第一章电磁场的媒质边界条件

电磁场边界条件的推导
电磁场边界条件的推导
1、电荷边界条件
电荷边界条件指的是在一个给定时刻，电场空间分布的边界处，电荷的分布应符合一定的规律，常表示为
E（r,t）=ρ（r,t）/ε
其中，E（r,t）为电场在位置r处和时刻t时的电场强度，ρ（r,t）为该位置处以及时刻t时的电荷密度，ε为真空介质的介电常数。

2、磁荷边界条件
磁荷边界条件指的是在一个给定时刻，磁场空间分布的边界处，磁荷的分布应符合一定的规律，常表示为
B（r,t）=μ㎡（r,t）
其中，B（r,t）为磁场在位置r处和时刻t时的磁场强度，μ㎡（r,t）为该位置处以及时刻t时的磁荷密度，μ为真空介质的磁导率。

3、电流边界条件
电流边界条件指的是在一个给定时刻，电流空间分布的边界处，电流密度的分布应符合一定的规律，常表示为
j（r,t）=σ（r,t）/ε
其中，j（r,t）为电流密度在位置r处和时刻t时的电流密度，σ（r,t）为该位置处以及时刻t时的电荷密度，ε为真空介质的介电常数。

4、磁流边界条件
磁流边界条件指的是在一个给定时刻，磁流空间分布的边界处，磁流密度的分布应符合一定的规律，常表示为
m（r,t）=μφ（r,t）
其中，m（r,t）为磁流密度在位置r处和时刻t时的磁流密度，φ（r,t）为该位置处以及时刻t时的磁荷密度，μ为真空介质的磁导率。

电磁场的边界条件姓名：学号：专业：班级：提交日期：桑薇薇0990*******通信工程电工 1401 2016.5.28成绩：电磁场的边界条件1.引言2.边界条件分类3.边界条件的作用4.结束语5.参考文献1. 引言在两种不同媒质的分界面上，场矢量E,D,B,H 各自满足的关系，称为电磁场的边界条件。

在实际的电磁场问题中， 总会遇到两种不同媒质的分界面 （例如： 空气与玻璃的分界面、导体与空气的分界面等） ，边界条件在处理电磁场问题中占据十分重要的地位。

2. 边界条件分类1、电场法向分量的边界条件如图 3.9 所示的两种媒质的分界面， 第一种媒质的介电常数、磁导率和电导率分别为1，1和1，第二种媒质的介电常数、磁导率和电导率分别为2，2和 2 。

在这两种媒质分界面上取一个小的柱形闭合面，图 3.9 电场法向分量的边界条件如图 3.9 所示，其高h 为无限小量，上下底面与分界面平行，并分别在分界面两侧， 且底面积 S 非常小，可以认为在 S 上的电位vv v移矢量 D和面电荷密度S是均匀的。

n 1 n 2分别为上下底面的外法线单位矢量， ， 在柱形闭合面上应用电场的高斯定律? v vv v S v vSSD gdS n 1 gD 1 n 2 gD 2 SS故v v v vn 1gD 1 n 2 gD 2S(3.48a)vv vvv若规定 n 为从媒质Ⅱ指向媒质Ⅰ为正方向，则 n 1 n ，n2n，式 (3.48a) 可写为v vvng(D 1D 2 )S(3.48b)或D1nD2nS(3.48c)式 (3.48 ) 称为电场法向分量的边界条件。

vvv 因为 DE ，所以式 (3.48) 可以用 E 的法向分量表示v v v v1n 1gE 12 n 2 gE 2S(3.49a)或1E 1n2 E 2nS(3.49b)若两种媒质均为理想介质时， 除非特意放置， 一般在分界面上不存在自由面电荷，即S，所以电场法向分量的边界条件变为D1nD2n(3.50a)或1E1n 2E2 n(3.50b)若媒质Ⅰ为理想介质，媒质Ⅱ为理想导体时， 导体内部电场为零，即E2，D2，在导体表面存在自由面电荷密度，则式(3.48) 变为v vn 1 gD 1 D 1nS(3.51a)或1E1ns(3.51b)2 、电场切向分量的边界条件在两种媒质分界面上取一小的矩形闭合回路 abcd ，如图 3.10 所示，该回路短边 h 为无限小量，其两个长边为l ，且平行于分界面，并分别在分界面两侧。

1)麦克斯韦方程组可以应用于任何连续的介质内部。

2)在两种介质界面上，介质性质有突变，电磁场也会突变。

3)分界面两边按照某种规律突变，称这种突变关系为电磁场的边值关系或边界条件。

4)推导边界条件的依据是麦克斯韦方程组的积分形式。

一、边界条件的一般形式 1、B 的边界条件:2、D 的边界条件结论：电位移矢量 在不同媒质分界面两侧的法向分量不连续，其差值等于分界面上自由电荷面密度。

3. H 的边界条件h∆→n-2B11220B dS B dS ⇒⋅+⋅=120B n B n ⇒⋅-⋅=210lim S h D H l H l J sl t→∂⇒⋅-⋅=⋅-⋅∂2t t SH H J⇒-=12()S n H H J⇒⨯-=21,S H l H l J s l n s⇒⋅-⋅=⋅=⨯()C sD H dl J dSt∂=+∂⎰⎰μ1μ2Hn1Hh →ls12()S n H H J⨯-=12()D D n σ-⋅=⇒2εε2D 1D n S∆n-n12n n D D σ⇔-=0S B dS ⋅=⎰12()0n B B ⋅-=21n nB B⇒=SD dS q =⋅⎰⇒⇒式中： S J 为介质分界面上的自由电流面密度。

结论：磁场强度 D 在不同媒质分界面两侧的切向分量不连续，其差值等于分界面上的电流面密度S J4.E 的边界条件结论：电场强度E 在不同每只分界面两侧的切向分量连续。

二、理想介质是指电导率为零的媒质，0=γ2)在理想介质内部和表面上，不存在自由电荷和自由电流。

结论：在理想介质分界面上，E 、H 矢量切向连续； 在理想介质分界面上，B 、D 矢量法向连续。

三、理想导体表面上的边界条件1)理想介质是指电导率为无穷大的导体，12t t E E⇒=12()0n E E ⇒⨯-= 2ε1ε2En1E2θl sl S BE dl d St∂⋅=-⋅∂⎰⎰12()0n E E ⨯-=⇒12t t EE=0s J =0ρ=12t t H H =⇒12n n D D=12()0n D D ⋅-=⇒12()0n B B ⋅-=12n n B B=⇒12()0n H H ⨯-=2)电场强度和磁感应强度均为零。

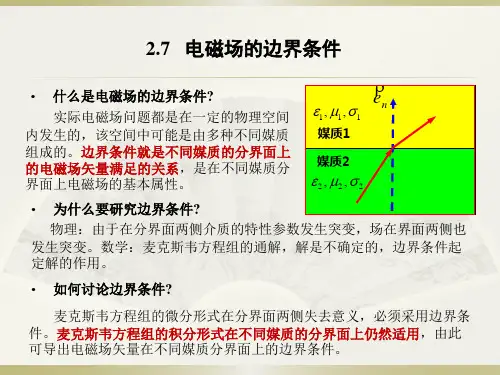
媒质分界面连接条件和媒质界限条件1.2.1 媒质分界面连接条件在求解电磁场问题时，在不一样媒质分界面上场的解答一定般配，已学过的有：电场：n E2E10n D2D1磁场：n H2H1J Sn B2B10电流场(恒定电场 )n E2E10n J2J10下边进一步剖析媒质分界面上场矢量发生突变的一般状况。

1．面散度场源可能惹起场磁量法向重量的突变：在电场中，散度场源D b( r ) 存在。

设电场中两种媒质之间存在一个过渡层，媒质性能参数由、、连续变化为、、1112 22 ，厚度h很小，取h 为一扁盒圆柱面的高，为过渡层内体自由电荷密度。

如下图，规定分界面上的正法向方向。

由高斯通量定理n 1D 2D ds D 2s 2 D 1s 1S2nD 2 D 1 sVD dVh s2、2、 2hn (D 2 D 1 )h1、 1、1s议论：D 11(1) 若为有限值，则当 h0，即n 2媒质参数发生跃变时，扁盒内的电荷量q = h 0n D 2 D 1 0D 2 n D 1 n 6(2) 若当 h 0 时， q 保持定值不变，即 h 0 ， 不停增大，使 h 保持定值，定义它为面自由电荷密度lim ( h)h 0上边的界限条件式变成：n ( D 2 D 1 ) lim ( h)lim ( hD )h 0hD 的法向重量突变，也可用标量电位表示为n2 2 1 1将以上结论引伸到一般矢量场 F 中，当 h 0 时成为一广泛性界限条件公式：n F 2 F 1lim (hb)lim ( hF )h 0h 0称上述极限突变值为 面散度源 ，可知“矢量场的面散度源可能惹起场的法向重量改变，无散场的法向重量必定连续 (假如没有偶极矩阵 )”。

2. 面旋度源可能惹起场矢量切向重量的突变由斯托克斯定理：F dlF dsc(r ) dsn lSS设磁场中两种媒质间存在一过H 2n渡层，其厚为 h 很小，如下图。

l n跨分界面作矩形闭合曲线 l ，其长、 22 Jt边为 l ，宽边为 h ，且 n 、 t和1、1hsn 呈右旋关系 tn n ，有lH 1H dlH 2 l 2 H 1 l 1lH 2 H 1 t l(H ) dsSc ( r ) dsc ( r ) n h lSt H 2H 1 n n H 2 H 1n nH 2 H 1 n c r hn [n ( H 2 H 1 ) c(r )h]因 l 回路设定的随意性，上式建立，在 h →0 时，必有：n ( H 2H 1 ) lim [ hc ( r )] lim [ h(H )]h 0h 0lim [ h( JD)]ht式中 D D 老是有限的， h0 ， h D0 。

电磁场三类边界条件介绍在电磁学中，边界条件是解决电磁场问题时的重要问题之一。

电磁场三类边界条件指的是麦克斯韦方程组在不同介质之间的边界上的满足条件。

这些条件在电磁场问题的求解中起到了关键的作用。

在本文中，我们将详细探讨电磁场三类边界条件的定义和应用。

一、第一类边界条件第一类边界条件也称为电磁场的法向边界条件。

其主要定义了电场和磁场在边界上的法向分量之间的关系。

具体表达如下：1.在介质边界上，电场的法向分量E n1和E n2满足：E n1=E n2；2.在介质边界上，磁场的法向分量H n1和H n2满足：H n1=H n2。

第一类边界条件体现了介质边界上的电场和磁场的连续性。

二、第二类边界条件第二类边界条件也称为电磁场的切向边界条件。

其主要定义了电场和磁场在边界上的切向分量之间的关系。

具体表达如下：1.在介质边界上，电场的切向分量E t1和E t2满足：E t1ϵ1=E t2ϵ2；2.在介质边界上，磁场的切向分量H t1和H t2满足：H t1μ1=H t2μ2。

其中，ϵ1和ϵ2分别为两个介质的介电常数，μ1和μ2分别为两个介质的磁导率。

第二类边界条件体现了介质边界上的电场和磁场的连续性和切向分量之间的比例关系。

三、第三类边界条件第三类边界条件也称为电磁场的混合边界条件。

其主要定义了电场和磁场在边界上的法向分量和切向分量之间的关系。

具体表达如下：1.在介质边界上，电场的法向分量E n1和E n2满足：E n1=E n2；2.在介质边界上，磁场的法向分量H n1和H n2满足：H n1=H n2；3.在介质边界上，电场的切向分量E t1和E t2满足：E t1ϵ1=E t2ϵ2；4.在介质边界上，磁场的切向分量H t1和H t2满足：H t1μ1=H t2μ2。

第三类边界条件综合了第一类和第二类边界条件，体现了介质边界上的电场和磁场的连续性以及法向分量和切向分量之间的比例关系。

四、应用举例电磁场三类边界条件在电磁学中的应用非常广泛，下面我们以几个实际问题为例，说明其应用方法：例一：平行板电容器考虑一对平行金属板构成的电容器，两板之间填充了介电常数为ϵ的均匀介质。