电磁场与电磁波第三章媒质的电磁性质和边界条件
- 格式:ppt
- 大小:1.41 MB
- 文档页数:41


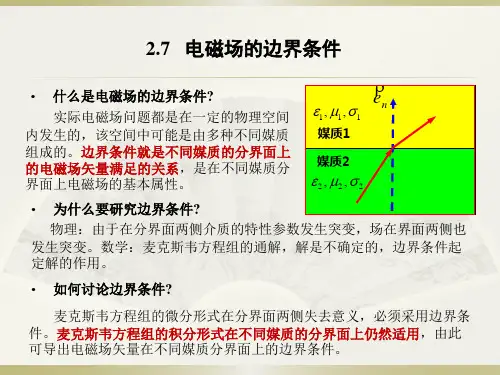


在两种媒质的边界上,电磁场所满足的边界条件一、定义电磁场,又称为电动场、磁和电场,是指一种可以在空气、介质或空间中产生或存在,以影响另一种物体表现或反应出来的能量场。
边界条件是指在一种媒质和另一种媒质之间的边界时,电磁场所满足的条件。
二、理论边界条件是建立在四种基本电动场和磁场的假设基础上的。
它的含义是,对于电动场的三个维度,即横向(Ex),纵向(Ey)和深向(Ez),在媒质的边界上,正好满足电动场的“接触分离”以及“跳变”原理;在边界上,磁力线的改变受到性质不同的两个媒质的影响,所以必须要满足磁力线不断、定向和磁场密度在方向上的改变,这三个对媒质之间的边界条件是不变的原则。
从另外一个角度来看,虽然单独的电动场和磁力线落实自身各自的电荷和磁矩,但是它们之间不可分割,相互影响,边界条件表明,电动场受到磁场的制约,具有界限概念,如果电动场沿某方向理想的存在,那么磁场也应遵守电动场,同样存在某种界限状态。
三、应用电磁场边界条件的应用非常广泛,它可以用来计算媒质区域内的电动场和磁场的交互作用,以及在电磁边界面上的电荷分布情况。
具体而言,电磁场边界条件被广泛应用于电子设备设计、高频通信与调制的研究、航天与卫星技术的发展、太阳能传感器的建立、声学行业中的声振调节、电动机驱动等方面。
电磁场边界条件所提供的数学知识为人类社会技术发展提供了最基础的理论和工具,广泛应用于这些方面有助于解决人类社会中技术上的挑战和问题。
四、总结由此可见,电磁场边界条件不仅具有实用性,而且非常有效。
它不仅可以帮助人们更好地理解及控制电磁场,而且可以用来设计更高效的系统并解决工程中的复杂问题,帮助技术的飞速发展。
历史证明,电磁场边界条件为人们在技术革新的道路上提供了巨大的支持和助力,取得了非常优秀的成果。



《电磁场与电磁波》名词解释不完全归纳(By Hypo )第一章 矢量分析1.场:场是遍及一个被界定的或无限扩展的空间内的,能够产生某种物理效应的特殊的物质,场是具有能量的。
2.标量:一个仅用大小就能够完整描述的物理量。
标量场:标量函数所定出的场就称为标量场。
(描述场的物理量是标量)3.矢量:不仅有大小,而且有方向的物理量。
矢量场:矢量场是由一个向量对应另一个向量的函数。
(描述场的物理量是矢量)4.矢线(场线):在矢量场中,若一条曲线上每一点的切线方向与场矢量在该点的方向重合,则该曲线称为矢线。
5.通量:如果在该矢量场中取一曲面S ,通过该曲面的矢线量称为通量。
6.拉梅系数:在正交曲线坐标系中,其坐标变量(u1 ,u2,u3)不一定都是长度, 可能是角度量,其矢量微分元,必然有一个修正系数,称为拉梅系数。
7.方向导数:函数在其特定方向上的变化率。
8.梯度:一个大小为标量场函数在某一点的方向导数的最大值,其方向为取得最大值方向导数的方向的矢量,称为场函数在该点的梯度,记作 9.散度:矢量场沿矢线方向上的导数(该点的通量密度称为该点的散度)10.高斯散度定理:某一矢量散度的体积分等于该矢量穿过该体积的封闭表面的总通量。
11.环量:在矢量场中,任意取一闭合曲线 ,将矢量沿该曲线积分称之为环量。
12.旋度: 一矢量其大小等于某点最大环量密度,方向为该环的一个法线方向,那么该矢量称为该点矢量场的旋度。
13.斯托克斯定理:一个矢量场的旋度在一开放曲面上的曲面积分等于该矢量沿此曲面边界的曲线积分。
14.拉普拉斯算子:在场论研究中,定义一个标量函数梯度的散度的二阶微分算子,称为拉普拉斯算子。
第二章 电磁学基本理论1.电场:存在于电荷周围,能对其他电荷产生作用力的特殊的物质称为电场。
2.电场强度:单位正试验电荷在电场中某点受到的作用力(电场力),称为该点的电场d grad d n a nφφ=强度。
3.电位差:单位正电荷由P 点移动到A 点,外力所做的功称为A 点和P 点之间的电位差。


第三章 媒质的电磁性质和边界条件众所周知,物质是由原子核和电子组成的,原子核带正电,电子带负电。
就是说任何物质材料,不论是气体、液体还是固体都含有带电粒子,这些带电粒子的周围一定存在着电场;同时电子一方面绕原子核运动,另一方面也作自旋运动,电荷的运动形成电流,这些电流周围存在磁场。
从微观上看,材料中这些带电粒子是存在电磁效应的,但从宏观上看,由于相邻原子产生的场相互抵消,及大量带电粒子热运动的平均结果,使自然状态下的物质仍呈现电中性。
倘若存在外加电磁场,则由于带电粒子和外加电磁场的相互作用,介质的分子电矩和磁矩将部分或全部取向一致,引起宏观电或磁效应,相当于在材料内部存在附加的场源,这样就需要对真空中的电磁学定律作进一步推广。
在第二章中,我们研究了在真空(或近似真空的空气)中电磁场各场量,如H B D E和,,所遵循的普遍规律,并得到一组麦克斯韦方程组。
麦克斯韦方程组的积分形式描述大尺度(如一个线段、曲面或体积)上的电磁特性,而微分形式描写空间任意一点的电磁场,但归根结底两者描述的仍然是宏观电磁现象。
这一章我们要研究物质的微观模型和性质,把麦克斯韦方程组推广到一般电磁材料中去.本章先研究由材料中带电粒子和电磁场的相互作用而产生的三个基本现象:传导、极化和磁化。
每一种物质在电磁场中均有传导、极化和磁化三种现象,根据某种主要的现象,可将材料分为导体、半导体、电介质和磁介质等。
讨论材料的电磁性质之后,我们可获得三个物态方程和一般媒质中的麦克斯韦方程组。
最后我们研究在不均匀媒质中电磁场所遵循的规律——边界条件。
§3.1 电场中的导体导体是一种含有大量可以自由移动的带电粒子的物质。
导体可分为两种——金属导体和电解质导体。
金属导体的导电靠的是自由电子,由于自由电子的质量比原子核的质量小得多,所以导电过程中没有明显的质量迁移,也不伴随任何化学变化。
而碱、酸、和盐溶液等电解液则属于第二种导体,其导电靠的是带电离子,导电过程中伴随有质量迁移,也要发生化学变化。