下载文档原格式
专用汽车设计常用计算公式汇集1.负载能力计算：
负载能力=轴重×轴数
2.强度计算：
强度=承载能力/安全系数
3.随载荷的车辆的弯曲刚度计算：
弯曲刚度=轮距×反曲率
4.弹性模量计算：
弹性模量=受力/受力产生的应变
5.轮胎筋度计算：
筋度=载荷/平均轮胎接地面积
6.轴间距计算：
轴间距=轴距/轴数
7.动力计算：
动力=扭矩×转速
8.燃油消耗计算：
燃油消耗=燃油消耗率×行驶距离
9.悬挂系统设计中的均布荷载计算：
均布荷载=最大悬挂荷载/悬挂系统自重
10.制动系统设计中的制动力计算：
制动力=负荷×制动系数
11.车辆加速度计算：
加速度=净推力/质量
12.转向半径计算：
转向半径=转向角度×轴距
13.刹车距离计算：
刹车距离=初速度²/(2×刹车力×摩擦系数)
14.路面阻力计算：
路面阻力=风阻+滚动阻力+坡道阻力+惯性阻力
15.加重系数计算：
加重系数=充油重量/空车重量
这些公式可以帮助设计师进行专用汽车的设计和计算，以确保其满足设计要求和安全标准。
然而，需要注意的是，实际应用中还需要考虑许多其他因素，如材料的强度特性、零部件的可行性、摩擦系数等，并且可能需要进行进一步的工程分析和测试。
因此，在设计专用汽车时，应综合考虑各种因素，以确保所设计的汽车能够满足用户需求和安全要求。
汽车传动轴临界转速的有限元法计算季 钢摘要 用有限元方法分析和计算汽车传动轴的临界转速,给出了相应的计算模型,并将计算的结果与实验结果相比较,为传动轴的设计与其临界转速的测定和计算提供了一种新的方法。
关键词:汽车传动轴 临界转速 有限元汽车传动轴的临界转速直接关系到汽车的高速性与平稳性。
传动轴系统在常用转速区出现共振,会使轴系和传动齿轮承受极大的交变冲击力,发生较强的机械振动与噪声,严重时还会导致断轴或断齿,造成事故。
目前国内较注重传动轴的动平衡,但对传动轴的共振频率的分布却研究甚少。
而事实上在大多数情况下,共振问题的产生往往是由于传动系统自振频率布置不当造成的,为了避免发生共振,通常可以修正系统的动力学参数(例如转动惯量和轴段与部件的刚度等),调整自振频率。
这些工作若能在汽车动力传动轴系的设计阶段加以解决,则最为经济和方便。
计算传动轴的临界转速相当于计算它的固有频率,计算轴系的固有频率有很多方法,本文介绍有限元方法进行分析和计算。
一、有限元法动力分析有限元法是最近三四十年发展起来的一门数值分析技术,是借助高速电子计算机解场问题的近似计算方法。
它运用离散的概念,使整个问题由整体连续到分段连续,由整体解析转化为分段解析,从而使数值法与解析法互相结合,互相渗透,形成一种新的数值计算方法。
首先把连续体离散化,把连续体假想分割成数目有限的小块单元,而单元之间只在数目有限的指定点处相互连结。
其次,选择一个较简单的函数来近似地表示其位移的分布规律,并用物理学中的基本方程建立起单元上节点力与位移的关系。
最后,借助于矩阵方法集合起来,利用各种方法求解方程组,得到所要求的结果。
动力学分析是有限元法的一个重要应用范围,结构的动力方程可由节点平衡条件来导出。
节点上的作用力可分为两类,作用于节点上的外载荷与相关单元对该节点的作用力。
汇集所有的节点方程,便得到结构的动力平衡方程,用矩阵符号可表示为: [M][ ]+[C][ ]+[K][ ]=[R](1)!!!其中[ ],[],[ ]分别是结构的节点位移、节点速度、节点加速度向量;[R]是结构的整体载荷向量,是t的函数;[K]是结构的整体刚度矩阵,由各个单元刚度矩阵集合而成;[C]是结构的整体阻尼矩阵,由各个单元阻尼矩阵集合而成;[M]是结构的整体质量矩阵,由各个单元质量矩阵集合而成;式(1)是用有限元法求解结构动力问题的基本方程,它是一个大型的二阶常微分方程组,简称为动力方程。
——动力学应用专题基本内容1、单自由度系统的自由振动2、固有频率的计算3、单自由度系统有阻尼的自由振动4、单自由度系统的受迫振动5、隔振与减振基本要求1、会应用动力学基本理论建立单自由度系统的振动微分方程2、掌握自由振动、受迫振动的特征3、会计算振动周期、固有频率和振幅4、掌握共振和临界转速的概念5、了解隔振的概念引言一、振动的现象与定义1、振动：物体（或系统）在其平衡位置附近周期性的往复运动。
振动是日常生活和工程实际中常见的物理现象。
例如：钟表的摆动；汽车行驶时车厢的上、下颠簸，左、右晃动；电机、机床等工作时的振动，狂风吹得旗帜哗哗作响、对瓶口吹气引起发声；以及地震时引起的建筑物的振动等。
利：振动给料机弊：磨损，减少寿命，影响强度振动筛引起噪声，影响劳动条件振动打桩机等消耗能量，降低精度等。
3. 研究振动的目的：研究并掌握振动规律，消除或减小有害的振动，充分利用振动为人类服务。
2、振动的利弊：引言一、振动的定义与现象引言二、振动的模型与分析方法xmgstlmgm k单自由度质量弹簧系统km三、振动的分类：按振动产生的原因分类：自由振动：无阻尼的自由振动，有阻尼的自由振动（衰减振动）强迫振动：无阻尼的强迫振动有阻尼的强迫振动按振动方程：可分为线性振动和非线性振动。
单自由度系统的振动多自由度系统的振动弹性体的振动按振动系统的自由度分类引言§17-1 单自由度系统的自由振动一、自由振动的概念：质量—弹簧系统一、自由振动的概念：弹簧－质量系统，物块的质量为m ,弹簧的刚度系数为k ,物块自平衡位置的初始速度为v0。
运动过程中，其方向恒指向物体平衡位置的力称为恢复力。
物体受到初干扰后，仅在恢复力作用下于其平衡位置附近的往复运动称为无阻尼自由振动。
二、自由振动微分方程及其解l0mk v0一、自由振动的概念：∑=iix F xm 0=kx xm ＋ 以弹簧未变形时的平衡位置为原点建立Ox 坐标系，将物块置于任意位置x > 0 处。
机械零件的工作能力和计算准则引言机械零件是现代机械工程中不可或缺的组成部分，它们承担着各种功能和载荷。
了解机械零件的工作能力和计算准则对于设计和制造高效可靠的机械系统至关重要。
本文将介绍机械零件的工作能力和计算准则，以帮助读者理解和应用。
工作能力机械零件的工作能力指的是其在各种工作条件下所能承受的外力和载荷。
了解机械零件的工作能力对于避免失效和保证机械系统的安全运行至关重要。
以下是一些常见的机械零件的工作能力：1. 钢材的抗拉强度钢材的抗拉强度是指其在拉伸过程中所能承受的最大外力。
在设计机械零件时，需要确保所选用的钢材的抗拉强度能够满足实际工作条件下的外力要求。
2. 轴承的承载能力轴承是机械系统中常见的零件，它们承担着支撑和传递载荷的任务。
轴承的承载能力是指其在工作过程中能够承受的最大载荷。
在选择和设计轴承时，需要考虑所需承载能力以及预计的工作条件。
3. 齿轮的承载能力齿轮是传动系统中重要的元件，它们负责传递动力和承受转矩。
齿轮的承载能力是指其在工作过程中能够承受的最大转矩。
在设计齿轮时，需要确保其承载能力能够满足实际工作条件下的转矩要求。
为了保证机械零件的工作能力，我们可以使用一些计算准则来评估其在各种工作条件下的性能。
以下是常见的机械零件计算准则：1. 安全系数安全系数是指机械零件的实际工作能力与设计要求之间的比值。
通常，我们会给机械零件设置一个合适的安全系数，以确保其在工作过程中有足够的余量。
安全系数的选取应考虑到工作条件和材料性能等因素。
2. 疲劳寿命疲劳寿命是指机械零件在连续循环加载下能够承受的次数。
疲劳寿命与工作负载、材料强度和设计几何形状等因素有关。
通过计算疲劳寿命，可以评估机械零件在实际工作条件下的寿命。
应力分析是用于评估机械零件受力情况的一种方法。
通过应力分析，可以计算出机械零件在工作过程中所受到的应力，进而评估其工作能力。
常见的应力分析方法包括有限元分析和解析计算等。
结论机械零件的工作能力和计算准则对于设计和制造可靠的机械系统至关重要。
机械零件的承载能力计算一、零件的强度和刚度条件（一）拉（压）杆的强度计算在进行强度计算中，为确保轴向拉伸（压缩）杆件有足够的强度，把许用应力作为杆件实际工作应力的最高限度，即要求工作应力不超过材料的许用应力。
于是，强度条件为：≤（3-19）应用强度条件进行强度计算时会遇到以下三类问题。
一是校核强度。
已知构件横截面面积，材料的许用应力以及所受载荷，校核（3-31）式是否满足，从而检验构件是否安全。
二是设计截面。
已知载荷及许用应力?，根据强度条件设计截面尺寸。
三是确定许可载荷。
已知截面面积和许用应力，根据强度条件确定许可载荷。
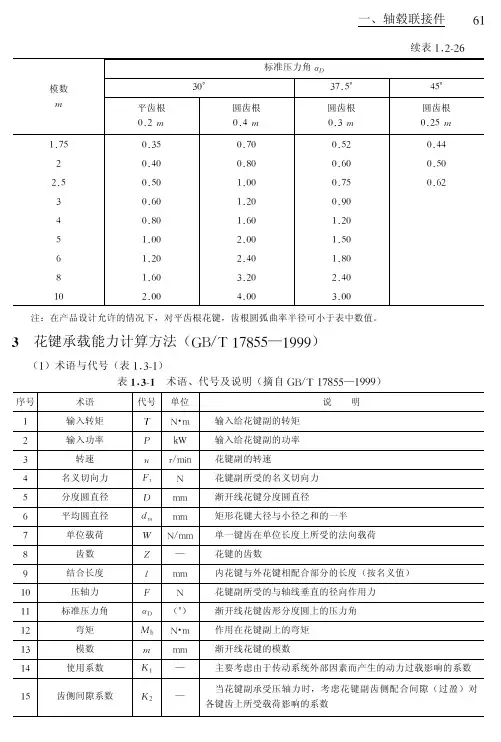
例3-6? 某冷镦机的曲柄滑块机构如图3-49（a）所示。
连杆接近水平位置时，镦压力=3.78MN( l MN=106N)。
连杆横截面为矩形，高与宽之比（图3-49（b）所示），材料为45号钢，许用应力=90MPa，试设计截面尺寸和。
解? 由于镦压时连杆AB近于水平，连杆所受压力近似等于镦压力，轴力=3.78MN。
根据强度条件可得：A≥(mm2)以上运算中将力的单位换算为，应力的单位为MPa或N/mm2，故得到的面积单位就是（mm2）注意到连杆截面为矩形，且，故(mm2)=173.2(mm)，=1.4=242(mm)所求得的尺寸应圆整为整数，取=175mm，h=245mm。
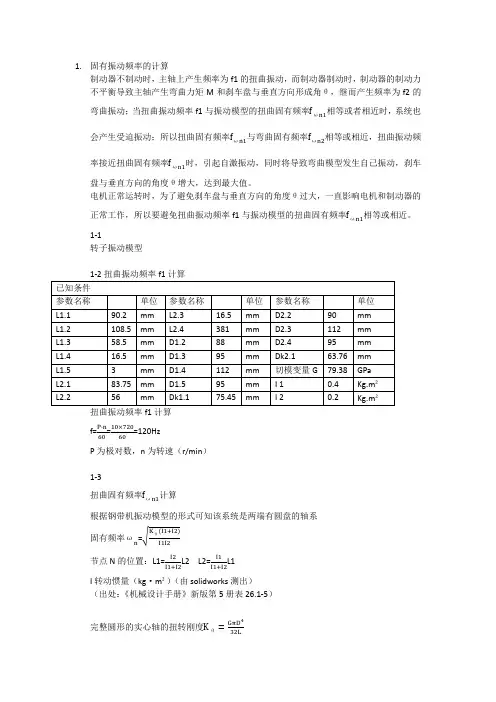
1.某张紧器（图3-50）工作时可能出现的最大张力=30kN ( lkN=103N)，套筒和拉杆的材料均为钢，=160MPa，试校核其强度。
解? 此张紧器的套筒与拉杆均受拉伸，轴力=30kN。
由于截面面积有变化。
必须找出最小截面。
对拉杆，20螺纹内径=19.29mm，=292mm2，对套筒，内径=30mm，外径=40mm，故=550mm2 。
最大拉应力为：故强度足够。
例3-7? 某悬臂起重机如图3-51（a）所示。
撑杆为空心钢管，外径105mm，内径95mm。
钢索1和2互相平行，且钢索1可作为相当于直径=25mm的圆杆计算。
