泊松分布的概念及表和查表方法

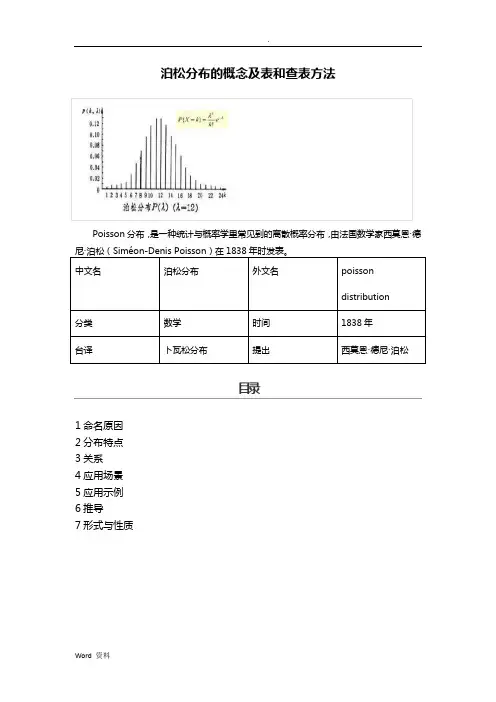
泊松分布的概念及表和查表方法目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布（Poisson distribution），台译卜瓦松分布（法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等），是一种统计与概率学里常见到的离散机率分布（discrete probability distribution）。

泊松分布是以18～19 世纪的法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）命名的，他在1838年时发表。

这个分布在更早些时候由贝努里家族的一个人描述过。

分布特点泊松分布的概率函数为：泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。

泊松分布适合于描述单位时间内随机事件发生的次数。

泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。

通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。

事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。

应用场景在实际事例中，当一个随机事件，例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。

因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位（在早期学界认为人类行为是服从泊松分布，2005年在nature上发表的文章揭示了人类行为具有高度非均匀性）。

应用示例泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。

泊松分布的概念及表和查表方法目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布（Poisson distribution），台译卜瓦松分布（法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等），是一种统计与概率学里常见到的离散机率分布（discrete probability distribution）。

泊松分布是以18～19 世纪的法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）命名的，他在1838年时发表。

这个分布在更早些时候由贝努里家族的一个人描述过。

分布特点泊松分布的概率函数为：泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。

泊松分布适合于描述单位时间内随机事件发生的次数。

泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。

通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。

事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。

应用场景在实际事例中，当一个随机事件，例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。

因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位（在早期学界认为人类行为是服从泊松分布，2005年在nature上发表的文章揭示了人类行为具有高度非均匀性）。

应用示例泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。

每天一点统计学——泊松分布公式在生活中的应用泊松分布的定义泊松概率分布是考虑在连续时间和空间单位上发生的随机事件的概率。

通俗解释：基于过去的经验，预测该随机事件在新的同样长的时间或同样大的空间中发生N次的概率。

泊松分布包括以下条件：1.单独事件在给定区间内随机、独立地发生，给定区间可以是时间或空间，例如可以是一个星期，也可以是一公里；2.已知该区间的事件平均发生次数，且为有限数值，该事件平均发生次数通常用希腊字母λ（lambda）表示。

泊松分布公式某事件在给定区间内平均发生λ次，在求给定区间内发生r次事件的概率时，使用以下公式：泊松分布公式泊松分布公式用到了指数函数ex，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828。

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。

如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数等等。

泊松分布公式的应用已知某家小杂货店，平均每周售出2个水果罐头。

请问该店水果罐头的最佳库存量是多少？解：假定不存在季节因素，可以近似认为，这个问题满足以下三个条件：（1）顾客购买水果罐头是小概率事件。

（2）购买水果罐头的顾客是独立的，不会互相影响。

（3）顾客购买水果罐头的概率是稳定的。

各个参数的含义：•P：每周销售r个罐头的概率；•X：水果罐头的销售变量；•r：每周销售罐头数的取值（0，1，2，3…）；•λ：每周水果罐头的平均销售量（数学期望），是一个常数，本题为2；根据公式，计算得到每周销售不同数量罐头数的概率及累计概率：从上表可见，如果存货4个罐头，95%的概率不会缺货（5%＝1/20，即平均19周发生一次）；如果存货5个罐头98%的概率不会缺货（2%＝1/50，即平均49周发生一次）。

泊松分布1. 引言泊松分布是概率论和统计学中一种常见的离散概率分布，由法国数学家西蒙·泊松于1838年首次提出。

泊松分布适用于描述特定时间段内某个事件发生的次数，例如一段时间内客户到达的数量、电话呼叫的次数或人员受伤的次数等。

本文将详细介绍泊松分布的定义、性质、用途和计算方法。

2. 定义泊松分布是指在一定时间段或空间区域内，事件发生的次数服从离散分布的概率模型。

它具有以下特点：- 定义域为非负整数集合。

- 事件在任意时间段内相互独立。

- 事件在不同时间段内的发生概率相等。

- 事件的平均发生率是已知的。

3. 概率质量函数泊松分布的概率质量函数表示某个事件发生k次的概率。

设λ为单位时间内该事件的平均发生率，则泊松分布的概率质量函数可表示为：P(k;λ) = (λ^k * e^(-λ)) / k!其中，k表示事件发生的次数，e是自然对数的底数约等于2.71828，!表示阶乘运算。

4. 期望值和方差泊松分布的期望值和方差可以通过发生率λ来计算。

期望值E(X)等于λ，方差Var(X)也等于λ。

这意味着，在一个给定的时间段内，事件的平均发生次数和方差相等。

5. 用途泊松分布在实际中有广泛的应用，例如：- 模拟客流量：在公共交通系统中，可以使用泊松分布来模拟乘客到达的数量，从而评估和优化运输系统。

- 预测事故发生率：在保险业中，可以使用泊松分布来预测车祸的发生率，从而进行合理的保险费用评估。

- 网络流量建模：在计算机网络领域，可以使用泊松分布来建模和分析网络流量，以便更好地管理和优化网络资源。

- 生物学分析：在生物学研究中，可以使用泊松分布来描述细胞分裂或突变事件的发生。

6. 计算方法泊松分布的计算方法主要有两种：- 使用概率质量函数：根据泊松分布的概率质量函数，可以直接计算某个事件发生k次的概率。

通过遍历所有可能的k值，可以得到泊松分布的概率分布情况。

- 使用近似方法：在一些情况下，计算泊松分布的概率质量函数可能较为繁琐。

标准泊松分布表
介绍
标准泊松分布是概率论和统计学中常用的一种离散性概率分布。

它描述了在一定时间内一个事件发生的次数的概率分布情况，适用
于一些与时间相关的事件，如电话的呼叫次数、邮件的收件次数等。

计算方法
计算标准泊松分布的概率可以借助泊松分布表来进行。

泊松分
布表是一个包含了不同事件发生次数的概率值的表格，可以用于计
算特定事件发生次数的概率。

标准泊松分布表一般以参数λ表示，其中λ为单位时间内该事
件平均发生的次数。

通过查表，可以找到给定λ值和特定事件发生
次数的概率。

使用示例
假设某项事件在一分钟内平均发生5次，我们想要知道在该分
钟内发生0次、1次、2次等事件的概率。

我们可以通过标准泊松
分布表来找到相应的概率。

使用该表格，我们可以快速找到特定事件发生次数的概率，从而对事件发生的概率进行分析和预测。

注意事项
在使用标准泊松分布表时，需要确保所使用的λ值符合标准泊松分布的要求。

此外，使用该表格进行计算时，需要注意查找正确的事件发生次数和相应的概率值。

总结
标准泊松分布表是一种用于计算标准泊松分布概率的工具。

通过查表，可以快速找到特定事件发生次数的概率，从而进行概率分析和预测。

在使用该表格时，需要注意参数λ的正确性和查找准确的概率值。

泊松分布是一种离散概率分布，常用于描述在给定时间间隔或空间内发生的事件的数量。

以下是泊松分布表格，其中λ表示事件发生的平均发生率，表格中的数字表示在给定λ值下，不同k值（事件发生的次数）的概率。

k λ=1 λ=2 λ=3 λ=4 λ=5
0 0.3679 0.2706 0.1821 0.1253 0.0864
1 0.2419 0.3477 0.2704 0.1888 0.1309
2 0.135
3 0.2453 0.2987 0.2446 0.1868
3 0.0732 0.1599 0.2362 0.2675 0.2353
4 0.041
5 0.1118 0.1849 0.2562 0.2684
... ... ... ... ... ...
以上表格中的数字是泊松分布的概率值，这些数字可以用来说明在给定λ值下，不同k值所对应的概率。

例如，当λ=2时，k=1时的概率为0.3477。

需要注意的是，泊松分布在一些情况下可能不适用。

例如，当事件的发生不是相互独立时，或者当事件发生的概率随时间变化时，泊松分布可能不准确。

在这种情况下，可能需要使用其他概率模型来描述事件的发生。

泊松分布与指数分布的计算方法概论当我们需要分析一些随机出现的事件时，常常需要用到随机变量的概念。

常见的随机变量包括离散型随机变量和连续型随机变量。

在离散型随机变量中，泊松分布是一种经典的模型，在连续型随机变量中，指数分布同样具有重要的意义。

在本文中，我们将讨论如何计算泊松分布和指数分布相关的问题。

泊松分布定义：泊松分布是一种离散型概率分布，描述了在一段固定时间内，某件事情发生的次数，比如，在一段时间内，某个路口的车辆通过次数、某个网站的点击次数等。

公式表达：$$P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}$$其中，$\lambda$ 表示单位时间内某事件发生的平均次数，$k$ 表示该事件发生了 $k$ 次的概率。

该公式称为泊松分布的概率质量函数（Probability Mass Function，PMF）。

计算方法：当我们需要计算泊松分布的概率时，有两种方法：查表法和计算法。

查表法是相对简单的方法，但只适用于已经有预制表格的情况。

计算法则需要先确定 $\lambda$ 值，然后按照公式计算。

查表法：我们以 $\lambda=3$，$k=4$ 为例，查表法的计算过程如下：在预制的泊松分布表格（$\lambda=3$）中找到 $k=4$ 上方的值，为 0.1680。

于是我们得到了 $P(X=4)=0.1680$。

表格如下所示：$k$|0|1|2|3|4|5|$\cdots$--|--|--|--|--|--|--|--$P(X=k)$|0.0498|0.1494|0.2241|0.2241|0.1680|0.1008|$\cdots$计算法：我们以 $\lambda=3$，$k=4$ 为例，计算法的计算过程如下：$$P(X=4)=\frac{3^4}{4!}e^{-3}=0.1680$$其中，$e$ 是欧拉数，约等于 $2.71828$。

指数分布定义：指数分布是一种连续型概率分布，广泛应用于描述独立随机事件之间时间间隔的概率分布，比如上一次农产品售出时间和下一次时间之间的间隔，网络请求的响应时间等。

泊松分布公式掌握泊松分布的关键公式泊松分布是概率论中的一种离散概率分布，用于描述在一个固定间隔内，事件在单位时间内发生的次数的概率分布情况。

泊松分布公式是求解泊松分布概率的关键公式。

本文将详细介绍泊松分布公式及其应用。

一、泊松分布的基本概念在介绍泊松分布公式之前，我们先来了解一下泊松分布的基本概念。

泊松分布是一种离散型概率分布，它描述了在一个固定时间或空间间隔内，事件发生的次数的概率分布情况。

泊松分布适用于以下条件：1. 事件在不同时间或空间间隔内独立发生；2. 在每个小的时间或空间间隔内，事件发生的概率非常小；3. 在整个时间或空间区间内，事件发生的次数不受前一次事件发生与否的影响。

泊松分布的概率质量函数可以用以下公式表示：P(X=k) = (e^(-λ) * λ^k) / k!其中，P(X=k)表示事件发生k次的概率，λ为单位时间或单位空间间隔内事件的平均发生次数。

二、泊松分布公式的推导泊松分布公式的推导过程比较复杂，这里我们只给出最终的公式结果。

通过对泊松分布的概率质量函数进行数学推导，可以得到以下泊松分布公式：P(X=k) = (e^(-λ) * λ^k) / k!其中，P(X=k)表示事件发生k次的概率，λ为单位时间或单位空间间隔内事件的平均发生次数。

三、泊松分布公式的应用泊松分布公式在实际问题中有着广泛的应用。

以下是一些应用场景的例子：1. 网络流量管理在网络流量管理中，泊松分布可用于描述网络中数据包到达的概率分布情况。

通过泊松分布公式，可以计算出单位时间内到达指定网口的数据包数目的概率。

2. 声音信号处理在声音信号处理领域，泊松分布可用于描述声音信号中事件（例如声音片段、语音信号等）的出现频率。

通过泊松分布公式，可以计算出在给定时间段内出现特定声音片段的概率。

3. 电话呼叫量预测在电话通信领域，泊松分布可用于预测特定时间段内的总呼叫量或某个时间间隔内的呼叫数量。

通过泊松分布公式，可以计算出在给定时间段内呼叫特定数量的概率。

泊松分布表泊松分布表是用于计算泊松分布概率函数的一种工具。

泊松分布是概率论中非常重要的一种分布，它可以描述独立随机事件发生的次数。

泊松分布表是一张包含各种泊松分布概率函数值的表格，可供科学家、工程师等专业人士进行数学计算和研究。

下面介绍泊松分布表的构造和使用方法。

首先我们来了解一下泊松分布概率函数。

泊松分布的概率函数为：P(x;λ) = (λ^x * e^(−λ))/x!其中，x表示随机事件发生的次数，λ表示该事件在一定时间内平均发生的次数，e为自然常数，x!表示x的阶乘。

泊松分布表根据不同的λ值和x值，列出了对应的概率函数值。

例如，当λ=2时，x=0时概率为P(0;2) = 0.135，x=1时概率为P(1;2) = 0.271，x=2时概率为P(2;2) = 0.270，以此类推。

泊松分布表的构造方法是通过计算泊松分布概率函数进行填表。

一般来说，泊松分布表的列数为不同的x值，行数为不同的λ值。

通常情况下，λ值的范围为0到10，x值的范围为0到20。

泊松分布表的构建需要使用统计软件或者手动计算，具体方法可以参考概率论教材或在线教程。

使用泊松分布表的方法是以λ值和x值为输入，查找对应的概率函数值。

例如，当λ=3，x=2时，从泊松分布表中可以找到对应的概率函数值为P(2;3) = 0.224，即随机事件发生2次的概率为0.224。

泊松分布表在很多领域都有广泛的应用。

例如，在计算机网络领域，泊松分布可用于描述消息到达某一节点的随机性。

在物理学和化学领域，泊松分布可用于描述放射性衰变和化学反应发生的随机性。

在经济学领域，泊松分布可用于描述突发事件的发生概率等。

总之，泊松分布表是一个极为实用的数学工具，在科学研究、工程设计等领域都有重要的应用价值。

泊松分布知识点总结1. 泊松分布的基本概念泊松分布是指在一个单位时间或单位空间内，某种随机事件发生的次数的概率分布规律。

具体来说，设随机变量X表示在单位时间内或单位空间内发生某种事件的次数，则X服从泊松分布的概率质量函数为：P(X=k) = (λ^k * e^(-λ)) / k!其中，λ是单位时间或单位空间内平均发生的事件次数，k=0,1,2,...是事件发生的次数。

泊松分布具有以下几个特点：（1）事件是离散的，即事件发生的次数只能是0,1,2,...无穷个；（2）事件是相互独立的，即事件在单位时间或空间内发生的次数与其他时间段无关；（3）事件是稀有的，即在很短的时间或空间内，事件发生的概率较小；（4）λ是事件发生的强度参数，表示在单位时间或空间内事件发生的平均次数。

2. 泊松分布的性质（1）数学期望：泊松分布的随机变量X的数学期望为E(X) = λ；（2）方差：泊松分布的随机变量X的方差为Var(X) = λ；（3）与二项分布的关系：当二项分布的n很大，p很小时，二项分布近似于泊松分布，当n趋向无穷大，p趋向0，np=λ时，二项分布B(n,p)可近似表示泊松分布P(λ)。

3. 泊松分布的应用泊松分布在实际应用中有着广泛的用途，主要包括以下几个方面：（1）电话交换机呼叫数目：当电话交换机平均每小时接到λ个呼叫时，每小时接到k个呼叫的概率可以用泊松分布来描述；（2）交通事故发生数目：假设某地区平均每天发生λ起交通事故，每天发生k起事故的概率可以用泊松分布来描述；（3）放射性原子核衰变数目：放射性核物质的衰变数目服从泊松分布；（4）网络数据包到达数目：网络数据包到达的数目服从泊松分布，可以用来描述网络通信中的数据包到达模式。

4. 泊松分布的推导与证明泊松分布的推导通常涉及到概率论和数理统计领域的知识，接下来我们对泊松分布的推导过程进行简要介绍。

设事件在一个很小的时间段Δt内发生的概率为λΔt (λ为单位时间内事件发生的平均次数)，设事件在不重叠的时间段内发生的次数是相互独立的随机变量，那么在nΔt时间段内，事件发生k次的概率可以表示为：P(X=k) = C(n, k) * (λΔt)^k * (1-λΔt)^(n-k)其中C(n, k)为组合数。

泊松分布的概念及表和查表方法Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩•德尼•泊松(Sim 的n-Denis Poisson) 在1838 年时发表。

中文名泊松分布外文名poisson distribution 分类数学时间1838 年台译卜瓦松分布提出西莫恩•德尼•泊松目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布(Poisson distribution ),台译卜瓦松分布(法语：loi de Poisson,英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等)，是一种统计与概率学里常见到的离散机率分布( discrete probability distribution )。

泊松分布是以18〜19世纪的法国数学家西莫恩•德尼•泊松( Sim 6on-Denis Poisson)命名的，他在1838年时发表。

这个分布在更早些时候由贝努里家族的一个人描述过。

分布特点泊松分布的概率函数为：卩(X = k)二巨旷一斤二0丄…I泊松分布的参数入是单位时间 (或单位面积)随机事件的平均发生次数。

泊松分布适合于描述单位时间随机事件发生的次数。

泊松分布的期望和方差均为丸特征函数为呦仃二gp*占一1}}「关系泊松分布泊松分布与二项分布当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中入为np。

通常当n± 20,pW 0.05时，就可以用泊松公式近似得计算。

事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。

应用场景在实际事例中，当一个随机事件，例如某交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率入（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）出现的次数或个数就近似地服从泊松分布P（入）。

* *泊松分布的概念及表和查表方法Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Sim éon-Denis Poisson）在 1838年时发表。

中文名泊松分布外文名poissondistribution分类数学时间1838 年台译卜瓦松分布提出西莫恩·德尼·泊松目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质* *命名原因泊松分布实例泊松分布（Poisson distribution），台译卜瓦松分布（法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等），是一种统计与概率学里常见到的离散机率分布（ discrete probability distribution）。

泊松分布是以18 ～19世纪的法国数学家西莫恩·德尼·泊松（Sim éon-Denis Poisson）命名的，他在1838年时发表。

这个分布在更早些时候由贝努里家族的一个人描述过。

分布特点泊松分布的概率函数为：泊松分布的参数λ是单位时间 (或单位面积 )内随机事件的平均发生次数。

泊松分布适合于描述单位时间内随机事件发生的次数。

泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n 很大而 p 很小时，泊松分布可作为二项分布的近似，其中λ为np 。

通常当 n ≧20,p ≦0.05 时，就可以用泊松公式近似得计算。

事上，泊松分布正是由二分布推而来的，具体推程参本条相关部分。

应用场景在事例中，当一个随机事件，例如某交台收到的呼叫、来到某公共汽站的乘客、某放射性物射出的粒子、微下某区域中的白血球等等，以固定的平均瞬速率λ（或称密度）随机且独立地出，那么个事件在位（面或体）内出的次数或个数就近似地服从泊松分布P(λ)。

泊松分布定义
泊松分布是一种离散型概率分布，它描述了在一段时间内或者某个区域内某一事件发生的次数。

泊松分布的定义如下：
设随机变量X表示在一个固定时间或者区域内某一事件发生的次数，如果满足以下条件：
1. 事件在任意时间或者区域内独立发生；
2. 事件在任意时间或者区域内的发生概率相等；
3. 事件在任意时间或者区域内的发生次数不受之前事件的影响。

那么X就服从泊松分布。

泊松分布的概率质量函数为：
P(X=k)=e^(-λ) * λ^k / k!
其中，λ表示单位时间或者单位区域内事件的平均发生次数，k表示事件发生的次数。

泊松分布的期望和方差都等于λ，即E(X)=λ，Var(X)=λ。

这意味着，泊松分布的分布形状和参数λ有关，当λ越大时，分布的峰值越靠近λ，分布的形状越陡峭。

泊松分布在实际应用中有着广泛的应用，例如：
1. 电话交换机中电话的到达次数；
2. 一段时间内道路上发生的交通事故次数；
3. 一段时间内某个网站的访问次数；
4. 一段时间内某个区域内的犯罪次数等。

在实际应用中，我们可以通过观察历史数据来估计λ的值，然后利用泊松分布来预测未来事件的发生次数。

例如，我们可以利用泊松分布来预测下一个小时内某个网站的访问次数，或者下一个月某个区域内的犯罪次数。

总之，泊松分布是一种非常重要的概率分布，它在实际应用中有着广泛的应用。

通过了解泊松分布的定义和性质，我们可以更好地理解和应用这一概率分布。