泊松分布表
- 格式：doc
- 大小：176.50 KB
- 文档页数：2
下载文档原格式
合集下载
泊松分布表
计算概率
根据查找到的概率值计算所需事件的概率。例如，如果需要计算平均值为λ的标准正态分布下，距离平均值2个标准差范围内的概率，可以通过查找λ值对应的概率，然后将其与标准正态分布曲线下的面积相乘得到概率值。
确定参数
首先需要确定所需的置信水平和所需的样本数量n。置信水平通常选择95%或99%，样本数量n则根据实际情况而定。
对于具有依赖性和集群性的事件，可以考虑使用更复杂的模型，如负二项式分布、帕累托分布等，以更好地描述事件的发生。
使用更复杂的模型
为了处理事件发生的时空变化，可以考虑引入时变参数，根据时间、地点等因素的变化来调整参数值。
引入时变参数
可以结合其他理论或方法，如聚类分析、关联规则等，以更全面地考虑事件发生的影响因述了服务台前顾客到达的次数。
排队论
保险精算
自然灾害
在保险精算中，泊松分布被用来计算在一定时间段内发生特定事件（如死亡、理赔等）的概率。
在预测自然灾害（如地震、洪水等）的频率时，泊松分布也具有应用价值。
03
02
01
$f(k) = \frac{{e^{- \lambda}\lambda^{k}}}{k!}$
累积分布函数
泊松分布的累积分布函数表现为一条从0开始缓慢上升的曲线，随着λ的增加，曲线逐渐变得陡峭。这条曲线与横轴之间的面积表示事件发生的概率。
泊松分布的数学推导
03
VS
f(k) = λ^k * e^(-λ) / k!
泊松分布的概率质量函数
p(k) = λ^k * e^(-λ) / k!
泊松分布的概率密度函数
常见用途
泊松分布在自然和社会科学中都有广泛的应用，如人口统计学、生物统计学、经济学等。通过使用泊松分布表，可以方便地查询和计算在给定参数下的概率分布。
泊松分布表计算
泊松分布表计算
泊松分布是一种描述随机事件发生次数的概率分布，通常用于描述事件的稀有性，如单位时间内发生的交通事故数、电话呼叫数等。
泊松分布的概率密度函数为：
P(X=k)= e^(-λ) * λ^k / k!
其中，X为事件发生的次数，λ为单位时间内该事件的平均发生次数，k为发生次数。
为了方便计算，可以使用泊松分布表，该表列出了不同λ和k值下的概率值。
使用泊松分布表进行计算时，只需查找对应的λ和k值，即可得到相应的概率值。
例如，当λ=2，k=3时，从泊松分布表中查找，可得概率值为
0.180.
需要注意的是，泊松分布适用于事件发生次数很少的情况，当λ较大时，正态分布更为适用。
在实际应用中，泊松分布可用于预测和控制随机事件的发生次数，如交通事故发生率、银行柜员的服务时间等。
- 1 -。
泊松分布的概念及表和查表方法
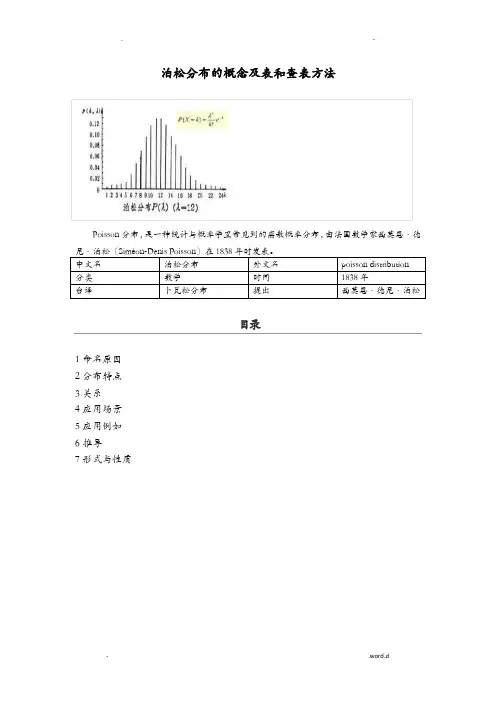
泊松分布的概念及表和查表方法Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松〔Siméon-Denis Poisson〕在1838年时发表。
中文名泊松分布外文名poisson distribution 分类数学时间1838年台译卜瓦松分布提出西莫恩·德尼·泊松目录1命名原因2分布特点3关系4应用场景5应用例如6推导7形式与性质命名原因泊松分布实例泊松分布〔Poisson distribution〕，台译卜瓦松分布〔法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等〕，是一种统计与概率学里常见到的离散机率分布〔discrete probability distribution〕。
泊松分布是以18～19 世纪的法国数学家西莫恩·德尼·泊松〔Siméon-Denis Poisson〕命名的，他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为：泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。
通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。
事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关局部。
应用场景在实际事例中，当一个随机事件，例如某交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ〔或称密度〕随机且独立地出现时，那么这个事件在单位时间〔面积或体积〕内出现的次数或个数就近似地服从泊松分布P(λ)。
泊松分布的概念及表和查表方法
泊松分布的概念及表和查表方法Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩•德目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布(Poisson distribution)，台译卜瓦松分布(法语： loi de Poisson ，英语:Poisson distributio n，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等)，是一种统计与概率学里常见到的离散机率分布(discreteprobability distribution)。
泊松分布是以 18〜19世纪的法国数学家西莫恩•德尼•泊松(Sim eon-Denis Poisson )命名的，他在1838年时发表。
这个分布在更早些时候由贝努 里家族的一个人描述过。
分布特点泊松分布的概率函数为：卩(X 二k)二厉旷—斤二0 1 (I)泊松分布的参数入是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为丸特征函数为岸⑴二即|川凸-1}}「关系当二项分布的n 很大而p 很小时，泊松分布可作为二项分布的近似，其中入为 常当n 120,p 再.05时，就可以用泊松公式近似得计算。
np 。
通泊松分布与二项分布事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。
应用场景在实际事例中，当一个随机事件，例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率入（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P（力。
因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位（在早期学界认为人类行为是服从泊松分布，2005年在nature上发表的文章揭示了人类行为具有高度非均匀性）。
泊松分布表格
泊松分布是一种离散概率分布，常用于描述在给定时间间隔或空间内发生的事件的数量。
以下是泊松分布表格，其中λ表示事件发生的平均发生率，表格中的数字表示在给定λ值下，不同k值（事件发生的次数）的概率。
k λ=1 λ=2 λ=3 λ=4 λ=5
0 0.3679 0.2706 0.1821 0.1253 0.0864
1 0.2419 0.3477 0.2704 0.1888 0.1309
2 0.135
3 0.2453 0.2987 0.2446 0.1868
3 0.0732 0.1599 0.2362 0.2675 0.2353
4 0.041
5 0.1118 0.1849 0.2562 0.2684
... ... ... ... ... ...
以上表格中的数字是泊松分布的概率值，这些数字可以用来说明在给定λ值下，不同k值所对应的概率。
例如，当λ=2时，k=1时的概率为0.3477。
需要注意的是，泊松分布在一些情况下可能不适用。
例如，当事件的发生不是相互独立时，或者当事件发生的概率随时间变化时，泊松分布可能不准确。
在这种情况下，可能需要使用其他概率模型来描述事件的发生。
POSSION分布
k10 k!
e55k 0.068 k9 k!
于是得 m+1=10, m=9件
这一讲，我们介绍了泊松分布 n重贝努里试验中稀有事件出现的次数近 似地服从泊松分布.
我们给出了泊松分布产生的一般条件
泊松分布在管理科学、运筹学以及自然 科学的某些问题中都占有重要的地位 .
让我们回忆一下上一讲介绍的泊松定理：
设
是一个正整数，pn
n
，则有
lnimCnk
pnk (1
pn)nk e
k ,
k!
k0,1,2,,
等式右端给出的概率分布，是又一种重要 的离散型分布： 泊松分布
一、泊松分布的定义及图形特点
设随机变量X所有可能取的值为0 , 1 , 2 , … , 且概率分布为：
P( X k) e k , k0,1,2,,
在实际中，许多随机现象服从或近 似服从泊松分布.
我们把在每次试验中出现概率很小的事 件称作稀有事件. 如地震、火山爆发、特大洪水、意外事故等等
由泊松定理，n重贝努里试验中稀有事件 出现的次数近似地服从泊松分布.
请看演示 “二项分布与泊松分布”
三、泊松分布产生的一般条件 在自然界和人们的现实生活中,经常要遇 到在随机时刻出现的某种事件.我们把在随机 时刻相继出现的事件所形成的序列,叫做随机 事件流. 若事件流具有平稳性、无后效性、普通性， 则称该事件流为泊松事件流（泊松流）.
下面简要解释平稳性、无后效性、普通性.
平稳性:
在任意时间区间内，事件发生k次(k≥0)的 概率只依赖于区间长度而与区间端点无关.
无后效性: 在不相重叠的时间段内，事件的发生是相 互独立的. 普通性:
如果时间区间充分小，事件出现两次或 两次以上的概率可忽略不计.
e55k 0.068 k9 k!
于是得 m+1=10, m=9件
这一讲，我们介绍了泊松分布 n重贝努里试验中稀有事件出现的次数近 似地服从泊松分布.
我们给出了泊松分布产生的一般条件
泊松分布在管理科学、运筹学以及自然 科学的某些问题中都占有重要的地位 .
让我们回忆一下上一讲介绍的泊松定理：
设
是一个正整数，pn
n
，则有
lnimCnk
pnk (1
pn)nk e
k ,
k!
k0,1,2,,
等式右端给出的概率分布，是又一种重要 的离散型分布： 泊松分布
一、泊松分布的定义及图形特点
设随机变量X所有可能取的值为0 , 1 , 2 , … , 且概率分布为：
P( X k) e k , k0,1,2,,
在实际中，许多随机现象服从或近 似服从泊松分布.
我们把在每次试验中出现概率很小的事 件称作稀有事件. 如地震、火山爆发、特大洪水、意外事故等等
由泊松定理，n重贝努里试验中稀有事件 出现的次数近似地服从泊松分布.
请看演示 “二项分布与泊松分布”
三、泊松分布产生的一般条件 在自然界和人们的现实生活中,经常要遇 到在随机时刻出现的某种事件.我们把在随机 时刻相继出现的事件所形成的序列,叫做随机 事件流. 若事件流具有平稳性、无后效性、普通性， 则称该事件流为泊松事件流（泊松流）.
下面简要解释平稳性、无后效性、普通性.
平稳性:
在任意时间区间内，事件发生k次(k≥0)的 概率只依赖于区间长度而与区间端点无关.
无后效性: 在不相重叠的时间段内，事件的发生是相 互独立的. 普通性:
如果时间区间充分小，事件出现两次或 两次以上的概率可忽略不计.