仿射变换
- 格式:doc
- 大小:557.50 KB
- 文档页数:9


高中数学仿射变换一、引言仿射变换是高中数学中的重要概念之一,它在几何变换和线性代数中有着广泛的应用。
本文将介绍仿射变换的基本概念、性质以及应用,帮助读者更好地理解和掌握这一知识点。
二、基本概念1. 定义:仿射变换是指保持直线平行性质的变换。
简单来说,它是由平移、旋转、缩放和投影四种基本变换组成的变换。
2. 仿射变换的代数表示:设二维平面上有一个点P(x, y),经过仿射变换后得到点P'(x', y'),则有如下代数表示:x' = a*x + b*y + cy' = d*x + e*y + f其中a、b、c、d、e、f为常数。
三、性质1. 保直线性质:仿射变换保持直线的性质,即直线经过仿射变换后仍然是直线。
例如,一条直线上的三个点经过仿射变换后仍然共线。
2. 保平行性质:仿射变换保持平行线的性质,即平行线经过仿射变换后仍然平行。
例如,两条平行线经过仿射变换后仍然平行。
3. 保比例性质:仿射变换保持线段的比例关系。
例如,一条线段上的两个点经过仿射变换后线段上的其他点的比例关系仍然成立。
四、应用1. 几何变换:仿射变换在几何变换中有着广泛的应用,可以用来描述平面上的旋转、缩放、平移等操作。
例如,我们可以利用仿射变换来实现图片的旋转、缩放和平移。
2. 图像处理:仿射变换在图像处理中也有着重要的应用,可以用来进行图像的扭曲、校正和纠正等操作。
例如,我们可以利用仿射变换来对图像进行透视校正,使得图像中的平行线在处理后仍然保持平行关系。
3. 计算机图形学:仿射变换在计算机图形学中扮演着重要的角色,可以用来进行三维物体的平面投影、旋转和缩放等操作。
例如,我们可以利用仿射变换来实现计算机图形学中的三维模型的投影效果。
五、总结通过本文的介绍,我们了解了高中数学中的仿射变换的基本概念、性质以及应用。
仿射变换作为一种保持直线平行性质的变换,在几何变换、图像处理和计算机图形学等领域都有着广泛的应用。

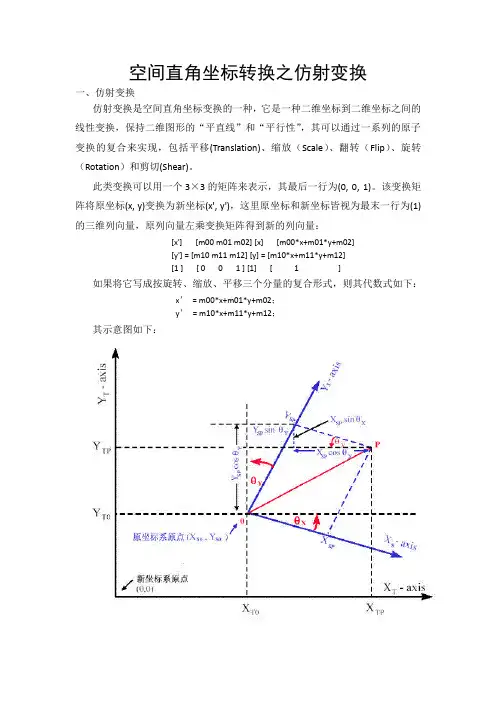
空间直角坐标转换之仿射变换一、仿射变换仿射变换是空间直角坐标变换的一种,它是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直线”和“平行性”,其可以通过一系列的原子变换的复合来实现,包括平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和剪切(Shear)。
此类变换可以用一个3×3的矩阵来表示,其最后一行为(0, 0, 1)。
该变换矩阵将原坐标(x, y)变换为新坐标(x', y'),这里原坐标和新坐标皆视为最末一行为(1)的三维列向量,原列向量左乘变换矩阵得到新的列向量:[x'] [m00 m01 m02] [x] [m00*x+m01*y+m02][y'] = [m10 m11 m12] [y] = [m10*x+m11*y+m12][1 ] [ 0 0 1 ] [1] [ 1 ]如果将它写成按旋转、缩放、平移三个分量的复合形式,则其代数式如下:x’= m00*x+m01*y+m02;y’= m10*x+m11*y+m12;其示意图如下:几种典型的仿射变换:1.public static AffineTransform getTranslateInstance(double tx, double ty)平移变换,将每一点移动到(x+tx, y+ty),变换矩阵为:[ 1 0 tx ][ 0 1 ty ][ 0 0 1 ](译注:平移变换是一种“刚体变换”,rigid-body transformation,中学学过的物理,都知道啥叫“刚体”吧,就是不会产生形变的理想物体,平移当然不会改变二维图形的形状。
同理,下面的“旋转变换”也是刚体变换,而“缩放”、“错切”都是会改变图形形状的。
)2.public static AffineTransform getScaleInstance(double sx, double sy)缩放变换,将每一点的横坐标放大(缩小)至sx倍,纵坐标放大(缩小)至sy倍,变换矩阵为:[ sx 0 0 ][ 0 sy 0 ][ 0 0 1 ]3.public static AffineTransform getShearInstance(double shx, double shy)剪切变换,变换矩阵为:[ 1 shx 0 ][ shy 1 0 ][ 0 0 1 ]相当于一个横向剪切与一个纵向剪切的复合[ 1 0 0 ][ 1 shx 0 ][ shy 1 0 ][ 0 1 0 ][ 0 0 1 ][ 0 0 1 ](译注:“剪切变换”又称“错切变换”,指的是类似于四边形不稳定性那种性质,街边小商店那种铁拉门都见过吧?想象一下上面铁条构成的菱形拉动的过程,那就是“错切”的过程。

一、简介Halcon是一种功能强大的机器视觉软件,广泛应用于工业自动化、医疗影像、安防监控等领域。
在Halcon中,仿射变换是一种常见的图像处理技术,用于实现图像的旋转、缩放、平移等操作。
二、仿射变换的基本原理1. 仿射变换是一种线性变换,可以通过矩阵运算来描述。
给定一个二维坐标系下的点P(x, y),经过仿射变换后,其坐标变为P'(x', y'),可以表示为:x' = a*x + b*y + cy' = d*x + e*y + f其中a、b、d、e为线性变换矩阵的元素,c、f为平移向量的偏移量。
2. 仿射变换可以实现图像的平移、旋转、缩放、错切等操作,是图像处理中常用的技术之一。
三、 Halcon中的仿射变换1. 在Halcon中,可以通过使用affine_trans_image函数来实现图像的仿射变换。
该函数接受输入图像、变换矩阵以及插值方式等参数,可以对图像进行指定的仿射变换操作。
2. 通过设置不同的变换矩阵,可以实现图像的不同变换效果。
通过调整平移向量的偏移量,可以实现图像的平移操作;通过调整线性变换矩阵的元素,可以实现图像的旋转、缩放等操作。
3. Halcon还提供了inverse_affine_trans_image函数,用于实现仿射变换的逆变换操作。
通过逆变换,可以将经过仿射变换后的图像还原到原始状态,实现图像的修正和恢复。
四、仿射变换在机器视觉中的应用1. 仿射变换在机器视觉中具有重要的应用价值。
在工业自动化领域,通过对图像进行仿射变换,可以实现对产品进行检测、定位和识别;在医疗影像领域,可以通过仿射变换对医学图像进行修正和分析;在安防监控领域,可以实现对监控图像的处理和分析等。
2. 通过使用Halcon中的仿射变换技术,可以实现对图像的精准操作和处理,为机器视觉系统的性能和效果提供有力支持。
五、总结1. 仿射变换是图像处理领域常用的技术之一,通过线性变换和平移操作,可以实现图像的平移、旋转、缩放等操作。

新高考数学大一轮复习第28讲 仿射变换一、问题综述设椭圆2222:1(0)x y C a b a b +=>>,作变换:x x ayy b ϕ⎧'=⎪⎪⎨⎪'=⎪⎩得单位圆22:1C x y '''+=,记点1122(,),(,)A x y B x y 在变换ϕ下的对应点分别为1122(,),(,)A x y B x y '''',设直线AB 和A B ''的斜率分别为,k k '(斜率存在且非零),AOB ∆和A OB '''∆的面积分别为,S S '.则变换ϕ有以下性质:性质1:共线结合性,即AB AC A B A C λλ''''=⇔=;1212////l l l l ''⇔;A C A C '∈⇔∈.性质2:b k k a'=或k bk a ='.证明:21212121()()y y b y y b k k x x a x x a ''--'===''--.性质3:线段AB 中点E 变成线段A B ''中点E '. 性质4:直线与曲线的位置关系保持不变.性质5:直线AB 上线段成比例,则变成直线A B ''上对应的线段仍成比例. 性质6:S abS '=或Sab S =', 证明:因为122112211122S x y x y ab x y x y abS '''''=-=-=,即证之. 性质7:设线段AB 在伸缩变换ϕ下的像为A B '',显然在伸缩变换下线段的长度关系不具有确定的关系,但是我们可以利用斜率的不变关系(性质2)寻找,AB A B ''的关系:即设线段AB 所在直线斜率为k,则A B A BAB x x A B x x -===''''-二、典例分析类型1:取值范围型【例1】设直线1y kx =-和椭圆2214x y m +=有且仅有一个公共点,求k 和m 的取值范围.解析:令2xx y y ⎧'=⎪⎪⎨⎪'=,则已知椭圆和直线变为相应的圆22:1O x y '''+=和直线210kx ''-=,要使已知的直线与椭圆有且仅有一个公共点,只要相应的直线与圆相切.1=,即214m k =-,故得01m <≤, 即20141k <-≤,解得1122k -<<.【方法小结】转化到直线与圆相切,建立参数关系式,利用二次函数最值求解.类型2:三角形面积最值型【例2】若,,A B C 是椭圆()222210x y a b a b +=>>上的三点,求ABC ∆面积的最大值.解析:对椭圆()222210x y a b a b +=>>做伸缩变换x x ayy b ⎧'=⎪⎪⎨⎪'=⎪⎩,椭圆就变成圆221x y ''+=.此时椭圆的内接ABC ∆就变成圆的内接A B C '''∆, 而圆的内接三角形以内接正三角形面积最大, 从而A B C S '''∆, 还原到椭圆中,由伸缩变换对应多边形面积比的不变性可知,ABCS ∆. 【例3】已知椭圆()222210x y a b a b+=>>,面积为2ab 的椭圆内接四边形有( ).A .1个B .2个C .3个D .4个 解析:对椭圆()222210x y a b a b +=>>做伸缩变换x x ayy b ⎧'=⎪⎪⎨⎪'=⎪⎩,椭圆就变成圆221x y ''+=,此时相应的椭圆内接四边形就变成圆的内接四边形, 当椭圆的内接四边形的面积2ab 时, 其对应的圆内接四边形的面积就是122ab ab⨯=, 由平面几何知识知圆的内接正方形的面积为2, 而这样的内接正方形有无数个,还原到椭圆可知对应的椭圆内接四边形也有无数个,【例4】(2014年高考全国新课标1卷理第20题)已知点()0,2A -,椭圆E :22221(0)x y a b a b+=>>的离心率为32,F 是椭圆E 的右焦点,直线AF 的斜率为233,O 为坐标原点. (Ⅰ)求E 的方程;(Ⅱ)设过点A 的直线l 与E 相交于,P Q 两点,当OPQ ∆的面积最大时,求l 的方程. 解析:(Ⅰ)椭圆E 的方程为2214x y +=.(Ⅱ)由伸缩变换:2xx y y ϕ⎧'=⎪⎨⎪'=⎩,椭圆2214x y +=(如下图)变成了单位圆221x y ''+=, ()0,2A -变为()0,2A '-,设直线P Q ''的方程为2y kx ''=-.原点O '到直线P Q ''的距离为21d k =+圆与直线相交,则需要满足1d <, 从而易得23k >,则2222223211211k P Q d k k ⎛⎫-''=-=- ⎪ ⎪++⎝⎭则2222221213222112324332142O P Q SP Q d k k k k k k '''''=-=⋅++-==--≤= 23k -=7k =()1S=,此时直线l 的斜率为72b k a ±=±,且()()()maxmaxmax21OPQ O P Q O P Q Sab SS''''''===.又直线l 过点()0,2A -, 所以直线l 的方程为722y x =-或722y x =--. 【方法小结】对于求三角形面积和直线方程问题,可以用性质2和6求解.类型3:四边形面积型【例5】(2013年高考全国新课标2卷理科第20题)平面直角坐标系xOy 中,过椭圆2222:1(0)x y M a b a b +=>>右焦点的直线30x y +-=交M 于,A B 两点,P 为AB 的中点,且OP 的斜率为12.(Ⅰ)求M 的方程;(Ⅱ),C D 为M 上的两点,若四边形ACBD 的对角线CD AB ⊥,求四边形的最大值. 解析: 在伸缩变换:x x ay y b ϕ⎧'=⎪⎪⎨⎪'=⎪⎩下,椭圆(如下图)变成圆,(Ⅰ)由伸缩变换性质知,2A B AB O P OP a a a ak k k k b b b b''''==-==, 又在椭圆中P 为AB 的中点,则在单位圆中P '为A B ''的中点, 则O P A B ''''⊥,故2212A B O P a k k b''''=-=-,即222a b =,又因为直线30x y +过椭圆的右焦点, 则3c ,于是6,3a b = 则椭圆M 的方程为221x y +=.(Ⅱ)由CD AB ⊥知1CD k =,则在单位圆中,A B AB C D CD k k ''''===设AB '与C D ''间的夹角为α,则tanα==则sinα=又直线AB 变换为直线A B ''10y ''+-=,则O '到直线A B ''的距离d==, 则A B ''=又1sin 2A B C D S A B C D D α''''''''''=≤当CD ''为圆的直径时取等号, 由伸缩变换的性质知, ABCD A B C D A B C D S abS ''''''''==≤. 【方法小结】对于四边形面积问题,在单位圆中利用三角函数的有界性和性质6求解.类型4:距离型【例6】在椭圆22147x y +=上求一点,使它到直线:32160l x y --=的距离最短,并求此距离.解析:作仿射变换2xx y ⎧'=⎪⎪⎨⎪'=⎪⎩,则已知椭圆和直线l 变为相应的圆221x y ''+=和直线:6160l x '''--=,从而所求问题变为:在圆221x y ''+=上求一点到直线:6160l x '''--=的距离的最短问题, 由平面几何知识可知,过圆221x y ''+=的圆心()0,0O 作直线l '的垂线段,交圆于点(),P x y ''', 点P '到垂足的距离最短,由直线l '的垂线:OP y '''=和圆221x y''+=相交, 解方程可求得点P '为3,⎛ ,则相应椭圆所求的点P 为37,24⎛⎫- ⎪⎝⎭,所求最短距离为()22373216813241332⨯+⨯-=+-. 【方法小结】距离最短,转化为单位圆中的垂线段最短,联立方程后得到点的坐标,用点到直线的距离求解即可.类型5:证明型【例7】如图,椭圆2222:1(0)x y C a b a b +=>>(其中)与过点()()2,0,0,1A B 的直线有只且只有1个公共点T ,且椭圆的离心率32e =. (Ⅰ)求椭圆的方程;(Ⅱ)设12,F F 分别为椭圆的焦点,M 为线段2AF 的中点,求证:1ATM AFT ∠=∠. 解析: (Ⅰ)如下图利用伸缩变换x x ayy b ⎧'=⎪⎪⎨⎪'=⎪⎩,椭圆上的点,,A T B 变换为圆,,A T B '''上的点,因为切线AB 的方程为12x y +=,所以切线A B ''的方程为12ax by ''+=, 由点O '到切线A B ''距离22112d a b ==⎛⎫+ ⎪⎝⎭,得2244a b +=,又32c e a ==,解得2212,2a b ==, 从而椭圆方程为22212x y +=.因为,O A O B O T A B ''''''''=⊥, 所以12A T AB ''''=. 由性质2可知1522AT AB ==, 在椭圆中易得1661,242AM AF =-=+, 从而21AT AF AM =,即1AT AM AF AT=,又1TAF M AT ∠=∠,从而1TAF MAT ,得1ATM AFT ∠=∠.【方法小结】用坐标伸缩变换将椭圆问题化作圆处理,解答过程完全退去了代数运算的成分,而是通过图形的几何性质进行解答,化繁为简,事半功倍类型6:相切轨迹型【例8】(2014年广东省数学高考理科试题第20题)已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点为()5,0,离心率为53. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)若动点00(,)P x y 为椭圆C 外一点,且点P 到椭圆的两条切线互相垂直,求点P 的轨迹方程. 解析:(Ⅰ)22194x y +=(Ⅱ)如图,设点,,A P B 在伸缩变换32xx yy ⎧'=⎪⎪⎨⎪'=⎪⎩下的像分别为,,A P B ''',可知00,32x y P ⎛⎫' ⎪⎝⎭,339224P A P B PA PB k k k k ''''==-,直线,P A PB ''与圆O '相切,设过点P 的圆的切线方程为0023y x y k x ⎛⎫-=- ⎪⎝⎭,即0066320kx y y kx -+-=, 从而圆心O '到切线的距离为1d ==,即()2220000436129360xk x y k y --+-=,根据韦达定理知, 202093694436P A P B y k k x ''''-==--, 化简得22013x y +=, 故点的轨迹方程为2213x y +=.【方法小结】在单位圆中得到切线方程,用点到直线的距离建立二次方程,用韦达定理得到202093694436P A P B y k k x ''''-==--,即可求得轨迹方程为2213x y +=.类型7:定值型【例9】(2011年重庆卷理科第20题) 如题(20)图,椭圆的中心为原点O,离心率e =,一条准线的方程为x =(Ⅰ)求该椭圆的标准方程;(Ⅱ) 设动点P 满足:2OP OM ON =+,其中,M N 是椭圆上的点,直线OM 与ON 的斜率之积为12-,问:是否存在两个定点12,F F ,使得12PF PF +为定值?若存在,求12,F F 的坐标;若不存在,说明理由. 解析:(Ⅰ)所求椭圆的方程为22142x y +=(Ⅱ)在伸缩变换2x x y ⎧'=⎪⎪⎨⎪'=⎪⎩的作用下(如下图)椭圆22142x y +=变为圆:221x y ''+=,12OM ON k k =-变为1O M O N k k ''''⋅=-,点,,M N P 变为点,,M N P '''.在圆中,由1O M O N k k ''''=-,知O M O N ''''⊥,设()(),,cos ,sin ,cos ,sin 22P x y M N ππαααα⎛⎫⎛⎫⎛⎫'''''++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即()sin ,cos N αα'-,因为2O P O M O N ''''''=+, 所以cos 2sin sin 2cos x y αααα'=-⎧⎨=+⎩,两式平方相加,得225x y ''+=, 即点P '的轨迹为圆225x y ''+=, 由伸缩变换知,在椭圆中,点P 的轨迹为椭圆2212010x y +=,所以存在两个定点())1210,0,10,0F F -,使得1245PF PF +=【方法小结】利用单位圆的参数方程得到点P '的轨迹为圆225x y ''+=,通过伸缩变换得到点P 的轨迹为椭圆2212010x y +=,所以存在两个定点()()1210,0,10,0F F -,使得125PF PF +=三、巩固练习1.(2014年浙江省数学高考理科试题第21题)如图,设椭圆2222:1(0)x y C a b a b+=>>,动直线l 与椭圆C 只有一个公共点P ,且点P 在第一象限.(Ⅰ)已知直线l 的斜率为k ,用,,a b k 表示点P 的坐标;(Ⅱ)若过原点O 的直线1l 与l 垂直,证明:点P 到直线1l 距离的最大值为a b -.2、(2011年江苏卷理科第18题)如图,在平面直角坐标系xOy 中,,M N 分别是椭圆22142x y +=的顶点,过坐标原点的直线交椭圆于,P A 两点,其中P 在第一象限,过P 作x 轴的垂线,垂足为C ,连接AC ,并延长交椭圆于点B ,设直线PA 的斜率为k . (Ⅰ)当直线PA 平分线段MN 时,求k 的值; (Ⅱ)当2k =时,求点P 到直线AB 的距离d ; (Ⅲ)对任意0k >,求证:PA PB ⊥.3.(2013年山东高考理文科第22题)在平面直角坐标系xOy 中,已知椭圆C 的中心在原点,焦点在x 轴上,短轴长是2. (Ⅰ)求椭圆C 的方程;(Ⅱ)A ,B 是椭圆C 上满足三角形AOB的任意两点,E 为线段AB 的中点,射线OE 交椭圆C 于点P .设OP tOE =,求实数t 的值.(第21题图)参考答案:1.第1小题的伸缩变换解法如下:解析:(Ⅰ)如图,设切点()00,P x y ,在伸缩变换x x a y y b ⎧'=⎪⎪⎨⎪'=⎪⎩的作用下,椭圆2222:1(0)x y C a b a b +=>>变换为圆221x y ''+=,椭圆上的点()00,P x y 变换为圆上的点0,x y P a b ⎛⎫' ⎪⎝⎭,过点P 的切线l 变换为过点P '的切线l ',且l l a ak k k b b '==,由点P '在圆221x y ''+=上得2200221x ya b += ①,由O P l '''⊥得1O P l k k '''=-, 从而001ay ak bx b=-,即2002a kyx b =-,代入①式可得点22222222,a k b P a k b a k b ⎛⎫- ⎪ ⎪++⎝⎭.2.解析:(Ⅰ)(Ⅱ)略.(Ⅲ)在伸缩变换2:2xx y y ϕ⎧'=⎪⎪⎨⎪'=⎪⎩的作用下,椭圆22142x y +=(如图)变成了单位圆221x y ''+=,()()0011,,,P x y B x y 变为,P B '',在圆中,由21P A B A B A P B k k k k ''''''''=⎧⎨=-⎩,得2P A P B k k ''''=-, 得001001222y y y x x x '''-=-'''-,00122222=-⋅-, 即0010011y yy x x x -⋅=--,即1PA PB k k =-,故PA PB ⊥.3. 解析:(Ⅰ)略(Ⅱ)将椭圆2212x y +=伸缩变换成221x y +=,设,,,,O A B E P 分别对应于点,,,,O A B E P ''''', 考虑到1,2AOB A B B A S x y x y =-则12A O B A B B A S x y x y '''''''=-由OP tOE =,有OP tOE ''=, 设A O E α'''∠=,由于2O E A π'''∠=, 故1O E O E O A O P t α''''==''''cos =又1=11sin 22A O B S α'''⨯⨯⨯=故sin 2α=,又2α为三角形内角, 故2=3πα或23π,则=6πα或3π,综上,1cos t α==或2,即,t =2t =.。

相似变换和仿射变换相似变换和仿射变换是几何中的两个重要概念,它们在图形变换中起着非常重要的作用。
本文将从定义、性质、应用等多个方面进行详细介绍。
一、相似变换1.1 定义相似变换是指在平面或空间中,保持两个图形之间的每一对对应点之间的距离比不变的变换。
简单来说,就是将一个图形按照比例因子进行缩放、旋转和平移后得到的新图形与原图形相似。
1.2 性质(1)保持距离比不变;(2)保持角度不变;(3)保持面积比不变。
1.3 应用相似变换在实际生活中有着广泛的应用。
例如地图缩放、建筑设计等都需要利用相似性进行计算和设计。
二、仿射变换2.1 定义仿射变换是指在平面或空间中,保持两个图形之间的每一对对应点之间的距离比和直线上点之间的距离比不变的线性变换。
简单来说,就是将一个图形通过平移、旋转、缩放和错切等操作得到一个新图形。
2.2 性质(1)保持距离比不变;(2)保持角度不变;(3)保持平行线仍为平行线。
2.3 应用仿射变换在计算机图形学中有着广泛的应用。
例如图像处理、计算机视觉等都需要利用仿射变换进行处理和分析。
三、相似变换与仿射变换的区别相似变换和仿射变换是两个重要的几何概念,在定义和性质上有所不同,可以通过以下几点进行区分:(1)相似变换只能进行缩放、旋转和平移操作,而仿射变换还包括错切操作;(2)相似变换只能保持距离比不变,而仿射变换还能保持直线上点之间的距离比不变;(3)相似变换只能将一个图形按照比例因子进行缩放、旋转和平移后得到一个新图形与原图形相似,而仿射变换可以将一个图形通过平移、旋转、缩放和错切等操作得到一个新图形。
四、总结相似变换和仿射变换是几何中的两个重要概念,它们在实际生活中和计算机图形学中都有着广泛的应用。
相似变换只能进行缩放、旋转和平移操作,而仿射变换还包括错切操作;相似变换只能保持距离比不变,而仿射变换还能保持直线上点之间的距离比不变;相似变换只能将一个图形按照比例因子进行缩放、旋转和平移后得到一个新图形与原图形相似,而仿射变换可以将一个图形通过平移、旋转、缩放和错切等操作得到一个新图形。

仿射变换公式仿射变换公式是数学中一种常见的变换公式,使用它可以对一个坐标系中的原点进行变换,从而将它转化为另一个坐标系下的点。
它有助于解决不同的图形学问题、实现图形的转换,也可以用于将两个不同的坐标系之间的数据进行转换。
仿射变换公式的定义如下:设A、B、C是三个二维空间的仿射变换,那么ABC的变换公式为:XA=XB+XC,YA=YB+YC。
其中XA、YA是原坐标系中点P的横纵坐标,XB、YB是原坐标系中点P’的横纵坐标,XC、YC是新坐标系中点P’的横纵坐标(新坐标系相对于原坐标系的平移量)。
仿射变换公式的另一种表示形式为:XA=AXB+BYC,YA=CXB+DYC。
其中XA、YA是原坐标系中点P的横纵坐标,XB、YB是原坐标系中点P’的横纵坐标,XC、YC是新坐标系中点P’的横纵坐标(新坐标系相对于原坐标系的平移量),A、B、C、D是四个不同的仿射变换系数。
仿射变换公式可以用来实现一些基本的图形变换,例如平移、旋转、缩放、拉伸及剪切等。
它也可以用于将两个不同的坐标系之间的数据进行转换,以统一处理某个问题。
例如,在机器视觉中,经常需要将输入的图像从一个坐标系转换到另一个坐标系中进行处理,这就要求把原始图像仿射变换到目标坐标系中。
此外,仿射变换公式还可以用于自然图像的空间变换或是像素点之间的坐标变换。
仿射变换公式的应用非常广泛,它极大地方便了图形学领域中的许多应用,也提供了图形学问题求解的一种重要方法。
例如,多层次变换(MLT)是一种常用的图形学变换技术,它可以用仿射变换公式表示为:XMLT=XL+TR,YMLT=YL+TR,其中XL、YL是原始图像的坐标,TR是与仿射变换相关的参数,XMLT、YMLT是MLT变换后的结果。
仿射变换是一种有效的图形变换手段,它的应用范围很广,在图形学、机器人控制、图像处理等领域都有重要的应用。
它可以用来实现两个不同坐标系之间的数据转换,也可以用于像素点之间的坐标变换,是一种非常重要的变换公式,也是图形学问题求解中不可或缺的工具。

仿射变换方程怎么解以仿射变换方程怎么解引言:仿射变换是一种常见的几何变换方法,可以用于对图像进行旋转、平移、缩放和错切等操作。
本文将介绍仿射变换方程的解法,帮助读者更好地理解和应用仿射变换。
一、什么是仿射变换?仿射变换是指在平面上对点进行旋转、平移、缩放和错切等操作的变换方式。
它可以通过一个线性变换和一个平移向量来表示。
具体而言,对于平面上的点 (x, y),经过仿射变换后的点 (x', y') 可以通过以下公式计算得出:x′=xx+xx+xx′=xx+xx+x其中,a、b、c、d、e 和 f 是仿射变换的参数。
二、仿射变换方程的解法1.已知三对点坐标的情况下当给定三对点的坐标时,我们可以利用这些已知点来求解仿射变换方程的参数。
假设已知的点分别为 (x1, y1) -> (x1', y1'),(x2, y2) -> (x2', y2') 和 (x3, y3) -> (x3', y3'),则可以得到以下三个方程:x1′=xx1+xx1+xx1′=xx1+xx1+xx2′=xx2+xx2+xx2′=xx2+xx2+xx3′=xx3+xx3+xx3′=xx3+xx3+x通过解这个方程组,我们可以求解出a、b、c、d、e 和f 的值,从而得到仿射变换的参数。
2.已知变换矩阵的情况下除了通过已知点来求解仿射变换方程的参数,我们还可以通过已知变换矩阵的方式来解方程。
假设已知的变换矩阵为 M,即[x′1 x′1] = [x1 x1 1] x其中,[x′1 x′1] 是经过仿射变换后的点的坐标,[x1 x1 1] 是原始点的齐次坐标。
则根据仿射变换的定义,可以得到以下方程:x′1=x1x+x1x+xx′1=x1x+x1x+x通过解这个方程组,我们可以求解出仿射变换的参数。
三、应用实例仿射变换在计算机图形学和计算机视觉领域有着广泛的应用。

大招六 仿射变换仿射变换,通俗来讲,就是将一个空间内的图形按照一定法则变换,就会在另一个空间内得到与之对应的新图形。
在高考数学解析几何题目中,我们可以利用仿射变换将一部分有关椭圆的问题转化为圆的问题,这样就可以借助圆中的特有的一些性质解决问题,从而使问题的解决过程大大简化。
椭圆222210x y a b a b +=>>(),经过仿射变换''ax x by y=⎧⎨=⎩,则椭圆变为了圆22(')(y')1x += 有如下对应关系:(1) 点00(,)P x y 变为00'(,)x y P a b(2) 直线斜率k 变为'a k k b =(3) 图形面积S 变为1'S S ab= (4) 点、线、面位置不变(中点依然是中点、相切依然是相切)注:仿射变换高考中如果使用,有可能扣分,勇哥建议大家可以利用仿射变换快速得出答案,过程还是采用正常方法。
例1、 设、分别是椭圆的左、右焦点. (1)若P 是该椭圆上的一个动点,求的取值范围; (2)设,是它的两个顶点,直线与AB 相交于点D,与椭圆相交于E 、F 两点.求四边形AEBF 面积的最大值. 例2、已知圆,定点,A 是圆上的一动点,线段的垂直平分线交半径于P 点.(Ⅰ)求P 点的轨迹C 的方程;(Ⅱ)四边形EFGH 的四个顶点都在曲线C 上,且对角线EG,FH 过原点O,若,求证:四边形EFGH 的面积为定值,并求出此定值.例3、已知A,B 分别为椭圆的左、右顶点,P 为椭圆C 上异于A,B 两点的任意一点,直线PA,PB 的斜率分别记为,(1)求; (2)过坐标原点O 作与直线PA,PB 平行的两条射线分别交椭圆C 于点M,N,问:的面积是否为定值?请说明理由.例4、平面直角坐标系xOy 中,已知椭圆2222:1(0)x y C a b a b +=>>的离心率为,左、右焦点分别是12,F F ,以1F 为圆心,以3为半径的圆与以2F 为圆心,以1为半径的圆相交,交点在椭圆C 上.(Ⅰ)求椭圆C 的方程;(Ⅱ)设椭圆2222:144x y E a b +=,P 为椭圆C 上的任意一点,过点P 的直线y kx m=+交椭圆E 于A,B 两点,射线PO 交椭圆E 于点Q.(ⅰ)求||||OQ OP 的值;(ⅱ)求ABQ ∆面积最大值.。
第四章保距变换和仿射变换本章教学目的:通过本章的学习,使学生掌握保距变换和仿射变换这两类重要的几何变换,从而深化几何学的研究,并掌握解决几何问题的一个有效方法。
本章教学重点:(1)保距变换和仿射变换的定义和性质;(2)仿射变换的基本定理;(3)保距变换和仿射变换的变换公式;(4)图形的仿射分类与仿射性质。
本章教学难点:仿射变换的性质和基本定理;仿射变换的变换公式的求法。
本章教学内容:§1 平面的仿射变换与保距变换1.1――对应与可逆变换集合X到集合Y的一个映射f:X→Y是把X中的点对应到Y中的点的一个法则,即∀x ∈X,都决定Y中的一个元素f(x),称为点x在f下的像。
对X的一个子集A,记f(A)={f(a)|a∈A},它是Y的一个子集,称为A在f下的像。
对Y的一个子集B,记f-1(B)={x∈X|f(x)∈B},称为B在F下的完全原像,它是X的子集。
如果f是X到Y的映射,g上Y到Z的映射,则它们的复合上X到Z的映射,记作g f: X→Z,规定为g f(x)=g(f(x)),∀x∈X.对A⊂X,g f(A)=g(f(A));对C⊂Z,(g f)-1(C)=f-1(g-1(C)).映射的复合无交换律,但有结合律。
映射f: X→X称为X上的一个变换,id X: X→X,∀x∈X,id X(x)=x,称为X的恒同变换。
对映射f: X→Y,如果有映射g: Y→X,使得g f= id X:X→X,f g=id Y:Y→Y,则说f是可逆映射,称g是f的逆映射。
如果在映射f: X→Y下X的不同点的像一定不同,则称f是单射。
如果f(X)=Y,则称f 是满射。
如果映射f: X→Y既是单射,又是是满射,则称f为——对应。
此时∀f-1f=id X,, ff-1= id Y,于是f是可逆映射,并且f的逆映射是f-1。
一个集合X到自身的可逆映射称为X上的可逆变换。
1.2平面上的变换群平移取定平行于平面的一个向量u,规定π的变换P u: π→π为:∀A∈π,令P u(A)AP(A)=u的点。
仿射变换详解warpAffine今天遇到一个问题是关于仿射变换的,但是由于没有将仿射变换的具体原理型明白,看别人的代码看的很费解,最后终于在师兄的帮助下将原理弄明白了,我觉得最重要的是理解仿射变换可以看成是几种简单变换的复合实现,具体实现形式即将几种简单变换的变换矩阵M相乘,这样就很容易理解啦定义:仿射变换的功能是从二维坐标到二维坐标之间的线性变换,且保持二维图形的“平直性”和“平行性”。
仿射变换可以通过一系列的原子变换的复合来实现,包括平移,缩放,翻转,旋转和剪切。
这类变换可以用一个3*3的矩阵M来表示,其最后一行为(0,0,1)。
该变换矩阵将原坐标为(x,y)变换为新坐标(x',y'),即OpenCV中相应的函数是:void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize,int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, constScalar& borderValue=Scalar())¶Parameters:∙src –input image.∙dst –output image that has the size dsize and the same type as src .∙M – transformation matrix,最重要的东东了,本文中着重讲M的构造∙dsize –size of the output image.ansformation ( ).∙borderMode – pixel extrapolation method (see borderInterpolate()); when borderM ode=BORDER_TRANSPARENT , it means that the pixels in the destination image correspon ding to the “outliers” in the source image are not modifi ed by the function.∙borderValue –value used in case of a constant border; by default, it is 0.下面介绍一些典型的仿射变换:(1)平移,将每一点移到到(x+t , y+t),变换矩阵为(2)缩放变换将每一点的横坐标放大或缩小s x倍,纵坐标放大(缩小)到s y倍,变换矩阵为(3)旋转变换原点:目标图形围绕原点顺时针旋转Θ 弧度,变换矩阵为(4) 旋转变换:目标图形以(x , y )为轴心顺时针旋转θ弧度,变换矩阵为相当于两次平移与一次原点旋转变换的复合,即先将轴心(x,y)移到到原点,然后做旋转变换,最后将图片的左上角置为图片的原点,即有的人可能会说为什么这么复杂呢,那是因为在opencv的图像处理中,所有对图像的处理都是从原点进行的,而图像的原点默认为图像的左上角,而我们对图像作旋转处理时一般以图像的中点为轴心,因此就需要做如下处理如果你觉得这样很麻烦,可以使用opencv中自带的Mat getRotationMatrix2D(Point2f center, double angle, double scale)函数获得变换矩阵M,center:旋转中心angle:旋转弧度,一定要将角度转换成弧度scale:缩放尺度它得到的矩阵是:其中α = scale * cos( angle ) , β = scale* sing( angle ) , ( center.x , center.y ) 表示旋转轴心但是不得不说opencv的文档以及相关书籍中都把这个矩阵写错了,如下:建议大家自己通过下式验证一下,即首先将轴心(x,y)移到原点,然后做旋转平绽放变换,最后再将图像的左上角转换为原点没有去研究该函数的源码,不晓得源码中到底怎么写的,但是在别人的博客中看到这个函数貌似需要修正opencv中还有一个函数:Mat getAffineTransform(InputArray src, InputArray dst)¶它通过三组点对就可以获得它们之间的仿射变换,如果我们在一组图像变换中知道变换后的三组点,那么我们就可以利用该函数求得变换矩阵,然后对整张图片进行仿射变换还有一种与仿射变换经常混淆的变换为透视变换,透视变换需要四组点对才能确定变换矩阵,由于仿射变换保持“平直性”与“平行性”,因此只需要三组点对,而透视变换没有这种约束,故需要四组点对warpPerspective函数主要作用:对图像进行透视变换,就是变形函数的调用形式:C++:void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize,int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, constScalar& borderValue=Scalar())参数详解:InputArray src:输入的图像OutputArray dst:输出的图像InputArray M:透视变换的矩阵Size dsize:输出图像的大小int flags=INTER_LINEAR:输出图像的插值方法,combination of interpolation methods (INTER_LINEAR or INTER_NEAREST) and the optionalflag WARP_INVERSE_MAP, that sets M as the inverse transformation ( )int borderMode=BORDER_CONSTANT:图像边界的处理方式const Scalar& borderValue=Scalar():边界的颜色设置,一般默认是0函数原理:透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane),也称作投影映射(Projective Mapping)。
159仿射变换与双曲线的标准方程22221x y a b 相比椭圆的标准方程22221x y a b 在形式上极为接近圆的标准方程222x y r .在这一讲,我们着重讲述利用仿射变换将椭圆变换为圆,再利用圆的良好几何性质解决问题的方法.对椭圆的标准方程22221x y a b ,我们需要在y 轴进行伸缩变换x x b y y a得到方程22221x y a a .伸缩变换不会改变直线与圆锥曲线的交点个数、也不会改变共线线段长度的比例关系、平行和直线共点关系等等,但是伸缩变换会改变线段的长度,这需要引起充分的注意.【备注】仿射变换(Affine Transform )是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直性”(译注: straightness ,即变换后直线还是直线不会打弯,圆弧还是圆弧)和“平行性”(译注:parallelness ,其实是指保二维图形间的相对位置关系不变,平行线还是平行线,而直线上点的位置顺序不变,另特别注意向量间夹角可能会发生变化.仿射变换可以通过一系列的原子变换的复合来实现,包括:平移(Translation )、缩放(Scale )、翻转(Flip )、旋转(Rotation )和错切(Shear ).【备注】在伸缩变换①下,椭圆方程2222:1x y E a b变为圆222:E x y a ,椭圆上的点 00,P x y 变为00,a P x y b,因此过圆E 上一点P 的圆的切线方程为:l 200a x x y y a b该直线通过伸缩变换①就可以得到过椭圆E 上一点P 的椭圆的切线方程22002:a l x x y y a b即00221x x y ya b典型例题160例1(2010年上海)已知椭圆22x y ⑴ 设直线l【解析】 ⑴ 作仿射变换,椭圆方程变为222x y a ,则121k k∴C D O E ,根据垂径定理,E 是弦C D 的中点于是E 是CD 的中点.⑵ 如下图,求作点1P 、2P 的步骤为:1.以O 为圆心,椭圆的长轴长a 为半径作圆;2.过O 作射线,使Ox 轴正方向到该射线的角为 ,射线与圆交于Q ;3.过圆与y 轴正向的交点作y 轴的垂线,过圆与x 轴负向的交点作x 轴的垂线,两条垂线交于点P ;4.连结P Q ,取其中点N ;认识仿射变换1615.连结ON ,过N 作与ON 垂直的直线,交圆于点1P 、2P ; 6.过点1P 、2P 作x 轴的垂线,交椭圆于点1P、2P 即为所求. 证明:这样作图相当于作了纵轴方向上的伸缩变换22b y y a,容易证明线段P Q 与12P P互相平分,而坐标轴方向上的伸缩变换不改变线段的比例,因此PQ 与12PP 互相平分.这样就有12121222PQ PN PP PP PP PP【备注】题⑴说明弦中点问题中由点差法得到的结论可以看做是椭圆的“垂径定理”;题⑵利用仿射变换完成纯几何...作图,注意椭圆的参数方程在仿射变换图形下获得了确切的几何意义.练习1(2012年湖北理)设A 是单位圆221x y 上的任意一点,l 是过点A 与x 轴垂直的直线,D 是直线l 与x 轴的交点,点M 在直线l 上,且满足DM m DA (0m ,且1m ).当点A 在圆上运动时,记点M 的轨迹为曲线C .求曲线C 的方程,判断曲线C 为何种圆锥曲线,并求焦点坐标.【解析】 曲线C 的方程为2221yx m. 当01m 时,曲线C 为焦点在x轴上的椭圆,焦点坐标为,0; 当1m 时,曲线C 为焦点在y轴上的椭圆,焦点坐标为 0,.通过仿射变换可以将椭圆内接三角形变为圆内接三角形,它们之间存在固定的比例关系.而求解圆内接三角形的面积运算量要低很多.例2 (2012年人大附开学考试)已知直线【解析】作仿射变换x x y,则直线l 是椭圆22334y x即2213944x y 的切线. 设O 到直线l 的距离为d ,23944d ≤(∵直线l 的斜率存在)12AOB A O B S d△△利用仿射变换处理面积问题162 等号当且仅当232d时取得. 因此AOB △.练习2(2010年朝阳一模文)已知椭圆22162x y 中有一内接三角形ABC ,其顶点C 的坐标1,AB.当ABC △的面积最大时,求直线AB 的方程.A'O【解析】 将椭圆通过仿射变换x x y y变成圆226xy ,则 A B C ABC S△△,1A B k,C 坐标为,.∵直线OC ∥直线A B ,∴A B C OA B S S △△ 设直线A B 的方程为0x y m ,则 O 到直线AB ,A B12OA B S△3≤∴当232m ,即m OA B S △取得最大值3,此时直线A B 的方程为0xy .因此OAB S△AB 的方程为0x .练习3 (2011年顺义二模)已知椭圆2214x y 的左、右顶点分别记为A 、B .过A 斜率为1的直线交椭圆于另一点S ,在椭圆C 上的T 满足:TSA △的面积为15.试确定点T 的个数.【解析】 将椭圆通过仿射变换12x x y y变成圆224x y ,则225S AT SAT S S △△.AS : 22y x ,即240x y∴圆心到直线ASAS163∴T 到直线AS的距离为25142,∴在优弧上存在两个T 点2 T 点.综上,点T 的个数也即点T 的个数是2.练习4 (2010年宣武一模文)直线:220l x y 与椭圆2214y x 的交点为A 、B .求使PAB 的面积为12的点P 的个数;【解析】 2.练习5(2011年西城二模)设直线l 与椭圆2219x y 交于A 、B 两点,且以AB 为直径的圆过椭圆的右顶点C ,求ABC △面积的最大值.【解析】 如图,将坐标系原点平移至C ,则椭圆方程变为22319x y 即22690x x y .设直线AB 的方程为x my a ,则联立直线方程与椭圆方程有22690x my x x y a ,即266910y m yx a x a而12121y y x x ,∴6910a ,35a ,因此35CD . 将椭圆通过变换3x x y y变为圆229x y ,则13ABC A B C S S △△ O (O')B'A'D (D')C (C')164 ∵35C D ,3O C ,∴3153435A B C O A B S C D S O D△△设O 到A B 的距离为d,1122O A B S A B d d △∴当且仅当29d 时,O A B S △取得最大值92于是13128ABC O A B S S △△≤,即ABC △面积的最大值为38.例3(2011年辽宁)如图,已知椭圆的短轴为MN ,且1C 、C 这四点按纵坐标从大到小依次为【解析】 ⑴ 设2MN a ,则椭圆1C :22211e x y a a ;椭圆2C :22211e x y a a ; 231e 4BC AD. ⑵ 对椭圆1C 作仿射变换x x y ,则1C :222x y a ;对椭圆2C 作仿射变换x x ,1y y ,则2C :222x y a .BO AN EO EN BO AN k k∥211e EO EN k k设点 cos ,sin E a a (0π ),则sin cos EO k,sin cos 1EN k利用仿射变换处理弦长问题165∴设cos 1cos EO EN k y k,则cos 1cos y , 1cos 1,11y 因此 ,02,y BO AN ∥2121e,∴当0<e时,不存在;当e 时,存在.利用仿射变换可以将一些题目中“平凡”的条件转化为对解题很有利的“特殊”条件,比如:① 利用仿射变换可以改变斜率,从而可以使得某些与椭圆相关的平行四边形转化为矩形,从而简化问题;② 利用仿射变化可以将椭圆变为圆,从而可以使某些与椭圆相关的平行四边形转化为菱形,从而简化问题. 例422x y【解析】 作仿射变换,椭圆方程变为224x y ,且OM ON .(理科)四边形OM P N 为正方形,于是OP M N∴P 点的轨迹方程为圆228x y , 因此P 点的轨迹方程为228x,即22184x y .∴存在符合题意的点1F 、2F ,坐标为 2,0 .(即椭圆的两个焦点) (文科)四边形OM P N 为矩形,OP M N ∴P 点的轨迹方程为圆2220x y ,因此P 点的轨迹方程为2220x,即2212010x y .∴存在符合题意的点F ,坐标为,0.(即椭圆的右焦点). 练习1(2011年海淀一模)设直线:l y kx m (12k ≤)与椭圆22143x y 相交于A 、B 两点,以线利用仿射变换凸显隐藏几何条件166 段OA ,OB 为邻边作平行四边形OAPB ,其中顶点P 在椭圆C 上,O 为坐标原点.求OP 的取值范围.【解析】 用仿射变换椭圆转化为圆,于是平行四边形OAPB 变为菱形OA P B ,由12AB k ≤得A B k ≤.根据菱形的对角线互相垂直,于是OP k ≥,因此1P x ≤.也就是说,1P P x x ≤ 于是22222231344P P P P Px x OP x y x133,4因此OP的取值范围是,.练习2(2012年海淀一模理)已知直线1l :1y kx m 与椭圆G :2212x y 交于A 、B 两点,直线2l :2y kx m (12m m )与椭圆G 交于C 、D 两点,且AB CD ,如图所示.⑴ 证明:120m m ;⑵ 求四边形ABCD 的面积S 的最大值.【解析】 考虑用仿射变换.⑴ ABCD 为椭圆内接平行四边形,作仿射变换后变为圆内接平行四边形,为矩形.因此对角线为直径,也就是说椭圆内接平行四边形的对角线互相平分于原点,于是120m m ;⑵ 圆内接矩形当且仅当矩形为正方形时面积最大,最大值为4,于是椭圆内接平行四边形面积.【备注】也可以看作相关直线问题⑴ 设直线y kx m 与椭圆交于两点A 、B ,则联立直线与方程,有22212102k x kmx m∴22AB k22k167∴AB CD 等价于2212m m ,又12m m ,∴12m m ,即120m m⑵ 由①,AB 与CD 关于原点对称,四边形ABCD 为对称中心在原点的平行四边形.不妨设10m ,则4ABCD OABS S△21422k22211221412m k m k≤(当且仅当22112m k时取得等号). ∴四边形ABCD 的面积S 的最大值是例5Q【解析】 如图,将椭圆22182x y通过仿射变换2x x y y变成圆228x y ,则 2,2M 过M 作x 轴的垂线,垂足为H ,交圆228x y 于点N ,则易知 2,2N . ∵ 2,2N ,∴OM ON ,又OM A B ∥,∴ON A B 根据垂径定理,N 平分弧A B ,于是M N是A M B 的平分线.于是22MP M P M Q MQ k k k k ,又MH PQ ,∴MPQ △是等腰三角形,证毕.【备注】(2012年密云一模理)如图所示,已知椭圆的中心在原点,焦点在x 轴上,长轴长是短轴长的3倍,且经过点 3,1M .平行于OM 的直线l 在y 轴上的截距为m (0m ),且交椭圆于A 、B 两不同点.⑴ 求椭圆的方程; ⑵ 求m 的取值范围;⑶ 求证:直线MA 、MB 与x 轴始终围成一个等腰三角形.【解析】 ⑴ 221182x y ;168 ⑵ 设直线l :13y x m (0m ),则 2,00,2m ;⑶ 视为连线垂直问题的推广或用仿射变换均可解决.练习6(2011年四中高二期中考试)已知点 2,1M 是椭圆22182x y 上一点,直线102y x m m 与椭圆相交于A 、B 两点.求MAB 的内心的横坐标.【解析】 考虑到图形的特点与求解的问题,考虑使用仿射变换将椭圆转化为圆加以解决.在圆中,容易证明M Q 是B MA 的平分线;于是MQ 是BMA 的平分线.因此MAB 的内心的横坐标为M 的横坐标,也就是2.例6(201122x y【解析】 ⑴ 如图,作仿射变换x xC 变为圆C :223x y .∴32OP Q OPQ S S△△ 设O 到直线P Q 的距离为d ,则1322d ,解得d 于是P Q ,OP OQ ,因此2212x y ,2221x y 而222211223x y x y ,∴22221212x x x x 3,2222121223y y y y 2 .综合169⑵ 设PQ 的斜率为k ,则OM 的斜率为23k,OM PQ OM P Q333 设2249k m k ,则43m ≥.3OM PQ 52≤. ⑶∵ODE ODG OEG S S S△△△32OD E OD G OE G S S S △△△ ∴在圆C 中,D E 、D G 、E G 所对的圆心角均为90 因此,不存在满足题意的三角形.练习7 (2013北京昌平二模理)如图,已知椭圆22221x y a b(0a b )的长轴为AB ,过点B 的直线l 与x 轴垂直,椭圆的离心率e,F 为椭圆的左焦点,且1AF BF . ⑴ 求此椭圆的方程;⑵ 设P 是此椭圆上异于A B ,的任意一点,PH x 轴,H 为垂足,延长HP 到点Q 使得HP PQ . 连接AQ 并延长交直线l 于点,M N 为MB 的中点,判定直线QN 与以AB 为直径的圆O 的位置关系.【备注】设AQ 与椭圆交于点R ,则NR 与椭圆相切,此题与⑵均可以利用仿射变换解决.例7已知椭圆22143x y 上的两点A 、点.设直线PB 与椭圆相交于D ,证明:直线利用仿射变换将问题转化为几何问题170【解析】若点A 、B 为关于圆的直径HG 对称的两点,HG 所在直线上的一点P 与B 点的连线交圆于D ,则AD 与PH 交于定点E .证明如下:如图,连结AG 、GD ,设PA 与圆交于C .HG PDBECA∵G 为弧CD 和弧AB 的中点,∴AG 、DH 分别是A 和BDG 的平分线 而DG DH ,∴DG 是EDP 的平分线.于是AE DE EGAP DP GP,因此2AE DE EG AP DP GP , 而AE DE EG EH (相交弦定理),AP DP AP CP PG PH (切割线定理) 于是EG EH EG EG PG PH PG PG ,即EG PGEH PH .∵PG PH 为定值(在本例中为13),∴EGEH 为定值,E 为定点(在本例中 1,0E ).练习8 设直线l :y kx m 与椭圆2212x y 相交于M 、N 两点,F 是椭圆的右焦点,直线FM 与直线FN 的斜率互为相反数.求证:直线l 过定点,并求该定点的坐标.【解析】 直线l 过定点 2,0.本质与例题相同.练习9(2010年江苏)如图,在平面直角坐标系xOy 中,已知椭圆22195x y 的左、右顶点为A 、B ,右焦点为F .设过点 9,T m 的直线,TA TB 与此椭圆分别交于点 11,M x y 、 22,N x y ,其中0m ,10y ,20y .设9t ,求证:直线MN 必过x 轴的一定点(其坐标与m 无关).171【解析】 如下左图所示,利用坐标变换x xa y y b可以把椭圆22221x y a b 变换圆222x y a ,由于伸缩变换不改变共线以及线段长度的比,于是问题就转化为如下右图所示的:已知以AB 为直径圆O ,T 为与AB 垂直的圆外直线上任意一点,连结AT 、BT 与圆O 分别交于M 、N .求证MN 恒过定点D .x法1连结AN 、MB 并延长交于点T ,容易知道T 与T 在同一条垂直于AB 的直线上(B 为ATT △的垂心)CT'T对ABT △的割线MN ,根据梅涅劳斯定理有1AD BM T NDB MT NA ; 而AM 、NB 、T T 交于一点,根据赛瓦定理有1BM T N ACMT NA CB; 于是1AD CB DB AC ,即AD ACDB BC 为定值,因此D 为定点. 法2172 CT NM A BOD设4AC a ,TAC ,NAC ,则4cos aAT,2cos AM a ,2cos a BT ,2cos BN a ,AN AD ADN MDB AD AD DM AN AM MB MD AM DM DB MD DB MB BNADM NDB BN DB△∽△△∽△ 而AN AT ANT BMT BM BT △∽△,于是22824AD AT AM a DB BT BN a .法3PCD O BA M NT设2MOC ,2NOC ,则OC 到OP 的角为 ,以O 为极点,OC 为极径,那么直线MN 的方程为 cos ,d O MN , 即 cos cos AB 于是ODcos cos AB cos cos sin sin cos cos sin sin AB1tan tan 1tan tan AB而12TAC MAB MOB ,12NAB NOB ,∴tan TC AC ,tan tan BCBTC TC因此11BC AC OD AB BC AC,于是点D 为定点.。
仿射变换一、将坐标进行伸缩变换,实现化椭为圆b2仿射变换定理一:若经过椭圆的对称中心的直线构成的直径三角形,则两条弦的斜率乘积k AC-k BC=--a仿射变换定理二:-=-(拉伸短轴);-=-(压缩长轴).S b S a拉伸短轴后点的坐标变化:AO。
,%)T A’。
;。
,一%),横坐标不变,纵坐标拉伸一倍.b b斜率的变化:如图纵坐标拉伸了色倍,故k'=-k,由于k.-k..=-l.b b AC BCb b b2bk AC'k BC=~k AC'^k BC=——,S徵BC=一、函毗/(水平宽不变,铅垂高缩小)•a a a a压缩长轴后点的坐标变化:A(x0,y0)A'(—x0,y0),纵坐标不变,横坐标缩小'倍.a a斜率的变化:如图横坐标缩小了"倍,故k'=-k,由于k.-k RC.=-1.a b AC BCh h h ak AC,k BC=-k AC,-k BC=一~'S a ABC=检,,,(水平宽扩大,铅垂高不变).a a a b例1(2013-新课标)椭圆C:j+:=l的左、右顶点分别为A、劣,点P在C上且直线必2斜率的取值范围是[-2,-1],那么直线F&斜率的取值范围是()12~「°3"113,; B.; C.-,1; D.-,1_2'4__8'4_24例2(2016•北京)已知椭圆C:与+土=1过点A(2,0),5(0,1)两点.a b(1)求椭圆。
的方程及离心率;(2)设P为第三象限内一点且在椭圆。
上,直线PA与y轴交于点M,直线P3与x轴交于点N,求证:四边形A3NM的面积为定值.22A7例3(2014•新课标I)已知点A(0-2),椭圆E:二+二=1(。
〉力〉0)离心率为匚,F是椭圆的右a b2焦点,直线AF的斜率为全3,。
为坐标原点.3(1)求E的方程;(2)设过点A的直线/与E相交于P、。
仿射变换与透视变换1. 仿射变换1) 用途旋转 (线性变换),平移 (向量加).缩放(线性变换),错切,反转2) 方法仿射变换是一种二维坐标到二维坐标之间的线性变换,它保持了二维图形的“平直性”(直线经过变换之后依然是直线)和“平行性”(二维图形之间的相对位置关系保持不变,平行线依然是平行线,且直线上点的位置顺序不变)。
任意的仿射变换都能表示为乘以一个矩阵(线性变换),再加上一个向量(平移)的形式.公式中的m矩阵,是线性变换和平移的组合,m11,m12,m21,m22为线性变化参数,m13,m23为平移参数,其最后一行固定为0,0,1,因此,将3x3矩阵简化为2x3。
3) 举例a) 以原点为中心旋转,2x3矩阵为:[ cos(theta), -sin(theta), 0 ],[ sin(theta), cos(theta), 0 ]则x’= x * cos(theta) - sin(theta) * yy’= x * sin(theta) + cos(theta) * yb) 平移,2x3矩阵为[1,0,tx],[0,1,ty]则x’= x * 1 + y * 0 + tx = x + txy’= x * 0 + y * 1 + ty = y + ty4) 图形变换样式2. 透视变换(投影变换)1) 用途将2D矩阵图像变换成3D的空间显示效果,全景拼接.2) 方法透视变换是将图片投影到一个新的视平面,也称作投影映射.它是二维到三维再到另一个二维空间的映射。
相对于仿射变换,它提供了更大的灵活性,将一个四边形区域映射到另一个四边形区域(不一定是平行四边形).它不止是线性变换.但也是通过矩阵乘法实现的,使用的是一个3x3的矩阵,矩阵的前两行与仿射矩阵相同(m11,m12,m13,m21,m22,m23),也实现了线性变换和平移,第三行用于实现透视变换。
以上公式设变换之前的点是z值为1的点,它三维平面上的值是x,y,1,在二维平面上的投影是x,y,通过矩阵变换成三维中的点X,Y,Z,再通过除以三维中Z轴的值,转换成二维中的点。
仿射变换几何仿射变换是指在几何上保持直线、并比例保持距离的变换。
在二维空间中,一个仿射变换可以表示为以下矩阵形式:[x'] [a b c] [x] [e][y'] = [d e f] * [y] + [f][1] [0 0 1] [1] [1]其中,(x, y)是原始坐标,(x', y')是变换后的坐标,矩阵[a b c de f]是仿射矩阵。
仿射变换可以通过平移、旋转、缩放和剪切等基本变换来构成。
具体而言,1. 平移:通过添加平移向量(e, f)来将点(x, y)移动到点(x', y'),即(x', y') = (x + e, y + f)。
2. 旋转:以点(c, f)为中心,通过旋转角度θ将点(x, y)旋转到点(x', y')。
具体而言,(x', y') = (c + (x - c) * cosθ - (y - f) * sinθ, f + (x - c) * sinθ + (y - f) * cosθ)。
3. 缩放:以点(c, f)为中心,通过水平缩放比例sx和垂直缩放比例sy将点(x, y)缩放到点(x', y')。
具体而言,(x', y') = (c + (x - c) * sx, f + (y - f) * sy)。
4. 剪切:通过剪切因子a、b、c和d将点(x, y)剪切到点(x', y')。
具体而言,(x', y') = (a * x + b * y + e, c * x + d * y + f)。
通过组合这些基本变换,可以实现各种类型的仿射变换,如平移、旋转、缩放、翻转、拉伸等。
同时,仿射变换还可以应用于计算机图形学、计算机视觉等领域,用于图像处理、图像配准、人脸识别、图像校正等方面。
仿射变换————————————————————————————————作者:————————————————————————————————日期:第四章保距变换和仿射变换本章教学目的:通过本章的学习,使学生掌握保距变换和仿射变换这两类重要的几何变换,从而深化几何学的研究,并掌握解决几何问题的一个有效方法。
本章教学重点:(1)保距变换和仿射变换的定义和性质;(2)仿射变换的基本定理;(3)保距变换和仿射变换的变换公式;(4)图形的仿射分类与仿射性质。
本章教学难点:仿射变换的性质和基本定理;仿射变换的变换公式的求法。
本章教学内容:§1 平面的仿射变换与保距变换1.1――对应与可逆变换集合X到集合Y的一个映射f:X→Y是把X中的点对应到Y中的点的一个法则,即∀x∈X,都决定Y中的一个元素f(x),称为点x在f下的像。
对X的一个子集A,记f(A)={f(a)|a∈A},它是Y的一个子集,称为A在f下的像。
对Y的一个子集B,记f-1(B)={x∈X|f(x)∈B},称为B在F下的完全原像,它是X的子集。
如果f是X到Y的映射,g上Y到Z的映射,则它们的复合上X到Z的映射,记作gf: X→Z,规定为g f(x)=g(f(x)),∀x∈X.对A⊂X,gf(A)=g(f(A));对C⊂Z,(g f)-1(C)=f-1(g-1(C)).映射的复合无交换律,但有结合律。
映射f: X→X称为X上的一个变换,idX: X→X,∀x∈X,id X(x)=x,称为X的恒同变换。
对映射f: X→Y,如果有映射g:Y→X,使得g f= idX:X→X,fg=idY:Y→Y,则说f是可逆映射,称g是f的逆映射。
如果在映射f: X→Y下X的不同点的像一定不同,则称f是单射。
如果f(X)=Y,则称f是满射。
如果映射f: X→Y既是单射,又是是满射,则称f为——对应。
此时∀f-1f=id X,, ff-1= idY,于是f是可逆映射,并且f的逆映射是f-1。
一个集合X到自身的可逆映射称为X上的可逆变换。
1.2平面上的变换群平移取定平行于平面的一个向量u,规定π的变换P u:π→π为:∀A∈π,令P u AP(A)=u的点。
称P u为π上的一个平移,称向量u是P u的平移量。
(A)是使得u旋转取定π上一点O,取定角θ。
规定π的变换r:π→π为:∀A∈π,令r(A)是A饶O转角θ所得的点。
称变换r是π上的一个旋转,称O是其旋转中心,θ为转角,r是可逆变换,r-1也是以O为中心的旋转,转角为-θ。
θ=180°时,称r为关于中心O点的中心对称,此时r-1=r。
反射取定上的一条直线a,做π的变换f a:π→π为:∀A∈π,fa(A)是A关于a 的对称点.称f a为π上的一个反射,称a是它的反射轴.也fa是可逆变换,f a-1=fa.正压缩取定π上一条直线和一个正数k,做π的变换:g:π→π为:∀A∈π,令g(A)是下列条件决定的点:(1)Pg(A)与a垂直;(2)g(A)到a的距离d(g(A),a)=kd(A,a);(3)g(A)与A在的同一侧,称变换g为π上的一个正压缩,称a为压缩轴。
称k为压缩系数,g也是可逆变换。
并且g-1也是以a为压缩轴的压缩变换,压缩系数为k-1.定义4.1一个集合G,如果它的元素都是π上的可逆变换,并且满足条件:(1)G中任何元素的逆也在G中;(2)G中任何两个元素的复合也在G中,则称G是π上的一个变换群。
1.3 保距变换定义4.2平面π上的一个变换f如果满足:对π上的任意两点A,B,总有d(f(A),f(B))=d(A,B),则称f是π上的一个保距变换。
命题4.1保距变换是可逆变换.证明略保距变换f的逆f-1也是保距变换,于是平面π上的全体保距变换构成一个交换群,称为保距变换群。
1.4仿射变换定义4.3平面(空间)的一个可逆变换,如果把共线点组变为共线点组,则称为平面(空间)的一个仿射变换。
我们把平面间保持点组共线性的可逆映射称仿射映射。
位似变换取定平面π上一点O和一个不为0的实数k,规定π上的变换f:π→π为:∀P∈π令f(P)是由等式Of(P)=k O(P)决定的点。
称f是一个位似变换,称O为它的位似中心,k为位似系数。
相似变换平面的一个变换f:π→π称为相似变换,如果存在正数k,使得对π上任意两点A,B都有d(f(A),f(B))=kd(A,B),称k为f的相似比。
错切变换取定平面π上的一条直线a,并取定a的一个单位法向量n以及与a平行的一个向量u,规定变换f:π→π为: ∀P∈π令f(P)是满足等式Pf(P)=(M P.n)u的点,其中M0是a上一点,称此变换为以a为错切轴的一个错切变换。
命题4.2在仿射变换下,不共线三点的像也不共线。
推论仿射变换把直线变为直线,并保持直线的平行性.§2 仿射变换基本定理2.1 仿射变换决定的向量变换定义4.3 设f是平面π上的仿射变换,则对于任何平行于π的向量a,规定ff A f B,这里A,B是π上的点,使得(a)=()()AB=a这样,就得到全体平行于π的向量集合上的一个变换,称它为f决定的向量变换,仍记作f.从定义容易看出:a=0 〈═〉f(a)=0.定理4.1仿射变换决定的向量变换具有线性性质,即(1)∀向量a,b,f (a+b)= f(a)+f(b),f(a-b)=f(a)-f(b).(2)∀向量a,∀π∈R,πa)=πf(a).f(πa)= tf(a)则对任何非零向量b,都有f(πb)引理(1)如果对a≠0和实数π,f (=tf(b)(2)对任何a≠0,如果π>0,则t >0.推论仿射变换保持共线三点的简单比.2.2仿射变换基本定理定理4.2(仿射变换基本定理)设π是一张平面.(1)如果f:π→π是仿射变换,I=[O;e1,e2 ]是π上的一个仿射坐标系,则1I= .[f(O);f(e1),f(e2)]也是π的仿射坐标系,并且∀P∈π,P在I中的坐标和f(P)在I’中的坐标相同;(2)任取π上两个仿射坐标系I= [O; e1,e2]和1I=[ O’; e1’; e2’]规定f:π→π如下,∀P∈π,设P在I中的坐标是(x,y),令f(P)是在I’中的坐标为(x,y)的点,则f是仿射变换.2.3关于保距变换命题 4.3如果平面π上两个三角形ABC和EFG全等,则把ABC变为EFG (每个顶点变为对应顶点)的仿射变换是保距变换.推论任何保距变换都可分解为平移旋转及反射的复合.2.4二次曲线在仿射变换下的像命题 4.4 平面π上两条二次曲线Ⅰ与1I (不是空集)是同类二次曲线的充分必要条件是,存在仿射变换f,使得 f(Ⅰ)=Ⅰ′.2.5仿射变换的变积系数命题 4.5 在同一仿射变换f:π→π下,π上不同的图形(可计面积的)面积的变化率相同,即存在由变换f决定的常数k ,使得任一图形S 的像f (S)的面积是S 面积的k 倍.这个常数k 称为f 的变积系数.引理1 如果仿射变换h :π→π把某一个圆周S 变为等半径的圆周,则f 是保距变换.引理2 每个仿射变换都可分解为一个保距变换和两个正压缩的乘积.§3 用坐标法研究仿射变换3.1 仿射变换的变换公式 设f:π→π是一个仿射变换.取定π上的一个仿射坐标系I =[O ; e1 ,e2 ] ,记1I =[f (O); f(e1) ,f(e 2)设P在I 中的坐标为(x,y )则由基本定理知道,f(P)在I ’中的坐标也是(x,y).于是可通过坐标变换公式来求f(P)在I 中的坐标.记I 到I ’的过渡矩阵为 A=11122122a a a a ⎛⎫⎪⎝⎭,f(O)在I中的坐标为(b1 ,b2),则由第三章中点的坐标变换公式(3.2b ),f(P)在I中的坐标(1,x 1y)为111121121222x y x x a a b y a a b ⎧=++⎪⎨=++⎪⎩, (4.3)称此公式为仿射变换f在坐标系I中的点(坐标的)变换公式,称矩阵A 为f在坐标系I中的变换矩阵.类似可得仿射变换在坐标系I中的向量(坐标的)变换公式:1111212122x y x yx a a y a a ⎧=+⎪⎨=+⎪⎩ ,(4.4)也可用矩阵乘积形式给出11x y ⎡⎤⎢⎥⎢⎥⎣⎦=11122122a a a a ⎛⎫ ⎪⎝⎭⎥⎦⎤⎢⎣⎡y x 其中(x,y )是一个向量α在I 中的坐标,(1,x 1y)是f(α)的坐标.设一条曲线Γ在I 中的方程为F(α)=0,求其像f(Γ)的方程方法为:从公式(4.3)反解出x , y用1,x 1y表示的函数式,代入F (x,y )=0,就得到f (Γ)的方程.例4.1 已知在仿射坐标系I中,仿射变换f 的点变换公式为11435322x y x y x y ⎧=--⎪⎨=-+⎪⎩ 直线a的方程为3x+y-1=0,求f(a)的方程.解 方法1.从变换公式反解出111123163423x y y x y x ⎧=-+-⎪⎨⎪=-+-⎩代入a 的方程:3(-21x+31y-16)+(-31x+41y-23)-1=0整理后得91x -131y+72=0,于是f(a )的方程为9x-13y +72=0.方法2(待定系数法).设f(a)的方程为Ax+By+C=0,用变换公式(4.5)代人得到A 的方程A(4x-3y-5)+B(3x-2y+2)+C=0.它与3x+y-1=0都是a的方程,于是433A B +=321A B --521A B C-++- 从上式左边等式解出13A+9B=0.即A: B=9: 13,再由右边的等式求出A: C=1: 8.取A =9则B =-13,C=72,得f(A )的方程:9x -13y+72=03.2 变换矩阵的性质 引理 设1I和2I是平面π上的两个仿射坐标系,他们分别北仿射变换f 变为11I 和22I,则I到阵.1推论仿射变换f把坐标系I变为1I,则f在1I中的变换矩阵就是f在I中的变换矩阵.命题4.6如果仿射变换f,g在仿射坐标系I中的变换矩阵分别为A和B,则它们的乘积g f在I中的变换矩阵为BA.f-在I中的推论如果仿射变换f在仿射坐标系I中的变换矩阵为A,则它的逆变换1A-.变换矩阵为1命题4.7设仿射变换f在仿射坐标系I中的变换矩阵为A,I到仿射坐标1I的过渡矩H-AH.阵为H,则f在1I中的变换矩阵为1推论一个仿射变换f在不同坐标系中的变换矩阵的行列式相等.命题4.8仿射变换的变积系数等于它的变换矩阵的行列式所绝对值.3.3仿射变换的不动点和特征向量设f:π→π是仿射变换.∀P∈π,如果P在f下不动,即f(P)=P,就称P为f的一个不动点.如果非零向量u与f(u)平行,则称u为f的一个特征向量;此时有唯一实数λ,使得f(u)=λu,称λ为u的特征值.不动点和特征向量都是应用中常见的概念.3.4 保距变换的变换公式命题4.9 平面上第一类保距变换或是旋转,或是平移.命题4.10 第二类保距变换或是反射,或是滑反射§4图形的仿射分类与仿射性质4.1平面上的几何图形的仿射分类和度量分类定义4.4设Γ和1Γ是平面π上的两个几何图形,如果存在一个仿射变换f:π→π,使得f(Γ)=1Γ,则称Γ和1Γ是仿射等价的;如果存在一个保距变换f:π→π,使得f(Γ)=1Γ,则称Γ和1Γ是度量等价的.仿射等价和度量等价都是平面上的几何图形的集合中的一个“等价关系”,即它满足下列三个性质(1) 自反性. 即任何图形和自己仿射等价.(2)对称性. 即如果图形Γ和1Γ仿射等价,则1Γ和Γ也仿射等价.(3)传递性.即如果Γ和1Γ仿射等价,1Γ和2Γ仿射等价,则Γ和2Γ也仿射等价.4.2仿射概念与仿射性质几何学中有些概念是在仿射变换下不会改变的,我们把这种概念称为仿射概念.类似地,把在保距变换下不会改变的概念称为度量概念.几何图形的某种性质如果是用仿射概念刻画的,从而在仿射变换中保持不变。