单纯形替换法

改进的单纯形法迭代计算方法吴庆丰【摘要】对传统大M法进行改进，若计算检验数的表达式中含有M则只计算含有M的部分，从而简化计算，迭代过程中当人工变量由基变量变为非基变量时，直接去掉人工变量部分的表格然后继续计算，从而再一次降低计算量。

借鉴两阶段法的优点进一步给出了无需给出大M的迭代算法，此法不会破坏目标函数的一致性，而且可以避免传统大M法在利用计算机求解时由于M值的选取不当所导致的计算错误。

%Improved big-M method is presented. If expressions of the calculated test number contain M, the only portion containing M is calculated, and thereby the calculation is simplified. And when artificial variables become nonbasic variables by basic variables in the iterative calculation process, the artificial variables parts of the table can be directly removed and then the calculation is continued. Thus, the amount of computation is again reduced. Taking advantages of two-phase method, an iteration algorithm without giving the big M is further given. This method does not undermine the consistency of the objective function, and the calculation error can be avoided when using traditional big-M method combined with computer to solve, due to the improper selection of the value of M.【期刊名称】《计算机工程与应用》【年(卷),期】2014(000)018【总页数】5页(P59-62,69)【关键词】线性规划;单纯形法;大M法;两阶段法【作者】吴庆丰【作者单位】淮北师范大学数学科学学院，安徽淮北 235000【正文语种】中文【中图分类】O22单纯形法是求解线性规划的基本方法，许多文献对其不断改进。

1．搜索方法我们这里以二维为例说明搜索方法在二维情况下的单纯形有3个顶点：X GX L二维情况：三个顶点计算各点的函数值，设好点为x L, 最坏点为x H, 次坏点为x G 求除x H（最坏点）以外的其余各点的几何中心x Cx C=∑≠=nHjjxj n&01单形替换法主要有以下集中搜索方法（1）反射以x C为中心，将x H按一定比例反射，得x R;x R=x C+α( x C―x H) (通常α=1)（2）扩张若f(x R)< f(x L),则搜索方向正确，应扩张，（比最好点还要好）x E=x R+r ( x R―x C) r扩张系数r=1.2~2.0⎪⎩⎪⎨⎧≥<RL G H R R E E L G H E R E X X X X X X f X f X X X X X X f X f ,),()(,,),()(构成新的单纯形代替则以若构成新的单纯形代替则以若 （3） 收缩a) 若x R 比x L 差但比x G 好，即f(x L )< f(x R ) < f(x G )反射可行，用x R 替换x H ，新的单纯形x L x G x R b) 若x R 比x G 差但比x H 好，反射走的太远，应收缩反向距离，x K =x C +β( x R ―x C ) β收缩因子，通常β=0.5 ⎪⎩⎪⎨⎧K H K K L G H K X X X X X X X X 则不用差比若则新的单纯形好比若,,, c) 若x R 比x H 差,即反射点比最差点还差，应在x C 内部找收缩点x K ‘x K ‘= x C ―β( x C ―x H )⎪⎩⎪⎨⎧'''',,,K H K K L G H K X X X X X X X X 则不用差比若则新的单纯形好比若 （4） 压缩:若x H ，x C 方向上的所有点都比x H 差（即通过上述三种搜索方法均未找到好点），则压缩，以x L 为中心，其余各点均向x L 靠拢x j = x L ―0.5( x L ―x j ) j=0,1,…n j ≠L。

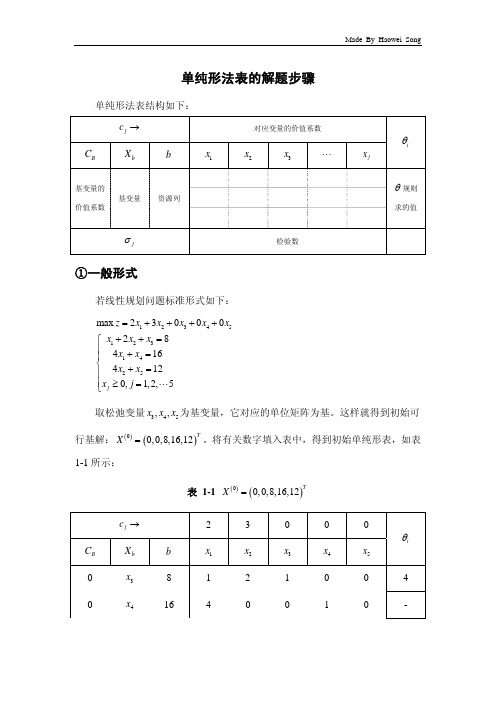
单纯形法表的解题步骤单纯形法表结构如下：j c →对应变量的价值系数i θB Cb Xb1x 2x 3x " j x基变量的价值系数基变量 资源列θ规则求的值j σ检验数①一般形式若线性规划问题标准形式如下：123451231425max 23000284164120,1,2,5j z x x x x x x x x x x x x x j =++++++=⎧⎪+=⎪⎨+=⎪⎪≥=⎩"取松弛变量345,,x x x 为基变量，它对应的单位矩阵为基。

这样就得到初始可行基解：()()00,0,8,16,12TX =。

将有关数字填入表中，得到初始单纯形表，如表1-1所示：表 1-1 ()()00,0,8,16,12TX =j c →2 3 0 0 0i θB C b X b1x 2x 3x 4x 5x0 3x 8 1 2 1 0 0 4 04x16 4 0 0 1 0 -5x12 0 [4] 0 0 1 3j σ2 3 0 0 0若检验数均未达到小于等于0，则对上表进行调整。

选择上表中检验数最大的列，该列对应的非变量为入基变量；再应用θ规则该列对应的各基变量对应的θ值，选出其中最小的一行，该行对应的基变量为出基变量。

修改单纯形表，对各行进行初等变换，确保基变量组成的矩阵为单为矩阵。

修改后的单纯形表如表1-2所示：表 1-2 ()()10,3,2,16,0TX =检验数12,0σσ>，则进行继续调整，调整后的单纯形法表如表1-3所示：表 1-3 ()()22,3,0,8,0TX =表1-3中， 50σ>，则继续进行调整，调整结果如表1-4所示：表 1-4 ()()34,2,0,0,4TX =检验数0j σ≤，这表示目标函数值已不可能再增大，于是得到最优解：()()3*4,2,0,0,4TX X ==*14z =②带人工变量现有线性规划问题：12312312313123min 321142321,,0z x x x x x x x x x x x x x x =−++−+≤⎧⎪−++≥⎪⎨−+=⎪⎪≥⎩ 将上述线性规划问题用大M 法求解，在约束条件中加入松弛变量4x ，剩余变量5x ，人工变量6x ，7x 得到：1234567123412356137min 300211423210,1,2,,7j z x x x x x Mx Mx x x x x x x x x x x x x x j =−++++++−++=⎧⎪−++−+=⎪⎨−++=⎪⎪≥=⎩"其中，M 是一个任意大的正数。

一维搜索:1精确一维搜索精确一维搜索可以分为三类：区间收缩法、函数逼近法（插值法）、以及求根法。

区间收缩法：用某种分割技术缩小最优解所在的区间(称为搜索区间)。

包括：黄金分割法、成功失败法、斐波那契法、对分搜索法以及三点等间隔搜索法等。

优化算法通常具有局部性质，通常的迭代需要在单峰区间进行操作以保证算法收敛。

确定初始区间的方法：进退法①已知搜索起点和初始步长；②然后从起点开始以初始步长向前试探，如果函数值变大，则改变步长方向；③如果函数值下降，则维持原来的试探方向，并将步长加倍。

1.1黄金分割法：黄金分割法是一种区间收缩方法(或分割方法)，其基本思想是通过取试探点和进行函数值比较，使包含极小点的搜索区间不断缩短以逼近极小值点。

具有对称性以及保持缩减比原则。

优点：不要求函数可微，除过第一次外，每次迭代只需计算一个函数值，计算量小，程序简单；缺点：收敛速度慢；函数逼近法（插值法）：用比较简单函数的极小值点近似代替原函数的极小值点。

从几何上看是用比较简单的曲线近似代替原的曲线，用简单曲线的极小值点代替原曲线的极小点。

1.2牛顿法：将目标函数二阶泰勒展开，略去高阶项后近似的替代目标函数，然后用二次函数的极小点作为目标函数的近似极小点。

牛顿法的优点是收敛速度快，缺点是需要计算二阶导数，要求初始点选的好，否则可能不收敛。

1.2抛物线法：抛物线法的基本思想就是用二次函数抛物线来近似的代替目标函数，并以它的极小点作为目标函数的近似极小点。

在一定条件下，抛物线法是超线性收敛的。

1.3三次插值法：三次插值法是用两点处的函数值和导数值来构造差值多项式，以该曲线的极小点来逼近目标函数的极小点。

一般来说，三次插值法比抛物线法的收敛速度要快。

精确一维搜索的方法选择：1如目标函数能求二阶导数：用Newton法，收敛快。

2如目标函数能求一阶导数：1如果导数容易求出，考虑用三次插值法，收敛较快；2对分法、收敛速度慢，但可靠；3只需计算函数值的方法：1二次插值法, 收敛快，但对函数单峰依赖较强；2黄金分割法收敛速度较慢，但实用性强，可靠；4减少总体计算时间：非精确一维搜索方法更加有效。

三、单纯形法的解题步骤第一步：作单纯形表.）（1）把原线性规划问题化为标准形式；）（2）找出初始可行基，通常取约束方程组系数矩阵中的单位矩阵；）（3）目标函数非基化；）（4）作初始单纯形表.第二步：最优解的判定.(1) 若所有检验数都是非正数，即，则此时线性规划问题已取得最优解.(2) 若存在某个检验数是正数，即，而所对应的列向量无正分量，则线性规划问题无最优解.如果以上两条都不满足，则进行下一步.第三步：换基迭代.，并确定所在列的非基变量为进基变量.（1）找到最大正检验数，设为（2）对最大正检验数所在列实施最小比值法，确定出主元，并把主元加上小括号.主元是最大正检验数所在列，用常数项与进基变量所对应的列向量中正分量的比值最小者；替换出基变量，从而得到新的基变量.也就是主元所在（3）换基：用进基变量（4）利用矩阵的行初等变换，将主元变为1，其所在列其他元素都变为零，从此得到新的单纯形表；（5）回到第二步，继续判定最优解是否存在，然后进行新一轮换基迭代，直到问题得到解决为止.例3 求.解（1）化标准型：令，引进松弛变量，其标准型为求（2）作单纯形表：在约束方程组系数矩阵中的系数构成单位矩阵，故取为基变量，目标函数已非基化了，作初始单纯形表并“换基迭代”（见表6.8）.表 6.8（3）最终结果：此时检验数均为非正数，线性规划问题取得最优解，最优解为标函数取得最优值.目性规划问题的最优解为：.原线目标函数的最优值为14，即.例4 用单纯形方法解线性规划问题.求.解此数学模型已是标准型了，其中约束方程含有一个二阶单位矩阵（1、2行，3、4列构成），取为基变量，而目标函数没有非基化.从约束方程找出，,代入目标函数, 经整理后，目标函数非基化了.作单纯形表，并进行换基迭代（见表6.9）.最大检验数，由最小比值法知：为主元，对主元所在列施以行初等变换，基变量出基，非基变量进基.表 6.9目前最大检验数，其所在列没有正分量，所以该线性规划问题没有最优解.例5用单纯形方法解线性规划问题.求解此数学模型已是标准型了，其中约束方程含有一个二阶单位矩阵，取为基变量，而目标函数没有非基化.从约束方程找出，,代入目标函数，经整理得,目标函数已非基化.作单纯形表，并进行换基迭代(见表6.10).最大检验数，由最小比值法知：为主元，对主元所在列施以行初等变换，基变量出基，非基变量x2进基，先将主元化为1，然后再将主元所在列的其他元素化为零.表 6.10至此，检验数均为非正数，故得基础可行解.原问题的最优解为：.最优值为6，即.如果我们再迭代一次，将基变量出基，非基变量进基（见表6.11）.表 6.11可得到另一个基础可行解,原问题的最优解为：，最优值仍为6，说明该线性规划问题有无穷多最优解，其最优解均为6.如何知道线性规划问题有无穷多最优解呢？这主要反映在单纯形表中.如果非基变量所对应的检验数为0，我们可对此列继续进行换基迭代，就可以得到另一个基础可行解.以此作下去，可得到许多基础可行解，即相对应的最优解有无穷多个.（4） 011 0。

三、单纯形法的解题步骤第一步：作单纯形表.）（1）把原线性规划问题化为标准形式；）（2）找出初始可行基，通常取约束方程组系数矩阵中的单位矩阵；）（3）目标函数非基化；）（4）作初始单纯形表.第二步：最优解的判定.（1）若所有检验数都是非正数，即，则此时线性规划问题已取得最优解.（2）若存在某个检验数是正数，即，而所对应的列向量无正分量，则线性规划问题无最优解.如果以上两条都不满足，则进行下一步.第三步：换基迭代.（1）找到最大正检验数，设为，并确定所在列的非基变量为进基变量.（2）对最大正检验数所在列实施最小比值法，确定出主元，并把主元加上小括号主元是最大正检验数所在列，用常数项与进基变量所对应的列向量中正分量的比值最小者；（3）换基：用进基变量替换出基变量，从而得到新的基变量.也就是主元所在列的非基变量进基，所在行的基变量出基；（4）利用矩阵的行初等变换，将主元变为1，其所在列其他元素都变为零，从此得到新的单纯形表；（5）回到第二步，继续判定最优解是否存在，然后进行新一轮换基迭代，直到问题得到解决为止.例3 求.解（1）化标准型：令，引进松弛变量，其标准型为求（2）作单纯形表：在约束方程组系数矩阵中的系数构成单位矩阵，故取为基变量，目标函数已非基化了，作初始单纯形表并“换基迭代” （见表 6.8）.表 6.81、2行，3、4 列 3） 最终结果：此时检验数均为非正数，线性规划问题取得最优解，最优解为目标函数取得最优值 .原线性规划问题的最优解为：.目标函数的最优值为 14，即.例 4 用单纯形方法解线性规划问题解 此数学模型已是标准型了，其中约束方程含有一个二阶单位矩阵（ 构成），取 为基变量，而目标函数没有非基化 .从约束方程找出，,代入目标函数,经整理后，目标函数非基化了 .作单纯形表，并进行换基迭代（见表 6.9） .最大检验数 ，由最小比值法知： 为主元，对主元所在列施以行初等变 换，基变量 出基，非基变量 进基 .量，x 1 x 2 x 3 x 4 常数x 31 -1 1 0 2x 4-3 (1) 0 1 4 S2 3 0 0 0x 3-2116x 2-3 1 0 1 4 S11-3126.9目前最大检验数 ，其所 在列没有正分量，所以该线性规划问题没有最优解例 5 用单纯形方法解线性规划问题 .求为基变解 此数学模型已是标准型了， 其中约束方程含有一个二阶单位矩阵， 取 而目标函数没有非基化 .从约束方程找出 表，,代入目标函数，经整理得,目标函数已非基化.作单纯形表，并进行换基迭代（见表 6.10）.最大检验数，由最小比值法知：为主元，对主元所在列施以行初等变换，基变量出基，非基变量x2进基，先将主元化为1，然后再将主元所在列的其他元素化为零.表 6.10至此，检验数均为非正数，故得基础可行解.原问题的最优解为：.最优值为6，即.如果我们再迭代一次，将基变量出基，非基变量进基（见表 6.11）表 6.11可得到另一个基础可行解,原问题的最优解为：，最优值仍为6，说明该线性规划问题有无穷多最优解，其最优解均为 6.如何知道线性规划问题有无穷多最优解呢？这主要反映在单纯形表中.如果非基变量所对应的检验数为0，我们可对此列继续进行换基迭代，就可以得到另一个基础可行解.以此作下去，可得到许多基础可行解，即相对应的最优解有无穷多个.如有侵权请联系告知删除，感谢你们的配合！。

最小化问题单纯形法求解步骤
最小化问题单纯形法求解步骤如下:
1.初始化:选择一个初始可行解，并将其带入目标函数中，计算出初始的目标函数值。

2.检查最优性:如果当前目标函数值已经达到最小，则停止迭代，当前解即为最优解。

否则，进入下一步。

3.迭代:根据当前解，通过单纯形法进行迭代，找到一个新的可行解。

4.更新解:用新的可行解替换原来的解，并带入目标函数中，计算出新的目标函数值。

5.返回步骤2，重复执行，直到找到最优解或达到预设的迭代次数。

以上是求解最小化问题的单纯形法的基本步骤，具体实现时可能还需要考虑一些细节问题，比如初始解的选择、迭代方向和步长的确定等。

最优化原理与方法首先讲几个问题：1>本部分以讲最优化原理和方法为主，联系金属加工工艺(轧钢)生产为辅。

因为最优化原理与方法不仅用于金属加工(轧钢生产)，而且适用于国民经济的各个部门。

2>最优化（原理）是近化应用数学的一个新的分支。

最优化主要是研究在给定的条件下，如何做出最好的决策去完成所给的任务。

本门课程的基础是微积分和线性代数，本门课程的计算工具是电子计算机。

因为用的数学知识和证明较多，我们在讲课中力求深入浅出，对有些证明我们予以省略，这一方面是由于学时有限，另一方面不要用过多的证明冲淡我们对方法的掌握，我们的重点是“实用”。

但要求对一些基本概念要有清晰的了解。

3>主要参考书是“轧制变形规程优化设计”(刘战英，冶金工业出版社)。

参考书是“最优化原理与方法”（东北工学院，薛嘉庆，冶金工业出版社）。

本书的规定学时是70学时，所以我们不能全讲，只讲其中一部分，有些内容还是这本书没有的。

另一本参考书是“最优化技术基础”（范鸣玉、张莹，清华大学出版社）4>学习方法a、认真听课，认真做笔记，基本概念和基本方法一定要掌握，要及时复习。

b、认真完成作业c、上机操作5>考核方式a、作业完成情况b、笔试（闭卷6>学习目的对优化技术入门，能编制简单的优化程序，最好能在毕业设计和论文中加以应用。

1最优化问题与数学预备知识1.1引言1.1.1什么是最优化问题做一切工作，我们总想从一切可能的方案中选出最优的方案，这就是最优化问题如1）安排生产计划方面，如何在现有人力、物力条件下，合理安排产品生产，使总产值为最高：2）产品设计方面，工字钢（截面抗弯能力，宽高比或面模量wx/f）机械零件；3）工厂布局、物资调动方面；4）配料方面，如何合理配料，在保证质量前提下使成本最低；5）自动控制中参数的设定：如轧钢自动控制系统中连轧机各架轧机压下量的设定；在坯料厚度H和成品限制条件都能满足的情况下，如何分配各架轧机的压下量，使达到最优工作状态；等等，由此可见，在各生产、科研领域中普遍存在着最优化问题。

单纯形法的一般描述和求解步骤：一般的线性规划问题的求解有以下几个步骤。

(1)确定初始基本可行解。

为了确定初始可行解，首先要找出初始可行基。

设一线性规划问题为⎪⎩⎪⎨⎧=≥==∑∑==nj xj b x P x c Z n j j j nj jj ,,2,1,0max 11（1-14）可分两种情况讨论。

1.若),,2,1(n j P j =中存在一个单位基，则将其作为初始可行基：⎪⎪⎪⎪⎪⎭⎫⎝⎛==100010001),,,(21m P P P B 2.若),,2,1(n j P j =中不存在一个单位基，则人为的构造一个单位初始基。

关于这个方法将在下面提到。

(2)检验最优解。

得到初始基本可行解后，要检验该解是否最优解。

如果是最优解，则停止运算；否则转入（3）基变换。

下面给出最优性判定定理。

一般情况下，经过迭代后可以得到以非基变量表示基变量的表达式∑+=='-'=nm j j iji i m i x ab x 1),,2,1(,(1-15)将式（1-15）代入式（1-14）的目标函数，整理后得j nm i ni ij i jmi i i x a c cb c Z ∑∑∑+==='-'+'=111)(max令∑='=m i i i b c Z 10,∑=+==mi ji i j n m j a c Z 1),,1(,于是j nm j j j x Z c Z Z ∑+=-+=10)(max再令),,1(,n m j Z c j j j +=-=σ则得到以非基变量表示的目标函数的表达式jnm j jx Z Z ∑+=+=10max σ由以上推导可得出下列最优解的判定定理。

(1)最优解的判定定理：若T m b b b X )0,,0,,,,(21)0( '''=为对应于基B 的一个基本可行解，且对于一切n m j ,,1 +=有0≤j σ，则)0(X 是最优解，称j σ为检验数。

1．搜索方法我们这里以二维为例说明搜索方法在二维情况下的单纯形有3个顶点：X GX L二维情况：三个顶点计算各点的函数值，设好点为x L, 最坏点为x H, 次坏点为x G 求除x H（最坏点）以外的其余各点的几何中心x Cx C=∑≠=nHjjxj n&01单形替换法主要有以下集中搜索方法（1）反射以x C为中心，将x H按一定比例反射，得x R;x R=x C+α( x C―x H) (通常α=1)（2）扩张若f(x R)< f(x L),则搜索方向正确，应扩张，（比最好点还要好）x E=x R+r ( x R―x C) r扩张系数r=1.2~2.0⎪⎩⎪⎨⎧≥<RL G H R R E E L G H E R E X X X X X X f X f X X X X X X f X f ,),()(,,),()(构成新的单纯形代替则以若构成新的单纯形代替则以若 （3） 收缩a) 若x R 比x L 差但比x G 好，即f(x L )< f(x R ) < f(x G )反射可行，用x R 替换x H ，新的单纯形x L x G x R b) 若x R 比x G 差但比x H 好，反射走的太远，应收缩反向距离，x K =x C +β( x R ―x C ) β收缩因子，通常β=0.5 ⎪⎩⎪⎨⎧K H K K L G H K X X X X X X X X 则不用差比若则新的单纯形好比若,,, c) 若x R 比x H 差,即反射点比最差点还差，应在x C 内部找收缩点x K ‘x K ‘= x C ―β( x C ―x H )⎪⎩⎪⎨⎧'''',,,K H K K L G H K X X X X X X X X 则不用差比若则新的单纯形好比若 （4） 压缩:若x H ，x C 方向上的所有点都比x H 差（即通过上述三种搜索方法均未找到好点），则压缩，以x L 为中心，其余各点均向x L 靠拢x j = x L ―0.5( x L ―x j ) j=0,1,…n j ≠L。