下载文档原格式
第二章常用统计参数第二章常用统计参数用参数来描述一组变量的分布特征，便于我们对数据分布状况进行更好的代表性的描述，也有利于我们更好地了解数据的特点。
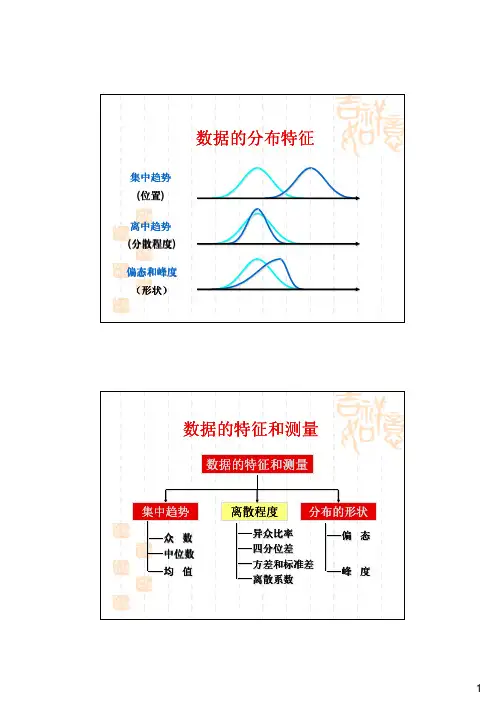
常见的统计参数包括三类：集中量数、差异量数、地位量数（相对量数X相关量数。
描述统计的指标通常有五类。
第一类集中量数：用于表示数据的集中趋势，是评定一组数据是否有代表性的综合指标，比如平均数、中数、众数等。
概述［不背］第二类差异量数：用于表示数据的离散趋势，是说明一组数据分散程度的指标，比如方差、标准差、差异系数等。
第三类地位量数：是反映个体观测数据在团体中所处位置的量数，比如百分位数、百分等级和标准分数等。
第四类相关量数：用于表示数据间的相互关系，是说明数据间关联程度的指标，比如积差相关、肯德尔和谐系数、①相关等。
第五类：是反映数据的分布形状，比如偏态量和峰度等（不作介绍I第一节集中量数（一）集中量数的定义（种类、作用）［湖南12名］描述数据集中趋势的统计量数称为集中量数。
集中量数能反映大量数据向某一点集中的情况。
常用的集中量数包括算术平均数、加权平均数、几何平均数、中数、众数等等，它们的作用都是用于度量次数分布的集中趋势。
（二）算术平均数（平均数、均数）（一级）简述算术平均数的定义和优缺点。
（1）平均数的含义算术平均数可简称为平均数或均数，符号可记为M。
算术平均数即数据总和除以数据个数，即所有观察值的总和与总频数之比。
只有在为了与其他几种集中.数洞区别时,如几何平均数、调和平均数、加权平均数，才全称为算术平均数。
如果平均数是由变量计算的,就用相应的变量表示，如又匕算术平均数是用以度量连续变量次数分布集中趋势及位置的最常用的集中量数，在一组数据中如果没有极端值, 平均数就是集中趋势中最有代表性的数字指标，是真值的最佳估计值。
（2）平均数的优缺点简述算术平均数的使用特点［含优缺点］算术平均数优点①反应灵敏。
观测数据中任1可一个数值或大或小的变化，甚至细微的变化，在计算平均数时，都能反映出来。
《考试统计学》课程考试大纲Ⅰ课程性质与设置目标一、课程的性质和特点考试统计学是研究大量考试现象的数量表现和数量关系的一门方法论科学，一种在事物的质与量的密切联系中主要从数量方面揭示考试客观规律的科学工具。
《考试统计学》以此为依据和目的，论述了考试统计学的基本理论，阐述了统计描述、统计推断、统计设计等方面的知识。
它为教育、劳动、人事等各级各类考试管理工作者和考试研究人员系统学习考试统计学知识，全面掌握考试信息资料采集、整理与分析的方法与技术，进一步提高考试管理水平和考试科研能力服务。
考试统计学与各有关相邻学科比较，其特点主要表现在：学科研究的实证性、数量关系的总体性、性质区分的规定性、现象测量的复杂性。
二、课程的基本要求本课程应达到的总体目标是：理解考试统计的基本概念和原理，掌握统计描述和统计推断以及统计设计的基本内容，为日后在工作中开展考试统计工作和考试统计研究奠定知识基础和能力基础。
三、课程与相关课程的关系考试管理专业的学生学习本课程应具备教育学、教育统计学、教育测量与评价学方面的知识。
因此本专业这门课程的先修课程是《教育学》、《统计分析概论》、《教育统计学》和《教育测量与评价》。
上述这些课程从内容上奠定了考试统计学的知识基础。
对于已具备考试管理专业专科水平的考生来说，本课程的重点是统计描述、统计推断、统计设计部分，难点是统计设计部分。
Ⅱ课程内容与考核目标（考核知识点、考核要求）第一章绪论一、学习目的和要求通过本章的学习，要牢固掌握统计的涵义，了解统计学的内容，深入理解考试统计学的对象和特点及其研究方法，领会学习考试统计学的意义和注意要点。
二、课程内容第一节统计的涵义和统计学内容（一）关于统计统计的概念。
统计概念所涵盖的三方面的关系。
（二）统计学内容统计学内容的三个组成部分。
各组成部分的含义及内容。
三者的关系。
第二节考试统计学的对象和特点（一）考试统计学的研究对象关于考试现象的数量表现。
关于考试现象的数量关系。
集中参数法名词解释
集中参数法是一种统计学中常用的方法，用于估计多个参数的值。
在集中参数法中，我们假设总体分布属于某个已知的参数化分布，然后利用样本数据对这些参数进行估计。
具体而言，集中参数法通过最大似然估计或最小二乘估计等方法，从样本数据中推断出总体参数的值。
这些参数可以代表总体的
均值、方差、比例等特征。
集中参数法的优点是能够通过样本数据对总体参数进行估计，
从而通过样本推断总体的特征。
它具有较好的数学性质和统计性质，并且通常在大样本情况下具有较好的效果。
然而，集中参数法也有一些限制。
首先，它要求总体分布属于
某个已知的参数化分布，这在实际问题中可能并不成立。
其次，集
中参数法对样本数据的分布和总体分布有一定的假设，如果这些假
设不满足，估计结果可能会有偏差。
总的来说，集中参数法是一种常用的统计估计方法，通过对样
本数据进行分析，可以推断出总体参数的估计值。
它在实践中有着广泛的应用，并且在合适的条件下可以提供可靠的估计结果。
第3章 集中量数与差异量数3.1 复习笔记一、集中量数集中量数又称集中趋势，是体现一组数据一般水平的统计量。
它能反映频数分布中大量数据向某一点集中的情况。
（一）算术平均数1．含义算术平均数（mean ）是最常用的，也是最容易理解的一个集中量数指标。
算术平均数是所有观察值的总和与总频数之商，也简称为平均数、均值或者均数。
可以用μ来表示；如果想表示变量X 的平均数，可以表示为X 。
2．计算公式假设X 1，X 2，…，X N 代表各次观测值，N 为观察的总频数，则其算术平均数为：123N X +X +X ++X =Nμ⋅⋅⋅ 记作： N 11=N i i X μ=∑ 其中，∑表示连加，1N i =∑表示从1i =到i N =的所有观测值i X 的总和。
3．性质（1）数据中如果每一个数据都加上一个常数C ，则算术平均数也需要加上C ，即∑=+=+ni C X C X n 1)(1 （2）数据中如果每一个数据都乘以一个常数C ，则算数平均数也需要乘以C ，即∑=⋅=⋅n i C X C X n 1)(1 （二）中数中数（median ）又称为中位数，它将数据分为数目相等的两半，其中一半的值比它小，另外一半的值比它大，等价于百分位数是50的那个数。
如果将所有数据按照大小顺序进行排列，那么中数正好位于正中间。
中数用M d 表示。
对于一个分布而言，中数将其分为大小相同的两个组。
对于没有经过处理的原始数据，需要先将所有数据按照大小顺序排成一个数列。
以下三种情况，中数有各自不同的求法。
1．数列的总个数为奇数假设数列共包含有n 个数（n 为奇数），如果处于数列中间的数跟相邻的值都不相等，则第21+n 个数就是这n 个值的中数。
2．数列的总个数为偶数如果n 是偶数，那么数列之中没有一个相应的值将该数列分成相等的两半，则取位于中间的两个数（第2n 和第12+n 个值）的平均数作为中数。
3．分布的中间有相等的数如果按照大小顺序排列好之后，位于数列中间的数与其相邻的数有相等的情况，则要进行一定的处理。
1第四章集中量数•定义：表示一组数据集中趋势的指标，或表示一组数据的典型情况。
•分类：• 1.算术平均数• 2.中数• 3.众数• 4.加权平均数• 5.几何平均数•6.调和平均数2一、算术平均数（样本用X ，M ；总体用U ）•（一）计算方法•（二）平均数的优缺点优点：（1）反应灵敏。
（2）确定严密。
•（3）简明易解。
（4）计算简单。
•缺点：（1）易受极端数据的影响。
•（2）数据模糊不清时，无法计算。
•3二、加权平均数•计算公式：∑∑=iii wWX W M •W 是权数，X 是原始分数计算加权平均数省区代码人数 平均分数1 627 982 268 603 400 824 670 965 411 806 314 657 610 968 500 88 ∑3800 665某课题组在8个省区进行一项调查，各省区的取样人数和平均数见下表，求该项调查的总平均数•解：A ：若果不加权，仅用八个省份的平均分数之和除以8，便可得到97.8638003304963800885006026898627==⨯+⋅⋅⋅+⨯+⨯=W M 13.838665==W M B ：A ，B 两种方法计算得到的平均值差异较大。
哪个正确？为什么？答：用A 方法计算的平均数不正确，实质上是假定每个省区的取样人数相等，这不符合实际情况6加权平均数的应用•选拔考试时，不同科目的考试分数最终合成总分时，可根据每个科目的重要性，赋予不同的权重。
•一题多解时，可赋予不同权重。
•难易度不同的几次考试，计算总成绩时可赋予不同权重。
•同一个题目让不同年龄的学生做时，应考虑权重。
•由各小组平均分计算总平均数是应用加权平均数的特例。
三、中数与众数中数（M d ）是按顺序排列在一起的一组数据中居于中间位置的数。
该数可能是数据中的某一个，也可能根本不是原有的数。
求中数的方法1.数据中无重复数值的情况（1）数据个数为奇数（2）数据个数为偶数2.数据中有重复数据的情况（1）重复值没有位于中间（2）重复数目位于中间，数据的个数为奇数（3）重复数目位于中间，数据的个数为偶数d N 12M =X +•求中数的方法•首先将数据按其取值大小排序，找出位于中间的那个数就是中数。
第2章常用统计参数【学习目标】1．了解各种集中量数、差异量数和地位量数的概念、性质和作用，理解各种量数的适用条件及特点。
2．识记相关、散点图及相关系数的概念与彼此之间的关系。
3．掌握各种量数的计算方法，并能够熟练使用各种量数对测量数据的数据特征进行描述。
4．掌握各种常见相关分析方法的适用条件及计算方法。
2.1复习笔记一组变量的次数分布，一般至少有以下两个方面的基本特征：中心位置：用以度量一组数据的集中趋势，描述它们的中心位于何处，故对其数量化描述称为位置度量数或集中量数。
离散性：反映一组数据的分散程度，即次数分布的离散程度。
对其数量化描述称为次数分布变异特性的度量或差异量数。
中心位置相同的次数分布，其离散程度不一定相同。
对任何一个已知的次数分布，均可以计算出反映上述统计特征的量数。
在教育与心理统计中，总体统计特征的量数称为参数，用希腊字母表示，如μ，σ2，ρ等；样本统计特征的量数称为统计量，用英文字母表示，如X，S2，r等。
一、集中量数集中量数是指描述数据集中趋势的统计量，包括算术平均数、加权平均数、几何平均数、中数，等等，其作用都是用于度量次数分布的集中趋势。
（一）算术平均数算术平均数（简称平均数、均数）是用以度量连续变量次数分布集中趋势的最常用的集中量数。
1．总体平均数与样本平均数（1）总体平均数如果一个总体X 包含N 个元素，x i 是这个总体中的第i 个元素，则称x i 为第i 次观测值，那么对x 来讲，该总体的算术平均数被定义为：11=Nii x N μ=∑式中：μ——总体算术平均数；N——总体容量；i x ——第i 次观测值。
（2）样本平均数当无法对总体进行全面观测时，对于样本X ，其算术平均数被定义为:11n i i X x n =∑式中：X ——样本平均数；n ——样本容量。
2．加权平均数若已知各组平均数和各组人数，要求总的平均数时，则要用加权平均数的方法，其计算公式为:式中：——总平均数（或加权平均数）；12,,,k n n n …——各组人数；12,k ,X X X …，——各组平均数；12t k n n n n =+++…——总人数。
【课程讲义】第三章集中量数【教学目标】明确一批数据的特征包括两个方面的内容：集中趋势、离散性；明确集中量数是描述数据集中趋势的量数，可以作为一批数据的代表值；明确算术平均数是所有集中量数中运用最广泛、最优的量数；明确各种集中量数的含义、计算方法、使用条件、性质及优缺点。
【学习方法】了解、理解、计算与应用。
【重点难点】算术平均数的概念及适用条件；算术平均数的计算方法；中位数的概念及适用条件；中位数的计算方法。
【讲义内容】前一章所讲的统计分组、统计表、统计图等，只是对研究工作中所获得的数据进行初步整理，其目的是对数据的性质、分布特征、差异情况及数据的一般规律有一直观和形象的认识。
因此说这一步还不是应用统计方法的步骤。
为了进一步发现和表示一组数据的规律性，需要计算出一些能够反映这组数据的统计特征的数字——称为统计量或特征数。
对于一组数据来讲，最常用的统计量有两类。
一类是表现数据集中性质或集中程度的，另一类是表现数据分散性质或分散程度的。
数据的集中情况指一组数据的中心位置。
集中趋势的度量，即确定一组数据的代表值。
描述数据集中情况的统计量有多种，包括算术平均数、中数、几何平均数等。
由于这些统计量的作用在于度量数据的集中趋势，因此它们都称为集中量数。
本章主要介绍几种常用的集中量数。
集中量数只描述数据的集中趋势和典型情况，它还不能说明一组数据的全貌。
数据除典型情况之外，还有变异性的特点。
对于数据变异性即离中趋势进行度量的一组统计量，称作差异量数，这些差异量数有方差、标准差、全距、平均差、四分差及各种百分差等等，下一章中将对常用的差异量数进行介绍。
第一节 算术平均数一、算术平均数的概念和适用条件（一）概念算术平均数一般简称为平均数或均数（Mean ）。
只有在与其他几种集中量数如几何平均数、加权平均数相区别的时候，才把它叫做算术平均数。
如果平均数是由X 变量计算的，就记为X （读作X 杠），若由Y 变量求得，则记为Y 。
研究：集中量数、差异量数、地位量数集中量数、差异量数、地位量数三种数据特征值的含义及包括的主要内容⼀、集中量数从次数分布表上可以看出，分布在各组的次数有多有少，但⼤部分数据趋向于中间的某⼀点。
这种向某点集中的趋向叫做集中趋势。
代表集中趋势的量数叫做集中量数。
集中量数⼜称代表值，它有两种功⽤。
（1）第⼀，可以⽤来描述和代表研究对象的⼀般⽔平，并为进⼀步统计分析打下基础。
（2）第⼆，⽤它与同质的另⼀研究对象作⽐较。
例如，就⼀个班来说，它是全班分数的代表，可以⽤它来代表这⼀班学⽣的程度和⽔平，并能⽤它与别的同类班作⽐较。
集中量数主要有：算术平均数、中数、众数、加数平均数和⼏何平均数等。
其中教育科学研究结果的处理中应⽤最多的是算术平均数。
⼆、差异量数差异量数是表⽰⼀组数据的差异情况或离散程度的量数，它反映数据分布的离中趋势。
集中量数的代表性如何，是要由差异量数来表明的。
（1）差异量数愈⼤，集中量数的代表性愈⼩；差异量数愈⼩，则集中量数的代表性愈⼤。
（2）差异量数⼀般包括：全距、平均差、四分差、标准差和⽅差。
其申以标准差和⽅差最为常⽤。
三、地位量数前⾯介绍的集中量数和差异量数都是描述样本或总体的整体特征的量数；⽽地位量数则是描述单个数据在样本或总体中的位置的，也称相对位置量数。
常⽤的地位量数主要有百分等级和标准分数。
（1）百分等级百分等级是指某观测值以下的个数与观测值总个数之⽐的百分数。
⽤符号P表⽰。
百分等级具有意义明确，容易理解，计算简便等优点，但是它只是⼀个顺序变量，不能进⾏代数运算，这给进⼀步分析⼯作带来困难。
（2）标准分数为解决百分等级不能进⾏代数运算的困难，有⼀种更为常⽤的地位量数，就是标准分数，⼜叫“基分数”或“Z分数”。
原⽂链接为https:///tiku/10609489.html补充：标准分数的计算⽅法：Z=（样本值-平均值）/标准差区别：分⼦为1的分数称为单位分数。
集中量数名词解释
集中量数名词指的是一类由文字或符号组成的表示数量的词语，它们能够反映出确定事物的数量。
集中量数名词具有明确的代表数量和物质量的含义，它不仅可以表示物质的数量，还可以用来指代抽象的概念。
集中量数名词在日常交流中得到了广泛的运用。
集中量数名词主要分为可数名词和不可数名词两大类，其中可数名词又被称为确定数量名词，指的是能够用一个汉字数字或者一个阿拉伯数字来表示具体数量的词语，它们可以通过加上序数词来表示物质数量的顺序，如“一只”、“第二个”等。
不可数名词也称作集体名词，指的是因为表示的是抽象概念，所以不能用汉字或者阿拉伯数字来表示具体的数量，如“收入”、“时间”等。
可数名词和不可数名词的使用是有规律的，用可数名词表示的是个别的事物或者是可以细分的量，如“一只狗”、“三朵花”；而不可数名词表示的是不可以细分的量，如“污水”、“人类的希望”。
在使用集中量数名词的过程中，我们还要注意一些具体的写作技巧，比如可数名词在使用时常用来表示总数，如“七位老师”；而不可数名词则可以用来表示平均数，如“每方草地上平均有十几只鸟”。
集中量数名词无论在文学、商务书面交流，还是日常生活中，都有着广泛的应用。
它能够准确表述出我们所想要表达的数量，起到表明大致范围和明确具体情况的作用。
对于对集中量数名词的使用，我们要把握使用的规律，不断的锻炼，这样才能正确准确的表达出自己想要表达的意思。
总之，集中量数名词拥有广泛的应用范围，不但可以用来表示物质客观世界中的数量，也可以用来指代较为抽象的概念，它的准确性能极大的提高文字表达的精准性。
我们要充分利用集中量数名词的特性，学会合理的使用这些词语，以实现有效的文字表达。
