平行六面体与长方体
- 格式:doc
- 大小:264.00 KB
- 文档页数:3

高中几何知识点总结一、空间几何体(一)棱柱、棱锥、棱台1、棱柱:一般地,由一个沿某一方向形成的空间几何体叫做棱柱。
(1)棱柱的底面、侧面、侧棱、表示方法、分类以及侧棱的性质(2)直棱柱、正棱柱、平行六面体的概念2、棱锥:叫做棱锥。
(1)棱锥的底面、侧面、侧棱、表示方法、分类以及侧棱的性质(2)正三棱锥与正四面体的概念3、棱台:叫做棱台。
(1)棱台的上下底面、侧面、侧棱、表示方法、分类以及侧棱的性质(2)正棱台的概念(3)棱台的检验方法(侧棱延长交于一点,上下底面相似且平行)(二)圆柱、圆锥、圆台、球1、旋转面:一般地,一条绕旋转所形成的2、旋转体:叫做旋转体。
3、圆柱、圆锥、圆台:将、、分别绕它的、、、所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台。
(1)圆柱、圆锥、圆台的轴、底面、侧面、母线(2)利用“平移”、“缩”、“截”的方法定义棱柱、棱锥、棱台4、球面:叫做球面。
球体:叫做球体,简称球。
5、圆柱、圆锥、圆台、球的轴截面与旋转面的关系(三)直观图画法1、消点:2、直观图画法步骤:二、点、线、面之间的位置关系1、平面基本性质公理1 如果一条直线上的公理2 如果两个平面有一个公共点,那么他们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线。
公理3 经过的三点,有且只有一个平面。
(2) 线面垂直:如果一条直线与一个平面内的任意一条直线都垂直,称为线面垂直,记作,垂线、垂面、垂足。
(3) 面面平行:如果两个平面没有公共点,那么就说这两个平面平行。
面面垂直:一般地,如果两个平面所成的二面角是直二面角,3、线线关系位置关系相交直线平行直线异面直线共面关系公共点个数4、线面关系位置关系公共点符号表示图形表示直线在平面内直线与平面相交直线与平面平行5、面面关系图形表示6、各类“平行”之间的转化条件线线平行结论如果∥b,b∥c,那么∥c如果∥b,,b,那么∥如果,b,面面平行∩b=P,cβ,如果,如果∥β,如果⊥ ,⊥β,如果∥ ,β,β∩=b,那么∥b 线面平行面面平行如果∥β,垂直关系线线平行∩γ=,β∩γ=b,那么∥b 如果∥β,,那么∥β 如果⊥ ,b⊥ ,那么∥b 线面平行———— b ,∩b=P,∥β,b∥β,那么∥β β∥γ,那么∥γ 那么∥βd β,c∩d=Q,∥c,b∥d,那么∥β7、各类“垂直”之间的转化条件线线垂直结论如果⊥ ,b,那么⊥b 如果三个平面两两垂直,那么它们交线两两垂直如果⊥β——那么⊥β如果⊥ ,β,那么β⊥ ——,如果∥b,⊥c,那么b⊥c 线面垂直面面垂直平行关系线线垂直——线面垂直如果⊥b,⊥c,b,c,b∩c=P,那么⊥ 定义(二面角等于90) 0α∩β=b,,⊥b,如果⊥ ,b∥ ,那么b⊥ 面面垂直——8、立体几何中的“角”(1) 异面直线所成的角:将两异面直线平移得到两相交直线,这两条香蕉直线所成的锐角或直角就是这两条异面直线所成的角。

数学立体几何解题技巧必看各个科目都有自己的学习方法,但其实都是万变不离其中的,基本离不开背、记,运用,数学作为最烧脑的科目之一,也是一样的。
下面是小编给大家整理的一些数学立体几何解题技巧的学习资料,希望对大家有所帮助。
高考数学答题技巧:立体几何解答立体几何篇高考立体几何试题一般共有4道(选择、填空题3道,解答题1道),共计总分27分左右,考查的知识点在20个以内。
选择填空题考核立几中的计算型问题,而解答题着重考查立几中的逻辑推理型问题,当然,二者均应以正确的空间想象为前提。
随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的发展。
从历年的考题变化看,以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题。
知识整合1、有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律--充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力。
2、判定两个平面平行的方法:(1)根据定义--证明两平面没有公共点;(2)判定定理--证明一个平面内的两条相交直线都平行于另一个平面;(3)证明两平面同垂直于一条直线。
3、两个平面平行的主要性质:(1)由定义知:“两平行平面没有公共点”。
(2)由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。
(3)两个平面平行的性质定理:”如果两个平行平面同时和第三个平面相交,那么它们的交线平行“。
(4)一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
(5)夹在两个平行平面间的平行线段相等。

第二十一章平行六面体的性质及应用【基础知识】平行六面体是平行四边形的一个三维类比模型,平行四边形的一系列有趣性质可推证到平行六面体中去.平行四边形与三角形有着极为密切的关系,因而平行六面体与四面体也有着极为密切的关系,这些构成了平行六面体一系列既有趣又有重要应用的性质.性质1平行六面体的四条对角线相交于一点,且在这一点互相平分,并称该点为中心.推论称侧面对角线的交点为侧面中心,则相对侧面中心的连线也交于平行六面体的中心,且在这一点互相平分.(见例5)性质2平行六面体所有对角线的平方和等于所有棱的平方和.推论1平行六面体所有侧面对角线的平方和等于其所有(体)对角线平方和的两倍.推论2平行六面体每一侧棱的平方等于与这侧棱共面的两侧面四条面对角线的平方和减去与这侧棱不共面而共端点的两条侧面对角线平方和所得差的四分之一.推论3平行六面体的每一对角线长的平方等于过这条对角线一端点的三条侧面对角线的平方和减去过另一端点的三条棱的平方和.性质3平行六面体的每一对角线长的平方等于共一端点的三条棱长的平方和减去这三条棱中每两条棱长及其所夹角余弦之积的两倍.性质4平行六面体的每一对角线通过与该对角线共端点的三条棱的另一端点构成的三角形截面的重心,且被这三角形截面分成三等分.性质5平行六面体的每个由三条侧面对角线构成的三角形截面面积平方的4倍,等于这截面所截三个侧面面积的平方和减去这三个侧面中每两个侧面面积及其所夹二面角余弦之积的两倍.推论平行六面体的八个由三条侧面对角线构成的三角形截面面积的平方和等于六个侧面面积的平方和. 性质6设平行六面体的全面积为S ,四条对角线长为1AC l 、1A C l 、1BD l 、1BD l 、1B D l ,则111122222AC A C BD B DS l l l l +++≤. 性质7通过平行六面体中心的任何平面,将平行六面体分成体积相等的两部分.推论1以平行六面体任一顶点及这顶点出发的三条棱的端点构成的四面体体积是平行六面体体积的六分之一.推论2以平行六面体任一顶点及这顶点出发的三条侧面对角线端点构成的四面体体积是平行六面体体积的三分之一.性质8平行六面体的体积等于底面积与高的乘积,或任一侧面面积与相对面距离之积. 推论设共一顶点的三条棱长为a 、b 、c ,每两条棱的夹角为α、β、γ,则体积V 为V abc ==若记()12θαβγ=++,则2V =. 性质9()11113/22222124AC A C BD B D V l l l l +++≤;3/26S V ⎛⎫ ⎪⎝⎭≤.推论l 表面积一定的平行六面体中,以正方体之体积为最大.推论2在各个侧面面积为定值的平行六面体中,以长方体之体积为最大.性质11由平行六面体的各顶点,至不截此体的一平面所引诸垂线段之和,等于由其对角线之交点至同平面所引垂线段之和的8倍.性质10在平行六面体1111ABCD A B C D -中,截面分别与AB 、AD 、1AA 、1AC 交于0B 、0C 、0A 、0D 各点,则110000AC AA AB AD AC AB AD AA =++u u u u r u u u r u u u r u u u r u u u ur u u u u r u u u u r u u u u r . 下面介绍平行六面体与四面体的密切关系. 1.对应关系作四面体的外接平行六面体,且使四面体的六条棱均成为平行六面体的侧面对角线.此时,四面体与其外接平行六面体是一一对应的.特别地,一个正四面体对应着一个正方体,一个等腰四面体(三对对棱分别相等的四面体)对应着一个长方体,一个两对对棱分别相等的四面体对应着一个直平行六面体,一个对棱均互相垂直的四面体(直角四面体或正三棱锥四面体)对应着一个菱形六面体等等.当四面体的共一顶点的三棱成为平行六面体的共顶点的三棱时,一个四面体对应着四个外接平行六面体,特别地,一个正四面体对应着一个一顶点面角均为60︒的菱形六面体,一个等腰四面体对应着两个一顶点面角之和为180︒的平行六面体等等. 2.隐显关系从本世纪初开始,人们试图将三角形的许多性质引申到四面体——最简单的多面体,事实证明发展四面体的几何学比三角形几何学困难得多,有些提法并不复杂的问题解答起来非常费劲,甚至未能解决.下面的例题将启示我们:四面体某些数量关系的发现及几何特征的显露,借助于其外接平行六面体的性质的运用是一种方便的重要途径.因此,可以说四面体的一些性质可以利其外接平行六面体来显现,平行六面体隐含了四面体的一些重要性质. 【典型例题与基本方法】例1在四面体ABCD 中,AB m =,CD n =,AD p =,BC q =,AC u =,BD u =.若AB 与CD 所成的角为θ,则()()2222cos 2pq u v mn+--=.证明如图211-,作四面体ABCD 的外接平行六面体A DB C AD BC ''''-,使四面体的棱都成为平行六面体的侧面对角线.显然,AB 与CD 所成的角θ就是A B ''与CD 所成的角,于是 ()()2222221/21/24cos 112222m n B D m n B D mn m n θ'+-⎡⎤⎡⎤'+-⎣⎦⎣⎦==⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭ 222222242222A D B D B D A D B D mn mn'''''+--==A'B'C 'D '图21-1DBA C()()22222222222222p q u v A D D D D D B D mn mn+--''''---==. 例2若四面体的六条棱长分别为a 、b 、c 、d 、e 、f ,体积为V ,则有333333a b c d e f +++++≥(Weisenbock 不等式的一种三维推广).证明如图211-,将四面体ABCD 补成平行六面体,则3ABCD V V =平行六面体.设平行六面体共顶点A 的三条棱长为l 、m 、n ,由前面的性质2的推论1,即有()2222222224a b c d e f l m n +++++=++.又由V l m n ⋅⋅平行六面体≤及幂平均值不等式,有113333332222223266a b c d e f a b c d e f ⎛⎫⎛⎫++++++++++ ⎪ ⎪⎝⎭⎝⎭≥.于是()322224212ABCD l m nV ⎡⎤++⎢⎥⎢⎥⎣⎦①()32222222112a b c d e f ⎡⎤=+++++⎢⎥⎣⎦()312233333331612a b c d e f ⎧⎫⎪⎪⎡⎤+++++⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭≤②)333333a b c d e f =+++++.故333333a b c d e f +++++≥.其中等号当且仅当①、②中满足l 、m 、n 互相垂直且l m n ==,即平行六面体为正方体,亦即a b c d e f =====时成立.类似上例,并运用前面的性质5的推论,可证明Weisenbock 不等式的另一种三维推广:若四面体各顶点A 、B 、C 、D 所对的面的面积分别为A S 、B S 、C S 、D S ,体积为V ,则33332A B C D S S S S +++ 例3空间四平面互相平行,相邻两面间距离都是h .今有一正四面体,它的四个顶点分别在这四个面上.求正四面体的棱长.解设正四面体ABCD 的外接正方体为'AC BD A CB D '''-.又设过棱D D '及B C '中点F 的截面为3α,过棱C C '及A D '中点E 的截面为2α,过棱A A ',过棱B B '且与3α、2α平行的平面分别为1α、4α,这样这四个平面即为两相邻距离都相等的互相平行的四平面.又设过A B ''的中点O '与CE 垂直的直线为l ,l 与4α、3α、2α、1α的交点分别为B ''、D ''、C ''、A '',如图21-2(b),则4α、3α、2α、1α两相邻平面间距离为B D ''''、D C ''''、C A ''''.当A C h ''''=时,可求得A E '=,从而A B ''=.这就是我们所要求的正四面体的棱长. 例4四面体ABCD 中,若AB CD ⊥,AC BD ⊥,则AD BC ⊥.(1957年天津市、1979年上海市中学竞赛题)证明如图211-,作四面体ABCD 的外接平行六面体A DB C AD BC ''''-.由平行六面体每一侧面两对角线所夹的角(锐角)的余弦值等于这侧面两相邻棱的平方差的绝对值除以这两条侧面对角线长的乘积,即¼()22cos A D DB A BCD A B CD''-'=''⋅.由AB CD ⊥,则¼()cos cos()0ABCD A B CD ''==撩妹妹?,从而A D DB ''=,即侧面A DB C ''为菱形,同理,由AC BD ⊥.有侧面A CC A ''为菱形,从而侧面A DD A ''也为菱形,故AD BC ⊥. 例5求证四面体的三双对棱中点连线必交于一点,且互相平分.证明如图213-,设E 、F 、G 、H 、M 、N 分别是四面体ABCD 的六条棱的中点.作四面体的外接平行六面体1A C ,则E 、F 、G 、H 、M 、N 分别是其六侧面对角线的交点.在11AAC C Y 中,连EF ,则11EF AA CC ∥∥,且过六面体对角线1A C 的中点O ,同时被O 平分.因六面体的四条对角线共点O ,于是同理可证GH 、MN 过O ,且被O 平分.例6立方体八个顶点中有四个恰是正四面体的顶点.求出立方体的表面积与四面体的表面积之比.(1980年美国中学生竞赛AHSME 第16题) 解设立方体表面积为S ,四面体表面积为0S ,由平行六面体所有三角形截面(三角形的边由六面体侧DEGO 'B"A"C "D "A'B'C 'D (b)(a)D图21-2CF 图21-3G N EH OCDBAC 1A 1D 1B 1MF面对角线组成)面积的平方和等于所有侧面面积的平方和,有2206/4264S S ⎛⎫⎛⎫⋅⋅= ⎪ ⎪⎝⎭⎝⎭,故0/S S =【解题思维策略分析】1.善于将四面体问题转化为平行六面体问题例7若A 、B 、C 、D 表示空间四点,AB 表示A 、B 两点间的距离,AC 表示A 、C 两点间的距离,⋯.证明:222222AC BD AD BC AB CD ++++≥.(第4届美国中学生竞赛题) 证明以空间四边形的边为侧面对角线构造平行六面体,由平行六面体所有侧面对角线的平方和等于所有棱的平方和的两倍及图213-,有222222222111444AC BD AD BC AB CD AD AA A B +++++=++()22242AD AB CD =++故222222AC BD AD BC AB CD ++++≥.当A 、B 、C 、D 共面时,10AD =,上式取等号.此时,可看作是压扁了的四面体.例8在四面体ABCD 中,BDC ∠是直角,由D 到ABC △所在的平面的垂线的垂足H 是ABC △的垂心,证明:()()22226AB BC CA AD BD CD ++++≤.(IMO 12-试题)证明如图214-,平行六面体1111AC BD B D AC -为四面体ABCD 的外接平行六面体.由题设,D 到ABC △所在的平面的垂线的垂足是ABC △的垂心,知这个四面体的对棱互相垂直,又BDC ∠是直角,即知四面体ABCD 的三面角D ABC -是直三面角,故此平行六面体为长方体.由()2222AD BD CD ++()()()222222AD BD BD CD CD AD =+++++222AB BC AC =++.故()()22222263AD BD CD AB BC AC ++=++222222AB BC CA AB BC BC CA AB CA +++⋅+⋅+⋅≥ ()2AB BC CA =++.例9若a 、b 、c 是四面体共顶点的三条棱的长,α、β、γ,是这三条棱组成的面角,ω是这三个面角和的一半,则四面体的体积为:13V abc =四面体证明如图21-4,设DA a =,DB b =,DC c =,BDC α∠=,ADC β∠=, ADB γ∠=.由平行六面体CDBC 1A 1D 1B 1图21-4H的体积公式()V abc S A =⋅平行六面体,其中()S A= 有16V V =四面体平行六面体1=3abc 2.善于构造平行六面体解答有关问题例10已知a 、b 、c +∈R ,且2221a b c ++=3a b c +++>.证明由2221a b c ++=3a b c +++>.参见图212- (a),构作长方体AB '.设对角线1AB '=,AD a '=,AC b '=,AA c '=,则A B ''=B C '',B D ''=.在A AB ''△中,A A A B B A ''''+>,即1c >.同理,1b >1a +>. 以上三式相加,即证.例11锐角α.β、γ满足222sin sin sin 1αβγ++=,求证:π3π24αβγ<++<. 证明构造长方体D AC B DA CB ''''-,参见图212- (a),使其长、宽、高分别为sin D A α'=,sin AC β'=,sin C C γ'=,则1AB D C ''==,D B A α''∠=,C B A β''∠=,C D C γ''∠=,且AB BA '>.sin sin sin D A D AD B A D BA B A BA α'''''∴=∠=<=∠', sin sin sin AC AC C B A C BA B A BAβ'''''=∠=<=∠'.从而D BA α'<∠,C BA β'<∠. 1π2D BA C BA αβ''∴+<∠+∠=.同理,π2βγ+<,π2αγ+<,即3π4αβγ++<. 设B A '与D C '相交于O ,则知2D OA α'∠=,2AOC β'∠=,2C OC γ'∠=.由于三面角的任意两个面角的和大于第三个面角,则 22D OA AOC D OC αβ'''+=∠+∠>∠.()2πD OC C OC αβγ''∴++=∠+∠=. 故π3π24αβγ<++<. 3.注意特殊平面体的性质的运用例12正方体1111ABCD A B C D -的棱长为1,求正方体底面ABCD 内切圆周上的点与过顶点1A 、C 和1B 的圆周上的点之间的最小距离.(第19届全苏奥林匹克题)解如图215-,考察两个圆周分别在以正方体的对称中心为球心的两个同心球面上,即与正方体各棱都)上,这两个球面上的点之间的最小距离是它们的半径之差12d =.如果两圆周上各有一点恰好在球心O 发出的同一射线上,那么d 即为最小值.考察在以O为位似比的变换下,小球面变为大球面,而小球面上的圆周的象集为大球面上的圆周.注意到ABCD 的内切圆1O e 与线段BD 的交点E 和F 在该位似变换下的象在平面1AB C 的两侧(因11145O OF BB O ∠=︒>∠,故射线OF 不与平面1AB C 相交),因此,1O e 的象集(圆周)将与过顶点A ,C 和1B 的圆周相交.设一交点为N ,而N 的原象为M ,那么M ,N 之间的距离就是考察的两圆周上的点之间的距离的最小值,其值为12d =.【模拟实战】习题A1.在正方体1111ABCD A B C D -中,O 是面ABCD 的中心,1O 是面11ADD A 的中心.求异面直线1D O 与1BO 所成角的余弦值.2.已知空间一个平面与一个正方体的12条棱的夹角都等于口α,求α的值.3.能否用一个平面去截一个正方体,使得截面为五边形?进一步,截面是否为正五边形?4.设一个平面截棱长为1的正方体1111ABCD A B C D -,过顶点1C ,交1A D 1中点于E ,1A A 距A 较近的一个三等分点于F ,AB 于G ,BC 于H .求截面1C EFGH 的周长.5.已知一个平面截棱长为1的正方体所得截面是—个六边形.证明:此六边形周长≥. 6.正三棱锥S ABC -的侧棱与底面边长相等,如果E ,F 分别为SC ,AB 的中点,那么异面直线EF 与SA 所成的角等于多少?图21-5C1A B7.已知111ABC A B C -是直三棱柱,90BAC ∠=︒,点1D ,1F 分别是11A B ,11B C 的中点.若1AB CA AA ==,求1BD 与1CF 所夹角的余弦值.8.已知ABCD 是边长为4的正方形,E ,F 分别是AB ,AD 的中点,GC ⊥面ABCD ,且2GC =.求点B 到面EFG 的距离.9.在四面体SABC 中,已知SA BC a ==,SC AB b ==,SB AC c ==,求此四面体的体积. 10.在四面体1234A A A A 中,相应对棱中点的三条连线分别为1m ,2m ,3m ,顶点i A 所对侧面的重心为i G ,其四面体体积记为V ,则(Ⅰ)1233m m m V ⋅⋅≥;(Ⅱ)421412716i j i i i j i A A AG =-∑∑≤≤≤≥(Ⅲ)421i i i AG =∑ 11.已知α,β,γ是锐角,且222cos cos cos 1αβγ++=.求证:(Ⅰ)tan tan tan αβγ⋅⋅≥ (Ⅱ)3ππ4αβγ<++<. 12.已知0a >,0b >,0c >,且1a b c ++=.习题B1.有一立方体,中心和边长为a b c <<的长方体的对称中心重合,诸界面与长方体各界面平行,求立方体的棱长,使得它与长方体的并的体积减去它与长方体的交的体积的差最小.(1979年捷克竞赛题) 2.证明:在棱长为a 的立方体内部可以作两个棱长为a 的正四面体,使得它们没有公共点.(1983年民主德国竞赛题)。

初中数学棱柱的知识点总结棱柱棱柱:有两个面相互平行,其余各面都是四边形,并且每相邻两个多边形的公共边都相互平行,由这些面所围成的多面体叫做棱柱。
棱柱用表示底面各顶点的字母来表示。
棱柱的底面:棱柱中两个相互平行的面,叫做棱柱的底面。
棱柱的侧面:棱柱中除两个底面以外的其余各个面都叫做棱柱的侧面。
棱柱的侧棱:棱柱中两个侧面的公共边叫做棱柱的侧棱。
棱柱的形成方式棱柱是由一个由直线构成的平面沿着不平行于此平面的直线整体平移而形成的。
棱柱的顶点在棱柱中,侧面与底面的公共顶点叫做棱柱的顶点。
棱柱的对角线:棱柱中不在表面同一平面上的两个顶点的连线叫做棱柱的对角线。
棱柱的高:棱柱的'两个底面的距离叫做棱柱的高。
棱柱的对角面:棱柱中过不相邻的两条侧棱的截面叫做棱柱的对角面。
棱柱的分类斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时,一般将侧棱画成不与底面垂直。
直棱柱:侧棱垂直于底面的棱柱叫做直棱柱。
画直棱柱时,应将侧棱画成与底面垂直。
正棱柱:底面是正多边形的直棱柱叫做正棱柱。
平行六面体:底面是平行四边形的棱柱。
直平行六面体:侧棱垂直于底面的平行六面体叫直平行六面体。
长方体:底面是矩形的直棱柱叫做长方体。
棱柱具有以下性质性质1)棱柱的各个侧面都是平行四边形,全部的侧棱都平行且相等;直棱柱的各个侧面都是矩形;正棱柱的各个侧面都是全等的矩形。
2)棱柱的两个底面与平行于底面的截面是对应边相互平行的全等多边形。
3)过棱柱不相邻的两条侧棱的截面都是平行四边形。
4)直棱柱的侧棱长与高相等;直棱柱的侧面及经过不相邻的两条侧棱的截面都是矩形。
知识要领总结:棱柱是由一个由直线构成的平面沿着不平行于此平面的直线整体平移而形成的。

第二十一章平行六面体的性质及应用【基础知识】平行六面体是平行四边形的一个三维类比模型,平行四边形的一系列有趣性质可推证到平行六面体中去.平行四边形与三角形有着极为密切的关系,因而平行六面体与四面体也有着极为密切的关系,这些构成了平行六面体一系列既有趣又有重要应用的性质.性质1平行六面体的四条对角线相交于一点,且在这一点互相平分,并称该点为中心.推论称侧面对角线的交点为侧面中心,则相对侧面中心的连线也交于平行六面体的中心,且在这一点互相平分.(见例5)性质2平行六面体所有对角线的平方和等于所有棱的平方和.推论1平行六面体所有侧面对角线的平方和等于其所有(体)对角线平方和的两倍.推论2平行六面体每一侧棱的平方等于与这侧棱共面的两侧面四条面对角线的平方和减去与这侧棱不共面而共端点的两条侧面对角线平方和所得差的四分之一.推论3平行六面体的每一对角线长的平方等于过这条对角线一端点的三条侧面对角线的平方和减去过另一端点的三条棱的平方和.性质3平行六面体的每一对角线长的平方等于共一端点的三条棱长的平方和减去这三条棱中每两条棱长及其所夹角余弦之积的两倍.性质4平行六面体的每一对角线通过与该对角线共端点的三条棱的另一端点构成的三角形截面的重心,且被这三角形截面分成三等分.性质5平行六面体的每个由三条侧面对角线构成的三角形截面面积平方的4倍,等于这截面所截三个侧面面积的平方和减去这三个侧面中每两个侧面面积及其所夹二面角余弦之积的两倍.推论平行六面体的八个由三条侧面对角线构成的三角形截面面积的平方和等于六个侧面面积的平方和.性质6设平行六面体的全面积为S ,四条对角线长为1AC l 、1A C l 、1BD l 、1BD l 、1B D l ,则111122222AC A C BD B DS l l l l +++≤. 性质7通过平行六面体中心的任何平面,将平行六面体分成体积相等的两部分.推论1以平行六面体任一顶点及这顶点出发的三条棱的端点构成的四面体体积是平行六面体体积的六分之一.推论2以平行六面体任一顶点及这顶点出发的三条侧面对角线端点构成的四面体体积是平行六面体体积的三分之一.性质8平行六面体的体积等于底面积与高的乘积,或任一侧面面积与相对面距离之积. 推论设共一顶点的三条棱长为a 、b 、c ,每两条棱的夹角为α、β、γ,则体积V 为V abc ==若记()12θαβγ=++,则2V =. 性质9()11113/22222124AC A C BD BDV l l l l +++≤;3/26S V ⎛⎫ ⎪⎝⎭≤.推论l 表面积一定的平行六面体中,以正方体之体积为最大.推论2在各个侧面面积为定值的平行六面体中,以长方体之体积为最大.性质11由平行六面体的各顶点,至不截此体的一平面所引诸垂线段之和,等于由其对角线之交点至同平面所引垂线段之和的8倍.性质10在平行六面体1111ABCD A B C D -中,截面分别与AB 、AD 、1AA 、1AC 交于0B 、0C 、0A 、0D 各点,则11000AC AA AB AD AC AB AD AA =++. 下面介绍平行六面体与四面体的密切关系. 1.对应关系作四面体的外接平行六面体,且使四面体的六条棱均成为平行六面体的侧面对角线.此时,四面体与其外接平行六面体是一一对应的.特别地,一个正四面体对应着一个正方体,一个等腰四面体(三对对棱分别相等的四面体)对应着一个长方体,一个两对对棱分别相等的四面体对应着一个直平行六面体,一个对棱均互相垂直的四面体(直角四面体或正三棱锥四面体)对应着一个菱形六面体等等.当四面体的共一顶点的三棱成为平行六面体的共顶点的三棱时,一个四面体对应着四个外接平行六面体,特别地,一个正四面体对应着一个一顶点面角均为60︒的菱形六面体,一个等腰四面体对应着两个一顶点面角之和为180︒的平行六面体等等. 2.隐显关系从本世纪初开始,人们试图将三角形的许多性质引申到四面体——最简单的多面体,事实证明发展四面体的几何学比三角形几何学困难得多,有些提法并不复杂的问题解答起来非常费劲,甚至未能解决.下面的例题将启示我们:四面体某些数量关系的发现及几何特征的显露,借助于其外接平行六面体的性质的运用是一种方便的重要途径.因此,可以说四面体的一些性质可以利其外接平行六面体来显现,平行六面体隐含了四面体的一些重要性质. 【典型例题与基本方法】例1在四面体ABCD 中,AB m =,CD n =,AD p =,BC q =,AC u =,BD u =.若AB 与CD 所成的角为θ,则()()2222cos 2p q u v mn+--=.证明如图211-,作四面体ABCD 的外接平行六面体A DB C AD BC ''''-,使四面体的棱都成为平行六面体的侧面对角线.A'B'C 'D '图21-1DA C显然,AB 与CD 所成的角θ就是A B ''与CD 所成的角,于是 ()()2222221/21/24cos 112222m n B D m n B D mn m n θ'+-⎡⎤⎡⎤'+-⎣⎦⎣⎦==⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭ 222222242222A D B D B D A D B D mn mn'''''+--==()()22222222222222p q u v A D D D D D B D mn mn+--''''---==. 例2若四面体的六条棱长分别为a 、b 、c 、d 、e 、f ,体积为V ,则有333333a b c d e f +++++≥(Weisenbock 不等式的一种三维推广).证明如图211-,将四面体ABCD 补成平行六面体,则3ABCD V V =平行六面体.设平行六面体共顶点A 的三条棱长为l 、m 、n ,由前面的性质2的推论1,即有()2222222224a b c d e f l m n +++++=++.又由V l m n ⋅⋅平行六面体≤及幂平均值不等式,有113333332222223266a b c d e f a b c d e f ⎛⎫⎛⎫++++++++++ ⎪ ⎪⎝⎭⎝⎭≥.于是()322224212ABCD l m nV ⎡⎤++⎢⎥⎢⎥⎣⎦①()32222222112a b c d e f ⎡⎤=+++++⎢⎥⎣⎦()312233333331612a b c d e f ⎧⎫⎪⎪⎡⎤+++++⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭≤②)333333a b c d e f =+++++.故333333a b c d e f +++++≥.其中等号当且仅当①、②中满足l 、m 、n 互相垂直且l m n ==,即平行六面体为正方体,亦即a b c d e f =====时成立.类似上例,并运用前面的性质5的推论,可证明Weisenbock 不等式的另一种三维推广:若四面体各顶点A 、B 、C 、D 所对的面的面积分别为A S 、B S 、C S 、D S ,体积为V ,则33332A B C D S S S S +++ 例3空间四平面互相平行,相邻两面间距离都是h .今有一正四面体,它的四个顶点分别在这四个面上.求正四面体的棱长.解设正四面体ABCD 的外接正方体为'AC BD A CB D '''-.又设过棱D D '及B C '中点F 的截面为3α,过棱C C '及A D '中点E 的截面为2α,过棱A A ',过棱B B '且与3α、2α平行的平面分别为1α、4α,这样这四个平面即为两相邻距离都相等的互相平行的四平面.又设过A B ''的中点O '与CE 垂直的直线为l ,l 与4α、3α、2α、1α的交点分别为B ''、D ''、C ''、A '',如图21-2(b),则4α、3α、2α、1α两相邻平面间距离为B D ''''、D C ''''、C A ''''.DEGO 'B"A"C "D "A'B'C 'D (b)(a)D图21-2CF当A C h ''''=时,可求得A E '=,从而A B ''=.这就是我们所要求的正四面体的棱长. 例4四面体ABCD 中,若AB CD ⊥,AC BD ⊥,则AD BC ⊥.(1957年天津市、1979年上海市中学竞赛题)证明如图211-,作四面体ABCD 的外接平行六面体A DB C AD BC ''''-.由平行六面体每一侧面两对角线所夹的角(锐角)的余弦值等于这侧面两相邻棱的平方差的绝对值除以这两条侧面对角线长的乘积,即()22cos A D DB A B CD A B CD''-'=''⋅.由AB CD ⊥,则()cos cos()0AB CD A B CD ''==,从而A D DB ''=,即侧面A DB C ''为菱形,同理,由AC BD ⊥.有侧面A CC A ''为菱形,从而侧面A DD A ''也为菱形,故AD BC ⊥. 例5求证四面体的三双对棱中点连线必交于一点,且互相平分.证明如图213-,设E 、F 、G 、H 、M 、N 分别是四面体ABCD 的六条棱的中点.作四面体的外接平行六面体1A C ,则E 、F 、G 、H 、M 、N 分别是其六侧面对角线的交点.图21-3G N EH OCDBAC 1A 1D 1B 1MF在11AAC C 中,连EF ,则11EF AA CC ∥∥,且过六面体对角线1A C 的中点O ,同时被O 平分.因六面体的四条对角线共点O ,于是同理可证GH 、MN 过O ,且被O 平分.例6立方体八个顶点中有四个恰是正四面体的顶点.求出立方体的表面积与四面体的表面积之比.(1980年美国中学生竞赛AHSME 第16题) 解设立方体表面积为S ,四面体表面积为0S ,由平行六面体所有三角形截面(三角形的边由六面体侧面对角线组成)面积的平方和等于所有侧面面积的平方和,有2206/4264S S ⎛⎫⎛⎫⋅⋅= ⎪ ⎪⎝⎭⎝⎭,故0/S S =【解题思维策略分析】1.善于将四面体问题转化为平行六面体问题例7若A 、B 、C 、D 表示空间四点,AB 表示A 、B 两点间的距离,AC 表示A 、C 两点间的距离,⋯.证明:222222AC BD AD BC AB CD ++++≥.(第4届美国中学生竞赛题) 证明以空间四边形的边为侧面对角线构造平行六面体,由平行六面体所有侧面对角线的平方和等于所有棱的平方和的两倍及图213-,有222222222111444AC BD AD BC AB CD AD AA A B +++++=++()22242AD AB CD =++故222222AC BD AD BC AB CD ++++≥.当A 、B 、C 、D 共面时,10AD =,上式取等号.此时,可看作是压扁了的四面体.例8在四面体ABCD 中,BDC ∠是直角,由D 到ABC △所在的平面的垂线的垂足H 是ABC △的垂心,证明:()()22226AB BC CA AD BD CD ++++≤.(IMO 12-试题)证明如图214-,平行六面体1111AC BD B D AC -为四面体ABCD 的外接平行六面体.由题设,D 到ABC △所在的平面的垂线的垂足是ABC △的垂心,知这个四面体的对棱互相垂直,又BDC ∠是直角,即知四面体ABCD 的三面角D ABC -是直三面角,故此平行六面体为长方体.CDBAC 1A 1D 1B 1图21-4H由()2222AD BD CD ++()()()222222AD BD BD CD CD AD =+++++222AB BC AC =++.故()()22222263AD BD CD AB BC AC ++=++222222AB BC CA AB BC BC CA AB CA +++⋅+⋅+⋅≥ ()2AB BC CA =++.例9若a 、b 、c 是四面体共顶点的三条棱的长,α、β、γ,是这三条棱组成的面角,ω是这三个面角和的一半,则四面体的体积为:13V abc =四面体证明如图21-4,设DA a =,DB b =,DC c =,BDC α∠=,ADC β∠=, ADB γ∠=.由平行六面体的体积公式()V abc S A =⋅平行六面体,其中()S A= 有16V V =四面体平行六面体1=3abc 2.善于构造平行六面体解答有关问题例10已知a 、b 、c +∈R ,且2221a b c ++=3a b c ++>.证明由2221a b c ++=3a b c ++>.参见图212- (a),构作长方体AB '.设对角线1AB '=,AD a '=,AC b '=,AA c '=,则A B ''B C ''=,B D ''.在A AB ''△中,A A A B B A ''''+>,即1c >.同理,1b >1a >.以上三式相加,即证.例11锐角α.β、γ满足222sin sin sin 1αβγ++=,求证:π3π24αβγ<++<. 证明构造长方体D AC B DA CB ''''-,参见图212- (a),使其长、宽、高分别为sin D A α'=,sin AC β'=,sin C C γ'=,则1AB D C ''===,D B A α''∠=,C B A β''∠=,C D C γ''∠=,且AB BA '>.sin sin sin D A D AD B A D BA B A BA α'''''∴=∠=<=∠', sin sin sin AC AC C B A C BA B A BAβ'''''=∠=<=∠'.从而D BA α'<∠,C BA β'<∠. 1π2D BA C BA αβ''∴+<∠+∠=.同理,π2βγ+<,π2αγ+<,即3π4αβγ++<. 设B A '与D C '相交于O ,则知2D OA α'∠=,2AOC β'∠=,2C OC γ'∠=. 由于三面角的任意两个面角的和大于第三个面角,则 22D OA AOC D OC αβ'''+=∠+∠>∠. ()2πD OC C OC αβγ''∴++=∠+∠=.故π3π24αβγ<++<. 3.注意特殊平面体的性质的运用例12正方体1111ABCD A B C D -的棱长为1,求正方体底面ABCD 内切圆周上的点与过顶点1A 、C 和1B 的圆周上的点之间的最小距离.(第19届全苏奥林匹克题)图21-5C1A B解如图215-,考察两个圆周分别在以正方体的对称中心为球心的两个同心球面上,即与正方体各棱都)上,这两个球面上的点之间的最小距离是它们的半径之差12d =.如果两圆周上各有一点恰好在球心O 发出的同一射线上,那么d 即为最小值.考察在以O 为位似比的变换下,小球面变为大球面,而小球面上的圆周的象集为大球面上的圆周.注意到ABCD 的内切圆1O 与线段BD 的交点E 和F 在该位似变换下的象在平面1AB C 的两侧(因11145O OF BB O ∠=︒>∠,故射线OF 不与平面1AB C 相交),因此,1O 的象集(圆周)将与过顶点A ,C 和1B 的圆周相交.设一交点为N ,而N 的原象为M,那么M ,N 之间的距离就是考察的两圆周上的点之间的距离的最小值,其值为12d =.【模拟实战】习题A1.在正方体1111ABCD A B C D -中,O 是面ABCD 的中心,1O 是面11ADD A 的中心.求异面直线1D O 与1BO 所成角的余弦值.2.已知空间一个平面与一个正方体的12条棱的夹角都等于口α,求α的值.3.能否用一个平面去截一个正方体,使得截面为五边形?进一步,截面是否为正五边形?4.设一个平面截棱长为1的正方体1111ABCD A B C D -,过顶点1C ,交1A D 1中点于E ,1A A 距A 较近的一个三等分点于F ,AB 于G ,BC于H .求截面1C EFGH 的周长.5.已知一个平面截棱长为1的正方体所得截面是—个六边形.证明:此六边形周长≥. 6.正三棱锥S ABC -的侧棱与底面边长相等,如果E ,F 分别为SC ,AB 的中点,那么异面直线EF 与SA 所成的角等于多少?7.已知111ABC A B C -是直三棱柱,90BAC ∠=︒,点1D ,1F 分别是11A B ,11B C 的中点.若1AB CA AA ==,求1BD 与1CF 所夹角的余弦值.8.已知ABCD 是边长为4的正方形,E ,F 分别是AB ,AD 的中点,GC ⊥面ABCD ,且2GC =.求点B 到面EFG 的距离.9.在四面体SABC 中,已知SA BC a ==,SC AB b ==,SB AC c ==,求此四面体的体积. 10.在四面体1234A A A A 中,相应对棱中点的三条连线分别为1m ,2m ,3m ,顶点i A 所对侧面的重心为i G ,其四面体体积记为V ,则 (Ⅰ)1233m m m V ⋅⋅≥;(Ⅱ)421412716i j i i i j i A A AG =-∑∑≤≤≤≥(Ⅲ)421i i i AG =∑ 11.已知α,β,γ是锐角,且222cos cos cos 1αβγ++=.求证:(Ⅰ)tan tan tan αβγ⋅⋅≥ (Ⅱ)3ππ4αβγ<++<. 12.已知0a >,0b >,0c >,且1a b c ++=.习题B1.有一立方体,中心和边长为a b c <<的长方体的对称中心重合,诸界面与长方体各界面平行,求立方体的棱长,使得它与长方体的并的体积减去它与长方体的交的体积的差最小.(1979年捷克竞赛题) 2.证明:在棱长为a 的立方体内部可以作两个棱长为a 的正四面体,使得它们没有公共点.(1983年民主德国竞赛题)。
长方体体积公式及外表积公式长方体是底面为长方形的直四棱柱〔或上、下底面为矩形的直平行六面体〕,其由六个面组成的,相对的面面积相等。
长方体是底面为长方形的直四棱柱〔或上、下底面为矩形的直平行六面体〕,其由六个面组成的,相对的面面积相等。
体积长方体的体积=长×宽×高。
设一个长方体的长、宽、高分别为a、b、c,那么它的体积:V=abc=Sh
因为长方体也属于棱柱的一种,所以棱柱的体积计算公式它也同样适用。
长方体体积=底面积×高,即V=Sh〔S是底面积〕外表积因为相对的2个面面积相等,所以先算上下两个面,再算前后两个面,最后算左右两个面。
设一个长方体的长、宽、高分别为a、b、c,那么它的外表积为S=(ab+bc+ca)×2,也等于2ab+2bc+2ca,还等于2〔ab+bc+ca〕;
公式:长方体的外表积=长×宽×2+宽×高×2+长×高×2,或:长方体的外表积=〔长×宽+宽×高+长×高〕×2。
性质(1)长方体有6个面。
每组相对的面完全一样。
(2)长方体有12条棱,相对的四条棱长度相等。
按长度可分为三组,每一组有4条棱。
(3)长方体有8个顶点。
每个顶点连接三条棱。
三条棱分别叫做长
方体的长,宽,高。
(4)长方体相邻的两条棱互相垂直。
第1单元空间几何体的结构〖要点梳理〗1.多面体:多面体是由若干个平面多边形所围成的几何体,围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点,连结不在同一面上的两个顶点的线段叫做多面体的对角线。
把一个多面体的任意一个面延展为平面,如果其余的各面都在这个平面的同一侧,则这样的多面体就叫做凸多面体。
2.有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点。
3.棱柱的高:如果棱柱的一个底面水平放置,则铅垂线与两底面的交点之间的线段或距离,叫做棱柱的高(通常用h表示)。
4.棱柱的一种分类按底面是三角形、四边形、五边形……的棱柱叫做三棱柱、四棱柱、五棱柱……。
另一种分类(按侧棱与底面的关系分):斜棱柱——侧棱与底面不垂直的棱柱。
直棱柱——侧棱与底面垂直的棱柱。
正棱柱——底面是正多边形的直棱柱。
5. 特殊的四棱柱:平行六面体——底面是平行四边形的棱柱叫做平行六面体。
侧棱与底面垂直的平行六面体叫做直平行六面体。
底面是矩形的直平行六面体是长方体,棱长都相等的长方体是正方体。
6. 棱锥:有一个面是多边形,其余各面都是的一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥,这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱。
7. 棱锥的高:如果把棱锥的底面水平放置,则顶点与过顶点的铅垂线和底面的交点之间的线段或距离,叫做棱锥的高(通常用h表示)。
8. 正棱锥:如果棱锥的底面是正多边形,并且水平放置,它的顶点又在过正多边形中心的铅垂线上,则这个棱锥叫做正棱锥。
正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高(通常用h′表示)。
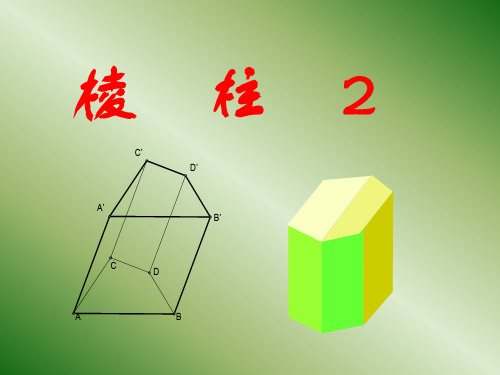
平行六面体与长方体
➢ 教学重点、难点:平行六面体、长方体的概念及性质.
➢ 教学过程: 一、复习
1.凸多面体的概念,棱柱的概念. 2.平行六面体的概念.
二、新课讲解
1.平行六面体、长方体、正方体
把学过的平行六面体与棱柱对照知:底面是平行四边形的四棱柱是平行六面体.侧棱与底面垂直的平行六面体叫直平行六面体,底面是矩形的直平行六面体长方体,棱长都相等的长方体叫正方体.
2.平行六面体、长方体的性质
定理:平行六面体的对角线交于一点,求证:对角线,,,AC BD CA DB ''''相交于一点,
且在点O 处互相平分.
证明:设O 是AC '的中点,则11()22
AO AC AB AD AA ''==++u u u r u u u u r u u u r u u u r u u u r
, 设,,P M N 分别是,,BD CA DB '''的中点,
同理:1()2AP AB AD AA '=++u u u r u u u r u u u r u u u r ,1()2AM AB AD AA '=++u u u u r u u u r u u u r u u u r
,
1()2
AN AB AD AA '=++u u u r u u u r u u u r u u u r ,
所以,,,,O P M N 四点重合,定理得证.
定理:长方体的一条对角线长的平方等于一个顶点上的三条棱长的平方和. 已知:长方体AC '中,AC '是一条对角线,求证:2
2
2
2
AC AB AD AA ''=++.
证明:∵AC AB AD AA ''=++u u u u r u u u r u u u r u u u r ,∴2||()()AC AB AD AA AB AD AA '''=++⋅++u u u u r u u u r u u u r u u u r u u u r u u u r u u u r
,
∵AB AD ⊥u u u r u u u r ,AB AA '⊥u u u r u u u r ,AA AD '⊥u u u r u u u r ,
∴2||AC AB AB AD AD AA AA '''=⋅+⋅+⋅u u u u r u u u r u u u r u u u r u u u r u u u r u u u r 222
||||||AB AD AA '=++,
即2
2
2
2
AC AB AD AA ''=++.
三、例题分析
例1.如图平行六面体ABCD A B C D ''''-中,,3
A A
B A AD BAD π
''∠=∠∠=
,
,AB AD a AA b '===,求对角面BB D D ''的面积. 解:∵BD AD AB =-u u u r u u u r u u u r
,
∴()AA BD AA AD AB ''⋅=⋅-u u u r u u u r u u u r u u u r u u u r ,
∵A AB A AD ''∠=∠,,AB AD a AA b '===,
∴()(cos cos )0AA BD AA AD AB ab A AB A AD ''''⋅=⋅-=∠-∠=u u u r u u u r u u u r u u u r u u u r
,
∴AA BD '⊥,∵//AA DD '',∴DD BD '⊥,
所以,对角面BB D D ''是矩形,它的面积是BD BB ab '⨯=.
例2.已知:正四棱柱ABCD A B C D ''''-的底面边长为2, (1)求二面角B AC B '--的大小;(2)求点B 到平面AB C '的距离。
解:(1)连结BD ,设,AC BD 交于O ,连结B O ',
∵ABCD 是正方形,∴BO AC ⊥, 又∵BB '⊥底面ABCD ,
∴B O AC '⊥,∴B OB '∠是二面角B AC B '--的平面角,
在Rt B OB '∆中,1
2
OB AC =
=BB '=, ∴45B OB '∠=o
,∴二面角B AC B '--为45o
.
(2)作BH B O '⊥于H ,∵AC ⊥平面B OB ',∴BH AC ⊥,
∴BH ⊥平面AB C ',即BH 为点B 到平面AB C '的距离,
在等腰直角三角形B OB '中,∵BB BO '==
∴1BH =,
所以,点B 到平面AB C '的距离为1. 四、本课小结
1.平行六面体与特殊四棱柱的关系. 2.平行六面体、长方体的性质. 五、作业补充
1.正方体1111ABCD A B C D -中,11AA =,M 为AD 中点,N 为1BD 上一点,
1:1:2D N NB =,MC BD P =I ,
(1)求证:NP ⊥平面ABCD ;
(2)求平面PNC 与平面11CC D D 所成的角; (3)求点C 到平面1D MB 的距离.
2.直平行六面体的两条对角线分别为9cm
,底面周长为18cm ,侧棱长为
4cm ,求它的表面积.
3.(1)长方体的有一个公共顶点的三个面的面积分别是3,4,5,求它的对角线长; (2)长方体的表面积是22,所有棱长和为24,求它的对角线长.
A C 1。