高二数学最新教案-如何把四面体补成平行六面体 精品

高中数学立体几何教案
教学内容：平行六面体
教学目标：
1. 了解平行六面体的定义和性质。

2. 掌握平行六面体的体积和表面积的计算方法。

3. 能够运用平行六面体的性质解决相关问题。

教学重点、难点：
重点：平行六面体的定义和性质、体积和表面积计算方法。

难点：运用平行六面体的性质解决相关问题。

教学过程：
一、导入（5分钟）
通过思考问题引入平行六面体的概念：什么是平行六面体？平行六面体有什么性质？平行六面体的体积和表面积如何计算？
二、讲解与示例（15分钟）
1. 讲解平行六面体的定义和性质，包括底面、侧面、顶面等概念。

2. 讲解平行六面体的体积计算公式：V = 底面积 × 高度。

3. 讲解平行六面体的表面积计算公式：S = 2 × 底面积 + 侧面积。

4. 举例说明如何计算平行六面体的体积和表面积。

三、练习与讨论（20分钟）
1. 给学生出一些计算平行六面体的体积和表面积的练习题，让学生在课堂上完成并相互讨论。

2. 引导学生设计一些实际生活中的问题，让他们运用平行六面体的性质解决问题，并与同学分享解决方法。

四、总结与作业布置（5分钟）
总结平行六面体的性质、体积和表面积的计算方法，强化学生对知识点的掌握。

布置作业：完成课后练习题，巩固所学知识。

教学反思：
教师应根据学生的实际水平和反应情况，灵活调整教学方法，合理安排教学过程，保证教学效果。

同时，要充分激发学生的学习兴趣，引导他们主动参与课堂活动，提高他们的学习积极性。

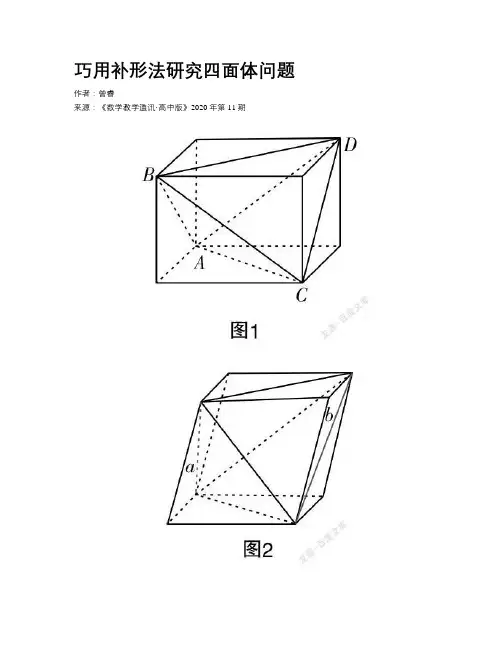
巧用补形法研究四面体问题作者：***来源：《数学教学通讯·高中版》2020年第11期[摘要] 立体几何问题中，有一类问题可以通过补形法，得到一个常见的几何体，使复杂的线面关系变得清晰明了. 文章从一道例题出发分析解决这类问题的方法，并在此基础上总结规律，归纳常见的一些四面体的补形方法.[关键词] 立体几何;四面体;补形教学中，遇到这样一个问题：已知在半径为2的球面上有A，B，C，D 四点，若AB=CD=2，则四面体ABCD的体积最大值为多少？这是某年数学全国卷的第12题，主要考查几何体的体积的计算、球的性质、异面直线间的距离，通过球这个载体考查学生的空间想象能力和推理计算能力.解答是这样的：过CD作平面PCD，使AB垂直于平面PCD，交AB于P. 设点P到CD的距离为h，则有V■=■×■×2×h×2=■h，当直径通过AB与CD中点时，h■=2■=2■，故V■=■.本小题这个解答当中，学生比较疑惑的有两点：（1）为什么可以过CD作平面PCD，使AB垂直于平面PCD，能这样作的前提是AB和CD要垂直，那为什么认定体积最大时AB和CD要垂直？（2）为什么直径通过AB与CD中点时，距离h最大？要解释清楚这两个疑点，首先需要补充说明一个公式.四面体体积公式：如果一个四面体的两条相对棱的长分别是a，b，它们的距离为d，所成的角为θ，那么它的体积为V■=■abdsinθ（证明见后）.根据这个公式，我们首先得到结论：AB和CD必须垂直，即sinθ=90°时才能得到最大的体积.其次，由于AB=CD=R（球的半径），所以连结球心O和四个顶点，则容易知道△OAB 和△OCD都是正三角形.设AB的中点为E，CD的中点为F，则OE⊥AB，OF⊥CD.设AB与CD间的距离为d，有d≤EF≤OE+OF. （异面直线间公垂线段最短）因此，OEF共线时，四面体的体积可以达到最大值，因为OE=OF=■，故V■=■.？摇？摇这样解决一个选择题比较花费时间，而且在高中数学教学中，不涉及四面体的体积公式，异面直线的距离即公垂线段的长度在教学中也仅仅要求了解.下面我们用补形的思路来解决这个问题.因为题目当中两条线段长度一样，所以考虑把这个四面体补形成一个长方体：如图1：则四面体的外接球即是长方体的外接球，四面体的体积是长方体的体积减去四个全等的小三棱锥的体积.设长方体的边长为a，b，c，体对角线即为外接球的直径，得到：a2+b2+c2=42，b2+c2=22，所以a=2■，则V■=V■-4V■=abc-4×■×■abc=■abc=■.又b2+c2=22 ，所以V■=■≤■（b2+c2）=■，当且仅当b=c=■时，等号成立.从等号成立的条件可以比较容易地看出是在AB和CD垂直时，四面体的体积取到了最大值.我们会发现，使用补形，一下子把陌生的几何体变得熟悉了，原本错综复杂的线面关系也变得清晰起来. 利用这一方法解决某些几何问题，思路清晰明朗，较其他方法简洁明了.比如刚才提到的四面体的体积公式也可以用补形法得到.一个四面体的两条相对棱的长分别是a，b，它们的距离为d，所成的角为θ，将四面体补形成平行六面体（因为相对棱的长度不确定，相等的时候才能补成长方体）.如图2：那么该平行六面体的底面积为S=■absinθ，平行六面体的体积为V■=■abdsinθ. 同样，该平行六面体由原四面体和四个全等的三棱锥构成. 三棱锥与平行六面体的高相等，底面积为平行六面体的一半，V■=■×■×■absinθ=■absinθ.所以V■=V■-4×V■=■absinθ.一起来看一下常见的几种四面体补形方式：一、把四面体的四个面各补上一个三棱锥，最后形成一个平行六面体. 其中正四面体是最特殊的形式，可以补成正方体. 而对棱相等的四面体则可以补形成一个长方体.例1：正四面体棱长为a，求外接球的半径R.正四面体补形为一个正方体，正四面体的外接球即为正方体的外接球.如图3：正方体的面对角线是正四面体的棱长，体对角线为外接球的直径.设正方体边长为b，则a=■b，2R=■b，所以R=■a.例2：在三棱锥A-BCD中，AB=CD=3，AD=BC=4，AC=BD=5，求三棱锥A-BCD外接球的半径.因为有三组对棱相等，把四面体补成一个长方形，如图4：长方体的三个面的面对角线是三棱锥的棱长，体对角线是外接球的直径.设长方体的棱长为a，b，c，外接球的半径为R，则a2+b2=32，b2+c2=42，a2+c2=52，（2R）2=a2+b2+c2，所以R=■.二、把四面体的一个角作为平行六面体的一个角补形成平行六面体.例3：四面体ABCD，侧棱AB，AC，AD两两垂直，AB=2，AC=3，AD=4，求四面体的外接球的半径R.因为四面体的侧棱两两垂直，所以可以把这个角看作长方体的一个角，把四面体补形成一个长方体，则四面体的外接球就是长方体的外接球四面体的三条侧棱就是长方体的长、宽、高，外接球的直径就是长方体的体对角线，则（2R）2=AB2+AC2+AD2=29，所以R=■.例4：若三棱锥S-ABC的所有顶点都在球O的球面上，SA⊥平面ABC，SA=2■，AB=1，AC=2，∠BAC=60°，求球O的半径R.根据已知条件可以得到△ABC是直角三角形，把四面体补成一个长方体，则四面体的外接球就是长方体的外接球，外接球的直径就是长方体的体对角线.则（2R）2=SA2+AC2=16，所以R=2.例5：已知四面体PABC的侧面PAC与平面ABC垂直，∠ABC=90°，BC=2■，AB=2，且PA⊥PC，PA=PC，求异面直线PC与AB所成角的余弦值.解答：把四面体补成如图所示平行六面体，异面直线PC与AB所成角即為PC与CD所成角的补角的余弦值.取AC中点M，PA=PC，则PM⊥AC，又因为平面PAC与平面ABC垂直，所以PM⊥平面ABC.△ABC中，∠ABC=90°，AB=2，BC=2■，所以∠ACB=30°，AC=4.△PAC中，PA⊥PC，PA=PC，AC=4，所以PM=2，PC=2■.底面四边形ABDC中，DM2=DC2+CM2-2DC·CM·cos120°，得到DM=2■.Rt△PMD中，PD=4.△PCD中，cos∠PCD=■= -■.所以异面直线PC与AB所成角的余弦值为■.此题也可以用空间向量法解答，用补形能更好地体现线面关系.三、把四面体补形成三棱柱例6：已知某几何体底面ABC是棱长为1的等边三角形，PA⊥平面ABC，PA=3，求该几何体的外接球的半径.解答：将该四面体补形成一个三棱柱四面体的外接球就是三棱柱的外接球.先求三棱柱底面三角形外接圆半径r=■·■=■.又因为PA⊥平面ABC，PA=3，所以三棱柱的外接球半径为R=■=■.四面体的问题可以通过补形变成正方体、长方体乃至平行六面体的问题.尤其在正方体和长方体中，点线面的关系是我们所熟悉的. 一些几何题的证明和求解，由原几何图形分析探究会比较烦琐，通过补形填补成一个新的几何图形，能使原问题的本质得到充分的体现，解决起来比较容易. 本文着重讨论四面体的补形问题，希望窥一斑而知全豹，探究立体几何中补形法这一重要的转化策略.。

平行六面体与长方体一、课题：平行六面体与长方体二、教学目标：1．掌握平行六面体、长方体、正方体的概念及性质；2．会利用平行六面体、长方体的性质解决有关长度与角度问题．三、教学重点、难点：平行六面体、长方体的概念及性质． 四、教学过程： （一）复习：1．凸多面体的概念，棱柱的概念； 2．平行六面体的概念． （二）新课讲解：1．平行六面体、长方体、正方体把学过的平行六面体与棱柱对照知：底面是平行四边形的四棱柱是平行六面体．侧棱与底 面垂直的平行六面体叫直平行六面体，底面是矩形的直平行六面体长方体，棱长都相等的 长方体叫正方体．2．平行六面体、长方体的性质定理：平行六面体的对角线交于一点，求证：对角线,,,AC BD CA DB ''''相交于一点，且在点O 处互相平分．证明：设O 是AC '的中点，则11()22AO AC AB AD AA ''==++u u u r u u u u r u u u r u u u r u u u r，设,,P M N 分别是,,BD CA DB '''的中点，同理：1()2AP AB AD AA '=++u u u r u u u r u u u r u u u r ，1()2AM AB AD AA '=++u u u u r u u u r u u u r u u u r，1()2AN AB AD AA '=++u u u r u u u r u u u r u u u r ，所以，,,,O P M N 四点重合，定理得证．定理：长方体的一条对角线长的平方等于一个顶点上的三条棱长的平方和．已知：长方体AC '中，AC '是一条对角线，求证：2222AC AB AD AA ''=++．证明：∵AC AB AD AA ''=++u u u u r u u u r u u u r u u u r ，∴2||()()AC AB AD AA AB AD AA '''=++⋅++u u u u r u u u r u u u r u u u r u u u r u u u r u u u r，∵AB AD ⊥u u u r u u u r ，AB AA '⊥u u u r u u u r ，AA AD '⊥u u u r u u u r ，D'C'B'A'DC BAH OA'D'C'B'DCBA∴2||AC AB AB AD AD AA AA '''=⋅+⋅+⋅u u u u r u u u r u u u r u u u r u u u r u u u r u u u r 222||||||AB AD AA '=++，即2222AC AB AD AA ''=++．（三）例题分析：例1．如图平行六面体ABCD A B C D ''''-中，,3A AB A AD BAD π''∠=∠∠=，,AB AD a AA b '===，求对角面BB D D ''的面积．解：∵BD AD AB =-u u u r u u u r u u u r ，∴()AA BD AA AD AB ''⋅=⋅-u u u r u u u r u u u r u u u r u u u r ，∵A AB A AD ''∠=∠，,AB AD a AA b '===，∴()(cos cos )0AA BD AA AD AB ab A AB A AD ''''⋅=⋅-=∠-∠=u u u r u u u r u u u r u u u r u u u r ，∴AA BD '⊥，∵//AA DD ''，∴DD BD '⊥，所以，对角面BB D D ''是矩形，它的面积是BD BB ab '⨯=． 例2．已知：正四棱柱ABCD A B C D ''''-的底面边长为2， （1）求二面角B AC B '--的大小；（2）求点B 到平面AB C '的距离。

D'C'B'A'DC BA平行六面体与长方体一、课题：平行六面体与长方体二、教学目标：1．掌握平行六面体、长方体、正方体的概念及性质；2．会利用平行六面体、长方体的性质解决有关长度与角度问题．三、教学重点、难点：平行六面体、长方体的概念及性质． 四、教学过程： （一）复习：1．凸多面体的概念，棱柱的概念； 2．平行六面体的概念． （二）新课讲解：1．平行六面体、长方体、正方体把学过的平行六面体与棱柱对照知：底面是平行四边形的四棱柱是平行六面体．侧棱与底 面垂直的平行六面体叫直平行六面体，底面是矩形的直平行六面体长方体，棱长都相等的 长方体叫正方体．2．平行六面体、长方体的性质定理：平行六面体的对角线交于一点，求证：对角线,,,AC BD CA DB ''''相交于一点，且在点O 处互相平分．证明：设O 是AC '的中点，则11()22AO AC AB AD AA ''==++， 设,,P M N 分别是,,BD CA DB '''的中点，同理：1()2AP AB AD AA '=++，1()2AM AB AD AA '=++，1()2AN AB AD AA '=++，所以，,,,O P M N 四点重合，定理得证．定理：长方体的一条对角线长的平方等于一个顶点上的三条棱长的平方和． 已知：长方体AC '中，AC '是一条对角线，求证：2222AC AB AD AA ''=++． 证明：∵AC AB AD AA ''=++，∴2||()()AC AB AD AA AB AD AA '''=++⋅++，∵AB AD ⊥，AB AA '⊥，AA AD '⊥，∴2||AC AB AB AD AD AA AA '''=⋅+⋅+⋅222||||||AB AD AA '=++，即2222AC AB AD AA ''=++．（三）例题分析：例1．如图平行六面体ABCD A B C D ''''-中，,3A AB A AD BAD π''∠=∠∠=，,AB AD a AA b '===，求对角面BB D D ''的面积．解：∵BD AD AB =-，∴()AA BD AA AD AB ''⋅=⋅-，∵A AB A AD ''∠=∠，,AB AD a AA b '===，H OA'D'C'B'DCBA∴()(cos cos )0AA BD AA AD AB ab A AB A AD ''''⋅=⋅-=∠-∠=， ∴AA BD '⊥，∵//AA DD ''，∴DD BD '⊥，所以，对角面BB D D ''是矩形，它的面积是BD BB ab '⨯=．例2．已知：正四棱柱ABCD A B C D ''''-的底面边长为2（1）求二面角B AC B '--的大小；（2）求点B 到平面AB C '的距离。

借助平行六面体模型解决四面体问题周益勇【摘要】四面体是最简单的多面体，而平行六面体特别是长方体是最熟悉的多面体，它们在立体几何中都有着非常重要的地位，以它们为载体考查立体几何的有关问题，在高考与竞赛中出现的频率很高．四面体经过补形可以成为平行六面体，平行六面体进行分割可以得到四面体，利用这种关系可以将四面体问题转化为平行六面体问题来解决．【期刊名称】《中学教研：数学版》【年(卷),期】2008(000)010【总页数】2页(P44-45)【关键词】平行六面体;四面体;立体几何;问题转化;多面体;长方体;补形;高考【作者】周益勇【作者单位】永嘉中学,浙江永嘉325114【正文语种】中文【中图分类】G633.6四面体是最简单的多面体，而平行六面体特别是长方体是最熟悉的多面体，它们在立体几何中都有着非常重要的地位，以它们为载体考查立体几何的有关问题，在高考与竞赛中出现的频率很高.四面体经过补形可以成为平行六面体，平行六面体进行分割可以得到四面体，利用这种关系可以将四面体问题转化为平行六面体问题来解决.1 利用平行六面体模型解决四面体问题若过四面体的每一条棱作平行于对棱的平面，则6个平面围成的几何体是平行六面体.例1 在四面体ABCD中，设直线AB与CD的距离为2，夹角为求四面体ABCD 的体积.(2003年全国数学竞赛试题)图1解如图1，把四面体补形成平行六面体，此时平行六面体的底面A1DB1C的面积为平行六面体的高即AB与CD的距离为2，因此平行六面体的体积为从而易得四面体ABCD的体积例2 求证：连结四面体任一顶点与它对面重心的线段交于一点，且这点将所在线段分成的比为3∶1，该点称为四面体的重心.图2分析如图2，将四面体A1BDC1补形成一个平行六面体，对角线AC1与面A1BD 交于点O，点G为平行六面体的中心，容易证得点O为△A1BD重心，且C1G∶GO=3∶1，同理可证另3条平行六面体的对角线也通过四面体的各面的重心，它们交于点G，同理可得比为3∶1，所以连结四面体任一顶点与它对面重心的线段交于一点，且这点将所在线段分成的比为3∶1.2 利用正方体模型解决正四面体问题过正四面体的每一条棱作平行于对棱的平面，则6个平面围成的几何体是正方体. 例3 金刚石是由碳原子组成的单质，在金刚石的晶体里，每个碳原子都被相邻的4个碳原子包围，且处于4个碳原子的中心，以共价键跟这4个碳原子结合.那么，在金刚石的晶体结构中，相邻的2个共价键之间的夹角(用反三角函数表示)是________.(第十五届希望杯数学竞赛试题)分析以相邻的4个碳原子为顶点构成正四面体，把该四面体补形成正方体，则该碳原子位于正方体的中心，相邻的2个共价键之间的夹角就是正方体2条对角线的夹角的补角，为例4 已知P是四面体ABCD内一点，且∠APB=∠APC=∠APD=∠BPC=∠BPD=∠CPD=θ，求sinθ的值.(1985年浙江省温州市数学竞赛试题)解在PA，PB，PC，PD上分别取点A1，B1，C1，D1，使得PA1=PB1=PC1=PD1，则四面体A1B1C1D1是正四面体.把它补形成正方体，则P为中心，同例3的解法可求得3 利用长方体模型解决直角四面体问题3条侧棱两两垂直的四面体(直角四面体)，以3条侧棱为边可以补成一个长方体. 例5 设P为直角四面体O-ABC的斜面ABC上的任意一点，则有下列结论成立：(1)若OP与OA，OB，OC所成的角依次为α,β,γ，则cos2α+cos2β+cos2γ=1；(2)若OP与3个直角面所成的角依次为α′，β′，γ′，则cos2α′+cos2β′+cos2γ′=2.图3分析如图3，该题可由直角四面体生成一个长方体，适当调整OA，OB，OC的长，使得OP所在直线为长方体的对角线，这样问题就转化为在长方体中，对角线与同一顶点发出的3条棱所成角的关系，对角线与同一顶点发出的3个面所成角关系.经过这样的转化，问题变得常规且简单，极易解决.引申已知S-ABC是3条棱两两互相垂直的三棱锥，O为底面ABC内一点，若∠OSA=α,∠OSB=β,∠OSC=γ，则tanαtanβtanγ的取值范围是( )(2007年全国高中数学联赛(吉林赛区)试题)解过点O分别作与SA,SB,SC平行的平面，得到一个长方体，且OS为长方体的对角线，因此cos2α+cos2β+cos2γ=1,于是sin2α=cos2β+cos2γ≥2cosβcosγ.同理sin2β=cos2α+cos2γ≥2cosαcosγ，sin2γ=cos2β+cos2α≥2cosβcosα，因此故选A．例6 在三棱锥S-ABC中，侧棱SA，SB，SC两两互相垂直，M为△ABC的重心，D为AB的中点，作与SC平行的直线DP．证明：(1)DP与SM相交；(2)设DP与SM的交点为D′，则D′为三棱锥S-ABC的外接球球心.(1993年高中数学竞赛试题)图4分析如图4，将三棱锥S-ABC补成长方体SAC′B-CB′S′A′，这时CSC′S′是长方形，AB与SC′互相平分于点D，且CD在平面CSC′S′上.因为DP∥SC，所以DP也在平面CSC′S′内，设SS′分别交PD,CD于H,N.由可得CN=2DN，因此N=M，H=D′.因为DP与SM相交于点D′,D′为SS′的中点，即长方体对角线的交点，所以D′为三棱锥S-ABC的外接球球心.4 利用长方体模型解决等腰四面体问题3组对棱分别相等的四面体(等腰四面体)过每一条棱作平行于对棱的平面，得到的平行六面体是长方体.例7 在三棱锥D-ABC中，AD=a,BD=b,AB=CD=c,且∠DAB+∠BAC+∠DAC=180°,∠DBA+∠ABC+∠DBC=180°.(1)求证：∠DCB+∠BCA+∠DCA=180°；(2)求异面直AD与BC所成角的大小.(2004年浙江省温州市数学竞赛试题)图5 图6解 (1)将三棱锥D-ABC的侧面沿各条侧棱剪开后,展在底面所在的平面上,如图6.由∠D1AB+∠BAC+∠D2AC=180°，可得D1,A,D2三点共线.又由∠D1BA+∠ABC+∠D3BC=180°，可得D1,B,D3三点共线.因为AD1=AD2,BD1=BD3,所以AB是△D1D2D3的中位线，即D2D3=2AB=2c.而CD2=CD3=c，因此CD2+CD3=D2D3，即D2,C,D3三点共线，从而∠DCB+∠BCA+∠DCA=180°.(2)由第(1)小题可知△ABD1≌△BCD3≌△ACD2，因此AD=BC=a,BD=AC=b.图7又AB=CD=c，所以三棱锥D-ABC的各对对棱均相等.将三棱锥放入如图7所示的长方体中,设长方体的长、宽、高分别为x,y,z,则解得因此故异面直AD与BC所成角的是由以上叙述可知，利用四面体与平行六面体之间的关系来认识四面体，研究四面体的性质，是一种重要的方法，这体现了转化的思想.参考文献【相关文献】[1] 虞关寿.四面体与平行六面体的关系探析[J].数学通讯，2005(9)：18-19.[2] 赵京育.四面体与它的外接平行六面体[J].高中数学教与学,2006(11)：9-10.。

第二十一章平行六面体的性质及应用【基础知识】平行六面体是平行四边形的一个三维类比模型，平行四边形的一系列有趣性质可推证到平行六面体中去．平行四边形与三角形有着极为密切的关系，因而平行六面体与四面体也有着极为密切的关系，这些构成了平行六面体一系列既有趣又有重要应用的性质．性质1平行六面体的四条对角线相交于一点，且在这一点互相平分，并称该点为中心．推论称侧面对角线的交点为侧面中心，则相对侧面中心的连线也交于平行六面体的中心，且在这一点互相平分．（见例5）性质2平行六面体所有对角线的平方和等于所有棱的平方和．推论1平行六面体所有侧面对角线的平方和等于其所有（体）对角线平方和的两倍．推论2平行六面体每一侧棱的平方等于与这侧棱共面的两侧面四条面对角线的平方和减去与这侧棱不共面而共端点的两条侧面对角线平方和所得差的四分之一．推论3平行六面体的每一对角线长的平方等于过这条对角线一端点的三条侧面对角线的平方和减去过另一端点的三条棱的平方和．性质3平行六面体的每一对角线长的平方等于共一端点的三条棱长的平方和减去这三条棱中每两条棱长及其所夹角余弦之积的两倍．性质4平行六面体的每一对角线通过与该对角线共端点的三条棱的另一端点构成的三角形截面的重心，且被这三角形截面分成三等分．性质5平行六面体的每个由三条侧面对角线构成的三角形截面面积平方的4倍，等于这截面所截三个侧面面积的平方和减去这三个侧面中每两个侧面面积及其所夹二面角余弦之积的两倍．推论平行六面体的八个由三条侧面对角线构成的三角形截面面积的平方和等于六个侧面面积的平方和．性质6设平行六面体的全面积为S ，四条对角线长为1AC l 、1A C l 、1BD l 、1BD l 、1B D l ，则111122222AC A C BD B DS l l l l +++≤． 性质7通过平行六面体中心的任何平面，将平行六面体分成体积相等的两部分．推论1以平行六面体任一顶点及这顶点出发的三条棱的端点构成的四面体体积是平行六面体体积的六分之一．推论2以平行六面体任一顶点及这顶点出发的三条侧面对角线端点构成的四面体体积是平行六面体体积的三分之一．性质8平行六面体的体积等于底面积与高的乘积，或任一侧面面积与相对面距离之积． 推论设共一顶点的三条棱长为a 、b 、c ，每两条棱的夹角为α、β、γ，则体积V 为V abc ==若记()12θαβγ=++，则2V =． 性质9()11113/22222124AC A C BD BDV l l l l +++≤；3/26S V ⎛⎫ ⎪⎝⎭≤．推论l 表面积一定的平行六面体中，以正方体之体积为最大．推论2在各个侧面面积为定值的平行六面体中，以长方体之体积为最大．性质11由平行六面体的各顶点，至不截此体的一平面所引诸垂线段之和，等于由其对角线之交点至同平面所引垂线段之和的8倍．性质10在平行六面体1111ABCD A B C D -中，截面分别与AB 、AD 、1AA 、1AC 交于0B 、0C 、0A 、0D 各点，则11000AC AA AB AD AC AB AD AA =++． 下面介绍平行六面体与四面体的密切关系． 1．对应关系作四面体的外接平行六面体，且使四面体的六条棱均成为平行六面体的侧面对角线．此时，四面体与其外接平行六面体是一一对应的．特别地，一个正四面体对应着一个正方体，一个等腰四面体（三对对棱分别相等的四面体）对应着一个长方体，一个两对对棱分别相等的四面体对应着一个直平行六面体，一个对棱均互相垂直的四面体（直角四面体或正三棱锥四面体）对应着一个菱形六面体等等．当四面体的共一顶点的三棱成为平行六面体的共顶点的三棱时，一个四面体对应着四个外接平行六面体，特别地，一个正四面体对应着一个一顶点面角均为60︒的菱形六面体，一个等腰四面体对应着两个一顶点面角之和为180︒的平行六面体等等． 2．隐显关系从本世纪初开始，人们试图将三角形的许多性质引申到四面体——最简单的多面体，事实证明发展四面体的几何学比三角形几何学困难得多，有些提法并不复杂的问题解答起来非常费劲，甚至未能解决．下面的例题将启示我们：四面体某些数量关系的发现及几何特征的显露，借助于其外接平行六面体的性质的运用是一种方便的重要途径．因此，可以说四面体的一些性质可以利其外接平行六面体来显现，平行六面体隐含了四面体的一些重要性质． 【典型例题与基本方法】例1在四面体ABCD 中，AB m =，CD n =，AD p =，BC q =，AC u =，BD u =．若AB 与CD 所成的角为θ，则()()2222cos 2p q u v mn+--=．证明如图211-，作四面体ABCD 的外接平行六面体A DB C AD BC ''''-，使四面体的棱都成为平行六面体的侧面对角线．A'B'C 'D '图21-1DA C显然，AB 与CD 所成的角θ就是A B ''与CD 所成的角，于是 ()()2222221/21/24cos 112222m n B D m n B D mn m n θ'+-⎡⎤⎡⎤'+-⎣⎦⎣⎦==⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭ 222222242222A D B D B D A D B D mn mn'''''+--==()()22222222222222p q u v A D D D D D B D mn mn+--''''---==． 例2若四面体的六条棱长分别为a 、b 、c 、d 、e 、f ，体积为V ，则有333333a b c d e f +++++≥(Weisenbock 不等式的一种三维推广)．证明如图211-，将四面体ABCD 补成平行六面体，则3ABCD V V =平行六面体．设平行六面体共顶点A 的三条棱长为l 、m 、n ，由前面的性质2的推论1，即有()2222222224a b c d e f l m n +++++=++．又由V l m n ⋅⋅平行六面体≤及幂平均值不等式，有113333332222223266a b c d e f a b c d e f ⎛⎫⎛⎫++++++++++ ⎪ ⎪⎝⎭⎝⎭≥．于是()322224212ABCD l m nV ⎡⎤++⎢⎥⎢⎥⎣⎦①()32222222112a b c d e f ⎡⎤=+++++⎢⎥⎣⎦()312233333331612a b c d e f ⎧⎫⎪⎪⎡⎤+++++⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭≤②)333333a b c d e f =+++++．故333333a b c d e f +++++≥．其中等号当且仅当①、②中满足l 、m 、n 互相垂直且l m n ==，即平行六面体为正方体，亦即a b c d e f =====时成立．类似上例，并运用前面的性质5的推论，可证明Weisenbock 不等式的另一种三维推广：若四面体各顶点A 、B 、C 、D 所对的面的面积分别为A S 、B S 、C S 、D S ，体积为V ，则33332A B C D S S S S +++ 例3空间四平面互相平行，相邻两面间距离都是h ．今有一正四面体，它的四个顶点分别在这四个面上．求正四面体的棱长．解设正四面体ABCD 的外接正方体为'AC BD A CB D '''-．又设过棱D D '及B C '中点F 的截面为3α，过棱C C '及A D '中点E 的截面为2α，过棱A A '，过棱B B '且与3α、2α平行的平面分别为1α、4α，这样这四个平面即为两相邻距离都相等的互相平行的四平面．又设过A B ''的中点O '与CE 垂直的直线为l ，l 与4α、3α、2α、1α的交点分别为B ''、D ''、C ''、A ''，如图21-2(b)，则4α、3α、2α、1α两相邻平面间距离为B D ''''、D C ''''、C A ''''．DEGO 'B"A"C "D "A'B'C 'D (b)(a)D图21-2CF当A C h ''''=时，可求得A E '=，从而A B ''=．这就是我们所要求的正四面体的棱长． 例4四面体ABCD 中，若AB CD ⊥，AC BD ⊥，则AD BC ⊥．（1957年天津市、1979年上海市中学竞赛题）证明如图211-，作四面体ABCD 的外接平行六面体A DB C AD BC ''''-．由平行六面体每一侧面两对角线所夹的角（锐角）的余弦值等于这侧面两相邻棱的平方差的绝对值除以这两条侧面对角线长的乘积，即()22cos A D DB A B CD A B CD''-'=''⋅．由AB CD ⊥，则()cos cos()0AB CD A B CD ''==，从而A D DB ''=，即侧面A DB C ''为菱形，同理，由AC BD ⊥．有侧面A CC A ''为菱形，从而侧面A DD A ''也为菱形，故AD BC ⊥． 例5求证四面体的三双对棱中点连线必交于一点，且互相平分．证明如图213-，设E 、F 、G 、H 、M 、N 分别是四面体ABCD 的六条棱的中点．作四面体的外接平行六面体1A C ，则E 、F 、G 、H 、M 、N 分别是其六侧面对角线的交点．图21-3G N EH OCDBAC 1A 1D 1B 1MF在11AAC C 中，连EF ，则11EF AA CC ∥∥，且过六面体对角线1A C 的中点O ，同时被O 平分．因六面体的四条对角线共点O ，于是同理可证GH 、MN 过O ，且被O 平分．例6立方体八个顶点中有四个恰是正四面体的顶点．求出立方体的表面积与四面体的表面积之比．（1980年美国中学生竞赛AHSME 第16题） 解设立方体表面积为S ，四面体表面积为0S ，由平行六面体所有三角形截面（三角形的边由六面体侧面对角线组成）面积的平方和等于所有侧面面积的平方和，有2206/4264S S ⎛⎫⎛⎫⋅⋅= ⎪ ⎪⎝⎭⎝⎭，故0/S S =【解题思维策略分析】1．善于将四面体问题转化为平行六面体问题例7若A 、B 、C 、D 表示空间四点，AB 表示A 、B 两点间的距离，AC 表示A 、C 两点间的距离，⋯．证明：222222AC BD AD BC AB CD ++++≥．（第4届美国中学生竞赛题） 证明以空间四边形的边为侧面对角线构造平行六面体，由平行六面体所有侧面对角线的平方和等于所有棱的平方和的两倍及图213-，有222222222111444AC BD AD BC AB CD AD AA A B +++++=++()22242AD AB CD =++故222222AC BD AD BC AB CD ++++≥．当A 、B 、C 、D 共面时，10AD =，上式取等号．此时，可看作是压扁了的四面体．例8在四面体ABCD 中，BDC ∠是直角，由D 到ABC △所在的平面的垂线的垂足H 是ABC △的垂心，证明：()()22226AB BC CA AD BD CD ++++≤．（IMO 12-试题）证明如图214-，平行六面体1111AC BD B D AC -为四面体ABCD 的外接平行六面体．由题设，D 到ABC △所在的平面的垂线的垂足是ABC △的垂心，知这个四面体的对棱互相垂直，又BDC ∠是直角，即知四面体ABCD 的三面角D ABC -是直三面角，故此平行六面体为长方体．CDBAC 1A 1D 1B 1图21-4H由()2222AD BD CD ++()()()222222AD BD BD CD CD AD =+++++222AB BC AC =++．故()()22222263AD BD CD AB BC AC ++=++222222AB BC CA AB BC BC CA AB CA +++⋅+⋅+⋅≥ ()2AB BC CA =++．例9若a 、b 、c 是四面体共顶点的三条棱的长，α、β、γ，是这三条棱组成的面角，ω是这三个面角和的一半，则四面体的体积为：13V abc =四面体证明如图21-4，设DA a =，DB b =，DC c =，BDC α∠=，ADC β∠=， ADB γ∠=．由平行六面体的体积公式()V abc S A =⋅平行六面体，其中()S A= 有16V V =四面体平行六面体1=3abc 2．善于构造平行六面体解答有关问题例10已知a 、b 、c +∈R ，且2221a b c ++=3a b c ++>．证明由2221a b c ++=3a b c ++>．参见图212- (a)，构作长方体AB '．设对角线1AB '=，AD a '=，AC b '=，AA c '=，则A B ''B C ''=，B D ''．在A AB ''△中，A A A B B A ''''+>，即1c >．同理，1b >1a >．以上三式相加，即证．例11锐角α．β、γ满足222sin sin sin 1αβγ++=，求证：π3π24αβγ<++<． 证明构造长方体D AC B DA CB ''''-，参见图212- (a)，使其长、宽、高分别为sin D A α'=，sin AC β'=，sin C C γ'=，则1AB D C ''===，D B A α''∠=，C B A β''∠=，C D C γ''∠=，且AB BA '>．sin sin sin D A D AD B A D BA B A BA α'''''∴=∠=<=∠'， sin sin sin AC AC C B A C BA B A BAβ'''''=∠=<=∠'．从而D BA α'<∠，C BA β'<∠． 1π2D BA C BA αβ''∴+<∠+∠=．同理，π2βγ+<，π2αγ+<，即3π4αβγ++<． 设B A '与D C '相交于O ，则知2D OA α'∠=，2AOC β'∠=，2C OC γ'∠=． 由于三面角的任意两个面角的和大于第三个面角，则 22D OA AOC D OC αβ'''+=∠+∠>∠． ()2πD OC C OC αβγ''∴++=∠+∠=．故π3π24αβγ<++<． 3．注意特殊平面体的性质的运用例12正方体1111ABCD A B C D -的棱长为1，求正方体底面ABCD 内切圆周上的点与过顶点1A 、C 和1B 的圆周上的点之间的最小距离．（第19届全苏奥林匹克题）图21-5C1A B解如图215-，考察两个圆周分别在以正方体的对称中心为球心的两个同心球面上，即与正方体各棱都）上，这两个球面上的点之间的最小距离是它们的半径之差12d =．如果两圆周上各有一点恰好在球心O 发出的同一射线上，那么d 即为最小值．考察在以O 为位似比的变换下，小球面变为大球面，而小球面上的圆周的象集为大球面上的圆周．注意到ABCD 的内切圆1O 与线段BD 的交点E 和F 在该位似变换下的象在平面1AB C 的两侧（因11145O OF BB O ∠=︒>∠，故射线OF 不与平面1AB C 相交），因此，1O 的象集（圆周）将与过顶点A ，C 和1B 的圆周相交．设一交点为N ，而N 的原象为M，那么M ，N 之间的距离就是考察的两圆周上的点之间的距离的最小值，其值为12d =．【模拟实战】习题A1．在正方体1111ABCD A B C D -中，O 是面ABCD 的中心，1O 是面11ADD A 的中心．求异面直线1D O 与1BO 所成角的余弦值．2．已知空间一个平面与一个正方体的12条棱的夹角都等于口α，求α的值．3．能否用一个平面去截一个正方体，使得截面为五边形？进一步，截面是否为正五边形？4．设一个平面截棱长为1的正方体1111ABCD A B C D -，过顶点1C ，交1A D 1中点于E ，1A A 距A 较近的一个三等分点于F ，AB 于G ，BC于H ．求截面1C EFGH 的周长．5．已知一个平面截棱长为1的正方体所得截面是—个六边形．证明：此六边形周长≥． 6．正三棱锥S ABC -的侧棱与底面边长相等，如果E ，F 分别为SC ，AB 的中点，那么异面直线EF 与SA 所成的角等于多少？7．已知111ABC A B C -是直三棱柱，90BAC ∠=︒，点1D ，1F 分别是11A B ，11B C 的中点．若1AB CA AA ==，求1BD 与1CF 所夹角的余弦值．8．已知ABCD 是边长为4的正方形，E ，F 分别是AB ，AD 的中点，GC ⊥面ABCD ，且2GC =．求点B 到面EFG 的距离．9．在四面体SABC 中，已知SA BC a ==，SC AB b ==，SB AC c ==，求此四面体的体积． 10．在四面体1234A A A A 中，相应对棱中点的三条连线分别为1m ，2m ，3m ，顶点i A 所对侧面的重心为i G ，其四面体体积记为V ，则 （Ⅰ）1233m m m V ⋅⋅≥；（Ⅱ）421412716i j i i i j i A A AG =-∑∑≤≤≤≥（Ⅲ）421i i i AG =∑ 11．已知α，β，γ是锐角，且222cos cos cos 1αβγ++=．求证：（Ⅰ）tan tan tan αβγ⋅⋅≥ （Ⅱ）3ππ4αβγ<++<． 12．已知0a >，0b >，0c >，且1a b c ++=．习题B1．有一立方体，中心和边长为a b c <<的长方体的对称中心重合，诸界面与长方体各界面平行，求立方体的棱长，使得它与长方体的并的体积减去它与长方体的交的体积的差最小．（1979年捷克竞赛题） 2．证明：在棱长为a 的立方体内部可以作两个棱长为a 的正四面体，使得它们没有公共点．（1983年民主德国竞赛题）。

第二十一章平行六面体的性质及应用【基础知识】平行六面体是平行四边形的一个三维类比模型，平行四边形的一系列有趣性质可推证到平行六面体中去．平行四边形与三角形有着极为密切的关系，因而平行六面体与四面体也有着极为密切的关系，这些构成了平行六面体一系列既有趣又有重要应用的性质．性质1平行六面体的四条对角线相交于一点，且在这一点互相平分，并称该点为中心．推论称侧面对角线的交点为侧面中心，则相对侧面中心的连线也交于平行六面体的中心，且在这一点互相平分．（见例5）性质2平行六面体所有对角线的平方和等于所有棱的平方和．推论1平行六面体所有侧面对角线的平方和等于其所有（体）对角线平方和的两倍．推论2平行六面体每一侧棱的平方等于与这侧棱共面的两侧面四条面对角线的平方和减去与这侧棱不共面而共端点的两条侧面对角线平方和所得差的四分之一．推论3平行六面体的每一对角线长的平方等于过这条对角线一端点的三条侧面对角线的平方和减去过另一端点的三条棱的平方和．性质3平行六面体的每一对角线长的平方等于共一端点的三条棱长的平方和减去这三条棱中每两条棱长及其所夹角余弦之积的两倍．性质4平行六面体的每一对角线通过与该对角线共端点的三条棱的另一端点构成的三角形截面的重心，且被这三角形截面分成三等分．性质5平行六面体的每个由三条侧面对角线构成的三角形截面面积平方的4倍，等于这截面所截三个侧面面积的平方和减去这三个侧面中每两个侧面面积及其所夹二面角余弦之积的两倍．推论平行六面体的八个由三条侧面对角线构成的三角形截面面积的平方和等于六个侧面面积的平方和．性质6设平行六面体的全面积为S ，四条对角线长为1AC l 、1A C l 、1BD l 、1BD l 、1B D l ，则111122222AC A C BD BDS l l l l +++≤． 性质7通过平行六面体中心的任何平面，将平行六面体分成体积相等的两部分．推论1以平行六面体任一顶点及这顶点出发的三条棱的端点构成的四面体体积是平行六面体体积的六分之一．推论2以平行六面体任一顶点及这顶点出发的三条侧面对角线端点构成的四面体体积是平行六面体体积的三分之一．性质8平行六面体的体积等于底面积与高的乘积，或任一侧面面积与相对面距离之积． 推论设共一顶点的三条棱长为a 、b 、c ，每两条棱的夹角为α、β、γ，则体积V 为V abc =若记()12θαβγ=++，则2V = 性质9()11113/22222124AC A C BD B D V l l l l +++≤；3/26S V ⎛⎫ ⎪⎝⎭≤．推论l 表面积一定的平行六面体中，以正方体之体积为最大．推论2在各个侧面面积为定值的平行六面体中，以长方体之体积为最大．性质11由平行六面体的各顶点，至不截此体的一平面所引诸垂线段之和，等于由其对角线之交点至同平面所引垂线段之和的8倍．性质10在平行六面体1111ABCD A B C D -中，截面分别与AB 、AD 、1AA 、1AC 交于0B 、0C 、0A 、0D 各点，则110000AC AA AB AD AC AB AD AA =++． 下面介绍平行六面体与四面体的密切关系． 1．对应关系作四面体的外接平行六面体，且使四面体的六条棱均成为平行六面体的侧面对角线．此时，四面体与其外接平行六面体是一一对应的．特别地，一个正四面体对应着一个正方体，一个等腰四面体（三对对棱分别相等的四面体）对应着一个长方体，一个两对对棱分别相等的四面体对应着一个直平行六面体，一个对棱均互相垂直的四面体（直角四面体或正三棱锥四面体）对应着一个菱形六面体等等．当四面体的共一顶点的三棱成为平行六面体的共顶点的三棱时，一个四面体对应着四个外接平行六面体，特别地，一个正四面体对应着一个一顶点面角均为60︒的菱形六面体，一个等腰四面体对应着两个一顶点面角之和为180︒的平行六面体等等． 2．隐显关系从本世纪初开始，人们试图将三角形的许多性质引申到四面体——最简单的多面体，事实证明发展四面体的几何学比三角形几何学困难得多，有些提法并不复杂的问题解答起来非常费劲，甚至未能解决．下面的例题将启示我们：四面体某些数量关系的发现及几何特征的显露，借助于其外接平行六面体的性质的运用是一种方便的重要途径．因此，可以说四面体的一些性质可以利其外接平行六面体来显现，平行六面体隐含了四面体的一些重要性质． 【典型例题与基本方法】例1在四面体ABCD 中，AB m =，CD n =，AD p =，BC q =，AC u =，BD u =．若AB 与CD 所成的角为θ，则()()2222cos 2p q u v mn+--=．证明如图211-，作四面体ABCD 的外接平行六面体A DB C AD BC ''''-，使四面体的棱都成为平行六面体的侧面对角线．A'B'C 'D '图21-1DA C显然，AB 与CD 所成的角θ就是A B ''与CD 所成的角，于是 ()()2222221/21/24cos 112222m n B D m n B D mn m n θ'+-⎡⎤⎡⎤'+-⎣⎦⎣⎦==⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭ 222222242222A D B D B D A D B D mn mn'''''+--==()()22222222222222p q u v A D D D D D B D mn mn+--''''---==．例2若四面体的六条棱长分别为a 、b 、c 、d 、e 、f ，体积为V ，则有333333a b c d e f +++++≥(Weisenbock 不等式的一种三维推广)．证明如图211-，将四面体ABCD 补成平行六面体，则3ABCD V V =平行六面体．设平行六面体共顶点A 的三条棱长为l 、m 、n ，由前面的性质2的推论1，即有()2222222224a b c d e f l m n +++++=++．又由V l m n ⋅⋅平行六面体≤及幂平均值不等式，有113333332222223266a b c d e f a b c d e f ⎛⎫⎛⎫++++++++++ ⎪ ⎪⎝⎭⎝⎭≥．于是()322224212ABCD l m nV ⎡⎤++⎢⎥⎢⎥⎣⎦①()32222222112a b c d e f ⎡⎤=+++++⎢⎥⎣⎦()312233333331612a b c d e f ⎧⎫⎪⎪⎡⎤+++++⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭≤②)333333a b c d e f =+++++．故333333a b c d e f +++++≥．其中等号当且仅当①、②中满足l 、m 、n 互相垂直且l m n ==，即平行六面体为正方体，亦即a b c d e f =====时成立．类似上例，并运用前面的性质5的推论，可证明Weisenbock 不等式的另一种三维推广：若四面体各顶点A 、B 、C 、D 所对的面的面积分别为A S 、B S 、C S 、D S ，体积为V ，则33332A B C D S S S S +++ 例3空间四平面互相平行，相邻两面间距离都是h ．今有一正四面体，它的四个顶点分别在这四个面上．求正四面体的棱长．解设正四面体ABCD 的外接正方体为'AC BD A CB D '''-．又设过棱DD'及B C '中点F 的截面为3α，过棱C C '及A D '中点E 的截面为2α，过棱A A '，过棱B B '且与3α、2α平行的平面分别为1α、4α，这样这四个平面即为两相邻距离都相等的互相平行的四平面．又设过A B ''的中点O '与CE 垂直的直线为l ，l 与4α、3α、2α、1α的交点分别为B ''、D ''、C ''、A ''，如图21-2(b)，则4α、3α、2α、1α两相邻平面间距离为B D ''''、D C ''''、C A ''''．DGO 'B"A"C "D "B'C 'D (b)(a)D图21-2CF当A C h ''''=时，可求得A E '=，从而A B ''=．这就是我们所要求的正四面体的棱长． 例4四面体ABCD 中，若AB CD ⊥，AC BD ⊥，则AD BC ⊥．（1957年天津市、1979年上海市中学竞赛题）证明如图211-，作四面体ABCD 的外接平行六面体A DB C AD BC ''''-．由平行六面体每一侧面两对角线所夹的角（锐角）的余弦值等于这侧面两相邻棱的平方差的绝对值除以这两条侧面对角线长的乘积，即 ()22cos A D DB A BCD A B CD''-'=''⋅．由AB CD ⊥，则 ()cos cos()0ABCD A B CD ''== ，从而A D DB ''=，即侧面A DB C ''为菱形，同理，由AC BD ⊥．有侧面A CC A ''为菱形，从而侧面A DD A ''也为菱形，故AD BC ⊥．例5求证四面体的三双对棱中点连线必交于一点，且互相平分．证明如图213-，设E 、F 、G 、H 、M 、N 分别是四面体ABCD 的六条棱的中点．作四面体的外接平行六面体1A C ，则E 、F 、G 、H 、M 、N 分别是其六侧面对角线的交点．图21-3G N EH OCDBAC 1A 1D 1B 1MF在11AA C C 中，连EF ，则11EF AA CC ∥∥，且过六面体对角线1A C 的中点O ，同时被O 平分．因六面体的四条对角线共点O ，于是同理可证GH 、MN 过O ，且被O 平分．例6立方体八个顶点中有四个恰是正四面体的顶点．求出立方体的表面积与四面体的表面积之比．（1980年美国中学生竞赛AHSME 第16题） 解设立方体表面积为S ，四面体表面积为0S ，由平行六面体所有三角形截面（三角形的边由六面体侧面对角线组成）面积的平方和等于所有侧面面积的平方和，有2206/4264S S ⎛⎫⎛⎫⋅⋅= ⎪ ⎪⎝⎭⎝⎭，故0/S S【解题思维策略分析】1．善于将四面体问题转化为平行六面体问题例7若A 、B 、C 、D 表示空间四点，AB 表示A 、B 两点间的距离，AC 表示A 、C 两点间的距离，⋯．证明：222222AC BD AD BC AB CD ++++≥．（第4届美国中学生竞赛题） 证明以空间四边形的边为侧面对角线构造平行六面体，由平行六面体所有侧面对角线的平方和等于所有棱的平方和的两倍及图213-，有222222222111444AC BD AD BC AB CD AD AA A B +++++=++()22242AD AB CD =++故222222AC BD AD BC AB CD ++++≥．当A 、B 、C 、D 共面时，10AD =，上式取等号．此时，可看作是压扁了的四面体．例8在四面体ABCD 中，BDC ∠是直角，由D 到ABC △所在的平面的垂线的垂足H 是ABC △的垂心，证明：()()22226AB BC CA AD BD CD ++++≤．（I MO 12-试题）证明如图214-，平行六面体1111AC BD B D AC -为四面体ABCD 的外接平行六面体．由题设，D 到ABC △所在的平面的垂线的垂足是ABC △的垂心，知这个四面体的对棱互相垂直，又BDC ∠是直角，即知四面体ABCD 的三面角D ABC -是直三面角，故此平行六面体为长方体．CDBC 1A 1D 1B 1图21-4H由()2222AD BD CD ++()()()222222AD BD BD CD CD AD =+++++222AB BC AC =++．故()()22222263AD BD CD AB BC AC ++=++222222AB BC CA AB BC BC CA AB CA +++⋅+⋅+⋅≥()2AB BC CA =++．例9若a 、b 、c 是四面体共顶点的三条棱的长，α、β、γ，是这三条棱组成的面角，ω是这三个面角和的一半，则四面体的体积为：13V abc =四面体证明如图21-4，设DA a =，DB b =，DC c =，BDC α∠=，ADC β∠=，ADB γ∠=．由平行六面体的体积公式()V abc S A =⋅平行六面体，其中()S A=有16V V =四面体平行六面体1=3abc 2．善于构造平行六面体解答有关问题例10已知a 、b 、c +∈R ，且2221a b c ++=3a b c ++>．证明由2221a b c ++=3a b c ++>．参见图212- (a)，构作长方体AB '．设对角线1AB '=，AD a '=，AC b '=，AA c '=，则A B ''=B C ''，B D ''=．在A AB ''△中，A A AB B A ''''+>，即1c >．同理，1b >1a >．以上三式相加，即证．例11锐角α．β、γ满足222sin sin sin 1αβγ++=，求证：π3π24αβγ<++<． 证明构造长方体D AC B DA CB ''''-，参见图212- (a)，使其长、宽、高分别为sin D A α'=，sin AC β'=，sin C C γ'=，则1AB D C ''=，D B A α''∠=，C B A β''∠=，C D C γ''∠=，且AB BA '>．sin sin sin D A D AD B A D BA B A BA α'''''∴=∠=<=∠'， sin sin sin AC AC C B A C BA B A BAβ'''''=∠=<=∠'．从而D BA α'<∠，C BA β'<∠． 1π2D BA C BA αβ''∴+<∠+∠=．同理，π2βγ+<，π2αγ+<，即3π4αβγ++<． 设B A '与D C '相交于O ，则知2D OA α'∠=，2AOC β'∠=，2C OC γ'∠=． 由于三面角的任意两个面角的和大于第三个面角，则 22D OA AOC D OC αβ'''+=∠+∠>∠． ()2πD OC C OC αβγ''∴++=∠+∠=．故π3π24αβγ<++<． 3．注意特殊平面体的性质的运用例12正方体1111ABCD A B C D -的棱长为1，求正方体底面ABCD 内切圆周上的点与过顶点1A 、C 和1B 的圆周上的点之间的最小距离．（第19届全苏奥林匹克题）图21-5C1A B解如图215-，考察两个圆周分别在以正方体的对称中心为球心的两个同心球面上，即与正方体各棱都）上，这两个球面上的点之间的最小距离是它们的半径之差12d =．如果两圆周上各有一点恰好在球心O 发出的同一射线上，那么d 即为最小值．考察在以O 为位似比的变换下，小球面变为大球面，而小球面上的圆周的象集为大球面上的圆周．注意到ABCD 的内切圆1O 与线段BD 的交点E 和F 在该位似变换下的象在平面1AB C 的两侧（因11145O OF BB O ∠=︒>∠，故射线OF 不与平面1AB C 相交），因此，1O 的象集（圆周）将与过顶点A ，C 和1B 的圆周相交．设一交点为N ，而N 的原象为M ，那么M ，N 之间的距离就是考察的两圆周上的点之间的距离的最小值，其值为12d =．【模拟实战】习题A1．在正方体1111ABCD A B C D -中，O 是面ABCD 的中心，1O 是面11ADD A 的中心．求异面直线1D O 与1BO 所成角的余弦值．2．已知空间一个平面与一个正方体的12条棱的夹角都等于口α，求α的值．3．能否用一个平面去截一个正方体，使得截面为五边形？进一步，截面是否为正五边形？4．设一个平面截棱长为1的正方体1111ABCD A B C D -，过顶点1C ，交1A D 1中点于E ，1A A 距A 较近的一个三等分点于F ，AB 于G ，BC于H ．求截面1C EFGH 的周长．5．已知一个平面截棱长为1的正方体所得截面是—个六边形．证明：此六边形周长≥． 6．正三棱锥S ABC -的侧棱与底面边长相等，如果E ，F 分别为SC ，AB 的中点，那么异面直线EF 与SA 所成的角等于多少？7．已知111ABC A B C -是直三棱柱，90BAC ∠=︒，点1D ，1F 分别是11A B ，11B C 的中点．若1AB CA AA ==，求1BD 与1CF 所夹角的余弦值．8．已知ABCD 是边长为4的正方形，E ，F 分别是AB ，AD 的中点，GC ⊥面ABCD ，且2GC =．求点B 到面EFG 的距离．9．在四面体SABC 中，已知SA BC a ==，SC AB b ==，SB AC c ==，求此四面体的体积． 10．在四面体1234A A A A 中，相应对棱中点的三条连线分别为1m ，2m ，3m ，顶点i A 所对侧面的重心为i G ，其四面体体积记为V ，则 （Ⅰ）1233m m m V ⋅⋅≥；（Ⅱ）421412716i j i i i j i A A AG =-∑∑≤≤≤≥（Ⅲ）421i i i AG =∑ 11．已知α，β，γ是锐角，且222cos cos cos 1αβγ++=．求证：（Ⅰ）tan tan tan αβγ⋅⋅≥ （Ⅱ）3ππ4αβγ<++<． 12．已知0a >，0b >，0c >，且1a b c ++=．习题B1．有一立方体，中心和边长为a b c <<的长方体的对称中心重合，诸界面与长方体各界面平行，求立方体的棱长，使得它与长方体的并的体积减去它与长方体的交的体积的差最小．（1979年捷克竞赛题） 2．证明：在棱长为a 的立方体内部可以作两个棱长为a 的正四面体，使得它们没有公共点．（1983年民主德国竞赛题）。

OA B C D E C BA SFz 四面体问题求解中的“嵌”与“补”江苏省姜堰中学 张圣官（225500）四面体（即三棱锥）是立体几何中最基本的一个几何体，而它又是与平行六面体密切相关的。

有些四面体问题，若将之放到平行六面体背景中，则往往能显现其中隐含的线面关系，从而使问题获得优解。

本文通过事例重点说明在正方体或长方体中如何巧解相关的四面体问题。

1． 将四面体“嵌入”到平行六面体中我们知道，任何一个四面体都可以“嵌入”到一个平行六面体中，而使四面体的六条棱分别是平行六面体六个面的一条面对角线。

例如，在证明“四面体顶点到对面三角形重心的四条连线交于一点”（此即为四面体重心）时，实施这种“嵌入”后，问题就转化为论证“平行六面体四条体对角线交于一点”，这就容易多了，而且易得四面体重心把四条连线都分成3：1的两部分。

下面看几例这种“嵌入”的应用。

例1（2000年全国高中数学联赛题）一个球与正四面体的六条棱都相切，若正四面体的棱长为a ，则这个球的体积是____________________。

分析：将正四面体ABCD “嵌入”到正方体中，使正四面体的六条棱分别是正方体六个面的面对角线（如图1），则球O 与正四面体的六条棱都相切等价于球O 与正方体的六个 面都相切。

易知正方体棱长为a 22，所以球半径为a 42，故 （图1）球的体积为363334a R ππ=。

例2（1990年全国高考题）正三棱锥S-ABC 的侧棱与底面边长相等，如果E 、F 分别为SC 、AB 的中点，那么异面直线EF 与SA 所成的角等于 （ ） A 900 B 600 C 450 D 300分析：本题的正三棱锥S-ABC 即为正四面体，将正 四面体SABC “嵌入”到正方体中，使正四面体的六条棱分别是正方体六个面的面对角线（如图2），易知EF 在正方体的两底面中心连线上，与正方体的一条侧棱平行。

而 SA 与该侧棱所成角是450，故异面直线EF 与SA 所成的 角等于450，选（C ）。