部分分式法综合无源网络
- 格式:doc
- 大小:157.50 KB
- 文档页数:2

二题目:已知()t t f 5.0=,则其()[]=t f L 【 】A. 25.0s s +B. 25.0sC.221sD. s 21 分析与提示:由拉氏变换的定义计算,可得()[]215.0s t f L = 答案:C题目:函数f (t )的拉氏变换L[f(t)]= 。
分析与提示:拉氏变换定义式。
答案:dt e t f st ⎰∞-0)(题目:函数()atet f -=的拉氏变换L[f(t)]= 。
分析与提示:拉氏变换定义式可得,且f(t)为基本函数。
答案:as +1题目:若te t tf 22)(-=,则()=)]([t f L 【 】A.22+s B.3)2(2+s C.22-s D.3)2(2-s 分析与提示:拉氏变换定义式可得,即常用函数的拉氏变换对,3)2(2)]([+=s t f L答案:B题目:拉氏变换存在条件是,原函数f(t)必须满足 条件。
分析与提示:拉氏变换存在条件是,原函数f(t)必须满足狄里赫利条件。
答案:狄里赫利题目:已知()15.0+=t t f ,则其()[]=t f L 【】A. 25.0s s +B. 25.0sC.ss 1212+D. s 21分析与提示:由拉氏变换的定义计算,这是两个基本信号的和,由拉氏变换的线性性质,其拉氏变换为两个信号拉氏变换的和。
()[]s st f L 115.02+= 答案:C题目:若()ss s s F ++=214,则()t f t ∞→lim )=( )。
【 】 A. 1 B. 4C. ∞D. 0分析与提示:根据拉氏变换的终值定理)(lim )(lim )(0s sF t f f s t →∞→==∞。
即有414lim )(lim 20=++=→∞→ss s st f s t答案:B题目:函数()t et f atωcos -=的拉氏变换L[f(t)]= 。
分析与提示:基本函数t ωcos 的拉氏变换为22ω+s s,由拉氏变换的平移性质可知()[]()22ω+++=a s as t f L 。


部分分式法综合无源网络作者:曾幸张利敏李晗琳来源:《科学与信息化》2017年第16期摘要对于一个比较复杂的网络函数,不能通过直接法进行综合,需要采用其他的方法进行综合。
其中一种常用的方法就是部分分式法。
用部分分式法综合无源网络的思路是:将网络的阻抗函数由通常的多项式表达形式分解为部分分式,而部分分式中的每一个因式可以通过直接综合法用一个电阻、电容、电感或它们的简单组合来实现,从而完成整个网络的综合。
利用部分分式法综合实现的网络称为福斯特网络。
其中,只包含电感和电容元件的福斯特网络称为LC福斯特网络。
根据阻抗表示式实现的福新特网络称为福斯特1型网络。
关键词部分分式法;综合无源网络引言滤波器广泛应用于我们的生活,随着网络函数越来越复杂,我们可以把复杂的函数简单化去解决。
2.2 网络的结构的确定也可以根据下面的方法,首先确定网络元件的数目,从而确定网络的结构(1)元件总数的确定LC福斯特1型网络元件数目由网络阻抗函数Z(s)的极点总数目(包括无穷大处极点的数目)确定。
其中,电容和电感的数目要么相等,要么差值为1。
(2)串联电感和串联电容的确定如果网络的极点数目为奇数,则网络所需元件数目为奇数,就需要一个串联电感串联电容。
具体可以根据Z(0)的值是零还是无穷大来确定网络的第一个串联元件是电感还是电容。
如果Z(0)=0,则网络中的第一个串联元件是电感。
如果Z(0)=∞,则网络中第一个串联元件是电容。
如果网络的极点数目为偶数,则串联电感和串联电容要么都需要,要么都不需要。
如果z (0)=∞或z(∞)=0,则串联电感和串联电容都需要。
如果Z(0)=0或Z(∞)=0,则串联电感和串联电容都不需要[2]。
(3)LC并联电路的个数的确定网络中LC并联电路的个数由阻抗函数共轭复数极点的数目来确定。
3 网络元件值的确定网络元件的数值由Z(s)的表达式或根据各元件的表达式确定。
参考文献[1] 陈邦媛.射频通信电路[M].北京:科学出版社,2006:12-13.[2] 杨志民,马义德,张新国.现代电路理论与设计[M].北京:清华大学出版2009:45-67,95-98。

无源网络分析与无源滤波器设计技巧无源网络是指不包含放大器或主动元件的电路或网络。
在电子工程领域中,无源网络的分析和设计是一项重要的技术,它可以帮助我们理解和设计各种类型的电路和系统。
本文将介绍无源网络的分析方法,以及无源滤波器的设计技巧。
一、无源网络分析方法无源网络的分析方法主要有基尔霍夫定律和等效电路法。
1. 基尔霍夫定律基尔霍夫定律是无源网络分析中的基本原理,它包括基尔霍夫的电流定律和基尔霍夫的电压定律。
基尔霍夫的电流定律(KCL)指出,在任何一个节点处,进入该节点的电流之和等于离开该节点的电流之和。
这个定律可以帮助我们分析节点处的电流分布,以及节点间的电流关系。
基尔霍夫的电压定律(KVL)指出,在任何一个闭合回路中,电压源的代数和等于电阻元件(包括电压源内部电阻)的电压代数和。
这个定律可以帮助我们分析回路中的电压分布,以及回路中各个元件之间的关系。
通过应用基尔霍夫定律,我们可以对无源网络进行电流和电压分布的分析,从而得到网络的行为和性能特征。
2. 等效电路法等效电路法是一种将复杂的无源网络转化为等效电路的方法。
通过将无源网络中的元件(如电阻、电容、电感)用等效电路替代,我们可以简化网络的分析和计算过程。
等效电路法的一种常见应用是将复杂的无源网络转化为Thévenin等效电路或Norton等效电路。
这种方法可以帮助我们以更简单和直观的方式分析无源网络的行为和性能。
二、无源滤波器设计技巧无源滤波器是一种通过使用电容、电感和电阻等被动元件来去除或改变信号中特定频率成分的电路。
在无源滤波器的设计过程中,我们需要考虑滤波器的类型、截止频率、频率响应等方面。
无源滤波器主要分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
设计每种类型的滤波器时,我们需要选择合适的元件数值和拓扑结构,以实现所需的频率特性。
1. 低通滤波器低通滤波器允许低频信号通过而阻止高频信号。
常见的低通滤波器包括RC低通滤波器和RL低通滤波器。

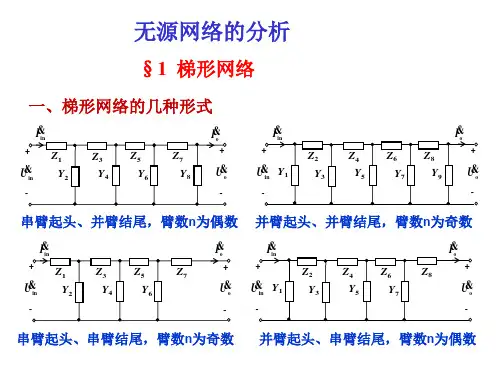




网络设计方法总结作者:吴金涛赵耀来源:《中国科技博览》2015年第27期[摘要]电网络对于信息处理系统、供配电系统都是非常重要的组成部分之一,电网络性能的差异将会对于整个系统产生深远的影响。
根据所用元件的不同,电网络又可被分为无源网络和有源网络两大类。
在本文中,对于无源网络和有源网络的综合方法进行了总结。
中图分类号:TN822 文献标识码:A 文章编号:1009-914X(2015)27-0132-011、无源网络的设计对于无源网络,其是由电阻、电容、电感三种基本元件通过一定的组合构成的,这一电路结构不提供能量。
无源单口网络的设计方法是建立在网络函数和频率特性的基础上,即设计的任务要求以网络函数的形式给出,设计的元件参数也用网络函数表达。
由于网络函数的零极点位置由电路的频率特性决定,因此,电路设计的关键是使得电路在指定位置上有所需要的零极点以实现性能指标要求的频率特性。
1.1 无源单口网络设计1.1.1 LC单口网络设计LC单口网络由于只包含电感与电容两种电抗元件,故而又被称为电抗单口网络。
在进行电路设计时,将需要达到的设计目标以网络函数的形式表达出来,进而分析网络函数的零极点位置。
通过结合电感与电容自身的频率特性,可以得到二者在复平面上的阻抗和导纳的零极点位置。
因此,进行设计的原理就是,通过电感与电容的组合,设计出LC单口网络,使其阻抗或导纳的零极点位置与待综合的网络函数的零极点位置相同。
设计LC单口网络的方法主要有福斯特法与考尔法:⑴福斯特法又称为部分分式法。
设计的基本步骤和方法是:①根据网络函数确定阻抗或导纳函数零极点的位置,画出阻抗或导纳的零极点图;②由电感、电容元件的零极点,确定在电路中应采用哪些元件与怎样的组合方式,由此确定网络的结构;③将阻抗或导纳函数改写成部分分式求和的形式;④与阻抗元件的函数表达式进行对比,确定对应的元件的参数值,确定最终的网络结构与元件参数值。
⑵考尔法是将极点交替移去以得到梯形网络结构的方法。
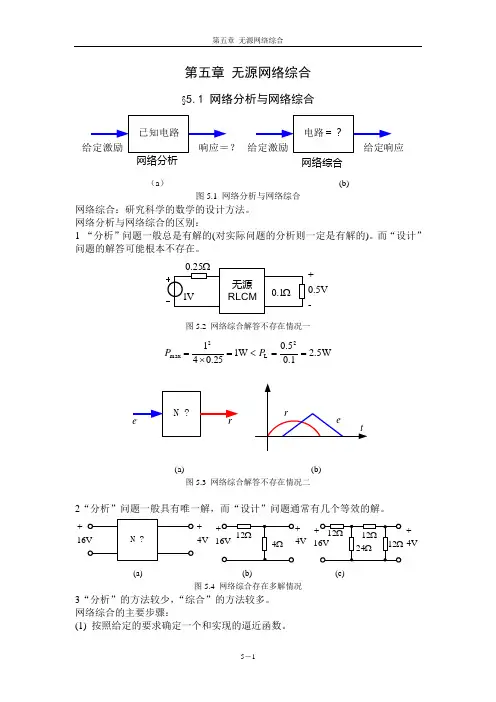
第五章 无源网络综合§5.1 网络分析与网络综合网络分析网络综合(a ) (b)图5.1 网络分析与网络综合网络综合:研究科学的数学的设计方法。
网络分析与网络综合的区别:1 “分析”问题一般总是有解的(对实际问题的分析则一定是有解的)。
而“设计”问题的解答可能根本不存在。
-V 5.0+图5.2 网络综合解答不存在情况一W 5.21.05.0W 125.0412L 2max==<=⨯=PP(a) (b)图5.3 网络综合解答不存在情况二2“分析”问题一般具有唯一解,而“设计”问题通常有几个等效的解。
-+-V 4+V 4+---V4+(a) (b) (c)图5.4 网络综合存在多解情况3“分析”的方法较少,“综合”的方法较多。
网络综合的主要步骤:(1) 按照给定的要求确定一个和实现的逼近函数。
(2) 寻找一个具有上述逼近函数的电路。
§5.2 网络的有源性和无源性输入一端口网络N 的功率()()()p t v t i t =从任何初始时刻0t 到t ,该网络的总能量0()()()()d tt W t W t v i τττ=+⎰式中0()W t 为在初始时刻0t 时该一端口储存的能量。
若对所有0t 以及所有时间0t t ≥,有()0,(),()W t v t i t ≥∀ (1)则此一端口N 为无源的。
如果一端口不是无源的,达就是有源的。
就是说,当且仅当对某个激励和某一初始值0t 以及某一时间0t t ≥,有()0W t <,则此一端口就是有源的。
换句话说,如果一个一端口是有源的,就一定能找到某一激励以及至少某一时间t ,式(1)对这个一端口不能成立。
在以上有关无源性的定义中必须计及初始储存能量0()W t 。
例如,对时不变的线性电容,设它的电容值为C ,则有0()00()22200()()()()()111()()()()222tv t t v t W t W t v i d W t C vdvW t Cv t Cv t Cv t τττ=+=+=+-=⎰⎰式中2001()()2W t Cv t =。
移动通信网络规划:5G有源、无源室分对比在当今数字化高速发展的时代,移动通信网络成为了人们生活和工作中不可或缺的一部分。
5G 技术的出现,更是带来了前所未有的高速率、低延迟和大容量连接的体验。
而在 5G 网络的建设中,室内覆盖是一个至关重要的环节,其中有源室分和无源室分是两种常见的解决方案。
接下来,让我们深入对比一下这两种技术,看看它们在 5G 移动通信网络规划中的各自特点和优势。
首先,我们来了解一下无源室分。
无源室分系统主要由馈线、功分器、耦合器和天线等无源器件组成。
它的工作原理相对简单,就是将基站发射的信号通过这些无源器件进行分配和传输,从而实现室内区域的信号覆盖。
无源室分的一个显著优点是成本相对较低。
由于其主要由无源器件构成,不需要额外的电源供应和复杂的控制设备,因此在初期建设成本上具有一定的优势。
而且,无源室分系统的稳定性较高,因为无源器件通常故障率较低,不需要频繁维护和更换。
然而,无源室分也存在一些局限性。
由于信号在传输过程中会有一定的损耗,尤其是在高频段的 5G 信号,这可能导致覆盖范围有限,特别是在大型复杂的室内场景中,可能会出现信号覆盖不均匀的情况。
而且,无源室分系统的容量相对较小,难以满足高容量需求的场景,如大型商场、会议厅等人流密集的区域。
接下来,我们看看有源室分。
有源室分系统则是由有源器件,如RRU(射频拉远单元)、POI(多系统合路平台)和天线等组成。
有源室分能够对信号进行放大和补偿,从而有效地解决了 5G 高频信号在传输过程中的损耗问题,大大提高了覆盖范围和覆盖质量。
有源室分的容量较大,可以支持更多的用户同时接入,满足高容量需求的场景。
同时,有源室分系统具有更好的灵活性和可扩展性。
通过软件配置,可以方便地调整系统的参数和覆盖范围,适应不同的室内环境和业务需求。
不过,有源室分也并非完美无缺。
其建设成本相对较高,不仅有源器件本身价格较高,而且还需要配套的电源供应和散热设备。
部分分式法综合无源网络
摘要对于一个比较复杂的网络函数,不能通过直接法进行综合,需要采用其他的方法进行综合。
其中一种常用的方法就是部分分式法。
用部分分式法综合无源网络的思路是:将网络的阻抗函数由通常的多项式表达形式分解为部分分式,而部分分式中的每一个因式可以通过直接综合法用一个电阻、电容、电感或它们的简单组合来实现,从而完成整个网络的综合。
利用部分分式法综合实现的网络称为福斯特网络。
其中,只包含电感和电容元件的福斯特网络称为LC福斯特网络。
根据阻抗表示式实现的福新特网络称为福斯特1型网络。
关键词部分分式法;综合无源网络
引言
滤波器广泛应用于我们的生活,随着网络函数越来越复杂,我们可以把复杂的函数简单化去解决。
2.2 网络的结构的确定也可以根据下面的方法,首先确定网络元件的数目,从而确定网络的结构
(1)元件总数的确定
LC福斯特1型网络元件数目由网络阻抗函数Z(s)的极点总数目(包括无穷大处极点的数目)确定。
其中,电容和电感的数目要么相等,要么差值为1。
(2)串联电感和串联电容的确定
如果网络的极点数目为奇数,则网络所需元件数目为奇数,就需要一个串联电感串联电容。
具体可以根据Z(0)的值是零还是无穷大来确定网络的第一个串联元件是电感还是电容。
如果Z(0)=0,则网络中的第一个串联元件是电感。
如果Z(0)=∞,则网络中第一个串联元件是电容。
如果网络的极点数目为偶数,则串联电感和串联电容要么都需要,要么都不需要。
如果z(0)=∞或z(∞)=0,则串联电感和串联电容都需要。
如果Z(0)=0或Z(∞)=0,则串联电感和串联电容都不需要[2]。
(3)LC并联电路的个数的确定
网络中LC并联电路的个数由阻抗函数共轭复数极点的数目来确定。
3 网络元件值的确定
網络元件的数值由Z(s)的表达式或根据各元件的表达式确定。
参考文献
[1] 陈邦媛.射频通信电路[M].北京:科学出版社,2006:12-13.
[2] 杨志民,马义德,张新国.现代电路理论与设计[M].北京:清华大学出版2009:45-67,95-98。