小波阈值去噪

2008年2月第2期电子测试E LECTRON I C TESTFeb .2008No .2几种基于小波阈值去噪的改进方法朱艳芹,杨先麟(武汉工程大学　武汉　430074)摘　要:传统小波阈值去噪分为硬阈值去噪和软阈值去噪,而在其去噪过程中,硬阈值函数在一些不连续点处有时会产生伪吉布斯现象;软阈值函数中估计的小波系数与信号的小波信号之间存在恒定偏差。

为了去除这些现象,本文提出了几种新阈值函数的改进方案。

实验结果表明,新阈值函数消噪后的视觉特性较好,并且信噪比提高,均方根误差有所降低。

从而说明这些方法的有效性。

关键词:小波变换;阈值消噪;门限规则中图分类号:TP274 文献标识码:BSeveral ne w methods based on wavelet thresholding denoisingZhu Yanqin,Yang Xianlin(W uhan I nstitute of Technol ogy,W uhan 430074,China )Abstract:The typ ical method of threshold in de 2noising has t w o kinds of ways,one of the m is hard one and the other is s oft.I n s ome cases,such as on the discontinuities points,the Gibbs phenomenon will exhibit when we use hard thresholding functi on t o re move noise of signals and s oft hresholding method als o has disadvantages .I n order t o re move the shortings,s ome ne w thresholding functi ons are p resented .The results of the experi m ent show that the visi on of de 2noising is better and the R MSE of signal has been decreased a l ot while the S NR has been increased,which indicates the methods p resented in this paper are effective .Keywords:wavelet transf or m;thresholding denoising;method of threshold0　引 言近年来,小波理论得到了迅速发展,而且由于小波具有低熵性、多分辨特性、去相关性和选基灵活性等特点,所以它在处理非平稳信号、去除图像信号噪声方面表现出了强有力的优越性。

小波阈值去噪的基本原理“哇，这声音也太吵了吧！”我嘟囔着。

旁边的小伙伴也跟着抱怨：“就是啊，这噪音真让人受不了。

”最近我们在做一个小实验，想把一段有很多噪音的音频变得清晰。

这时候，老师给我们介绍了一种神奇的方法——小波阈值去噪。

那小波阈值去噪到底是啥呢？咱就拿画画来打个比方吧。

一幅画如果被弄脏了，有很多乱七八糟的线条和斑点，就不好看了。

小波阈值去噪就像是一个神奇的橡皮擦，可以把那些不好看的线条和斑点擦掉，让画变得干净又漂亮。

它的结构呢，有一些关键部件。

就像一个小机器人，有脑袋、身体和手脚。

脑袋呢，就是那个分析声音的部分，它能把声音分成很多小块，就像把一个大蛋糕切成很多小块一样。

身体呢，就是那个决定哪些小块是噪音，哪些小块是有用的声音的部分。

手脚呢，就是把噪音去掉，把有用的声音留下来的部分。

它的主要技术和工作原理是这样的。

首先，它会把声音信号变成一种奇怪的样子，就像把一个苹果变成一个魔方一样。

然后，它会找到那些噪音的部分，就像在一堆糖果里找到坏掉的糖果一样。

接着，它会把噪音的部分变小或者去掉，就像把一个大胖子变成一个小瘦子一样。

最后，它会把处理好的声音信号变回原来的样子，就像把一个魔方变回一个苹果一样。

那小波阈值去噪在生活中有啥用呢？有一次，我和爸爸妈妈去公园玩。

公园里人很多，很热闹。

我们想拍一段视频，可是周围的声音太吵了，有小孩的哭声，有大人的说话声，还有风吹树叶的声音。

这时候，要是有小波阈值去噪就好了。

它可以把那些不需要的声音去掉，只留下我们想要的声音，比如小鸟的叫声，或者我们的笑声。

还有一次，我在听音乐的时候，发现音乐里有很多杂音，听起来很不舒服。

要是有小波阈值去噪，就可以把那些杂音去掉，让音乐变得更加动听。

小波阈值去噪真的好厉害啊！它可以让我们的生活变得更加美好。

以后我也要好好学习，掌握更多的知识，让这个世界变得更加精彩。

本文对各种去噪方法进行了比较，总结了两大类方法的基本思想及实现流程，详细介绍了应用最广的小波阈值去噪。

一、小波去噪主要方法1、基于小波分频的去噪方法——主要用来压制面波等规则干扰；2、小波域去噪方法——主要用于压制随机干扰，目前主要有三种方法： a) 模极大值去噪方法（Mallat 和Zhang ，1992）b) 尺度相关性分析方法（Xu ，1994）c) 小波阈值收缩方法（Dohono 和Johnstone ，1994）其中，小波阈值去噪方法能在最小均方误差意义下得到信号的近似最优估计，计算速度快，适应性广，因此应用最广泛。

二、方法实现的总体流程1、基于小波分频的去噪方法小波时频分析使信号在空间域和频率域同时具有良好的局部分析性质。

小波变换可以将信号分解到各个不同的尺度或各个不同的频段上，并且通过伸缩、平移聚焦到信号的任一细节加以分析。

小波分析的这些特长，结合传统的傅立叶去噪方法，为地球物理信号去噪提供了有效途径。

对于离散序列信号，其小波变换采用 Mallat 快速算法， 信号经尺度j ＝１,２,…,J 层分解后，得到)(2R L 中各正交闭子空间（1W 、2W 、…、J W 、J V ）， 若j j V A ∈代表尺度为j 的低频部分， j j W D ∈代表高频部分，则信号可以表示为J J D D A t f +++= 1)(，据此可重构出信号在尺度j ＝J 时的低频部分和j ＝1,2,…,J 的高频部分。

如果地震数据中的干扰波频率与有效波的频率成分是分开的，通过小波分频很容易消除干扰波；如果两种频率成分存在混叠，也可以用小波分频方法提取混叠部分，再用传统方法分离有效和干扰波。

这样可以最大限度的保留有效波能量。

2、小波域去噪方法小波域去噪方法是利用信号和噪声的小波系数在小波域不同特性来进行的。

信号和噪声的小波系数幅值随尺度变化的趋势不同，随着尺度的增加，噪声的小波系数很快衰减，而信号的小波系数基本不变。

自适应小波阈值去噪原理小波变换的出现为信号处理领域带来了新的处理方法，其中的小波阈值去噪技术由于其出色的去噪效果而备受关注。

该技术在如何确定阈值方面存在许多争议，为了解决这个问题，自适应小波阈值去噪技术应运而生。

本文将详细介绍自适应小波阈值去噪技术的原理和实现方式。

小波阈值去噪技术是基于小波变换的信号去噪方法，其基本原理是：将噪声信号通过小波变换转换到小波域，利用小波变换的分解性质将噪声和信号分开，通过加入阈值进行噪声的滤除，然后将小波域上的信号逆变换回时域，得到经过去噪后的信号。

具体来说，对于一个长度为N的信号$x(n)$，它可以进行小波变换得到其小波系数$CJ_k$，即：$$CJ_k = \sum_{n=0}^{N-1}x(n)\psi_{j,k}(n)$$$\psi_{j,k}(n)$为小波基函数，它们可以由小波变换的不同种类选择。

通过多层小波分解，可以得到多个小波系数矩阵$CJ_{nj}$，其中$n$表示小波变换的层数，$j$表示小波系数的关键字，$j=(n,j)$。

在小波域中，噪声和信号的表现方式不同。

通常情况下，信号的小波系数分布在某个范围内，而噪声则分布在零附近。

我们可以通过以零为中心的阈值将小波系数分为两部分：大于阈值的系数表示信号成分，小于阈值的系数表示噪声成分。

然后将小于阈值的小波系数清零，再通过逆变换将小波系数转换回原始信号。

小波阈值去噪技术的核心问题是如何确定阈值。

传统的小波阈值去噪技术采用全局阈值，所有小波系数均采用同一个阈值进行处理。

这种方法可能会使信号丢失部分重要信息，从而影响其质量。

如果在将全部小波系数同时处理时，不同频带的信号成分和噪声带宽差异较大，无法很好地选取合理的阈值。

为了解决这些问题，自适应小波阈值去噪技术应运而生。

该方法采用自适应阈值，在不同频带上分别应用不同的阈值，以便更好地保留信号信息。

自适应小波阈值去噪技术的步骤如下：1. 利用小波变换将噪声信号转换到小波域。

一维信号小波阈值去噪1、小波阈值处理基本理论所谓阈值去噪简而言之就是对信号进行分解，然后对分解后的系数进行阈值处理，最后重构得到去噪信号。

该算法其主要理论依据是：小波变换具有很强的去数据相关性，它能够使信号的能量在小波域集中在一些大的小波系数中;而噪声的能量却分布于整个小波域内。

因此，经小波分解后，信号的小波系数幅值要大于噪声的系数幅值。

可以认为，幅值比较大的小波系数一般以信号为主，而幅值比较小的系数在很大程度上是噪声。

于是，采用阈值的办法可以把信号系数保留，而使大部分噪声系数减小至零。

小波阈值收缩法去噪的具体处理过程为：将含噪信号在各尺度上进行小波分解，设定一个阈值，幅值低于该阈值的小波系数置为0，高于该阈值的小波系数或者完全保留，或者做相应的收缩（shrinkage）处理。

最后将处理后获得的小波系数用逆小波变换进行重构，得到去噪后的信号。

2、阈值函数的选取小波分解阈值去噪中，阈值函数体现了对超过和低于阈值的小波系数不同处理策略，是阈值去噪中关键的一步。

设w表示小波系数，T为给定阈值，sign（*）为符号函数，常见的阈值函数有：硬阈值函数：（小波系数的绝对值低于阈值的置零，高于的保留不变）软阈值函数：（小波系数的绝对值低于阈值的置零，高于的系数shrinkage处理）式（3-8）和式（3-9）用图像表示即为：值得注意的是：1）硬阈值函数在阈值点是不连续的，在下图中已经用黑线标出。

不连续会带来振铃，伪吉布斯效应等。

2）软阈值函数，原系数和分解得到的小波系数总存在着恒定的偏差，这将影响重构的精度同时这两种函数不能表达出分解后系数的能量分布，半阈值函数是一种简单而经典的改进方案。

见下图：选取的阈值最好刚好大于噪声的最大水平，可以证明的是噪声的最大限度以非常高的概率。

小波去噪常用方法目前，小波去噪的方法大概可以分为三大类：第一类方法是利用小波变换模极大值原理去噪，即根据信号和噪声在小波变换各尺度上的不同传播特性，剔除由噪声产生的模极大值点，保留信号所对应的模极大值点，然后利用所余模极大值点重构小波系数，进而恢复信号；第二类方法是对含噪信号作小波变换之后，计算相邻尺度间小波系数的相关性，根据相关性的大小区别小波系数的类型，从而进行取舍，然后直接重构信号；第三类是小波阈值去噪方法，该方法认为信号对应的小波系数包含有信号的重要信息，其幅值较大，但数目较少，而噪声对应的小波系数是一致分布的，个数较多，但幅值小。

基于这一思想，在众多小波系数中，把绝对值较小的系数置为零，而让绝对值较大的系数保留或收缩，得到估计小波系数，然后利用估计小波系数直接进行信号重构，即可达到去噪的目的。

1：小波变换模极大值去噪方法信号与噪声的模极大值在小波变换下会呈现不同的变化趋势。

小波变换模极大值去噪方法，实质上就是利用小波变换模极大值所携带的信息，具体地说就是信号小波系数的模极大值的位置和幅值来完成对信号的表征和分析。

利用信号与噪声的局部奇异性不一样，其模极大值的传播特性也不一样这些特性对信号中的随机噪声进行去噪处理。

算法的基本思想是，根据信号与噪声在不同尺度上模极大值的不同传播特性，从所有小波变换模极大值中选择信号的模极大值而去除噪声的模极大值，然后用剩余的小波变换模极大值重构原信号。

小波变换模极大值去噪方法，具有很好的理论基础，对噪声的依赖性较小，无需知道噪声的方差，非常适合于低信噪比的信号去噪。

这种去噪方法的缺点是，计算速度慢，小波分解尺度的选择是难点，小尺度下，信号受噪声影响较大，大尺度下，会使信号丢失某些重要的局部奇异性。

2：小波系数相关性去噪方法信号与噪声在不同尺度上模极大值的不同传播特性表明，信号的小波变换在各尺度相应位置上的小波系数之间有很强的相关性，而且在边缘处有很强的相关性。

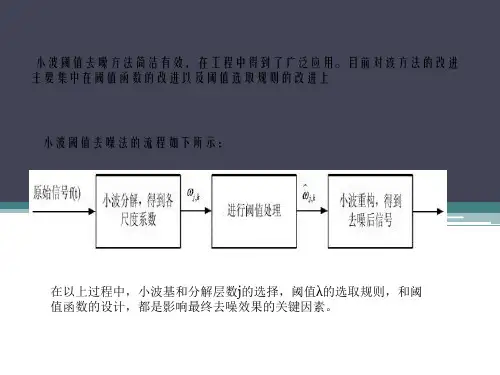
小波阈值去噪的基本原理_小波去噪阈值如何选取小波阈值去噪是利用小波变换的频率分析特性，将信号分解到不同的频带中进行处理并去除噪声的一种方法。

其基本原理是通过小波变换将原始信号分解为不同频带的子信号，然后对每个子信号进行阈值处理，将低幅值的信号置为零，最后通过反变换将处理后的信号恢复到原始信号的时域上。

小波去噪阈值如何选取：小波去噪的核心是选择合适的阈值来判断信号频带中的噪声与信号成分。

有许多常用的阈值函数可供选择，常见的有软阈值和硬阈值。

1.软阈值：对于一些频带的子信号，如果其绝对值小于一个特定的阈值，则将其置为零；如果绝对值大于阈值，则将其保留。

软阈值能有效地抑制较小的噪声，但可能会损失一些信号的微弱成分。

2.硬阈值：对于一些频带的子信号，如果其绝对值小于一个特定的阈值，则将其置为零；如果绝对值大于阈值，则将其保留。

与软阈值相比，硬阈值能更彻底地去除噪声，但可能会导致信号的失真。

选取合适的阈值是小波去噪的关键，一般来说1.基于固定阈值的去噪方法：根据经验或实验数据设定一个固定的阈值对信号进行去噪处理。

这种方法简单直观，但需要根据具体问题和实际情况选取合适的阈值。

2.基于百分比阈值的去噪方法：将小波系数按大小排序，并根据百分比选取阈值。

常用的方法有能量百分比法和极大值百分比法。

能量百分比法选择固定能量百分比并将小波系数按能量大小进行排序，然后选取对应百分位的小波系数作为阈值。

极大值百分比法选择相对于整个小波系数序列的极大值进行百分比计算，选取对应百分位的极大值作为阈值。

3. 基于信息准则的去噪方法：利用统计学原理，通过最大化似然函数或最小化信息准则（如Akaike信息准则、最小描述长度准则等）来选择最优的阈值。

这种方法较为复杂，但具有更好的理论依据。

综上所述，小波去噪阈值的选择需要根据具体情况和实际需求进行，可以根据经验、百分比法或信息准则等方法选取合适的阈值，以达到较好的去噪效果。

小波阈值去噪算法小波阈值去噪算法是一种常见的信号去噪方法，其基本思想是利用小波变换将信号转换到小波域，在小波域中对信号进行阈值处理，从而去除噪声成分，最后再将信号转换回时间域得到去噪后的信号。

本文将按照以下顺序介绍小波阈值去噪算法的相关内容：小波变换、信号去噪原理、小波阈值去噪算法步骤、小波阈值去噪算法的改进和应用等方面。

一、小波变换小波变换是一种多分辨率分析方法，在时频域上具有非常好的局部性和多尺度分析能力。

通过小波变换，可以将信号分解为不同频率分量，从而可以更好地分析和处理信号。

小波变换的基本思想是将原始信号通过一组基函数进行线性组合，得到信号在不同尺度和位置的频率分量。

小波变换中，通常采用小波函数作为基函数，小波函数具有局部性、正交性和可变性的特点，可以更好地适应信号的局部性质，从而在频域中更好地表现出信号的特性。

二、信号去噪原理在信号处理中，噪声是一个不可避免的问题，噪声会对信号的质量和精度产生很大的影响。

为了提高信号的质量和精度，需要对信号进行去噪处理。

信号去噪的基本原理是将噪声和信号进行分离，从而得到去噪后的信号。

在频域中，通过小波变换可以将信号分解为不同频率成分，在小波域中，信号的高频分量通常是噪声成分，低频成分通常是信号成分。

利用小波域中的分解性质，可以对信号的高频分量进行阈值处理，将低于一定阈值的高频成分置零，从而达到去除噪声的目的。

最后，将处理后的信号通过小波反变换回到时域中，得到去噪后的信号。

三、小波阈值去噪算法步骤小波阈值去噪算法的步骤如下：1. 采集原始信号并进行小波变换，得到信号的分解系数。

2. 对信号分解系数进行阈值处理，设置一个阈值T，将小于T 的分解系数置零。

3. 通过小波反变换将处理后的分解系数得到去噪后的信号。

四、小波阈值去噪算法的改进和应用小波阈值去噪算法是一种简单有效的信号去噪方法，但其存在一些问题，例如对于存在小幅度信号变化的信号，容易将低幅度的信号误判为噪声并去除，影响信号的重要信息。

小波去噪的原理
小波去噪是一种信号处理技术，它通过对信号进行小波变换，将信号分解成不同尺度的频率成分，然后根据信号的特点去除噪声成分，最后再进行小波逆变换得到去噪后的信号。

小波去噪的原理主要包括小波分解、阈值处理和小波重构三个步骤。

首先，小波分解是将原始信号分解成不同尺度的频率成分。

小波变换可以将信号分解成低频部分和高频部分，低频部分反映信号的整体特征，而高频部分则反映信号的细节特征。

通过小波分解，我们可以更清晰地观察信号的频率成分，从而更好地去除噪声。

其次，阈值处理是小波去噪的关键步骤。

在小波分解后，我们需要对每个尺度的频率成分进行阈值处理，将小于阈值的频率成分置零，而将大于阈值的频率成分保留。

这样可以有效去除信号中的噪声成分，同时保留信号的有效信息。

最后，小波重构是将经过阈值处理后的频率成分进行逆变换，得到去噪后的信号。

小波重构是通过将经过阈值处理后的频率成分进行小波逆变换，将去除噪声后的频率成分合成为最终的去噪信号。

经过小波重构后的信号，噪声成分得到了有效去除，同时保留了信号的有效信息。

总的来说，小波去噪利用小波变换将信号分解成不同尺度的频率成分，然后通过阈值处理去除噪声成分，最后再进行小波重构得到去噪后的信号。

这种方法在去除信号噪声的同时，尽可能地保留了信号的有效信息，因此在实际应用中具有较好的效果。

小波去噪的原理简单清晰，操作方便，因此在实际应用中得到了广泛的应用。

它不仅可以用于音频、图像等信号的去噪处理，还可以应用于地震信号处理、医学图像处理等领域。

随着数字信号处理技术的不断发展，小波去噪技术将会在更多领域得到应用，并发挥更大的作用。

第3章医学图像的小波阈值去噪3.1 常用医学图像格式医学影像是临床科室开展诊疗的第一参考资料，是开展教学、网上会诊的重要数据，特别是一些特殊病例的图像资料，在临床教学中尤为珍贵。

用什么格式将医学图像资料进行保存最好?以下介绍几种方式(1)BMP格式。

BMP是英文bitmap(位图)的简写，它是Windows操作系统中的标准图像文件格式，能够被多种Windows应用程序所支持。

随着Windows操作系统的流行与丰富的Windows应用程序的开发，BMP位图格式理所当然地被广泛应用。

这种格式的特点是包含的图像信息较丰富，几乎不进行压缩，但由此导致了它与生俱来的缺点，即占用磁盘空间过大。

(2)JPEG格式。

JPEG也是常见的一种图像格式，它由联合照片专家组(Joint Photographic Experts Group)开发。

JPEG文件的扩展名为．jpg或．jpeg，其压缩技术是用有损压缩方式去除冗余的图像和彩色数据，在获取极高压缩率的同时，能展现十分生动的像，换句话说，就是可以用最少的磁盘空间得到较好的图像质量。

由于JPEG格式是采样平衡像素之间的亮度色彩来压缩的，因而更有利于表现带有渐变色彩且没有清晰轮廓的图像。

(3)PNG格式。

PNG（protable network graphics）是一种新兴的网络图像格式，1996年10月1日由PNG向国际网络联盟提出，并得到推荐认可。

首先，PNG 是目前最不是真的格式，它汲取了GIF和JPG二者的优点，存储形式丰富，兼有GIF和JPG的色彩模式；其次，PNG能把图像文件压缩到极限以利于网络传输，但又能保留所有与图像品质有关的信息，由于PNG采用无损压缩方式来减少文件的大小，这一点与牺牲图像品质以换取高压缩率的JPG有所不同；第三，PNG的显示速度很快，只需下载1/64的图像信息就可以显示出低分辨率的预览图像，现在越来越多的软件支持这一格式。

(4)TIFF格式。

小波阈值去噪算法小波阈值去噪算法（Wavelet threshold denoising algorithm）是一种常用的信号去噪方法。

它基于小波变换（Wavelet transform）和阈值处理（Thresholding），通过将信号分解为不同频率的子带，并对子带系数进行阈值处理，从而去除信号中的噪声。

小波变换是一种多尺度分析的方法，可以将信号在时间和频率上进行分解。

它将信号分解为低频和高频部分，低频部分反映了信号的整体趋势，而高频部分则反映了信号的细节信息。

小波变换的一个优点是可以通过改变小波基函数的选择来适应不同类型的信号。

阈值处理是指对信号中的小波系数进行幅值截断的操作。

假设子带系数为c，阈值处理函数定义为T(x)，则阈值处理的过程可以用以下公式表示：d=c*T(，c，)其中，c，表示系数的幅值，T(x)为阈值处理函数，d为处理后的系数。

阈值处理函数一般有硬阈值（Hard thresholding）和软阈值（Soft thresholding）两种形式。

硬阈值函数定义如下：T(x) = 0, if ，x，< λT(x) = x, if ，x，≥ λ其中，λ为阈值。

软阈值函数定义如下：T(x) = 0, if ，x，< λT(x) = sign(x)(，x，-λ), if ，x，≥ λ其中，sign(x)为x的符号。

1.对输入信号进行小波变换，将其分解为不同尺度的子带。

2.对每个子带的系数进行阈值处理，得到处理后的系数。

3.对处理后的系数进行逆小波变换，得到去噪后的信号。

在实际应用中，选择合适的小波基函数和阈值值对去噪效果有重要影响。

常用的小波基函数包括Daubechies小波、Haar小波、Symlets小波等。

阈值的选择可以通过交叉验证的方法进行，或者根据信噪比等指标来确定。

总之，小波阈值去噪算法是一种基于小波变换和阈值处理的信号去噪方法。

通过对信号进行小波变换和阈值处理，可以去除信号中的噪声，保留信号的重要信息。

一种基于小波阈值降噪方法的图像降噪效果研究电子信息学院 赵华 2015201355一、引言数字图像处理(Digital Image Processing ，DIP)是指用计算机辅助技术对图像信号进行处理的过程。

数字图像处理最早出现于20世纪50年代，随着过去几十年来计算机、网络技术和通信的快速发展，为信号处理这个学科领域的发展奠定了基础，使得DIP 技术成为信息技术中最重要的学科分支之一。

在现实生活中，DIP 应用十分广泛，医疗、艺术、军事、航天等图像处理影响着人类生活和工作的各个方面。

然而，在图像的采集、获取、编码和传输的过程中，都存在不同程度被各种噪声所“干扰”的现象。

如果图像被干扰得比较严重，噪声会变成可见的颗粒形状，导致图像质量的严重下降。

根据研究表明，当一张图像信噪比(SNR)低于14.2dB 时，图像分割的误检率就高于0.5%，而参数估计的误差高于0.6%。

通过一些卓有成效的噪声处理技术后，尽可能地去除图像噪声，我们在从图像中获取信息时就更容易，有利于进一步的对图像进行如特征提取、信号检测和图像压缩等处理。

小波变换处理应用于图像去噪外，在其他图像处理领域都有着十分广泛的应用。

本文以小波变换作为分析工具处理图像噪声，研究数字图像的滤波去噪问题，以提高图像质量。

二、基本原理1.小波基本原理在数学上，小波定义为对给定函数局部化的新领域，小波可由一个定义在有限区域的函数ψ(x )来构造，ψ(x )称为母小波（mother wavelet ），或者叫做基本小波。

一组小波基函数， {ψa,b (x )}，可以通过缩放和平移基本小波来生成：⎪⎭⎫ ⎝⎛-ψ=ψa b x a x b a 1)(, 其中，a 为进行缩放的缩放参数，反映特定基函数的宽度，b 为进行平移的平移参数，指定沿x 轴平移的位置。

当a=2j 和b=ia 的情况下，一维小波基函数序列定义为：()()1222,-ψ=ψ--x x j j j i 其中，i 为平移参数，j 为缩放因子，函数f （x ）以小波ψ(x )为基的连续小波变换定义为函数f （x ）和ψa,b (x )的内积：()()dx a b x a x f f x W b a b a ⎪⎭⎫ ⎝⎛-ψ=ψ=⎰∞∞-1,,,与时域函数对应，在频域上则有：()()ωωa e a x j b a ψ=ψ-,可以看出，当|a|减小时，时域宽度减小，而频域宽度增大，而且ψa, b (x )的窗口中心向|ω|增大方向移动。

matlab小波阈值去噪
一、MATLAB小波阈值去噪
如今，MATLAB小波阈值去噪技术成为信号去噪研究中的一个热点。

事实上，MATLAB小波阈值去噪技术是一种近几年新兴的信号处理技术，它能有效地去除信号中的噪声。

本文首先介绍了MATLAB小波阈值去噪的基本原理，然后详细阐述了MATLAB小波阈值去噪的处理方法，最后结合实例对MATLAB小波阈值去噪进行了分析，并给出了实际应用中的一些技术指导意见。

1.MATLAB小波阈值去噪的基本原理
MATLAB小波阈值去噪是一种基于小波变换的去噪技术，它首先将原始信号进行小波变换，得到的结果是一组小波系数，通过比较这组小波系数和预定义的阈值，然后将比阈值小的系数置为零，最后将小波变换结果反向变换，就可以得到满足某种条件的去噪结果。

2.MATLAB小波阈值去噪的处理方法
(1)时域噪声提取
MATLAB小波阈值去噪的处理方法主要包括时域噪声提取、小波变换和小波阈值处理三个步骤。

其中，时域噪声提取是一个非常重要的步骤，主要是计算每个原始信号的均值和标准差，然后根据这些数据来进行时域噪声提取。

(2)小波变换
小波变换是MATLAB小波阈值去噪处理方法的核心步骤，这一步主要是进行小波变换，通过选择合适的小波分解级数，将原始信号分
解成不同尺度的小波子空间，然后比较这些子空间中每个小波系数的幅度大小，以确定哪些小波系数是噪声。

(3)小波阈值处理
小波阈值处理是小波变换步骤的重要结果，主要是比较不同小波系数的幅度和阈值，确定哪些系数应当被置零，从而有效地去除噪声。

之后，再将变换后的小波系数反向变换，从而得到去噪后的信号。

小波阈值规则
小波阈值规则在小波域信号处理中有着广泛应用。

根据信号与噪声在小波变换后的不同特性，选择一个合适的阈值进行小波系数的取舍，以达到去噪的目的。

1. 阈值选择规则：基于模型y=f(t)+e，其中e是高斯白噪声N(0,1)。

因此
可以通过小波系数、或者原始信号来进行评估能够消除噪声在小波域的阈值。

2. 常见的阈值选择方法：固定阈值估计、极值阈值估计、无偏似然估计以及启发式估计等。

极值阈值估计和无偏似然估计方法比较保守，当噪声在信号的高频段分布较少时，这两种阈值估计方法去噪效果较好，可以将微弱的信号提取出来。

固定阈值估计法和启发式阈值估计法去噪比较彻底，在去噪时显得更为有效，但是也容易把有用的高频信号误认为噪声而去除掉。

3. 阈值函数的选取：
硬阈值法：将信号的绝对值与阈值进行比较，小于阈值的点置为零，其他保持不变。

这种方法可以对图像的边缘和细节等局部信息进行保留，但图像会发生局部失真。

软阈值法：将信号的绝对值和阈值进行比较，小于阈值的点置为零，大于或等于阈值的点则向零收缩，变为该点值与阈值之差。

这种方法处理则相对平滑，但其又使得边缘模糊、图像失真。

以上内容仅供参考，如需获取更多信息，建议查阅小波变换相关书籍或咨询专业人士。