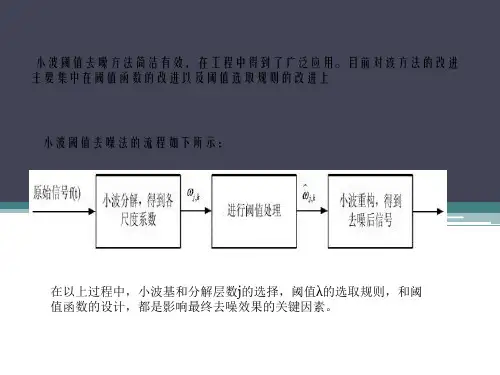
小波阈值去噪中新的阈值函数

基于EMD和小波熵阈值算法的超声回波信号降噪作者：杜必强孙立江来源：《中国测试》2017年第01期摘要：超声检测信号中通常包含大量噪声，而其中材料晶界散射的噪声是一种相关噪声。

鉴于传统的方法难以将这种噪声和缺陷回波信号区分，提出一种EMD和小波熵阈值联合降噪的算法。

该算法首先对目标信号进行EMD分解，提取具有噪声特性的IMF分量进行小波分解，利用含噪系统熵增的特性，在分解各尺度层的细节部分选用小波熵自适应阈值降噪，然后将剩余分量和降噪处理后的信号进行重构。

仿真信号结果表明：该降噪方法（EMD-WET）输出信号的信噪比（SNR）为7.9 dB、均方根误差（RMSE）为18.1、相似系数（NCC）为0.92，优于传统的小波软、硬阈值方法。

对实测信号进行处理，该方法降低信号中的大部分噪声，更好地还原回波信号的波形。

关键词：超声检测；降噪；小波熵；经验模态分解文献标志码：A 文章编号：1674-5124（2017）01-0101-05收稿日期：2016-06-18；收到修改稿日期：2016-07-25基金项目：中央高校基本科研业务费项目（2014MS118）作者简介：杜必强（1974-），男，江西吉安市人，副教授，博士，研究方向为旋转机械故障诊断、机器人标定及无人飞行器。

引言在现场超声检测中，技术人员通常根据回波信号来判断被检测对象是否存在缺陷。

作为一种典型的非线性、非平稳信号，回波信号本身含有许多突变成分，包含大量的有用信息，但超声波在材料晶界散射引起的微结构噪声以及采集仪器的散射噪声都会使回波信号包含大量噪声，严重干扰有用信号特征的提取，影响检测结果。

因此，采用有效的信号处理方法抑制回波信号携带的各种噪声，提高信噪比，有利于下一步对缺陷回波信号的特征提取，模式识别。

近年来，对非线性、非平稳信号降噪的方法有：EMD阈值去噪、小波阈值去噪、EMD和小波阈值联合去噪等。

李秋锋等[1]采用EMD对粗晶材料超声检测信号进行了去噪方法研究，取得了一定的效果。

2008年2月第2期电子测试E LECTRON I C TESTFeb .2008No .2几种基于小波阈值去噪的改进方法朱艳芹,杨先麟(武汉工程大学　武汉　430074)摘　要:传统小波阈值去噪分为硬阈值去噪和软阈值去噪,而在其去噪过程中,硬阈值函数在一些不连续点处有时会产生伪吉布斯现象;软阈值函数中估计的小波系数与信号的小波信号之间存在恒定偏差。

为了去除这些现象,本文提出了几种新阈值函数的改进方案。

实验结果表明,新阈值函数消噪后的视觉特性较好,并且信噪比提高,均方根误差有所降低。

从而说明这些方法的有效性。

关键词:小波变换;阈值消噪;门限规则中图分类号:TP274 文献标识码:BSeveral ne w methods based on wavelet thresholding denoisingZhu Yanqin,Yang Xianlin(W uhan I nstitute of Technol ogy,W uhan 430074,China )Abstract:The typ ical method of threshold in de 2noising has t w o kinds of ways,one of the m is hard one and the other is s oft.I n s ome cases,such as on the discontinuities points,the Gibbs phenomenon will exhibit when we use hard thresholding functi on t o re move noise of signals and s oft hresholding method als o has disadvantages .I n order t o re move the shortings,s ome ne w thresholding functi ons are p resented .The results of the experi m ent show that the visi on of de 2noising is better and the R MSE of signal has been decreased a l ot while the S NR has been increased,which indicates the methods p resented in this paper are effective .Keywords:wavelet transf or m;thresholding denoising;method of threshold0　引 言近年来,小波理论得到了迅速发展,而且由于小波具有低熵性、多分辨特性、去相关性和选基灵活性等特点,所以它在处理非平稳信号、去除图像信号噪声方面表现出了强有力的优越性。

改进阈值函数进行语音信号消噪，但是在程序运行过程中频频报错。

本人经验不足调试不出，希望求得各位指导改进函数表达式附图clear all; clc; close all;fs=8000;%语音信号采样频率为8000xx=wavread('lw1.wav');x1=xx(:,1);%取单声道t=(0:length(x1)-1)/8000;y1=fft(x1,2048);%对信号做2048点FFT变换f=fs*(0:1023)/2048;figure(1)plot(t,x1) %做原始语音信号的时域图形y=awgn(x1',10,'measured');%加10db的高斯白噪声[snr,mse]=snrmse(x1,y')%求得信噪比均方误差figure(2)plot(t,y) %做加噪语音信号的时域图形[c,l]=wavedec(y,3,'db1');%多尺度一维分解%用db1小波对信号进行3层分解并提取系数a3=appcoef(c,l,'db1',3);%a2=appcoef(c,l,'db1',2);%a1=appcoef(c,l,'db1',1);d3=detcoef(c,l,3);d2=detcoef(c,l,2);d1=detcoef(c,l,1);thr1=thselect(d1,'rigrsure');%阈值获取，使用Stein的无偏风险估计原理thr2=thselect(d2,'rigrsure');thr3=thselect(d3,'rigrsure');%利用改进阈值函数进行去噪处理gd1=Garrote_gg(d1,thr1);gd2=Garrote_gg(d2,thr2);gd3=Garrote_gg(d3,thr3);c1=[a3 gd3 gd2 gd1];y1=waverec(c2,l,'db1');%多尺度重构[snr,mse]=snrmse(x1,y1')%求得信噪比均方误差figure(3);plot(t,y1);function gd=Garrote_gg(a,b)%a为信号分解后的小波系数，b为获得的阈值m=0.2*((a*a)-(b*b));if (abs(a)>=b)gd=sign(a)*(abs(a)-b/exp(m));else (abs(a)<b)gd=0;endfunction [snr,mse]=snrmse(I,In)% 计算信噪比函数% I :原始信号% In:去噪后信号snr=0;Ps=sum(sum((I-mean(mean(I))).^2));%signal power Pn=sum(sum((I-In).^2));%noise powersnr=10*log10(Ps/Pn);mse=Pn/length(I);QQ截图20130516175535.png(11.18 KB, 下载次数: 0)改进函数表达式本帖最后由罗志雄于 2013-5-16 21:58 编辑function [snr,mse]=snrmse(I,In)% 计算信噪比函数% I :原始信号% In:去噪后信号snr=0;Ps=sum(sum((I-mean(mean(I))).^2));%signal power Pn=sum(sum((I-In).^2));%noise powersnr=10*log10(Ps/Pn);mse=Pn/length(I);修改后程序清单如下：clear all; clc; close all;fs=8000;%语音信号采样频率为8000xx=wavread('lw1.wav');x1=xx(:,1);%取单声道x1=x1-mean(x1);t=(0:length(x1)-1)/8000;y1=fft(x1,2048);%对信号做2048点FFT变换f=fs*(0:1023)/2048;figure(1)plot(t,x1) %做原始语音信号的时域图形y=awgn(x1',10,'measured');%加10db的高斯白噪声[snr,mse]=snrmsel(x1',y)%求得信噪比均方误差snr1=SNR_singlech(x1',y)figure(2)plot(t,y) %做加噪语音信号的时域图形[c,l]=wavedec(y,3,'db1');%多尺度一维分解%用db1小波对信号进行3层分解并提取系数a3=appcoef(c,l,'db1',3);%a2=appcoef(c,l,'db1',2);%a1=appcoef(c,l,'db1',1);d3=detcoef(c,l,3);d2=detcoef(c,l,2);d1=detcoef(c,l,1);thr1=thselect(d1,'rigrsure');%阈值获取，使用Stein的无偏风险估计原理thr2=thselect(d2,'rigrsure');thr3=thselect(d3,'rigrsure');%利用改进阈值函数进行去噪处理gd1=Garrote_gg(d1,thr1);gd2=Garrote_gg(d2,thr2);gd3=Garrote_gg(d3,thr3);c1=[a3 gd3 gd2 gd1];function gd=Garrote_gg(a,b)%a为信号分解后的小波系数，b为获得的阈值m=0.2*((a.*a)-(b*b));if (abs(a)>=b)gd=sign(a)*(abs(a)-b/exp(m));elsegd=zeros(size(a));endy1=waverec(c1,l,'db1');%多尺度重构[snr,mse]=snrmsel(x1',y1) %求得信噪比均方误差figure(3);plot(t,y1);小波去噪软阈值和硬阈值的matlab仿真程序硬阈值、软阈值这里有一段不知道有用没%设置信噪比和随机种子值snr=4;init=2055615866;%产生原始信号sref和高斯白噪声污染的信号s[sref,s]=wnoise(1,11,snr,init);%用db1小波对原始信号进行3层分解并提取系数[c,l]=wavedec(s,3,'db1');a3=appcoef(c,l,'db1',3);d3=detcoef(c,l,3);d2=detcoef(c,l,2);d1=detcoef(c,l,1);thr=1;%进行硬阈值处理ythard1=wthresh(d1,'h',thr);ythard2=wthresh(d2,'h',thr);ythard3=wthresh(d3,'h',thr);c2=[a3 ythard3 ythard2 ythard1];s3=waverec(c2,l,'db1');%进行软阈值处理ytsoftd1=wthresh(d1,'s',thr);ytsoftd2=wthresh(d2,'s',thr);ytsoftd3=wthresh(d3,'s',thr);c3=[a3 ytsoftd3 ytsoftd2 ytsoftd1];s4=waverec(c3,l,'db1');%对上述信号进行图示subplot(5,1,1);plot(sref);title('参考信号');subplot(5,1,2);plot(s);title('染噪信号');subplot(5,1,3);plot(s3);title('硬阈值处理');subplot(5,1,4);plot(s4);title('软阈值处理');matlab小波除噪，为何硬阈值和软阈值除躁信噪比一样了？load leleccum;index=1:1024;f1=leleccum(index); % 产生含噪信号init=2055615866;randn('seed',init);f2=f1+18*randn(size(x));snr=SNR_singlech(f1,f2) %信噪比subplot(2,2,1);plot(f1);title('含噪信号'); %axis([1,1024,-1,1]); subplot(2,2,2);plot(f2);title('含噪信号'); %axis([1,1024,-1,1]); %用db5小波对原始信号进行3层分解并提取系数[c,l]=wavedec(f2,3,'db6');a3=appcoef(c,l,'db6',3);d3=detcoef(c,l,3);d2=detcoef(c,l,2);d1=detcoef(c,l,1);sigma=wnoisest(c,l,1);thr=wbmpen(c,l,sigma,2);%进行硬阈值处理ythard1=wthresh(d1,'h',thr);ythard2=wthresh(d2,'h',thr);ythard3=wthresh(d3,'h',thr);c2=[a3 ythard3 ythard2 ythard1];f3=waverec(c2,l,'db6');%进行软阈值处理ytsoftd1=wthresh(d1,'s',thr);ytsoftd2=wthresh(d2,'s',thr);ytsoftd3=wthresh(d3,'s',thr);c3=[a3 ytsoftd3 ytsoftd2 ytsoftd1];f4=waverec(c3,l,'db6');%对上述信号进行图示subplot(2,2,3);plot(f3);title('硬阈值处理');%axis([1,1024,-1,1]); subplot(2,2,4);plot(f4);title('软阈值处理');%axis([1,1024,-1,1]); snr=SNR_singlech(f1,f3)snr=SNR_singlech(f1,f4)信噪比函数SNR_singlech(I,In)function snr=SNR_singlech(I,In)% 计算信噪比函数% I：riginal signal% In:noisy signal(ie. original signal + noise signal)snr=0;Ps=sum(sum((I-mean(mean(I))).^2));%signal powerPn=sum(sum((I-In).^2));%noise powersnr=10*log10(Ps/Pn);小波去噪程序Matlab小波去噪（默认，强制，给定三种情况）%% 利用小波分析对监测采集的信号进行去噪处理，恢复原始信号%小波分析进行去噪有3中方法：%1、默认阈值去噪处理。

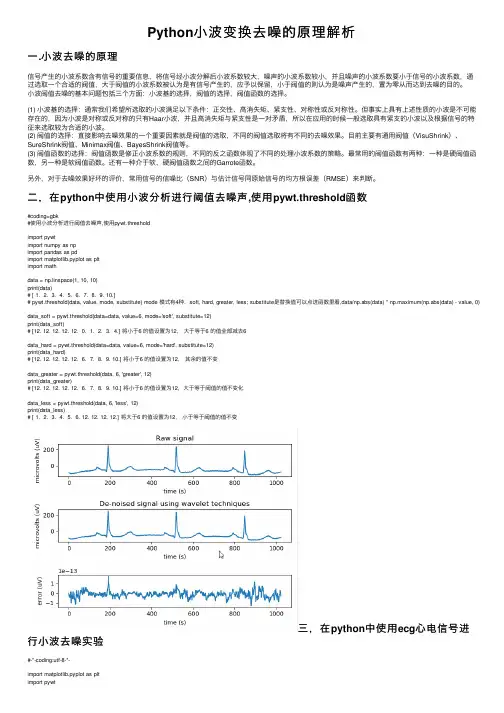
Python⼩波变换去噪的原理解析⼀.⼩波去噪的原理信号产⽣的⼩波系数含有信号的重要信息，将信号经⼩波分解后⼩波系数较⼤，噪声的⼩波系数较⼩，并且噪声的⼩波系数要⼩于信号的⼩波系数，通过选取⼀个合适的阀值，⼤于阀值的⼩波系数被认为是有信号产⽣的，应予以保留，⼩于阀值的则认为是噪声产⽣的，置为零从⽽达到去噪的⽬的。

⼩波阀值去噪的基本问题包括三个⽅⾯：⼩波基的选择，阀值的选择，阀值函数的选择。

(1) ⼩波基的选择：通常我们希望所选取的⼩波满⾜以下条件：正交性、⾼消失矩、紧⽀性、对称性或反对称性。

但事实上具有上述性质的⼩波是不可能存在的，因为⼩波是对称或反对称的只有Haar⼩波，并且⾼消失矩与紧⽀性是⼀对⽭盾，所以在应⽤的时候⼀般选取具有紧⽀的⼩波以及根据信号的特征来选取较为合适的⼩波。

(2) 阀值的选择：直接影响去噪效果的⼀个重要因素就是阀值的选取，不同的阀值选取将有不同的去噪效果。

⽬前主要有通⽤阀值（VisuShrink）、SureShrink阀值、Minimax阀值、BayesShrink阀值等。

(3) 阀值函数的选择：阀值函数是修正⼩波系数的规则，不同的反之函数体现了不同的处理⼩波系数的策略。

最常⽤的阀值函数有两种：⼀种是硬阀值函数，另⼀种是软阀值函数。

还有⼀种介于软、硬阀值函数之间的Garrote函数。

另外，对于去噪效果好坏的评价，常⽤信号的信噪⽐（SNR）与估计信号同原始信号的均⽅根误差（RMSE）来判断。

⼆，在python中使⽤⼩波分析进⾏阈值去噪声,使⽤pywt.threshold函数#coding=gbk#使⽤⼩波分析进⾏阈值去噪声,使⽤pywt.thresholdimport pywtimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport mathdata = np.linspace(1, 10, 10)print(data)# [ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]# pywt.threshold(data, value, mode, substitute) mode 模式有4种，soft, hard, greater, less; substitute是替换值可以点进函数⾥看,data/np.abs(data) * np.maximum(np.abs(data) - value, 0) data_soft = pywt.threshold(data=data, value=6, mode='soft', substitute=12)print(data_soft)# [12. 12. 12. 12. 12. 0. 1. 2. 3. 4.] 将⼩于6 的值设置为12，⼤于等于6 的值全部减去6data_hard = pywt.threshold(data=data, value=6, mode='hard', substitute=12)print(data_hard)# [12. 12. 12. 12. 12. 6. 7. 8. 9. 10.] 将⼩于6 的值设置为12，其余的值不变data_greater = pywt.threshold(data, 6, 'greater', 12)print(data_greater)# [12. 12. 12. 12. 12. 6. 7. 8. 9. 10.] 将⼩于6 的值设置为12，⼤于等于阈值的值不变化data_less = pywt.threshold(data, 6, 'less', 12)print(data_less)# [ 1. 2. 3. 4. 5. 6. 12. 12. 12. 12.] 将⼤于6 的值设置为12，⼩于等于阈值的值不变三，在python中使⽤ecg⼼电信号进⾏⼩波去噪实验#-*-coding:utf-8-*-import matplotlib.pyplot as pltimport pywtimport mathimport numpy as np#get Dataecg=pywt.data.ecg() #⽣成⼼电信号index=[]data=[]coffs=[]for i in range(len(ecg)-1):X=float(i)Y=float(ecg[i])index.append(X)data.append(Y)#create wavelet object and define parametersw=pywt.Wavelet('db8')#选⽤Daubechies8⼩波maxlev=pywt.dwt_max_level(len(data),w.dec_len)print("maximum level is"+str(maxlev))threshold=0 #Threshold for filtering#Decompose into wavelet components,to the level selected:coffs=pywt.wavedec(data,'db8',level=maxlev) #将信号进⾏⼩波分解for i in range(1,len(coffs)):coffs[i]=pywt.threshold(coffs[i],threshold*max(coeffs[i]))datarec=pywt.waverec(coffs,'db8')#将信号进⾏⼩波重构mintime=0maxtime=mintime+len(data)print(mintime,maxtime)plt.figure()plt.subplot(3,1,1)plt.plot(index[mintime:maxtime], data[mintime:maxtime])plt.xlabel('time (s)')plt.ylabel('microvolts (uV)')plt.title("Raw signal")plt.subplot(3, 1, 2)plt.plot(index[mintime:maxtime], datarec[mintime:maxtime])plt.xlabel('time (s)')plt.ylabel('microvolts (uV)')plt.title("De-noised signal using wavelet techniques")plt.subplot(3, 1, 3)plt.plot(index[mintime:maxtime],data[mintime:maxtime]-datarec[mintime:maxtime])plt.xlabel('time (s)')plt.ylabel('error (uV)')plt.tight_layout()plt.show()到此这篇关于Python⼩波变换去噪的⽂章就介绍到这了,更多相关Python⼩波去噪内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持！。

小波变换小波阈值去噪
小波变换是一种信号处理技术，可以将信号分解成不同频率的子信号，从而更好地分析和处理信号。

而小波阈值去噪则是小波变换的一种应用，可以通过去除信号中的噪声，提高信号的质量和可靠性。

小波阈值去噪的基本原理是，将信号分解成不同频率的子信号后，对
每个子信号进行阈值处理，将小于阈值的信号置为0，大于阈值的信号保留。

然后再将处理后的子信号合并，得到去噪后的信号。

小波阈值去噪的具体步骤如下：
1. 对信号进行小波分解，得到不同频率的子信号。

2. 对每个子信号进行阈值处理，将小于阈值的信号置为0，大于阈值
的信号保留。

3. 将处理后的子信号合并，得到去噪后的信号。

4. 可以根据需要对去噪后的信号进行重构，得到处理后的信号。

小波阈值去噪的优点是可以有效地去除信号中的噪声，提高信号的质
量和可靠性。

同时，小波阈值去噪还可以应用于图像处理、音频处理等领域，具有广泛的应用前景。

需要注意的是，小波阈值去噪的效果受到阈值的选择和小波基函数的选择等因素的影响。

因此，在实际应用中需要根据具体情况选择合适的阈值和小波基函数，以达到最佳的去噪效果。

总之，小波阈值去噪是一种有效的信号处理技术，可以去除信号中的噪声，提高信号的质量和可靠性。

在实际应用中，需要根据具体情况选择合适的阈值和小波基函数，以达到最佳的去噪效果。

小波阈值去噪matlab程序小波阈值去噪是一种常用的信号处理方法，可以在Matlab中使用Wavelet Toolbox来实现。

下面是一个简单的小波阈值去噪的Matlab程序示例：matlab.% 生成含有噪声的信号。

t = 0:0.001:1;y = sin(2pi100t) + randn(size(t));% 进行小波阈值去噪。

wname = 'db4'; % 选择小波基函数。

level = 5; % 选择分解的层数。

noisySignal = wdenoise(y, 'DenoisingMethod','UniversalThreshold', 'ThresholdRule', 'Soft', 'Wavelet', wname, 'Level', level);% 绘制结果。

figure.subplot(2,1,1)。

plot(t,y)。

title('含噪声信号')。

subplot(2,1,2)。

plot(t,noisySignal)。

title('去噪后信号')。

在这个示例中，首先生成了一个含有噪声的信号，然后使用`wdenoise`函数进行小波阈值去噪。

在`wdenoise`函数中，我们选择了小波基函数为db4，分解的层数为5，DenoisingMethod为UniversalThreshold，ThresholdRule为Soft。

最后绘制了含噪声信号和去噪后的信号。

需要注意的是，小波阈值去噪的具体参数选择和调整需要根据实际情况进行，上述示例仅供参考。

希望这个简单的示例可以帮助你开始在Matlab中实现小波阈值去噪。

小波变换的阈值选取与去噪效果评估方法小波变换是一种常用的信号分析方法，可以将信号分解成不同频率的子信号，从而实现信号的去噪和特征提取。

在小波变换中，阈值选取是一个重要的步骤，它决定了去噪效果的好坏。

本文将介绍小波变换的阈值选取方法，并探讨如何评估去噪效果。

一、小波变换的阈值选取方法小波变换的阈值选取方法有很多种，常用的有固定阈值法、基于统计特性的阈值法和基于小波系数分布的阈值法。

1. 固定阈值法固定阈值法是最简单的阈值选取方法，它将小波系数的绝对值与一个固定阈值进行比较，大于阈值的系数保留，小于阈值的系数置零。

这种方法简单直观，但对于不同信号的去噪效果不一致，需要根据实际情况进行调整。

2. 基于统计特性的阈值法基于统计特性的阈值法是根据信号的统计特性来选择阈值。

常用的方法有均值绝对偏差（MAD）和中值绝对偏差（MAD）。

MAD方法是通过计算小波系数的平均值和标准差来确定阈值。

具体步骤是先计算小波系数的平均值和标准差，然后将平均值加减一个倍数的标准差作为阈值。

一般情况下，取倍数为2或3可以得到较好的去噪效果。

3. 基于小波系数分布的阈值法基于小波系数分布的阈值法是根据小波系数的分布特点来选择阈值。

常用的方法有软阈值和硬阈值。

软阈值将小于阈值的系数置零，并对大于阈值的系数进行缩放。

这种方法可以保留信号的主要特征，同时抑制噪声。

硬阈值将小于阈值的系数置零，而大于阈值的系数保留。

这种方法对于信号的边缘特征保留较好，但可能会导致一些细节信息的丢失。

二、去噪效果评估方法选择合适的阈值选取方法可以实现较好的去噪效果，但如何评估去噪效果也是一个关键问题。

下面介绍两种常用的评估方法。

1. 信噪比（SNR）信噪比是一种常用的评估指标，它可以衡量信号与噪声的相对强度。

计算公式为SNR = 10 * log10(信号能量 / 噪声能量)。

当SNR值越大，说明去噪效果越好。

2. 均方根误差（RMSE）均方根误差是评估去噪效果的另一种指标。

小波阈值规则
小波阈值规则在小波域信号处理中有着广泛应用。

根据信号与噪声在小波变换后的不同特性，选择一个合适的阈值进行小波系数的取舍，以达到去噪的目的。

1. 阈值选择规则：基于模型y=f(t)+e，其中e是高斯白噪声N(0,1)。

因此
可以通过小波系数、或者原始信号来进行评估能够消除噪声在小波域的阈值。

2. 常见的阈值选择方法：固定阈值估计、极值阈值估计、无偏似然估计以及启发式估计等。

极值阈值估计和无偏似然估计方法比较保守，当噪声在信号的高频段分布较少时，这两种阈值估计方法去噪效果较好，可以将微弱的信号提取出来。

固定阈值估计法和启发式阈值估计法去噪比较彻底，在去噪时显得更为有效，但是也容易把有用的高频信号误认为噪声而去除掉。

3. 阈值函数的选取：
硬阈值法：将信号的绝对值与阈值进行比较，小于阈值的点置为零，其他保持不变。

这种方法可以对图像的边缘和细节等局部信息进行保留，但图像会发生局部失真。

软阈值法：将信号的绝对值和阈值进行比较，小于阈值的点置为零，大于或等于阈值的点则向零收缩，变为该点值与阈值之差。

这种方法处理则相对平滑，但其又使得边缘模糊、图像失真。

以上内容仅供参考，如需获取更多信息，建议查阅小波变换相关书籍或咨询专业人士。

一种改进的小波阈值去噪方法
曾守桢;朱建华
【期刊名称】《海洋技术》
【年(卷),期】2008(027)001
【摘要】利用D.L.Donoho和I.M.Johnstone提出的小波阈值去噪方法,构造了一个新的阈值函数.与传统的硬、软阈值函数相比,该阈值函数克服了硬阈值函数不连续的缺点,且同软阈值函数一样具有连续性,便于进行各种数学处理;同时还克服了软阈值函数中估计小波系数与分解小波系数之间存在着恒定偏差的缺陷,它具有硬、软阈值函数不可比拟的灵活性.仿真结果表明,新的阈值函数的去噪效果有效抑制了在信号奇异点附近产生的Pseudo-Gibbs现象,无论是在视觉效果上,还是在信噪比增益上均优于传统的硬、软阈值方法.
【总页数】3页(P37-39)
【作者】曾守桢;朱建华
【作者单位】天津农学院,天津,300072;国家海洋技术中心,天津,300012
【正文语种】中文
【中图分类】TB53
【相关文献】
1.一种基于小波阈值改进的图像去噪方法 [J], 张磊;邱书波;李萍
2.一种基于小波阈值改进的图像去噪方法 [J], 张磊;邱书波;李萍;;;
3.一种改进小波阈值去噪方法的研究 [J], 王旭;王昶
4.一种改进的小波阈值去噪方法及在气象仪器领域的应用 [J], 江虹;王奉宇;王新远;李进
5.一种改进小波阈值函数的图像去噪方法研究 [J], 周峡; 徐善顶
因版权原因，仅展示原文概要，查看原文内容请购买。

matlabwden函数原理matlab中的wden函数是一个基于小波变换的信号降噪工具。

在数字信号处理领域，信号的降噪是一个重要的任务，它可以帮助我们提取出信号中的有用信息，并去除掉其中的噪声干扰。

而小波变换作为一种强大的信号分析工具，可以将信号分解成不同频率的子信号，从而更好地进行信号处理和降噪。

wden函数的原理是基于小波阈值去噪的方法。

该方法将信号分解成多个尺度的小波系数，然后利用阈值来对小波系数进行处理。

具体而言，wden函数将信号分解成多个尺度的小波系数，然后根据阈值的设定，对小波系数进行阈值处理。

对于小于阈值的小波系数，将其置零；而对于大于阈值的小波系数，保留其数值。

最后，将处理后的小波系数进行逆变换，得到降噪后的信号。

在使用wden函数时，我们需要指定一些参数来进行信号降噪的设置。

首先是小波基函数的选择，可以根据信号的特性选择适合的小波基函数。

常用的小波基函数有haar、db、bior等。

其次是阈值的设定，可以根据具体的需求来调整阈值的大小。

通常情况下，较大的阈值可以更好地去除噪声，但可能会损失一些信号的细节信息；而较小的阈值则可以更好地保留信号的细节信息，但可能无法完全去除噪声。

因此，我们需要根据具体的信号特性和降噪要求来进行阈值的选择。

除了小波基函数和阈值的设定，wden函数还提供了其他一些参数来进行信号降噪的设置。

例如，我们可以选择使用软阈值还是硬阈值来对小波系数进行处理。

软阈值是指将小于阈值的小波系数置零，并对大于阈值的小波系数进行衰减处理；硬阈值则是将小于阈值的小波系数置零，而大于阈值的小波系数保留原值。

此外，wden函数还提供了是否进行过采样的选项，可以在降噪过程中进行信号的过采样，以提高降噪效果。

使用wden函数进行信号降噪的步骤如下：1. 导入信号数据并进行预处理，如去除直流分量、归一化等。

2. 选择合适的小波基函数，并设定阈值的大小。

3. 调用wden函数对信号进行降噪处理。