线性规划作业 3

第二章 线性规划73P 4. 将下面的线性规划问题化成标准形式12312312312max 2..236230316x x x s t x x x x x x x x −+⎧⎪−+≥⎪⎪+−≤⎨⎪≤≤⎪⎪−≤≤⎩解：将max 化为 min ， 3x 用45x x −代替，则1245124512451245min 2()..23()62()30316,0x x x x s t x x x x x x x x x x x x −+−−⎧⎪−+−≥⎪⎪+−−≤⎪⎨≤≤⎪⎪−≤≤⎪≥⎪⎩令221x x ′=+，则1245124512451245min12()..2(1)3()62(1)()30307,0x x x x s t x x x x x x x x x x x x ′−+−−−⎧⎪′−−+−≥⎪⎪′+−−−≤⎪⎨≤≤⎪⎪′≤≤⎪≥⎪⎩将线性不等式化成线性等式，则可得原问题的标准形式12451245612457182912456789min221..23342437,,,,,,,0x x x x s t x x x x x x x x x x x x x x x x x x x x x x ′−+−+−⎧⎪′−+−−=⎪⎪′+−++=⎪⎨+=⎪⎪′+=⎪′≥⎪⎩73P 5、用图解法求解下列线性规划问题：(1) 121212min 3..206122x x s t x x x x +⎧⎪+≥⎪⎨≤≤⎪⎪≥⎩解：图2.1的阴影部分为此问题的可行区域.将目标函数的等值线123x x c +=(c 为常数)沿它的负法线方向()13T−−，移动到可行区域的边界上.于是交点T），（812就是该问题的最优解，其最优值为36.75P 16. 用单纯形法求解下列线性规划问题：(1) 123123123123min 2..360210200,1,2,3j z x x x s t x x x x x x x x x x j ⎧=−−+⎪++≤⎪⎪−+≤⎨⎪+−≤⎪⎪≥=⎩解：将此问题化成标准形式123123412351236min 2..360210200,1,2,3,4,5,6j z x x x s t x x x x x x x x x x x x x j ⎧=−−+⎪+++=⎪⎪−++=⎨⎪+−+=⎪⎪≥=⎩以456,,x x x 为基变量，可得第一张单纯形表为以1x 为进基变量，5x 为离基变量旋转得以2x 为进基变量，6x 为离基变量旋转得1x 2x 3x 4x 5x 6x RHS z2 1 -1 0 000 4x 31 1 1 0060 5x 1-121010 6x 11 -1 0 01201x 2x 3x 4x 5x 6x RHS z0 3 -5 0 -20-204x 0 4 -5 1 -3030 1x 1-1 2 0 1010 6x 02-3-11101 注意单纯形表的格式！2 要用记号把转轴元标出来 3要记住在单纯形表的左边，用进基变量代替离基变量注（零行元素的获得）：先将目标函数化成求最小值的形式，再把所有变量移到等式左边，常数移到等式右边。

线性规划题及答案线性规划是一种数学优化方法，用于在给定的约束条件下，寻找一个线性目标函数的最优解。

在实际应用中，线性规划可以用于解决各种决策问题，如生产计划、资源分配、投资组合等。

以下是一个线性规划问题的示例：问题描述：某工厂生产两种产品A和B，每天的生产时间为8小时。

产品A每件需要2小时的加工时间，产品B每件需要3小时的加工时间。

每天的加工时间总共有16个小时。

产品A的利润为100元/件，产品B的利润为150元/件。

工厂的目标是最大化每天的总利润。

解决步骤：1. 定义变量：设产品A的生产数量为x，产品B的生产数量为y。

2. 建立目标函数：目标函数是每天的总利润，即：Z = 100x + 150y。

3. 建立约束条件：a) 加工时间约束：2x + 3y ≤ 16，表示每天的加工时间不能超过16小时。

b) 非负约束：x ≥ 0，y ≥ 0，表示产品的生产数量不能为负数。

4. 求解最优解：将目标函数和约束条件带入线性规划模型，使用线性规划算法求解最优解。

最优解及分析：经过计算，得到最优解为x = 4，y = 4，此时总利润最大为100 * 4 + 150 * 4 = 1000元。

通过最优解的分析可知，工厂每天应生产4件产品A和4件产品B，才能达到每天最大利润1000元。

同时，由于加工时间约束，每天的加工时间不能超过16小时，这也是生产数量的限制条件。

此外，也可以通过灵敏度分析来了解生产数量的变化对最优解的影响。

例如，如果产品A的利润提高到120元/件，而产品B的利润保持不变，那么最优解会发生变化。

在这种情况下，最优解为x = 6，y = 2，总利润为120 * 6 + 150 * 2 = 960元。

这表明，产品A的利润提高会促使工厂增加产品A的生产数量，减少产品B 的生产数量，以获得更高的总利润。

总结：线性规划是一种重要的数学优化方法，可以用于解决各种实际问题。

通过建立目标函数和约束条件，可以将实际问题转化为数学模型，并通过线性规划算法求解最优解。

作业1．第7题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.02．第8题下列不满足线性规划问题的典式要求的是（）。

A. 线性规划模型必须是标准形B. 基必须是单位矩阵。

C. 基变量可以出现在目标函数中D. 非基变量可以出现在目标函数中。

A.AB.BC.CD.D答案:C标准答案：C您的答案：题目分数：1.0此题得分：0.03．第13题A.AB.BC.CD.D答案:B标准答案：B 您的答案：题目分数：1.0 此题得分：0.04．第14题A.AB.BC.CD.D答案:D标准答案：D 您的答案：题目分数：1.0此题得分：0.05．第15题A.AB.BC.CD.D答案:A标准答案：A 您的答案：题目分数：1.0 此题得分：0.06．第16题A.AB.BC.CD.D答案:B标准答案：B 您的答案：题目分数：1.0 此题得分：0.07．第17题A.AB.BC.CD.D答案:A标准答案：A您的答案：题目分数：1.0此题得分：0.08．第18题若用二阶段法求没有可行解的线性规划问题，则在最后一张单纯表上（）。

A. 人工变量的检验数没有正数B. 人工变量的检验数没有负数C. 非基变量中有人工变量D. 基变量中有人工变量A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.09．第19题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.010．第20题若目标函数求极小值的线性规划问题没有最优解，则在最后一张单纯表上（）。

A. 对应非基变量的列上的系数没有正数B. 基变量的取值有负数C. 检验数没有负数D. 检验数为负的非基变量对应的列上的系数没有正数A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.011．第21题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0 此题得分：0.012．第26题A.AB.BC.CD.D答案:B标准答案：B您的答案：题目分数：1.0 此题得分：0.013．第28题A.AB.BC.CD.D答案:A标准答案：A您的答案：题目分数：1.0 此题得分：0.014．第33题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0 此题得分：0.015．第34题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0 此题得分：0.016．第35题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.017．第36题A.AB.BC.CD.D答案:A标准答案：A您的答案：题目分数：1.0此题得分：0.018．第46题检验有无迂回时，必须对（）进行。

例1 (任务安排)某厂计划在下月内生产4种产品B1，B2，B3，B4。

每种产品都可用三条流水作业线A1，A2，A3中旳任何一条加工出来．每条流水线（Ai）加工每件产品（Bj）所需旳工时数(i＝1,2,3,j=1,2,3,4)、每条流水线在下月内可供运用旳工时数及多种产品旳需求均列表于4.1中．又A1，A2，A3三条流水线旳生产成本分别为每小时7，8，9元。

现应怎样安排各条流水线下月旳生产任务，才能使总旳生产成本至少？例2 (外购协议)某企业下月需要B1，B2，B3，B4四种型号旳钢板分别为1000，1200，1500，2023吨。

它准备向生产这些钢板旳A1，A2，A3三家工厂订货。

该企业掌握了这三家工厂生产多种钢板旳效率（吨/小时）及下月旳生产能力（小时），如表4.2所示。

而它们销售多种型号钢板旳价格如表4.3所示。

该企业当然但愿能以至少旳代价得到自己所需要旳多种钢板，那么，它应当向各钢厂订购每种钢板各多少吨？假设该企业订购时采用如下原则，要么不订购，要么至少订购100吨以上。

该怎样处理这个问题。

若至少订购50吨，怎样处理？例3 (广告方式旳选择) 中华家电企业近来生产了一种新型洗衣机．为了推销这种新产品，该企业销售部决定运用多种广告宣传形式来使顾客理解新洗衣机旳长处。

通过调查研究，销售部经理提出了五种可供选择旳宣传方式．销售部门并搜集了许多数据。

如每项广告旳费用，每种宣传方式在一种月内可运用旳最高次数以及每种广告宣传方式每进行一次所期望得到旳效果等．这种期望效果以一种特定旳相对价值来度量、是根据长期旳经验判断出来旳．上述有关数据见表4．8中华家电企业拨了20230元给销售部作为第一种月旳广告预算费、同步提出，月内至少得有8个电视商业节目，15条报纸广告，且整个电视广告费不得超过12023元，电台广播至少隔日有一次，现问该企业销售部应当采用怎样旳广告宣传计划，才能获得最佳旳效果?例4 长城家电企业近来研制了一种新型电视机．准备在三种类型旳商场即一家航空商场、一家铁路商场和一家水上商场进行销售．由于三家商场旳类型不同样，它们旳批发价和推销费都不同样。

第五节 线性规划应用举例例1 生产计划问题某工厂可以生产n A A A 、、、 21共n 种产品，生产中需要消耗m B B B 、、、 21共m 种资源。

生产每单位产量的A j 产品需要消耗B i 种资源的数量为a ij ，各种产品每单位的利润分别为n c c c 、、、 21。

工厂的资源是有限的，每种资源的数量分别为m b b b 、、、 21。

上述情况可表示在如下生产情况表中。

解：设：n A A A 、、、 21的产量分别为n x x x 、、、 21。

问题的线性规划模型为：,,,z max 21221122222121112121112211≥≤+++≤+++≤++++++=n m n mn m m n n n n nn x x x b x a x a x a b x a x a x a b x a x a x a x c x c x c例2．货运问题某企业租用了一节火车车皮运送甲、乙两种货物到外地销售。

这两种货物每箱的重量分别为：甲—0.2吨，乙—0.3吨；每箱的体积分别为：甲—1米3，乙—0.6米3；每箱可获得的利润分别为：甲—500元，乙—400元。

一节车皮的有效载重为56吨，有效容积为180米3。

问：为获得最大利润，甲、乙各应运载多少箱？可将该问题视为一个生产计划问题，产品为甲、乙，资源为载重量和容积，可列出相应的生产情况表如下：解：设甲、乙货物的运送两分别为x 1、x 2。

模型为：,1805.0563.02.0400500z max 21212121≥≤+≤++=x x x x x x x x解得：x 1＝130，x 2＝100，z ＝105000例3：混合配料问题某饲养厂每天需要1000公斤饲料，其中至少要含7000克蛋白质、300克矿物质、1000毫克维生素。

现有五种饲料可供使用，各种饲料每公斤营养含量及价格如下表所示：解：设每天各种饲料的选用量依次为：54321,,,,x x x x x 。

线性规划题及答案引言概述：线性规划是一种优化问题求解的方法，广泛应用于经济学、管理学、工程学等领域。

本文将介绍线性规划题的基本概念和解题方法，并给出相关题目及其答案。

正文内容：1. 线性规划的基本概念1.1 目标函数：线性规划的目标是最大化或者最小化一个线性函数，称为目标函数。

目标函数常用来表示利润、成本等经济指标。

1.2 约束条件：线性规划的解必须满足一系列线性等式或者不等式，称为约束条件。

约束条件可以表示资源限制、技术限制等。

1.3 变量：线性规划的解是一组变量的取值，这些变量表示决策变量，用来描述问题的决策方案。

2. 线性规划的解题方法2.1 图形法：对于二维线性规划问题，可以使用图形法求解。

通过绘制目标函数和约束条件的图形，找到目标函数的最优解。

2.2 单纯形法：对于多维线性规划问题，可以使用单纯形法求解。

该方法通过迭代计算，逐步逼近最优解。

2.3 整数线性规划：当决策变量需要取整数值时，可以使用整数线性规划方法求解。

这种方法在实际问题中更具实用性。

3. 线性规划题目及答案3.1 例题1：某工厂生产两种产品，产品A每单位利润为10元，产品B每单位利润为15元。

生产A产品需要2小时，B产品需要3小时。

工厂每天有8小时的生产时间。

求如何安排生产，使得利润最大化。

答案：假设生产A产品x单位，B产品y单位，则目标函数为10x + 15y，约束条件为2x + 3y ≤ 8，x ≥ 0，y ≥ 0。

通过计算可得最优解为x = 2，y = 2，最大利润为70元。

3.2 例题2：某公司有两个部门，部门A和部门B。

部门A每月产生利润10万元，部门B每月产生利润15万元。

公司规定，部门A的人数不能超过100人，部门B的人数不能超过80人。

求如何分配人力资源，使得利润最大化。

答案：假设部门A的人数为x人，部门B的人数为y人，则目标函数为10x + 15y，约束条件为x ≤ 100，y ≤ 80，x ≥ 0，y ≥ 0。

1.（建模） Metalco 公司生产一种新的合金，新合金的成分为40%的锡、35%的锌和25%的请建立数学模型确定各种合金的比例，以使新产品的生产成本最低。

（财经社，数据模型与决策4.18，p137）2.用单纯形法求解下列线性规划问题。

（清华编写组，运筹学第三版，1.4，p45）（1）⎪⎩⎪⎨⎧≥≤+≤++=0,24261553.2max 21212121x x x x x x t s x x z （2） ⎪⎪⎩⎪⎪⎨⎧≥≤+≤≤+=0,18231224.52max 21212121x x x x x x t s x x z3.（同上，2.9，p76）现有线性规划问题⎪⎩⎪⎨⎧≥≤++≤++-++-=0,,)2(9010412)1(203..1355max 321321321321x x x x x x x x x t s x x x z先用单纯形法求出最优解，然后分析在下列条件下，最优解分别有什么变化？ （1） 约束条件（1）的右端常数由20变为30； （2） 约束条件（2）的右端常数由90变为70； （3） 目标函数中x3的系数由13变为8；（4） x1的系数列向量由⎪⎪⎭⎫ ⎝⎛-121变为⎪⎪⎭⎫⎝⎛50；（5） 增加一个约束条件（3）10010510321≤++x x x4.（蓝伯雄，管理数学（下），2.11，p90）某厂生产甲、乙两种产品，需要A 、B 两种原料，（1） 请构造数学模型使该厂利润最大，病求解该问题。

（2） 原料A 、B 的影子价格为多少？（3） 现有新产品丙，每件需消耗3千克原料A 和4千克原料B ，问该产品的销售价格至少为多少时才值得生产？（4） 工厂可在市场上买到原料A 。

工厂是否应该购买该原料以扩大生产？在保持原问题最优基不变的前提下，最多应购入多少？可增加多少利润？。

线性规划作业
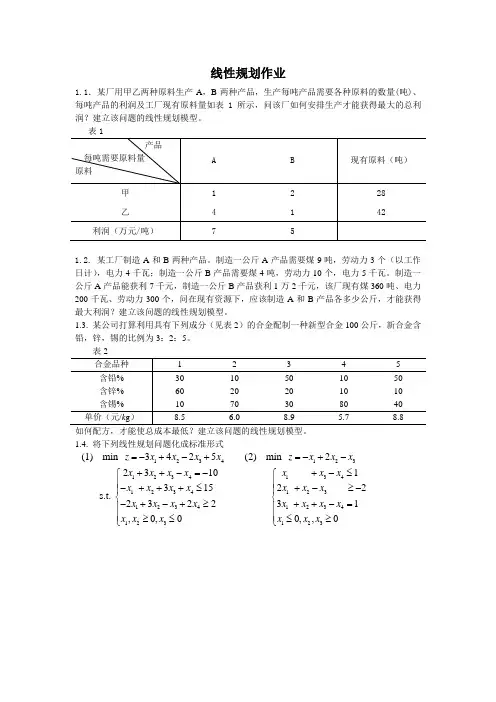
1.1．某厂用甲乙两种原料生产A ，B 两种产品，生产每吨产品需要各种原料的数量(吨)、每吨产品的利润及工厂现有原料量如表1所示，问该厂如何安排生产才能获得最大的总利润？建立该问题的线性规划模型。

表1
1.2. 某工厂制造A 和B 两种产品。

制造一公斤A 产品需要煤9吨，劳动力3个（以工作日计），电力4千瓦；制造一公斤B 产品需要煤4吨，劳动力10个，电力5千瓦。

制造一公斤A 产品能获利7千元，制造一公斤B 产品获利1万2千元，该厂现有煤360吨、电力200千瓦、劳动力300个，问在现有资源下，应该制造A 和B 产品各多少公斤，才能获得最大利润？建立该问题的线性规划模型。

1.3. 某公司打算利用具有下列成分（见表2）的合金配制一种新型合金100公斤，新合金含铅，锌，锡的比例为3：2：5。

1.4. 将下列线性规划问题化成标准形式
1234123412341234123 (1)min 3425 2310 315 s.t. 2322,0,0z x x x x x x x x x x x x x x x x x x x =-+-+++-=-⎧⎪-+++≤⎪⎨-+-+≥⎪⎪≥≤⎩ 123
134123
1234123(2) m i n 2
12 2 3 10,,0
z x x x x x x x x x x x x x x x x =-+-+-≤⎧⎪+-≥-⎪⎨
++-=
⎪⎪≤≥⎩。

某医院的护士值班计划
该医院护士上班分5个班次，每班8h，具体为：
第一班2:00-10:00；第二班6:00-14:00；第三班10:00-18:00；第四班14:00-22:00；第五班18:00-2:00（次日）。

每名护士每周上5个班，并被安排在不同日子。

有一名总护士长负责护士的值班安排。

值班方案要做到在人员或经济上比较节省，又做到尽可能合情合理。

下面是一些正在考虑中的值班方案。

方案1每名护士连续上班5天，休息2天，并从上班第一天起按从上第一班到第五班的顺序安排。

方案2考虑到按上述方案中每名护士在周末（周六周天）两天内休息安排不均匀，于是规定每名护士在周六周天两天内安排一天、且只安排一天休息，再在周一至周五间安排4个班，同样上班的5天内分别顺序安排5个不同班次。

在对第1、2方案建立线性规划模型并求解后，发现方案2虽然在安排周末休息时比较合理，但所需值班人数要比第1方案有较多增加，经济上不太合算，于是又提出了第3方案。

方案3 在方案2基础上，动员一部分护士放弃周末休息，即每周一至周五间由总护士长安排3天值班，加周六周天共上5个班，同样五个班分别安排不同班次。

作为奖励，规定放弃周末休息的护士，其工资和奖金总额比其他护士增加a%。

根据上述，帮助总护士长分析：
1 对方案1、2建立使值班护士人数最少的线性规划模型并求解。

2 对方案3，同样建立使值班护士人数最少的线性规划模型并求解，给出a值，使方案3较方案2更经济。

[ 课时作业 ][A组基础稳固 ]1．在△ ABC 中，三极点分别为A(2,4)， B(－ 1,2)， C(1,0)，点 P(x， y)在△ABC 内部及其边界上运动，则 m＝y－ x 的取值范围为 ()A ． [1,3]B ． [－3,1]C． [－ 1,3] D ．[－3，－ 1]分析：直线 m＝ y－ x 的斜率 k ＝ 1≥k ＝2，且 k ＝ 1＜kAC＝ 4，∴直线经过点C(1,0)时 m 最1AB31小，为－ 1，经过点 B(－1,2)时 m 最大，为 3.答案：Cx＋ y≥12．若变量 x、 y 知足拘束条件y－ x≤1，则 z＝ 2x－ y 的最小值为 ()x≤1A．－ 1 B ． 0C． 1 D ．2分析：由拘束条件作出可行域如下图，由图可知，目标函数在点 A 处获得最小值．联立x＋ y＝ 1 y－ x＝ 1，解得x＝ 0y＝ 1，∴ A(0,1)，因此z＝ 2x－ y 在点 A 处获得最小值为2×0－ 1＝－ 1.答案： Ax－y＋ 5≥0，3．已知 x，y 知足 x≤3，且 z＝ 2x＋ 4y 的最小值为－ 6，则常数 k＝ ()x＋y＋ k≥ 0.A ． 2B ． 9C．3 10 D ．0分析：由题意知，当直线z＝ 2x＋ 4y 经过直线 x＝ 3 与 x＋ y＋ k＝0 的交点 (3，－ 3－ k)时， z 最小，因此－ 6＝ 2×3＋ 4×(－ 3－ k)，解得 k＝ 0.答案： Dx－ 2y＋ 4≤0，4．已知变量 x， y 知足 x≥2，则 x2＋ y2的取值范围是 ()x＋ y－ 8≤0，A ． [13,40]B ． [13,40)C． (13,40) D ．(13,40]分析：作出可行域如图暗影部分所示．x2＋ y2能够当作点 (0,0)与点 (x，y)距离的平方，联合图形可知，点 (0,0)与可行域内的点 A(2,3) 连线的距离最小，即 x2＋y2最小，最小值为 13；点 (0,0) 与可行域内的点 B(2,6)连线的距离最大，即 x2＋ y2最大，最大值为40.因此 x2＋ y2的取值范围为[13,40] ．答案：A5．已知 ?ABCD 的三个极点为A(－ 1,2)， B(3,4) ，C(4，－ 2)，点 (x， y)在 ?ABCD 的内部，则z＝2x－ 5y 的取值范围是()A ． (－ 14,16)B ． (－14,20)C． (－ 12,18) D ．(－12,20)分析：如图，由 ?ABCD 的三个极点A(－ 1,2)， B(3,4)，C(4，－ 2)可知 D 点坐标为 (0，－ 4)，由 z＝ 2x－ 5y 知2z，y＝5x－52z∴当直线y＝5x－5过点 B(3,4)时，z min＝－ 14.2z当直线 y＝5x－5过点 D (0，－ 4)时， z max＝ 20.∵点 (x， y)在 ?ABCD 的内部不包含界限，∴z的取值范围为 (－ 14,20)．答案：B6．某公司生产甲、乙两种产品，已知生产每吨甲产品要用 A 原料 3 吨、 B 原料 2 吨；生产每吨乙产品要用 A 原料 1 吨、B 原料 3 吨．销售每吨甲产品可获取收益 5 万元、每吨乙产品可获取收益 3 万元，该公司在一个生产周期内耗费 A 原料不超出13 吨、 B 原料不超出18吨，那么该公司可获取的最大收益是________万元．分析：设生产甲产品x 吨、乙产品y 吨，则获取的收益为z＝ 5x＋3y.由题意得x≥0，y≥0，3x＋ y≤13，2x＋ 3y≤18，可行域如图暗影所示．由图可知当x、 y 在 A 点取值时， z 获得最大值，此时 x＝ 3，y＝ 4， z＝ 5×3＋ 3×4＝ 27(万元 )．答案：27x＋ y－2≤07．若 x， y 知足拘束条件x－ 2y＋1≤0，则 z＝ 3x＋ y 的最大值为 ________．2x－ y＋2≥0分析：作出可行域如图中暗影部分所示，作出直线l 0： 3x＋y＝ 0，平移直线l0，当直线l ： z＝ 3x＋ y 过点A 时， z 取最大值，由x＋ y－ 2＝0解得 A(1,1)，∴ z＝3x＋ y 的最大值为 4.x－ 2y＋1＝ 0答案： 4x≥1，8．已知 x，y 知足拘束条件x－ y＋1≤0，则 x2＋y2的最小值是 ________．2x－ y－ 2≤0，分析：画出知足条件的可行域如图中暗影部分所示，依据x2＋ y2表示可行域内一点到原点的距离，可知x2＋ y2的最小值是 |AO|2. 由x＝ 1，得 A(1,2)，因此 |AO |2＝ 5.x－ y＋ 1＝ 0，答案：5y≤2x9．已知实数x， y 知足y≥－ 2x.x≤3(1)求不等式组表示的平面地区的面积；(2)若目标函数为 z＝x－ 2y，求 z 的最小值．分析：画出知足不等式组的可行域如下图：(1)易求点 A、 B 的坐标为：A(3,6)， B(3，－ 6)，因此三角形OAB 的面积为：1S△OAB＝2×12×3＝ 18.1 1(2)目标函数化为： y＝2x－2z，作图知直线过 A 时 z 最小，可得 A(3,6)，∴z min＝－ 9.10．某工厂制造 A 种仪器 45 台， B 种仪器 55 台，现需用薄钢板给每台仪器配一个外壳．已知钢板有甲、乙两种规格：甲种钢板每张面积 2 m2，每张可作 A 种仪器外壳 3 个和 B 种仪器外壳 5 个，乙种钢板每张面积 3 m2，每张可作 A 种仪器外壳 6 个和B 种仪器外壳 6 个，问甲、乙两种钢板各用多少张才能用料最省？( “用料最省”是指所用钢板的总面积最小)分析：设用甲种钢板x 张，乙种钢板y 张，x， y∈N *依题意3x＋ 6y≥45，5x＋ 6y≥55钢板总面积z＝ 2x＋ 3y.作出可行域如下图．由图可知当直线z＝ 2x＋3y 过点 P 时，最小．3x＋ 6y＝ 45，x＝ 5由方程组得.5x＋ 6y＝ 55，y＝ 5因此，甲、乙两种钢板各用 5 张．[B 组能力提高]x2＋ y2－ 2x－ 2y＋ 1≥0，→→1．设 O 为坐标原点，A(1,1)，若点B(x， y)知足1≤x≤2，则OA·OB获得最1≤y≤2，小值时，点 B 的个数是 ()A ． 1B ． 2C． 3 D ．无数个分析：如图，暗影部分为点B(x， y)所在的地区．→ →∵OA·OB＝ x＋y，令 z＝ x＋ y，则 y＝－ x＋ z.由图可知，当点 B 在 C 点或 D 点时， z 取最小值，故点 B 的个数为 2.答案： B2．已知 a， b 是正数，且知足2<a＋ 2b<4.那么 a2＋ b2的取值范围是 ()416B ． (4，16)A．( ，5)55 C． (1,16)16， 4) D．( 52<a＋ 2b分析：原不等式组等价为，做出不等式组对应的平面地区如图暗影部分，a＋ 2b<4a2＋ b2表示地区内的动点P(a， b)到原点距离的平方，由图象可知当P 在 D 点时， a2＋ b2最大，此时 a2＋b2＝ 42＝ 16，原点到直线 a＋ 2b－ 2＝ 0 的距离最小，即d＝ |－ 2|2＝2，因此1＋25 222422422a＋ b＝d ＝，即 a＋ b的取值范围是 <a ＋ b <16，选 B.55答案： B3．已知实数x， y 知足不等式组x－ y＋ 2≥0，x＋ y－ 4≥0，目标函数z＝ y－ ax(a∈ R)．若取最大值时的独一最优解是(1,3)，则实数a 2x－ y－ 5≤0，的取值范围是 ________．分析：如下图，依题意直线x＋ y－ 4＝0 与x－ y＋2＝ 0 交于A(1,3)，此时取最大值，故a＞1.答案： (1，＋∞)x＋ 4y≥4，4．给定地区 D ： x＋ y≤4，令点集 T＝ {( x0， y0 )∈D |x0， y0∈ Z ，(x0， y0)是 z＝ x＋ y 在 D x≥0，上获得最大值或最小值的点} ，则 T 中的点共确立 ________条不一样的直线．分析：画出平面地区 D ，如图中暗影部分所示．作出 z ＝ x ＋ y 的基本直线l 0： x ＋ y ＝ 0.经平移可知目标函数z ＝ x ＋ y 在点A(0,1) 处获得最小值，在线段BC处获得最大值．而会合T 表示z ＝ x ＋y 获得最大值或最小值时的整点坐标，在取最大值时线段 BC 上共有5 个整点，分别为 (0,4)， (1,3)， (2,2) ， (3,1)， (4,0)，故 T 中的点共确立 6 条不一样的直线．答案：6x － y ＋ 2≥0，5．已知 x ＋ y － 4≥0，求：2x － y － 5≤0，(1) z ＝ x 2＋ y 2－ 10y ＋25 的最小值；y ＋ 1(2) z ＝ 的范围．分析 ：作出可行域如图，并求出极点的坐标 A(1,3)、 B(3,1)、 C(7,9)．(1) z ＝ x 2＋ (y － 5)2 表示可行域内任一点 (x ， y)到定点 M(0,5)的距离的平方，过 M 作直线 AC的垂线，易知垂足N 在线段 AC 上，故 z 的最小值是 |MN|2＝ 9.2(2) z ＝y －－表示可行域内任一点 ( x ， y)与定点 Q(－1，－ 1)连线的斜率，由于k QA ＝ 2，x － －1k QB ＝ ，故 z 的范围为 12， 2 .6．已知－ 1＜ x ＋ y ＜ 3，且 2＜ x －y ＜ 4，求 2x ＋ 3y 的范围．分析：在直角坐标系中作出直线x＋ y＝ 3， x＋ y＝－ 1， x－ y＝ 4，x－ y＝ 2，则不等式组－1＜ x＋y＜ 3表示的平面地区是矩形ABCD 地区内的部分．2＜ x－ y＜4设 2x＋ 3y＝ z，变形为平行直线系l ：2zy＝－3x＋3.由图可知，当 l 趋近于 A、C 两点时，截距z趋近于最大值与最小值，即z 趋近于最大值与最3小值．x－ y＝ 2，51由求得点 A( ， )．x＋ y＝ 3，22因此 z＜5113 2×＋3×＝2.22x－ y＝ 4，35由求得点 C(，－)．x＋ y＝－ 1，22因此 z＞35)＝－9. 2×＋3×(－2 22因此－9＜ 2x＋ 3y＜13 2 2.。

线性规划作业（数学规划作业一）1、用两种编程方式求解下列问题2、将下述问题化成标准线性规划问题3、奶制品的生产销售计划一奶制品加工厂用牛奶生产A 1、A 2两种奶制品，1桶牛奶可以在甲类生产设备上用12h 加工成3kg A 1种奶制品，或在在乙类生产设备上用8h 加工成4kg A 2种奶制品.若A 1、A 2两种奶制品全部能售出,且甲种奶制品售价24元/kg, 乙种奶制品售价16元/kg 。

现在工厂每天能得到50桶牛奶,每天正式工人总的劳动时间为480h,且甲类生产设备每天至多加工100kg 甲种奶制品, 乙类生产设备每天加工乙种奶制品没有限制.为了增加工厂的获利，开发了奶制品的深加工技术，用2h 和3元加工费，可将1kg A 1加工成0.8kg 高级奶制品B 1;也可将1kg A 2加工成0.75kg 高级奶制品B 2，B 1与B 2售价分别为44元与32元，试为该工厂制订一个生产计划,使每天获利最大.并进一步讨论以下3 个问题:（1）、若用30元买一桶牛奶，投资3元可以增加1h 劳动时间，是否投资？若每天投资150元，可获利多少？（2）、每kg 高级奶制品B 1与B 2的获利经常有10%的波动，对制订生产销售计划有影响？若B 2的获利下降10%，计划是否变化？（3）、若工厂已签订了每天销售10kg A 1的合同并且必须满足，该合同对工厂的获利有什么影响？4、供水问题某市从A 、B 、C 三个水库向甲、乙、丙、丁四个生活区供应自来水，C 不能向丁区供水.四个生活区每天的基本生活用水分别为30，70，10，10（单位103t ），并且每天申请了额外的用水量分别为50,70,20,40（单位103t ）;三个水库每天最多只能供应50,60,50（单位103t ）.由于地理位置不同,向各区送水所需的引水管理费不同(表1),其他管理费每单位(103t)450元,但向各区都统一收取每单位(103t)900元.问怎样制定供水方案,才能使获利最大?为了增加供水量,拟对水库进行改造,使各水库的最大供水量增加1倍,问怎样制定供水方案,才能使获利最大?表1 引水管理费(元/103t)⎪⎩⎪⎨⎧-≤+---≤-+--≤+--2143214321432132132..x x x x x x x x x x x x t s 4321432min x x x x z +++=),,,{min(max 11211i mi im i mi i i mi i x x a x a x a i∑∑∑=== ⎩⎨⎧=≥=+++m i x x x x t s im ,,2,1,01.215、货物装运问题某架货机有前、中、后三个货舱,所能装载的货物的最大重量和体积都有限制(见表1),且三个货舱实载货物的重量与其最大限载重量成比例.表1 最大限载量现有四类货物由本机装载,信息如表2:表2 四类货物装载信息问应如何装运,使本架货机获利最大?。

高三数学寒假作业（三）不等式、线性规划一、选择题1.(2012·枣庄模拟)设0＜b ＜a ＜1，则下列不等式成立的是( ) (A)ab ＜b 2＜1(B)1122log b log a 0＜＜ (C)2b ＜2a ＜2 (D)a 2＜ab ＜12.设实数x ，y 满足x 1x 2y 30y x ,≥⎧⎪-+≥⎨⎪≥⎩，，则x+2y 的最大值和最小值之和等于( )(A)12 (B)16 (C)8(D)143.(2012·湖南高考)设a ＞b ＞1，c<0，给出下列三个结论：c c ab①＞；② a c ＜b c ；③ log b (a-c)>log a (b-c)，其中所有的正确结论的序号是( ) (A)① (B)①② (C)②③ (D)①②③4.已知2b 211x a (a 2)y ()(b 0),a 22-=+=-＞，＜则x ，y 之间的大小关系是( )(A)x ＞y (B)x ＜y(C)x=y(D)不能确定5.已知x ＞0,y ＞0，lg 2x+lg8y=lg2,则11x3y+的最小值是( )(A)2(B) (C)4(D)6.(2012·福建高考)下列不等式一定成立的是( ) (A)21lg(x )lgx (x 0)4+＞＞ (B)1sin x 2(x k k Z )sin x+≥≠π∈，(C)x 2+1≥2|x|(x ∈R) (D)211(x R )x 1∈+＞7.函数()x 1(x 0),f x x 1(x 0),-+⎧=⎨-≥⎩，＜，则不等式x+(x+1)f(x+1)≤1的解集是( )(A){x |1x 1}-≤≤ (B){x|x ≤1}()()C {x |x 1}D {x |1x 1}≤≤≤8.(2012·山东高考)已知变量x ，y 满足约束条件x 2y 22x y 44x y 1,+≥⎧⎪+≤⎨⎪-≥-⎩，，则目标函数z=3x-y的取值范围是( )(A)362-［，］(B)312--［，］(C)［-1，6］(D)362-［，］9.(2012·日照模拟)如果不等式组x 0y 2x kx y 10≥⎧⎪≥⎨⎪-+≥⎩，，表示的平面区域是一个直角三角形，则该三角形的面积为( ) (A)1125或(B)1123或(C)1154或(D)1142或10.(2012·潍坊模拟)二次函数f(x)=ax 2+2x+c(x ∈R)的值域为［0，+∞),则a 1c 1ca+++的最小值为( ) (A)2(B)2+(C)4(D)2+二、填空题11.已知()lnx x 0f x x 2x 0>⎧=⎨+<⎩，，，，则f(x)>1的解集为_____________.12.设x ，y ∈R ，a ＞1，b ＞1，若a x =b y =3，a b +=则11xy+的最大值为_______.13.当x ∈(1，2)时，不等式x 2+mx+4＜0恒成立，则m 的取值范围是____________.14.(2012·德州模拟)设x ，y 满足约束条件x 0y 0x y13a 4a⎧⎪≤⎪≤⎨⎪⎪+≤⎩，，，若y 1z x 1-=-的最小值为14，则实数a 的值为__________.高三数学寒假作业（三）1. C.2.A.3. D.4. A.5. C.6. C.对于A:21lg(x )lg lgx ,4+≥=当且仅当21x 4=时，即1x 2=时等号成立, 故A 错误;对于B: 当sin x ＜0时，不可能有1sin x 2,sin x+≥故B 错误;对于C: 由基本不等式x 2+1=|x|2+1≥2|x|,故C 正确;对于D: 因为x 2+1≥1,所以211,x 1≤+故D 错误.7.【解析】选C.不等式转化为()()()x 10x 10x x 1x 1x x 1x 1+≥+<⎧⎧⎪⎪⎨⎨++≤++-≤⎪⎪⎩⎩，，或，解得1x 1-≤≤或x<-1.综上知x 1,≤故选C.8.【解析】选A.画出约束条件表示的可行域如图所示.由目标函数z=3x-y 得直线y=3x-z,当直线平移至点B(2,0)时, 目标函数z=3x-y 取得最大值为6, 当直线平移至点1A (3)2，时, 目标函数z=3x-y 取得最小值为3.2-所以目标函数z=3x-y 的取值范围是36.2-［，］9. C. 10.【解析】选C.由题意知a 0a 044ac 0ac 1>>⎧⎧⎨⎨∆=-==⎩⎩，即，则a 1c 1a ac c ac a c a c 4cacaca+++++=+=+++≥=，当且仅当a=c=1时等号成立.11.【解析】不等式f(x)>1等价于x 0x 0lnx 1x 21><⎧⎧⎨⎨>+>⎩⎩，，或，解得x>e 或-1<x<0.12.【解析】∵a x=b y=3,∴x=log a 3,y=log b 3， ∴23333a b 1111a b log a log b log ab log ()1,x y log 3log 32++=+=+=≤=当且仅当a b ==.故11xy+的最大值为1.答案：113.【解析】令f(x)=x 2+mx+4,则()()f 1m 50f 22m 80=+≤⎧⎪⎨=+≤⎪⎩，，∴m ≤-5，答案：(-∞,-5］14.【解析】由题意y 1z x 1-=-有最小值，故a ＜0，如图，故m in 011z ,3a 14-==-解得a=-1. 答案：-1。

线性规划练习1、在“家电下乡”活动中，某厂要将100台洗衣机运往邻近的乡镇，现有4辆甲型货车和8辆乙型货车可供使用。

每辆甲型货车运输费用400元，可装洗衣机20台；每辆乙型货车运输费用300元，可装洗衣机10台。

若每辆车至多只运一次，则该厂所花的最少运输费用为A.2000元B.2200元C.2400元D.2800元2、本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告，能给公司事来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？（）A.48万B.65万 C 70万 D 90万3、某糖果厂生产A、B两种糖果，A种糖果每箱获利润40元，B种糖果每箱获利润50元，其生产过程分为混合、烹调、包装三道工序，下表为每箱糖果生产过程中所需平均时间（单位：分钟）混合烹调包装A 1 5 3B 2 4 1每种糖果的生产过程中，混合的设备至多能用12小时，烹调的设备至多只能用30小时，包装的设备只能用机器15小时，试用每种糖果各生产多少箱可获得最大利润．（）A.18800元B.19800元 C19840元 D 21800元4、甲、乙、丙三种食物的维生素A、B含量及成本如下表：甲乙丙维生素A（单位/千克）600 700 400维生素B（单位/千克）800 400 500成本（元/千克）11 9 4某食物营养研究所想甲种食物，乙种食物，丙种食物配成100千克的混合食物，并使混合食物至少含56000单位维生素A和63000单位维生素B．使成本最低为多少元．（）A.850元B.860元 C870元 D 880元5、某工厂有甲、乙两种产品，按计划每天各生产不少于15t，已知生产甲产品1t需煤9t，电力4kW，劳力3个（按工作日计算）；生产乙产品1t需煤4t，电力5kW，劳力10个；甲产品每吨价7万元，乙产品每吨价12万元；但每天用煤最不得超过300吨，电力不得超过200kW，劳力只有300个．问每天应该怎么样安排生产甲、乙两种产品，才能既保定完成生产任务，又能为国家创造最多的财富．（）A.400万元B.412万元 C428万元 D 432万元6、某公司每天至少要运送180t 货物．公司有8辆载重为6t 的A 型卡车和4辆载重为10t 的B 型卡车，A 型卡车每天可往返4次，B 型卡车可往返3次，A 型卡车每天花费320元，B 型卡车每天花费504元，问如何调配车辆才能使公司每天花费最少．A.2560元B.2650元 C2460元 D 2740元07、某公司有60万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对项目乙投资的32倍，且对每个项目的投资不能低于5万元，对项目甲每投资1万元可获得0.4万元的利润，对项目乙每投资1万元可获得0.6万元的利润，该公司正确提财投资后，在两个项目上共可获得的最大利润为A.36万元B.31.2万元C.30.4万元D.24万元08、某企业生产甲、乙两种产品。

运筹学作业1、线性规划某快餐店坐落在一个旅游景点中。

这个旅游景点远离市区，平时游客不多，而在每个星期六游客猛增。

快餐店主要是为旅客提供低价位的快餐服务。

该快餐店雇佣了两名正式职工，正式职工每天工作八小时，其余工作有临时工来担任，临时工每班工作4小时。

在星期六，该快餐店从上午11点开始营业到下午10点关门。

根据游客就餐情况，在星期六每个营业小时所需职工数（包括正式工和临时工）如下表所示：表格 1已知一名正式职工11点开始上班，工作4小时后休息一小时，而后在工作4小时；另一名正式职工13点开始上班，工作4小时后休息一小时，而后在工作四小时。

又知临时工每小时的工资为4元。

（1）、在满足对职工需求的条件下如何安排临时工的班次，使得使用临时工的成本最小？（2）、如果临时工每班工作时间可以是3小时也可以是4小时，那么应如何安排临时工的班次，使得使用临时工的总成本最小？比（1）节省多少费用？这时应安排多少临时工班次？目标函数：min z=16（x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11）x1+x9+x10+x11>=8x1+x2+x10+x11>=8x1+x2+x3+x11>=7x1+x2+x3+x4>=1x2+x3+x4+x5>=2x3+x4+x5+x6>=1x4+x5+x6+x7>=5x5+x6+x7+x8>=10x6+x7+x8+x9>=10x7+x8+x9+x10>=6x8+x9+x10+x11>=6x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11>=0程序如下：Model:Sets:Row/1…11/:b;Arrange/1…11/:x,c;Link(row,arrange):a;EndsetsData:b=8,8,7,1,2,1,5,10,6,6;c=16,16,16,16,16,16,16,16,16,16,16;a=1,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0 ,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0, 0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0 ,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1;enddata[OBJ]min=@sum(arrange(j):c(j)*x(j));@for(row(i);@sum(arrange(j):a (i,j)x(i,j))>=b(i););@for(arrange(j):x(j)>=0;);End最优解为x=(2,1,0,0,1,0,9,0,1,0,5),最优值为z=304，即临时工班次为11:00~12:00开始上班2人，12:00~13:00开始上班1人，15:00~16:00开始上班1人，17:00~18:00开始上班9人，19：00~20：00开始上班1人，21:00~22:00开始上班5人，雇佣临时工19人，临时工的总工资为304元。

第二章 线性规划 作业及答案1、试述线性规划数学模型的组成部分及其特性答：线性规划数学模型由决策变量、约束条件和目标函数三个部分组成。

线性规划数学模型特征：（1） 用一组决策变量表示某一方案，这组决策变量均为非负的连续变量；（2） 存在一定数量（m ）的约束条件，这些约束条件可以用关于决策变量的一组线性等式或者不等式来加以表示；（3） 有一个可以用决策变量加以表示的目标函数，而该函数是一个线性函数。

2、一家餐厅24小时全天候营业，在各时间段中所需要的服务员数量分别为：2：00~6：00 3人 6：00~10：00 9人 10：00~14：00 12人 14：00~18：00 5人 18：00~22：00 18人 22：00~ 2：00 4人设服务员在各时间段的开始时点上上班并连续工作八小时，问该餐厅至少配备多少服务员，才能满足各个时间段对人员的需要。

试构造此问题的数学模型。

解：用决策变量1x ,2x ,3x ,4x ,5x ,6x 分别表示2：00~6：00， 6：00~10：00 ，10：00~14：00 ，14：00~18：00，18：00~22：00， 22：00~ 2：00 时间段的服务员人数。

其数学模型可以表述为：123456min Z x x x x x x =+++++16122334455612345639125184,,,,,0x x x x x x x x x x x x x x x x x x +>=+>=+>=+>=+>=+>=≥3、现要截取2.9米、2.1米和1.5米的元钢各100根，已知原材料的长度是7.4米，问应如何下料，才能使所消耗的原材料最省。

试构造此问题的数学模型。

解：圆钢的截取有不同的方案，用θ表示每种切割方案的剩余材料。

其切割方案如下所示： 2.9 2.1 1.5 θ 1' 1 1 1 0.9 2' 2 0 0 0.1 3' 1 2 0 0.3 4' 1 0 3 0 5' 0 1 3 0.8 6'41.47' 0 2 2 0.2 8' 0 3 0 1.1 目标函数为求所剩余的材料最少，即12345678min 0.90.10.300.8 1.40.2 1.1Z x x x x x x x x =+++++++1234135781245671234567821002231003342100,,,,,,,0x x x x x x x x x x x x x x x x x x x x x x x +++>=++++>=+++++>=≥4、某糖果厂用原料A 、B 、C 加工成三种不同牌号的糖果甲、乙、丙。

《运筹学》书上有关线性规划的作业题目一、将给出的线性规划问题化为标准型和对偶型两种类型： Min Z = X 1 + 3X 2 + 2X 3 + 4X 42X 1 + 3X 2 - X 3 + X 4 = 10 S.t. 3X 1 - 2X 2 + 2X 3 - X 4 ≥ -5X 1 - X 2 + X 3 - X 4 ≤ -3X 1≥0 ， X 2≤ 0， X 3 ≥0 ，X 4符号不限解：（1）令444x x x '''=-，其中440,0x x '''≥≥， 在第二个约束不等式左边加上松弛变量5x ， 在第三个约束不等式左边减去松弛变量6x ， 令z z '=-，化min z 为max z '，则标准型为：12344max 3244z x x x x x ''''=+++- 123441234451234461234456231032215..30,0,,,,,0x x x x x x x x x x x s t x x x x x x x x x x x x x '''+-+-=⎧⎪'''-+-++=⎪⎨'''-+-+-=-⎪⎪'''≥≤≥⎩（2）设对偶变量为123,,y y y ，对偶问题模型为：Max 1231053w y y y =--123123123123123231323..2240,0,0y y y y y y s t y y y y y y y y y ++=⎧⎪--≤⎪⎪-++≤⎨⎪--≤⎪⎪≥≤≥⎩ 二、已知某线性规划问题的约束条件为：2X 1 + X 2 - X 3 = 30 -X 1 + 2X 2 + X 3 - X 4 = 55X 2 + X 3 - 2X 4 - X 5 = 60 X j ≥0 ， j = 1, 2, … ,5判断下列各点是否为该线性规划问题可行域的顶点。