- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 0所, 以当0 | x x0 | 2
| h(时x) ,A|有 则
h(x) A .
②
由条件(1)知, 当0 | x x0 | r
时,有
g(x) f (x) h(x). ③
取 min{r,1,2}, 当 0 | x x0 |
①, ②时,,③式同时成立. 故
A g(x) f (x) h(x) A ,
h(x)
A
A
g(x)
f (x)
A
•
x0
•
r
•
•
•
x0
•
r
•
o
x0 1 x0 2
x0 x0 2 x0 1
x4
证明
0,
因 lim g(x) A, x x0
所以由极限的定义,1 0,
时,有| g(x) A| , 则
A g(x).
①
0 |当x x0 | 1
又因为 lim h(x) A, x x0
lim
n
xn
a.
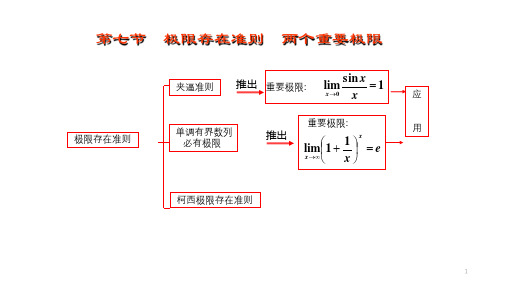
定理1和定理2称为夹逼准则(也称为两边夹法则).
利用夹逼
准则求极限关键是
构造出合适y的n, zn ,
或 g(x), h(x).
6
四、应用
例1 a设n
1 n2 1
1 n2 2
1, n2 n
求极限
lim
n
an.
解 因为 而
n n2n n n2 n
an an
n ,
n 2n 1 n2 1
y
B
因 为 ,所以
SAOB S扇形AOB SAOC
1 sin x 1 x 1 tan x,
2
22
即 sin x x tan x, 对不等式进行变形有
x
o
D
此式对 x 0 也成立. 2 由夹逼准则知,
cos x sin x 1, x
因 limcos x 1 x0
lim sin x 1. x0 x
lim
n
bn
b,则
⑴ nlim[an bn ] a b;
⑵ nlim[an bn ] a b;
⑶ lim an a , 其中 b 0.
b n n
b
2
二、问题
(1)设an
1 n2 1
1 n2 2
1 n2
n
,
求极限
lim
n
an
.
(2)求极 lim sin x .
限
x0 x
3
lim1 1 与
x0
C Ax
,
9
四、小结
1. 夹逼准则
定理1 如果函数f (x), g(x) h(x) 及
满足下列条件:
⑴ 当x U o (x0, r) g(x) f (时x), h(x)
⑵ lim g(x) A, lim h(x) A,
x x0
x x0
那么函数 f (x) 的极限存在,且 lim f (x) A. xx0
即
| f (x) A| .
注 x 当
所以 lim f (x) A. x x0
定理1类似成立.
5
定理2 如果数列{xn}, {yn} {zn} 及
满足下列条件:
(1) N0 N , n N0 当
yn xn zn ;
时,有
(2)
lim
n
yn
a,
lim
n
zn
a,
那么数列{xn } 的极限存在,且
三、夹逼准则
定理1 如果函数f (x), g(x) h(x) 及
满足下列条件:
⑴ 当x U o (x0,r), g(x) f (x) h(x),
⑵ lim g(x) A, lim h(x函数 f (x) 的极限存在,且 lim f (x) A.
y x x0
《高等数学》
极限存在的夹逼准则
1
一、回顾
定理3 设 lim f (x) A,lim g(x) B,则 ⑴ lim[ f (x) g(x)] A B; ⑵ lim[ f (x) g(x)] A B; ⑶ lim f (x) A , 其中B 0.
g(x) B
定理4
设
lim
n
an
a,
lim n lim 1 1, lim n lim 1 1,
n n2 n
n 1 1 n
n
n2 1
n
1
1 n2
所以,由夹逼准则得
lim
n
an
1.
7
例2 求极限lim sin x . x0 x
y
C
B
x
o
D
A
x
8
解 设0x ,
2
由图知,
sin x BD, x AB, tan x AC.
2.一个重要极限: lim sin x 1.
x0 x
五、作业 P56 4(1),(2) .
10
11