空间与图形的知识树

初中数学空间图形知识点梳理空间图形是初中数学中重要的一部分，它涵盖了很多基本概念和重要的几何原理。

在初中数学中，学生需要掌握和应用这些知识点来解决各种与空间图形相关的问题。

本文将介绍初中数学中空间图形的主要知识点，包括几何体的性质、分类和计算等。

1. 点、线、面和空间在几何学中，点是最基本的图形单位，没有大小和形状。

线是由无数点连成的，它没有宽度，只有长度。

面是由无数条线围成的，它有宽度和长度。

空间是由无数面围成的，它有三个维度：长度、宽度和高度。

2. 平行和垂直线平行线指在同一个平面内永远不会相交的两条直线。

垂直线是两条线的夹角为90度的情况。

垂直线之间可以画出一个直角。

3. 四边形的性质四边形是一个有四条边的封闭图形。

它的性质包括相对的边平行、对角线的关系和角的性质。

对于平行四边形，相对的两条边是平行的。

对于矩形和正方形，对角线相等且互相垂直。

对于菱形，对角线相等而且互相垂直，也有90度角。

4. 三角形的性质三角形是一个有三条边的封闭图形。

它的性质包括三个角的和为180度、角的分类和边的关系等。

根据边的长度，三角形可以分为等边三角形、等腰三角形和普通三角形。

根据角的大小，三角形可以分为直角三角形、锐角三角形和钝角三角形。

5. 几何体的分类几何体是由面围成的三维图形。

常见的几何体包括球体、立方体、长方体、圆柱体和圆锥体等。

这些几何体有各自的性质和计算公式。

例如，球体的体积公式是V = 4/3πr³，其中r是球体的半径。

6. 平行和垂直面平行面是在空间中永远不相交的两个平面。

垂直面是两个平面的交线是直角的情况。

两个垂直面之间可以形成一个直角。

7. 空间图形的投影空间图形的投影是指将三维图形在一个平面上的映射。

常见的空间图形投影包括正投影和斜投影。

正投影是指将图形投影到垂直于投影平面的平面上。

斜投影是指将图形投影到不垂直于投影平面的平面上。

8. 旋转体的性质旋转体是由将一个平面图形绕着一条轴旋转而成的图形。

六年级空间与图形知识点一、点、线、面及图形的基本概念空间与图形是数学中的重要知识点，它们的基本概念是我们学习和认识其他几何知识的基础。

在学习空间与图形之前，我们需要了解以下基本概念。

1.1 点点是空间中最基本的概念，它没有长、宽、高，也没有体积和表面积，是形状最简单的图形。

1.2 线段与直线线段是由两个点确定的线段，具有长度，用两个点的名称表示，如AB。

直线是由无数个点连在一起的轨迹，没有起点和终点，用一条直线符号表示。

1.3 面与平面面是由三条线段相交而成的图形，有长和宽，但没有厚度。

平面是由无数个点连成的表面，可以表示为一个无限大的四边形。

1.4 图形图形是空间中的一个实体，可以是二维图形或三维图形。

常见的二维图形有：圆、三角形、正方形、矩形等；常见的三维图形有：长方体、立方体、球体等。

二、空间与图形的性质及判断方法了解了空间与图形的基本概念后，我们需要进一步学习它们的性质以及判断方法。

2.1 图形的周长与面积图形的周长是指图形边界上所有边的长度之和，可以通过直接累计边长来求解。

图形的面积是指图形所围成的区域的大小，可以通过具体的公式来计算。

2.2 图形的对称性对称性是指图形在某个直线、点或平面上成像是完全重合的性质。

常见的对称性有：线对称、点对称、中心对称等。

2.3 图形的相似性图形的相似性是指两个图形的形状相似，但大小可能不同。

相似的图形具有相等的形状比例，即对应边的长度成比例。

2.4 图形的旋转与平移图形的旋转是指将图形围绕一个中心点按一定的角度进行旋转；图形的平移是指将图形沿着一条直线进行平行移动。

旋转和平移不改变图形的形状和大小，只改变其位置和方向。

三、空间与图形的应用空间与图形的知识在实际生活中有许多应用。

以下是几个常见的应用场景。

3.1 建筑设计在建筑设计中，空间与图形的知识被广泛应用。

建筑师需要根据设计要求，绘制建筑平面图、立面图等，确保建筑的结构稳定、美观。

3.2 地图导航地图导航是利用空间与图形的知识来确定路径和方向。

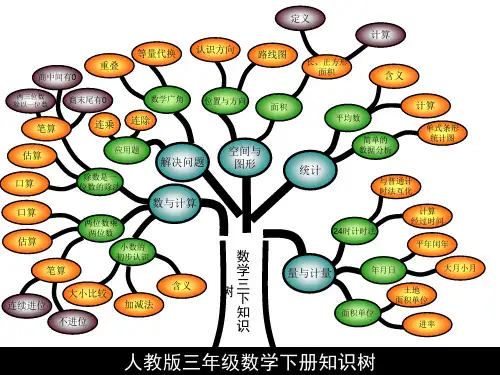
空间与图形知识点考点分析1、直线、射线和线段2、垂直与平行在同一平面内，不相交的两条直线叫做平行线，也可以说这两条直线互相平行。

3、角的意义及分类从一点引出的两条射线所组成的图形叫做角。

角的大小与边的长短无关，与两边叉开的大小有关。

45、画平面图形的高6、三角形的内角和求三角形中未知的一个角或几个角的度数，涉及到综合运用直角三角形的特征，等腰三角形的特征以及有关比的知识。

7、把多边形分成几个简单的图形。

8、常见四边形的周长和面积求法:9、圆的周长和圆的面积:圆的周长=直径×圆周率;圆的面积=半径的平方×圆周率。

10、平面图形面积公式推导过程。

11、常见的长度、面积计量单位。

（1）名数 测量的结果用数字表示，在后面加上单位名称，合起来就是名数。

（2）名数种类 名数有单名数和复名数之分。

（3）单名数之间的改写 高级单位改写成低级单位要乘进率，低级单位改写成高级单位要除以进率。

（4）复名数、单名数互化。

13、圆柱和圆锥的特征 14、长方体、正方体和圆柱体的表面积的意义。

15、长方体、正方体和圆柱体的表面积的计算方法。

16、物体的体积和物体的容积的意义。

体积：物体所占空间的大小。

容积：容器所能容纳的物体的体积。

17、物体的体积和物体的容积之间的联系和区别。

18、体积和容积单位及其相邻单位之间的进率。

19、计量单位换算的方法。

20、立体图形体积计算方法：长方体的体积＝长×宽×高（V ＝abh ） 正方体的体积＝棱长×棱长×棱长(V ＝a 3) 圆柱的体积＝底面积×高(V ＝Sh)圆锥的体积＝底面积×高×13 (V ＝13Sh) 21、长方体、正方体、圆柱体积公式的统一：V ＝Sh22、解决几何体体积和表面积的综合实际问题（注意表面积与体积的联系和区别）。

小学数学空间与图形知识点总结:空间与图形知识点是小学学习数学时期的主要知识点之一，主要包括认识位置与方向、图形的直观认识、直线和线段、角的初步认识、长方形与正方形、平行四边形、垂线、平行线、三角形、圆、圆柱、圆锥、球、轴对称图形、作图题（操作题）、棱锥、等，以下是各具体知识点总结的理解和分析。

空间与图形全部知识点认识位置与方向：三视图位置的认识认识方向三视图：三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形。

位置的认识：能正确地用上下、前后、左右等词描述物体所在的位置。

认识方向：感知东，南，西，北四个方位。

图形的直观认识：长方体正方体圆柱球长方形正方形三角形圆长方体：相邻两面的面积不同的叫长方体。

正方体：底面是正方形的直平行六面体叫正方体，即棱长都相等的六面体，又称“立方体”、“正六面体”。

圆柱：以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱。

球：在空间中到定点的距离等于或小于定长的点的集合叫做球体，简称球。

长方形：有一个角是直角的平行四边形是矩形。

正方形：在平面几何学中，正方形是具有四条相等的边和四个相等内角的多边形。

正方形是正多边形的一种，即正四边形。

三角形：由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫做三角形。

圆：当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹叫做圆。

根据定义，通常用圆规来画圆直线和线段：直线、线段、射线测量距离数轴直线，线段，射线：直线是两端都没有端点、可以向两端无限延伸、不可测量长度的。

直线上两个点和它们之间的部分叫做线段数轴：规定了唯一的原点，唯一的正方向和唯一的单位长度的直线叫数轴。

角的初步认识：角的度量角的分类角的度量：顶点重合，一条边重合。

角的分类：平角、周角以及锐角、直角。

长方形与正方形：四棱锥的体积正方形、长方形的特征正方形、长方形的周长正方形、长方形的面积正方体、长方体的表面积正方体、长方体的体积四棱锥的体积：计算公式是底面积乘以高的三分之一。

图形的基本认识1、图形的形成过程：点：一个点沿着一定的方向运动形成一条线。

（直线、曲线）如：线：一条线沿着一定的方向移动形成面（直面、曲面）如：面：一个面沿着一定的方向移动，或者绕着一条轴旋转形成体（长方体、正方体……）如：图形的形成过程是：点→线→面→体2、点＿＿＿＿大小，常用＿＿＿＿＿＿＿＿表示。

3、线，包括＿＿＿＿、＿＿＿＿、＿＿＿＿三种。

4、直线＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿，常用＿＿＿＿＿＿＿＿＿＿＿＿表示。

如：5、射线＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

常用＿＿＿＿＿＿＿＿表示。

如：6、线段＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

常用＿＿＿＿＿＿＿＿＿＿＿＿＿＿表示。

如：7、长方形：对边＿＿＿＿，四个角是＿＿＿＿，对角线＿＿＿＿＿＿＿＿＿＿，有＿＿＿＿对称轴。

8、正方形：四条边＿＿＿＿，四个角是＿＿＿＿，对角线＿＿＿＿＿＿＿＿＿＿＿，有＿＿＿＿对称轴。

9、平行四边形：两组对边＿＿＿＿＿＿＿＿，对角＿＿＿＿，相邻两个角的和是＿＿＿＿。

对角线＿＿＿＿，＿＿＿＿对称轴。

它有＿＿＿＿条高。

10、菱形：是特殊的＿＿＿＿＿＿，对角线＿＿＿＿＿＿＿＿。

11、三角形：由＿＿＿＿首尾顺次连接所构成的＿＿＿＿＿叫做三角形。

它有＿＿＿＿条高，三个内角的和是＿＿＿＿。

两个＿＿＿＿＿＿＿的三角形可以拼成一个＿＿＿＿＿＿＿。

三角形＿＿＿＿＿＿＿大于＿＿＿＿，＿＿＿＿＿＿＿＿小于＿＿＿＿。

等腰三角形，＿＿＿＿相等，＿＿＿＿＿＿相等。

等边三角形，＿＿＿＿相等，＿＿＿＿＿＿相等且都是＿＿＿＿度。

等腰直角三角形，三个内角分别是＿＿＿＿＿＿＿＿。

钝角三角形，＿＿＿大于90度。

锐角三角形的＿＿＿＿＿＿＿＿＿。

直角三角形＿＿＿＿＿＿＿＿＿。

12、梯形，＿＿＿＿＿＿＿＿＿＿＿＿的图形叫做梯形。

它有＿＿＿＿高。

两个＿＿＿＿＿＿＿＿的梯形可以拼成一个＿＿＿＿＿＿＿。

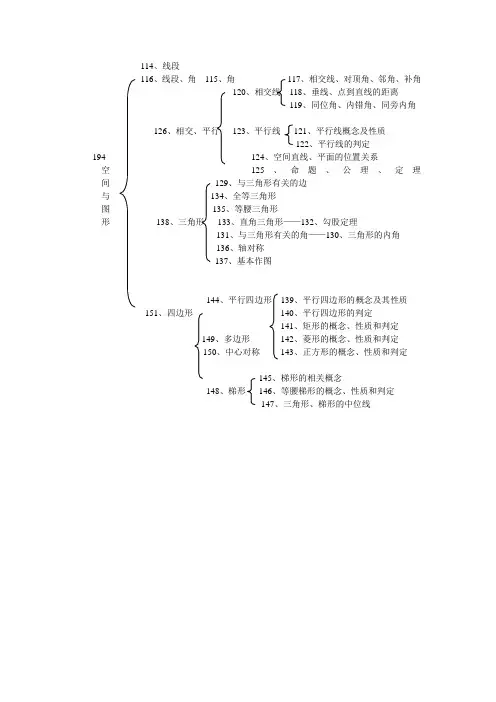
114、线段
116、线段、角115、角117、相交线、对顶角、邻角、补角
120、相交线118、垂线、点到直线的距离
119、同位角、内错角、同旁内角
126、相交、平行123、平行线121、平行线概念及性质
122、平行线的判定
194 124、空间直线、平面的位置关系空125、命题、公理、定理间129、与三角形有关的边
与134、全等三角形
图135、等腰三角形
形138、三角形133、直角三角形——132、勾股定理
131、与三角形有关的角——130、三角形的内角
136、轴对称
137、基本作图
144、平行四边形139、平行四边形的概念及其性质151、四边形140、平行四边形的判定
141、矩形的概念、性质和判定
149、多边形142、菱形的概念、性质和判定
150、中心对称143、正方形的概念、性质和判定
145、梯形的相关概念
148、梯形146、等腰梯形的概念、性质和判定
147、三角形、梯形的中位线。

空间与图形知识点（一）平面图形1、长方形的周长=（长+宽）×2 C= (a+b)×2长方形的面积=长×宽S=a×b2、正方形的周长=边长×4 C=a×4正方形的面积=边长×边长S=a×a3、平行四边形的面积=底×高S= a×h4、三角形的面积=底×高÷2S= a×h÷25、梯形的面积=(上底+下底)×高÷2s=(a+b)×h÷2（二）立体图形1、长方体的棱长总和=（长＋宽＋高）×4长方体的表面积=(长×宽+长×高+宽×高)×2S=（a×b＋a×h＋b×h）×2长方体的体积=长×宽×高=底面积×高V=a×b×h=S×2、正方体的棱长总和=棱长×12正方体的表面积=棱长×棱长×6 S= a×a×6正方体的体积=棱长×棱长×棱长V=a×a×a3、圆形的周长=直径×π=2×π×半径C=πd=2πr半圆的周长=πr+2r圆的面积=π×半径S=π×r²4、圆柱的表面积==侧面积+底面积×2圆柱的侧面积=底面周长×高圆柱的体积=底面积×高=π×半径²×高V=s×h=π×r²×h 5、圆锥体的体积=底面积×高÷3 =π×半径²×高÷3V=s×h÷3=π×r²×h÷3。

空间与图形知识点梳理1、圆柱和圆锥（（2）圆柱的表面积和体积①要点：圆柱的侧面积 = 底面周长 × 高圆柱的表面积 = 侧面积 + 底面积 × 2圆柱所占空间的大小是圆柱的体积，圆柱的体积（容积） = 底面积 × 高，用含有字母的式子表示是：V = sh 或者V = лr ²h 。

②例题：用铁皮制作一个圆柱形烟囱，要求底面直径是3分米，高是15分米，制作这个烟囱至少需要铁皮多少平方分米？（接头处不计，得数保留整平方分米）侧面积：3.14 × 3 × 15 = 141.3（平方分米）≈ 142（平方分米）例题：一个圆柱形蓄水池，底面周长是25.12米，高是4米，将这个蓄水池四周及底部 抹上水泥。

如果每平方米要用水泥20千克，一共要用多少千克水泥？底面积：25.12 ÷ 3.14 ÷ 2 = 4（米）3.14 × 4 ² = 50.24（平方米）侧面积：25.12 × 4 = 100.48（平方米）表面积：50.24 + 100.48 = 150.72（平方米）水泥质量： 150.72 × 20 = 3014.4千克例题：在直径0.8米的水管中，水流速度是每秒2米，那么1分钟流过的水有多少立方米？3.14 ×（0.8÷2）² × 2 × 60 = 60.288（立方米）（3）圆锥的体积①要点：圆锥所占空间的大小是圆锥的体积，圆锥的体积是与它等底等高的圆柱体积的三分之一。

即V = 31sh 或者V = 31лr ²h 。

②例题：一个圆锥体的体积是a 立方米，和它等底等高的圆柱体体积是( ) 例题：把一段圆钢切削成一个最大的圆锥体，圆柱体体积是6立方米，圆锥体体积是( )立方米例题：一个圆锥形沙堆，高是1.5米，底面半径是2米，每立方米沙重1.8吨。

空间与图形知识点六年级上空间与图形知识点是六年级上学期数学的重要内容之一，它包含了一系列与空间和图形相关的知识和概念。

通过学习和掌握这些知识点，学生将能够提高他们的几何思维能力和问题解决能力。

本文将对六年级上学期的空间与图形知识点进行综述，并提供一些相关的练习题供学生们巩固和复习。

一、平面图形的认识在六年级上学期，学生将进一步学习和认识不同的平面图形，如三角形、四边形、圆等。

他们需要了解每种图形的特点、性质和命名规则。

例如，学生应该知道三角形有三条边和三个内角，并且根据边的长度和角的大小可以将三角形分为等边三角形、等腰三角形和一般三角形。

二、图形的周长和面积计算学生在学习了不同图形的特点后，应该学会如何计算图形的周长和面积。

对于任何一个四边形，学生需要掌握计算周长的方法，即将四条边的长度相加。

而对于三角形和圆形，学生需要学会计算其周长和面积的特殊方法。

例如，学生可以通过计算底边乘以高的一半来计算三角形的面积，而圆的面积可以通过半径的平方乘以π来计算。

三、立体图形的认识在六年级上学期，学生还将学习和认识一些常见的立体图形，如长方体、正方体、圆柱体等。

他们需要了解每种立体图形的特点、性质和命名规则。

例如，学生应该知道长方体有六个面、八个顶点和十二条棱，并且能够通过计算面积和体积来解决与长方体相关的问题。

四、图形的投影投影是指将一个物体在光线的照射下所形成的影子或者在某个平面上的投射。

六年级上学期，学生将学习如何通过观察和绘制图形的投影来判断图形的形状和位置。

他们需要了解正投影和侧投影的概念，并能够根据给定的图形和光源方向来画出相应的投影图。

五、图形的折叠与展开折纸是六年级上学期空间与图形中一个有趣且重要的内容。

学生将学习如何通过折纸来制作不同的图形，并能够根据已折好的图形还原出原始的平面图形。

这将培养学生的几何思维和操作能力，提高他们的学习兴趣和动手能力。

练习题：1. 有一个正方形的边长为5厘米，计算它的周长和面积。