(完整版)六年级下册相交线与平行线综合复习测试(有答案)

相交线与平行线一、选择题（本大题共8小题，每小题只有一个正确选项，每小题3分，共24分）1．在下面各图中，∠1与∠2是对顶角的是（）A．B．C．D．2．如图，直线a、b相交于点O，若∠1＝30°，则∠2等于（）A．60°B．30°C．140°D．150°3．如图，直线a，b相交于点O，若∠1＝40°，则∠2＝（）A．40°B．50°C．60°D．140°4．如图，点P在直线l外，点A，B在直线l上，PA＝3，PB＝7，点P到直线l的距离可能是（）A．2 B．4 C．7 D．85．如图，直线a∥b，∠1＝50°，则∠2的度数为（）A．40°B．50°C．55°D．60°6．如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b．理由是（）A．连接直线外一点与直线上各点的所有线段中，垂线段最短B．在同一平面内，垂直于同一条直线的两条直线互相平行C．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线D．经过直线外一点，有且只有一条直线与这条直线平行7．如图，已知ON丄a，OM丄a，所以OM与ON重合的理由是（）A．两点确定一条直线B．经过一点有且只有一条线段垂直于己知直线C．过一点只能作一条垂线D．垂线段最短8．如图，直线AB∥CD，∠A＝70°，∠E＝30°，则∠C等于（）A．30°B．40°C．60°D．70°二、填空题（本大题共6小题，每小题3分，共18分）9．如图所示，在铁路旁边有一李庄，现要建一火车站，为了使李庄人乘火车最方便（即距离最近），请你在铁路旁选一点来建火车站（位置已选好），说明理由：．10．如图，已知O是直线AB上一点，∠1＝30°，OD平分∠BOC，则∠2＝．11．如图，直线AB、CD相交于点O，EO⊥AB，∠AOC＝25°。

第七章相交线与平行线综合测评一、选择题（本大题共10小题，每小题3分，共30分）1.如图1，直线a，b被直线c所截，∠1与∠2的位置关系是（）A．同位角B．内错角C．同旁内角D．对顶角图1 图22.有下列说法：①对顶角相等；②在同一平面内，垂直于同一条直线的两直线平行；③有且只有一条直线平行于已知直线；④同位角相等.其中错误的有（）A．1个B．2个C．3个D．4个3.如图2，已知OA⊥OB，若∠1=40°，则∠2的度数是（）A.20°B.40°C.50°D.60°4.已知直线AB，CB，l在同一平面内，若AB⊥l，垂足为点B，CB⊥l，垂足也为点B，则符合题意的图形可以是（）A B C D5.如图3，网格中的两个图形可以互相平移而得到，它们平移的距离是（）A.3格B.4格C.5格D.6格图3 图46.如图4，在三角形ABC中，已知∠ACB=90°，CD∥AB，若∠ACD=40°，则∠B的度数为（）A．40°B．50°C．60°D．70°7. 图5是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）A．同位角相等，两直线平行B．内错角相等，两直线平行C．两直线平行，同位角相等 D.两直线平行，内错角相等图５图６8.若∠l=∠2，下列选项中可以使AB∥CD的是（）ＡＢＣＤ9.如图６，已知BE平分∠ABC，DE∥BC，图中相等的角共有（）A.3对B.4对C.5对D.6对10.小明、小亮、小刚、小颖一起研究一道数学题．如图７，已知EF⊥AB，CD⊥AB．小明说：“如果还知道∠CDG=∠BFE，则能得到∠AGD=∠ACB．”小亮说：“把小明的已知和结论倒过来，即由∠AGD=∠ACB，可得到∠CDG=∠BFE．”小刚说：“∠AGD一定大于∠BFE．”小颖说：“如果连接GF，则GF一定平行于AB．”他们四人中，说法正确的有（）A．1人B．2人C．3人D．4人图７二、填空题（本大题共8小题，每小题4分，共32分）11. 如图8，当剪子口∠AOB增大15°时，∠COD增大度，其根据是.图8 图912.已知∠A与∠B互余，若∠A=20°15′，则∠B的度数为.13.如图9，直线AB，CD相交于点O，OM⊥AB，若∠MOD=45°，则∠COB= 度.14.如图10，在4×6的正方形网格中，点A，B，C，D，E，F都在格点上，连接C，D，E，F中任意两点得到的所有线段中，与线段AB平行的线段是.图10 图1115.已知AB∥CD，直线EF分别交AB，CD于点M，N，将一个含有45°角的直角三角尺按图11所示的方式摆放，若∠EMB=75°，则∠PNM= °.16.图12是运动员的领奖台，最高处的高为1 m，底边宽为2 m，为了美观要在上面铺上红地毯（图12中的阴影处），则至少需要红地毯m.图12 图1317.将一副三角尺和一张对边平行的纸条按图13所示的方式摆放，两个三角尺的一直角边重合，含30°角的直角三角尺的斜边与纸条一边重合，含45°角的三角尺的一个顶点在纸条的另一边上，则∠1的度数是．18.在同一平面内有2017条直线a1，a2，…，a2017，若a1∥a2，a2⊥a3，a3∥a4，a4⊥a5，……，则a1与a2017的位置关系是.三、解答题（本大题共5小题，共58分）19.如图14所示，已知∠AED=∠C，∠1=∠B，说明：EF∥AB.请结合图形，补全下面说理过程．因为∠AED=∠C，根据“”，所以DE∥.根据“”，所以∠1=∠.又因为∠1=∠B，所以∠B=∠.根据“”，所以EF∥AB.20.（10分）一辆汽车在笔直的公路上由A向B行驶，M，N分别是位于公路AB两侧的学校，如图15所示.（1）汽车在公路上行驶时，会对两所学校的教学都造成影响，当汽车行驶到何处时，分别对两所学校的影响最大?在图上标出来.（2）当汽车从A向B行驶时，在哪一段上对两个学校的影响越来越大?哪一段上对M学校的影响逐渐减小，而对N学校的影响逐渐增大?图1521. （12分）如图16，已知∠1＝∠2，试说明DE∥BF的理由.22.（12分）如图17，直线ＡＢ，ＣＤ，ＥＦ相交于点Ｏ．若∠ＡＯＣ∶∠ＡＯＥ＝2∶1，∠ＥＯＤ＝90°，求∠ＢＯＣ的度数．22.（14分）一张四边形纸片ABCD，∠B=∠D=90°，把纸片按图18所示折叠，使点B落在AD边上的B＇点，AE是折痕．（1）试判断B＇E与DC的位置关系，并说明理由.（2）若∠C=130°，求∠AEB的度数．图18附加题（15分，不计入总分）已知直线ｌ１∥ｌ２，且ｌ３与ｌ１，ｌ２分别交于Ａ，Ｂ两点，点Ｐ在ｌ３上．如图１9，试找出∠１，∠２，∠３之间的数量关系，并说明理由.（广东龙海平）参考答案一、1.B 2.B 3.C 4.C 5.C 6.B 7.A 8.C 9.C 10. B二、11. 15 对顶角相等 12. 两个角是同一个角的补角 这两个角相等 13. 13514. FD 15. 30 16．4 17. 15° 18. a 1∥a 2017三、19. 同位角相等，两直线平行 BC 两直线平行，内错角相等 EFC EFC 同位角相等，两直线平行20. 解：（1）如图1，过点M 作MC ⊥AB 于点C ，过点N 作ND ⊥AB 于点D ，根据垂线段最短，可 得在点C 处对M 学校的影响最大，在点D 处对N 学校的影响最大.图1（2）由点A 向点C 行驶时，对两个学校的影响逐渐增大；由点C 向点D 行驶时，对M 学校的影响 逐渐减小，对N 学校的影响逐渐增大.２1． 解：根据“对顶角相等”可得∠1=∠DMC.因为∠1=∠2，所以∠2=∠DMC.根据“同位角相等，两直线平行”，所以DE ∥BF.22． 解：由∠ＣＯＥ与∠ＥＯＤ互为补角，得∠ＣＯＥ＝１８０°－∠ＥＯＤ＝１８０°－９０°＝９０°． 因为∠ＡＯＣ∶∠ＡＯＥ＝２∶１，且∠ＡＯＣ＋∠ＡＯＥ＝∠ＣＯＥ＝９０°，所以∠ＡＯＥ＝31∠ＣＯＥ＝31×９０°＝３０°． 所以∠ＡＯＤ＝∠ＡＯＥ＋∠ＥＯＤ＝３０°＋９０°＝１２０°．由∠ＡＯＤ与∠ＢＯＣ互为对顶角，得∠ＢＯＣ＝∠ＡＯＤ＝１２０°．23. 解：（1）B ＇E ∥DC.理由如下：由折叠前后对应角相等，得∠AB ＇E=∠B=90°.又∠D=90°，所以∠AB ＇E=∠D ，所以B ＇E ∥DC.（2）因为B ＇E ∥DC ，所以∠BEB ＇=∠C=130°.由折叠前后对应角相等，得∠AEB=∠AEB ＇=21∠BEB ＇=21×130°=65°. 24.∠１＋∠２＝∠３．理由：如图2，过点Ｐ作ｌ１的平行线ＰＱ．因为ｌ１∥ｌ２，所以ｌ１∥ｌ２∥ＰＱ．所以∠１＝∠４，∠２＝∠５．又∠４＋∠５＝∠３，所以∠１＋∠２＝∠３．。

第七章相交线与平行线综合测评（二）时间：分钟满分：120分班级：姓名：得分：一、选择题（每小题4分，共３2分）1. 如图1所示，下列说法中正确的是（）A. 图中没有同位角、内错角、同旁内角B. 图中没有同位角和内错角，但有一对同旁内角C. 图中没有内错角和同旁内角，但有三对同位角D. 图中没有同位角和内错角，但有三对同旁内角2. 如图2所示，下列说法正确的是（）A. 若AB∥CD，则∠B＋∠A＝180°B. 若AD∥BC，则∠B＋∠C＝180°C. 若AB∥CD，则∠B＋∠D＝180°D. 若AD∥BC，则∠B＋∠A＝180°3. 如图3所示，已知AB∥CD，CE平分∠ACD，∠A＝110°，则∠ECD的度数等于（）A. 110°B. 70°C. 55°D. 35°４．如图4，已知直线ＡＢ，ＣＤ相交于点Ｏ，ＯＡ平分∠ＥＯＣ，若∠ＥＯＣ＝１２０°，则∠ＢＯＤ的度数是（）Ａ．１２０°Ｂ．４０°Ｃ．６０°Ｄ．８０°５．如图5，已知ＡＢ⊥ＢＣ，ＡＢ＝３０ｃｍ，ＢＣ＝４０ｃｍ，ＡＣ＝５０ｃｍ，点Ｍ从点Ａ出发，沿直线ＡＣ向点Ｃ移动，则线段ＢＭ的最小值为（）Ａ．２０ｃｍＢ．２４ｃｍＣ．３０ｃｍＤ．４０ｃｍ6．如图6，直线ＡＢ，ＣＤ被直线ＥＦ所截，下面的条件中，不能得到ＡＢ∥ＣＤ的是（）Ａ．∠２＋∠３＝１８０°Ｂ．∠１＝∠４Ｃ．∠４＋∠２＝１８０°Ｄ．∠２＝∠３７．两条平行直线被第三条直线所截，如果一对同旁内角的度数之比为３∶７，那么这两个角的度数分别是（）Ａ．３０°，７０°Ｂ．６０°，１４０°Ｃ．５４°，１２６°Ｄ．６４°，１１６°8. 两条平行线被第三条直线所截，角平分线互相垂直的是（）A. 内错角B. 同旁内角C. 同位角D. 内错角或同位角二、填空题（每小题４分，共32分）9．如图7，∠DAB和∠B是直线DE和BC被直线所截而成的角.10. 两条直线相交所成的角中，若有一组对顶角互补，则这两条直线的位置关系是.11.如图8所示，点A，C，B在同一直线上，DC⊥CE于点C，∠ACD＝53°，则∠BCE＝．12. 如图9所示，四边形ABCD中，∠1＝∠2，∠D＝72°，则∠BCD＝．13. 如图10所示，a∥b，∠1＝3∠2，则∠1＝，∠2＝．１4．如图11所示，AB∥CD∥EF，AC∥DF，∠BAC=120°，则∠EFD= .１５．图12中的左图是连续弯路的交通标志，画成几何图形如图12的右图所示，已知ＡＢ∥ＣＤ∥ＥＦ，ＢＣ∥ＤＥ，若∠ＡＢＣ＝α，则∠ＢＣＤ＋∠ＣＤＥ＋∠ＤＥＦ＝．16. 设a，b，c为平面内三条不同的直线．①若a∥b，c⊥a，则c与b的位置关系是；②若c⊥a，c⊥b，则a与b的位置关系是；③若a∥b，则c与b的位置关系是．三、解答题（共5６分）１７．（7分）已知∠α，∠β（如图１3），求作一个角，使它等于２∠β－∠α．（要求尺规作图，不写作法，保留作图痕迹）１８．（9分）图１4是汽车车灯的原理图，由点Ｍ处的灯泡发出的光线ＭＡ，MN，ＭＣ经过凹面镜反射后，反射光线平行，即ＡＢ∥ＮＭ∥ＣＤ.已知∠ＢＡＭ＝４０°，∠ＭＣＤ＝２０°，求∠ＡＭＣ的度数．１９．（9分）如图15所示，已知ＡＢ⊥ＢＣ，ＢＣ⊥ＣＤ，∠１＝∠２，试判断ＢＥ与ＣＦ的位置关系，并说明理由．２0．（9分）如图16所示，已知ＡＢ∥ＣＤ，直线ＥＦ⊥ＣＤ于点Ｆ，∠１＝２∠２，求∠２的度数．21．（１０分）如图１7，已知直线ＡＢ与直线ＣＤ相交于点Ｏ，ＯＥ平分∠ＡＯＣ，ＯＥ⊥ＯＦ，∠ＡＯＥ＝２０°．（１）求∠ＢＯＦ的度数；（２）∠ＣＯＦ与∠ＢＯＦ有怎样的数量关系？并说明理由．２２．（１2分）如图１8，已知直线ＡＢ与ＣＤ相交于点Ｏ，点Ｅ，Ｆ分别在直线ＡＢ上，且ＣＥ∥ＤＦ．（１）利用三角尺过点Ｏ画直线ＭＮ⊥ＥＣ，垂足为Ｇ，ＭＮ交ＤＦ于点Ｈ，判断直线ＭＮ与ＤＦ的位置关系，并说明理由．（２）如果∠ＡＥＣ＝１４０°，求∠ＤＦＢ的度数．(拟题刘书妹)《第七章相交线与平行线综合测评（二）》答案一、1. D 2. D 3. D 4. C 5. B 6. A7. C 8. B二、9. AB 内错10. 垂直11. 37°12. 108°13. 135°45°14. 120°15. 3α16. 垂直平行平行或相交三、17. 解：如下图所示，∠AOB即为所求.18. 解：因为AB∥MN，所以∠AMN=∠BAM=40°.又MN∥CD，所以∠NMC=∠MCD=20°.所以∠AMC=∠NMC+∠AMN=20°+40°=60°.19. 解：因为AB⊥BC，BC⊥CD，所以∠ABC＝∠BCD＝90°.因为∠1＝∠2，根据“等角的余角相等”，可得∠EBC＝∠BCF.根据“内错角相等，两直线平行”，可得BE∥CF．20. 解：因为AB∥CD，所以∠1＝∠CFG.因为∠1＝2∠2，所以∠CFG=2∠2.因为EF⊥CD，所以∠CFE＝∠CFG＋∠2＝2∠2＋∠2＝3∠2＝90°，所以∠2＝30°．21. 解：（1）因为OE⊥OF，所以∠EOF=90°.因为∠AOE=20°，所以∠AOF=∠AOE+∠EOF=20°+90°=110°.所以∠BOF=180°-∠AOF=180°-110°=70°.（2）∠COF=∠BOF.理由如下：因为OE平分∠AOC，所以∠COE=∠AOE=20°.因为∠EOF=90°，所以∠COF=90°-∠COE=90°-20°=70°.所以∠COF=∠BOF.22. 解：（1）如图所示，MN⊥DF.理由如下：因为EC⊥MN，所以∠EGM=90°.因为CE∥DF，所以∠DHM=∠EGM=90°.所以MN⊥DF.（2）因为∠AEC=140°，所以∠OEC=180°－∠AEC=40°.又EC∥DF，所以∠OFD=∠OEC=40°.所以∠DFB=180°－∠OFD=140°.。

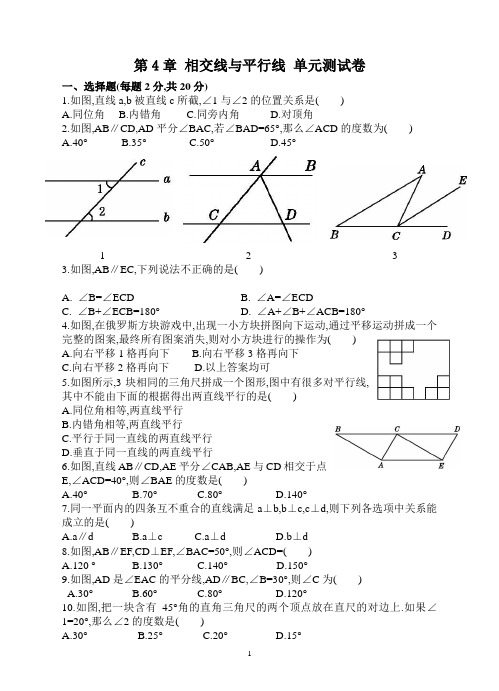
第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1.如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D.对顶角2.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD的度数为()A.40°B.35°C.50°D.45°1 2 33.如图,AB∥EC,下列说法不正确的是()A. ∠B=∠ECDB. ∠A=∠ECDC. ∠B+∠ECB=180°D. ∠A+∠B+∠ACB=180°4.如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整的图案,最终所有图案消失,则对小方块进行的操作为()A.向右平移1格再向下B.向右平移3格再向下C.向右平移2格再向下D.以上答案均可5.如图所示,3块相同的三角尺拼成一个图形,图中有很多对平行线,其中不能由下面的根据得出两直线平行的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.平行于同一直线的两直线平行D.垂直于同一直线的两直线平行6.如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是()A.40°B.70°C.80°D.140°7.同一平面内的四条互不重合的直线满足a⊥b,b⊥c,c⊥d,则下列各选项中关系能成立的是()A.a∥dB.a⊥cC.a⊥dD.b⊥d8.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120 °B.130°C.140°D.150°9.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为()A.30°B.60°C.80°D.120°10.如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是()6 8 9 10二、填空题(每题3分,共21分)11.如图所示,某地一条小河的两岸都是直的,小明和小亮分别在河的两岸,他们拉紧了一根细绳,当测出∠1和∠2满足关系________时,河岸的两边才是平行的.12.同一个平面内的三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=________.13.在测量跳远成绩时,从落地点到起跳线所拉的皮尺应当与起跳线________.14.如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A'B'C'的位置时,B'C=3 cm,则三角形ABC平移的距离为cm.11 14 1515.如图是我们常用的折叠式小刀,刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是度.16.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=°.17.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是第1个图案经过平移而得,那么第2015个图案中有白色六边形地面砖块.三、解答题(22~24题每题9分,其余每题8分,共59分)18.如图,在一条公路l的两侧有A,B两个村庄.(1)现在镇政府为民服务,沿公路开通公共汽车,同时修建A,B两个村庄到公路的道路,要使两个村庄村民乘车最为方便,请你设计道路路线,在图中画出(标明①),并标出公共汽车停靠点的位置,说出你这样设计的理由;(2)为方便两村物流互通,A,B两村计划合资修建一条由A村到达B村的道路,要使两个村庄物流、通行最为方便,请你设计道路路线,在图中画出(标明②),说出你这样设计的理由.19.如图所示,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.20.如图,CD⊥AB,EF⊥AB,∠E=∠EMC,说明:CD是∠ACB的平分线.21.如图,已知点A,O,B在同一直线上,OC是从点O出发的任意一条射线,OD是∠AOC的平分线,OE是∠COB的平分线,试确定OD和OE的位置关系,并说明理由.22.如图,∠E=∠3,∠1=∠2,试说明:∠4+∠BAP =180°.23.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时,入射光线与平面镜的夹角等于反射光线与平面镜的夹角(∠1=∠2,∠3=∠4).请说明为什么进入潜望镜的光线和离开潜望镜的光线是平行的.24.如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①②③④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(1)当动点P落在第①部分时,如图①,试说明:∠APB=∠PAC+∠PBD;(2)当动点P落在第②部分时,如图②,∠APB=∠PAC+∠PBD是否成立?若不成立,请说明理由.参考答案一、1.【答案】B 2.【答案】C3.【答案】B解：根据两直线平行,同位角相等,得出A正确;根据两直线平行,同旁内角互补,得出C正确;根据两直线平行,内错角相等,得出∠A=∠ACE,而∠ACE+∠B+∠ACB=180°,则∠A+∠B+∠ACB=180°.得出D正确.故选B.4.【答案】C5.【答案】C6.【答案】B7.【答案】C8.【答案】C9.【答案】A10.【答案】B二、11.【答案】∠1=∠212.【答案】4解：a=3,b=1.13.【答案】垂直14.【答案】215.【答案】9016.【答案】14017.【答案】8062三、18.解:(1)画图如图,P,Q即为公共汽车停靠点的位置垂线段最短;(2)画图如图,两点之间,线段最短.19.解:因为AB∥CD,所以∠ECD=∠A=37°,又因为DE⊥AE,所以∠CED=90°,所以∠D=180°-90°-37°=53°.20.解:因为CD⊥AB,EF⊥AB,所以CD∥EF(垂直于同一直线的两直线平行).相等),又因为∠E=∠EMC,所以∠BCD=∠ACD(等量代换).所以CD是∠ACB的平分线(角平分线定义).21.解:OD和OE互相垂直,即OD⊥OE.理由如下:因为点A,O,B在同一直线上,所以∠AOB=180°.又因为OD是∠AOC的平分线,OE是∠COB的平分线,所以∠DOC=∠AOC,∠COE=∠COB.所以∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB=×180°=90°,所以OD⊥OE.22.解:因为∠ENM=∠3(对顶角相等),∠E=∠3(已知),所以∠ENM=∠E(等量代换),所以AE∥HM(内错角相等,两直线平行).所以∠EAM=∠AMH(两直线平行,内错角相等).又因为∠1=∠2,所以∠EAM+∠1=∠AMH+∠2(等式性质),即∠BAM=∠AMC.所以AB∥CD(内错角相等,两直线平行).所以∠AMD+∠BAP=180°(两直线平行,同旁内角互补).因为∠4=∠AMD(对顶角相等),所以∠4+∠BAP=180°(等量代换).23.解:根据题意,作出如图所示的几何图形,已知:AB∥CD,∠1=∠2,∠3=∠4.试说明:EF∥GH.说明过程:因为AB∥CD(已知),所以∠2=∠3(两直线平行,内错角相等).又因为∠1=∠2,∠3=∠4,所以∠1=∠2=∠3=∠4.因为∠5=180°-(∠1+∠2),∠6=180°-(∠3+∠4),所以∠5=∠6,所以EF∥GH(内错角相等,两直线平行).即进入潜望镜的光线和离开潜望镜的光线是平行的.24.解:(1)如图①:过点P作MP∥AC,则MP∥BD,因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,①②(2)不成立.理由如下:如图②,过点P作MP∥AC,则MP∥BD, 因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,即:360°-∠APB=∠PAC+∠PBD.所以∠APB=∠PAC+∠PBD不成立.。

第七章相交线与平行线综合测评一、选择题（本大题共10小题，每小题3分，共30分）1.如图1，直线a，b被直线c所截，∠1与∠2的位置关系是（）A．同位角B．内错角C．同旁内角D．对顶角图1 图22.有下列说法：①对顶角相等；②在同一平面内，垂直于同一条直线的两直线平行；③有且只有一条直线平行于已知直线；④同位角相等.其中错误的有（）A．1个B．2个C．3个D．4个3.如图2，已知OA⊥OB，若∠1=40°，则∠2的度数是（）A.20°B.40°C.50°D.60°4.已知直线AB，CB，l在同一平面内，若AB⊥l，垂足为点B，CB⊥l，垂足也为点B，则符合题意的图形可以是（）A B C D5.如图3，网格中的两个图形可以互相平移而得到，它们平移的距离是（）A.3格B.4格C.5格D.6格图3 图46.如图4，在三角形ABC中，已知∠ACB=90°，CD∥AB，若∠ACD=40°，则∠B的度数为（）A．40°B．50°C．60°D．70°7. 图5是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）A．同位角相等，两直线平行B．内错角相等，两直线平行C．两直线平行，同位角相等 D.两直线平行，内错角相等图５图６8.若∠l=∠2，下列选项中可以使AB∥CD的是（）ＡＢＣＤ9.如图６，已知BE平分∠ABC，DE∥BC，图中相等的角共有（）A.3对B.4对C.5对D.6对10.小明、小亮、小刚、小颖一起研究一道数学题．如图７，已知EF⊥AB，CD⊥AB．小明说：“如果还知道∠CDG=∠BFE，则能得到∠AGD=∠ACB．”小亮说：“把小明的已知和结论倒过来，即由∠AGD=∠ACB，可得到∠CDG=∠BFE．”小刚说：“∠AGD一定大于∠BFE．”小颖说：“如果连接GF，则GF一定平行于AB．”他们四人中，说法正确的有（）A．1人B．2人C．3人D．4人图７二、填空题（本大题共8小题，每小题4分，共32分）11. 如图8，当剪子口∠AOB增大15°时，∠COD增大度，其根据是.图8 图912.已知∠A与∠B互余，若∠A=20°15′，则∠B的度数为.13.如图9，直线AB，CD相交于点O，OM⊥AB，若∠MOD=45°，则∠COB= 度.14.如图10，在4×6的正方形网格中，点A，B，C，D，E，F都在格点上，连接C，D，E，F中任意两点得到的所有线段中，与线段AB平行的线段是.图10 图1115.已知AB∥CD，直线EF分别交AB，CD于点M，N，将一个含有45°角的直角三角尺按图11所示的方式摆放，若∠EMB=75°，则∠PNM= °.16.图12是运动员的领奖台，最高处的高为1 m，底边宽为2 m，为了美观要在上面铺上红地毯（图12中的阴影处），则至少需要红地毯m.图12 图1317.将一副三角尺和一张对边平行的纸条按图13所示的方式摆放，两个三角尺的一直角边重合，含30°角的直角三角尺的斜边与纸条一边重合，含45°角的三角尺的一个顶点在纸条的另一边上，则∠1的度数是．18.在同一平面内有2017条直线a1，a2，…，a2017，若a1∥a2，a2⊥a3，a3∥a4，a4⊥a5，……，则a1与a2017的位置关系是.三、解答题（本大题共5小题，共58分）19.如图14所示，已知∠AED=∠C，∠1=∠B，说明：EF∥AB.请结合图形，补全下面说理过程．因为∠AED=∠C，根据“”，所以DE∥.根据“”，所以∠1=∠.又因为∠1=∠B，所以∠B=∠.根据“”，所以EF∥AB.20.（10分）一辆汽车在笔直的公路上由A向B行驶，M，N分别是位于公路AB两侧的学校，如图15所示.（1）汽车在公路上行驶时，会对两所学校的教学都造成影响，当汽车行驶到何处时，分别对两所学校的影响最大?在图上标出来.（2）当汽车从A向B行驶时，在哪一段上对两个学校的影响越来越大?哪一段上对M学校的影响逐渐减小，而对N学校的影响逐渐增大?图1521. （12分）如图16，已知∠1＝∠2，试说明DE∥BF的理由.22.（12分）如图17，直线ＡＢ，ＣＤ，ＥＦ相交于点Ｏ．若∠ＡＯＣ∶∠ＡＯＥ＝2∶1，∠ＥＯＤ＝90°，求∠ＢＯＣ的度数．22.（14分）一张四边形纸片ABCD，∠B=∠D=90°，把纸片按图18所示折叠，使点B落在AD边上的B＇点，AE是折痕．（1）试判断B＇E与DC的位置关系，并说明理由.（2）若∠C=130°，求∠AEB的度数．图18附加题（15分，不计入总分）已知直线ｌ１∥ｌ２，且ｌ３与ｌ１，ｌ２分别交于Ａ，Ｂ两点，点Ｐ在ｌ３上．如图１9，试找出∠１，∠２，∠３之间的数量关系，并说明理由.（广东龙海平）参考答案一、1.B 2.B 3.C 4.C 5.C 6.B 7.A 8.C 9.C 10. B二、11. 15 对顶角相等 12. 两个角是同一个角的补角 这两个角相等 13. 13514. FD 15. 30 16．4 17. 15° 18. a 1∥a 2017三、19. 同位角相等，两直线平行 BC 两直线平行，内错角相等 EFC EFC 同位角相等，两直线平行20. 解：（1）如图1，过点M 作MC ⊥AB 于点C ，过点N 作ND ⊥AB 于点D ，根据垂线段最短，可 得在点C 处对M 学校的影响最大，在点D 处对N 学校的影响最大.图1（2）由点A 向点C 行驶时，对两个学校的影响逐渐增大；由点C 向点D 行驶时，对M 学校的影响 逐渐减小，对N 学校的影响逐渐增大.２1． 解：根据“对顶角相等”可得∠1=∠DMC.因为∠1=∠2，所以∠2=∠DMC.根据“同位角相等，两直线平行”，所以DE ∥BF.22． 解：由∠ＣＯＥ与∠ＥＯＤ互为补角，得∠ＣＯＥ＝１８０°－∠ＥＯＤ＝１８０°－９０°＝９０°． 因为∠ＡＯＣ∶∠ＡＯＥ＝２∶１，且∠ＡＯＣ＋∠ＡＯＥ＝∠ＣＯＥ＝９０°，所以∠ＡＯＥ＝31∠ＣＯＥ＝31×９０°＝３０°． 所以∠ＡＯＤ＝∠ＡＯＥ＋∠ＥＯＤ＝３０°＋９０°＝１２０°．由∠ＡＯＤ与∠ＢＯＣ互为对顶角，得∠ＢＯＣ＝∠ＡＯＤ＝１２０°．23. 解：（1）B ＇E ∥DC.理由如下：由折叠前后对应角相等，得∠AB ＇E=∠B=90°.又∠D=90°，所以∠AB ＇E=∠D ，所以B ＇E ∥DC.（2）因为B ＇E ∥DC ，所以∠BEB ＇=∠C=130°.由折叠前后对应角相等，得∠AEB=∠AEB ＇=21∠BEB ＇=21×130°=65°. 24.∠１＋∠２＝∠３．理由：如图2，过点Ｐ作ｌ１的平行线ＰＱ．因为ｌ１∥ｌ２，所以ｌ１∥ｌ２∥ＰＱ．所以∠１＝∠４，∠２＝∠５．又∠４＋∠５＝∠３，所以∠１＋∠２＝∠３．。

第七章相交线与平行线综合检测一、选择题（本大题共10小题，每小题3分，共30分）1.如图1，过点A画直线l的平行线，一共能画（）A.2条以上B.2条C.1条D.0条图1①②③④2.如图2，直线a，b，c交于一点，a⊥b，若∠1=40°，则∠2的度数为（）A.30°B.40°C.50°D.60°3.在图3所示的四个图中，∠1与∠2是同位角的是（）A．①②③④B．仅①②③C．仅①②D．仅①③4.如图4，若直线a∥b，c⊥a，则c与b相交所形成的∠1的度数为（）A．45°B．60°C．90°D．120°5.如图5，笔直的公路一旁是电线杆，若电线杆都和电线杆①平行，则判断其余电线杆两两平行的根据是（）A.同位角相等，两直线平行B.内错角相等，两直线平行C.同旁内角互补，两直线平行D.平行于同一条直线的两直线平行6.如图6，有下列条件：①∠B+∠BFE=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5．其中能判定AB∥EF的有（）A．1个B．2个C．3个D．4个7.如图7，分别过长方形ABCD（BC∥AD）的顶点A，D作直线l1，l2，使l1∥l2，l2与边BC交于点P，若∠1=38°，则∠BPD的度数为（）A．162°B．152°C．142°D．128°8.如图7，直线AC∥BD，AO，BO分别是∠BAC，∠ABD的平分线，下列结论中错误的是（）A．∠BAO与∠CAO相等B．∠BAC与∠ABD互补C．∠BAO与∠ABO互余D．∠CAO与∠DBO相等图7 图8 图99.某小区大门的栏杆示意图如图8，当栏杆抬起时，BA垂直于地面AE，CD平行于地面AE，则∠ABC+∠BCD的度数为（）A．180°B．270°C．300°D．360°10.如图9，点D，E分别在BA，BC上，已知∠ADF=α，∠CEG=β，∠ABC=γ，若DF∥EG，则α，β，γ之间的关系为（）A．α+β+γ=180°B．α+β=γ C．α+β+γ=90°D．2α+2β-γ=45°二、填空题（本大题共6小题，每小题3分，共18分）11.有下列说法：①对顶角相等；②同旁内角互补；③互为补角的两个角的度数之和是180°；④两直线平行，同位角相等.其中正确的是（填序号）.12.如图10，已知AB⊥l1，AC⊥l2，则点A到直线l1的距离是线段的长度．图10 图1113.如图11，已知∠1+∠2=180°，若∠3=110°，则∠4=．14.如图12，已知AB∥DC，若∠1=39°，∠C与∠D互余，则∠D=，∠B=．15.如图13，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COE，若∠BOF=30°，则∠AOC=°．16. 如图14，一块长方形的玻璃（其中AB∥CD，AD∥BC）因震动发生两条裂痕，即折线EFGH和线段EM，已知∠1=130°，∠G=∠F，EM⊥EF，则∠2=_______，∠3=_______.三、解答题（本大题共6小题，共52分）17. （6分）如图15，以点B为顶点，射线BC为一边，利用尺规作∠EBC，使∠EBC=∠A．（尺规作图，不写作法，但保留作图痕迹）18.如图16，已知∠1=∠2，∠3=∠4，∠5=∠6，试说明ED∥FB的理由．将下列过程补充完整.解：因为∠3=∠4，根据“内错角相等，两直线平行”，所以CF∥.根据“”，所以∠5+∠CAB=180°.又∠5=∠6，所以∠6+∠CAB=180°.根据“同旁内角互补，两直线平行”，所以∥CD.根据“”，所以∠2= .因为∠1=∠2，所以∠1=∠EGA. 根据“”，所以ED∥FB．19.如图17，已知AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E．求证：AD∥BC．20.如图18，已知直线AB，CD相交于点O，OE平分∠BOD，∠AOC=70°，OF⊥CD．（1）写出图中互余的角；（2）求∠EOF的度数．21.（8分）如图19，已知四边形ABCD，延长DA到E，延长BC到F，连接EF，分别交AB，CD 于点G，H，若∠BGE+∠CHF=180°，∠B=∠D，试说明∠E=∠F.22.（12分）将一个含30°角的三角尺按如图20所示放置，已知AB∥EF，∠2比∠1大10°，∠3比∠1的2倍少40°.（1）试判断直线CD与EF的位置关系，并说明理由；（2）求∠AGH的度数.图18附加题（共20分，不计入总分）1.（6分）在同一平面内，若一个角的两边与另一个角的两边分别平行，那么这两个角的数量关系为（）A.相等B.互补C.相等或互补D.无法确定2.（14分）如图，点C，D分别在射线OA，OB上，不与点O重合，CE∥DF.（1）如图①，探究∠ACE，∠AOB，∠ODF的数量关系，并证明你的结论；（2）如图②，DP平分∠ODF，若∠ACE=α，∠AOB=β，请用含α，β的式子表示∠PDO=．（直接写出结果）①②参考答案一、1. C2. C3. D 4. C 5. D 6.C7.C 8.D 9.B10. B 提示：如图1，过B作BH∥DF，则BH∥EG.因为DF∥EG，所以∠ADF=∠1.又BH∥EG，所以∠CEG=∠2，所以∠ADF+∠CEG=∠1+∠2=∠ABC，即α+β=γ.图1二、11. ②12. AB13. 110°14. 39°15.8016. 50°40°三、17.解：如图所示，∠CBE即为所求．18. 解：BD 两直线平行，同旁内角互补AB ∠EGA 两直线平行，同位角相等同位角相等，两直线平行19.解：∵AE平分∠BAD（已知），∴∠1=∠2（角平分线的定义）.又AB∥CD（已知），∴∠1=∠CFE（两直线平行，同位角相等）.∵∠CFE=∠E（已知），∴∠2=∠E（等量代换）.∴AD∥BC（内错角相等，两直线平行）．20. 解：（1）图中互余的角有∠AOC与∠BOF，∠BOD与∠BOF，∠EOF与∠EOD，∠BOE与∠EOF. （2）因为∠AOC与∠BOD互为对顶角，所以∠BOD=∠AOC=70°.因为OF⊥CD，所以∠COF=90°，所以∠BOF=180°-70°-90°=20°.所以∠EOF=∠BOE+∠BOF=35°+20°=55°．21. 解：因为∠GHC+∠CHF=180°，∠BGE+∠CHF=180°，所以∠GHC=∠BGE.所以AB∥CD，所以∠B+∠BCD=180°.又∠B=∠D，所以∠D+∠BCD=180°.所以DE∥BF，所以∠E=∠F.22. 解：（1）设∠1=x°，则∠2=（x+10）°，∠3=（2x-40）°.因为∠1+∠HMG+∠2=180°，所以x+30+x+10=180，解得x=70.所以∠1=70°，∠2=70°+10°=80°，∠3=2×70°-40°=100°.所以∠2+∠3=80°+100°=180°.所以CD∥EF.（2）因为CD∥EF，所以∠MHD=∠1=70°.所以∠GHD=90°-∠MHD=90°-70°=20°.因为AB∥EF，CD∥EF，所以AB∥CD.所以∠AGH=∠GHD=20°.附加题1.C2. 解：（1）∠ODF+∠AOB+∠ACE=360°．理由如下：过点O 作直线OG ∥FD.因为OG ∥FD ，所以∠ODF+∠DOG=180°.又OG ∥FD ，CE ∥FD ，所以OG ∥CE ，所以∠GOC=∠OCE. 因为∠ACE+∠OCE=180°，所以∠ACE+∠GOC=180°.所以∠ODF+∠DOG+∠ACE+∠GOC=360°，即∠ODF+∠AOB+∠ACE=360°.（2）180°-21α-21β提示：因为DP 平分∠ODF ，所以∠POD=21∠ODF=21（360°-α-β）=180°-。

鲁教版五四制六年级下册第七章相交线与平行线复习习题（含答案解析）学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，将一张含有30∘角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2= 44∘，则∠1的大小为（）A．14∘B．16∘C．90∘−αD．α−44∘2．如图，BE平分∠DBC，点A是BD上一点，过点A作AE∥BC交BE于点E，∠DAE=56°，则∠E的度数为（）A．56°B．36°C．26°D．28°3．如图，直线a∥b，一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°，则∠2的度数为( )A．105°B．110°C．115°D．120°4．如图，已知∠1+∠2=180°，∠3=55°．那么∠4的度数是（）A．45°B．125°C．35°D．55°5．下列说法：①两点之间，线段最短；②同旁内角互补；③若AC=BC，则点C是线段AB的中点；④经过一点有且只有一条直线与这条直线平行，其中正确的说法有( ) A．1个B．2个C．3个D．4个6．如图，下列四个条件中，能判断DE//AC的是( )．A．∠3=∠4B．∠1=∠2C．∠EDC=∠EFC D．∠ACD=∠AFE7．如图，下列条件中不能判定AB∥CD的是（）A．∠3＝∠4B．∠1＝∠5C．∠3＝∠5D．∠1＋∠4＝180°8．将一条两边沿平行的纸带如图折叠，若∠1=62∘，则∠2等于()A．62∘B．56∘C．45∘D．30∘9．如图，已知AB、CD、EF互相平行，且∠ABE =70°，∠ECD = 150°，则∠BEC是（）A．30°B．40°C．50°D．60°10．如图，在下列条件中：①∠1=∠2；②∠BAD+∠ADC=180°；③∠ABC=∠ADC；④∠3=∠4，能判定AB∥CD的有( )A．1个B．2个C．3个D．4个11．为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产--“抖空竹”引入阳光特色大课间.下面左图是某同学“抖空竹”时的一个瞬间，小聪把它抽象成右图的数学问题：已知AB//CD，∠EAB=80∘，∠ECD=110∘，则∠E的度数是()A．30∘B．40∘C．60∘D．70∘12．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯的角∠A是120°，第二次拐弯的角∠B是150°，第三次拐弯的角是∠C，这时道路恰好和第一次拐弯之前的道路平行，则∠C是（）度A．120B．130C．140D．15013．如图，a∥b，AC⊥AB，∠1=60°，则∠2的度数是( )A．50°B．45°C．35°D．30°14．一个两边平行的纸条，如图那样折叠一下，则∠1的度数是（）A．30°B．40°C．50°D．60°15．如图，直线a∥b，∠1=75°，∠2=40°，则∠3的度数为（）A．75°B．50°C．35°D．30°16．如图，已知直线a∥b，△ABC的顶点B在直线b上，∠C=90°，∠1=36°，则∠2的度数是（）A．54°B．44°C．36°D．64°17．如图，直线c与直线a，b相交，不能判断直线a，b平行的条件是( )A．∠2＝∠3 B．∠1＝∠4C．∠1＋∠3＝180°D．∠1＋∠4＝180°18．将一副三角板和一张对边平行的纸条按如图摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是( )A．15°B．22.5°C．30°D．45°19．将一把直尺与一块三角板如图所示放置，若∠1=40°，则∠2的度数为（）A．50°B．110°C．130°D．140°20．如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为( )A．85°B．70°C．75°D．60°21．如图，已知直线AB、CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB、CD、AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，，④360°﹣α﹣β，∠AEC的度数可能是（）A．①②③B．①②④C．①③④D．①②③④22．如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30︒角直角三角板的斜边与纸条一边重合，含45︒角的三角板的一个顶点在∠的度数是（）纸条的另一边，则1A．14°B．15°C．20°D．30°23．23．如图所示，AB∥CD，EF，HG相交于点O，∠1=40°，∠2=60°，则∠EOH的角度为（）A．80°B．100°C．140°D．120°24．①如图1,AB∥CD,则∠A +∠E +∠C=180°；②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E－∠1=180° ；④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )A．、1个B．2个C．3个D．4个25．三条互不重合的直线的交点个数可能是（）A．0，1，3B．0，2，3C．0，1，2，3D．0，1，226．点P为直线MN外一点,点A、B、C为直线MN上三点,PA=4厘米,PB=5厘米,PC=2厘米,则P到直线MN的距离为（）A．4厘米B．2厘米C．小于2厘米D．不大于2厘米27．如图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．108°B．114°C．116°D．120°28．如图，在△ABC中，AB=AC，CD∥AB，点E在BC的延长线上.若∠A=30°，则∠DCE的大小为（）A．30°B．52.5°C．75°D．85°29．一辆汽车在笔直的公路上行驶，两次拐弯后的方向与原来的方向相反．．，那么两次拐弯的角度可能是是（）A．第一次右拐60°，第二次左拐120°B．第一次左拐60°，第二次右拐60°C．第一次左拐60°，第二次左拐120°D．第一次右拐60°，第二次右拐60°30．两条平行线被第三条直线所截，则下列说法错误的是（）A．一对邻补角的平分线互相垂直B．一对同位角的平分线互相平行C．一对内错角的平分线互相平行D．一对同旁内角的平分线互相平行二、填空题31．（题文）如图，m∥n，∠1=110°，∠2=100°，则∠3=_______°．32．如图，四边形ABCD中，点MN分别在AB，AC上，∠C=80°，按如图方式沿着MN折叠，使FN∥CD，此时量得∠FMN=40°，则∠B的度数是_____．33．如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5；则一定能判定AB∥CD的条件有_____(填写所有正确的序号)．34．如图，把一块含有30°角（∠A=30°）的直角三角板ABC的直角顶点放在长方形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1=40°，那么∠AFE=______35．如图，DA⊥CE于点A，CD∥AB，∠1=30°，则∠D=_____．36．如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为_____．37．如图，直线AB，CD相交于点O，OA平分∠EOC，∠EOD＝120°，则∠BOD=________ °38．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=48°，则∠AED为°．39．将如图1的长方形ABCD纸片沿EF折叠得到图2，折叠后DE与BF相交于点P. 如果∠EPF=70°，则∠PEF的度数为_________ .40．直线l1∥l2，一块含45°角的直角三角板如图放置．若∠1=85度，则∠2=________度．41．在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角板画平行线AB、CD, 并说出自己做法的依据. 小琛、小萱、小冉三位同学的做法如下：小琛说：“我的做法的依据是内错角相等，两直线平行. ”小萱做法的依据是______________________.小冉做法的依据是______________________.42．如图，四边形ABCD中，点M、N分别在AB、BC上，将△BMN沿MN翻折，得△FMN，若MF//AD，FN//DC，则∠D的度数为______ ∘.43．如图，已知，AB∥CD∥EF，∠E=140°，∠A=115°，则∠ACE=______度.44．如图，已知AB∥DE，∠ABC＝70º，∠CDE＝140º，则∠BCD的值为_______.45．如图，AF∥CD，BC平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：①BC平分∠ABE；②AC∥BE；③∠BCD+∠D = 90°；④∠DBF = 2∠ABC．其中正确的结论有______________．46．一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D 在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是_____．47．如图，已知AB//DE，∠BAC=m∘，∠CDE=n∘，则∠ACD=________________ ∘．48．如图所示,同位角有a 对,内错角有b 对,同旁内角有c 对,则a+b+c 的值是_______.49．如图，直线 1l ∥2l ，∠1=40°，则∠2+∠3= °．50．如图，正五边形ABCDE ，AF ∥CD 交BD 的延长线于点F ，则∠DFA ＝ 度。

相交线与平行线练习题（附答案）【知识积累】一、相交线1、邻补角：如下图，∠1和∠2（或∠3和∠4、或∠5和∠6、或∠7和∠8、或∠1和∠3、或∠2和∠4、或∠5和∠7、或∠6和∠8）有一条公共边，它们的另一边互为反向延长线（∠1和∠2互补），具有这种关系的两个角，互为邻补角。

2、对顶角：如上图，∠1和∠4（或∠2和∠3、或∠5和∠8、或∠6和∠7）有一个公共顶点，并且∠1的两边分别是∠4的两边的反向延长线（∠1和∠4相等），具有这种位置关系的两个角，互为对顶角。

3、同位角：如上图，∠1和∠5（或∠3和∠7、或∠2和∠6、或∠4和∠8），这两个角分别在直线的同一侧，即左侧（或左侧、或右侧、或右侧），并且在另外两条直线的同一方，即上方（或下方、或上方、或下方），具有这种位置关系的一对角叫做同位角。

4、内错角：如上图，∠3和∠6（或∠4和∠5），这两个角都在两条直线之间，并且分别在中间直线的两侧，具有这种位置关系的一对角叫做内错角。

5、同旁内角：如上图，∠3和∠5（或∠4和∠6），这两个角都在两条直线之间，并且分别在中间直线的同侧，具有这种位置关系的一对角叫做同旁内角。

二、垂直1、定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

符号语言记作：如图所示：AB⊥CD，垂足为O。

垂直定义的两层含义：（1）∵∵AOC=90°（已知），∵AB∵CD（垂直的定义）（2）∵AB∵CD（已知），∵∵AOC＝90°（垂直的定义）2、性质：（1）过一点有且只有一条直线与已知直线垂直。

（2）连接直线外一点与直线上各点的所有线段中，垂线段最短。

简称：垂线段最短。

3、垂线段的概念：由直线外一点向直线引垂线，这点与垂足间的线段叫做垂线段。

4、点到直线的距离：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。

三、平行1、定义：在同一平面内，不相交的两条直线叫做平行线，直线a与直线b互相平行，记作a∵b。

相交线与平行线测试题及答案1. 单选题：在平面上，两条互相垂直的直线称为（）。

A. 平行线B. 垂直线C. 相交线D. 对称线答案：B. 垂直线2. 单选题：下面哪种说法是正确的？A. 平行线永远不会相交B. 相交线永远不会平行C. 平行线和相交线可以同时存在D. 平行线和相交线不能同时存在答案：C. 平行线和相交线可以同时存在3. 多选题：判断下列述句是否正确。

1) 平行线没有交点。

2) 相交线可以有无数个交点。

3) 两条垂直线的交点一定是直角。

A. 正确的有1）、2）、3）B. 正确的有1）、3）C. 正确的有2）、3）D. 正确的只有3）答案：B. 正确的有1）、3）4. 填空题：两条互相垂直的直线所成的角度为（）度。

答案：90度5. 判断题：两条平行线的夹角为180度。

答案：错误6. 判断题：两条相交直线一定不平行。

答案：正确7. 计算题：已知直线L1与直线L2互相垂直，L1的斜率为2，过点（1，3）的直线L2的斜率为（）。

答案：-1/28. 计算题：已知直线L1过点（1，2）且斜率为3/4，直线L2与L1平行且过点（3，5），求直线L2的斜率。

答案：3/49. 解答题：请解释什么是相交线和平行线，并举例说明。

答案：相交线是指两条直线或线段在平面上有唯一一点相交。

例如，在平面上有两条直线，一条通过点A和点B，另一条通过点C和点D，如果点A与点C不重合并且点B与点D不重合，则这两条直线相交于点E。

平行线是指在平面上没有任何交点的两条直线。

例如，在平面上有一条直线通过点A和点B，另一条直线通过点C和点D，如果两条直线没有任何一点相交，则这两条直线是平行线。

10. 解答题：如何通过直线的斜率来判断两条直线是否平行或垂直？答案：两条直线平行的充要条件是它们的斜率相等，即斜率相同的两条直线是平行线。

两条直线垂直的充要条件是它们的斜率的乘积为-1，即斜率之积为-1的两条直线是垂直线。

总结：在平面几何中，相交线是指两条直线或线段在平面上有唯一一点相交，平行线是指在平面上没有任何交点的两条直线。