数据库关系代数表达式学习资料
- 格式:docx
- 大小:23.79 KB
- 文档页数:5

【数据库复习】关系代数
关系代数
问:为何称为代数?
答:因为存在操作符和操作数,操作数为表,操作符为交、并等;
关系代数有分为基于集合的关系代数和基于包的关系代数;
关系代数的基本操作:并、选择、投影、笛卡尔积、差、重命名;
基本操作的意思是其他的操作符可以通过基本操作推出;
注意:如果我们使用并、交、差运算,必须保证R和S的属性集合是相同的,当然如果不同,也可以通过重命名操作;
补充:1.自然连接
2. θ连接
3.重命名
表达式树
基于包的关系代数
1.并
如果元组t在R中出现m次,S中出现n次,则在R∪S中出现m+n次;
2.交
如果元组t在R中出现m次,S中出现n次,则R∩S中出现min(m,n)次;
3.差
如果元组t在R中出现m次,S中出现n次,则R-S中出现(1)如果m>n,则出现m-n次;(2)如果m<>
4.消除重复操作符
δ(R) 能对关系R消除重复元组;
5.聚集操作符
SUM(A)
AVG(A)
MIN(A)
MAX(A)
COUNT(A)
其中A为某个属性;
6.分组操作符
γ
包含了以某个属性作为分组属性,还有聚集操作符;
7.排序元组
τA(R) 表示根据A属性进行排序;
8.外连接
左外连接:
右外连接:
9.扩展投影运算
关系代数表达式的分步表示
因为用一个表达式直接表示复杂的代数表达式会很不清楚,因此我们可以通过分步表示;
比如:
可以表示为:。

数据库SQL---关系模型与关系代数1、关系数据库:表的集合,即关系的集合。
关系数据库=关系数据库模式(型)+关系数据库内容(值)1)域:一组具有相同数据类型的值的集合。
2)笛卡尔积:对集合进行穷举外变一次内变一边,是一张二维表,表中的一行对应于一个元组,表中的一列的值来自于同一个域。
给定一组域D1,D2,...,Dn的笛卡尔积为D1×D2×...×Dn={(d1,d2,...,dn)|di€Di,i=1,2,...,n},其中集合中的每一个元素(d1,d2,...,dn)称为一个n元组,简称元组,元组中的每一个值di 称为一个分量。
3)关系:笛卡尔积的子集,是一张二维表。
2、关系模式:简记为r(U)或r(D1,D2,...,Dn),其中r是关系的名字,U是属性名(D1,D2,...,Dn)的集合,n是关系的目(或度),当n=1时,称该关系为单元关系;当n=2时,称该关系为二元关系。
3、码1)超码:属性集A可以唯一地标识关系r中的一个元组,则称属性A为关系r的超码。
2)全码:所有属性加在一起组成的候选码。
3)候选码:属性集A是关系r的超码,且属性集A的任意真子集都不能称为关系r的超码,则称属性集A为候选码。
候选码是最小的超码,即最小属性组。
候选码的诸属性称为主属性,不能为空。
不包含在任何候选码中的属性称为非码属性。
4)主码:若一个关系有多个候选码,则可选定其中一个候选码作为该关系的主码。
5)外码:F是关系r的一个属性,Ks是关系s的主码,若F与Ks 相对应,则称F是关系r参照关系s的外码,简称F是关系r的外码,并称关系r为参照关系,关系s为被参照关系或目标关系。
4、关系完整性约束关系模式中3类数据完整性约束:实体完整性、参照完整性、用户自定义完整性,其中前两种称为关系的两个不变性。
1)实体完整性:若属性集A是关系r的主码,则A不能取空值null,即主属性不能为空。
2)参照完整性:主键与外键的关系,外码的取值要么为空,要么为与之对应的主码的值。


关系代数操作复习实例:职工(职工编号,职工姓名,年龄,性别);E(ENO ,ENAME,AGE,SEX);社团(社团编号,社团名称);C(CNO ,CNAME);参加(职工编号,社团编号,参加时间);EC(ENO ,CNO,TIME);说明:(1)加粗的为主键;(2)参加表中的职工编号参照职工表中的职工编号,参加表中的社团编号参照社团表中的社团编号写出如下检索关系代数表达式:(1)检索年龄在30到50岁之间的职工编号和职工姓名AGE '30'AGE '50',((E))ENO ENAME σ>=∧<=∏(2)检索年龄在30到50岁之间的职工参加的社团名称AGE '30'AGE '50'((E C EC))CNAME σ>=∧<=∞∞∏(3)检索参加‘妇女之家’的职工编号''(())CNAME ENO C EC σ=∞∏妇女之家(4)检索参加‘书法社’或‘篮球队’的职工姓名''''AME ((E C EC))CNAME CNAME EN σσ=∨=∞∞∏书法社篮球队(5)检索既参加‘书法社’又参加‘篮球队’的职工姓名''''AME AME ((E C EC))((E C EC))CNAME CNAME EN EN σσ==∞∞∞∞∏∏ 书法社篮球队注意:不能将结果写成:''''AME ((E C EC))CNAME CNAME EN σσ=∧=∞∞∏书法社篮球队不能使指定的社团名称既是‘书法社’又是‘篮球队’。
假设社团表的信息如下:‘篮球队’,从表格中可以看出一个名称对应一个编号!(6)检索‘2014’年参加社团的职工信息'2014'NO,ENAME,AGE,SEX ((C EC))TIME E σ=∞∏(7)检索‘王小毛’参加的社团名称ENAME ''CNAME ((E C EC))σ=∞∞∏王小毛(8)检索没有参加任何社团的职工编号ENO ENO (E)-(EC)∏∏(9)检索没有参加‘篮球队’的职工姓名CNAME=''ENAME ENAME (E)-(E C EC )σ∞∞∏∏篮球队()。


用关系代数式表示查询语句
关系代数式用于表示数据库查询语句,以下是一些常见的关系代数式:
1. 选择(Select):σ<条件>(关系)表示从关系中选择符合条件的元组。
例如,σ年龄>18 (学生) 表示选择学生关系中年龄大于18的学生。
2. 投影(Project):π<属性列表>(关系)表示从关系中选择指定的属性。
例如,π姓名, 年龄 (学生) 表示选择学生关系中的姓名和年龄属性。
3. 连接(Join):ρ属性名1.属性名2(关系1 ⨝条件关系2)表示根据条件连接两个关系的元组。
例如,ρS.学号(E ⨝ S.学号=E.学号) 表示根据学号将学生和成绩关系连接起来,得到学生关系中每个学生的成绩。
4. 自然连接(Natural Join):ρ属性名(关系1 ⨝关系2)表示根据两个关系的公共属性自动连接。
例如,ρS(E ⨝ S) 表示根据学号连接学生和成绩关系,得到学生关系中每个学生的成绩。
5. 差集(Difference):关系1 - 关系2表示关系1中去除与关系2中相同元组的结果。
例如,学生 - 选课表示去除已选课学生的学生关系。
6. 笛卡尔积(Cartesian Product):关系1 ×关系2表示关系1和关系2的所有可能组合。
例如,学生 ×选课表示学生关系和选课关系的笛卡尔积。
这些关系代数式可以组合使用,构建复杂的查询语句。

数据库关系代数表达式学习关系代数是关系数据库系统查询语言的理论基础一、关系代数的9种操作:关系代数中包括了:并、交、差、乘、选择、投影、联接、除、自然联接等操作。
五个基本操作:并(∪)、差(-)、笛卡尔积(×)、投影(σ)、选择(π)四个组合操作:交(∩)、联接(等值联接)、自然联接(R S)、除法(÷)注2:等值连接表示先做笛卡尔积(×)之后,对相应列进行选择或等值关联后的结果(仅筛选行、不筛选列) 注2:自然连接表示两个关系中若有相同名称的属性,则自动作为关联条件,且仅列出一列二、关系代数表达式:由关系代数运算经有限次复合而成的式子称为关系代数表达式。
这种表达式的运算结果仍然是一个关系。
可以用关系代数表达式表示对数据库的查询和更新操作。
三、举例说明:设教学数据库中有3个关系:学生关系S(SNO, SNAME,AGE,SEX)学习关系SC(SNO,CNO,GRADE)课程关系C(CNO,CNAME,TEACHER)(1) 检索学习课程号为C2的学生学号与成绩------------------------------------SELECT SNO,GRADEFROM SCWHERE CNO='C2'------------------------------------π SNO, GRADE (σ CNO='C2' (SC))************************************(2) 检索学习课程号为C2的学生学号与姓名------------------------------------SELECT SC.SNO,S.SNAMEFROM SC,SWHERE SC.SNO=S.SNOAND O='C2'------------------------------------π SNO,SNAME (σ CNO='C2' (S SC))此查询涉及S和SC,先进行自然连接,然后再执行选择投影操作。
关系代数表达式总结一、并例1 求选修了课程号为1或2的课程的学生学号。
分析:可以先求出选修了课程号为1的课程的学生学号,再求出选修了课程号为2的课程的学生学号,最后使用并运算的方法求出选修课程号为1或2的课程的学生学号。
本例也可以使用或条件来表示。
πSno(σCno=’1’(SC))∪πSno(σCno=’2’(SC)) 或πSno(σCno=’1’∨ Cno=’2’(SC))二、交例2 检索至少选修课程号为2和3的课程的学生学号。
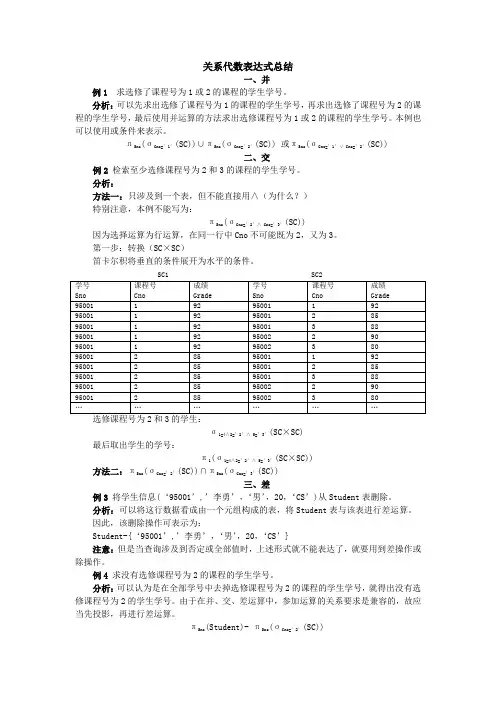
分析:方法一:只涉及到一个表,但不能直接用∧(为什么?)特别注意,本例不能写为:πSno(σCno=’2’∧ Cno=’3’(SC))因为选择运算为行运算,在同一行中Cno不可能既为2,又为3。
第一步:转换(SC×SC)笛卡尔积将垂直的条件展开为水平的条件。
SC1 SC2选修课程号为2和3的学生:σ1=4∧2=’2’∧ 5=’3’(SC×SC)最后取出学生的学号:π1(σ1=4∧2=’2’∧ 5=’3’(SC×SC))方法二:πSno(σCno=’2’(SC))∩πSno(σCno=’3’(SC))三、差例3 将学生信息(‘95001’,’李勇’,‘男’,20,‘CS’)从Student表删除。
分析:可以将这行数据看成由一个元组构成的表,将Student表与该表进行差运算。
因此,该删除操作可表示为:Student-{‘95001’,’李勇’,‘男’,20,‘CS’}注意:但是当查询涉及到否定或全部值时,上述形式就不能表达了,就要用到差操作或除操作。
例4 求没有选修课程号为2的课程的学生学号。
分析:可以认为是在全部学号中去掉选修课程号为2的课程的学生学号,就得出没有选修课程号为2的学生学号。
由于在并、交、差运算中,参加运算的关系要求是兼容的,故应当先投影,再进行差运算。
πSno(Student)- πSno(σCno=’2’(SC))特别注意,本题不能写为:πSno(σCno≠’2’(SC))。

数据库关系代数:是一种抽象的查询语言,用对关系的运算来表达查询。
关系代数运算的是关系,运算结果亦是关系。
关系代数的基本关系包括:并、交、差、笛卡尔积、选择、投影、连接、除法运算。
由于并、交、差运算很简单,这里不再赘述,只说明了几个容易遗忘和混淆的运算。
1、笛卡尔积
计算两个关系R和S的笛卡尔积,R的元数为r,S的元数为s,则R×S是一个(r+s)元的元组集合
2、选择
选择是根据某些条件对关系做水平切割
3、投影π
投影与选择正好相反,是对关系的一种垂直切割,消去某列,并重新安排列的顺序。
投影用(π)表示。
4、连接
连接运算:从两个关系的笛卡尔积中选取属性间满足一定条件的元组,用(R ⋈S)表示,连接分为两种,一种是等值连接(有的书上写的是连接),另一种是自然连接。
等值连接:条件AθB中的θ为‘=’的连接;自然连接:关系R与S选取A、B属性值相等的那些元组。
自然连接:一般自然连接使用在R和S有公共属性时,如果没有公共属性,自然连接就转为笛卡尔积操作。
5、除法
经过总结之后,发现其实关系之间的运算并不难,关键在于要认
真分析,将符号与我们的实际找到联系,只有对各种符号印象深刻之后,这些关系之间的运算也就变得很简单。
在平时要多找联系多总结,方是正道。

数据库关系代数表达式
数据库关系代数表达式是一种简单的数学表达式,它可以用来描述数据库表之间的关系,以及它们之间的操作。
它可以被用来查询或更新数据库,并且能够让数据库变得容易管理和操作。
数据库关系代数表达式主要包括6种基本操作:选择(select),投影(project),交集(intersect),并(union),差(difference)和笛卡尔积(cartesian product)。
选择操作可以从数据库中提取满足特定条件的记录。
投影操作可以从数据表中抽取特定的属性,以便只展示需要的信息。
交集操作可以将两个表中的重复的记录提取出来。
并操作可以将两个表中的内容进行合并,以查看它们的所有内容。
差操作则可以排除两个表中的重复记录,以便分离出不同的记录。
最后,笛卡尔积操作可以将两个表中的记录进行全部组合,以便更好地查看它们之间的关系。
数据库关系代数表达式的最大优势在于它的灵活性,它可以被用来实现各种各样的操作,并且能够被用来构建复杂的查询和更新数据库的功能。
此外,它还可以被用来实现多表查询,以及查询结果的进一步操作,这使得它十分强大。
数据库关系代数表达式是一种十分实用的数据库操作工具,它可以帮助开发人员更轻松地管理数据库,而且能够实现多种复杂的操作。
因此,它是数据库开发过程中非常重要的一部分,应该被充分利用。
•登录关系数据库关系代数之前在学习数据库时接触过关系代数,只是在经过很长一段时间不应用之后,不能很快从大脑中将知识调出来,今天就来了个再次学习总结加深自己的印象。
关系代数:是一种抽象的查询语言,用对关系的运算来表达查询。
关系代数运算的是关系,运算结果亦是关系。
关系代数的基本关系包括:并、交、差、笛卡尔积、选择、投影、连接、除法运算。
由于并、交、差运算很简单,这里不再赘述,只说明了几个容易遗忘和混淆的运算。
1、笛卡尔积计算两个关系R和S的笛卡尔积,R的元数为r,S的元数为s,则R×S是一个(r+s)元的元组集合,如下例所示:结果:由结果分析:笛卡尔积得到的结果元数为r+s即:3+3=6;记录数为:R中的记录数与S中的记录数相乘,即:3×2=6。
2、选择选择是根据某些条件对关系做水平切割,例如δ2 > '4'(R),表示从R中挑选第二个分量值(也就是R中B列的值)大于4的元组所构成关系。
结果:3、投影π投影与选择正好相反,是对关系的一种垂直切割,消去某列,并重新安排列的顺序。
投影用(π)表示。
例如:π3,1(R)表示的结果如下:由结果可以看出:查询表达式中的下标可以用数字表示,也可以用列的名字表示,返回列的名字,而其他的列在结果关系中被去掉,也可以通过投影来重新布局关系的排列。
4、连接连接运算:从两个关系的笛卡尔积中选取属性间满足一定条件的元组,用(R ⋈S)表示,连接分为两种,一种是等值连接(有的书上写的是连接),另一种是自然连接。
等值连接:条件AθB中的θ为‘=’的连接;自然连接:关系R与S选取A、B属性值相等的那些元组。
数据库关系代数表达式学习关系代数是关系数据库系统查询语言的理论基础一、关系代数的9种操作:关系代数中包括了:并、交、差、乘、选择、投影、联接、除、自然联接等操作。
五个基本操作:并(∪)、差(-)、笛卡尔积(×)、投影(σ)、选择(π)四个组合操作:交(∩)、联接(等值联接)、自然联接(R S)、除法(÷)注2:等值连接表示先做笛卡尔积(×)之后,对相应列进行选择或等值关联后的结果(仅筛选行、不筛选列) 注2:自然连接表示两个关系中若有相同名称的属性,则自动作为关联条件,且仅列出一列二、关系代数表达式:由关系代数运算经有限次复合而成的式子称为关系代数表达式。
这种表达式的运算结果仍然是一个关系。
可以用关系代数表达式表示对数据库的查询和更新操作。
三、举例说明:设教学数据库中有3个关系:学生关系S(SNO, SNAME,AGE,SEX)学习关系SC(SNO,CNO,GRADE)课程关系C(CNO,CNAME,TEACHER)(1) 检索学习课程号为C2的学生学号与成绩------------------------------------SELECT SNO,GRADEFROM SCWHERE CNO='C2'------------------------------------π SNO, GRADE (σ CNO='C2' (SC))************************************(2) 检索学习课程号为C2的学生学号与姓名------------------------------------SELECT SC.SNO,S.SNAMEFROM SC,SWHERE SC.SNO=S.SNOAND O='C2'------------------------------------π SNO,SNAME (σ CNO='C2' (S SC))此查询涉及S和SC,先进行自然连接,然后再执行选择投影操作。
并、差、笛卡儿积、投影、选择是关系代数的5种基本的运算,其他运算,即交、连接、除都可以通过基本的运算推导运算出。
1、并,设有两个关系R和S,它们具有相同的结构,R和S的并是由属于R或属于S的元组组成的集合;2、差,R和S的差是由属于R但不属于S的元组组成的集合;3、笛卡尔积,两个集合X和Y的笛卡尓积,又称直积,表示为X 与Y相乘,第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员;4、选择,从关系中找出满足给定条件的那些元组称为选择;其中的条件是以逻辑表达式给出的,值为真的元组将被选取;5、投影,从关系模式中挑选若干属性组成新的关系称为投影。
数据库系统(二)--关系型数据库之关系代数关系型数据库-关系操作集合1、基本的关系操作关系模型中常用的关系操作包括查询(Query)操作和插入(Insert)、删除(Delete)、修改(Update)操作两大部分。
查询操作分为:选择、投影、连接、除、并、差、交、笛卡尔积等;五种基本操作:选择、投影、并、差、笛卡尔积;关系操作的特点是集合操作方式,即操作的对象和结果都是集合、这种操作方式也称为一次一集合的方式。
2、关系数据语言的分类关系操作是通过关系语言来实现的。
关系语言的特点是高度非过程化,即:(1)用户不必请求数据库管理员为其建立特殊的存取路径,存取路径的选择由 DBMS 的优化机制来完成;(2)用户也不必求助于循环和递归来完成数据的重复操作。
关系操作的能力可以用两种方式来表示:代数方式和逻辑方式。
关系代数、元组关系演算和域关系演算均是抽象的查询语言。
结构化查询语言SQL充分体现了关系数据语言的特点和优点,是关于数据库的标准语言。
关系数据语言可以分为三类:关系代数语言、关系演算语言以及兼具两者双重特点的语言。
三类语言的共同特点是语言具有完备的表达能力,是非过程化的集合操作语言,功能强,能够独立使用也可以嵌入高级语言中使用。
3、关系代数操作包含三大要素:操作对象、操作符、操作结果。
数据库关系代数表达式数据库关系代数表达式:1. 什么是数据库关系代数表达式?Solid State Drives(SSDs)是一种快速读写和存储用的计算机存储介质,它使用关系代数表达式(RELATION ALGEBRA)来表达多个表之间的关系。
它使用关系运算符来反映数据间的逻辑关系,有助于在数据库中的查询操作的效率和可靠性。
2. 关系代数表达式的基础上概念数据库关系代数表达式的基本概念,主要包括关系(relation)、运算符(operators)、连接(joins)、窗口函数(window functions)和子查询等。
(1)关系(relation):关系代数的核心概念是关系,关系也就是数据表,比如学生表、课程表等,每一行数据都可以看作是表的一个实例。
(2)运算符(operators):运算符用于对关系中的行数据作选择、连接、聚合等操作,常见的运算符有并集 union 、交集 intersect 、差集difference 、选择 selection 、投影 projection 、笛卡尔积 cartesian product 、条件 join 。
(3)连接(joins):连接是两个或多个关系之间的链接方式,包括内连接 inner join、左外连接 left outer join、右外连接 right outer join和全外连接full outer join等。
(4)窗口函数(window functions):窗口函数是一种特殊的运算符,它能够把一行数据拆分成多行,并对每一行的数据进行计算,窗口函数可用于实现排序、聚合、求平均值等操作。
(5)子查询(subqueries):子查询是SQL语句中的一种特殊查询,它可以将一个查询语句的结果作为另一个查询语句的输入,它也可以把表中一行数据或列数据嵌入另一个查询语句中。
3. 数据库关系代数表达式的应用(1)查询和更新操作:数据库关系代数可以实现快速查询和更新操作,可大大提高查询效率和可靠性。
数据库管理系统中的关系代数随着互联网的快速发展,数据已经成为了一个组织和管理大量信息的重要工具。
数据库管理系统是一种专门用于处理数据的软件,可以帮助用户在存储和管理大量数据时,更加方便地使用和操作这些数据。
关系型数据库是目前最常使用的数据库类型,其中的关系代数是用于操作关系型数据库的一种基本工具。
本文将介绍关系代数的基本概念、运算和应用。
一、关系代数的基本概念关系代数是用于操作关系型数据库的一种基本工具,它代表了数据库中的关系,并定义了一些操作来处理这些关系。
关系代数的基本概念包括:1. 关系关系是指数据表中的一组列或字段,每列都有一个对应的域类型和一个域值的集合。
关系通常用一个表格符号来表示,其中每个数据被表示为一个固定数量的列或字段。
每个字段都有一个域类型,可以是整数、文本或其他格式的数据类型。
2. 元组元组是指数据表中的一行数据,包括表中每个字段的值。
在关系代数中,每个元组都是关系的一部分,可以进行排序、查找和修改。
3. 属性属性是数据表中的一列数据,存储每个元组中的一个值。
在关系代数中,属性通常指代表数据表中的一个列。
4. 关系代数运算关系代数的操作包括一些基本运算,如选择、投影、并、差和笛卡尔积等。
这些基本运算可以通过组合和嵌套来实现更复杂的查询。
二、关系代数的运算1. 选择运算选择运算是通过指定一个属性值和一个运算符,从关系中选择满足条件的元组。
例如,从员工表中选择工资大于5000元的员工:σ(薪水>5000)(员工表)2. 投影运算投影运算是指从一张关系中提取所需的属性,生成一个新的关系。
例如,从员工表中仅选择姓名和性别两个属性:π(姓名,性别)(员工表)3. 连接运算连接运算是通过将两个关系的行组合在一起,生成一个新的关系。
连接运算通常用于关系之间有关联的情况。
例如,从员工表和部门表中获取员工所在的部门名字:员工表 JOIN 部门表 ON 员工表.部门ID=部门表.部门ID4. 并运算并运算是指从两个关系中选择所有元组,生成一个新的关系。
数据库关系代数表达式学习
关系代数是关系数据库系统查询语言的理论基础
一、关系代数的9种操作:
关系代数中包括了:并、交、差、乘、选择、投影、联接、除、自然联接等操作。
五个基本操作:
并(∪)、差(-)、笛卡尔积(×)、投影(σ)、选择(π)
四个组合操作:
交(∩)、联接(等值联接)、自然联接(R S)、除法(÷)
注2:等值连接表示先做笛卡尔积(×)之后,对相应列进行选择或等值关联后的结果(仅筛选行、不筛选列)
注2:自然连接表示两个关系中若有相同名称的属性,则自动作为关联条件,且仅列出一列
二、关系代数表达式:
由关系代数运算经有限次复合而成的式子称为关系代数表达式。
这种表达式的运算结果仍然是一个关系。
可以用关系代数表达式表示对数据库的查询和更新操作。
三、举例说明:
设教学数据库中有3个关系:
学生关系S(SNO, SNAME,AGE,SEX)
学习关系SC(SNO,CNO,GRADE)
课程关系C(CNO,CNAME,TEACHER)
(1) 检索学习课程号为C2的学生学号与成绩
------------------------------------
SELECT SNO,GRADE
FROM SC
WHERE CNO='C2'
------------------------------------
π SNO, GRADE (σ CNO='C2' (SC))
************************************
(2) 检索学习课程号为C2的学生学号与姓名
------------------------------------
SELECT SC.SNO,S.SNAME
FROM SC,S
WHERE SC.SNO=S.SNO
AND O='C2'
------------------------------------
π SNO,SNAME (σ CNO='C2' (S SC))
此查询涉及S和SC,先进行自然连接,然后再执行选择投影操作。
----
π SNO,SNAME (S)(π SNO (σ CNO='C2' (SC)))
自然连接的右分量为"学了C2课的学生学号的集合"。
此表达式比前一个表达式优化,执行起来要省时间、省空间。
************************************
(3) 检索选修课程名为MATHS的学生学号与姓名
------------------------------------
SELECT SC.SNO,S.SNAME
FROM SC,S,C
WHERE SC.SNO=S.SNO
AND O=O
AND AME='MATHS'
------------------------------------
π SNO, SANME (σ CNAME='MATHS' (S SC C))
************************************
(4) 检索选修课程号为C2或C4的学生学号
------------------------------------
SELECT SNO
FROM SC
WHERE CNO='C2'
OR CNO='C4'
------------------------------------
π SNO (σ CNO='C2'∨CNO='C4' (SC))
************************************
(5) 检索至少选修课程号为C2或C4的学生学号
------------------------------------
SELECT SA.SNO
FROM SC AS SA,SC AS SB
WHERE SA.SNO=SB.SNO
AND O='C2'
AND O='C4'
------------------------------------
π 1 (σ 1=4∧2='C2'∧5='C4' (SC×SC))
************************************
(6) 检索不学C2课的学生姓名与年龄
------------------------------------
SELECT SNAME,AGE
FROM S
MINUS
SELECT S.SNAME,S.AGE
FROM SC,S
WHERE SC.SNO=S.SNO
AND O='C2'
(Oracle)
------------------------------------
π SNAME, AGE (S)-π SNAME, AGE (σ CNO='C2' (S SC)) ************************************
(7) 检索学习全部课程的学生姓名
------------------------------------
这个定义用SQL表示比较麻烦,略过
------------------------------------
π SNO, CNO (SC)÷π CNO (C)
先用除法取出选取所有课程的SNO集(除法可以理解为一个Filter) π SNAME (S(π SNO,CNO (SC)÷π CNO (C)))
再关联S表取出SNAME
************************************
(8) 检索所学课程包含S3所学课程的学生学号
------------------------------------
这个定义用SQL表示比较麻烦,略过
------------------------------------
π SNO,CNO (SC)÷ π CNO (σ SNO='S3' (SC))
同样运用了除法的特性
************************************
(9) 将新课程元组( 'C10','PHYSICS','YU') 插入到关系C中
------------------------------------
INSERT INTO C VALUES('C10','PHYSICS','YU')
------------------------------------
(C∪('C10','PHYSICS','YU'))
记住该符号的用法
************************************
(10) 将学号S4选修课程号为C4的成绩改为85分
------------------------------------
UPDATE SC SET GRADE=85
WHERE SNO='S4'
AND CNO='C4'
------------------------------------
(SC-('S4','C4',? )∪('S4','C4',85))
先用'-'实现DELETE功能,再用'∪'实现INSERT功能
注意使用?来表示检索时忽略该字段值
************************************
四、关系代数表达式的优化:
目的:为了系统在执行时既省时间又能提高效率。
基本策略:先做选择,运用投影去除多余属性等等。
优化算法:语法树( 尽量提前做选择操作;在每个操作后,应做个投影操作,去掉不用的属性值) 例如:
π SNO ,SNAME (σ GRADE>60 (S SC)) 进行优化后转换为:
π SNO ,SNAME (π SNO ,SNAME (S) π SNO (σ GRADE>60 (SC)))
--即提前做选择操作;在每个操作后,应做个投影操作,去掉不用的属性值
又如:
S(S#,SNAME,AGE,SEX)
SC(S#,C#,GRADE)
C(C#,CNAME,TEACHER)
π CNAME,TEACHER (σ SEX='女' (S SC C)) 进行优化后转换为:
π CNAME, TEACHER (C π C# (π S#,C# (SC) π S# (σ SEX='女' (S))))
优化前和优化后的语法树如下所示:。