第3节条件概率讲解

解读条件概率条件概率可以说是统计学中独具特色的概念，其定义为在前项已发生的条件下后项发生的可能性大小。

它的计算公式十分简单，只有P（A|B）=P（A∩B）/P（B）。

它作为一个重要的概念，已经应用到许多方面，如贝叶斯网络建模中用来表达变量之间的相关性，以及在机器学习领域中经常用来做分类。

首先，为了对条件概率进行解读，让读者能够理解条件概率的原理，我们可以从简单的实例，如抛硬币来进行讨论。

让我们假设有一枚硬币，其正反面各有probability=0.5的概率出现。

因此，其基本概率P（正）= P（反）=0.5。

让我们来看一个有趣的变形，如果给了某个硬币一次抛掷的先决条件，即正面朝上，我们也可以确定下一次抛掷的结果，即P（正|正）=1，P（反|正）=0，即在这个条件下，后项的可能性等于所给的前项的概率。

同样的道理，我们可以在概率学中用来计算一个不同的条件下，后项的概率。

比如，给定一个事件A，已知A的概率是P(A)，如果给定A发生的条件B，那么A在B条件下发生的概率就可以用条件概率来计算：P（A| B）=P（A∩ B）/P（ B）。

其次，关于条件概率，比如计算多个事件的组合，就需要用到乘积定理，该定理指出，在多个事件的条件下同时发生的概率是每个事件本身发生概率的乘积。

比如，有一个事件A，A的概率为P（A），有另一个独立的事件B，B的概率为P（B），那么A和B同时发生的概率就是P（A）×P（B）。

此外，还有贝叶斯定理，它是条件概率概念的推广应用，它可以让我们通过计算多个事件发生的概率，来估计一个事件发生的概率，增强我们对各种事件可能性的了解。

最后，条件概率的一个重要应用是做决策，这就要求我们根据自己获得的信息，计算每个决策结果发生的概率，然后根据概率进行选择，以便使最终结果达到最大化。

总之，条件概率是一个重要的概念，用于表达不同事件之间的相关性，我们可以根据条件概率，来计算每种可能性发生的概率，从而做出更好的决策。

条件概率知识点一、条件概率的定义。

1. 概念。

- 设A、B为两个事件，且P(A)>0，称P(BA)=(P(AB))/(P(A))为在事件A发生的条件下事件B发生的条件概率。

- 例如，扔一个骰子，事件A为“骰子的点数为偶数”，P(A)=(3)/(6)=(1)/(2)，事件B为“骰子的点数小于4”，AB表示“骰子的点数为2”，P(AB)=(1)/(6)。

那么在A发生的条件下B发生的条件概率P(BA)=(P(AB))/(P(A))=(frac{1)/(6)}{(1)/(2)}=(1)/(3)。

2. 性质。

- 非负性：对于任意事件B，A（P(A)>0），有P(BA)≥slant0。

- 规范性：P(ΩA) = 1，这里Ω是样本空间。

- 可列可加性：如果B_1,B_2,·s是两两互不相容的事件，则P(bigcup_i =1^∞B_iA)=∑_i = 1^∞P(B_iA)。

二、条件概率的计算方法。

1. 公式法。

- 直接根据定义P(BA)=(P(AB))/(P(A))计算。

- 例如，有一批产品共100件，其中次品10件，从中不放回地抽取两次，每次取一件。

设事件A为“第一次取到次品”，P(A)=(10)/(100)=(1)/(10)；事件B为“第二次取到次品”。

AB表示“第一次和第二次都取到次品”，P(AB)=(10)/(100)×(9)/(99)=(1)/(110)。

那么P(BA)=(P(AB))/(P(A))=(frac{1)/(110)}{(1)/(10)}=(1)/(11)。

2. 缩减样本空间法。

- 当直接计算P(AB)和P(A)比较复杂时，可以考虑缩减样本空间。

- 还是以上面抽取产品的例子，在A发生的条件下，即第一次已经取到了次品，此时样本空间就缩减为99件产品，其中次品还有9件，所以P(BA)=(9)/(99)=(1)/(11)。

三、条件概率的乘法公式。

1. 公式。

- 由P(BA)=(P(AB))/(P(A))可得P(AB)=P(A)P(BA)（P(A)>0）。

一、条件概率生活中很多概率都是在某些特殊条件下的概率。

比如你想知道你在家感染新冠的概率，这是取决于很多方面的，比如，政策有没有放开、是否位于高风险区等等。

只有在这些条件的限制下，我们才能较为准确的求出你想知道的概率。

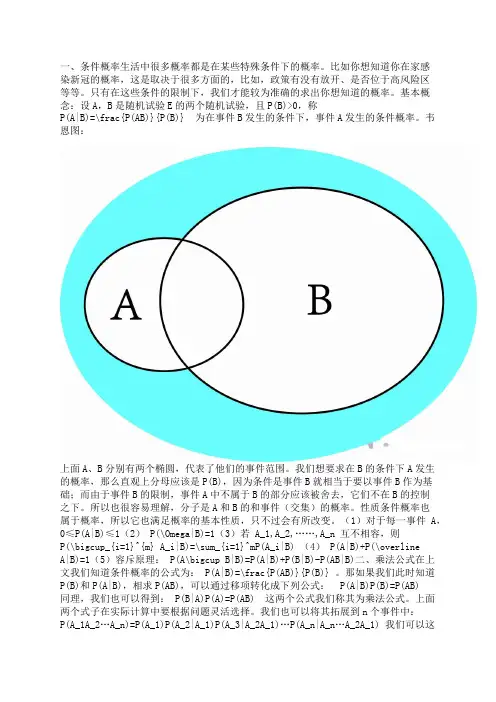
基本概念：设A，B是随机试验E的两个随机试验，且P(B)>0，称P(A|B)=\frac{P(AB)}{P(B)} 为在事件B发生的条件下，事件A发生的条件概率。

韦恩图：上面A、B分别有两个椭圆，代表了他们的事件范围。

我们想要求在B的条件下A发生的概率，那么直观上分母应该是P(B)，因为条件是事件B就相当于要以事件B作为基础；而由于事件B的限制，事件A中不属于B的部分应该被舍去，它们不在B的控制之下。

所以也很容易理解，分子是A和B的和事件（交集）的概率。

性质条件概率也属于概率，所以它也满足概率的基本性质，只不过会有所改变。

（1）对于每一事件A，0≤P(A|B)≤1（2） P(\Omega|B)=1（3）若A_1,A_2,……,A_n 互不相容，则P(\bigcup_{i=1}^{m} A_i|B)=\sum_{i=1}^mP(A_i|B) （4） P(A|B)+P(\overlineA|B)=1（5）容斥原理： P(A\bigcup B|B)=P(A|B)+P(B|B)-P(AB|B)二、乘法公式在上文我们知道条件概率的公式为： P(A|B)=\frac{P(AB)}{P(B)} 。

那如果我们此时知道P(B)和P(A|B)，相求P(AB)，可以通过移项转化成下列公式： P(A|B)P(B)=P(AB)同理，我们也可以得到： P(B|A)P(A)=P(AB) 这两个公式我们称其为乘法公式。

上面两个式子在实际计算中要根据问题灵活选择。

我们也可以将其拓展到n个事件中：P(A_1A_2…A_n)=P(A_1)P(A_2|A_1)P(A_3|A_2A_1)…P(A_n|A_n…A_2A_1) 我们可以这样理解：$P(A_1)$是假设A1正确，$P(A_2|A_1)$是假设A1正确的情况下A2正确，以此类推三、全概率公式有限划分基本概念：设 \Omega 为随机试验E的样本空间，B1，B2 ，…，Bn为E的一组事件，若(1) Bi∩Bj =f ,i ≠ j(2) B_1∪B_2 ∪…∪B_n=\Omega则称B1，B2，…，Bn 为 \emptyset 的一个有限划分，或称完备事件组。

第三节 条件概率一）1、教学目的与要求：理解条件概率的概念，掌握乘法公式并会利用该公式进行计算2、教学重点：条件概率 乘法公式教学难点：条件概率3、教学课时：2课时4、授课手段：师生互动，讲练结合二）授课过程1、 回顾：上节课我们学习了概率的定义，其中最主要的有两个知识点：1）什么情况的事件概率适用古典概率去求？（生答）2)古典概率适用，则如何求其概率，关键是什么？（生答）2、 导入：前面我们学习了概率的相关概念，给出了概率的古典定义基本事件总数包含的基本事件个数事件）＝（A A P 但是很多时候有些事件的发生还被其他事件影响着，这样的事件概率如何求，就是本节我们要讨论的内容。

3、 新授：一 、 条件概率1、概念及计算公式引例：一批同类产品共14件，其中有甲厂提供的6件产品中有4件优质品；由乙厂提供的8件产品中有5件优质品。

试考察下列事件的概率：1)从全部产品中任抽1件是优质品2)从甲厂提供的产品中任抽1件而被抽的这1件为优质品解：设B ＝｛抽到产品是优质品｝，A ＝｛抽到甲厂提供的产品｝1)抽取在全部产品中进行，故样本空间 中有14个基本事件，B 中包括有9个，则所求概率为149； （此处为上一节课内容，可以让学生回答解决问题） 2)这里考察的是在事件A 发生下事件B 发生的概率，则此时概率为64 （生答）定义：一般地，若P （A ）>0，则把事件A 已经发生的条件下，事件B 发生的概率称为条件概率，记为：P （B|A ）。

说明：（重点、难点解决） 定义用图示法理解为：事件的样本点已落在图形A 中（事件A 已发生），问落在B （事件B ）中的概率。

由于样本点已经落在A 中，且又要求落在B 中，于是只能落在AB 中，则其概率计算公式为 P(A)AB P A |B P ）（）＝（ （P(A)>0）（给出结论之前，让学生思考试答） 类似地， P(B)AB P B |A P ）（）＝（ （P(B)>0）（学生思考试答） 注：1）注意P(B|A ）与P(B)的区别。

条件概率理解
嘿，朋友！今天咱就来好好唠唠条件概率这个玩意儿，你可得竖起耳朵听好喽！
咱先说个例子哈，就比如彩票，你买了一张彩票，中头奖的概率那可是
相当低。

但如果我告诉你，这张彩票是从某个特定的机器里出来的，而这个机器之前出过头奖，那你会不会觉得你中奖的概率好像瞬间就增加了呢？这就是条件概率！
再举个例子，你想啊，假如你知道一个人总是很守时，那么你是不是就
会觉得他这次也会大概率守时呢？就好像你和朋友约好出去玩，他平常都不怎么迟到，这次你就会更相信他会按时出现。

咱生活中到处都是条件概率的影子呢！比如你看天气预报说第二天有雨，那你出门带伞的可能性就会大大提高，因为这个“第二天有雨”的条件改变了你对“带不带伞”这件事的概率判断。

嘿，你想想是不是这个理儿？条件概率就像一个隐藏的小开关，一旦打开，事情的可能性就变了。

可以说它就像是给我们的判断加上了一层滤镜。

我记得有一次，我和几个朋友一起玩猜硬币的游戏。

我们都先猜正面，
然后有个朋友说他知道这枚硬币之前连续三次都是正面，这时候，大家瞬间觉得这次还是正面的概率好像大了很多呢！
我觉得啊，理解条件概率真的超级重要！它能让我们更理性地看待事情，而不是盲目地去判断。

不然的话，我们可能就会做出一些不太明智的决定。

所以，咱可得好好琢磨琢磨这个条件概率，让它为我们的生活服务呀！怎么样，你是不是也觉得条件概率很有意思呢？是不是也对它有了更深的理解呢？。

一、条件概率的定义条件概率是指，在某个事件A已经发生的前提下，另一个事件B发生的概率。

用数学符号表示为：P(B|A) = P(AB) / P(A)其中，P(B|A)表示条件概率，P(AB)表示事件A和事件B同时发生的概率，P(A)表示事件A发生的概率。

二、条件概率的性质1. 非负性：条件概率的值总是大于等于0，即0 ≤ P(B|A) ≤ 1。

2. 有界性：条件概率的值不会超过1，即P(B|A) ≤ 1。

3. 乘法公式：条件概率与全概率之间存在乘法公式，即：P(AB) = P(A) P(B|A)4. 奥卡姆剃刀法则：在已知条件概率的情况下，事件A和事件B同时发生的概率最小，即：P(AB) ≤ P(A) P(B|A)5. 条件概率的逆：在已知条件概率的情况下，可以求出逆条件概率，即：P(A|B) = P(AB) / P(B)三、条件概率的计算方法1. 根据条件概率的定义计算：直接利用条件概率的定义公式进行计算。

2. 利用乘法公式计算：根据乘法公式，先计算P(AB)，再计算P(A)，最后代入公式计算P(B|A)。

3. 利用全概率公式计算：根据全概率公式，先计算P(A)，再计算P(B|A)，最后代入公式计算P(B)。

四、条件概率的应用1. 生物学：在遗传学中，条件概率可以用来计算某种基因型出现的概率。

2. 经济学：在经济学中，条件概率可以用来分析市场风险、投资收益等。

3. 保险：在保险行业中，条件概率可以用来计算保险事故发生的概率，从而确定保险费率。

4. 统计学：在统计学中，条件概率可以用来计算样本数据的可靠性、检验假设等。

5. 人工智能：在人工智能领域，条件概率可以用来计算某个事件发生的概率，从而进行决策和预测。

五、条件概率的局限性1. 实际应用中，条件概率的计算往往需要大量的数据支持，否则难以准确计算。

2. 条件概率的计算可能受到样本选择、样本量等因素的影响，从而导致计算结果的不稳定性。

3. 条件概率的应用往往需要满足一定的假设条件，如独立性、条件独立性等。

概率论中的条件概率和贝叶斯公式——概率论知识要点概率论是数学的一个分支，研究的是随机现象的规律性。

在概率论中，条件概率和贝叶斯公式是两个重要的概念和工具。

本文将介绍条件概率和贝叶斯公式的概念和应用，并总结概率论中的一些重要知识要点。

一、条件概率条件概率是指在一个事件发生的条件下，另一个事件发生的概率。

设A和B是两个事件，且P(A)≠0，称P(B|A)为在事件A发生的条件下事件B发生的条件概率，表示为P(B|A)。

条件概率的计算公式为：P(B|A) = P(A∩B) / P(A)其中，P(A∩B)表示事件A和事件B同时发生的概率，P(A)表示事件A发生的概率。

条件概率的计算方法可以通过样本空间和事件的定义来进行推导和计算。

在实际应用中，条件概率常常用于解决复杂问题，如生病的概率、产品质量的判断等。

二、贝叶斯公式贝叶斯公式是一种用于计算事件的后验概率的方法，即在已知某些条件下，计算其他条件的概率。

贝叶斯公式的表达式如下：P(A|B) = P(B|A) * P(A) / P(B)其中，P(A|B)表示在事件B发生的条件下事件A发生的概率，P(B|A)表示在事件A发生的条件下事件B发生的概率，P(A)表示事件A发生的概率，P(B)表示事件B发生的概率。

贝叶斯公式的应用非常广泛，尤其在统计学和机器学习中有着重要的地位。

它可以用于推断未知的参数，分类问题，以及数据的模型选择等。

三、概率论知识要点除了条件概率和贝叶斯公式，概率论还涉及到许多其他重要的知识点。

以下是一些概率论中的知识要点：1. 事件与样本空间：事件是指某个结果或者一些结果的集合，样本空间是指所有可能结果的集合。

2. 随机变量与概率分布：随机变量是指对随机现象结果的一种数学描述，概率分布是指随机变量取各个值的概率。

3. 期望与方差：期望是指随机变量的平均值，方差是指随机变量与其期望之间的差异程度。

4. 独立事件与互斥事件：独立事件是指两个事件的发生不会互相影响，互斥事件是指两个事件不能同时发生。