下载文档原格式
概率论与数理统计主讲：四川大学四川大学第10讲条件概率(III): 全概率公式贝叶斯公式1§1.5 条件概率四川大学第10讲条件概率(III): 全概率公式贝叶斯公式3第10讲条件概率(III)全概率公式贝叶斯公式四川大学四川大学第10讲条件概率(III): 全概率公式贝叶斯公式4四川大学第10讲条件概率(III): 全概率公式贝叶斯公式5在前面两讲，我们讲了条件概率和乘法公式。
现在来讲全概率公式和贝叶斯公式()()(|)P AB P A P B A =(()0)P A >（一）全概率公式四川大学第10讲条件概率(III): 全概率公式贝叶斯公式6A ()(|)B P A B1AB 2AB 3AB 4AB 5AB )B1AB2AB 3AB 4AB 5AB四川大学第10讲条件概率(III): 全概率公式贝叶斯公式11全概率公式的意义事件A 的发生有各种可能的原因B i (i =1,…,n )。
如果A 是由原因B i 引起，则A 发生的概率为()()(|)i i i P AB P B P A B 每一个原因都可能导致A 发生，故A 发生的概率是全部原因引起A 发生的概率的总和，即为全概率公式。
由此可以形象地把全概率公式看成是“由原因推结果”的公式，每个原因对结果的发生有一定的作用，结果发生的可能性与各种原因的作用大小有关，全概率公式就表达了它们之间的关系。
四川大学四川大学第10讲条件概率(III): 全概率公式贝叶斯公式12在很多实际问题中，P (A )不容易直接求得，但却容易找到S 的一个划分B 1, B 2,…, B n ，且P (B i )和P (A |B i )容易求得，那么就可以用全概率公式求出P (A )。
使用全概率公式的关键是作出S 的一个划分。
何时用全概率公式求A 的概率？四川大学1()()(|)ni i i P A P B P A B ==∑四川大学第10讲条件概率(III): 全概率公式贝叶斯公式16例2 有12个足球都是新球，每次比赛时取出3个，比赛后又放回去，求第三次比赛时取到的3 个足球都是新球的概率。
一、条件概率生活中很多概率都是在某些特殊条件下的概率。
比如你想知道你在家感染新冠的概率，这是取决于很多方面的，比如，政策有没有放开、是否位于高风险区等等。
只有在这些条件的限制下，我们才能较为准确的求出你想知道的概率。
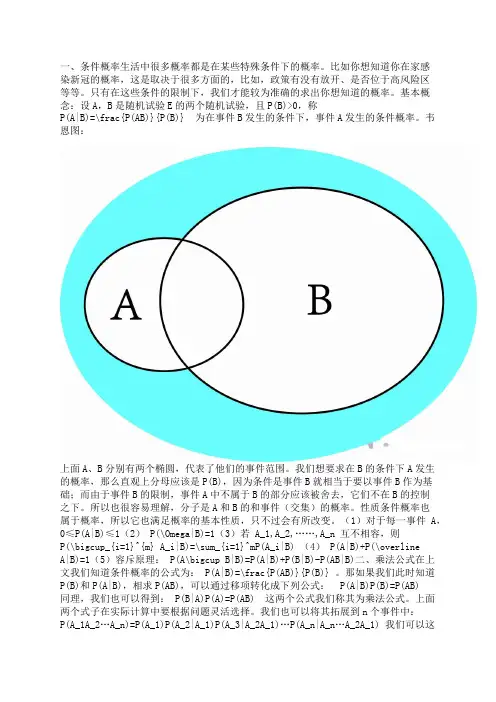
基本概念：设A，B是随机试验E的两个随机试验，且P(B)>0，称P(A|B)=\frac{P(AB)}{P(B)} 为在事件B发生的条件下，事件A发生的条件概率。
韦恩图：上面A、B分别有两个椭圆，代表了他们的事件范围。
我们想要求在B的条件下A发生的概率，那么直观上分母应该是P(B)，因为条件是事件B就相当于要以事件B作为基础；而由于事件B的限制，事件A中不属于B的部分应该被舍去，它们不在B的控制之下。
所以也很容易理解，分子是A和B的和事件（交集）的概率。
性质条件概率也属于概率，所以它也满足概率的基本性质，只不过会有所改变。
（1）对于每一事件A，0≤P(A|B)≤1（2） P(\Omega|B)=1（3）若A_1,A_2,……,A_n 互不相容，则P(\bigcup_{i=1}^{m} A_i|B)=\sum_{i=1}^mP(A_i|B) （4） P(A|B)+P(\overlineA|B)=1（5）容斥原理： P(A\bigcup B|B)=P(A|B)+P(B|B)-P(AB|B)二、乘法公式在上文我们知道条件概率的公式为： P(A|B)=\frac{P(AB)}{P(B)} 。
那如果我们此时知道P(B)和P(A|B)，相求P(AB)，可以通过移项转化成下列公式： P(A|B)P(B)=P(AB)同理，我们也可以得到： P(B|A)P(A)=P(AB) 这两个公式我们称其为乘法公式。
上面两个式子在实际计算中要根据问题灵活选择。
我们也可以将其拓展到n个事件中：P(A_1A_2…A_n)=P(A_1)P(A_2|A_1)P(A_3|A_2A_1)…P(A_n|A_n…A_2A_1) 我们可以这样理解：$P(A_1)$是假设A1正确，$P(A_2|A_1)$是假设A1正确的情况下A2正确，以此类推三、全概率公式有限划分基本概念：设 \Omega 为随机试验E的样本空间，B1，B2 ，…，Bn为E的一组事件，若(1) Bi∩Bj =f ,i ≠ j(2) B_1∪B_2 ∪…∪B_n=\Omega则称B1，B2，…，Bn 为 \emptyset 的一个有限划分，或称完备事件组。
