当前位置：文档之家 › 2010秋第12章波动光学

2010秋第12章波动光学

  • 格式：doc
  • 大小：3.29 MB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

第十二章波动光学_1课件

第十二章波动光学_1课件
中心位置： D
5 4 3 2
x k D k 0,1,2
1 0
d
-1
（2）暗条纹： xd (2k 1)
-2 -3
中心位置： D
2
x (2k 1) D k 1,2,3
-4 -5
（3）条纹间距：
2d
相邻明纹中心或相邻暗纹中心的距离称为条纹间距x D
纹。
•半波损失
现象：当屏幕W移至B处，从
S 和 S’ 到B点的光程差为零，
但是观察到暗条纹，验证了反
射时有半波损失存在。
光栏
p
S
p'
Q'
d
A MB
S'
L
Q
W
原因：当光从光疏介质射向光 密介质时，反射光的相位发生 了π跃变，或者反射光产生了 λ/2附加的光程差，即“半波 损失”。 解释：光的电磁理论（菲涅耳 公式）可以解释半波损失。
两光波在P点的波程差为： S1
x
δ= r2-r1
d
r2
O
r12=D2+(x-d/2)2 r22=D2+(x+d/2)2
S2
D
所以 r22- r12=2xd
即
(r2- r1)( r2+r1)=2xd
采用近似 波程差为：
r2+r1≈2D


r2
r1

xd D
4、干涉条纹的位置
（1）明条纹： xd k
激光光源是 相干光源
2、杨氏双缝干涉实验装置
1801年，杨氏巧妙地设计了一种把单个波阵面分 解为两个波阵面以锁定两个光源之间的相位差的方法 来研究光的干涉现象。杨氏用叠加原理解释了干涉现 象，在历史上第一次测定了光的波长，为光的波动学 说的确立奠定了基础。

波动光学

波动光学
光的干涉
光的衍射 光栅 光的偏振
r 2 r1 2k 1
k 0,1,2,3, 称为条纹级次。
幕上明暗条纹的位置。由图得
k
加强，即明纹条件。 消弱，即暗纹条件。
2
a r D x 2 a s r D x 2 a 2 2 s r 2 r1 2ax
2
近似考虑。令
r1 r 2 2D 2r2 r 1 D 2ax
00
2
得
Dd n 1 x a
例：在双缝实验中，波长为λ的平面波单色光垂直入射到双缝上 ，在幕上呈现明暗相间的干涉条纹，当使平面光斜入射到双缝 上时，发现幕上的原来的第5级明纹处被零级明纹占据，求光斜 入射时的入射角（用双缝间距a和波长λ 表示）。
第二节
由薄膜的彩色谈起
薄膜干涉
一 劈尖干涉（等厚干涉) 解释形成机理
单色光近似垂直入射
b
a
p
劈形薄膜
e

劈尖角
从劈尖的上下二表面上反射的二光 a b来自同一光，二者频 率相同，振动方向相同，在相遇点处有固定的位相差，故为相干 光。二光在劈尖的上表面附近相遇，形成干涉条纹。 沿着入射光的方向看去，看到明，暗相间的干涉直条纹在上表 面附近形成。
f a
中央明纹宽度
2f a
例 14—10 用波长为 632 .8nm 的单色平行光垂直入射于宽 度为 a 0.15mm 的单缝上，透镜焦距为 f 40cm ，求第三级暗 纹在屏幕上的位置。 解：考虑到各级的衍射角小，可用近似计算。 暗纹位置
明纹位置
相邻明纹（或相邻暗纹）的间距
r n rn
2 1 1
例 14—1 若双缝干涉实验在折射率为 n 1.33的水中进行， 讨论干涉条纹分布。 k 明 解：

大学物理 第十二章 波动光学2

大学物理 第十二章 波动光学2

电磁波是横波。
X E u Z H
引起视觉和化学效 应的是电磁波中的 Y 电场强度矢量E， 因此，常把 E 矢 量称为“光矢量”。
二、电磁波谱
波长： ~ 105 电磁波：工业电 10-3 m ~ 770 nm
红外线 10-7 ~ 10-13 X射线
104 ~ 1 无线电波 760 ~ 400 nm
1 ~ 10-3 (m) 微波 400 ~ 1 nm
1
1
2
2
例：杨氏双缝实验中，P为屏上第五级亮纹所在位置。现将
一 玻璃片插入光源 S1发出的光束途中，则P点变为中央
亮条纹的位置，求玻璃片的厚度。 已知:
0.6m
玻璃
n 1.5
S1 S2
解：没插玻璃片之前二光束的光程差为
r1
r2
P
r2 r1 5
插玻璃片之后二光束的光程差为
r2 r1 d nd r2 r1 d n 1 0
5 d (1.5 1) 0
d 10 6m

§12.4
薄膜干涉（一）
o r环 P f
—— 等倾条纹 一. 点光源照明时的干涉条纹分析
光束1、2的光程差：
2 e AB BC S cos r i AD AC sin i 2e tg r sin i n 2ne 2n e sin r sin i n > n cos r cos r 2 n n sin i n sin r 折射定律
= (E2-E1)/h
E1 波列长L = c (≈10-8 s)
1. 普通光源：自发辐射
· ·
独立(不同原子发的光) 独立(同一原子先后发的光)

第十二 波动光学

第十二 波动光学
o
en 1 r2 r1
en 1 d x
D 0
x en 1D
d
4.0
106 1.5 11.5
0.30 103
m
1.0 102 m
这表示干涉条纹整体向下平移了10mm.
12.1.3 光程和光程差(optical path and optical path difference)
光波在某一介质中所经过的几何路程 r 与该介质折射率的乘积 nr ,称为光程.
m
1.5m
⑵在S2未被玻璃片遮盖时,中央亮条纹的中心应 处于x=0的地方, r r2 r1 0
S2被玻璃片遮盖后,中央亮条纹下移至 O处.若
设薄玻璃片的厚度为e,厚度e之后的波程分别 为r1、r2,这时的中央亮条纹波程差应表示为
r ne r2 e r1
S1
S
r2 S2 e
r1
o
x
n2
r1
)
n1
2
(n2r2
n1r1 )
令 Δ n2r2 n1r1 叫光程差
决定明暗条纹的条件:
亮条纹 2 2k .k 1,2,...
暗条纹 2 (2k 1) .k 1,2,...
• 若直接用光程差表示：
亮条纹： n2r2 n1r1 k, k 1,2,...
透镜
观测屏
x2
1
x1
设d为相邻两条亮条纹或暗条纹对应的空气隙
厚度差, 有
2d k 1
2
k
1
2dk
2
k
两式相减得
d dk1 dk 2
dk
d d
dk+1
L
若测出相邻亮条纹或相邻暗条纹的距离l, 则两块平板玻璃之间的夹角为

第12章-波动光学3

第12章-波动光学3

第十二章 波动光学
B
i
A
C
光轴
无双折射现象
光轴
P.36/70
由惠更斯原理解释双折射现象：
第十二章 波动光学
o光和e光都不折射，但速度和折射率不同， 所以两波面并不重合。
P.37/70
o光、e光的一些性质
第十二章 波动光学
1、o光、e光传播速度一般不同，但沿光轴方向传播 方向速度相同（此时无双折射现象）
第十二章 波动光学
d d
P.50/70
四分之一波片
第十二章 波动光学
圆偏振光通过四分之
一波片后，变为线偏振 光，其振动方向与光轴 方向成45°角。
d
椭圆偏振光通过四分 之一波片后，变为线偏 振光，其振动方向与光 轴方向的夹角不等于45 °角。
Ex Ey
I Ix Iy
P.5/70
第十二章 波动光学
自然光可用两个相互独立、没有固定相位关系、 等振幅且振动方向相互垂直的线偏振光表示。
自然光的表示：
部分偏振光：某一方向的光振动比与之相垂直的另 一方向的光振动占优势。
平行纸面振动占优的部分偏振光 垂直纸面振动占优的部分偏振光
P.6/70
I
I
I
I
I
cos2
30
4I1
3 4
3I1
I
I
cos2
30
3I1
3 4
9 4 I1
P.16/70
第十二章 波动光学
例13. 一束光由自然光和线偏振光混合组成，当它通 过一偏振片时，发现透射光的强度随偏振片的转动可 以变化到五倍。求入射光中自然光和线偏振光的强度 各占入射光强度的几分之几？
解： 设入射光强度：I0 ； 自然光强度：I10 ； 偏振光强度 : I20

第12章 波动光学

第12章 波动光学
-------------------------------------------------------------------------------
五、光程与光程差
干涉现象决定于两束相干光的位相差 两束相干光通过不同的介质时，位相差不能单纯 由几何路程差决定。
S1
r1
n1
S2
r2 P n2
第12章 波动光学
§12.1 杨氏双缝干涉 §12.2 薄膜干涉 §12.3 光的衍射 §12.4 光栅衍射 §12.5 光的偏振
-------------------------------------------------------------------------------
光的干涉和衍射现象说明是光具有波动性， 光的偏振现象显示出光的横波性.
(3) D,d一定时，由条纹间距可算出单色光的波长。
方法一： xd /(kD) 方法二： xd / D
-------------------------------------------------------------------------------
四、其他分波阵面干涉装置
1. 菲涅尔双镜
-------------------------------------------------------------------------------
§12.1 杨氏双缝干涉 一、光源
1.光源的发光机理
光源的最基本发光单元是分子、原子
E2
波列
hv
E1
= (E2-E1)/h
L=c
持续时间约为 10-8秒,但典型 值内约包含 5106 个振动周期.
s1
r1
s

第十二章 波动光学

第十二章 波动光学

第十二章 波动光学§12.1 光的电磁理论、相干光的获得[教学要求]1、 了解光的电磁理论、光源的概念；2、 理解用扬氏双缝干涉实验和络埃镜实验获得相干光；3、 掌握确定扬氏干涉条纹的位置的方法。

[重点、难点]重点：分析确定扬氏干涉条纹的位置。

难点：扬氏双缝干涉实验和络埃镜实验获得相干光；[教学方法]运用机械波有关知识，对比讲述光的相关内容。

[教学过程]上一章我们学过波动的一些初步知识。

波动就是振动或场在介质中的传播，如果波传播的振动是电场或者磁场时，我们就称这种波为电磁波。

电磁波里面有一个非常重要的波段就是我们今天要学习的光波。

研究光的本性，发射、传播和吸收的规律的光学是物理学中的一个分支。

根据所研究的内容的不同，光学又分为几何光学、波动光学和量子光学。

其中几何光学是以光的直线传播为基础研究光在透明介质中传播；波动光学是以光的波动性质为基础研究光的传播；量子光学是以光和物质相互作用时显示的粒子性为基础研究光的传播。

波动光学和量子光学又统称为物理光学。

§12.1 光的电磁理论、相干光的获得 (板书)一、光学的分类几何光学光学 波动光学 (板书)量子光学光是电场E 和磁场H 的传播形式，因此光是一种电磁波。

主要表现在二、光是电磁波 (板书) 光具备波动特性（干涉、衍射，在不同介质分界面上可反射和折射）。

光在真空中的速度与电磁波速度相同 c=3×108m/s.光学的研究对象是人肉眼可以看到的可见光，其波长在400nm —760nm.不同波长(频率)的光具有不同的颜色，波长有长到短依次是红、橙、黄、绿、青、蓝、紫。

日常生活中的白光是各种颜色的光组成的复色光。

光学中还有一个概念是光源。

所谓光源就是能发光的物体。

三、光源 (板书) 普通光源 (板书)激光光源光源的发光是光源中大量原子或分子从较高能量状态跃迁到较低能量状态辐射出来的。

这种辐射有两个特点：(1) 同一时刻不同原子发出的光频率振幅和相位都不同，而且随机分布。

波动光学课件

波动光学课件

第九章 波动光学内容：1．光波及其相干条件 2．杨氏双缝干涉 3．薄膜干涉 4．迈克尔孙干涉仪 5．单缝衍射 6．光栅衍射 7．X 光衍射 8．自然光与偏振光 9．起偏与检偏 10．反射光与折射光的偏振 重点与难点：1．杨氏双缝干涉2．等倾干涉； 3．等厚干涉； 4．迈克尔孙干涉仪的应用 5．单缝衍射 6．光栅衍射 7．马吕斯定律； 8．布儒斯特定律； 要求：1．掌握等倾干涉、等厚干涉的本质； 2．掌握薄膜干涉、劈尖干涉、牛顿环干涉； 3．了解迈克尔孙干涉仪。

4．掌握夫琅和费单缝衍射5．了解圆孔衍射艾理斑公式及光学仪器的分辨率； 6．掌握光栅衍射的基本规律；7．理解X 光衍射 8．了解光的偏振性；9．了解起偏与检偏，掌握马吕斯定律；10．了解反射光与折射光的偏振，掌握布儒斯特定律。

§9－1 光的相干性 光程一、光波1．光波的概念：光波是电磁波的一部分，仅占电磁波谱很小的一部分，它与无线电波、X 射线等其它电磁波的区别只是频率不同，能够引起人眼视觉的那部分电磁波称为可见光。

● 1.1666年，牛顿研究光的色散，用棱镜将太阳光分解为由红到紫的可见光谱（V isible Light ）。

●2.1800年，J.F .W. Hershel 发现在可见光谱的红端以外，还有能够产生热效应的部分，称为红外线（Infrared Ray ）。

● 3.1802年，J.W . Ritter 与W .H. Wollaston 发现，在可见光的紫端以外，还有能够产生化学效应的部分，称为紫外线（Ultraviolet Ray ）红外光：波长λ>0.76μm可见光：波长λ在0.40μm 与0.76μm 之间 紫外光：波长λ<0.40μm广义而言，光包含红外线与紫外线。

2．光的颜色光的颜色由光的频率决定，而频率一般仅由光源决定，与介质无关。

单色光（Monochromatic light ）——只含单一波长的光，如激光 复色光——不同波长单色光的混合，如白光 3．光的速度与折射率： 光在介质中传输时的速度为 εμ1=v真空中，1800100.31-⋅⨯==s m c με介质中，r r r r c v μεμμεεεμ//1/100===其中r r n με/1=为介质的折射率（Refractive index ），由介质本身的性质决定，如 真空 1=n 空气 1≈n 水 33.1=n玻璃0.2~50.1=n折射率大的物质，称为光密介质；折射率小的物质，称为光疏介质。

波动光学

波动光学

光具有波粒二象性机制都不起作用，介质的相对磁导率μr 1800s m 1058924997.21−⋅×==μεc 真空电容率μ0：真空磁导率光速（在介质中）rr μεcu =真空中光速ucn =介质的相对电容率μ是介质的相对磁导率可见光的范围基态原子能级及发光跃迁Δ=10 L⇒称波列长度L为相干长度普通光源的相干长度：理论证明cm 1010→⋅λΔλ=2L 可达几百公里1S 2S P激光的相干长度：L>Δ来自于原子辐射发光的时间有限，所以波列有一定的长度L 。

两列波能发生干涉的最大波程差λλλδΔ==2M M k λ：中心波长钠Na 光，波长589.6nm ，相干长度3.4*10-2m 氦氖激光，波长632.8nm ，相干长度40 *102m2.相干时间光通过相干长度所需时间§3.2 光程一. 光程、光程差媒质λπλϕ2nr =Δ光程:L = nr 在介质中传播的波长，折算成真空中的波长介质的折射率光在介质中传播的距离折算成真空中的长度。

)(1122r n r n −=Δ)(21122λλπϕr r −=ΔδλπλπΔ=−=0112202)(2r n r n杨(Thomas Young) ，英国物理学家、考古学家、医生。

在1801 年做了双孔和双缝干涉实验，首先提出波干涉和波长概念，论证了光的波动性，解释了牛顿环的成因和薄膜的彩色。

他还第一个测量了7 种颜色光的波长。

λ，D >> d (d ∼10 m, D ∼m )波程差：Dxd d d r r ⋅=≈≈−=θθδtg sin 12相位差：πλδϕ2=ΔLL,2,1,0,2,1,02)12(==⎪⎩⎪⎨⎧+±±==k k k k x D d 暗纹明纹λλδp(1)一定时，若变化,则将怎样变化？'d d 、λx Δλd Dx =Δ(2) 一定时,条纹间距与的关系如何？x Δd 'd 、λ白光入射的杨氏双缝干涉照片红光入射的杨氏双缝干涉照片四、杨氏干涉可用于测量波长)2sin (πλθϕd =Δ紧靠镜端处总是产生暗纹，说明在镜端处反射光与入射光的相位差为，相当于光程差，称为半波损失1、劳埃镜实验真空中：12r r −2)12(λ+λk k minmaxL2,1,0±±=k =λ+2介质中：12)()(i i i i r n r n ∑−∑2λ+L =1s s 1020例2：杨氏双缝实验中，测得双缝间距d=0.2mm ，双缝到观察屏的距离D=4m ，折射率n=1.0，1）若同侧的第一级明纹中心到第4级明纹中心的距离为3.0cm ，求单色光的波长。

大学物理(波动光学知识点总结)

大学物理(波动光学知识点总结)

2）若浸入 水中，lf 且n1.33
na l2 1 5 .3 8 3 1 1 9 3 0 1 0 0 0 0 .88 17 3 0 m
[例5]在单缝夫琅和费衍射实验中，垂直入射的光有两种波长， λ1 = 4000 Å，λ2 = 7600Å。单缝缝宽a = 1.0×10－2cm。 透镜焦距f = 50 cm，求1）两种光第一级衍射明纹中心之间 的距离。2）若用d = 1.0×10－3 cm的光栅替换单缝，其他条 件和上一问相同。求两种光第一级主极大之间的距离。
厚度。2）此时零级明条纹的位置。
E
解：1）入射光到达双缝时已有光程差：
1dsin 30
S
30
1
1
o
经双缝后，又产生附加光程差：
2(n1)e
S2
D
两束光在点O处相聚时的光程差为：
2 1 ( n 1 ) e d s3 in 0
由题意知：点O处为第8 级明条纹，即：
(n 1 )e d s3 i n 0 8
解：1）由单缝衍射明条纹公式知：
f
xk (2k1)2a
xk1
(21)
f1
2a
xk2
(21)
f2
2a
x3f(21)
2a
5 0 3 (764 00 0 ) 0 1 8 0
2 1 2 0
0 .2c7m
2）光栅方程： dsin k
ds in 1k1 ds in 2k2 (k 1)
因为 1、2很小。则s有 i ntg
N 1 ab
7、在单缝的夫琅和费衍射示意图中所画的各条正入射光线间距
相等，那么光线1 和 3 在屏上P点相遇时的相位差为 2 ，
P点应为 暗 点。

大学物理(少学时) 第4版教学课件第12章 波动光学01

大学物理(少学时) 第4版教学课件第12章 波动光学01

r2 r1 d sin
x D (n 1)t d
d tan d
n 1 x d tD
x D
22
三、劳埃德镜
P'
P
s1
d
s2
ML
D
与双缝干涉对比： ① 明暗条纹位置反转。 一路光在平面镜反射时，有“半波损失”，光波 相位有π的突变。
② 条纹分布区域限于屏的上半部分。 23
第十二章 波动光学
明纹，求(1)该明纹的干涉级;(2)新的零级明纹的位置。
S1 nt d
解：（1）
X
r1
P nt t
r2 O
x
(n 1)t
O
k
S2 D
k (n 1)t
21
S1 nt d S2
r1
r2
D
X P
x O
O
k (n 1)t
（2） r2 r1 nt t 0 新的零级明纹位置
r2 r1 nt t n 1 t
12
3. 获得相干光方法 普通光源的发光特点:
（1） 一个原子每一次发光只能发出一个波列 （2） 原子的发光是断续的 （3） 各原子的各次发光是完全相互独立的
两个普通光源或同一普通光源的不同部分所发 出的光是不相干的
从普通光源获得相干光方法:
分波前法 分振幅法
13
相干光源的获得 —— (1)分波面法：
当 e、n2、n1 确定， 则 相同入射角的入射光线有相同光程差。
它们在透镜焦平面上构成同一级条纹，称等倾干涉。
➢ 两束透射相干光的光程差：
2e n22 n12 sin2 i
——透射光相干图样与反射光相干图样“互补”
27
等倾干涉实验： 2e

波动光学

波动光学


r 2 nr
2
从相位改变的角度来看，光在折射率为n的 介质中通过了几何路程r，相当于它在真空中通过了nr的几何路程。
'

第十二章 波动光学
光程：折射率n和光所通过的几何路程r的乘积
L nr
2.光程差 • 两束光的光程之差称为光程差，常用 表示。 • 决定光波相位和相位变化的不只是几何路程，而是光 程和光程差。 2 • 相位差与光程差的关系为：
第十二章 波动光学
3.条纹位置 • 第k级暗纹位置： xk f tg f sin k f

a
• 第k级明纹位置： xk (2k 1) f

2a
k=1, 2, 3, ……
k=1, 2, 3, ……
• 明条纹宽度：即相邻两暗纹中心间距。
x ' x k 1 x k
2 k x 2 d sin d D (2k 1) 2
x δ= r2 r1 d sin d tan d D
( k 0,1, 2,) 相干加强,明纹 ( k 1, 2, 3,) 相干削弱 , 暗纹
(r1 l n l ) r2 (n 1) l
(n 1) l k
(1.30 1) 0.01 103 5 7 6.00 10


第十二章 波动光学
四、劳埃德镜实验
S1 和 S2相当于两个相干光源，屏上相遇区域观 察到明暗相间的干涉条纹。 实验结果还表明：光从空气射向玻璃发生反射 时，反射光有大小为 的相位突变。 相当于光波多走（或少走）了半个波长的距离， 这个现象称为半波损失。

波 动 光 学

波 动 光 学
波动光学
1
光学是研究光的传播以及它和物质相互作用 问题的学科。 光学通常分为以下三个部分：
以光的直线传播规律为基础，主要 ▲ 几何光学：
研究各种成象光学仪器的理论。 研究光的电磁性质和传播规律， 特别 ▲ 波动光学： 是干涉、衍射、偏振的理论和应用。 以光的量子理论为基础， 研究光与 ▲ 量子光学： 物质相互作用的规律。
I 4 I 0 cos 2
2
(
d si n

2π )
I
光强曲线
-4 -2 -2 -1
4I0
-2 /d - /d
x 2
x 1
0 0 0 0
2 1
4 2
/d 2 /d sin
x1
x2
k
x
15
三. 干涉问题分析的要点：
（1）搞清发生干涉的光束； （2）计算波程差（光程差）； （3）搞清条纹特点： 形状、 位置、 级次分布、条纹移动等； （4）求出光强公式、画出光强曲线。
16
△ 四.
其他分波面干涉实验（自学书P128—129）
要求明确以下问题： 1.如何获得的相干光； 2.明、暗纹条件； 3.干涉条纹特点： 形状、间距、 级次位置分布； 4.劳埃镜实验说明了什么？ 重点搞清劳埃镜实验。
17
（temporal coherence） §3.3 时间相干性 一. 光的非单色性
· ·
2 2 2 I E0 , 又 I1 E10，I 2 E20
光强 I I1 I 2 2 I1 I 2 cos
干涉项
7
非相干光源： cos 0
I = I
1
+ I
2
—非相干叠加

第十二章(二)波动光学

第十二章(二)波动光学

第十二章（二） 波动光学班号 学号 姓名 日期一、选择题1．一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是(A) 紫光； (B) 绿光； (C) 黄光； (D) 红光。

( )2．在光栅光谱中，假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上，因而实际上不出现，那么此光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系为(A) b a =； (B) b a 2=； (C) b a 3=； (D) a b 2=。

( )3．设一平面透射光栅，当入射的平行单色光从垂直于光栅平面入射变为斜入射时，能观察到的光谱线的最高级次k(A) 变小； (B) 变大； (C) 不变； (D) 无法确定。

( )4．一束光强度为I 0的自然光垂直穿过两个偏振片，此两偏振片的偏振化方向成45︒角，若不考虑偏振片的反射和吸收，则穿过这两个偏振片后的光强度I 为(A) 420I ； (B) 40I ； (C) 20I ； (D) 220I 。

( )5．自然光以60︒的入射角照射到某两介质交界面时，反射光为完全偏振光，则知折射光为(A) 完全偏振光且折射角是30︒；(B) 部分偏振光、且只是在该光由真空入射到折射率为3的介质时，折射角是30︒；(C) 部分偏振光，但须知两种介质的折射率才能确定折射角；(D) 部分偏振光、且折射角是30︒。

( )6．一束光强度为I 0的自然光，相继通过三个偏振片P 1、P 2、P 3后，出射光的光强度为80I I =，已知P 1和P 3的偏振化方向相互垂直，若以入射光线为轴，旋转P 2，则它至少要转过多大角度，才能使出射光的光强度为零。

(A) 30︒； (B) 45︒； (C) 60︒； (D) 90︒ 。

()7．一束自然光自空气射向一块平板玻璃（如图所示），设入射角等于布儒斯特角i 0，则在界面2的反射光为(A) 自然光； (B) 完全偏振光、且光矢量的振动方向垂直于入射面；(C) 完全偏振光、且光矢量的振动方向平行于入射面； (D) 部分偏振光。

大学物理高校出版社罗圆圆主编-第12章波动光学PPT课件

大学物理高校出版社罗圆圆主编-第12章波动光学PPT课件

现象：一系列平行的明暗相间的条纹； 不太大时条纹等间距.
24
干涉条纹定量分析：
（1）条纹(中心)的位置
s
s
d
1
（在 较小的情况下） s 2
波程差：
r1
p
r2
x
o
D
r2r1dsin dt gdD x
Δ20 10 2 π(r2r1) 现已有 20 - 10=0
25
亮纹: （相长干涉）
2kπ (k0,1,2, ) 或波程 r2差 r1k
13
P点处：
E 1E 1c 0 o ts (1)
E 2E 2c 0 o ts (2)
r1
· 1
r2
· 2
E20
·P
E0
EE1E2
EE0cos(t)
2 1 E10
14
E 0 2E 1 2 0E 2 2 02E 1E 0 2c 0 os
其中：21
I E 0 2 = 1 0 E 2 0 d t = 1 0 [E 1 2 0 E 2 2 0 2 E 1 0 E 2 0 c o s ] d t
电磁谐波 EE0cots(k)x
电磁波的强度：
I
wu1
2
E02u
在同一介质中通常把强度直接写成
I
E
2 0
说明：与物质作用的主要物理量是电矢量 通常称 E为光矢量
按波长或频率的次序把这些电磁波排列成谱
----称为电磁波谱。
可见光的范围
4000埃~7600埃，
:40~076n0m只占很小的一段 :7.51104~4.31104Hz 8
2
波动光学
第一部分 光的干涉 第二部分 光的衍射 第三部分 光的偏振

第十二章波动光学

第十二章波动光学

第十二章波动光学本章前言◆本章学习目标1、由原子或分子发光特点理解普通光源是非相干光源。

2、了解几种获得相干光的方法。

3、掌握计算明、暗条纹的光程差条件。

4、理解薄膜干涉是由膜的上、下两表面分别反射的两束光的干涉。

5、理解等厚干涉条纹的特征及实际中的应用。

6、理解光的衍射与单缝衍射明、暗条纹的角位置。

7、理解光栅衍射公式。

8、理解自然光和线偏振光，理解马吕斯定律及布儒斯特定律。

了解线偏振光的获得方法和检验方法。

◆本章教学内容1、光的干涉、杨氏双缝干涉1.1 光的干涉1.2 杨氏双缝干涉2、光程、薄膜干涉、等厚条纹(劈尖及牛顿环)3、迈克耳孙干涉仪4、光的衍射、惠更斯一菲涅耳原理、单缝夫琅禾费衍射、光学仪器的分辨率5、光栅衍射、平面透射光栅6、光的偏振、自然光和线偏振光、起偏和检偏、马吕斯定律、布儒斯特定律◆本章重点薄膜干涉明、暗纹的计算、单缝衍射明、暗纹的计算及光栅公式。

◆本章难点光程与光程差的计算，半波损失的分析。

光衍射的本质。

光栅衍射分析。

§12.1 光的干涉、杨氏双缝干涉12.1.1光的相干性一、光源发射光波的物体，也即光波的源称为光源。

普通光源发光的机理是原子（或分子）的自发辐射。

原子、分子在吸收能量后处于一种不稳定的激发态，即使没有任何外界作用，它们也会自发地回到低激发态或基态，同时向外发出光波。

可见光源和我们前面学过的机械波的波源有很大的区别，机械波的波源往往是一个振动的物体，而光源却是千千万万的原子随几地、此起彼伏地发光。

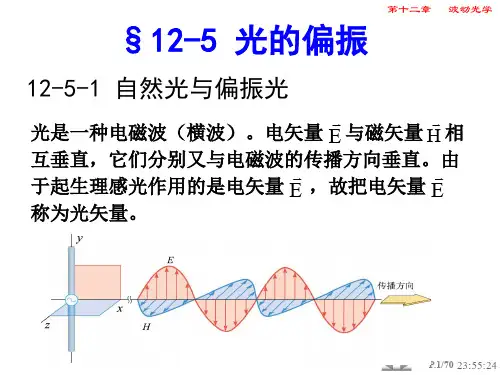
二、光波光波是电磁波，是相互激发的电场E的波和磁场H的波。

通常我们用电场E 作为光的代表，称为光矢量。

之所以选取电场，一方面是由于电场E和磁场H是紧密相关的，如前所述，如果确定了电场，则磁场也能随即确定。

另一方面是在人的视觉以及光化学反应中，电场的作用是主要的。

光波有间断性，不是连续的。

一个原子的一次发光的时间极短，一般在10–11~10–8s，发出的光波的长度也比较短，把发光时间乘以光速可知，光波的长度大约在毫米到米的范围，我们把这一段光波称为一个光波列。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、填空题、简答题
1.从同一光源获得相干光的方法有两种，一种叫 分波阵面法 ，另一种叫 分振幅法 ，杨氏双缝实验获得相关光属于哪一种（分波阵面法）？薄膜干涉又属于那一种（分振幅法）？
2.在双缝干涉中，两缝间距离为d ，双缝与屏幕之间的距离为()D D d >>，波长为λ的平行单色光垂直照射到双缝上，屏幕上干涉条纹中第3级明纹中心的位置x =
d
D λ3，第5级明纹与第8级明纹
之间的距离为d
D λ3。

3.两初相位相同的相关光源
1S 和2S （如左图所示），发出波长都为λ的光，经路程10.4r =m 和20.3r =m 到达P 点，在1S 与P 间插入厚度为
0.1x =m
、折射角为2n =的薄玻璃片，则光从1S 到P 点的光程=0.5 ， 从
1S 和2S 发出的光到P
点的光程差δ=0.2 ，在P 点的相位差ϕ∆=
λ
π52。

4.将杨氏双缝实验干涉实验上方的缝后贴上一薄的透明云母片，干涉条纹间距有无变化（无变化）？中央条纹位置有何变化（上移）？
5.一束波长为λ的单色光从空气中垂直入射到折射率为n 的透明薄膜上，要使反射光线得到增加，薄膜的厚度应为
()......3,2,1412=-k n
k λ。

6. 用波长为λ的平行单色光垂直照射折射率n 的劈尖薄膜，形成等厚干涉条纹。

若测得两相邻干涉条纹间距为l ，则劈尖角θ=
nl
2λ。

7. 两块玻璃构成空气劈尖, 左边为棱边, 用单色平行光垂直入射, 若上面的平玻璃慢慢向上平移, 则干涉条纹向 左 方向平移，条纹间隔 不变 (填“变大”、“变小”或“不变”)。

8.用半波带法讨论单缝衍射条纹中心的条件时，与中央明条纹旁第2暗纹中心相对应的半波带的数目是 4 。

9. 一单色平行光垂直入射一单缝，其衍射第三级明纹位置恰好与波长为600 nm 的单色光垂直入射该缝时衍射的第二级明纹位置重合，则该单色光的波长为nm 6.428.
10.已知地月距离约为53.010⨯ km ，用口径为1.0m 的天文望远镜能分辨月球表面两点的最小距离是
m 8
1066.3⨯λ。

11. 波长为550 nm 的单色光垂直入射于光栅常数为41.010-⨯ cm 的光栅上，可能观察到得光谱线的最大级次为 1 .
12. 一束平行单色光垂直入射到光栅上，当光栅常数d 与缝宽a 的比值
d a =
3 时，
36k =±± 、
等级次的主极大缺失. 二、计算题
13.迎面而来的两辆汽车的车头灯距离为1.0m ，问在汽车离人多远时，它们刚能为人眼所分辨？设瞳孔直径为3.0mm ，光的波长为500nm 。

14.用很薄的云母片()1.58n =覆盖在双缝实验中的一条缝上，这时屏幕上的零级明条纹移到第七级明条纹的位置上。

如果入射光波长为500nm ，试问此云母片的厚度为多少？
15.在棱镜()1 1.52n =表面镀一层增透膜()2 1.30n =，如使此增透膜适用于氦氖激光器发出的激光
()632.8λ=nm ，膜的厚度应取何值？
16.制造半导体元件时，常需要精确地测定硅片上的二氧化硅()2SiO 薄膜的厚度，这时可把二氧化硅()2SiO 薄膜的一部分腐蚀掉，使它成为劈尖，利用等厚干涉条纹测出其厚度。

如图，已知S i 的折射率为3.42，2SiO 的折射率为1.5.用氦氖激光()632.8λ=nm 垂直照射，在反射光中观察到在腐
蚀区域内有8条暗纹，求2SiO 薄膜的厚度。

解：反射光在劈尖上表面形成干涉暗纹满足的条件：
()
22212
sio n d k λ
=+，012k = （、、），
在腐蚀区域内总共有8条暗纹， 则7k =对应的厚度既为2SiO 薄膜的厚度：()
22712 1.582
sio d n m
λ
μ=⨯+=
17. 有一单缝，缝宽0.1m m a =，缝后放一焦距为50cm 的会聚透镜，用波长546.1nm
λ=的平行光垂
直照射单缝，试求位于透镜焦平面处屏上中央明纹的宽度及第4级暗纹中心所在位置？ 解：单缝衍射暗纹满足的条件：()sin , 123a k k θ
λ=±= 、、，
由上式可得第1级暗纹中心对应的衍射角1
a
λθ=
，第1级暗纹中心所在位置1
11tan x f f f
a
λθθ=≈=，
所以中央明纹的宽度为上下两第1级暗纹中心的间距:3
122 5.46110 m
x x f a
λ-∆===⨯.
第4级暗纹中心所在位置m
a
f
f x 2
4410
1.14-⨯±=±=±=λθ。

18.已知一个每厘米刻有4000条缝的光栅，利用这个光栅可以产生多少个完整的可见光谱
()400~760λ=nm ？
解：由题意可知光栅常量6
1 2.510
4000
d cm m
-=
=⨯，因衍射角2
π
θ≤
，由光栅方程：
()sin , 0123d k k θλ==±±±± 、、、
可知对某一波长的可见光最大级次d
k λ
≤
，（1）当400λ= nm 得光入射， 6.25
d
k λ
≤
=，取整数6
k
=；
（2）当700λ= nm 的光入射， 3.57
d
k λ
≤=，取整数3
k
=，分析可得利用这个光栅可以产生3个完
整的可见光谱.。