单自由度机械振动系统习题课
- 格式:doc
- 大小:413.50 KB
- 文档页数:3
第一章 概论1-1概念1. 机械振动系统由哪几部分组成?其典型元件有哪些?2. 机械振动研究哪三类基本问题?3. 对机械振动进行分析的一般步骤是什么?4. 在振动分析中,什么叫力学模型,什么叫数学模型?5. 惯性元件、弹性元件、阻尼元件的基本特性各是什么?6. 什么叫离散元件或集中参数元件?7. 什么叫连续体或分布参数元件?8. 建立机械振动系统力学模型的基本原则有哪些?9.建立机械振动系统力学模型需要考虑的基本问题?并分析建立下图中的系统的力学模型。
一台机器(看为一个整体)平置于一块板上,板通过两个垂直的支撑块放置在地面上,试建立其力学模型。
10. 如果一个振动系统是线性的,它必须满足什么条件?11. 如果一个振动系统的运动微分方程是常系数的,它必须满足什么条件? 12. 试讨论:若从车内乘客的舒适度考虑,该如何建立小轿车的振动模型?1-2简谐运动及其运算1求下列简谐函数的单边复振幅和双边复振幅 (1))3sin(2πω+=t x (2))410cos(4ππ+=t x (3))452cos(3︒+=t x π答案:(1)111,,2222S B B X j X j X j +-==-=+ (2),,S B B X X X +-== (3),,224444S B B X j X j X j +-=+=+=-2通过简谐函数的复数表示,求下列简谐函数之和,并用“振动计算实用工具”对(2)(3)进行校核(1))3sin(21πω+=t x )32s i n (32πω+=t x (2)t x π10sin 51=)410cos(42ππ+=t x(3))302sin(41︒+=t x π )602sin(52︒+=t x π)452cos(33︒+=t x π)382cos(74︒+=t x π )722cos(25︒+=t x π答案:(1))6.6cos(359.412︒+=t x ω (2))52.4710cos(566.312︒-=t x π (3))22.92cos(776.1412345︒+=t x π3试计算题1中)(t x 的一阶导数和二阶导数对应的复振幅,并给出它们的时间历程4设)(t x 、)(t f 为同频简谐函数,并且满足)(t f cx x b x a =++ 。

习题课-单自由度系统1.图示系统质量块质量为m=10kg,弹簧刚度为k=30kN/m并且弹簧质量可以忽略,质量块被向左方向推离位置1mm后放手,求此系统的固有频率、周期和响应,以及弹簧所受的力。
2.如果前题的系统必须考虑该弹簧的质量,弹簧单位长度的质量等于 =0.1kg,弹簧的长度为L=10mm。
求系统的固有频率并与上题比较,误差有多大?提示:质量块的位移用)(t x 来表示。
假设在振动过程中弹簧位移是线性的。
显然左端不动、右端与质量块一致,则可设在距离弹簧左端ξ处取一质量为ξρd 的微单元,则该单元位移为Lt x ξ)(,则系统的动能为:)(321L 3)(21)(21)(21)(21T 2232222200t xL m t x t x m d t xL t x m L L ⎪⎭⎫ ⎝⎛+=+=⎰+=⎪⎪⎪⎭⎫ ⎝⎛ρξρξρξ系统的势能为:)t)(212t kx V =系统机械能:)(21)(32122t kx t x L m V T E ++=+=⎪⎪⎪⎭⎫ ⎝⎛ ρ 由根据机械能守恒原理0=dtdE得到系统振动微分方程为:0)()(3=++⎪⎪⎪⎭⎫⎝⎛t kx t xL m ρ代入数据可得:t)时间间隔内受到突加的矩形脉冲力激励如3.设无阻尼质量-弹簧系统在(0,1图所示。
F01(1)求系统响应;解:(1) 由图可知11(0)()()F t t F t t t ≤≤⎧=⎨≥⎩当10t t ≤≤时,由杜哈梅积分得0()()()tx t F h t d τττ=-⎰则001()sin ()tn nx t F t d m ωττω=-⎰解得()(1cos )n F x t t kω=- 当1t t ≥时,由杜哈梅积分分段积分得到11()()()()()t tt x t F h t d F h t d ττττττ=-+-⎰⎰ 110011()sin ()0sin ()t t n n t n nx t F t d t d m m ωττωττωω=-+⨯-⎰⎰10001()cos ()|[cos ()cos ]t n n n F x t t kF t t t kωτωω=-=--由此可以写出系统响应1011(1cos )0()[cos ()cos ]n n nF t t t kx t F t t t t t kωωω⎧-≤≤⎪⎪=⎨⎪--≥⎪⎩(2) 求系统在该激励下的响应谱; 当脉冲力作用时间1t 超过系统的半周期即12Tt >时,位移响应()x t 的驻值发生在()0m x t =,即2m T t =时刻亦即12m t T =,位移的最大值为02()2F T x k =。


1 / 21第二章 单自由度系统习题2.1 弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:2n=g/δ运动微分方程(式2.5):x +2nx=0初始条件:x (0)=3δ,x(0)=0 由式2.8有:A=2020)(ωnxx +=3δ=arctgnx xω00 =0由式2.7有: 响应:x =3δcos(δg t)2.2 弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:ω2n =g/δ=9.8/0.2=49运动微分方程(式2.5):x +ω2n x=0 初始条件:x (0)=-0.2,x(0)=0 由式2.8有:振幅:A=2020)(ωnxx +=0.2ϕ=arctgnx xω00 =0由式2.7有: 响应:x=0.2cos(7t) 周期:T=2/ωn弹簧刚度:k=mg/δ=19.8/0.2=49(N/m)最大弹簧力:F Smax =-kA=-490.2=9.8(N)2.3 重物m l 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物m 2从高度为h 处自由落到m l 上而无弹跳,如图T —2.3所示,求其后的运动。
图 T —2.3解:ω2n =k/(m 1+m 2)运动微分方程(式2.5):x+2nx=0初始条件:x (0)=- m 2g/km 2gh=21(m 1+m 2)x2(0)⇒ x (0) (以下略)2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆3 / 21心受到一弹簧k 约束,如图T —2.4所示,求系统的固有频率。
图 T —2.4解:系统的势能:U=21kr 2θ2系统的动能:E t =21I •θ2+21mr2•θ2由d(U+E t )=0得:(I+ mr 2)••θ+kr 2θ=0ω2n =22m r I kr +2.5 均质杆长L 、重G ,用两根长h 的铅垂线挂成水平位置,如图T —2.5所示,试求此杆相对铅垂轴OO 微幅振动的周期。

2.1 弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则:mg k δ=,即:n ω==取系统静平衡位置为原点0x =,系统运动方程为: δ⎧+=⎪=⎨⎪=⎩00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-= 所以:9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=其中,初始条件:(0)0.2(0)0x x =-⎧⎨=⎩ (参考教材P14) 所以系统的响应为:()0.2cos ()n x t t m ω=-弹簧力为:()()cos ()k n mg F kx t x t t N ω===-因此:振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有: 2121()2T E m m x =+ 212U kx =由()0T d E U +=可知:12()0m m x kx ++= 即:12/()n k m m ω=+系统的初始条件为:⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m (能量守恒得:221201()2m gh m m x =+) 因此系统的响应为:01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即:ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。

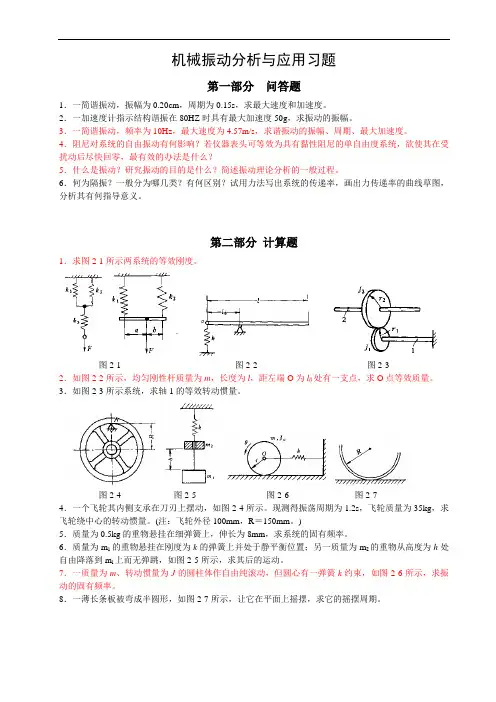
机械振动分析与应用习题第一部分问答题1.一简谐振动,振幅为0.20cm,周期为0.15s,求最大速度和加速度。
2.一加速度计指示结构谐振在80HZ时具有最大加速度50g,求振动的振幅。
3.一简谐振动,频率为10Hz,最大速度为4.57m/s,求谐振动的振幅、周期、最大加速度。
4.阻尼对系统的自由振动有何影响?若仪器表头可等效为具有黏性阻尼的单自由度系统,欲使其在受扰动后尽快回零,最有效的办法是什么?5.什么是振动?研究振动的目的是什么?简述振动理论分析的一般过程。
6.何为隔振?一般分为哪几类?有何区别?试用力法写出系统的传递率,画出力传递率的曲线草图,分析其有何指导意义。
第二部分计算题1.求图2-1所示两系统的等效刚度。
图2-1 图2-2 图2-32.如图2-2所示,均匀刚性杆质量为m,长度为l,距左端O为l0处有一支点,求O点等效质量。
3.如图2-3所示系统,求轴1的等效转动惯量。
图2-4 图2-5 图2-6 图2-74.一个飞轮其内侧支承在刀刃上摆动,如图2-4所示。
现测得振荡周期为1.2s,飞轮质量为35kg,求飞轮绕中心的转动惯量。
(注:飞轮外径100mm,R=150mm。
)5.质量为0.5kg的重物悬挂在细弹簧上,伸长为8mm,求系统的固有频率。
6.质量为m1的重物悬挂在刚度为k的弹簧上并处于静平衡位置;另一质量为m2的重物从高度为h处自由降落到m l上而无弹跳,如图2-5所示,求其后的运动。
7.一质量为m、转动惯量为J的圆柱体作自由纯滚动,但圆心有一弹簧k约束,如图2-6所示,求振动的固有频率。
8.一薄长条板被弯成半圆形,如图2-7所示,让它在平面上摇摆,求它的摇摆周期。
图2-8 图2-99.长度为L 、重量为W 的均匀杆对称地支承在两根细绳上,如图2-8所示。
试建立杆相对于铅垂轴线o-o 的微角度振动方程并确定它的周期。
10.求图2-9所示系统的等效刚度和固有频率。
11.用能量法求图2-10所示均质圆柱体振荡的固有频率。
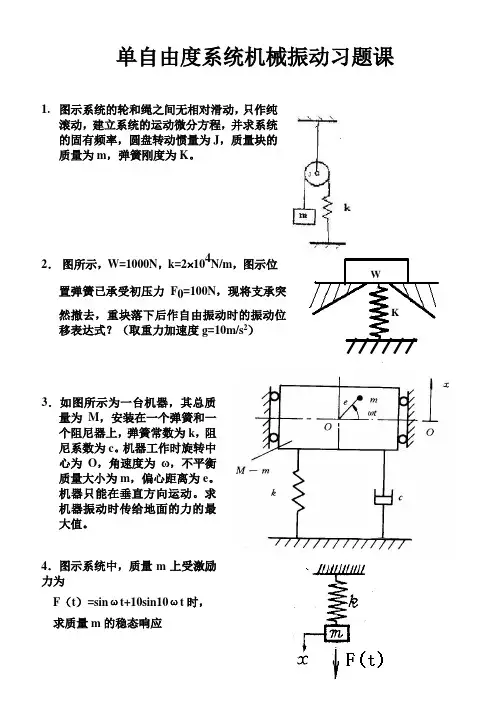
单自由度系统机械振动习题课1. 图示系统的轮和绳之间无相对滑动,只作纯滚动,建立系统的运动微分方程,并求系统的固有频率,圆盘转动惯量为J ,质量块的质量为m ,弹簧刚度为K 。
2. 图所示,W=1000N ,k=2 104N/m ,图示位置弹簧已承受初压力F 0=100N ,现将支承突然撤去,重块落下后作自由振动时的振动位移表达式?(取重力加速度g=10m/s 2)3.如图所示为一台机器,其总质量为M ,安装在一个弹簧和一个阻尼器上,弹簧常数为k ,阻尼系数为c 。
机器工作时旋转中心为O ,角速度为ω,不平衡质量大小为m ,偏心距离为e 。
机器只能在垂直方向运动。
求机器振动时传给地面的力的最大值。
4.图示系统中,质量m 上受激励力为F (t )=sin ωt+10sin10ωt 时,求质量m 的稳态响应WK5.图示系统的轮和绳之间无相对滑动,只作纯滚动,建立系统的运动微分方程,并求系统的固有频率,圆盘转动惯量为J,质量块的质量为m,弹簧刚度为K6.一重块与两弹簧相连,W=490N,k=9800N/m,图示位置弹簧不受力,现将支承突然撤去,重块落下后作自由振动时的振动位移表达式?7. 如图所示为一台机器,其总质量为m,通过一个弹簧和一个阻尼器安装在基础上,弹簧常数为k,阻尼系数为c。
基础的运动为y(t)=Ysinωt,机器只能在垂直方向运动。
求基础振动时传给机器的力的最大值。
8.图示系统中,质量m上受激励力为F(t)=sinωt+10sin10ωt时,求质量m的稳态响应。
WKK9.一般振动问题,如图所示:三类振动问题分别是:(1)振动分析,已知,求;(2)振动环境预测或载荷分析,已知,求;(3)系统识别,已知,求。
10. 振动问题的分类,根据自由度数分,有,和。
11. 简谐振动x=Asin(ωt+φ),其中的振动位移为,振幅为,振动频率为为,振动的初相位为12. n个自由度振动系统有个固有频率,有个固有振型,其中的第i阶主振型有个节点。
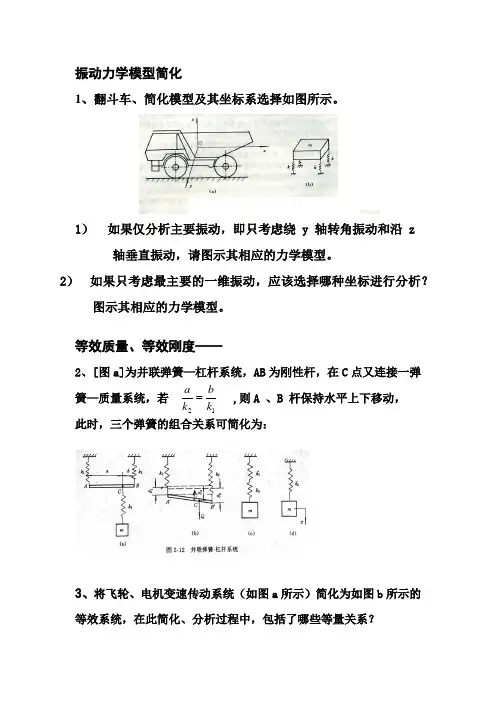
振动力学模型简化1、翻斗车、简化模型及其坐标系选择如图所示。
1)如果仅分析主要振动,即只考虑绕 y 轴转角振动和沿 z 轴垂直振动,请图示其相应的力学模型。
2)如果只考虑最主要的一维振动,应该选择哪种坐标进行分析?图示其相应的力学模型。
等效质量、等效刚度——2、[图a]为并联弹簧—杠杆系统,AB为刚性杆,在C点又连接一弹簧—质量系统,若 ,则A 、B 杆保持水平上下移动,此时,三个弹簧的组合关系可简化为:3、将飞轮、电机变速传动系统(如图a所示)简化为如图b所示的等效系统,在此简化、分析过程中,包括了哪些等量关系?21a bk k[试从能量、受力、运动等方面进行总结] 。
简谐振动表述(余弦函数)用余弦函数表示的简谐振动, 参数所表达的物理意义和用正弦函数表示的简谐振动有无区别?公式(1-10)中,代表的是 在 图(a)中哪个轴上的投影?扭转振动分析——1、已知:系统由固定端垂直轴与水平圆盘连接而成,轴的长度为 L 、 直径为 d 、 剪切模量为 G ,圆盘转动惯量为 I (略去轴的质量,不记阻尼) 。
该结构(固定端直轴)的扭转刚度为: 求 :系统固有频率f ;自由扭转振动微分方程;()cos (110)x A t ωϕ=+-0A ωϕ、、A x lG d k 324πθ=飞轮电机单质体受迫振动受力分析与方程列写凸轮以等角速度 转动,顶杆的运动规律为(图2-36b )。
设某瞬时 均不为零,单独考虑两个弹簧对质体所传递的弹性力,1、画出质体受力图;2、列写质体运动方程,并推导至下列标准方程形式:固有频率求解——2、静变形法求解固有频率适用于( )情形;能量法求解固有频率适用于( )情形; 瑞利法求解固有频率适用于( )情形。
3、瑞利法求解固有频率时,为什么要作弹性元件的变形曲线假设?122()()()m x r x k k x Q t k y t +++==()y t ω()()x t y t 、曲线性质分析___幅频曲线性质、瞬态振动曲线、拍振曲线的演变1、图2-19是简谐激励无阻尼受迫振动稳态响应的幅频曲线,纵坐标为,在、及处曲线取值的物理含义2、图2-22(a)、(b)分别为、时稳态受迫振动和伴生振动叠加的瞬态振动曲线,试给出相应的稳态振动曲线。

胡海岩主编---机械振动基础课后习题解答_第2章习题第2章习题含答案习题2-1 定常力作用下的单自由度系统1. 一个单自由度系统的质量m=2kg,刚度k=1000N/m,阻尼系数c=10N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解:根据公式,该系统的固有频率可计算为:ωn = √(k/m) = √(1000/2) ≈ 22.36 rad/s阻尼比可计算为:ξ = c/(2√(mk)) = 10/(2√(2×1000)) ≈ 0.158振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时,系统为欠阻尼;当ξ=1时,系统为临界阻尼;当ξ>1时,系统为过阻尼。
2. 一个单自由度系统的质量m=5kg,刚度k=500N/m,阻尼系数c=20N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解:根据公式,该系统的固有频率可计算为:ωn = √(k/m) = √(500/5) = 10 rad/s阻尼比可计算为:ξ = c/(2√(mk)) = 20/(2√(5×500)) ≈ 0.141振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时,系统为欠阻尼;当ξ=1时,系统为临界阻尼;当ξ>1时,系统为过阻尼。
习题2-2 强迫振动的幅值和相位1. 一个单自由度系统的质量m=3kg,刚度k=2000N/m,阻尼系数c=30N·s/m。
给定的外力F(t) = 10sin(5t)N。
试求该系统在稳态时的振动幅值和相位。
解:首先求解系统的强迫响应,即对外力F(t)进行拉氏变换:F(s) = L{F(t)} = L{10sin(5t)} = 10L{sin(5t)} = 10×(5/(s^2+25))根据公式,系统的强迫响应可计算为:X(s) = F(s)/((s^2+ωn^2)+2ξωns)其中,ωn=√(k/m)为系统的固有频率,ξ=c/(2√(mk))为系统的阻尼比。
习题课及考前复习(24题)
一、考试知识点
二、考题分布情况
三、作业题
四、课堂练习题
五、经典例题
一、考试知识点
第一章
1、单自由度系统振动方程。
2、无阻尼单自由度系统的自由振动。
3、等效单自由度系统。
4、有阻尼单自由度系统的自由振动。
5、简谐力激励下的受迫振动。
6、基础简谐激励下的受迫振动。
第二章
1、多自由度系统的振动方程。
2、建立系统微分方程的方法。
3、无阻尼系统的自由振动。
4、无阻尼系统的受迫振动。
二、考题分布情况
1、主要围绕作业题、课堂练习题、经典例题题型展开。
2、复习时把握每章知识要点,理解基础题型解题方法。
3、考卷共6道大题。
习题课及考前复习(24题)
一、考试知识点
二、考题分布情况
三、作业题
四、课堂练习题
五、经典例题
m
222(2)m l θ= ⎧⎨⎩211
(2)m l θ= 212(22)2k l l l θθ−⋅−⋅⋅11k l l θ−⋅221(22)2k l l l
θθ−⋅−⋅⋅
习题课及考前复习(24题)
一、考试知识点
二、考题分布情况
三、作业题
四、课堂练习题
五、经典例题
m
m
m
m
m
m
习题课及考前复习(24题)
一、考试知识点
二、考题分布情况
三、作业题
四、课堂练习题
五、经典例题
m。
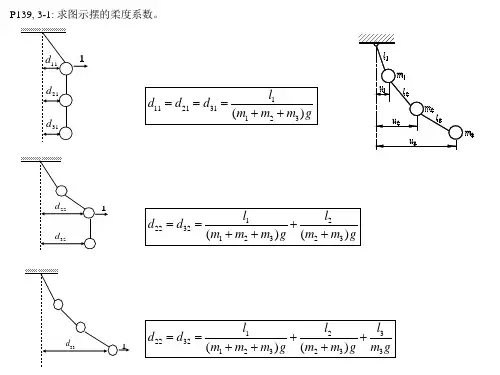
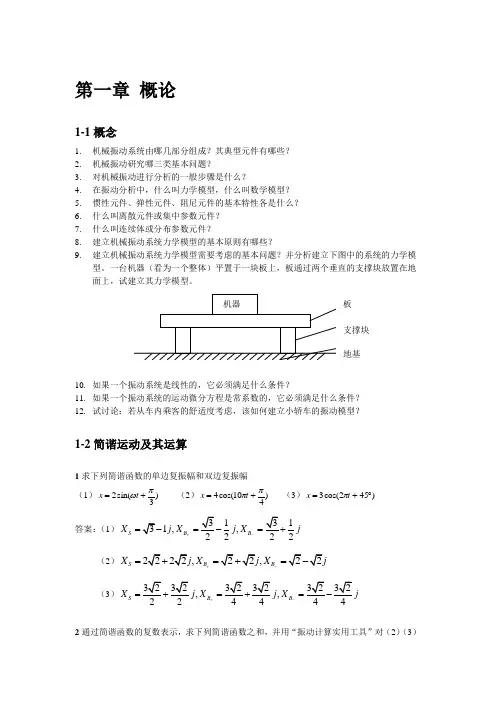
习 题1-1一单层房屋结构可简化为题1-1图所示的模型,房顶质量为m ,视为一刚性杆;柱子高h ,视为无质量的弹性杆,其抗弯刚度为EJ 。
求该房屋作水平方向振动时的固有频率。
解:由于两根杆都是弹性的,可以看作是两根相同的弹簧的并联。
等效弹簧系数为k 则 mg k δ=其中δ为两根杆的静形变量,由材料力学易知δ=324mgh EJ=则k =324EJh设静平衡位置水平向右为正方向,则有 "m x kx =- 所以固有频率3n 24mhEJp =1-2 一均质等直杆,长为 l ,重量为W ,用两根长h 的相同的铅垂线悬挂成水平位置,如题1-2图所示。
试写出此杆绕通过重心的铅垂轴作微摆动的振动微分方程,并求出振动固有周期。
解:给杆一个微转角2a =h2F cos α=mg由动量矩定理:aha mg a mg Fa M ml I M I 822cos sin 12122-=-≈⋅-====αθαθ题1-1图题1-2图F sin α2θhmg其中12cossin ≈≈θααhl ga p ha mg ml n 22222304121==⋅+θθ g ha l ga h l p T n 3π23π2π222===1-3求题1-3图中系统的固有频率,悬臂梁端点的刚度分别是k 1和k 3,悬臂梁的质量忽略不计。
解:悬臂梁可看成刚度分别为k 1和k 3的弹簧,因此,k 1与k 2串联,设总刚度为k 1ˊ。
k 1ˊ与k 3并联,设总刚度为k 2ˊ。
k 2ˊ与k 4串联,设总刚度为k 。
即为21211k k k k k +=',212132k k kk k k ++=',4241213231421432421k k k k k k k k k k k k k k k k k k k k ++++++=)(42412132314214324212k k k k k k k k k k m k k k k k k k k k p ++++++=1-4求题1-4图所示的阶梯轴一圆盘系统扭转振动的固有频率。
单自由度系统机械振动习题课
1. 图示系统的轮和绳之间无相对滑动,只作纯
滚动,建立系统的运动微分方程,并求系统
的固有频率,圆盘转动惯量为J ,质量块的
质量为m ,弹簧刚度为K 。
2. 图所示,W=1000N ,k=2 104N/m ,图示位
置弹簧已承受初压力F 0=100N ,现将支承突
然撤去,重块落下后作自由振动时的振动位
移表达式?(取重力加速度g=10m/s 2)
3.如图所示为一台机器,其总质
量为M ,安装在一个弹簧和一
个阻尼器上,弹簧常数为k ,阻
尼系数为c 。
机器工作时旋转中
心为O ,角速度为ω,不平衡
质量大小为m ,偏心距离为e 。
机器只能在垂直方向运动。
求
机器振动时传给地面的力的最
大值。
4.图示系统中,质量m 上受激励
力为
F (t )=sin ωt+10sin10ωt 时,
求质量m 的稳态响应
W
K
5.图示系统的轮和绳之间无相对滑动,只作纯滚
动,建立系统的运动微分方程,并求系统的固
有频率,圆盘转动惯量为J,质量块的质量为m,弹簧刚度为K
6.一重块与两弹簧相连,W=490N,k=9800N/m,
图示位置弹簧不受力,现将支承突然撤去,重块落下后作自由振动时的振动位移表达式?
7. 如图所示为一台机器,其总质量为m,通
过一个弹簧和一个阻尼器安装在基础上,弹
簧常数为k,阻尼系数为c。
基础的运动为
y(t)=Ysinωt,机器只能在垂直方向运动。
求
基础振动时传给机器的力的最大值。
8.图示系统中,质量m上受激励力为
F(t)=sinωt+10sin10ωt时,
求质量m的稳态响应。
W
K
K
9.一般振动问题,如图所示:
三类振动问题分别是:
(1)振动分析,已
知,求;
(2)振动环境预测或载荷分析,已知,求;
(3)系统识别,已知,求。
10. 振动问题的分类,根据自由度数分,有,和。
11. 简谐振动x=Asin(ωt+φ),其中的振动位移为,振幅为,
振动频率为为,振动的初相位为
12. n个自由度振动系统有个固有频率,有个固有振型,
其中的第i阶主振型有个节点。
13.图示单自由度系统,在0时刻时,M的位移是x.。
,初速度为0,求系统的固有频率和
在初始条件下的系统的稳态响应。
14.图示系统中,质量m上受激励力为
F(t)=sinωt时,
求质量m的稳态响应。