当前位置：文档之家 › 信息学奥赛NOIP动态规划入门

信息学奥赛NOIP动态规划入门

  • 格式：pptx
  • 大小：2.22 MB
  • 文档页数：37

下载文档原格式

  / 37

合集下载

NOIP普及讲座3-动态规划1

NOIP普及讲座3-动态规划1


• （1）划分阶段：按照问题的时间或空间特征，把 问题分为若干个阶段； • （2）确定状态和状态变量：将问题发展到各个阶 段时所处的各种情况用不同状态表示出来； • （3）确定决策并写出状态转移方程：一般是根据 相邻两个阶段各状态之间的关系来确定决策； • （4）寻找边界条件：给出的状态转移方程是一个 递推式，必须有一个递推的边界条件； • （5）编写程序。
从搜索到动态规划
引例（数塔问题）
• 设有一个三角形的数塔，顶点为根结点，每个结 点有一个整数值。从顶点出发，可以向左走或向 右走，从根结点13出发向左、向右的路径长度可 以是： 13 13－11－7－14－7，其和为52 11 8 13－11－12－14－13，其和为63 • 若要求从根结点开始， 26 7 12 请找出一条路径，使 8 15 6 14 路径之和最大,输出路 24 7 13 径的长度。 12
输入 第一行是一个整数N（不超过15），表示导弹数。 第二行包含N个整数，为导弹依次飞来的高度（雷达给出的高 度数据是不大于30000的正整数）。 输出 一个整数，表示最多能拦截的导弹数。 样例输入 8 389 207 155 300 299 170 158 65 样例输出 6
【问题分析】 状态： f[i]代表打下第i颗导弹最多能打多少颗导弹 方程： f[i]=max(f[j])+1(1<=j<i)且第i颗导弹的高度要高于 第j颗导弹的高度
11
• 【问题分析】 （1）贪心法
• 【问题分析】 （2）搜索：
• 【问题分析】 （3）动态规划：
Байду номын сангаас
13 11 12 7 14 7 15 8 26 8 24
6 12
13
11
CCF中学生计算机程序设计能力评级信息学奥赛NOIP动态规划算法及优化

CCF中学生计算机程序设计能力评级信息学奥赛NOIP动态规划算法及优化

1 ≤ n ≤ 5000, 1 ≤ b, ci, di ≤ 109。
动态规划算法 及优化
Codeforces 815C Karen and Supermarket
背包类问题 数据结构优化 决策单调性 计数
可以发现依赖关系形成了一棵树，因此可以考虑在树上
进行 DP。需要注意的是，本题中物品的价格可能非常大， 但是每个物品的收益只有 1，因此我们 DP 时第二维表示的 应当是买了多少个物品。
动态规划算法 及优化
背包类问题 数据结构优化 决策单调性 计数
动态规划算法及优化
动态规划算法 及优化
背包问题
背包类问题 数据结构优化 决策单调性 计数
01 背包：n 个物品，每个物品有价格 ci 及收益 wi ，问 m 元最多能得到多少收益。
完全背包：n 种物品，每种物品有价格 ci 及收益 wi，并 且每种物品能买无限个，问 m 元最多能得到多少收益。
n ≤ 500, m ≤ 4000, di ≤ 100。
动态规划算法 及优化
BZOJ4182 Shopping
背包类问题 数据结构优化 决策单调性 计数
先考虑我们知道必选某个节点时怎么做。可以把这个点
当成根，那么问题就转化为了一个树上依赖背包问题。 考虑用和上一题类似的方法进行 DP。令 fi,j 表示在节点
背包类问题 数据结构优化 决策单调性 计数
树上依赖背包其实还有一个经典的做法。考虑一边 dfs 一边 DP。dfs 到节点 i 的时候，我们先把 DP 数组拷贝一份， 表示不选 i 的子树时的背包。接着我们用多重背包的做法加 入商品 i，并且强制至少买一个商品 i。然后我们再依次 dfs 进每个儿子的子树中，回溯到 i 时我们就得到了在 i 的子树 中买了物品的背包，把它与原先拷贝的背包取个 max 即可。 这样复杂化即可。这样加入一个物品的复杂度是 O(m)
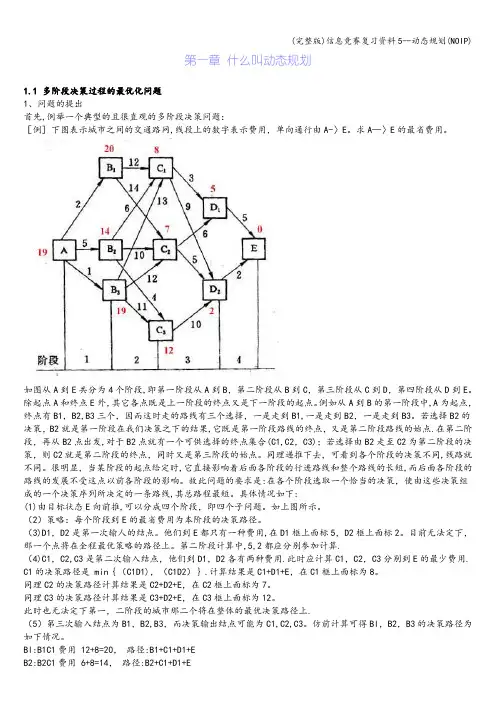
(完整版)信息竞赛复习资料5--动态规划(NOIP)

(完整版)信息竞赛复习资料5--动态规划(NOIP)

第一章什么叫动态规划1.1 多阶段决策过程的最优化问题1、问题的提出首先,例举一个典型的且很直观的多阶段决策问题：［例] 下图表示城市之间的交通路网,线段上的数字表示费用，单向通行由A-〉E。

求A—〉E的最省费用。

如图从A到E共分为4个阶段,即第一阶段从A到B，第二阶段从B到C，第三阶段从C到D，第四阶段从D到E。

除起点A和终点E外，其它各点既是上一阶段的终点又是下一阶段的起点。

例如从A到B的第一阶段中,A为起点，终点有B1，B2,B3三个，因而这时走的路线有三个选择，一是走到B1,一是走到B2，一是走到B3。

若选择B2的决策，B2就是第一阶段在我们决策之下的结果,它既是第一阶段路线的终点，又是第二阶段路线的始点.在第二阶段，再从B2点出发,对于B2点就有一个可供选择的终点集合(C1,C2，C3)；若选择由B2走至C2为第二阶段的决策，则C2就是第二阶段的终点，同时又是第三阶段的始点。

同理递推下去，可看到各个阶段的决策不同,线路就不同。

很明显，当某阶段的起点给定时,它直接影响着后面各阶段的行进路线和整个路线的长短,而后面各阶段的路线的发展不受这点以前各阶段的影响。

故此问题的要求是:在各个阶段选取一个恰当的决策，使由这些决策组成的一个决策序列所决定的一条路线,其总路程最短。

具体情况如下:(1)由目标状态E向前推,可以分成四个阶段，即四个子问题。

如上图所示。

（2）策略：每个阶段到E的最省费用为本阶段的决策路径。

（3)D1，D2是第一次输人的结点。

他们到E都只有一种费用,在D1框上面标5，D2框上面标2。

目前无法定下，那一个点将在全程最优策略的路径上。

第二阶段计算中,5,2都应分别参加计算.（4)C1，C2,C3是第二次输入结点，他们到D1，D2各有两种费用.此时应计算C1，C2，C3分别到E的最少费用. C1的决策路径是 min｛（C1D1)，（C1D2）｝.计算结果是C1+D1+E，在C1框上面标为8。

最新信息学奥赛NOIP动态规划入门教学文案

最新信息学奥赛NOIP动态规划入门教学文案


阶段4
阶段4：F(D1)=3;F(D2)=4;F(D3)=3 阶段3：F(C1)=min{F(D1)+C1到D1的路径长度，
F(D2)+C1到D2的路径长度} F(C2)……
阶段1
阶段2
阶段3
阶段4
我们把F(x) 称为当前x的状态；
在这个例子中每个阶段的选择依赖当前的状态，又 随即引起状态的转移，一个决策序列(E –D3-C4B2-A)就是在变化的状态中产生的，故有“动态”的 含义。
方各有个数，从第一行的数开始，每次可以选择
向左下或是向右下走一格，一直走到最下行，把
沿途经过的数全部加起来。如何走才能使得这个
和尽量大？。
穷举？贪心？搜索？
数字三角形
数组存储
格子编号
深搜（递归实现）
程序清单： void f( int i, int j )
{ s=s+a[ i ][ j ]; if ( i==4 ) if ( s > max ) max = s; else { f( i+1, j ); s=s-a[ i+1] [ j ]; f( i+1, j+1); s=s-a[ i+1] [ j+1]; }
if( i == n ) return a[i][ j];
if(d[ i ][ j ] >= 0) return d[i][ j];
d[i][ j] = a[i][ j]+max(solve ( i+1, j ), solve ( i+1 , j +1) );
这样做是正确的， 可惜时间效率太低 。低效的原因在于
重复计算。
重复计算
dt(1,1) 的调用关系树
《noip动态规划讲解》PPT课件

《noip动态规划讲解》PPT课件

位同学排成合唱队形。 合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1，2…，K，
他 们 的 身 高 分 别 为 T1，T2，…，TK， 则 他 们 的 身 高 满 足 T1<...<Ti>Ti+1>…>TK(1<=i<=K)。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可 以使得剩下的同学排成合唱队形。 【输入文件】
精选PPT
5
设有由n个不相同的整数组成的数列，记为: a(1)、a(2)、……、a(n)且a(i)<>a(j) (i，j<=n) 例如3，18，7，14，10，12，23，41，16，24。 若存在i1<i2<i3< … < ie 且有a(i1)<a(i2)< … <a(ie)则称为长度为e的不下降序列。如上例中3， 18，23，24就是一个长度为4的不下降序列，同时 也有3，7，10，12，16，24长度为6的不下降序列。 最长的不下降序列就是求长度最长的子序列。
If f[j]<f[j-a[i]]+b[i] Then f[j]:=f[j-a[i]]+b[i];
精选PPT
15
Sample Problem4
金明的预算方案（NOIp2006）
【问题描述】 金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己
专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购 买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。今天一早，金明 就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个 主件的。如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件 可以有0个、1个或2个附件。附件不再有从属于自己的附件。金明想买的东西很 多，肯定会超过妈妈限定的N元。于是，他把每件物品规定了一个重要度，分为 5等：用整数1~5表示，第5等最重要。他还从因特网上查到了每件物品的价格 （都是10元的整数倍）。他希望在不超过N元（可以等于N元）的前提下，使每 件物品的价格与重要度的乘积的总和最大。
信息学奥赛——动态规划实例分析及程序实现

信息学奥赛——动态规划实例分析及程序实现

全国青少年信息学奥林匹克联赛动态规划实例分析及程序实现一、数字三角形（图３.１－１）示出了一个数字三角形。

请编一个程序计算从顶至底的某处的一条路径，使该路径所经过的数字的总和最大。

●每一步可沿左斜线向下或右斜线向下走；●1＜三角形行数≤100；●三角形中的数字为整数0，1，…99；输入数据：由INPUT.TXT文件中首先读到的是三角形的行数。

在例子中INPUT.TXT表示如下：573 88 1 02 7 4 44 5 2 6 5输出数据：把最大总和（整数）写入OUTPUT.TXT文件。

上例为：30７３８８１０２７４４４５２６５（图３.１－１）二、算法分析只要对该题稍加分析，就可以得出一个结论：如果得到一条由顶至底的某处的一条最佳路径，那么对于该路径上的每一个中间点来说，由顶至该中间点的路径所经过的数字和也为最大。

因此该题是一个典型的多阶段决策最优化的问题。

我们采用动态规划中的顺推解法。

按三角形的行划分阶段。

若行数为n, 则可把问题看作一个n-1个阶段的决策问题。

从始点出发，依顺向求出第一阶段、第二阶段，……，第n-1阶段中各决策点至始点的最佳路径，最终求出始点到终点的最佳路径。

设：ｆk（Ｕk）━━从第ｋ阶段中的点Ｕk至三角形顶点有一条最佳路径，该路径所经过的数字的总和最大，ｆk（Ｕk）表示为这个数字和；由于每一次决策有两个选择，或沿左斜线向下，或沿右斜线向下，因此设Ｕk1━━ｋ－１阶段中某点Ｕk沿左斜线向下的点；Ｕk2━━ｋ－１阶段中某点Ｕk沿右斜线向下的点；ｄk（Ｕk1）━━ｋ阶段中Ｕk1的数字；ｄk（Ｕk2）━━ｋ阶段中Ｕk2的数字；因而可写出顺推关系式ｆk（Ｕk）＝ｍａｘ｛ｆk-1（Ｕk）＋ｄk（Ｕk1），ｆk-1（Ｕk）＋ｄk（Ｕk2）｝ｆ0（Ｕ0）＝０；Ｋ＝１，２，３，４，……ｎ经过一次顺推，便可分别求出由顶至底Ｎ个数的Ｎ条路径，在这Ｎ条路径所经过的Ｎ个数字和中，最大值即为正确答案。

三、程序分析根据上述顺推关系，我们编写程序如下：Program ID1P1;ConstMaxn = 100;TypeNode = RecordVal, Tot : Integer{ 当前格数字; 从[1,1]到当前格的路径所经过的数字和} End;VarList : Array [1..Maxn, 1..Maxn] of Node; { 计算表} N, Max, { 行数, 最大总和}I, J : Integer; { 辅助变量}Fi : Text; { 文件变量}Procedure Init;BeginAssign(Fi, 'INPUT.TXT'); { 文件名和文件变量连接} Reset(Fi); { 文件读准备}Readln(Fi, N); { 读三角形行数}For i := 1 to N Do { 读入三角形各格的数字}For j := 1 to i DoRead(Fi, List[i, j].Val);Close(Fi)End;{init}Procedure Main;BeginList[1, 1].Tot := List[1, 1].Val; { 从[1,1]位置开始往下顺推}For i := 2 to N DoFor j := 1 to i Do BeginList[i, j].Tot := -1; { 从[1,1]至[i,j]的数字和初始化}If (j <> 1) And(List[i - 1, j - 1].Tot + List[i, j].Val > List[i, j].Tot) ThenList[i, j].Tot := List[i - 1, j - 1].Tot + List[i, j].Val;{ 若从[i-1,j-1]选择右斜线向下会使[1,1]至[i,j]的数字和最大,则决策该步} If (j <> i) And(List[i - 1, j].Tot + List[i, j].Val > List[i, j].Tot) ThenList[i, j].Tot := List[i - 1, j].Tot + List[i, j].Val{ 若从[i-1,j]选择左斜线向下会使[1,1]至[i,j]的数字和最大,则决策该步} End; {for}Max := 1;{ [1,1]至底行各点的N条路径所经过的数字和中,选择最大的一个输出} For i := 2 to N DoIf List[N, i].Tot > List[N, Max].Tot ThenMax := i;Writeln(List[N, Max].Tot) { 输出最大总和}End; {main}BeginInit; { 读入数字三角形}Main { 求最大总和}End.{main}二、Problem : 打鼹鼠Contents: 有个n*n个格子，在m个时间点上的不定格子里有数量不等的鼹鼠出现，机器人每次只能向前后左右移动一个格子，问最多机器人能打多少鼹鼠？(n<=1000, m<=10000)Type: 动态规划Difficulty: 2Source: HNOI2004_day_*_*Solution :a)记得学OI不到几个月，高一刚上来就做的这道题..着实郁闷了半天,有一个思路是开1000*1000 的数组乱搞…忘了可以过几个来着..b)又翻到这道题的时候是2月份了..发现f[i]表示：如果机器人最后打死的老鼠是第i只，这种情况下机器人最多可以打死多少老鼠。

全国信息学奥赛NOI培训教程(最新整理)

全国信息学奥赛NOI培训教程(最新整理)

全国信息学奥赛NOI培训教程（最新整理）使用”视图"—--—"文档结构图"可大大方便阅读本文档目录计算机基础知识-———--—-—--——---———-———---—-——6 第一章计算机基础常识第二章操作系统简介第三章计算机网络第四章计算机信息安全基础知识Pascal 语言-——————————--—-————---——-———-——-——-19Pascal语言概述与预备知识第一章开始编写pascal语言程序第二章Pascal语言基础知识第三章顺序结构程序设计第四章选择结构程序设计第五章循环结构程序设计第六章数组与字符串第七章函数和过程第八章子界与枚举类型第九章集合类型第十章记录与文件类型第十一章指针第十二章程序调试常用算法与策略———-——--———-—--—-———-————————--——--56第一章算法的概念第二章递归第三章回溯第四章排序第五章查找第六章穷举策略第七章贪心算法第八章分治策略数据结构-————-—-——-——--——--————---———-—————101第一章什么是数据结构第二章线性表第三章栈第四章队第五章树第六章图动态规划-——————---———----———-—-—-—---—-—-——144第一章什么叫动态规划第二章用动态规划解题第三章典型例题与习题第四章动态规划的递归函数法第五章动态规划分类1数学知识及相关算法第一章有关数论的算法第二章高精度计算第三章排列与组合第四章计算几何第五章其它数学知识及算法图论算法-————---—--—---—————-—-——-—-—-—————192第一章最小生成树第二章最短路径第三章拓扑排序（AOV网）第四章关键路径(AOE网）第五章网络流第六章图匹配搜索算法与优化——-———————————--——-—-—---—-—--—-—-—218第一章双向广度优先搜索第二章分支定界法第三章A＊算法青少年信息学奥林匹克竞赛情况简介信息学奥林匹克竞赛是一项旨在推动计算机普及的学科竞赛活动,重在培养学生能力，使得有潜质有才华的学生在竞赛活动中锻炼和发展。

信息学奥赛简介NOIP及C++基础知识第一讲

信息学奥赛简介NOIP及C++基础知识第一讲


6. p=(a+b+c)/2;
思考：语句5和6可以交换吗？
7. s=sqrt(p*(p-a)*(p-b)*(p-c));
8. printf("%0.3lf\n",s);
9. return 0;
10.}
1. #include<cstdio> 2. #include<cmath> 3. int main(){
渡河的方法与步骤： 第一步：农夫带 过河 第二步：农夫划船回来 第三步：农夫带 过河 ……
猜数字（1..1000)
• 回答大了或小了
猜 生 日？
月？ 日？
二分法
每次舍弃“一半”不符合条件的情况，逐渐缩小范围， 最后找到问题的解
枚举算法
基本思想： 按照问题本身的性质，一一列举出该问题所有可
能的解，并根据问题的条件对各解进行逐个检验，从 中挑选出符合条件的解，舍弃不符合条件的解。
开，最后用分号结束。
知识点1：格式化输入函数scanf
格式： scanf("格式化字符串"，地址列表);
说明： 1）地址列表中给出各变量的地址（即变量名的前面加“&”
符号）。 2）格式控制符由%和格式符组成，作用是将要输入的字符
按指定的格式输入，如%d，%lf等 3）格式字符和和变量的类型一一对应：类型和个数一致。
{
double r,s;
//定义实型变量
scanf("%lf",&r);
//输入r的值，&符号不能漏掉
s=PI*r*r;
//计算圆的面积
printf("%.2lf\n",s); //显示计算结果，结果保留2位小数
noip动态规划1

noip动态规划1

一个加法 F[n] = F[n-1]+F[n-2] 即可。
➢ 例１ 最短路径问题。下图中给出一个地图，地图中每个顶点代表 一个城市，两个城市之间的连线表示道路，连线上的数值代表道路 的长度。现在，想从城市A到城市E，怎样走路程最短，最短路程 的长度是多少？
➢ 现在，我们想从城市A到达城市E。怎样走才能使得路径最短，最 短路径的长度是多少？
fk ( s k )op g fk t 1 T k ( s k ,u k ) ,u k
u k D k ( s k )
fn(sn) 某个初始值 （边界条件）
➢ 其中Sk是第k段的某个状态，Uk是从Sk出发的允许决 策集合Dk(Sk)中的一个决策，Tk(Sk,Uk)是定义在数值 x和决策Uk上的一个函数，而函数opt表示最优化， 根据具体问题分别表示为max或min。例中最短路径
noip动态规划1
第一章 回归分析的性质
➢动态规划
➢ 与递归程序相类，将对问题求解分解为对子问 题求解；不同之处在于把子问题的解存起来， 用空间换时间。
➢ 例：Fibonacci数
F(0)=0; F(1)=1; F(n)=F(n-1)+F(n-2); 递归: F(n-1)和F(n-2)分别求到底一次 动态规划：用数组将前n-1个数存起来，每次只用
由常识知，最短路有一个重要特性：最短路上的任一（后部）子
路也是最短的。即
若 A---B3---C1---D1---E 是 A---E 最短，
则
B3---C1---D1---E 是 B3---E 最短路，
C1---D1---E 也是C1---E 最短路.
利用最短路的这一特性，构造寻找 A---E 最短路的方法，即为：
D3
noip知识点

noip知识点

noip知识点NOIP（全国青少年信息学奥林匹克竞赛）是中国信息学竞赛中最重要的赛事之一，也是许多计算机爱好者所瞩目的目标。

对于参加NOIP的选手来说，掌握一些基础的知识点是非常必要的。

本文将从准备阶段、算法设计、数据结构、编程语言和调试技巧等方面来谈谈NOIP的一些重要知识点。

在准备阶段，一个好的准备是成功的一半。

首先，选手要熟悉并掌握编程语言（如C++）的基础知识，能够完成常见的输入输出操作、常见的数据类型和运算符的使用。

其次，选手要了解算法的基本概念和思想，掌握一些常见的算法模板，如贪心算法、动态规划等。

此外，选手还需要刷一些NOIP历年真题，熟悉考试的题型和难度。

通过反复练习，选手可以提高自己的解题能力和编程速度。

在算法设计方面，选手需要学会分析问题，找出问题的规律和特点。

常见的算法设计思想有：贪心算法、分治算法和动态规划。

贪心算法是指每一步都选择当前状况下最优的解，但不能保证一定能得到全局最优解；分治算法是将问题分解成若干个相似的子问题，通过解决子问题来解决原问题；动态规划是通过维护中间状态，避免重复计算，从而提高效率。

选手需要熟练运用这些算法思想，灵活应用于不同的问题场景。

数据结构也是NOIP中一个重要的考点。

常见的数据结构有：数组、链表、栈、队列、树和图等。

选手需要了解不同数据结构的特点和应用场景，能够根据问题需求选择合适的数据结构并进行操作。

例如，对于查找问题，可以使用二分查找；对于维护顺序的问题，可以使用排序算法等。

选手还需要了解常见的数据结构算法，如快速排序、堆排序等，以及这些算法的时间复杂度和空间复杂度。

对于编程语言的掌握，选手需要熟悉编程语言的语法和特性。

C++是NOIP常用的编程语言，具有强大的功能和高效的执行速度。

选手需要掌握C++的基本语法、函数的定义和调用、类的使用等。

此外，选手还应该了解一些C++的高级特性，如模板、STL（标准模板库）等，以便在解题过程中能够灵活运用。

信息学奥赛中的动态规划

信息学奥赛中的动态规划



有什么想法没？
为什么不记录下相同的状态时的最优策略呢？

在使用相同的容量和处理了相同的物品后，剩下的搜索过程应该是相 同的，假如共有n个物品，我们已经处理了m个，那么还需要处理的物 品数量就是n-m，但是在背包剩余体积为v的情况下，剩下n-m个物品 产生的最优解应该是相同的，这样就可以简化搜索过程，但是前面的 怎么办呢？前面的当然要最好的！ 于是，我们得到一条结论： 在其他状态均相同的情况下，选择最好的总是对的！
有没有更好的方法呢？

背包问题可以用一维数组解决你造吗？ 由于重量没有负数，所以可以直接向后转移，而且不用向下 转移了，但这样就有可能重复处理一个物品，怎么办？ 很简单，改变下方向，从后往前处理就可以啦~

至此，01背包完满完成~
难度增加的背包问题
更加喜(sang)闻(xin)乐(bing)见(kuang)的背包问题
金明的预算方案(NOIP2006提高组)
题目描述 Description 金明今天很开心，家里购臵的新房就要领钥匙了，新房里 有一间金明自己专用的很宽敞的房间。更让他高兴的是， 妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布 臵，你说了算，只要不超过N元钱就行”。今天一早，金明 就开始做预算了，他把想买的物品分为两类：主件与附件 ，附件是从属于某个主件的，右图就是一些主件与附件的 例子。 如果要买归类为附件的物品，必须先买该附件所属的主件 。每个主件可以有0个、1个或2个附件。附件不再有从属 于自己的附件。金明想买的东西很多，肯定会超过妈妈限 定的N元。于是，他把每件物品规定了一个重要度，分为5 等：用整数1~5表示，第5等最重要。他还从因特网上查到 了每件物品的价格（都是10元的整数倍）。他希望在不超 过N元（可以等于N元）的前提下，使每件物品的价格与重 要度的乘积的总和最大。 设第j件物品的价格为v[j]，重要度为w[j]，共选中了k 件物品，编号依次为j1，j2，……，jk，则所求的总和为： v[j1]*w[j1]+v[j2]*w[j2]+ …+v[jk]*w[jk]。（其 中*为乘号） 请你帮助金明设计一个满足要求的购物单。

noi知识大纲

NOI（全国青少年信息学奥林匹克竞赛）知识大纲是针对NOI系列比赛制定的大纲，旨在帮助学生和老师明确学习目标和教学方向。

NOI大纲将知识点分为三个级别：入门级、提高级和NOI级，分别适用于不同的竞赛阶段。

以下是NOI知识大纲的主要内容：1. 入门级知识点：适用于CSP-J（入门级选手），主要涉及计算机基础、编程语言、数据结构与算法等方面。

2. 提高级知识点：适用于NOIP、CSP-S（提高级选手），包括算法策略、数据结构、算法设计与分析、编程实践等。

3. NOI级知识点：适用于NOI及以上竞赛，包括IOI、CTS、NOI冬令营、国家集训队集训等。

主要涉及高级算法、复杂问题分析与解决、竞赛技巧等。

NOI大纲还对知识点进行了难度系数的标注，帮助学生和老师更好地了解各知识点的学习难度。

同时，大纲对知识点进行了术语规范化的调整，使得选手和教师能够更加清晰地理解竞赛知识体系。

为了更好地备战NOI竞赛，选手可以根据NOI大纲进行有针对性的学习和训练，确保在学习过程中能够全面掌握各个级别的知识点。

同时，多参加模拟赛和真题训练，提高自己的编程能力和解题技巧，才能在竞赛中取得好成绩。

各个级别知识点的具体内容。

入门级知识点：计算机基础：计算机组成原理、操作系统、计算机网络等。

编程语言：C/C++语言基础，如变量、数据类型、运算符、控制结构等。

数据结构与算法：数组、链表、栈、队列、树、图等基本数据结构，以及排序、查找等基本算法。

提高级知识点：算法策略：动态规划、贪心算法、分治算法、回溯算法等。

数据结构：高级数据结构，如字典树、并查集、线段树、树状数组等。

算法设计与分析：算法复杂度分析、数学证明等。

编程实践：编程技巧、调试方法、代码优化等。

NOI级知识点：高级算法：涉及图论、字符串、动态规划、组合数学等高级算法领域。

复杂问题分析与解决：涉及各种竞赛题目类型，如构造题、计算题、优化题等。

竞赛技巧：比赛策略、时间管理、心理素质等。

信息学奥赛系列课程(三阶段)-2019_02_21_第3版

信息学奥赛NOIP系列课程（三阶段）第一阶段C++语言及数据结构与算法基础课本:1、信息学奥赛一本通+训练指导教程C++版第五版--2017年出版(两本）第1部分C++语言（50课时）适于：零基础的初中或高中的学生，当然有C语言或scratch、Python语言基础更好授课：相关内容讲授+实例+题目现堂训练（每次课2-3题，题目较大可能是1题）第1章C++语言入门（2－3课时）第2章顺序结构程序设计（6课时）第3章程序控制结构（3课时）NOIP2017复赛普及组第1题成绩https:///problem-12334.htmlNOIP2018复赛普及组第1题标题统计方法一https:///problem-12393.htmlNOIP1996普及组第1题https:///WDAJSNHC/article/details/83513564https:///yuyanggo/article/details/47311665第4章循环结构（5课时）NOIP2018复赛普及组第1题标题统计方法二https:///problem-12393.htmlNOIP2016复赛普及组第1题买铅笔https:///problem-12121.htmlNOIP2015复赛普及组第1题金币/ch0105/45/NOIP2002复赛普及组第1题级数求和/ch0105/27/NOIP2013复赛普及组第1题计数问题https:///problem-11005.html?tdsourcetag=s_pcqq_aiomsgNOIP2012复赛普及组第1题质因数分解/ch0105/43/NOIP2011复赛普及组第1题数字反转/ch0105/29/NOIP2010复赛普及组第1题数字统计https:///problem-10012.htmlNOIP1999普及组第1题Cantor表/ch0201/8760/https:///problemnew/show/P1014NOIP1997普及组第1题棋盘问题https:///problemnew/show/P1548NOIP1995普及组复赛第1题https:///secret_zz/article/details/76862335https:///WDAJSNHC/article/details/83513896NOIP1997普及组第2题数字三角形https:///ber_bai/article/details/76722379第5章数组（9－10课时）NOIP2014复赛普及组第1题珠心算测验https:///problem-12091.htmlNOIP2009复赛普及组第1题多项式输出/ch0113/39/NOIP2006复赛普及组第1题明明的随机数/ch0110/09/NOIP2005复赛普及组第1题陶陶摘苹果/ch0106/02/NOIP2004复赛普及组第1题不高兴的津津/ch0109/03/NOIP2003年普及组第1题乒乓球/ch0113/37/NOIP1998年普及组第1题三连击（枚举）https:///problemnew/show/P1008NOIP1995普及组复赛第2题方阵填数https:///WDAJSNHC/article/details/79381876NOIP1996普及组第2题格子问题https:///WDAJSNHC/article/details/79381843?utm_source=blogxgwz5NOIP2016复赛普及组第2题回文日期https:///problem-12122.htmlhttps:///problemnew/show/P2010NOIP2015普及组第2题P2670扫雷游戏/ch0108/14/https:///problemnew/show/P2670https:///problem-12105.htmlNOIP2012普及组第2题_P1076寻宝/ch0112/06/https:///problemnew/show/P1076第6章函数（5课时）NOIP2008复赛普及组第1题ISBN号码/ch0107/29/NOIP2000提高组第1题P1017进制转换https:///problemnew/show/P1017NOIP2000普及组第1题计算器的改良https:///problemnew/show/P1022https:///yuyanggo/article/details/47856785https:///u012773338/article/details/41749421NOIP2018普及组第2题龙虎斗https:///problemnew/show/P5016https:///problem-12394.html机器翻译【1.12编程基础之函数与过程抽象07】Noip2010提高组第1题/ch0112/07/Vigenère密码【1.12编程基础之函数与过程抽象08】Noip2012提高组第1题/ch0112/08/笨小猴【1.9编程基础之顺序查找06】NOIP2008提高组第1题/ch0109/06/第7章文件和结构体（5课时）NOIP2011复赛提高组第1题铺地毯/ch0109/14/NOIp2008提高组第2题火柴棒等式https:///problemnew/show/P1149https:///Mr_Doublerun/article/details/52589778第8章指针及其应用（8课时）第9章C++实用技巧与模版库（5课时）NOIP2007复赛普及组第1题奖学金/ch0110/04/NOIP2017复赛普及组第2题图书管理员（STL、排序）https:///problem-12335.htmlhttps:///problemnew/show/P3955NOIP1999普及组第2题回文数https:///problemnew/show/P1015***模拟NOIP2017年提高组第2题时间复杂度（模拟）https:///problem-12333.htmlhttps:///problemnew/show/P3952NOIP2011普及组第3题P1309瑞士轮（模拟、快拍、归并排序）/ch0401/4363/https:///problemnew/show/P1309NOIP2018复赛普及组第3题摆渡车(模拟)https:///problem-12395.htmlhttps:///problemnew/show/P5017NOIP2016普及组第3题海港（port）--枚举https:///problemnew/show/P2058NOIP2006年提高组第3题P1065作业调度方案(模拟)https:///problemnew/show/P1065NOIP2013提高组第4题P1969积木大赛（模拟贪心）https:///problem-12071.htmlhttps:///problemnew/show/P1969NOIP2014提高组第4题P2038无线网络发射器选址（模拟）https:///problemnew/show/P2038第2部分NOIP基础算法（39课时）第1章高精度计算（2-3课时）【例1.6】回文数(Noip1999):8088/problem_show.php?pid=1309NOIP2003普及组第4题P1045麦森数(分治、高精度运算)https:///problemnew/show/P1045NOIP2005普及组第4题P1050循环(高精度运算、数论、快速幂) https:///problemnew/show/P1050第2章数据排序（3课时）NOIP2014复赛普及组第1题珠心算测验https:///problem-12091.html第3章递推算法（2-3课时）1314：【例3.6】过河卒(Noip2002):8088/problem_show.php?pid=1314NOIP2011普及组第4题P1310表达式的值(栈、表达式计算、递推) https:///problemnew/show/P1310NOIP2011提高组第6题P1315观光公交(递推分析、贪心)https:///problemnew/show/P1315第4章递归算法（2-3课时）【例4.6】数的计数(Noip2001普及组第1题):8088/problem_show.php?pid=1316第5章搜索与回溯算法（2-3课时）NOIP2015day1T3_斗地主P2668斗地主https:///problemnew/show/P2668NOIP2017年普及组第3题棋盘https:///problemnew/show/P3956https:///problem-12336.htmlNOIP2015年提高组第2题P2661信息传递（Tarjen bfs/dfs（图论））https:///problem-12107.htmlhttps:///problemnew/show/P2661NOIP2016年提高组第2题天天爱跑步（Lca/dfs（图论）树结构最近公共祖先）https:///problem-12208.htmlhttps:///problemnew/show/P1600NOIP2000普及组第4题P1019单词接龙(深搜)https:///problemnew/show/P1019NOIP2000年提高组第3题单词接龙(DFS,字符串,模拟)https:///problemnew/show/P1019NOIP2014普及组第4题P2258子矩阵(搜索或dp)https:///problemnew/show/P2258NOIP2018年提高组第3题P5021赛道修建(搜索深度优先搜索)https:///problem-12392.htmlhttps:///problemnew/show/P5021第6章贪心算法（3课时）删数问题（NOIP1994）P1106删数问题https:///problemnew/show/P1106:8088/problem_show.php?pid=1321NOIP2010复赛普及组第2题接水问题/ch0109/15/NOIP1999年提高组第1题导弹拦截https:///problemnew/show/P1020https:///huashanqingzhu/p/6728652.html https:///qq_33927580/article/details/51853345 https:///Darost/article/details/52086240https:///yuyanggo/article/details/48739029NOIP2002提高组第1题均分纸牌P1031均分纸牌https:///problemnew/show/P1031NOIP2007普及组第2题_P1094纪念品分组https:///problem-12007.htmlhttps:///problemnew/show/P1094NOIP2008普及组第2题_P1056排座椅https:///problem-12008.htmlhttps:///problemnew/show/P1056NOIP2012年提高组第2题国王游戏（贪心、排序后列出）https:///problemnew/show/P1080NOIP2013年提高组第2题P1966火柴排队(逆序对、贪心、排序) https:///problem-12083.htmlhttps:///problemnew/show/P1966NOIP2010普及组第4题P1199三国游戏(贪心)https:///problemnew/show/P1199第7章分治算法（3课时）NOIP2001提高组第1题P1024一元三次方程求解/ch0204/7891/https:///problemnew/show/P1024NOIP2011年提高组第2题P1311选择客栈(二分查找)https:///problemnew/show/P1311NOIP2003普及组第4题P1045麦森数(分治、高精度运算)https:///problemnew/show/P1045第8章广度优先搜索算法（2-3课时）NOIP2002年提高组第2题P1032字串变换(BFS,字符串)https:///problemnew/show/P1032NOIP2013提高组第6题P1979华容道(广搜\最短路:图论)https:///problem-12212.htmlhttps:///problemnew/show/P1979第9章动态规划（15课时）第一节动态规划的基本模型1260：【例9.4】拦截导弹(NOIP1999):8088/problem_show.php?pid=1260NOIP2013普及组第3题P1982小朋友的数字https:///problemnew/show/P1982NOIP2003复赛普及组第2题_P1043数字游戏数字游戏（Game.cpp）https:///problemnew/show/P1043NOIP2006年提高组第2题P1064金明的预算方案(资源分配DP,构造) https:///problemnew/show/P1064NOIP2013普及组第3题P1982小朋友的数字（动态规划、子段和）https:///problemnew/show/P1982NOIP2007普及组第3题P1095守望者的逃离(动态规划或枚举）https:///problemnew/show/P1095NOIP2009普及组第4题P1070道路游戏(动态规划)https:///problemnew/show/P1070NOIP2004年提高组第3题P1091合唱队形(子序列DP)https:///problemnew/show/P1091第二节背包问题NOIP2018提高组第2题货币系统https:///problem-12391.htmlNOIP2006普及组第2题_P1060开心的金明题解https:///problemnew/show/P1060NOIP2005普及组第3题P1048采药(0/1背包)/ch0206/1775/https:///problem-12062.htmlhttps:///problemnew/show/P1048NOIP2001普及组第4题P1049装箱问题(0/1背包或枚举)https:///problemnew/show/P1049NOIP2014年提高组第3题P1941飞扬的小鸟(背包DP)https:///problem-12087.htmlhttps:///problemnew/show/P1941第三节动态规划经典题NOIP2000年提高组第2题P1018乘积最大（资源分配DP）https:///problemnew/show/P1018NOIP2000普及组第3题P1018乘积最大(划分动态规划)https:///problemnew/show/P1018NOIP2001年提高组第2题P1025数的划分（资源分配DP,多维状态DP）/ch0206/8787/https:///problemnew/show/P1025NOIP2001年提高组第3题统计单词个数(资源分配DP,字符串) https:///problemnew/show/P1026NOIP2005年提高组第2题P1052过河(子序列DP,贪心优化)https:///problemnew/show/P1052NOIP2010年提高组第2题P1541乌龟棋(动态规划优化)https:///problemnew/show/P1541NOIP2014年提高组第2题P1351联合权值（动态规划搜索图结构树形DP图的遍历遍历（图论）,二次展开式）https:///problem-12086.htmlhttps:///problem-12210.htmlhttps:///problemnew/show/P1351NOIP2008普及组第3题P1057传球游戏（动态规划）https:///problemnew/show/P1057NOIP2012普及组第3题摆花（动态规划）https:///problem-12366.htmlhttps:///problemnew/show/P1077NOIP2002普及组第4题P1002过河卒(棋盘动态规划)https:///problemnew/show/P1002NOIP2008年提高组第3题P1006传纸条(多维状态DP动态规划图结构最短路网络流)https:///problem-12110.htmlhttps:///problemnew/show/P1006NOIP2000提高组第4题方格取数(多维状态DP)/ch0206/8786/https:///problem-12186.htmlhttps:///problemnew/show/P1004NOIP2002提高组第4题P1034矩形覆盖(动态规划/贪心/搜索剪枝) /ch0405/1793/https:///problemnew/show/P1034第3部分NOIP数据结构（19课时）第1章栈（3课时）NOIP2011普及组第4题P1310表达式的值(栈、表达式计算、递推) https:///problemnew/show/P1310第2章队列（3-5课时）NOIP2016普及组第3题海港（port）https:///problemnew/show/P2058第3章树（3课时）第一节树的概念第二节二叉树第三节堆及其应用NOIP2015普及组第4题P2672推销员(枚举、堆)https:///problemnew/show/P2672NOIP2001普及组第3题P1030求先序排列(树的遍历)https:///problemnew/show/P1030NOIP2004普及组第3题P1087FBI树(二叉树的遍历)https:///problemnew/show/P1087第4章图论算法（8课时）第一节基本概念第二节图的遍历第三节最短路径算法NOIP2002普及组第3题P1037产生数(最短路、高精度)https:///problemnew/show/P1037NOIP2012普及组第4题P1078文化之旅(搜索、最短路(图论)、动规) https:///problemnew/show/P1078NOIP2009年提高组第3题P1073最优贸易(最短路:图论）https:///problemnew/show/P1073NOIP2001提高组第4题P1027Car的旅行路线(最短路,实数处理)https:///problemnew/show/P1027NOIP2007提高组第4题P1099树网的核(最短路,树的直径)https:///problemnew/show/P1099第四节图的连通性问题第五节并查集NOIP2010年提高组第3题P1525关押罪犯(二分答案或并查集)https:///problemnew/show/P1525NOIP2017提高组第4题P3958奶酪（数据结构树结构并查集）https:///problem-12205.htmlhttps:///problemnew/show/P3958第六节最小生成树第七节拓朴排序与关键路径NOIP2013普及组第4题P1983车站分级(图论、拓扑排序) https:///problemnew/show/P19831390：食物链【NOI2001】:8088/problem_show.php?pid=1390NOIP2004年提高组第2题P1090合并果子(最优哈夫曼树，排序，贪心)https:///problemnew/show/P1090NOIP2013年提高组第3题P1967货车运输(最大生成树,最近公共祖先)https:///problemnew/show/P1967NOIP2018提高组第4题P5022旅行（搜索图结构）https:///problem-12397.htmlhttps:///problemnew/show/P5022NOIP2018提高组第6题P5024保卫王国(图结构)https:///problem-12399.htmlhttps:///problemnew/show/P50242、啊哈！算法--2014-06（35-50小时）第二阶段算法与数据结构提高1、《信息学奥赛一本通·提高篇》（80-100课时，不一定一次都讲完）第一部分基础算法第1章贪心算法NOIP2002提高组第1题P1031均分纸牌(贪心,模拟)https:///problemnew/show/P1031NOIP2010普及组第3题P1158导弹拦截（排序+枚举，贪心）https:///problemnew/show/P1158NOIP2012提高组第6题P1084疫情控制(二分答案，贪心，倍增)https:///problemnew/show/P1084第2章二分与三分NOIP2010年提高组第3题P1525关押罪犯(二分答案或并查集)https:///problemnew/show/P1525NOIP2008提高组第4题P1155双栈排序(枚举,贪心/二分图)https:///problemnew/show/P1155NOIP2015提高组第4题P2678跳石头（二分查找、二分答案）https:///problem-12198.htmlhttps:///problemnew/show/P2678第3章深搜的剪枝技巧NOIP2018普及组第4题对称二叉树（搜索树结构深度优先搜索）https:///problem-12396.htmlhttps:///problemnew/show/P5018NOIP2011年提高组第3题P1312Mayan游戏(深搜、剪支)https:///problemnew/show/P1312NOIP2015年提高组第3题P2668斗地主(分情况,剪枝)https:///problemnew/show/P2668NOIP2003提高组第4题P1041传染病控制(随机贪心/搜索剪枝)https:///problemnew/show/P1041NOIP2004提高组第4题P1092虫食算（搜索搜索与剪枝）https:///problem-12414.htmlhttps:///problemnew/show/P1092第4章广搜的优化技巧NOIP2017年普及组第3题棋盘（搜索搜索与剪枝广度优先搜索）https:///problemnew/show/P3956https:///problem-12336.htmlNOIP2009提高组第4题P1074靶形数独(搜索优化)https:///problemnew/show/P1074NOIP2010提高组第4题P1514引入水域（广搜+动态规划，判断有解和无解）https:///problemnew/show/P1514第二部分字符串算法第1章哈希表第2章KMP算法第3章Trie字典树第4章AC自动机NOIP2005提高组第4题P1054等价表达式(字符串,抽样检测,表达式) /practice/1686/https:///problemnew/show/P1054NOIP2008普及组第4题P1058立体图(字符输出)https:///problemnew/show/P1058NOIP2006普及组第3题P1061Jam的计数法(数学、字符串)https:///problemnew/show/P1061NOIP2007年提高组第2题字符串的展开（字符串模拟）https:///problem-11016.htmlhttps:///problemnew/show/P1098NOIP2003年提高组第2题P1039侦探推理(枚举,模拟,字符串)https:///problemnew/show/P1039NOIP2011普及组第2题_P1308统计单词数/ch0112/05/https:///problemnew/show/P1308第三部分图论第1章最小生成树第2章最短路径NOIP2016年提高组第3题P1850换教室(最短路/Dp)https:///problemnew/show/P1850NOIP2017年提高组第3题P3953逛公园(搜索图结构记忆化搜索最短路)https:///problem-12337.htmlhttps:///problemnew/show/P3953NOIP2014提高组第5题P1351联合权值(遍历,二次展开式)https:///problem-12086.htmlhttps:///problemnew/show/P1351第3章SPFA算法的优化第4章差分约束系统第5章强连通分量第6章割点和桥第7章欧拉回路第四部分数据结构第1章树状数组第2章RMQ问题第3章线段树NOIP2012提高组第5题P1083借教室(枚举、线段树、树状数组、二分) https:///problem-12069.htmlhttps:///problemnew/show/P1083NOIP2017提高组第6题P3960列队(数据结构平衡树线段树)https:///problem-12339.htmlhttps:///problemnew/show/P3960第4章倍增求LCANOIP2015提高组第6题P2680运输计划(Lca或线段树)https:///problem-12213.htmlhttps:///problemnew/show/P2680第5章树链剖分第6章平衡树Treap第五部分动态规划第1章区间类型动态规划NOIP2007年提高组第3题P1005矩阵取数游戏(区间DP,高精度)https:///problemnew/show/P1005第2章树型动态规划NOIP2003年提高组第3题P1040加分二叉树(树,区间DP)https:///problemnew/show/P1040第3章数位动态规划第4章状态压缩类动态规划NOIP2017提高组第5题P3959宝藏(动态规划搜索贪心状态压缩DP枚举)https:///problem-12340.htmlhttps:///problemnew/show/P3959NOIP2016提高组第6题愤怒的小鸟(状态压缩动态规划)https:///problemnew/show/P2831第5章单调队列优化动态规划NOIP2016提高组第5题蚯蚓(单调队列)https:///Mrsrz/p/7517155.htmlhttps:///m0_38083668/article/details/82557281NOIP2017普及组第4题P3957跳房子（数据结构动态规划单调队列队列）https:///problem-12338.htmlhttps:///problemnew/show/P3957第6章利用斜率优化动态规划NOIP2012年提高组第3题P1081开车旅行(离线深搜，动态规划、倍增)https:///problemnew/show/P1081NOIP2015提高组第5题P2679子串(Dp+滚动数组)https:///problemnew/show/P2679第六部分数学基础第1章快速幂第2章素数第3章约数第4章同余问题第5章矩阵乘法第6章组合数学NOIP2009年提高组第2题P1072Hankson的趣味题(初等数论,质因数,组合数学)https:///problemnew/show/P1072NOIP2006提高组第4题P10662^k进制数(动态规划/组合数学,高精度) https:///problemnew/show/P1066NOIP2011提高组第4题P1313计算系数（组合、二项式系数）/practice/4036/https:///problemnew/show/P1313NOIP2016提高组第4题P2822组合数问题（杨辉三角）https:///problemnew/show/P2822第7章博弈论NOIP2004普及组第4题P1088火星人(数学:排列、stl)https:///problemnew/show/P1088NOIP2009普及组第3题P1069细胞分裂（数论）https:///problemnew/show/P1069NOIP2000提高组第1题P1017进制转换(初等代数,找规律)https:///problemnew/show/P1017NOIP2001提高组第1题P1024一元三次方程求解(数学,枚举,实数处理) /ch0204/7891/https:///problemnew/show/P1024NOIP2003普及组第3题P1044栈(数学:卡特兰数）https:///problemnew/show/P1044NOIP2018年提高组第2题货币系统(数论)https:///problem-12391.htmlhttps:///problemnew/show/P5020NOIP2014年普及组复赛第3题螺旋矩阵（数学分析）https:///problem-12341.htmlhttps:///problemnew/show/P2239NOIP2015年普及组第3题求和（数学：数列）https:///problemnew/show/P2671NOIP2004普及组第4题P1088火星人(数学:排列、stl)https:///problemnew/show/P1088NOIP2005普及组第4题P1050循环(高精度运算、数论、快速幂) https:///problemnew/show/P1050NOIP2006普及组第4题P1062数列(数学:进制转换)https:///problemnew/show/P1062NOIP2007普及组第4题P1096$Hanoi$双塔问题(数学、高精度) https:///problemnew/show/P1096NOIP2016普及组第4题P2119魔法阵(数学分析、枚举)https:///problemnew/show/P2119NOIP2002年提高组第3题P1033自由落体(数学,物理,模拟,实数处理) https:///problemnew/show/P1033NOIP2005年提高组第3题P1053篝火晚会(置换群,贪心)https:///problemnew/show/P1053NOIP2012提高组第4题P1082同余方程（数论、递归，扩展欧几里得）https:///problemnew/show/P1082NOIP2011提高组第5题P1314聪明的质监员(部分和优化)/practice/4037/https:///problemnew/show/P1314NOIP2013提高组第5题P1970花匠(序列)https:///problem-12072.htmlhttps:///problemnew/show/P1970NOIP2018提高组第5题P5023填数游戏（DP）https:///problem-12398.htmlhttps:///problemnew/show/P50232、NOIP历年真题讲解（30-50小时）---包括初赛和复赛3、《骗分导论》（推荐指数：5颗星）--电子书（可以作为学习的参考资料）第三阶段算法与数据结构高级专题（选择性学习）1、信息学奥赛之数学专题2、高级数据结构(C++版)3、动态规划专题注：上面的内容也可能要交叉的进行讲解在线题库：1、OpenJudge在线题库/2、信息学奥赛一本通在线评测系统:8088/3、洛谷https:///4、啊哈编程/tiku/5、《信息学奥赛一本通（提高篇）》在线评测OJhttps://loj.ac/注：本系列课程将根据行业发展状况，及时优化调整课程内容，具体课程设置以实际为准。

全国信息学奥林匹克联赛NOIP计算机基础知识

全国信息学奥林匹克联赛NOIP计算机基础知识全国信息学奥林匹克联赛（National Olympiad in Informatics in Provinces，简称NOIP）是全国性的计算机竞赛，旨在选拔优秀的信息学选手并培养他们的计算机基础知识。

下面我们将从计算机基础知识的概念、NOIP的意义以及如何提高计算机基础知识等方面进行论述。

一、计算机基础知识的概念计算机基础知识是指计算机科学与技术领域中的一系列基本概念、原理和技能。

它包括计算机硬件和软件基础、数据结构与算法、操作系统、计算机网络、数据库等方面的知识。

掌握计算机基础知识是进行信息学竞赛和计算机相关工作的基础，也是计算机科学与技术教育的重要组成部分。

二、NOIP对计算机基础知识的要求NOIP作为全国性的信息学竞赛，要求选手具备扎实的计算机基础知识。

在NOIP的赛题中，涉及到算法设计与实现、数据结构、操作系统等多个方面的知识。

选手需要通过分析问题、设计算法、编写代码的方式来解决问题。

因此，提高计算机基础知识对参加NOIP具有重要意义。

三、NOIP对个人发展的意义NOIP能够促进个人对计算机基础知识的深入理解和掌握。

通过参加NOIP，选手需要深入学习和应用各种算法和数据结构，拓宽自己的计算机知识面。

这不仅有助于提高个人的编程能力和解决问题的能力，还培养了选手的团队协作精神和创新思维能力。

此外，NOIP的竞赛经历对于参加高考、申请国内外名校、从事与计算机相关工作都有积极的影响。

四、提高计算机基础知识的方法1. 学习课程教材：通过认真学习计算机基础知识的课程教材，了解计算机硬件和软件的基本原理，掌握重要的数据结构和算法，熟悉常用的操作系统和网络知识。

2. 刷题练习：通过大量的练习，提高编程能力和解题能力，掌握各种常用算法和数据结构的实现方法。

3. 参加竞赛训练：积极参加NOIP等信息学竞赛，通过实际解决问题的训练，提高计算机基础知识的应用能力和创新能力。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

最大连续子序列和（Maximum Continuous Subsequence Sum）

转移方程： dp[i]= max { A[i] , dp[i-1] + A[i] } 边界：dp[0]=A[0] 代码： dp[0] = A[0]; for (int i=1 ; i < n ; i++){ dp[i]= max ( A[i] , dp[i-1] + A[i] ) }
阶段4：F(D1)=3;F(D2)=4;F(D3)=3 阶段3：F(C1)=min{F(D1)+C1到D1的路径长度， F(D2)+C1到D2的路径长度} F(C2)……
阶段1 阶段2 阶段3
阶段4
我们把F(x) 称为当前x的状态； 在这个例子中每个阶段的选择依赖当前的状态，又 随即引起状态的转移，一个决策序列(E –D3-C4B2-A)就是在变化的状态中产生的，故有“动态”的 含义。
如何选呢？
其中较大的一个，再加上a(i,j)的值就是d[i,j]。
d[i,j]=a[i,j]+max{d[i+1,j],d[i+1,j+1]}
思考：边界条件？
思想：从上向下思考，从底向上计算
24 16
8
13
23
21
数字三角形
方法1：递推计算
void solve () { int i , j; for( j = 1; j <= n; j ++) d[n][j ] = a[n][j]; for(i = n -1; i >= 1; i - -) for( j = 1; j <= i; j ++) d[i][j ] = a[i][j ] + max (d[i +1][ j], d[i +1][ j +1]); }
格子编号
分析：考察 设以格子(i,j)为首的“子三角形”的最大和为d[i,j] （我们将不加区别的把这个子问题(subproblem) 本 身也称为d[i,j]），则原问题的解是d[1,1]我们关心 的是从某处出发到底部的最大和： 从(2,1)点出发的最大和记做d[2,1]; 从(2,2)点出发的最大和记做d[2,2]; 从（1，1）出发有两种选择（2，1）或（2，2） 在已知d[2,1]和d[2,2]的情况下，应选择较大的一个。
方法2：递归计算
dt(1,1) 的调用关系树
方法3：记忆化搜索
这个方法和直接递归非常类似，但加入了记忆 化(memoization) ，保证每个结点只访问一次。
// initially , all d[i][j] are -1
int solve ( int i , int j)
{ if( i == n ) return a[i][j]; if(d[ i ][ j ] >= 0) return d[i][j]; d[i][j] = a[i][j]+max(solve ( i+1, j ), solve ( i+1 , j +1) ); return d[i][j]; } 时间复杂度O（n2） 不必事先确定各状态的计算顺序
问题转换为dp[0],dp[1],…,dp[n-1]中的最大 者。
最大连续子序列和（Maximum Continuous Subsequence Sum）
dp[i]表示以A[i]作为末尾的连续序列的最大和（ A[i]必须作为序列的末尾）; 只有两重情况： 1、这个最大和的连续序列只有一个元素，即以A[i] 开始，以A[i]结尾；最大和就是A[i]本身。 2、这个最大和的连续序列有多个元素，从前面某处 A[p]开始（p<i)；一直到A[i]结尾。 也就是 dp[i-1]+A[i]; A[p]+…+A[i-1]+A[i]=dp[i-1]+A[i];
程序清单： void f( int i, int j ) { s=s+a[ i ][ j ]; if ( i==4 ) if ( s > max ) max = s; else { f( i+1, j ); s=s-a[ i+1] [ j ]; f( i+1, j+1); s=s-a[ i+1] [ j+1]; } }
需要考虑两个部分：一是递推的顺序，二是递归边界（也是递推 起点）。
•从直接递归和后两种方法的比较可以看出：重叠子问题
(overlapping subprob-lems) 是动态规划展示威力的关键。
考察：d(1,1)；d(2,1)；d(2,2)……这些问题 的共性：都是求从一个位置出发到底部的最大 值；是一个共同的问题。
思考：考虑更一般的情况，当前位置（i，j）看 成一个状态， 定义状态（i，j）的指标函数d(i，j) 为从 格子（i，j）出发时能得到的最大和（包含格 子（i，j）本身的值）。 原题的解：？d（？，？）
d[1，1]
格子编号
思考：观察不同状态如何转移的。 从格子（i，j）出发有两种决策。 如果（i，j）格子里的值为a (i ，j) 向左走需要求“从（i+1，j）出发的最大和”， 就是d[i+1，j]。 向右走需要求“从（i+1，j+1）出发的最 大和”，就是d[i+1，j+1]。
时间复杂度O（n2） 在计算d[i][j]前，d[i+1][j],d[i+1][j+1]已计算好了！
int solve ( int i , int j) { if (i == n) return a[i][j]; else return a[i][j] + max( solve (i+1,j), solve (i+1 , j +1)); }这样做是正确的， 可惜时间效率太低。 低效的原因在于重 复计算。 重复计算
最短路径问题---求A到E的最短路的长度
穷举？贪心？搜索？
阶段1 阶段2 阶段3
阶段4
思考： 仔细观察本图路径的特殊性，可以分成4个阶段： 第一阶段：A经过A-B1或A-B2到B 第二阶段：B1有三条路通……；B2有两条通路……
阶段1
阶段2
阶段3
阶段4
思考：倒着推；设F(x)表示x到E的最短路径的长度
样例输入： 8 389 207 155 300 299 170 158 65 样例输出： 6（最多能拦截的导弹数）
题目分析： 给定一个正整数序列，求出其中最长下降序列：例如： 389 207 155 300 299 170 158 65 389 300 299 170 158 65 所求的问题：从某一个位置开始的最长下降序列 寻找一个状态？
d(2,1) d(2,2)
重叠子问题
考察：d(1,1)；d(2,1)；d(2,2）；可以发现 每个子问题结果都是最优的。
d(2,Байду номын сангаас)
d(2,2)
最优子结构
什么是动态规划？
动态规划是求解包含重叠子问题的最优化方法 动态规划的性质？ 子问题重叠性质：在用递归算法自顶向下对问题进行
求解是，每次产生的子问题并不总是新问题，有些子问题 可能被重复计算多次。动态规划算法利用此性质，对每个 子问题只计算一次，然后将其结果保存起来以便高效重用。 最优化子结构性质：若问题的最优解所包含的子问题 的解也是最优的，则称该问题具有最优子结构性质（即满 足最优化原理）。 能用动态规划解决的求最优解问题，必须满足最优解 的每个局部也都是最优的
{ 第1列} {对角线}
思考：最后的结果：？？ max{d[n][1],d[n][2]……d[n][n]}
这种方法本 质就是递推
例3:最大连续子序列和（Maximum Continuous Subsequence Sum）



给定k个整数的序列{A1,A2,...,Ak }，其任意连续 子序列可表示为{ Ai, Ai+1, ...,Aj }，其中 1 <= i <= j <= k。最大连续子序列是所有连续子序 中元素和最大的一个。 例如给定序列{ -2, 11, -4, 13, -5, -2 }，其 最大连续子序列为{11,-4,13}，最大连续子序列 和即为20。 暴力枚举？时间复杂度为？能优化吗？复杂度？
向上考虑，观察不同状态如何转 移的。从格子（i，j）出发有两 种决策。
d(i,j)为：取d(i-1,j) 和d(i-1,j-1)中较 大的一个加上a(i,j)的和。
思考：边界情况：？？
d[1][1]=a[1][1] d[i][1]=d[i-1][1]+a[i][1] d[i][i]=d[i-1][i-1]+a[i][i]
例2: 数字三角形 一个由非负数组成的三角形，第一行只有 一个数，除了最下行之外每个数的左下方和右下 方各有个数，从第一行的数开始，每次可以选择 向左下或是向右下走一格，一直走到最下行，把 沿途经过的数全部加起来。如何走才能使得这个 和尽量大？。 穷举？贪心？搜索？
数字三角形
数组存储
格子编号
深搜（递归实现）
1.动态规划比穷举具有较少的计算次数 从数塔问题可以看出，层数为k时， 穷举算法求路径的条数2k-1 动态规划计算的次数为: k (k 1) 2
穷举最多计算到n=20，动态规划可以算到n=100 2.递归需要很大的栈空间，而动规的递推法不需要栈 空间；使用记忆化搜索比较容易书写程序。
思考： 还有一种思考方法，从下
动态规划初步
引入：走楼梯
已知一个楼梯有n级，从下往上走，一步可以走一级 ，也可以走两级，走到第N级楼梯有多少种走法？ 【输入格式】 一行一个整数n。 【输出格式】 一行仅有一整数，表示走到第n级有多少种走法。 【输入样例】 【输出样例】 2 2 【数据规模】 对100%的数据满足：0 ＜ n ≤ 30。