信息学奥赛NOIP普及组历届试题分析
- 格式:ppt
- 大小:112.50 KB
- 文档页数:32


NOIP普及组初赛历年试题及答案阅读题篇阅读程序写结果(共4 题,每题8 分,共计32 分)阅读程序题是得分的关键,因为不是让你上机去运行程序,所以要一步步地读程序,记录相关变量值的变化情况。
因为程序的运行结果只有输出语句才有输出,所以只写出输出语句的结果。
有时要找出规律才能写出结果,特别是循环次数多的情况,另外要注意边界值,不能多算一步也不能少算一步。
解决这类问题的关键在于能够分析程序的结构以及程序段的功能。
常见的有列表法、画流程图法等。
完成这类题目的方法和步骤如下:1、从头到尾通读程序,大致把握程序的算法、找出这个题目的即这个程序想干什么。
抓住了它,不仅得出答案变得较容易,而且对自己的结果也会比较有信心。
2、通过给程序分段、理清程序的结构和层次,达到读懂程序的目的。
3、阅读程序中特别注意跟踪主要变量的值的变化,可以用列表的方法,了解变量变化和程序的运行结果,注意发现规律。
所谓列表法,就是将各变量名作为表头,在程序的执行过程中,将各变量值的变化记录在相应变量的下方。
4、按照程序中输出格式的要求,写出运行结果,并带着结果回到程序进行检查。
在阅读程序时,要特别注意过程、函数所完成的子任务以及和主程序之间的参数传递关系。
在阅读程序中,比较好的方法是首先阅读主程序,看其需要调用的过程或函数是什么,最后要求输出变量是什么;其次在阅读程序中,将较长的程序分成几个程序段(特别注意循环结构、判断结构),阅读理解各程序段的功能以及各程序之间的关联。
NOIP2011-1.#include<iostream>using namespace std;int main(){int i,n,m,ans;cin>>n>>m;i=n;ans=0;while(i<=m){//从i=10~20,共循环计数11次ans+=i;//每次循环,ans累加一次i 值i++;}cout<<ans<<endl;//此时ans值应为(10+20)*11/2,即165 return 0;}输入: 10 20输出: 165NOIP2011-2.#include<iostream>#include<string>using namespace std;int main(){string map= "2223334445556667778889999";//数组中元素位置是从0开始计数的string tel;int i;cin>>tel;for(i=0;i<tel.length();i++)if((tel[i]>='0') && (tel[i]<='9') )//如果输入的tel是0~9,直接输出tel值cout<<tel[i];else if( (tel[i]>='A') && (tel[i]<='Z'))cout<<map[tel[i]-'A'];//如果输入的tel是A~Z,则输出一个map数组中对应的元素//输出元素在map数组中位置为“输入字母与A的ASCII码的差值”//如果输入的是其他字符,比如“-”,则不符合循环条件,无输出cout<<endl;return 0;}输入: CCF-NOIP-2011输出: 22366472011NOIP2011-3.#include<iostream>#include<cstring>using namespace std;const int SIZE= 100;int main(){int n,i,sum,x,a[SIZE];cin>>n;memset(a,0,sizeof(a));for(i=1;i<=n;i++){cin>>x;a[x]++;}//循环结束时数组中的值为:a[1]=1,a[2]=2,a[3]=3,a[4]=2,a[5]=1,a[6]=2 i=0;sum=0;while(sum<(n/2+1)){//当sum值大于等于n/2+1,即sum>=6的时候,循环结束i++;sum+=a[i];}cout<<i<<endl;//输出循环结束时i 的值(不是sum的值)return 0;}输入:114 5 6 6 4 3 32 3 2 1输出: 3NOIP2011-4.#include<iostream>using namespace std;int solve(int n,int m){int i,sum;if(m==1) return 1;//递归函数solve(i,m)中m=1时返回函数值为1sum=0;for(i=1;i<n;i++)//递归函数solve(i,m)中i=1时不循环,sum=0sum+= solve(i,m-1);return sum;//可递归求得sum=solve(1,3)+(2,3)+(3,3)+(4,3)+(5,3)+(6,3)}int main(){int n,m;cin>>n>>m;cout<<solve(n,m)<<endl; //输出函数值,即sum值return 0;}输入: 7 4输出: 20NOIP2012-1.#include<iostream> using namespace std; int a, b, c, d, e, ans; int main(){cin>>a>>b>>c;d = a+b;e = b+c;ans = d+e;//ans=a+b+b+ccout<<ans<<endl;return 0;}输入: 1 2 5输出: 10NOIP2012-2.#include<iostream>using namespace std;int n, i, ans;int main(){cin>>n;ans = 0;for (i = 1; i <= n; i++)if (n % i == 0)ans++;//统计1~18中18的因数个数cout<<ans<<endl;return 0;}输入: 18输出: 6NOIP2012-3.#include<iostream>using namespace std;int n, i, j,a[100][100];int solve(int x,int y){int u, v;if(x == n)return a[x][y];//递归边界:当x=5时,solve(5,y)=a[5][y]u= solve(x + 1, y);v= solve(x + 1, y + 1);if(u > v)return a[x][y] + u;elsereturn a[x][y] + v;//用递归最终求得solve(1,1)=a[1][1]+solve(2,2)=2+12=14 }int main(){cin>>n;for(i = 1; i <= n; i++) for (j = 1; j <= i; j++) cin>>a[i][j];cout<<solve(1,1)<<endl; return 0;}输入:52-1 42 -1 -2-1 6 4 03 2 -1 5 8输出: 14NOIP2012-4.#include<iostream>#include<string> using namespace std; int n, ans, i, j;string s;char get(int i){if(i < n)return s[i];elsereturn s[i-n];//i<8时,get(i)返回s[i];i>=8时,get(i)返回s[i-8],从第一个开始返回}int main(){cin>>s;n= s.size();ans= 0;for(i = 1; i <= n-1; i++){for (j = 0; j <= n-1; j++)if (get(i+j) < get(ans+j)){ans = i;break;}else if (get(i+j) > get(ans+j))break;}//此循环执行完毕,ans=7for(j = 0; j <= n-1; j++)cout<<get(ans+j);//1,ans+j<8,输出s[7+0];2,ans+j=8,输出s[8-8];3,ans+j=9,输出s[9-8]……cout<<endl;return 0;}输入: CBBADADA输出: ACBBADADNOIP2013-1.#include<iostream>using namespace std;int main(){inta, b;cin>>a>>b;cout<<a<<"+"<<b<<"="<<a+b<<endl;return 0;}//输出:3+5=8输入: 3 5输出: 3+5=8NOIP2013-2.#include<iostream>using namespace std;int main(){int a, b, u, i, num;cin>>a>>b>>u;num = 0;for (i = a; i <= b; i++)if ((i % u) == 0)num++;//1-100之间有多少数是15的倍数cout<<num<<endl;return 0;}输入: 1 100 15输出: 6NOIP2013-3.#include<iostream>using namespace std;int main(){const int SIZE = 100;int n, f, i, left, right, middle, a[SIZE]; cin>>n>>f;for (i = 1; i <= n; i++)cin>>a[i];left = 1;right = n;do {middle= (left + right) / 2;if(f <= a[middle])right = middle;elseleft = middle + 1;}while (left < right);// middle=6,17>a[6],则left=7// middle=9,17<a[9],则right=9 // middle=8,17<a[8],则right=8// middle=7,17=a[7],则right=7 // left=right,直接输出leftcout<<left<<endl;return 0;}输入:12 172 4 6 9 11 15 1718 19 20 21 25 输出: 7NOIP2013-4.#include<iostream>using namespace std;int main(){constint SIZE = 100;intheight[SIZE], num[SIZE], n, ans; cin>>n;for(int i = 0; i < n; i++) {cin>>height[i];num[i] = 1;for (int j = 0; j < i; j++) {if ((height[j] < height[i]) && (num[j] >= num[i]))num[i] = num[j]+1;}}//两两相比,得出num[0], num[1], num[2], num[3], num[4], num[5]ans= 0;for(int i = 0; i < n; i++) {if (num[i] > ans) ans = num[i];}//得出num中最大值,即在数组height中第几位数值最大cout<<ans<<endl;return 0;}输入:62 53 11 12 4输出: 4不懂算法?跟踪变量!列表模拟!遇到递归?画树形图!注意边界!找到规律了?还会流程图?恭喜你,32分到手了!NOIP2014-1.#include <iostream>using namespace std;int main(){int a, b, c, d, ans;cin>> a >> b >> c;d = a - b; //将a-b=-1赋值给d a = d + c; //将d+c=3赋值给a ans = a * b; //ans=a*b=3*3=9 cout<< "Ans = " << ans << endl; return 0;}输入:2 3 4输出: Ans=9NOIP2014-2.#include <iostream>using namespace std;int fun(int n){if (n == 1)return 1; //边界fun(1)=1if (n == 2)return 2; //边界fun(2)=2 return fun(n - 2) - fun(n - 1); } //fun(n)=fun(n-2)-fun(n-1) int main(){int n;cin >> n;cout << fun(n) << endl;//fun(7)=fun(5)-fun(6)=-11 return 0;}输入: 7输出: -11NOIP2014-3.#include <iostream>#include <string>using namespace std;int main(){int i, len;getline(cin, st);len = st.size();for(i = 0; i < len; i++){if (st[i] >= 'a' && st[i] <= 'z')st[i] = st[i] - 'a' + 'A';} //如果字符串st中字母小写,则替换成大写cout<< st << endl;return 0;}输入: Hello, my name is Lostmonkey.输出: HELLO, MY NAME IS LOSTMONKEY.NOIP2014-4.#include <iostream>using namespace std;const int SIZE =100;int main(){int p[SIZE];int n, tot, i, cn;cin>> n;for(i = 1; i <= n; i++)p[i] = 1; //p[1]-p[30]中所有元素赋值1 for(i = 2; i <= n; i++){if (p[i] == 1)tot++; //计数cn = i * 2; //找出2-30中所有2i while (cn <= n) {p[cn] = 0;cn += i; //找出2-30中所有3i}}//对2-30中素数计数,并输出个数cout<< tot << endl;return 0;}输入: 30输出: 10NOIP2015-1.#include <iostream>using namespace std;int main(){int a, b, c;a = 1;b = 2;c = 3;if(a > b) //不符合循环条件,不执行if(a > c)cout << a << ' ';elsecout << b << ' ';cout << c << endl;return 0;}输出: 3NOIP2015-2.#include <iostream>using namespace std;struct point{int x;int y;}; //声明结构体类型pointint main(){int a, b, c;struct EX{int a;int b;point c;}e; //声明结构体类型EXe.a = 1; //结构体变量e中变量ae.b = 2; //结构体变量e中变量be.c.x = e.a + e.b;//结构体变量e中的结构体变量c中的变量x e.c.y = e.a * e.b;//结构体变量e中的结构体变量c中的变量y cout << e.c.x << ','<< e.c.y << endl; return 0;}输出: 3,2NOIP2015-3.#include <iostream>#include <string>using namespace std;int main(){string str;int i;int count;count = 0;getline(cin, str);for(i = 0; i < str.length();i++)if(str[i] >= 'a' &&str[i] <= 'z')count++; //统计字符串中小写字母数量cout << "It has "<< count << " lowercases" << endl; return 0;}输入: NOI2016will be held in Mian Yang.输出: It has 18 lowercasesNOIP2015-4.#include <iostream>#include <string>using namespace std;void fun(char *a, char *b){a = b;(*a)++;} //指针题int main(){char c1, c2, *p1, *p2;c1 = 'A';c2 = 'a';p1 = &c1;p2 = &c2;fun(p1, p2);//p1=p2=&c2,把c2的地址赋值给指针变量p1 //p1++,则有&’a’+1=&’b’, 所以,c2=’b’,cout << c1 << c2<< endl;return 0;}输出: AbNOIP2016-1.#include <iostream>using namespace std;int main(){int max, min, sum, count = 0;int tmp;cin>> tmp;if(tmp == 0)return0; //如果输入的数字是0,程序退出max= min = sum = tmp;count++;while(tmp != 0) {cin>> tmp;if(tmp != 0) {sum += tmp; //求和count++;//计数if(tmp > max)max = tmp; //找出最大值if(tmp < min)min = tmp; //找出最小值}}cout<< max << "," << min << ","<< sum / count << endl; //输出“最大值, 最小值, 平均值”return 0;}输入: 1 2 3 4 5 6 0 7输出: 6,1,3NOIP2016-2.#include <iostream>using namespace std;int main(){int i = 100, x = 0, y = 0;while (i > 0) {i--;x = i % 8;if (x == 1)y++;} //统计1-100中有多少数是“8的倍数+1”cout << y << endl;return 0;}输出: 13NOIP2016-3.#include <iostream>using namespace std;int main(){int a[6] = {1, 2, 3, 4, 5, 6};int pi = 0;int pj = 5;int t , i;while(pi < pj) {t =a[pi];a[pi]= a[pj];a[pj]= t;pi++;pj--;} //把数组a[6]中的数字顺序颠倒过来for(i = 0; i < 6; i++)cout<< a[i] << ",";cout<< endl;return 0;}输出: 6,5,4,3,2,1,NOIP2016-4.#include <iostream>using namespace std;int main(){int i, length1, length2; strings1, s2;s1= "I have a dream.";s2 = "I Have A Dream."; length1 = s1.size();length2 = s2.size();for (i = 0; i < length1; i++)if (s1[i] >= 'a' && s1[i]<= 'z') s1[i] -= 'a' - 'A';//把s1里的小写字母全部换成大写for (i = 0; i < length2; i++)if (s2[i] >= 'a' && s2[i]<= 'z') s2[i] -= 'a' - 'A';//把s2里的小写字母全部换成大写if (s1 == s2)cout << "=" <<endl;else if (s1 > s2)cout << ">" <<endl;elsecout << "<" <<endl;return 0;}输出: =。







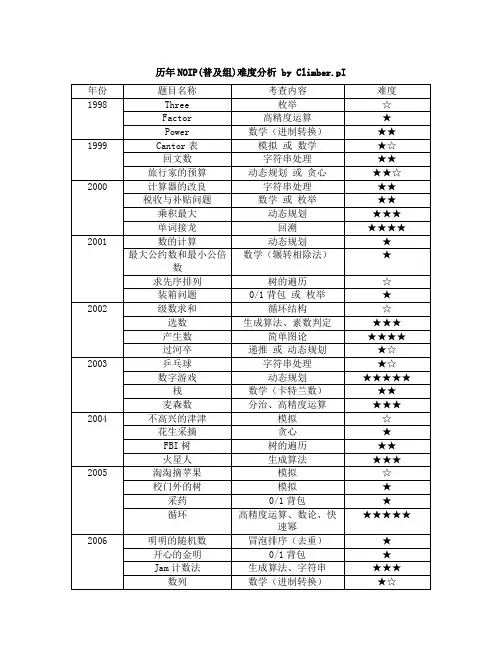
历年NOIP(普及组)难度分析 by Climber.pINOIP提高组复赛考察点详细分析动态规划:12 模拟:10数学:5 图论:4搜索:4 构造:3贪心:2【动态规划】平均难度系数:0.55此项为历届NOIP考察次数最多的知识点。
主要有 1.区间模型 2.子序列模型 3.资源分配模型以及一些简单的多维状态设计技巧。
动态规划可以与图,树,高精度等知识点配合出题。
【模拟】平均难度系数:0.76平均每届NOIP都会出现1个模拟题。
这种题一般算法很简单,需要选手细心理解题目意思,注意细节。
考察选手的代码实现能力。
【数学】平均难度系数:0.46需要掌握质数及其性质,基础的实属操作,加法原理和乘法原理。
此类题需要选手对数学规律的灵感。
【图论】平均难度系数:0.50历届考察点基本上都是 1.最短路问题和 2.特殊图的性质。
特殊图包括树,拓扑图,二分图等。
历届NOIP在图论上的考察并不是很多。
【搜索】平均难度系数:0.38历届搜索题一般都比较难,搜索算法本身简单,于是题目会提高选手对其他方面的要求。
主要有搜索优化和模拟。
写搜索题时应该以尽量多得分为目标。
【构造】平均难度系数:0.27构造类题目一般没有明确的算法,需要选手仔细分析题目的实质,并得出解法。
这个解法通常不是唯一的。
有时一个好的贪心可以得相当多的分。
有时搜索剪枝可以很大的提高效率。
同样以多得分为目标。
【【贪心】平均难度系数:0.75此类题需要选手对算法的直觉,贪心正确性一旦被证明,通常题目就简单了。

NOIP普及组初赛历年试题及答案求解题篇问题求解:每次共2题,每空5分,共计10分。
每题全部答对得 5 分,没有部分分。
注:答案在文末在NOIP初赛问题求解中,经常会遇到排列组合问题。
这一类问题不仅内容抽象,解法灵活,而且解题过程极易出现“重复”和“遗漏”的错误,这些错误甚至不容易检查出来,所以解题时要注意不断积累经验,总结解题规律。
解答排列组合问题,首先必须认真审题,明确是属于排列问题还是组合问题,或者属于排列与组合的混合问题,其次要抓住问题的本质特征,灵活运用基本原理和公式进行分析解答。
同时还要注意讲究一些策略和技巧,比如采用分类、分步、捆绑等方法,也可以借助表格、方程等工具,使一些看似复杂的问题迎刃而解。
NOIP2011-1. 每份考卷都有一个8位二进制序列号。
当且仅当一个序列号含有偶数个1时,它才是有效的。
例如,0000000、01010011都是有效的序列号,而11111110不是。
那么,有效的序列号共有______个。
NOIP2011-2. 定义字符串的基本操作为: 删除一个字符、插入一个字符和将一个字符修改成另外一个字符这三种操作。
将字符串A变成字符串B的最少操作步数,称为字符串A到字符串B的编辑距离。
字符串“ ABCDEFG ”到字符串“BADECG ”的编辑距离为_______。
NOIP2012-1. 如果平面上任取n 个整点(横纵坐标都是整数) ,其中一定存在两个点,它们连线的中点也是整点,那么n至少是_____。
NOIP2012-2. 在NOI期间,主办单位为了欢迎来自全国各地的选手,举行了盛大的晚宴。
在第十八桌,有5名大陆选手和5名港澳选手共同进膳。
为了增进交流,他们决定相隔就坐,即每个大陆选手左右相邻的都是港澳选手、每个港澳选手左右相邻的都是大陆选手。
那么,这一桌共有_____种不同的就坐方案。
注意:如果在两个方案中,每个选手左边相邻的选手均相同,则视为同一个方案。
NOIP2013-1. 7 个同学围坐一圈,要选2 个不相邻的作为代表,有_____种不同的选法。
noip普及组初赛试题导语:NOIP(全国青少年信息学奥林匹克竞赛)普及组初赛试题是一个重要的竞赛,对于参与者来说具有很大的挑战性。
本文将为大家提供NOIP普及组初赛试题的详细说明和解析,希望对大家在备战竞赛中起到一定的帮助和指导。
一、试题背景NOIP普及组初赛试题是国内一项重要的信息学竞赛,它旨在选拔出具有较高综合素质和较强信息学能力的学生,为他们提供机会参加进一步的培训和比赛,进一步提高其信息学水平。
本次试题包含多个题目,涉及算法、数据结构、编程等多个方面的知识点。
二、试题内容1. 题目一:数学运算要求:编写一个程序,输入两个整数a和b,输出它们的和。
注意:a和b的范围在-1000到1000之间。
2. 题目二:查找元素要求:编写一个程序,输入一个整数n和一个由n个整数组成的数组,再输入一个整数x,输出x在数组中的索引位置。
若x不存在于数组中,则输出-1。
3. 题目三:字符串处理要求:编写一个程序,输入一个字符串s,输出字符串s的第一个字母和最后一个字母。
若字符串s为空,则输出空字符串。
4. 题目四:文件操作要求:编写一个程序,从输入文件input.txt中读取n个整数,将其从小到大排序后输出到输出文件output.txt中。
输入文件input.txt的第一行为一个整数n,接下来的n行为n个整数。
5. 题目五:模拟游戏要求:编写一个程序,模拟一个游戏。
游戏开始时,玩家位于位置0,玩家可以输入命令"l"向左移动一格,输入命令"r"向右移动一格。
玩家的移动轨迹将被输出到控制台上。
直到玩家输入命令"q"退出游戏。
三、解题思路1. 题目一:数学运算这是一个非常简单的题目,只需要使用基本的数学运算符进行相加操作即可。
首先,接收用户输入的两个整数a和b,然后使用加法运算符将其相加,最后将结果输出即可。
2. 题目二:查找元素这是一个查找问题,我们可以使用线性搜索的方法来解决。
一、进制(这种题型你们可以看复印的资料上比较详细)(十一届)3.和十进制数23的值相等的二进制数是(D )。
A. 10110B.11011C.11011D.10111E.10011(十一届)18.(3725)8+(B)16的运算结果是(B )。
A.(3736)8B.(2016)10C.(1111110000)2D.(3006)10E.(7B0)16(十二届)15. 与十进制数1770对应的八进制数是(C )。
A. 3350B.3351C.3352D.3540(十二届)18.(2010)16 +(32)8的结果是(A )。
A.(8234)10B.(202B)16C.(20056)8D. (100000000110)2(十三届)17.与十进制数1770对应的八进制数是(C)。
A.3350 B.3351 C.3352 D.3540(十三届)19.(2070)16 + (34)8 的结果是(A)。
A.(8332)10 B.(208A)16 C.(100000000110)2D.(20212)8(十四届)8.与十进制数28.5625相等的四进制数是( D )。
A.123.21 B.131.22 C.130.22 D.130.21(十四届)12.(2008)10+(5B)16的结果是( A )。
A.(833)16 B.(2089)10 C.(4163)8 D.(100001100011)2二、字符串(十一届)1.在字符串“ababacbabcbdecced”中出现次数最多的字母出现了(B)次。
A.6B.5C.4D.3E.2(十四届)2.设字符串S=”Olympic”,S的非空字串的数目是(A )。
A.28 B.29 C.16 D.17三、(“∧”逻辑与也称交运算若A 为真且B 为真,则命题A ∧B 为真;否则为假;“∨”逻辑或也称并运算只要A 或者B 之中一个为真,则命题A ∧B 为真;否则为假)(十一届)2.设全集I={a,b,c,d,e,f,g,h},集合A={a,b,c,d,e,f},B={c,d,e},C={a,d},那么集合A∩B∩~C为(A)。
NOIP部份试题分析和解答南宁三中孙国强QQ: 393936008竞赛试题名称算法N01P2004津津的储蓄计划模拟合并果子排序+二分杏找合唱队形动态规划虫食算搜索N01P2005谁拿了最多奖学金模拟过河数学或动态规划篝火晚会图论或数学等价表达式分治NOIP2006能量项链动态规划金明的预算方案动态规划作业调度方案模拟2”k进制数数学+高精N01P2007统计数字排序字符串的展开模拟知阵取数游戏动态规划+高精树网的核图论N01P2008笨小猴模拟火柴棒等式搜索或数学传纸条动态规划双栈排序图论一、枚举:I 1 1 e ! 11 It I H It 1 LJ n. -i "i JIJ iri j注意:1.加号与等号各自需要两根火柴棍2.如果A,B,则A+B=C与B+A=C视为不同的等式(A、B、0=0)3.n根火柴棍必须全部用上【输入】输入文件matches.in共一行,乂一个整数n (nv=24)。
【输出】输出文件matches.out共一行,表示能拼成的不同等式的数目。
【输入输出样例1 ]matches, in matches, out142【输入输出样例1解释】2个等式为0+1=1和1+0=1 □【输入输出样例2】matches, in matches, out189【输入输出样例2解释】9个等式为: 0+4=4 0+11=11 1+10=112+2=42+7=94+0=47+2=9 10+1=11 11+0=11既然我们用枚举的方法,就要确定枚举什么?枚举的数量(范)有多少,估算时间和空间复杂度。
2.举例:一-年一度的高一YL杯超级篮球赛开赛了。
当然,所谓超级,意思是参赛人数可能多余5人。
小三对这项篮球非常感兴趣,所以一场都没有落下。
每个中午都准时守侯在篮球场看比赛。
经过一个星期的研究,小三终于对篮球的技战术找到了一丝丝感觉了。
他发现打YL 杯的每个班都有一奁相似的进攻战术:1:控球后卫带球到前场,找到一个最佳攻击点(x,y)2:所有除控卫以外的队员都从各自的当前位置迅速向(x,y)移动3:控球后卫根据场上情况组织进攻这个战术对于一般情况是非常奏效的,但是每个队员毕竞不像小三一样每天精力过剩, 每个队员都有一个疲劳指数W,显然对于每个队员的移动需要消耗一些能量。
历届信息学奥赛试题评析—阅读程序写结果第一题:var n,i,temp,sum:integer;a:array[1..100] of integer;beginreadln(n);for i:=1 to n doread(a[i]);for i:=1 to n-1 doif a[i]>a[i+1] thenbegintemp:=a[i];a[i]:=a[i+1];a[i+1]:=temp;end;for i:=n downto 2 doif a[i]<a[i-1] thenbegin temp:=a[i];a[i]:=a[i-1];a[i-1]:=temp;end;sum:=0;for i:=2 to n-1 doinc(sum,a[i]);writeln(sum div (n-2)); { div 表示整除} end.输入:840 70 50 70 20 40 10 30输出:点评:考查选择语句、循环语句、数组等内容,计算量中等。
难度:中等题。
第二题:program ex2;var n,i,ans:integer;function gcd(a,b:integer):integer;beginif a mod b =0then gcd:=belse gcd:=gcd(b,a mod b); { mod表示取余数}end;beginreadln(n);ans:=0;for i:=1 to n doif gcd(n,i)=ithen begin writeln(i); ans:=ans+1; end;writeln(ans);end.输入:120输出:点评:考查选择语句、循环语句、函数、递归等内容,计算量中等。
难度:中等题。
第三题:vardata:array[1..20] of integer;n,i,h,ans:integer;procedure merge;begindata[h-1]:=data[h-1]+data[h];dec(h); { dec(h) 表示h:=h-1 }inc(ans); { inc(ans) 表示ans:=ans+1 } end;beginreadln(n);h:=1;data[h]:=1;ans:=0;for i:=2 to n dobegin inc(h);data[h]:=1;while (h>1) and (data[h]=data[h-1]) domerge;end;writeln(ans);end.输入:8输出:点评:考查循环语句、数组、过程等内容,计算量较大。
历届“问题求解”解析(2013竞赛辅导)问题求解是信息学竞赛初赛中常见题型,它共两题,每题5分,共10分,十六届增加了比重,有三题,占15分。
诸如寻找假币、博弈原理、抽屉原理、容斥问题、排列组合、逻辑推理、递推关系等问题出现在问题求解中。
(相关问题的具体讲解根据需要考虑发讲义) 第一届(逻辑推理问题)1. 有标号为A 、B 、C 、D 和1、2、3、4的8个球,每两个球装一盒,分装4盒。
标号为字母的球与标号为数字的球有着某种一一对应的关系(称为匹配),并已知如下条件: ① 匹配的两个球不能在一个盒子内。
② 2号匹配的球与1号球在一个盒子里。
③ A 号和2号球在一个盒子里。
④ B 匹配的球和C 号球在一个盒子里。
⑤ 3号匹配的球与A 号匹配的球在一个盒子里。
⑥ 4号是A 或B 号球的匹配球。
⑦ D 号与1号或2号球匹配。
请写出这四对球匹配的情况。
第四届(递推、树、图)1. 已知一个数列U 1,U 2,U 3,…,U N ,… 往往可以找到一个最小的K 值和K 个数a 1,a 2,…,a n 使得数列从某项开始都满足: U N+K =a 1U N+K-1+a 2U N+K-2+……+a k U N (A)例如对斐波拉契数列1,1,2,3,5,…可以发现:当K=2,a 1 =1,a 2 =1时,从第3项起(即N>=1)都满足U n+2 =U n+1+U n 。
试对数列13,23,33,…,n 3,…求K 和a 1,a 2, …,a K 使得(A )式成立。
当K= 4,a 1,a 2,…,a k 为a 1=4, a 2=6, a 3=4,a 4=-1对数列132333,…,n 3,…(A )成立。
2.给出一棵二叉树的中序遍历:DBGEACHFI 与后序遍历:DGEBHIFCA 画出此二叉树。
3.用邻接矩阵表示下面的无向图:表示该无向图的邻接矩阵为 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 1 1 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 1 0第五届(递推)将Ln 定义为求在一个平面中用n 条直线所能确定的最大区域数目。