当前位置：文档之家 › NOIP普及组历届试题分析

NOIP普及组历届试题分析

  • 格式：ppt
  • 大小：328.00 KB
  • 文档页数：105

下载文档原格式

  / 105

合集下载

信息学奥赛NOIP普及组历届试题分析

信息学奥赛NOIP普及组历届试题分析
53
二、模拟类试题
有些问题，我们很难建立数学模型，或者很难 用计算机建立递推、递归、枚举、回溯法等算 法。在这种情况下，一般采用模拟策略。
所谓模拟策略就是模拟某个过程，通过改变数 学模型的各种参数，进而观察变更这些参数所 引起过程状态的变化，由此展开算法设计。
金币 (noip2015普及组第一题)
输入样例：
70 3 71 100
69 1 12
输出样例：
3
（1 <= T <= 1000） （1 <= M <= 100）
采药 （noip2005普及组第三题）
题目大意：共m株草药，每株草药有一个价值 和采摘的时间，问t时间能采摘到的草药的最大 价值。
采药 （noip2005普及组第三题）
输入格式：
第一行有两个整数T和M，T代表总共能够用来采药的时间，M 代表山洞里的草药的数目。接下来的M行每行包括两个在1到 100之间（包括1和100）的整数，分别表示采摘某株草药的时 间和这株草药的价值。
输出格式：
一行只包含一个整数，表示在规定的时间内，可以采到的草药 的最大总价值。
螺旋方阵试题分析
本题首先让我们想到传统的模拟，从[1,1]开 始往数组中填充数字，但对于[30000,30000] 的数组，直接爆零。
对于读入的n, x, y，先判断(x,y)在第几圈， 再模拟圈内的数字。
螺旋方阵试题分析
如：n=4, (2,2)在第2圈，(3,1)在第1圈。 n=6，(4,5)在第2圈
移动；如果前方是未曾经过的格子，则继续前进， 否则右转；重复上述操作直至经过矩阵中所有格子。 根据经过顺序，在格子中依次填入1,2,3,....，便构 成了一个螺旋矩阵。 现给出矩阵大小n以及i和j，请你求出该矩阵中第 i行第j列的数是多少。 下图是一个n=4时的螺旋矩阵。

【通用】信息学奥赛NOIP普及组历届试题分析.ppt

【通用】信息学奥赛NOIP普及组历届试题分析.ppt
枚举法其实是最简单的搜索算法。
.,.,
4
珠心算测验 (noip2014普及组第一题)
珠心算是一种通过在脑中模拟算盘变化来完成快 速运算的一种计算技术。珠心算训练，既能够开 发智力，又能够为日常生活带来很多便利，因而 在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加 法能力的测验方法。他随机生成一个正整数集合， 集合中的数各不相同，然后要求学生回答：其中 有多少个数，恰好等于集合中另外两个（不同的） 数之和？ 最近老师出了一些测验题，请你帮忙求 出答案。
不过，如果把调查结果就以这种方式呈现出来，大 多数人肯定不会满意。因为这个比例的数值太大， 难以一眼看出它们的关系。对于上面这个例子，如 果把比例记为 5:3，虽然与 真实结果有一定的误差， 但依然能够较为准确地反映调查结果，同时也显得 比较直观。
现给出支持人数 A，反对人数 B，以及一个上限 L， 请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均 不大于 L 且 A’和 B’互质（两个整数的最大公约数 是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - A/B 的值 尽可能小。
输入样例 2 23 ?*? *??
输出样例 2 mine.out 2*1 *21
对于 100%的数据，1≤n≤100，1≤m≤100
.,.,
10
比例简化 (noip2014普及组第二题)
在社交媒体上，经常会看到针对某一个观点同意与 否的民意调查以及结果。例如，对某 一观点表示 支持的有 1498 人，反对的有 902 人，那么赞同与 反对的比例可以简单的记为1498:902。
.,.,
11
比例简化 (noip2014普及组第二题)
输入格式 输入共一行，包含三个整数 A，B，L，每两个整

NOIP试题分析.doc

NOIP试题分析.doc

八 1/ | （初中部分）1排序：（有些排序因涉及贪心，所以我放在贪心那一节里了）历届试题：NOIP分数线划定奖学金明明的随机数排序法使用：选择排序。

快速排序。

桶排序。

分析：1.分数线划定：ci）这是一道具有代表性的排序题，可使用选择或快排，使用选择排序整体难度较小，但因此题数据量较大，选择排序不可过全部数据。

（2）使用快速排序是解决本题的最好方法，但不可直接套用，因为有儿个排序条件，排序内最好添加几个辅助变量。

2.奖学金：（1）这道题和上题大体相同，但其测试数据较小，可使用选择排序得全分。

3.明明的随机数：（1）本题可用选择或快排，但代码设计较难，使用桶排序解绝此题是较为理想的选择。

2模拟：分为三类：〈1〉普通模拟（完全模拟的较少，大多为结合贪心。

排序的，贪心。

排序的不单独讨论）历届试题：NOIP多项式输出数列1. NOIP多项式输出.：（1）多项式输出:这道题想要拿分很容易，但要注意一下模拟过程，此题实际上需有4个判段过程，其中有一个是极易遗漏的。

（2）数列:这道题竟是第4题，很简单的模拟题，还可用转成2进制的方式直接算.〈2〉罕符模拟历届试题：NOIP ISBN号码Jam记数法立体图（1）ISBN号码：总体难度不大，这道题如果是使用C语言的话，可以用每个字符都减去字符0的方式，直接把它们从字符转为数字，再进行处理。

（2）Jam记数法:很绝对的模拟，一开始我还认为是数学知识模拟题,就是从后往前推.（3）立体图:很难的很考细心的一道模拟题,没说的，就是上机不断的调程序.〈3〉数学知识模拟历届试题：NOIP细胞分裂（1）初中组目前唯一一道数学知识模拟题，掌握了相关的知识就应该不难，这道题要满分还是比较难的，需要高精度运算（用LONG LONG型不知道可不可以），还有一定要注意时间问题，这道题极易超时.3贪心：历届试题：NOIP排座椅纪念品分组守望者的逃离.注意：任何贪心之前都必需排序。

（1）排座椅:这道题初看不像一道贪心，但实际上只要细细的看，就可以发现了,跟实际生活联系很紧密的一道题。

1995-2008 历届NOIP试题及详解

1995-2008 历届NOIP试题及详解
98765
N=6
正整数化为二进制数，在此二进制数中，我们将数字 16 17 18 19 20 1
1
于数字
0
的个数的这类二进制数称为 15 30 31 32 21 2
A
类数，否则就称
数。
14 29 36 33 22 3
（13）10=1（3 1218013）5 234 23 4
的个数为132，207 的26个2数5 为241，5则称此数为 A 类数；
提示：文档已分节，可用 word 跳转节功能 本文为本人将 1995-2008 年历届 NOIP 试题、研究成果整理而成，由于“年代久远”所以有不少 资料没有找到。但本人都尽量整理最有价值的信息记录于此。 资料来源皆为网络，若引用请注明出处 一不注意就 208 页了呢~ 其实最初只是想方便自己，看着一下午的成果，就忍不住放到了网络 上。由于赶时间，质量不太好，而且历届 NOIP 的排版也不一样，只是做了粗略的整理、排 版，若有错误之处，敬请谅解。 回首历届 NOIP，甚至比我自己出生的还早的老题，一代代 OIer 就从这条路上走过，作为一个 不大努力的 OIer，我甚至为自己感到愧疚。总之，为了报答一代代出题人、教师、主办方以及 OIer 们，在努力一把也不迟啊。
96
109
108
1 <2> 本题 18 分（4%+6%+8%）
① 输入 N=1 （4%） 结果：
② 输入 N=3 （6%） 结果：
1
781
692
543 ③ 输入 N=10（8%）
结果： 28 29 30 31 32 33 34 35 36 1
27 58 59 60 61 62 63 64 37 2
26 57 80 81 82 83 84 65 38 3

历年noip普及组(c++)完善程序题总结归纳

历年noip普及组(c++)完善程序题总结归纳

完善程序题总结归纳By：七（6） yx一、【题目】（哥德巴赫猜想）哥德巴赫猜想是指，任一大于2的偶数都可写成两个质数之和。

迄今为止，这仍然是一个著名的世界难题，被誉为数学王冠上的明珠。

试编写程序，验证任一大于2且不超过n的偶数都能写成两个质数之和。

#include<iostream>using namespace std;int main(){const int SIZE=1000;int n,r,p[SIZE],i,j,k,ans;bool tmp;cin>>n;r=1;p[1]=2;for(i=3;i<=n;i++){① ;for(j=1;j<=r;j++)if(i% ② ==0){tmp=false;break;}if(tmp){r++;③ ;}}ans=0;for(i=2;i<=n/2;i++){tmp=false;for(j=1;j<=r;j++)for(k=j;k<=r;k++)if(i+i== ④ ){tmp=true;break;}if(tmp)ans++;}cout<<ans<<endl;return 0;}若输入n为2010，则输出⑤时表示验证成功，即大于2且不超过2010的偶数都满足哥德巴赫猜想。

【算法】先for一遍，找出质数，然后对每一个偶数进行一一匹配（2除外），效率O（n^3）【代码】1、tmp=1；2、p[j];3、p[r]=j;4、p[j]+p[k]5、1004【年份】2010年二、【题目】(过河问题) 在一个月黑风高的夜晚,有一群人在河的右岸,想通过唯一的一根独木桥走到河的左岸.在伸手不见五指的黑夜里,过桥时必须借照灯光来照明,不幸的是,他们只有一盏灯.另外,独木桥上最多能承受两个人同时经过,否则将会坍塌.每个人单独过独木桥都需要一定的时间,不同的人要的时间可能不同.两个人一起过独木桥时,由于只有一盏灯,所以需要的时间是较慢的那个人单独过桥所花费的时间.现在输入N(2<=N<1000)和这N个人单独过桥需要的时间,请计算总共最少需要多少时间,他们才能全部到达河左岸.例如,有3个人甲、乙、丙,他们单独过桥的时间分别为1、2、4,则总共最少需要的时间为7.具体方法是:甲、乙一起过桥到河的左岸,甲单独回到河的右岸将灯带回,然后甲、丙在一起过桥到河的左岸,总时间为2+1+4=7.#include<iostream>#include<cstring>using namespace std;const int size=100;const int infinity = 10000;const bool left=1;const bool right =0;const bool left_to_right=1;const bool right_to_left=0;int n,hour[size];bool pos[size];int max(int a,int b){return a>b?a:b;}int go(bool stage){int i,j,num,tmp,ans;if(stage==right_to_left){num=0;ans=0;for(i=1;i<=n;i++)if(pos[i]==right){num++;if( hour[i]>ans)ans=hour[i];}if( ① )return ans;ans=infinity;for(i=1;i<=n-1;i++)if(pos[i]==right)for(j=i+1;j<=n;j++)if(pos[j]==right){pos[i]=left;pos[j]=left;tmp=max(hour[i],hour[j])+ ②; if(tmp<ans)ans=tmp;pos[i]=right;pos[j]=right;}return ans;}if(stage==left_to_right){ans=infinity;for(i=1;i<=n;i++)if( ③ ){pos[i]=right;tmp= ④ ;if(tmp<ans)ans=tmp;⑤;}return ans;}return 0;}int main(){int i;cin>>n;for(i=1;i<=n;i++){cin>>hour[i];pos[i]=right;}cout<<go[right_to_left)<<endl;return 0;}【算法】利用深搜，左右交替寻找最优解（maybe是动态规划）【代码】1、num<=2;2、go[1];3、pos[j]==1;4、hour[i]+go[0];5、pos[i]=1;【年份】2010年三、【题目】（子矩阵）给输入一个n1*m1的矩阵a，和n2*m2的矩阵b，问a中是否存在子矩阵和b相等。

信息学奥赛NOIP普和组历届试题分析报告PPT35页

信息学奥赛NOIP普和组历届试题分析报告PPT35页
信息学奥赛NOIP普和组历 届试题分析报告
26、机遇对于有准备的头脑有特别的 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一， 也是成 功的利 器之一 。没有 它，天 才也会 在矛盾 无定的 迷径中 ，徒劳 无功。-。 30、我奋斗，所以我快乐。--格林斯 潘。
16、业余生活要有意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
END

1995-2008 历届NOIP试题及详解

② 由编码求原数组：共 15 分（5%+5%+5%）
a 输入：N=5 B=（0，0，0，0，0）
输出： A=（4，3，2，1，0）
b 输入：N=10 B=（0，1，2，3，4，5，6，7，8，9）
输出： A=（0，1，2，3，4，5，6，7，8，9）
c 输入：N=7 B=（0，0，0，0，4，5，6）
R
Y Y
P2=B R N2R=2
Y
P3=Y R N3=R1
Y
Q
RR
Y
排列方案： 排列总数： 105×2=210
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y BB
① 输10入5×2=210 3 4R 4 R4 4R 3 4 B B
1 2R 2 R2 2R 2 1 3B B
应打印出完整的图形R：（R12 分R）
BB
15 1R6 1R6 1R5 4 B B
Y Y Y Y Y
7 8 R 8R 8 R 7 7
BB
Y
3 4 R4 R4 R4 3 4 B B
Y
1 2 2R 2 R 2 R 2 1
19 18 17 16 15 14 13 12 11 10 <3> 本题 14 分

普及组近5年NOIP试题分析试题分析


1≤ L ≤ R≤10000。
NOIP2010——数字统计
从L到R枚举每一个数i,对i进行分离数字，直接
统计有多少个2......

分离数字的过程
void count(int n)
{while (n>0) {if (n%10==2) ans++; n/=10; }
}
NOIP2010——接水问题

NOIP2012——寻宝

藏宝楼共有N+1层，最上面一层是顶层，顶层有一个 房间里面藏着宝藏。除了顶层外，藏宝楼另有 N层， 每层M个房间，这M个房间围成一圈并按逆时针方向 依次编号为0，…，M-1。其中一些房间有通往上一 层的楼梯，每层楼的楼梯设计可能不同。每个房间里 有一个指示牌，指示牌上有一个数字x，表示从这个 房间开始按逆时针方向选择第x个有楼梯的房间（假 定该房间的编号为k），从该房间上楼，上楼后到达 上一层的k号房间。比如当前房间的指示牌上写着2， 则按逆时针方向开始尝试，找到第2个有楼梯的房间， 从该房间上楼。如果当前房间本身就有楼梯通向上层， 该房间作为第一个有楼梯的房间。
NOIP2010——三国

输入样例
输出样例
8
42 24 10 29 27 12 58
1
77
31 8 16 26 80 6
25 3 36 11 5 33 20 17 13 15 77 9 4 50
19
NOIP2010——三国
显然每个武将对应的最大默契值都无法选到，
但是可以保证能选到次大的。所以就在次大的 中选一个最大的作为答案咯。这样计算机肯定 也得不到更大的值所以一定是可以获胜的。
NOIP2012——质因数分解

历届NOIP试题及详解


间的整数，且 A[i]≠A[j]（当 i≠j 时）。
例如：N=6 时，有：
A=（4，3，0，5，1，2）
此时，数组 A 的编码定义如下：
A[0]的编码为 0；
A[i]的编码为：在 A[0]，A[1]，……A[i-1]中比 A[i]的值小的个数（i=1，2……N-1）
∴上面数组 A 的编码为：
B=（0，0，0，3，1，2）
输出： A=（3，2，1，0，4，5，6）
<5> 本题共 30 分（10%+10%+10%）
① 数据输入： N=6
P1=R
N1=1
Q
排列方案： R ② 排数列据总输数入=：6 N=6 R
P1=R
NR1=2
P2=Y
N2=1 R
Q
R
排列方案： R ③ 排数列据总输数入=：12N=1R2
P1=RR
R
Y
R R N1= 3
③ 同一种颜色的灯不能分开；
④ 不同颜色的灯之间至少要有一个空位置。
例如：N=8（格子数） R=2（红灯数） B=3（蓝灯数）
放置的方法有：
R-B 顺序
RR
BBB
RR
BBB
RR
BBB
RR
BBB
RR
BBB
B-R 顺序
RR
BBB
BBB
RR
BBB
RR
BBB
RR
BBB
RR
BBB
RR
放置的总数为 12 种。 数据输入的方式为：
提示：文档已分节，可用 word 跳转节功能 本文为本人将 1995-2008 年历届 NOIP 试题、研究成果整理而成，由于“年代久远”所以有不少 资料没有找到。但本人都尽量整理最有价值的信息记录于此。 资料来源皆为网络，若引用请注明出处 一不注意就 208 页了呢~ 其实最初只是想方便自己，看着一下午的成果，就忍不住放到了网络 上。由于赶时间，质量不太好，而且历届 NOIP 的排版也不一样，只是做了粗略的整理、排 版，若有错误之处，敬请谅解。 回首历届 NOIP，甚至比我自己出生的还早的老题，一代代 OIer 就从这条路上走过，作为一个 不大努力的 OIer，我甚至为自己感到愧疚。总之，为了报答一代代出题人、教师、主办方以及 OIer 们，在努力一把也不迟啊。

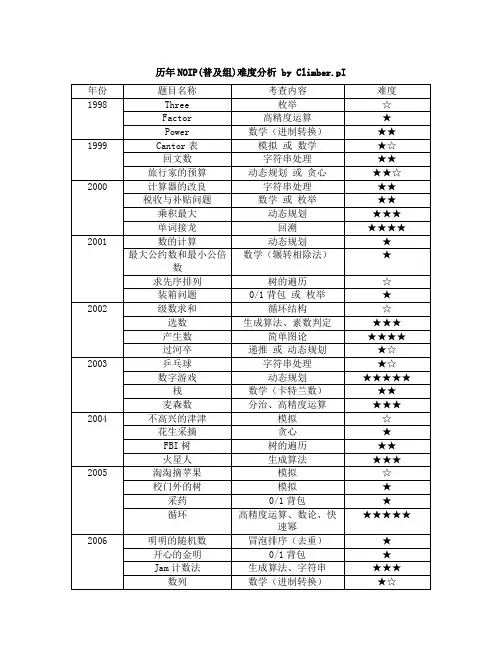
历年NOIP(普及组提高组)试题难度列表

历年NOIP(普及组)难度分析 by Climber.pINOIP提高组复赛考察点详细分析动态规划：12 模拟：10数学：5 图论：4搜索：4 构造：3贪心：2【动态规划】平均难度系数：0.55此项为历届NOIP考察次数最多的知识点。

主要有 1.区间模型 2.子序列模型 3.资源分配模型以及一些简单的多维状态设计技巧。

动态规划可以与图,树,高精度等知识点配合出题。

【模拟】平均难度系数：0.76平均每届NOIP都会出现1个模拟题。

这种题一般算法很简单，需要选手细心理解题目意思，注意细节。

考察选手的代码实现能力。

【数学】平均难度系数：0.46需要掌握质数及其性质，基础的实属操作，加法原理和乘法原理。

此类题需要选手对数学规律的灵感。

【图论】平均难度系数：0.50历届考察点基本上都是 1.最短路问题和 2.特殊图的性质。

特殊图包括树，拓扑图，二分图等。

历届NOIP在图论上的考察并不是很多。

【搜索】平均难度系数：0.38历届搜索题一般都比较难，搜索算法本身简单，于是题目会提高选手对其他方面的要求。

主要有搜索优化和模拟。

写搜索题时应该以尽量多得分为目标。

【构造】平均难度系数：0.27构造类题目一般没有明确的算法，需要选手仔细分析题目的实质，并得出解法。

这个解法通常不是唯一的。

有时一个好的贪心可以得相当多的分。

有时搜索剪枝可以很大的提高效率。

同样以多得分为目标。

【【贪心】平均难度系数：0.75此类题需要选手对算法的直觉，贪心正确性一旦被证明，通常题目就简单了。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

对于100%的数据，3 ≤ n ≤ 100 测验题给出的正整数大小不超过10,000。
试题分析

题意大意：给你n个数，在这n个数中，找 到满足A+B=C的C的个数，注意不是这个 等式的个数。
样例中，1,2,3,4有1+2=3，1+3=4两个。

由于本题数据规模n<=100，我们可以直接
枚举C, A, B，三层循环解决问题。
扫雷游戏 (noip2015普及组第二题)
输入样例 1 33 *?? ??? ?*? 输入样例 2 23 ?*? *??
输出样例 1 mine.out *10 221 1*1 输出样例 2 mine.out 2*1 *21
对于 100%的数据，1≤n≤100，1≤m≤100
问题分析：
本题也是简单的枚举类试题。 我们从雷区的第一行第一列(1,1)开始，判断它周围 有多少个地雷。 由于本题读入的是字符，读入时需要注意： readln(n,m); for i=1 to n do begin for j=1 to m do read(a[i][j]); readln; end;
比例简化 (noip2014普及组第二题)



在社交媒体上，经常会看到针对某一个观点同意与 否的民意调查以及结果。例如，对某 一观点表示 支持的有 1498 人，反对的有 902 人，那么赞同与 反对的比例可以简单的记为1498:902。 不过，如果把调查结果就以这种方式呈现出来，大 多数人肯定不会满意。因为这个比例的数值太大， 难以一眼看出它们的关系。对于上面这个例子，如 果把比例记为 5:3，虽然与 真实结果有一定的误差， 但依然能够较为准确地反映调查结果，同时也显得 比较直观。 现给出支持人数 A，反对人数 B，以及一个上限 L， 请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均 不大于 L 且 A’和 B’互质（两个整数的最大公约数 是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - A/B 的值 尽可能小。
质因数分解(2012p1)、细胞分裂(2009p3) Hanoi双塔问题(2007p4)、数列(2006p4) 循环(2005p4) 、栈(2003p3卡特兰数) 表达式求值(2013p2)、表达式的值(2011p4) FBI树(2004p1)、求先序排列(2001p2) 车站分级(2013p4 拓扑排序) 文化之旅(2012p4 floyd算法)



试题分析
题目大意是给定a,b，统计a,b之间数字2出现 的次数。 从a到b直接枚举每一个数，判断这个数中含 有几个2。 for i=a to b do{ 求i中含2的个数t; ans=ans+t; } 输出t;
参考程序：
1. 2. 3.
4.
5. 6. 7. 8. 9. 10. 11. 12. 13.
数字统计 (noip2010普及组第一题)
请统计某个给定范围[L, R]的所有整数中，数字2出现 的次数。 比如在给定范围[2, 22]，数字2在数2中出现了1次，在 数12中出现了1次，在数20中出现了1次，在数21中出 现了1次，在数22中出现了2次，所以数字2在该范围内 一共出现了6次。 输入格式 输入共一行，为两个正整数L和R，之间用一个空格隔 开。 输出格式 输出共1行，表示数字2出现的次数。 样例输入：2 22 样例输出：6
问题分析：
一个格子的周围格子包括其上、下、左、右、左 上、右上、左下、右下八个方向上与之直接相 邻的格子。判断如下：



if a[i][j-1]='*' then inc(s); if a[i][j+1]='*' then inc(s); if a[i+1][j-1]='*' then inc(s); if a[i+1][j+1]='*' then inc(s); if a[i+1][j]='*' then inc(s); if a[i-1][j-1]='*' then inc(s); if a[i-1][j+1]='*' then inc(s); if a[i-1][j]='*' then inc(s);
NOIP普及组历届试题分析
安徽省六安第一中学 江家和
引言
noip复赛的知识面很广泛，对选手的综合
素质考核要求更为严格，难度和分数的
阶梯层次更趋科学合理，对信息学活动 的推动力和社会公信力更为增强。
NOIP普及组题型分布
题型 枚举 题目 扫雷游戏(2015p2)、珠心算测验(2014p1) 数字统计(2010p1)、比例简化(2014p2) 金币(2015p1)、 螺旋方阵(2014p3)、计数问题(2013p1)、 寻宝(2012p2)、接水问题(2010p2) 数字反转(2011p1)、统计单词个数(2011p2) ISBN号码(2008p1)、乒乓球(2003p1) 排座椅(2008p2)、纪念品分组(2007p2)
var i,a,b,ans:longint; begin readln(a,b); ans:=0; for i:=a to b do begin if i mod 10=2 then inc(ans); if i div 10 mod 10=2 then inc(ans); if i div 10 div 10 mod 10=2 then inc(ans); if i div 10 div 10 div 10 mod 10=2 then inc(ans); end; writeln(ans); end.

方法2：两层循环
两层循环枚举a,b的值，判断a+b是否存在：
for a=1 to n do for b=1 to n do if (vis[f[a]+f[b]]=1) and (a<>b) then begin inc(ans); vis[f[a]+f[b]]=2; //避免出现重复的等式 end;
数学/数论
数据结构 图论（提高组）
一、枚举类试题

枚举法的基本思想是根据提出的问题枚举所
有可能的解，并用问题给定的条件检验哪些
解是需要的，哪些解是不需要的。能使条件
成立，即为其解。

枚举法其实是最简单的搜索算法。
珠心算测验 (noip2014普及组第一题)

珠心算是一种通过在脑中模拟算盘变化来完成快 速运算的一种计算技术。珠心算训练，既能够开 发智力，又能够为日常生活带来很多便利，因而 在很多学校得到普及。
方法2：参考代码
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.
var i, n, a, b, ans:longint; vis:array[0..20005]of 0..2; f:array[0..105]of longint; begin readln(n); fillchar(vis,sizeof(vis),0); for i:=1 to n do begin read(f[i]); vis[f[i]]:=1; end; ans:=0; for a:=1 to n do for b:=1 to n do if (vis[f[a]+f[b]]=1)and(a<>b) then begin inc(ans); vis[f[a]+f[b]]:=2; end; writeln(ans); end.
某学校的珠心算老师采用一种快速考察珠心算加 法能力的测验方法。他随机生成一个正整数集合， 集合中的数各不相同，然后要求学生回答：其中 有多少个数，恰好等于集合中另外两个（不同的） 数之和？ 最近老师出了一些测验题，请你帮忙求 出答案。

珠心算测验 (noip2014普及组第一题)



【输入】 输入共两行，第一行包含一个整数n，表示测试 题中给出的正整数个数。 第二行有n个正整数，每两个正整数之间用一个 空格隔开，表示测试题中给出的正整数。 【输出】 输出共一行，包含一个整数，表示测验题答案。 【样例输入】 【样例输出】 4 2 1234
28. 29. 30.
else begin if a[i][j-1]='*' then inc(s); if a[i][j+1]='*' then inc(s); if a[i+1][j-1]='*' then inc(s); if a[i+1][j+1]='*' then inc(s); if a[i+1][j]='*' then inc(s); if a[i-1][j-1]='*' then inc(s); if a[i-1][j+1]='*' then inc(s); if a[i-1][j]='*' then inc(s); write(s); end; end; writeln; end; end.
方法1：三层循环

考试中，有许多选手的程序是这样的，错 在哪里？
ans:=0; for c:=1 to n do for a:=1 to n do for b:=1 to n do if (f[c]=f[a]+f[b])and(c<>a)and(a<>b)and(c<>b) then inc(ans); writeln(ans);
扫雷游戏 (noip2015普及组第二题)
扫雷游戏是一款十分经典的单机小游戏。 在 n 行 m 列的雷区中有一些格子含有地雷 （称之为地雷格） ，其他格子不含地雷（称之 为非地雷格） 。玩家翻开一个非地雷格时，该 格将会出现一个数字——提示周围格子中有多 少个是地雷格。 游戏的目标是在不翻出任何地 雷格的条件下，找出所有的非地雷格。 现在给出n行m列的雷区中的地雷分布， 要 求计算出每个非地雷格周围的地雷格数。 注：一个格子的周围格子包括其上、下、左、 右、左上、右上、左下、右下八个方向上与之 直接相邻的格子。