大学物理位置矢量位移

大学物理1(上)知识点总结一维运动学参考系是用来确定物体位置的物体。

为了进行定量描述，需要在参考系上建立坐标系。

位置矢量（位矢）是从坐标原点引向质点所在位置的有向线段，用矢量r表示。

位矢用于确定质点在空间中的位置。

位矢与时间t的函数关系为：r = r(t) = x(t)i + y(t)j + z(t)k其中i、j、k是坐标轴的单位向量。

运动方程是指位移矢量Δr = r(t+Δt) - r(t)。

位移矢量是质点在时间Δt内的位置改变。

轨道方程是质点运动轨迹的曲线方程。

速度是质点位矢对时间的变化率。

平均速度定义为单位时间内的位移，即Δr/Δt。

速率是质点路程对时间的变化率，即v = ds/dt。

加速度是质点速度对时间的变化率，即a = dv/dt。

在圆周运动中，有法向加速度和切向加速度。

法向加速度的方向沿半径指向曲率中心（圆心），反映速度方向的变化。

切向加速度的方向沿轨道切线，反映速度大小的变化。

角速度的方向沿轨道切线，反映速度方向的变化。

对于两个相互作平动的参考系，有r'pk = rpk + rkk'，vpk= vpk' + vkk'，apk = apk' + akk'。

掌握位置矢量、位移、速度、加速度、角速度、角加速度等描述质点运动和运动变化的物理量，明确它们的相对性、瞬时性和矢量性。

理解法向加速度和切向加速度的物理意义；掌握圆周运动的角量和线量的关系，并能灵活运用计算问题。

理解XXX坐标、速度变换，能分析与平动有关的相对运动问题。

功是力和位移的标积，即dA = F·dr = Fds·cosθ。

对质点在力作用下的有限运动，力作的功为A = ∫F·dr。

在直角坐标系中，此功可写为。

角动量定理指出，质点所受的合外力矩等于它的角动量对时间的变化率。

其中，质点的角动量可以表示为L=r×p=r×mv，其中r为质点到某一固定点的位置矢量，p为质点的动量。

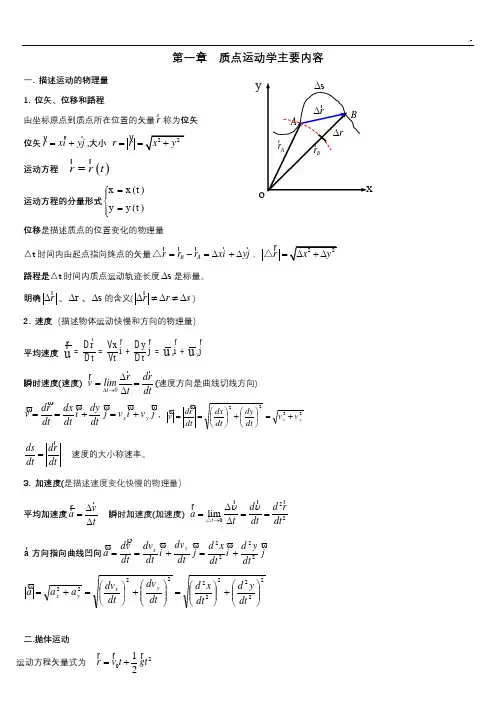
y第一章 质点运动学主要内容一.描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r r称为位矢位矢r xi yj =+r v v ,大小 r r ==v 运动方程()r r t =r r运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆r rr r r△，r =r△路程是△t 时间内质点运动轨迹长度s ∆是标量。

明确r ∆r 、r ∆、s ∆的含义(∆≠∆≠∆rr r s ) 2. 速度（描述物体运动快慢和方向的物理量）平均速度 x y r x y i j i j t t tu u u D D ==+=+D D r r r r r V V r 瞬时速度(速度) t 0r dr v lim t dt∆→∆==∆r r r(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x ϖϖϖϖϖϖ+=+==，2222y x v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==ϖϖ ds dr dt dt=r 速度的大小称速率。

3. 加速度(是描述速度变化快慢的物理量）平均加速度va t ∆=∆rr 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆r r r r △ a r方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x ϖϖϖϖρϖ2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x ϖ二.抛体运动运动方程矢量式为 2012r v t gt =+r rr分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量：线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。

大学物理学习指导第一章 质点的运动本章基本要求：掌握位置矢量、位移、速度、加速度、角速度、角加速度、切向加速度、法向加速度等描述质点运动状态的物理量。

能借助于直角坐标系计算质点在平面内运动时的速度、加速度。

能计算质点作园周运动时的角速度、角加速度、切向加速度、法向加速度。

理解运动的相对性。

本章重点：1、已知速度和加速度及初始条件，求质点的运动方程；2、已知质点运动方程，求质点的位移、速度、加速度等物理量；3、匀变速直线运动、抛体运动的规律。

解题指导：本章的习题一般分两大类：第一类是已知质点的运动方程，利用微分法求各物理量（速度、加速度等）；第二类是已知速度和加速度及初始条件利用积分法求运动方程。

第二类问题及学会用速度合成定理处理运动的矢量性和相对性问题是本章的难点。

质点运动学问题的一般解题顺序为：a. 审清题意，确定研究对象，分析研究对象的运动情况。

b. 建立适当的坐标系。

c. 根据所求物理量的定义列式并求解。

或根据运动的特点和题设条件列方程求解。

d. 必要时进行分析讨论。

第二章 牛顿运动方程本章基本要求：掌握牛顿三定律及适用条件，掌握运用微积分方法求解一维变力作用下质点的动力学问题。

本章重点：1、质量和力的概念以及力学中常见的三种力——万有引力、弹性力和摩擦力的特点。

2、牛顿运动定律及其适用条件。

3、练运用隔离法分析物体受力，正确列出物体受力方程，求解简单的质点动力学问题。

解题指导：（一）物体的受力分析画物体受力图的步骤：a. 隔离出研究对象，并画出已知力；b. 画重力；c. 考察并画出研究对象与周围物体相接触处的弹性力和摩擦力。

d. 应注意：每画出一力必须能找出该力的施力物体。

（二）牛顿运动定律的应用牛顿运动定律主要解决二类问题： 1、 1、 已知运动求力，即已知物体的运动现象或规律（运动方程()t r r =r = r(t)），求作用于物体的外力。

一般可先求得a 后再求力。

2、 2、 已知力求力运动，即求物体的加速度、速度和运动方程，这可用积分法得。

第一章 质点运动学一、 基本要求1．掌握位矢、位移、速度、加速度，角速度和角加速度等描述质点运动和运动变化的物理量。

2． 能借助于直角坐标计算质点在平面内运动时的速度、加速度。

3．能计算质点作圆周运动时的角速度和角加速度，切向加速度和法向加速度。

4．理解伽利略坐标，速度变换。

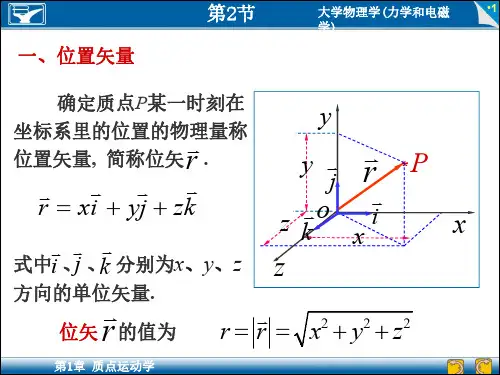
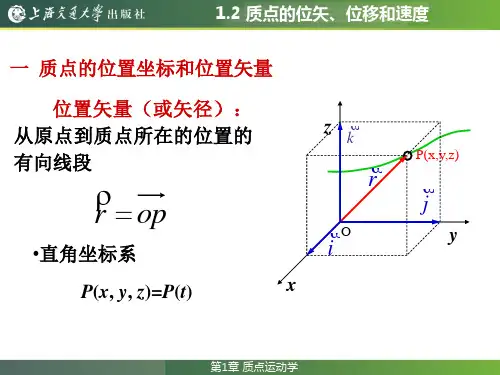
二、 基本内容1．位置矢量（位矢）位置矢量表示质点任意时刻在空间的位置，用从坐标原点向质点所在点所引的一条有向线段r 表示。

r 的端点表示任意时刻质点的空间位置。

r同时表示任意时刻质点离坐标原点的距离及质点位置相对坐标系的方位。

位矢是描述质点运动状态的物理量之一。

注意：（1）瞬时性：质点运动时，其位矢是随时间变化的，即()t r r=；（2）相对性：用r描述质点位置时，对同一质点在同一时刻的位置，在不同坐标系中r 可以是不相同的。

它表示了r的相对性，也反映了运动描述的相对性；（3）矢量性：r为矢量，它有大小，有方向，服从几何加法。

在直角坐标系Oxyz 中k z j y i x r++= 222z y x r r ++==r z r y r x ===γβαcos ,cos ,cos质点运动时， ()t r r= （运动方程矢量式）()()()⎪⎩⎪⎨⎧===t z z t y y t x x （运动方程标量式）。

２．位移()(),j y i x t r t t r r ∆+∆=-∆+=∆ r∆的模()()22y x r ∆+∆=∆ 。

注意：（１）r∆与r ∆：前者表示质点位置变化，是矢量，同时反映位置变化的大小和方位；后者是标量，反映质点位置离开坐标原点的距离的变化。

（２）r∆与s ∆：s ∆表示t —t t ∆+时间内质点通过的路程，是标量，只有质点沿直线运动时两者大小相同或0→∆t 时，s r ∆=∆。

3. 速度dtrd v =是描述位置矢量随时间的变化。

在直角坐标系中k v j v i v k dtdz j dt dy i dt dx dt r d v z y x++=++==222222z y x v v v dt dz dt dy dt dx v v ++=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==v的方向：在直线运动中，v>0表示沿坐标轴正向运动，v <0表示沿坐标轴负向运动。

大学物理知识点总结 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIANBr ∆A rB ryr ∆第一章质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程 ()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△，2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。

明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s )2. 速度（描述物体运动快慢和方向的物理量）平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==，2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。

3. 加速度(是描述速度变化快慢的物理量）平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量：线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。

第一章质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r r称为位矢位矢r xi yj =+rv v ,大小r r ==v 运动方程 ()r r t =r r运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B Ar r r xi yj =-=∆+∆r r r r r △，r =r △路程是△t 时间内质点运动轨迹长度s ∆是标量。

明确r ∆r 、r ∆、s ∆的含义(∆≠∆≠∆rr r s )2. 速度（描述物体运动快慢和方向的物理量）平均速度 x y r x y i j i j t t tu u u D D ==+=+D D r r r r r V V r 瞬时速度(速度) t 0r dr v lim t dt∆→∆==∆r r r(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x ϖϖϖϖϖϖ+=+==，2222y x v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==ϖϖ ds dr dt dt=r 速度的大小称速率。

3. 加速度(是描述速度变化快慢的物理量）平均加速度va t∆=∆rr 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆r r r r △ a r方向指向曲线凹向二.抛体运动运动方程矢量式为 2012r v t gt =+r rr分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量：线位移s 、线速度ds v dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。

Br ∆ A rB ryr ∆第一章 质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△，2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。

明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s ) 2. 速度（描述物体运动快慢和方向的物理量）平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==，2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。

3. 加速度(是描述速度变化快慢的物理量）平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量：线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。

《大学物理学C 》课程基本内容第一章 质点的运动1．直角坐标系、极坐标系、自然坐标系※2．质点运动的描述：位置矢量r 、位移矢量r ∆=)()(t r t t r-∆+、运动方程)(t r r =。

在直角坐标系中,k t z j t y i t x t r)()()()(++=速度：t rv d d=； 加速度：22d d d d t r t v a == 在直角坐标系中，速度k v j v i v v z y x ++=,加速度k a j a i a a z y x++=自然坐标系中，速度 τ v v =＝τts d d ，加速度t n a a a +==n r v t v 2d d +τ 在极坐标系中,角量的描述：角速度t d d θω=，角加速度22d d d d t t θωα==3．运动学的两类基本问题：第一类问题:已知运动方程求速度、加速度等。

此类问题的基本解法是根据各量定义求导数。

第二类问题:已知速度函数(或加速度函数)及初始条件求运动方程。

此类问题的基本解法是根据各量之间的关系求积分。

例如据txv d d =，可写出积分式⎰x d ＝⎰t v d .由此求出运动方程)(t x x =。

4．相对运动：位移:t u r r ∆+'∆=∆ ，速度：u v v+'=,加速度：0a a a +'=第七章 气体动理论1．对“物质的微观模型”的认识；对“理想气体”的理解。

※2．理想气体的压强公式23132v n p k ρε==，其中221v m k =ε※理想气体物态方程：RT MmpV =或 nkT p =理解压强与微观什么有关，即压强的物理含义是什么.※3．理想气体分子的平均平动动能与温度的关系：kT k 23=ε 理解温度与微观什么有关，即温度的物理含义。

※4．能量均分定理：气体处于平衡态时，分子每个自由度上的平均能量均为2kT概念：自由度※理想气体内能公式：RT iM m E 2=5．麦克斯韦气体分子速率分布律 ※麦克斯韦气体分子速率分布函数：定义：vNN v f d d 1)(=函数：22232π2π4)(v v v kTm ekT m f -⎪⎭⎫⎝⎛= 以及v v f NNd )(d =；v v Nf N d )(d =；⎰21d )(v v v v Nf ；⎰21d )(v v v v f 等表示的物理含义。

如何用大学物理的角度去认识位移矢量（一）引言概述：大学物理中，位移矢量是一个基本的概念。

它描述了物体从一个位置到另一个位置的变化，具有大小和方向。

通过用大学物理的角度去认识位移矢量，我们可以更好地理解和应用它。

本文将从五个大点出发，深入探讨如何用大学物理的角度去认识位移矢量。

正文：1. 位移的定义和性质- 位移的定义及其与距离的区别- 位移矢量的表示法和单位- 位移矢量的性质和运算法则- 正、负位移的概念及其物理意义- 绝对位移和相对位移的区别2. 位移的运动学分析- 位移和时间的关系- 平均速度和瞬时速度的概念- 位移和速度之间的关系式- 平均加速度和瞬时加速度的定义- 加速度和速度之间的关系式3. 位移与矢量运算- 矢量的加法和减法运算- 分解矢量的方法和意义- 矢量的数量积和叉积运算- 应用矢量运算求解位移问题的例题分析- 位移与力的关系及其在牛顿第二定律中的应用4. 位移的相关概念及定理- 位移曲线的绘制和特征- 相关速度和相关加速度的概念- 相关速度和相关加速度与位移的关系- 阶梯式位移问题的解析- 直线运动和曲线运动中位移的计算方法5. 位移的应用领域- 位移在机械工程中的应用- 位移在电子工程中的应用- 位移在建筑工程中的应用- 位移在地震学和天文学中的应用- 位移在生物学和医学中的应用总结：通过大学物理的角度去认识位移矢量，我们深入了解了位移的定义和性质，探讨了位移与运动学分析、矢量运算、相关概念及定理的关系，以及位移在各个领域的应用。

这些知识和理解将帮助我们更好地应用位移矢量，并且为相关领域的研究和实践提供基础。