二端口网络的传输参数矩阵

二端口网络z参数求解技巧二端口网络是指由两个端口组成的网络，其中一个端口为输入端口，另一个端口为输出端口。

在分析和设计二端口网络时，我们常常使用参数化方法，其中最常见的是使用z参数。

z参数是指输入端口和输出端口之间的电压和电流之间的关系。

在二端口网络中，输入端口的电流I1和电压V1以及输出端口的电流I2和电压V2之间存在以下关系：```V1 = Z11 * I1 + Z12 * I2V2 = Z21 * I1 + Z22 * I2```其中，Z11、Z12、Z21和Z22是参数矩阵，代表了电路元件的特性。

我们可以利用这些参数来分析和计算二端口网络的性能。

接下来，我将介绍一些求解二端口网络z参数的技巧。

1. 网络简化：首先，我们要对二端口网络进行简化，即将网络中的电路元件替换为等效电路，以便更方便地分析。

我们可以使用电路分析方法，如电压分压法、电流分流法等，将网络简化为电阻、电容和电感等基本元件的串并联组合。

2. 确定输入和输出量：在分析二端口网络时，我们需要确定输入和输出量。

输入和输出量可以是电流和电压之间的关系，也可以是功率和电阻之间的关系。

通过确定输入和输出量，我们可以更准确地描述和计算二端口网络的特性。

3. 确定参数值：在求解z参数时，我们需要确定参数矩阵Z11、Z12、Z21和Z22的具体值。

参数值可以通过实验或仿真等方式获取。

如果我们已经知道了电路元件的数值，我们可以直接使用电路分析方法求解参数值。

如果我们只知道电路的结构和拓扑关系，我们可以使用矩阵分析方法求解参数值。

4. 参数矩阵运算：一旦确定了参数值，我们就可以进行参数矩阵的运算。

参数矩阵的运算包括矩阵加法、矩阵减法、矩阵乘法和矩阵逆运算等。

通过参数矩阵的运算，我们可以得到输入端口和输出端口之间的关系。

5. 分析和计算：最后，我们可以利用参数矩阵进行分析和计算。

例如，如果我们已知输入端口的电流和电压，我们可以使用参数矩阵得到输出端口的电流和电压。

三、 二端口网络的T 方程和T 参数在上述内容中我们已经介绍了Y 参数和Z 参数的求法，Y 参数和Z 参数都可用来描述一个二端口网络的端口外特性。

但在许多工程实际问题中，往往还要求知道一个端口的电流、电压与另一个端口的电流、电压之间的直接关系。

若把Y 参数方程：22212122121111U Y U Y I U Y U Y I +=+=的第二式化为2212212211I Y U Y Y U +-= 代入Y 参数方程第一式中，整理可得：221112212211121)(I Y Y U Y Y Y Y I +-= 把以上两式写成下列形式⎪⎩⎪⎨⎧-=-=221221I D U C I I B U A U式中 ⎪⎪⎩⎪⎪⎨⎧-=-=-=-=2111212211212121221Y Y D Y Y Y Y C Y B Y Y AA 、B 、C 、D 称为二端口网络的一般参数、传输参数、T 参数或A 参数。

它们的具体含义可用下式说明：0221==I U U A A 是输出端开路时，输入电压与输出电压的比值；0221=-=I I U B B 是输出端短路时，输入端对输出端的转移阻抗；0221==I U I C C 是输出端开路时，输入端对输出端的转移导纳；0221==U I I D D 是输出端短路时，输入电流与输出电流的比值。

可见，A 是一个量纲为一的量纲；B 的量纲为Ω；C 的量纲为s ；D 也是量纲为一的量。

对于无源线性二端口网络A 、B 、C 、D 只有3个是独立的，因为Y 11＝Y 22，故A ＝D 。

所以T 参数方程为：其中 ⎥⎦⎤⎢⎣⎡=D C B A T ，称为T 参数矩阵。

AD BC 可逆时，-=1AD BC A D =对称时满足:-=1,【例】 求例1中电路的T 参数【解】：方法一：根据定义求解（略）方法二：根据KCL 直接列方程求解（略）方法三：根据T 参数与Y 参数或Z 参数的转换公式(可在表6-1中查到)求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∆---=2111212121221Y Y Y Y Y Y Y T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆=1222212121111Z Z Z Z Z Z Z T 其中 2112221122211211Y Y Y Y Y Y Y Y Y -==∆2112221122211211Z Z Z Z Z Z Z Z Z -==∆因为已知例1的 s Y ⎥⎦⎤⎢⎣⎡--=4.02.02.04.0 12.004.016.0=-=∆Y所以 ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=26.0522.04.02.012.02.012.04.0T⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2211D I U C B A I U【例 】：已知...1111122...2211222(1)(2)U Z I Z I U Z I Z I =+=+ ，求T 参数。

实验一电路元件伏安特性的测量一、实验目的1．学习测量电阻元件伏安特性的方法；2．掌握线性电阻、非线性电阻元件伏安特性的逐点测试法；3．掌握直流稳压电源和直流电压表、直流电流表的使用方法。

二、实验原理在任何时刻，线性电阻元件两端的电压与电流的关系，符合欧姆定律。

任何一个二端电阻元件的特性可用该元件上的端电压U与通过该元件的电流I之间的函数关系式I＝f(U)来表示，即用I－U平面上的一条曲线来表征，这条曲线称为电阻元件的伏安特性曲线。

根据伏安特性的不同，电阻元件分为两大类：线性电阻和非线性电阻。

线性电阻元件的伏安特性曲线是一条通过坐标原点的直线，如图1-1（a）所示。

该直线的斜率只由电阻元件的电阻值R决定，其阻值R为常数，与元件两端的电压U和通过该元件的电流I无关；非线性电阻元件的伏安特性曲线不是一条经过坐标原点的直线，其阻值R不是常数，即在不同的电压作用下，电阻值是不同的。

常见的非线性电阻如白炽灯丝、普通二极管、稳压二极管等，它们的伏安特性曲线如图1-1（b）、（c）、（d）所示。

在图1-1中，U ＞0的部分为正向特性，U＜0的部分为反向特性。

(a)线性电阻(b)白炽灯丝绘制伏安特性曲线通常采用逐点测试法，电阻元件在不同的端电压U 作用下，测量出相应的电流I ，然后逐点绘制出伏安特性曲线I ＝f (U )，根据伏安特性曲线便可计算出电阻元件的阻值。

三、实验设备与器件1 台2.直流电压表 1 块3.直流电流表 1 块4.万用表 1 块5.白炽灯泡 1 只6. 二极管 1 只7.稳压二极管 1 只8.电阻元件 2 只四、实验内容1．测定线性电阻的伏安特性 按图1-2接线。

调节直流稳压电源的输出电压U ，从0伏开始缓慢地增加（不得超过10V ），在表1-1中记下相应的电压表和电流表的读数。

表1-1 测定线性电阻的伏安特性U （V ） 0 1 2 3 4 5 6 7 8 9 10 I （mA ） 012．测定白炽灯泡的伏安特性将图1-2中的1kΩ线性电阻R 换成一只的灯泡，重复1的步骤，在表1-2中记下相应的电压表和电流表的读数。

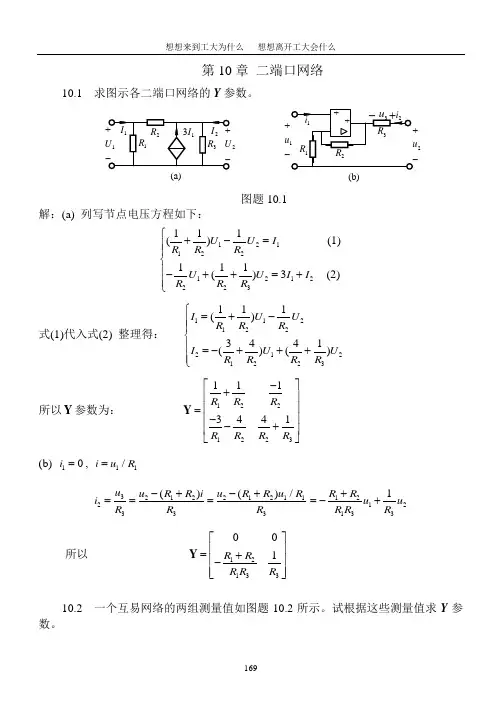
第10章 二端口网络10.1 求图示各二端口网络的Y 参数。

22u (b)图题10.1解：(a) 列写节点电压方程如下：1211221212223111() (1)111()3 (2)U U I R R R U U I I R R R ⎧+-=⎪⎪⎨⎪-++=+⎪⎩ 式(1)代入式(2) 整理得： 1121222121223111()3441()()I U U R R R I U U R R R R ⎧=+-⎪⎪⎨⎪=-+++⎪⎩所以Y 参数为：12212231113441R R R R RR R -⎡⎤+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦Y (b) 10i =, 11/i u R =3212212112333()()/u u R R i u R R u R i R R R -+-+===12121331R R u u R R R +=-+ 所以12133001R R R R R ⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦Y10.2 一个互易网络的两组测量值如图题10.2所示。

试根据这些测量值求Y 参数。

(a)(b)22-+U图题10.2解：图(a)中11222A,j2V 2j5j 10V j5A I U U I ===⨯==-,,由Y 参数方程得：11112221222j2j 10 (1)j5j2j 10 (2)I Y Y I Y Y ⎧==⨯+⨯⎨=-=⨯+⨯⎩ 由图(b)得 222jA 1V I Y ==⨯ (3) 对互易网络有：1221Y Y = (4)由式(3) 得： 22j 1S Y =，代入式(2) 得：2112( 2.5j5)S Y Y ==-- 再代入式(１)得：11(12.5j24)S Y =+ 所以12.5j2425j52.5j5j1.+--⎡⎤=⎢⎥--⎣⎦Y S 10.3 求图示各二端口网络的Z 参数。

(b)图题10.3解 (a)：按网孔列写KVL 方程得1211221(2)2 (1)2(2)3 (2)R R I RI U RI R R I U U ++=⎧⎨++=+⎩ 将式(1)代入式(2)整理得1122123273U RI RI U RI RI =+⎧⎨=--⎩ 所以 3273RR R R ⎡⎤=⎢⎥--⎣⎦Z(b) 将∆联接的三个阻抗转换成Y 形联接，如图(c)所示，由此电路可直接写出Z 参数1j j j 0+⎡⎤=⎢⎥⎣⎦Z Ω10.4求图示各二端口网络的A 参数。

姓名班级学号实验日期节次教师签字成绩互易二端口网络特性的研究一. 实验目的:1.学习掌握线性无源二端口网络传输参数的测量方法；2.用实验的方法验证二端口网络的等效电路定理；3.了解二端口网络的特性和二端口网络级联的特性；二.总体设计方案和技术路线:(1) 二端口网络是一种使用广泛的电路形式，其外部性能取决于两个端口电压电流的之间的相互关系，这种关系可以由网络本身一些参数来表示，利用这些参数可以比较方便了解端口网络在传递电能和信号方面的特性。

(2)二端口网络的传输参数方程：如上图传输参数方程是用输出端口电压U2与电流I2来表示输入端电压U1与电流I1的方程U1=A11U2-A12I2I1=A21U2-A22I2其中A11 A12 A21 A22 为二端口网络的传输参数，这些参数可以表示二端口网络的所有特性。

21011101021i U A R I A ===21121122S S Su U A R I A ===12022202021i U A R I A ===12122211S S Su U A R I A ===考虑到远距离输电线二端口测量采用同时测量法比较费力麻烦，故本次实验采用间接测量法并验证其准确性。

在二端口网络的AA ’端口接上直流电源，在BB ’端开路和短路的情况下分别得到开路阻抗10R 及短路阻抗1S R ，即：再把电源接在BB ’端口，在AA ’端口开路和短路的情况下分别得到开路阻抗20R 及短路阻抗2S R ，即：上述四个参数只有三个是独立的，由此可以计算得到二端口的传输参数。

(3)线性无源二端口网络可以用T 型电路和π型电路等效，由电路理论基础知识可知111211A R A -=； 222211A R A -= ； 3211R A = ； π型电路三个电阻参数由以下公式给出：121221A R A =- ；221R A = ； 123111A R A =- ；T 型电路π型电路搭建T 型和π型电路，测出其传输参数与原二端口网络电路的传输参数比较分析。

[考研类试卷]电路历年真题试卷汇编151 (清华大学2007年考研试题)求如图16—6所示二端口网络的传输参数方程。

2 (清华大学2007年考研试题)如图16—7所示，A为一含独立源线性网络。

当Z=0时，测得；当Z=∞时，测得。

试求当Z为任意值时的电压。

3 (清华大学2006年考研试题)如图16一10所示电路中，已知二端口N的传输参数(1)求R L为多少时其上可获得最大的功率，并求此最大功率值；(2)求此时5A电流源发出的功率。

4 (清华大学2005年考研试题)电路如图16—12(a)所示，其中N为仅含电阻的对称二端口网络。

当R f=50Q时，它可获得最大功率P max=20W。

(1)求二端口网络N的传输参数；(2)当R f断开时，为了使电压源发出的功率不变，需在输入端并上一个电阻R，如图16—12(b)所示，求此电阻R的值。

5 (北京大学2006年考研试题)试求图16-14中电路ab端的等效电阻值。

6 (北京大学2005年考研试题)如图16一16所示的含受控电压源(一R m I1)双端口网络，其1-1'端用电压源激励，2-2'端以R L为负载。

求：(1)该双端口网络的Z参量；(2)从1一1'端看进去的输入阻抗；(3)2-2'端的开路电压。

7 (华中科技大学2006年考研试题)如图16一17所示电路，N为线性电阻性二端口网络，已知U S=20V。

当R=∞时，I1=0．4A，U S=8V；当R=0时，I1=IA，I2=-0．5A。

试确定R=10Ω时的输入电阻R i和输出电阻R0。

8 (华中科技大学2005年考研试题)如图16一18所示含理想变压器的电路中，N为线性无源对称双口网络，Z1=Z2=0．5Z3=Z，2—2'端口的开路电压为，2—2'端口图示方向下的短路电流为。

试确定双口网络N的Z参数。

假定、Z已知。

9 (武汉大学2007年考研试题)在如图16—20(a)所示的电路中，N1和N2是两个完全相同的仅含线性电阻的对称双口网络，已知条件如图16-20(a)中所示。

第七章二端口网络§7-2 二端口网络的参数方程及参数一、导纳参数方程、导纳参数如图7-4所示无源线性二端口电路中，电压、电流参考方向如图所示，电路已达稳定。

假设端口电压、为已知量，、为待求量，用、表示、时，1U 2U 1I 2I 1U 2U 1I 2I 根据叠加定理，二端口网络的方程为22212122121111U Y U Y I U Y U Y I +=+=式中系数具有导纳性质，称为二端口网络的导纳参数（参数），所以上式称为导纳方程或方程。

无源二端口网络的Y 参数，仅与网络的内部结构、元件参数、工作频率有关，而与输入信号的振幅、负载的情况无关。

因此，这些参数描述了二端口网络本身的电特性。

所以导纳方程可以用矩阵形式表示为⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2221121121Y Y Y Y I I ⎥⎥⎦⎤⎢⎢⎣⎡21U U UY I =⎥⎥⎦⎤⎢⎢⎣⎡=21I I I ⎥⎥⎦⎤⎢⎢⎣⎡=21U U U 22122111⎥⎦⎤⎢⎣⎡=Y Y Y Y Y 为端口电流列向量；为端口电压列向量；为导纳矩阵或Y 矩阵011112==U U I Y 012212==U UIY 022221==U UIY 021121==U UIY 由于每个Y 参数都是在一个端口短路情况下分析得到的，因此参数也称为短路导纳参数。

对于无源线性二端口网络可以证明，输入和输出互换位置时，不会改变由同一激励所产生的响应。

由此得出2112Y Y =即在参数中，只有三个参数是独立的，这样的网络具有互易性，称为互易网络。

如果二端口网络是对称的（即对称二端口网络），则输出端口和输入端口互换位置后，电压和电流均不改变，有2211Y Y =对互易且对称二端口网络中，则参数中只有两个参数是独立的。

【例7-1】求图7-5所示二端口网络的导纳矩阵。

解将端口2短路sj U I Y U )42(011112-=== sj U I Y U 4012212=== sj U I Y U 4021121=== sj U I Y U 3022221-=== S将端口1短路。