高等传热学作业.(DOC)

高等传热学作业修订版 IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】第一章1-4、试写出各向异性介质在球坐标系)(ϕθ、、r 中的非稳态导热方程，已知坐标为导热系数主轴。

解：球坐标微元控制体如图所示：热流密度矢量和傅里叶定律通用表达式为：→→→∂∂+∂∂+∂∂-=∆-=k T r k j T r k i r T k T k q r ϕθθϕθsin 11'' （1-1）根据能量守恒：st out g in E E E E ••••=-+ϕθθρϕθθϕϕθθϕθd drd r tT c d drd r q d q d q dr r q p r sin sin 22∂∂=+∂∂-∂∂-∂∂-• （1-2） 导热速率可根据傅里叶定律计算：ϕθθθθd r dr Tr k q sin ⋅∂∂-= （1-3） 将上述式子代入（1-4-3）可得到)51(sin sin )sin ()sin (sin )(222-∂∂=+⋅⋅∂∂∂∂+⋅⋅∂∂∂∂+⋅⋅∂∂⋅∂∂⋅ϕθθρϕθθϕθϕθϕϕθθθθϕθθϕθd drd r t T c d drd r q d rd dr T r k rd d dr T r k d d dr r T r k r p r 对于各向异性材料，化简整理后可得到：tTc q T r k T r k r T r r r k pr ∂∂=+∂∂+∂∂∂∂+∂∂∂∂⋅ρϕθθθθθϕθ2222222sin )(sin sin )( （1-6）第二章2-3、一长方柱体的上下表面(x=0，x=δ)的温度分别保持为1t 和2t ，两侧面(L y ±=)向温度为1t 的周围介质散热，表面传热系数为h 。

试用分离变量法求解长方柱体中的稳态温度场。

解：根据题意画出示意图：（1）设f f f t t t t t t -=-=-=2211,,θθθ，根据题意写出下列方程组⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+∂∂==∂∂======∂∂+∂∂00000212222θθλθθθδθθθθh y L y y y x x y x （2-1）解上述方程可以把θ分解成两部分I θ和∏θ两部分分别求解，然后运用叠加原理∏+=θθθI 得出最终温度场，一下为分解的I θ和∏θ两部分： （2）首先求解温度场I θ用分离变量法假设所求的温度分布),(y x I θ可以表示成一个x 的函数和一个y 的函数的乘积，即)()(),(11y Y x X y x I =θ （2-2）将上式代入I θ的导热微分方程中，得到012121212=+X dy Y d Y dx X d ，即21''11''1ε=-=Y Y X X ，上式等号左边是x 的函数，右边是y 的函数，只有他们都等于一个常数时才可能成立，记这个常数为2ε。

传热学作业第一章绪论能量平衡分析1-8.有两个外形相同的保温杯A与B，注入同样温度、同样体积的热水后不久，A杯的外表面就可以感觉到热，而B杯的外表面则感觉不到温度的变化，试问哪个保温杯的质量较好？答：Ｂ：杯子的保温质量好。

因为保温好的杯子热量从杯子内部传出的热量少，经外部散热以后，温度变化很小，因此几乎感觉不到热。

导热1-10 一炉子的炉墙厚13cm，总面积为20m2，平均导热系数为1.04w/m.k，内外壁温分别是520℃及50℃。

试计算通过炉墙的热损失。

如果所燃用的煤的发热量是2.09×104kJ/kg，问每天因热损失要用掉多少千克煤？解：根据傅利叶公式每天用煤Q??A?t1.04?20?(520?50)??75.2KW?0.1324?3600?75.2?310.9Kg/d4 2.09?10 1-12 在一次测定空气横向流过单根圆管的对流换热实验中，得到下列数据：管壁平均温度tw=69℃，空气温度tf=20℃，管子外径d=14mm，加热段长80mm，输入加热段的功率8.5w，如果全部热量通过对流换热传给空气，试问此时的对流换热表面传热系数多大？解：根据牛顿冷却公式q?2?rlh?tw?tf? qh??dtw?tf＝49.33W/(m2.k) 所以热阻分析1-21 有一台气体冷却器，气侧表面传热系数h1＝95W/(m2.K)，壁面厚?＝2.5mm，??46.5W/(m.K)水侧表面传热系数h2?5800W/(m2.K)。

设传热壁可以看成平壁，试计算各个环节单位面积的热阻及从气到水的总传热系数。

你能否指出，为了强化这一传热过程，应首先从哪一环节着手？解：R1?111?0.010526;R20.0025?5.376?10?5;R31.724?10?4;h1h25800?46. 5K?则111h1h2?＝94.7W/(m2.K)，应强化气体侧表面传热。

第二章稳态热传导平板导热2-2 一冷藏室的墙由钢皮矿渣棉及石棉板三层叠合构成，各层的厚度依次为0.794mm.,152mm及9.5mm，导热系数分别为45W/(m.K),0.07W/(m.K)及0.1W/(m.K)。

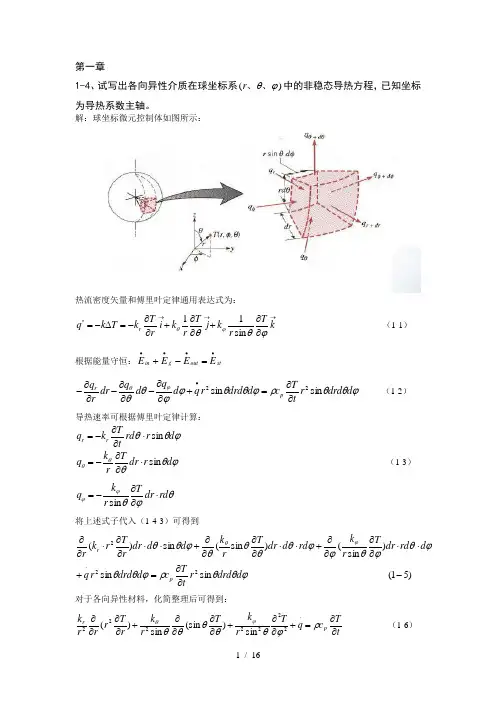
1-4、试写出各向异性介质在球坐标系)(ϕθ、、r 中的非稳态导热方程，已知坐标为导热系数主轴。

解：球坐标微元控制体如图所示：热流密度矢量和傅里叶定律通用表达式为：→→→∂∂+∂∂+∂∂-=∆-=k T r k j T r k i r T k T k q r ϕθθϕθsin 11'' （1-1）根据能量守恒：st out g in E E E E ••••=-+ϕθθρϕθθϕϕθθϕθd drd r tT c d drd r q d q d q dr r q p r sin sin 22∂∂=+∂∂-∂∂-∂∂-• （1-2） 导热速率可根据傅里叶定律计算：ϕθθd r rd t Tk q rr sin ⋅∂∂-= ϕθθθθd r dr T r k q sin ⋅∂∂-= （1-3）θϕθϕϕrd dr Tr k q ⋅∂∂-=sin将上述式子代入（1-4-3）可得到)51(sin sin )sin ()sin (sin )(222-∂∂=+⋅⋅∂∂∂∂+⋅⋅∂∂∂∂+⋅⋅∂∂⋅∂∂⋅ϕθθρϕθθϕθϕθϕϕθθθθϕθθϕθd drd r tT c d drd r q d rd dr Tr k rd d dr T r k d d dr r T r k r p r 对于各向异性材料，化简整理后可得到：tTc q T r k T r k r T r r r k p r ∂∂=+∂∂+∂∂∂∂+∂∂∂∂⋅ρϕθθθθθϕθ2222222sin )(sin sin )( （1-6）2-3、一长方柱体的上下表面(x=0，x=δ)的温度分别保持为1t 和2t ，两侧面(L y ±=)向温度为1t 的周围介质散热，表面传热系数为h 。

试用分离变量法求解长方柱体中的稳态温度场。

解：根据题意画出示意图：（1）设f f f t t t t t t -=-=-=2211,,θθθ，根据题意写出下列方程组⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+∂∂==∂∂======∂∂+∂∂00000212222θθλθθθδθθθθh y L y y y x x y x（2-1）解上述方程可以把θ分解成两部分I θ和∏θ两部分分别求解，然后运用叠加原理∏+=θθθI 得出最终温度场，一下为分解的I θ和∏θ两部分：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+∂∂==∂∂======∂∂+∂∂00000212222I I I I I I I h y L y y y x x y x θθλθθθδθθθθ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧=+∂∂==∂∂======∂∂+∂∂∏∏∏∏∏∏∏∏0000002222θθλθθδθθθθh y L y y y x x y x （2）首先求解温度场I θ用分离变量法假设所求的温度分布),(y x I θ可以表示成一个x 的函数和一个y 的函数的乘积，即)()(),(11y Y x X y x I =θ （2-2）将上式代入I θ的导热微分方程中，得到012121212=+X dyY d Y dx X d ，即21''11''1ε=-=Y Y X X ，上式等号左边是x 的函数，右边是y 的函数，只有他们都等于一个常数时才可能成立，记这个常数为2ε。

高等传热学导热练习题1. 试求圆柱坐标),,(z r φ的拉梅系数。

圆柱坐标(,,)r z φ和直角坐标(,,)x y z 的 关系是：cos x r φ=，sin y r φ=，z z = 解：由题目条件得：2222221cos sin 1x y z a r r r φφ∂∂∂⎛⎫⎛⎫⎛⎫=++=+= ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭得：11a =()()22222222sin cos x y z a r r r φφφφφ⎛⎫⎛⎫⎛⎫∂∂∂=++=−+= ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭得：2a r =222231x y z a z z z ∂∂∂⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭得：31a =123a a a a r ==3. 一维无限大平板，0≤x ≤L ，初始温度为F(x)。

当时间0>τ时，x=0处与x=L 处的边界温度维持零度。

试求时间0>τ时，平板内温度),(τx t 的表达式。

并求当初始温度F(x)=t 0=常数这种特殊情况下的温度),(τx t 。

解：该导热问题的数学描写为：()()()()()()22,,1,0,00,0,0,0t x t x x L x t t L t x F x τττατττ⎧∂∂=<<>⎪∂∂⎪⎪=⎨⎪=⎪⎪=⎩ 分离变量：()()(),t x X x ττ=⋅Γ 代入温度微分方程得：()()()()22211d X x d const X x dx d τβαττΓ==−=Γ得时间函数：()2e αβττ−Γ=空间变量的特征值问题为：()()()()222000d X x X x dxX X L β⎧+=⎪⎨⎪==⎩查表得：()(),sin m m X x x ββ=，()12m N Lβ=，m β是()sin 0m L β=的正根 温度通解为：()()21,,m m m m t x c X x e αβττβ∞−==∑代入初始条件可得：()()(),Lm mm X x F x dxc N ββ=⎰将上式代入温度的通用级数解，可得：()()()()2012,sin sin m L m m m t x x F x dx x e Lαβττββ∞−='''=⋅⋅∑⎰ 对于()0F x const t ==的情形，可得：()()()2011cos 2,sin m m m m m L t t x x e Lαβτβτββ∞−=−=⋅∑4. 一维无限大平板，0≤x ≤L ，初始温度为F(x)。

传热学实验试题及答案高中一、选择题（每题2分，共10分）1. 传热的基本方式有哪些？A. 导热、对流、辐射B. 导热、对流、蒸发C. 导热、对流、扩散D. 蒸发、对流、辐射2. 以下哪个不是影响导热速率的因素？A. 材料的导热系数B. 温度差C. 材料的厚度D. 材料的颜色3. 对流换热的特点是什么？A. 只发生在固体内部B. 只发生在液体和气体中C. 需要流体的流动D. 与流体的流动无关4. 辐射换热的特点是？A. 需要介质B. 与温度无关C. 可以在真空中进行D. 只发生在固体表面5. 以下哪个公式用于计算稳态导热的热流量？A. Q = h * A * ΔTB. Q = k * A * ΔT / dC. Q = c * ρ * ΔTD. Q = m * L * ΔT / t答案：1-5 A B C C B二、填空题（每空1分，共10分）1. 导热的基本定律是________，表达式为Q = k * A * ΔT / d。

2. 当流体的流动状态发生变化时，换热方式可能由________转变为对流换热。

3. 辐射换热不需要介质，可以在________中进行。

4. 影响对流换热的因素包括流体的________、________和流速。

5. 稳态导热条件下，物体内部某点的温度随时间________。

答案：1. 傅里叶定律 2. 导热 3. 真空 4. 温度、压力 5. 不变三、简答题（每题5分，共20分）1. 简述导热、对流和辐射三种传热方式的区别。

2. 描述稳态导热和非稳态导热的特点。

3. 解释为什么说辐射换热是所有物体都具有的自然现象。

4. 举例说明在日常生活中如何应用对流换热的原理。

答案：1. 导热是热量通过物体内部分子振动和自由电子运动传递的过程，主要发生在固体中；对流是流体中温度不同的各部分之间通过宏观位移传递热量的过程，主要发生在液体和气体中；辐射是物体因温度产生的电磁波向外传递热量的过程，可以在真空中进行，所有物体都具有辐射能力。

第九章4．一工厂中采用0.1MPa 的饱和水蒸气在—金属竖直薄壁上凝结，对置于壁面另一侧的物体进行加热处理。

已知竖壁与蒸汽接触的表面的平均壁温为70 ℃，壁高1.2m ，宽300 mm 。

在此条件下，一被加热物体的平均温度可以在半小时内升高30℃，试确定这一物体的平均热容量(不考虑散热损失)。

解:本题应注意热平衡过程，水蒸气的凝结放热量应等于被加热物体的吸热量。

P=0.1Mpa=105Pa,t s =100℃,r=2257.1kJ/kg, t m =21( t s + t w )= 21(100+70) ℃=85℃。

查教材附录5，水的物性为：ρ=958.4kg/m 3;λ=0.683 W ／(m 2·℃);µ=282.5×10-6N·s/m 2假设流态为层流：4132)(13.1⎥⎦⎤⎢⎣⎡-=w s t t l r g h μλρ416332)70100(2.1105.282102257683.081.94.95813.1⎥⎦⎤⎢⎣⎡-⨯⨯⨯⨯⨯⨯⨯=- W ／(m 2·℃) =5677 W ／(m 2·℃)36102257105.2822.13056774)(4Re ⨯⨯⨯⨯⨯⨯=-=-r t t hl w s c μ=1282<1800流态为层流，假设层流正确Φ=ωl t t h w s )(-=5677×（100−70）×1.2×0.3W=61312W凝结换热量=物体吸热量Φ∆τ=mc p ∆t61068.330603061312⨯=⨯⨯=∆Φ∆=t mc p τJ/℃ 16．当液体在一定压力下做大容器饱和沸腾时，欲使表面传热系数增加10倍，沸腾温差应增加几倍?如果同一液体在圆管内充分发展段做单相湍流换热，为使表面传热系数增加10倍，流速应增加多少倍?维持流体流动所消耗的功将增加多少倍?设物性为常数。

1-5 椭球坐标系（),,ϕθη由η=常数的椭球面，θ=常数的双曲线面和ϕ=常数的平面组成。

如果椭球坐标系与直角坐标系的关系为：θηϕθηϕθηcos sin sin cos sin Ach z Ash y Ash x === 试证明该椭球坐标系的拉梅系数为：1H =ηH =2222cos sin θηθηsh ch A + θH H =12222cos sin θηθηsh ch A += ψH H =1θηsin Ash =并证明椭球坐标系中拉普拉斯算子的表达式为：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+∂∂+=∇θθθηηηθηθηt t t cth t sh ch A t cot )cos sin (12222222222ψθη22222sin 1∂∂+tsh A 解：（1）由式1 -2-18知 2221)()()(ηηηη∂∂+∂∂+∂∂==zy x H H 22222222222sin sin cos cos cos θηψθηψθηch A sh A sh A ++=θηsin Ash =（2）由式1 -2 - 25知ψθηθθθηηηθηθηψθηθθηθηθηθηθηηθηθηψθθθηηηψψψθθθηηηψψηθηη22222222222222222222222222222223332233222122321321223322333212322212312sin 1cot )cos sin (1sin 1sin cos sin sin )cos sin (11]11[1])([1)( )()([1)3,2,1()(1∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+∂∂+=∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+∂∂+=∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂=∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂+∂∂∂∂=∂∂∂∂+∂∂∂∂+∂∂∂∂==∂∂∂∂=∇∑=tsh A t t t cth t sh ch A tsh A t Ash Ach t t Ash Ach t sh ch A t H t H H t t H H t H H t H H H t H H H t H t H t H t H H H H tH H t H H t H H H i x t H H x Ht ii i i3-2 大平壁的初始温度均匀为0t ，从某一时刻起其两表面的温度突然降为w t 并保持不变，试求:（1）写出该导热问题的数学描述； （2）用分离变量法求解平壁中的温度场。

传热学大作业二维稳态计算练习东南大学院系：能源与环境学院二维稳态计算练习1、原始题目及要求二维平壁的节点划分及边界条件如上图所示，计算要求如下：1. 写出各未知温度节点的代数方程2. 分别给出G-S迭代和Jacobi迭代程序3. 程序中给出两种自动判定收敛的方法4. 考察三种不同初值时的收敛快慢5. 上下边界的热流量（λ=1W/(m℃））6. 绘出最终结果的等值线报告要求如下：1. 原始题目及要求2. 各节点的离散化的代数方程3. 源程序4. 不同初值时的收敛快慢5. 上下边界的热流量（λ=1W/(m℃））6. 计算结果的等温线图7. 计算小结2. 各节点的离散化的代数方程将上图二维平壁的节点编号如下各节点的离散化代数方程如下：t i−1,j+t i+1,j+t i,j−1+t i,j+1−4t i,j=0 2≤i≤4，2≤j≤4t i,j=200 i=1，1≤j≤5t i,j=100 1≤i≤5， j=52t i,j+1+t i−1,j+t i+1,j−(4+2ℎ△xλ)t i,j+2ℎ△xλt∞=0 2≤i≤4， j=1t i,j−1+t i,j+1+2t i−1,j−4t i,j=0 i=5，2≤j≤4由于（5，1）为歧义点，现将其近似认为对流边界外部拐点，其节点离散化代数方程为：t4,1+t5,2−(2+2ℎ△xλ)t5,1+2ℎ△xλt∞=0△x=△y=1 λ=1Wℎ=10W23.源程序（1）、G-S迭代算法Matlab源程序：t=zeros(5,5);t0=zeros(5,5);e=0.001;h=10;tf=10;for j=1:5 %上边界节点t(1,j)=200;endfor i=1:5 %右边界节点t(i,5)=100;endfor k=1:100for i=2:4 %内部节点for j=2:4t(i,j)=(t(i-1,j)+t(i+1,j)+t(i,j-1)+t(i,j+1))/4;endendfor i=2:4;%左边界节点t(i,1)=(2*t(i,2)+t(i-1,1)+t(i+1,1)+2*h*tf/n)/(4+2*h/n); endfor j=2:4; %下边界节点t(5,j)=(t(5,j-1)+t(5,j+1)+2*t(4,j))/4;endt(5,1)=(t(4,1)+t(5,2)+2*h*tf/n)/(2+2*h/n); %(5,1)节点dtmax=0;for i=1:5for j=1:5dtmax=max(abs(t(i,j)-t0(i,j)),dtmax);endendcontour(t',30);t0=t;tpause;if dtmax<e break; endend（2）Jacobi迭代Matlab源程序t=zeros(5,5);t0=zeros(5,5);e=0.001;h=10;n=1;tf=10;Num=0;for j=1:5 %上边界节点t(1,j)=200;for i=1:5 %右边界节点t(i,5)=100;endt0=t;for k=1:100for i=2:4 %内部节点for j=2:4t(i,j)=(t0(i-1,j)+t0(i+1,j)+t0(i,j-1)+t0(i,j+1))/4;endendfor i=2:4;%左边界节点t(i,1)=(2*t0(i,2)+t0(i-1,1)+t0(i+1,1)+2*h*tf/n)/(4+2*h/n); endfor j=2:4; %下边界节点t(5,j)=(t0(5,j-1)+t0(5,j+1)+2*t0(4,j))/4;endt(5,1)=(t(4,1)+t(5,2)+2*h*tf/n)/(2+2*h/n); %(5,1)节点dtmax=0;for i=1:5for j=1:5dtmax=max(abs(t(i,j)-t0(i,j)),dtmax);endendcontour(t',30);t0=t;tpause;Num=Num+1;Numif dtmax<e break; endend比较两种方法的收敛速度：G-S法最终输出结果如下：t =200.0000 200.0000 200.0000 200.0000 100.000026.2727 107.4214 135.1054 135.4873 100.000015.7010 68.3085 97.5138 106.8443 100.000013.9343 52.5990 79.7981 94.3766 100.000013.5242 48.3564 74.7042 90.8644 100.0000Num =29Jacobi法最终结果如下：t =200.0000 200.0000 200.0000 200.0000 100.000026.2695 107.3899 135.0717 135.4675 100.000015.6897 68.2189 97.4308 106.7988 100.000013.8464 52.3668 79.6357 94.2985 100.000011.8916 47.7681 74.4495 90.7611 100.0000Num =53由此可见，G-S法比Jacobi法收敛速度快，就本题初值为0而言，收敛速度大概为其两倍左右。

Homework 5.21. Slug flow in a tube(u(r) = V) with a fully developed temperature profile:- Constant heat flux - What is T(r)?·Remember dT m /dx = constant·Use dT/dr = 0 at r = 0 and T w at r = R to get ingration constants - What is Nu? A: 根据能量方程，221p p T T T T c u c v k rk r x r r rx ρρ∂∂∂∂∂⎛⎫+=+ ⎪∂∂∂∂∂⎝⎭(1) 对于充分发展的管内弹状流，u=0, 且由于mdT T x dx∂=∂= constant ，因此(1)式可化简为： 1m p dT Tc Vk r dx r r rρ∂∂⎛⎫= ⎪∂∂⎝⎭(2) 解之可得，212(r)ln 4p m V c dT T r C r C k dxρ=⋅⋅++ (3) 根据边界条件，0,, T(r)=T w Tr rr R ∂==∂= 代入(3)中，得到C 1=0, 224p m w V c dT C T R k dxρ=-⋅平均温度201()2Rm T T r rdr R ππ=⎰ 28()m w m p dT kT T dx V c Rρ=- 因此，得到22222(r)(1)22()4m w m w w m dT VR r r T T T T T T dx R Rα=+⋅⋅-=-+-2288q''h()()()222p p m w m w m w m p mc c R V dT k kT T T T T T R dx R V c R Rρπππρ=-=⋅=⋅-=- 28h d h R Nu k k⋅⋅===2. Fully developed Poiseuille flow between parallel plates- Constant heat flux- Top and bottom at the same temperature - Neglect viscous dissipation - What is T(y)?·Remember dT m /dx = constant·Use T w at y = 0 and y = h to get integration constants - What is Nu? A: 根据能量方程，2222()p p T T T T c u c v k x y x yρρ∂∂∂∂+=+∂∂∂∂ (1)对于x 方向充分发展的Poiseuille 流，v=w=0 由于mdT T x dx∂=∂= constant ，(1)式可化为： 22p T T c u k x yρ∂∂=∂∂ (2)根据01()hm u u y dy h =⎰，且22()6()m u y y y u h h=-，代入得到22226()m m p dT y y Tu c k h h dx yρ∂-=∂解得温度分布为34122()()2p m m c u dT y y T y C y C k dx h h ρ=⋅-++ (3)根据Poiseuille 流边界条件：0,w y T T == ,w y h T T ==带入(3)式中解得，12p m mc u dT C h kdxρ=-, 2w C T =因此，得到温度分布为342()()22p m p m m m w c u c u dT dT y y T y y T k dx h h k dxρρ=⋅--⋅+ 根据342220011()()6()22h hp m p m m m m w m m m c u c u dT dT y y y y T T y udy y T u dy hu hu k dx h h k dx h h ρρ⎡⎤⎡⎤==⋅--+-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰∴2140()17m w m m p dT kT T dx u c hρ=- ∴ 140q''h()()17p m w m w m mc dT kT T T T L dx L =-=⋅=- Nu 14017=Homework 5.31. Find the equation for the boundary layer thickness δ and for C f for:23()u y a b c d Uηηη=+++ Compare to the exact values and the fourth order equation solutions. A: 对于23()u y a b c d Uηηη=+++，根据边界条件， 0, u=0y =，∴ a = 0,y u U δ==，∴ 1 = b + c + d 对于平板，有220y uy =∂=∂，∴ c = 0根据0y u yδ=∂=∂，∴ b + 3d = 0由此可得，a = 0, b = 1.5, c = 0, d = -0.5.3()3122u y U ηη=- 2200333()222w y y u y UU yμτμμδδδ==∂=-=-⋅-=-∂1039(1)280i u u y d U U δδδ=-=⎰ 对于U = constant ，23-2i w UU x δδμρτδδ∂==∂积分后得到，xδ=与精确解相差7.2%，与4级近似解相差20.5%02223=1122y f uy U C U U U μτμδρρρ=∂∂==，且x δ=f C ==与精确解相差2.6%，与4级近似解相差5.5%2. Derive the ordinary differential equation and the boundary conditions for the Blasius solution energy equation for flow over a flat plate. (See pages 29-30) A: 根据能量方程，22()k p T T T c u v x y yρ∂∂∂+=∂∂∂w w T T T T θ∞-=-，22()k p c uv x y y θθθρ∂∂∂+=∂∂∂ 常壁温边界条件：0,0,1y y θθ===∞=根据Blasius solution δη≈===3/22222221122x x x x y y U y y y x θθηθθηηηηθθηθηηθθηθθηηνη∂∂∂∂-∂⎛⎫⎛⎫===⋅-⋅ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭∂∂∂∂==∂∂∂∂⎛∂∂∂∂∂∂==⋅=⋅ ∂∂∂∂∂∂⎝代入能量方程中得到，)1'''''2p p U c f U c f f k x vx ηρθρηθθ⎛⎫-+-= ⎪⎝⎭即 2''Pr '0f θθ+= 边界条件为00;1ηθηθ===∞=，，3. Start from the local friction coefficient for flow over a flat plate, C f , on slide 31 andderive the average friction coefficient over the entire plate, C L . Show your work. A:2(x)12f C U τρ===01LL C L ==⎰4. A projectile in the form of a bluff-ended cylinder 20 cm in diameter and 60 cm long, moves through the air in the direction of its long axis at a velocity U of 100 m/s.212Dfrontal F C A U ρ=The drag coefficient, C, is equal to 1.0 for this object. Frontal area=πD 2/4, F D = total dragAssuming that the boundary layer thickness over the cylindrical surface of the projectile at a distance x from the leading edge is given by:xδ=and that the momentum thickness of the boundary layer is given by:772i δδ=Find what proportion of the total drag on the projectile is attributable to skin friction over the curved surface, assuming no pressure gradient in the boundary layer in the streamline direction.Data. Air kinematic viscosity is 0.15 cm 2/s Air density is 1.15 Kg/m 3Assumptions: Assume this is like a flat plate, then use the equation on slide 15.A: 22*()i w U dU U x dxδρρδτ∂+=∂ 若将圆柱表面看成平板，U = constant,0dUdx=，则22()772i w U U x xδδτρρ∂∂==∂∂因为xδ=∴4155x x x δ-⎛⎫⎛⎫∂∂∂=== ⎪ ⎪∂∂∂⎝⎭125772w U τρ-=1125500070.131372LLL w f dx U dx x dx τρ--====⎰⎰⎰12.16N22142D F D U πρ=⋅=180.64N DfF =6.7%Homework 5.41. Derive the equation relating q” to the temperature difference for natural convection driven flow in a round tube (like on slide 19 for parallel plates). - water properties at 25 C - tube length = 100 cm - tube diameter = 1 mm - constant heat flux- fully developed flow in a tube (from the first homework)a) Plot ∆T and Q (m 3/s) versus heat flux for fluxes of 500 to 5000 W/m 2 b) Is the assumption of fully developed flow valid? - hint: is L/(D Re) > 0.05c) Is the Boussinesq approximation valid here? A: 圆管内充分发展的流体，其速度分布为 22214R p r u z R μ⎛⎫∂=- ⎪∂⎝⎭平均速度2222201(1)2r 48RR p r R p u dr R z R zππμμ∂∂=⋅⋅-=-⋅∂∂⎰体积流量为44288R p R pQ R u z Lπππμμ∂∆===∂()()()22L LL L Lp gdy g T T dy g T T g T ρρρβρβρβ∞∞∞∞∞∞∆=-=-=-=∆⎰⎰ 根据能量平衡，''2p Qc T q RL ρπ∆=即4''28p R pc T q RL L πρπμ∆∆=将p ∆代入，得到()232''32p c gR q T Lρβμ∞=∆Pr ''''32R cond Gr q q =，''cond T q R λ∆= a) 根据以上推导过程可以得到，T ∆=Q =分别作出当2''500~5000/q W m =时T ∆与Q 随q’’变化的曲线，如下图所示。