3三角形的中线、

三角形高，中线，角平分线的定义
定义如下：
1、高：三角形的一个顶点向对边做的一条垂线段叫三角形的高。

2、中线：连接顶点和它，所对的边的中点，所得的线段，叫做三角形的中线。

3、角平分线：将一个叫分成相等的两份。

其他定义
三角形(triangle)是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形，在数学、建筑学有应用。

常见的三角形按边分有普通三角形（三条边都不相等），等腰三角（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）；按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

三角形的中线定理三角形的中线定理是指：三角形的三条中线交于一点，且交点到三个顶点的距离相等，等于各边边长的一半。

中线是连接三角形的一个顶点与对边中点的线段。

对于任意一个三角形ABC，它的三条中线分别连接顶点A与对边BC的中点D，顶点B与对边AC的中点E，以及顶点C与对边AB的中点F。

根据中线定理，我们可以得出以下结论：1. 三条中线交于一点：在三角形ABC中，连接三条中线AD、BE和CF的交点为点G。

根据中线定理，点G是三条中线的交点。

2. 交点到三个顶点的距离相等：点G到顶点A的距离等于点G到顶点B的距离，且等于点G到顶点C的距离。

3. 交点到三个顶点的距离等于各边边长的一半：例如，点G到顶点A的距离等于边BC的长度的一半，即AG = 0.5 * BC。

同样地，AG = 0.5 * AC，BG = 0.5 * AC，CG = 0.5 * AB，DG = 0.5 * AB，EG = 0.5 * BC。

根据中线定理，我们可以推导出许多有用的性质和定理。

下面，我们来介绍一些常用的推论：1. 三条中线的交点是三角形重心：三角形的重心是三条中线的交点。

重心是三角形内部到三个顶点距离之和最小的点。

记三条中线的交点为点G，那么点G就是三角形的重心。

2. 重心到顶点的距离比例为2:1：重心到顶点A的距离为AG，到顶点B的距离为BG，到顶点C的距离为CG。

根据中线定理可知AG = 2/3 * GD，BG = 2/3 * GE，CG = 2/3 * GF。

因此，重心到顶点的距离比例为2:1。

3. 重心将中线划分为2:1的比例：以顶点为端点的两条中线的交点即为重心，且重心将中线划分为2:1的比例。

例如，重心G将中线AD 分成AG:GD = 2:1的比例。

4. 重心到顶点的距离之和最小：对于任意点P在三角形内部，P到三个顶点的距离之和大于或等于重心G到三个顶点的距离之和。

即PA + PB + PC >= GA + GB + GC，其中等号成立的条件是点P与重心G重合。

三角形的中线在几何学中，三角形是最基本、最常见的图形之一。

它由三条直线段组成，每两条直线段的交点被称为三角形的顶点。

三角形的中线是连接三角形的每条边的中点的线段。

三角形有三条边，我们可以将中线分别连接三角形的三个顶点。

这样，我们可以得到三个中线，分别称为三角形的重心线、垂心线和媒介线。

接下来，我们将探讨这些中线的性质和应用。

一、重心线以三角形的三个顶点为起点，连接三个顶点到对边中点的线段，得到的三条线段交于一点，称为重心，连接重心与三个顶点的线段分别称为重心线。

在标准笛卡尔坐标系中，重心的坐标是三个顶点坐标的平均值。

重心线有以下性质：1. 重心线三条线段交于一点，该点与三角形的重心重合。

2. 重心线平分对应边，即重心到对边中点的线段长度相等。

重心线在三角形中起到平衡作用。

在平面上，三个人均匀站在三角形的顶点上，通过绳子将每个人与重心相连，可以保持平衡。

因此，重心被称为三角形的“几何中心”。

二、垂心线以三角形的三个顶点为起点，连接三个顶点到对边的垂线的交点，得到的三条线段交于一点，称为垂心，连接垂心与三个顶点的线段分别称为垂心线。

垂心线有以下性质：1. 垂心线三条线段交于一点，该点与三角形的垂心重合。

2. 垂心线互相垂直，即三条垂心线两两垂直。

垂心线在三角形中起到垂直作用。

垂心可以看作是三角形的“垂直投影中心”，通过垂心线可以得到三角形的三个顶点到对边的垂直距离。

三、媒介线以三角形的三个顶点为起点，连接三个顶点到非相邻顶点的中点的线段，得到的三条线段互相平行，称为媒介线。

三角形的媒介线有三条，连接三个媒介线交点的线段被称为媒介线三角形。

媒介线有以下性质：1. 媒介线三条线段互相平行，且等于对边的一半。

媒介线在三角形中起到平行作用。

当我们绘制媒介线后，可以将三角形分割为三个面积相等的小三角形。

总结：三角形的中线包括重心线、垂心线和媒介线，它们分别连接三角形的顶点和对边的中点。

这些中线具有独特的性质，如重心线的平分性、垂心线的垂直性和媒介线的平行性，可以帮助我们研究三角形的性质和解决与三角形相关的问题。

三角形的中线中线的性质和应用三角形是初中数学中的基础概念之一。

在三角形中，中线是一条连接一个顶点与其对边中点的线段。

每个三角形都有三条中线，互相交于一个点，我们称之为重心。

本文将探讨三角形的中线中线的性质和应用。

一、三角形中线的定义与性质1. 定义：三角形的中线是一条连接一个顶点与其对边中点的线段。

2. 性质1：三角形的三条中线互相交于一个点，这个点被称为三角形的重心。

重心划分每条中线的长度比为2:1，即重心到顶点的距离是重心到中点距离的两倍。

3. 性质2：三角形的重心离每条边的距离相等。

4. 性质3：三角形的中线长度满足关系式：m₁+m₂+m₃=3m（其中，m₁、m₂、m₃分别表示三角形的三条中线的长度，m表示三角形的周长）。

二、三角形中线中线的应用1. 面积计算：利用三角形中线中线的性质，我们可以简化计算三角形面积的步骤。

设三角形的三条边长分别为a、b、c，三条中线的长度分别为m₁、m₂、m₃，则三角形的面积S可以通过以下公式计算得到：S = 1/4 * √(2a²+2b²-c²) * √(2a²+2c²-b²) * √(2b²+2c²-a²)这个公式称为三角形中线长公式，可以大大简化我们计算三角形面积的过程。

2. 相似三角形比较：利用三角形中线对应线段相等的性质，我们可以判断两个三角形是否相似。

如果两个三角形的中线等分对应边的比例相等，那么这两个三角形就是相似的。

例如，如果一个三角形的一个中线等分了对应边，而另一个三角形的对应中线等分了对应边的同一比例，那么这两个三角形就是相似的。

3. 证明三角形性质：三角形中线中线的性质也可以用来证明其他三角形的性质。

例如，我们可以利用中线的长度比是2:1，来证明三角形重心到两边距离的关系。

假设三角形ABC的重心为G，连接AG、BG、CG分别和边BC、AC、AB交于点D、E、F。

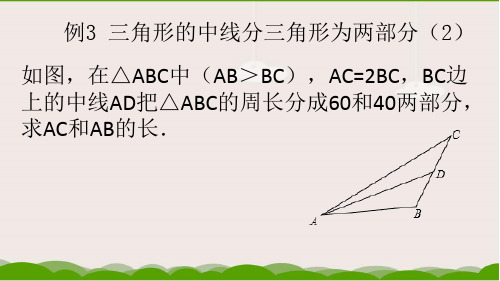
三角形的中线与高的关系在几何学中，三角形是最基本的图形之一。

它由三条边和三个角组成。

三角形的中线和高是三角形的重要特征之一。

本文将讨论三角形的中线与高的关系，并通过几何证明来验证这一关系。

一、什么是三角形的中线与高1. 中线：三角形的中线是连接三角形某两个顶点与对边中点的线段。

即对于三角形ABC，连接AB的中点D与C点的线段为三角形ABC的中线。

2. 高：三角形的高是从三角形某一顶点引垂线到对边的线段。

即对于三角形ABC，从顶点A引垂线到对边BC所得线段为三角形ABC的高。

二、中线与高的关系中线和高有一定的关系，它们可以相互影响和表达。

具体而言，当我们将三角形的中线和高联系起来时，可以得出以下结论：1. 中线长度关系：三角形的三个中线的长度相等。

证明：设三角形ABC的中线分别为AD、BE和CF。

我们需要证明AD=BE=CF。

首先，由中线的定义可知，AD是BC的中点。

由于三角形ABC中，AD和BC平行且等长，根据平行线之间的性质，可得△ADC与△ABC是全等三角形。

因此，△ADC的角A和△ABC的角A相等，即∠ADC=∠ABC。

又因为AD和BC是平行线，所以∠BCA=∠CDA。

由此可得，△ADC与△ABC的三个角相等，因此两个三角形全等。

根据全等三角形的性质，可得对应的边也相等，即AD=BE。

同理可证，BE=CF，因此三角形ABC的三个中线相等，即AD=BE=CF。

2. 高的长度关系：三角形的三条高对应的边长成反比。

证明：设三角形ABC的高分别为AD、BE和CF。

我们需要证明AD:BE:CF=BC:AC:AB。

首先，由高的定义可知，AD是从顶点A引垂线到对边BC所得线段。

根据相似三角形的性质，我们可以得出以下比例关系：△ADB∼△AEC∼△AFB。

根据相似三角形的比例关系可得，AD:BE:CF=BD:AE:AF。

进一步，根据垂直平分线定理可知，BD=DC，AE=EC，AF=BF。

因此，我们可以得到AD:BE:CF=DC:EC:BF。

三角形的中线：在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。

由于三角形有三条边，所以一个三角形有三条中线。

且三条中线交于一点。

这点称为三角形的重心。

每条三角形中线分得的两个三角形面积相等。

角平分线：三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线。

三角形的角平分线不是角的平分线，是线段。

角的平分线是射线。

高线：从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。

线段的垂直平分线：经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

注意：要证明一条线为一个线段的垂直平分线，应证明两个点到这条线段的距离相等且这两个点都在要求证的直线上才可以证明巧计方法：点到线段两端距离相等。

三角形中线性质定理：1、三角形的三条中线都在三角形内。

2、三角形的三条中线长：ma=(1/2)√2b2+2c2 -a2 ；mb=(1/2)√2c2 +2a2 -b2 ；mc=(1/2)√2a2 +2b2 -c2 。

(ma,mb,mc分别为角A,B,C所对的中线长）3、三角形的三条中线交于一点，该点叫做三角形的重心。

4、直角三角形斜边上的中线等于斜边的一半。

5.三角形中线组成的三角形面积等于这个三角形面积的3/4.定理内容：三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。

角平分线线定理：定理1：在角平分线上的任意一点到这个角的两边距离相等。

逆定理：在一个角的内部（包括顶点），且到这个角的两边距离相等的点在这个角的角平分线上。

定理2：三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例，如：在△ABC中，BD平分∠ABC，则AD：DC=AB：BC注：定理2的逆命题也成立。

三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等！(即内心)。

垂直平分线的性质：1.垂直平分线垂直且平分其所在线段。

三角形的三线在数学的世界里，三角形是一个基础且重要的图形。

而三角形的三线，即三角形的高线、中线和角平分线，更是深入理解三角形性质和解决相关问题的关键。

让我们先来聊聊三角形的高线。

高线，简单来说，就是从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段就叫做三角形的高线。

每个三角形都有三条高线，并且这三条高线所在的直线会相交于一点。

锐角三角形的三条高线都在三角形的内部；直角三角形有两条高线就是它的两条直角边，另一条高线在三角形的内部；钝角三角形有两条高线在三角形的外部，一条在内部。

高线在计算三角形的面积时非常有用。

我们都知道三角形的面积等于底乘以高除以二，如果知道了三角形的底和对应的高，就能轻松算出它的面积。

接下来是中线。

中线是连接三角形顶点和它对边中点的线段。

一个三角形有三条中线，这三条中线也相交于一点，并且这个交点位于三角形的内部。

中线的一个重要性质是，它把三角形分成了两个面积相等的部分。

为什么呢？因为中线平分了对边，所以以中线为底边的两个小三角形，高是相同的，底边也相等，面积自然就相等了。

在解决一些与三角形面积相关的问题或者证明一些线段关系时，中线的这个性质常常能发挥很大的作用。

最后要说的是角平分线。

角平分线就是三角形一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段。

每个三角形同样有三条角平分线，它们也相交于一点，这个点也在三角形的内部。

角平分线的一个重要性质是，角平分线上的点到角两边的距离相等。

这个性质在很多几何证明和计算中都是很关键的依据。

为了更好地理解三角形的三线，我们不妨通过一些具体的例子来看看。

假设我们有一个等边三角形，它的边长是 6 厘米。

由于等边三角形的三条边相等，三个角也相等，都是 60 度。

那么它的三条高线、中线和角平分线是重合的。

我们先求它的面积。

根据等边三角形的面积公式，面积等于根号 3 乘以边长的平方除以 4，计算可得面积约为 9 倍根号3 平方厘米。

三角形的中线与中位线在解析几何中，三角形是一个基础而重要的概念，而其中线和中位线则是三角形中的两个重要线段。

本文将介绍三角形的中线和中位线，并探讨它们的性质和应用。

一、中线的定义和性质中线是连接三角形两个顶点与对应边中点的线段。

在任意三角形ABC中，连结A与BC的中点D，B与AC的中点E，C与AB的中点F，则线段DE称为三角形ABC的中线。

中线有以下几个重要性质：1. 中线长度相等在任意三角形中，三条中线的长度是相等的。

这一性质可以用中位线定理进行证明。

假设DE为中线，在三角形ABC中，连接EF和FD，由中位线定理可知，EF和FD分别是AC和AB的中位线，所以EF=FD=1/2AC=1/2AB，因此DE与EF长度相等。

2. 中线互相平分在任意三角形中，三条中线相互平分。

换句话说，三条中线的交点是三角形的重心。

设三条中线相交于点G，则可以证明GD:GA=GE:GB=GF:GC=1:2。

3. 中线与对应边平行在任意三角形中，中线与对应边是平行的。

即DE∥AB，EF∥BC，FD∥AC。

这一性质可以通过向量法进行证明，利用向量的平行性质和中点的定义可以推导出这一结论。

二、中位线的定义和性质中位线是连接三角形的两个边中点的线段。

在任意三角形ABC中，连结AB的中点D，AC的中点E，BC的中点F，则线段DE称为三角形ABC的中位线。

中位线有以下几个重要性质：1. 中位线长度相等在任意三角形中，三条中位线的长度是相等的。

由于中位线连接对边的中点，而对边的长度相等，所以中位线的长度也相等。

2. 中位线与对边平行在任意三角形中，中位线与对边是平行的。

即DE∥BC，DF∥AC，EF∥AB。

这一性质同样可以通过利用向量法进行证明。

3. 中位线与中线交点在任意三角形中，三条中位线的交点是三角形的重心。

与中线类似，重心是三角形内部的一个特殊点，可以用中位线的交点来确定。

重心具有平分中线和平分面积的性质，是三角形的一个重要参考点。