用计算器求立方根-
- 格式:ppt
- 大小:377.50 KB
- 文档页数:8


用计算器求立方根数学教案
标题:使用计算器求立方根的数学教案
一、教学目标:
1. 让学生了解立方根的基本概念
2. 学会使用计算器求立方根的方法
3. 培养学生的实际操作能力和解决实际问题的能力
二、教学内容:
1. 立方根的概念和性质
2. 使用计算器求立方根的操作步骤
3. 实际应用举例
三、教学过程:
1. 引入新课:通过一些生活中的实例引入立方根的概念,激发学生的兴趣。
2. 讲解新知:讲解立方根的基本概念和性质,引导学生理解立方根的意义。
3. 演示操作:教师演示如何使用计算器求立方根,让学生跟随操作,确保每个学生都能掌握操作方法。
4. 学生实践:布置一些简单的练习题,让学生使用计算器求立方根,教师巡回指导。
5. 课堂小结:总结本节课的学习内容,强调立方根的重要性和计算器的使用技巧。
6. 课后作业:布置一些与立方根相关的实际问题,让学生在家中尝试解决。
四、教学评估:
1. 通过课堂观察和提问,了解学生对立方根的理解程度。
2. 通过学生的操作表现,评价他们使用计算器求立方根的能力。
3. 通过课后作业的完成情况,评价学生解决实际问题的能力。
五、教学反思:
分析教学过程中的优点和不足,思考如何改进教学方法和策略,以提高教学效果。


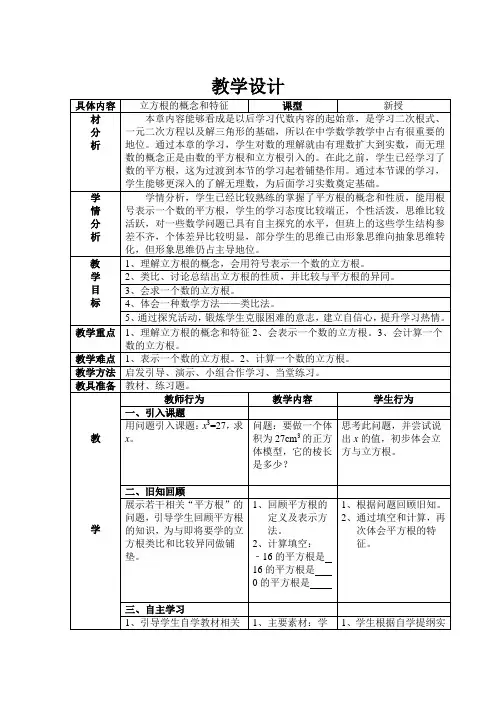
6.2 立方根第二课时教学设计一、教材分析:这节课的内容是人教版数学七年级下册第六章实数中6.2立方根的第2课时。
由于本章的前两节“平方根”“立方根”在内容上基本是平行的,知识的展开顺序基本相同,因此可以充分利用类比的方法:在第一课时类比得出立方根的概念、开立方运算、立方与开立方运算的互逆关系等的基础上。
类比平方根估算方法研究立方根的估算方法,类比平方根计算器的使用研究立方根计算器的使用,类比平方根的小数点的移动研究立方根的小数点的移动等。
通过类比旧知识学习新知识,使学生的学习形成正迁移。
二、学情分析:本节课需要面向七年级学生进行教学,由于七年级学生年龄低、好表现、具有形象思维等特征,所以这节课我主要采用情境教学法、动手操作法、探究交流法。
通过创设生动有趣的情境,本着结论让学生得,疑难让学生议,思路让学生想,错误让学生析,规律让学生找,小结让学生讲的原则,在方法的设计上,把重点放在了逐步展示知识的形成过程上,激发学生对数学学习的兴趣。
三、学习目标:1.知识与技能:熟练掌握求一个数立方根的方法。
会用计算器求一个数的立方根。
2.过程与方法:经历探究被开方数与立方根的关系,能够运用规律解决实际问题。
3.情感、态度与价值观:学生经历观察、动手操作、发现讨论等数学活动,感受数学活动充满探索性与创造性。
并通过小组互助学习培养学生的合作意识和解决问题的能力。
教学重点:探究被开方数与立方根的关系的过程。
教学难点:运用探索的规律解决实际问题。
四、教学方法:归纳和类比的方法。
五、教学过程:活动一、自主学习,探究规律预习课本第50~51页,自学完成下列问题。
问题1:如果一个正方体的体积是2㎝³,则这个正方体的棱长是多少呢?解:设这个正方体的棱长为xcm,则有 x3 =2解得:。
归纳:1.实际上,很多有理数的立方根是无限不循环小数,如,等都是无限不循环小数。
我们可以用有理数近似的表示它们。
2.要求一个数的立方根(或近似值),我们可以利用计算器中的键来计算。


用计算器求立方根计算立方根是一种常见的数学运算,它可以帮助我们找到一个数的立方根。
在本文中,我们将介绍如何使用计算器来进行立方根的计算。
简介立方根是指一个数的立方等于给定数的运算,即 n^3 = x,其中 x 为给定数。
计算立方根可以帮助我们解决很多实际问题,例如在几何学中计算体积,或者在工程学中进行三维尺寸的估算。
计算器求立方根的方法在现代科技发达的时代,智能手机和计算器已经成为我们生活中必备的工具之一,计算立方根也可以通过计算器来快速完成。
下面是一些使用计算器求立方根的方法:1. 普通计算器大多数普通计算器都具有立方根功能。
要使用此功能,您只需要按下相应的按键,然后输入要计算的数值即可。
通常,立方根键的标识为“∛”,您可以在计算器的说明书中查找到正确的键位和使用方法。
2. 科学计算器科学计算器通常比普通计算器更复杂,提供了更多的功能和运算符。
要使用科学计算器来计算立方根,您需要按下立方根键(通常标识为“∛”或“^(1/3)”),然后输入要计算的数值。
在某些科学计算器中,您还可以使用表示立方根的函数,例如“cbrt(x)” 或“sqrt(x, 3)”。
3. 在线计算器除了手机和手持计算器外,互联网上还提供了许多在线计算器,您可以通过浏览器来使用这些在线计算器。
在搜索引擎中输入“在线立方根计算器”或类似的关键词,您将找到许多可供使用的计算器。
在这些在线计算器中,您只需输入要计算的数值,然后按下计算按钮即可求得立方根。
解决实际问题中的立方根求解立方根计算不仅仅是一个独立的数学问题,它在实际生活和工程中也具有重要的应用。
1. 几何学问题在几何学中,我们经常需要计算三维对象的体积。
例如,计算正方体或长方体的体积,我们可以通过立方根计算来找到边长对应的体积大小。
使用计算器可以快速计算出正确的结果,从而帮助我们在几何学问题中更好地应用立方根。
2. 工程学问题在工程学中,立方根计算可以帮助我们进行三维尺寸的估算。

教你如何在计算器上运用算法求立方根立方根不仅是数学运算中的基本概念之一,也是我们日常生活中常常需要使用到的计算方法。
而现代计算器已经为我们提供了一种方便、灵活的计算方式,掌握计算器运用算法求立方根的方法对您的生活和工作都将非常实用。
让我来告诉大家如何在计算器上运用算法求立方根。
第一步:了解立方根的概念在数学上,立方根是指一个数的三次方的算术平方根。
例如,数字8的立方根是2,因为2的立方等于8。
类似的,数字27的立方根是3,因为3的立方等于27。
一般情况下,如果一个数字的立方根是x,这个数字的三次方等于x的立方。
第二步:掌握计算器的立方根功能现代计算器大多数都具有求立方根的功能,可以直接输入数字并按下“立方根”键来计算。
这种方法简单、方便,对于一些常用数字的计算非常有用。
第三步:使用牛顿切线法求立方根如果计算的数字不是简单,或者没有相应的立方根功能,我们需要使用一些算法来计算。
其中一种最常用的算法是牛顿切线法。
下面是具体步骤:1. 假设我们要求一个数字a的立方根,将其记为x。
我们可以先猜测一个与答案相近的数值x0。
2. 使用下面的公式来生成下一个数值x1:x1 = (2x0^3 + a) / (3x0^2)3. 使用类似的方法得到下一个数值x2,x3……,直到x(n)和x(n-1)之间的差距足够小。
4. 令x(n)等于所求的立方根。
下面是一个简单的例子,假设我们要求数字27的立方根:1. 假设x0为3,则x1为(2*3^3+27)/(3*3^2)=4.333。
2. x2则为(2*4.333^3+27)/(3*4.333^2)=3.26193. x3为(2*3.2619^3+27)/(3*3.2619^2)=3.000027的立方根为3.0000。
第四步:使用二分法求立方根除了牛顿切线法,我们还可以使用二分法来求立方根。
其基本思路是利用二分法来逼近所求的立方根。
下面是具体步骤:1. 设定一个起始范围,假设我们要求数字a的立方根。

立方根(2)----用计算器求立方根、用有理数估计一个数立方根的大小说课稿各位评委:大家上午好!今天我说课的题目是《§6.2立方根(2)》。
我将从“教材分析、学情分析、教法分析、学法指导、教学过程的设计与实施”五方面进行本节课的说课。
一、教材分析:1、说教材的地位和作用这一节课是人教版(2012年版)义务教育教科书数学七年级下册第六章《实数》§6.2立方根,本节共两课时,这节课的内容为第二课时。
本章内容是在前面学习有理数的基础上,把有理数的范围进行扩大,也可以看成是其后的代数内容的起始章,是学习二次根式、一元二次方程以及解三角形的基础,因此本章内容起着承上启下的作用,在中学数学中占有重要的地位。
通过本章的学习,学生对数的范围的认识就由有理数扩大到实数,而无理数的概念正是由数的平方根和立方根引入的。
在此之前,学生已学习了数的平方根内容和研究方法,这为过渡到本节的学习起着铺垫作用。
通过本节课的学习,学生可以更深入的了解无理数,为后面学习实数奠定基础。
2、说教学目标知识与技能:(1)会正确使用计算器求一个数的立方根。
(2)能用有理数估计一个立方根的大致范围,使学生形成估算的意识,培养估算能力。
过程与方法:经历运用计算器探求数学规律的过程,发展合情推理能力。
情感态度与价值观:培养学生严谨的数学学习态度,科学的探索精神。
4、说教学重点和难点(1)重点:计算器的使用方法和用有理数估计一个立方根的大致范围。
(2)难点:探索立方根的变化规律及应用。
二、学情分析七年级具有学生年龄低、好奇心强、发言积极、爱好表现,有话就说,小组合作初步形成,兼有一定的形象思维和初步的逻辑思维能力,知识经验不够丰富的特点,因此探索的结论还需要同学公认和老师把关。
三、教法分析针对以上学生基础知识薄弱,主动参与学习的积极性高,学习探究能力较差的这种情况及本节课的特点,我采用“类比探究----验证结论-----归纳概括----巩固应用”为主线的教学程序。


怎样用没有开立方根按键的计算器开立方根和高效方根4黑龙江电子技术1993年第4期怎样用没有开立方根按键的计算器开立方根和高次方根黑龙江省经济管理干部学院洪永样————————一摘耍7p手一II培出T一种用开平方键开土方厦高次方根的技书,为走不增加任何硬件,巧用现有谩奋辑决问题的道路提供T一个示倒.关键词:开立方开高次方计算器—一.—/——一现在电子计算器的使用已十分普遍.很多计算器上都设有开平方根的按键(常用符号团表示),开起平方来十分方便.然而,是否每个计算器上都有开立方根的按键就不一定了.至于开更高次方根的按键,对于普及型计算器则几乎都未l殳置.遇到这种情况,如果想开立方或更高次方根怎么办?下面介绍一种用回按键解决这一问题的办法.一,用开平方根按键开立方的依据设A是不等于l的被开立方的正数,IAr.,A卜I,A.,Al,……是j的第一,值.其中lAI.1A"AI.2iIIA,A"A.1j!IA…A..Ai即我们想求出_'或写为;I2……第二,第卜2,第卜l,第i,第1个正近似即;的每个新近似值都是用;乘以原近似值的次幂求出.下面两个基于以上约定的论断是本方法的依据,现叙述和证明如下(I)(2)(3)论断一:当A>l时,若A是比A『_l更逼近i的过剩近似值,则AI必定是比A, 】II更逼近j的过剩近似值.用数学式子表示即是t若>i且<卜J则必有t>Aj 且A1<AID1993年第4期黑龙扛电子技术?5?l正明lI】①l>Aj.即A什l是的过剩近似值.一.!l1I?II1I固fi>(),tII~A;>.两边皆乘以,A?A>;?即I.fI>.根据上边的(3)式,不等号左边是州,所以+l>A.②Hl<Af.tIIJA,+I~L-I:Al更逼近i的过剩近值.因,<一,,故,<卜.i.两边各乘以,:.,j<i.Hj,依据前边(3)式和(2)式得Al<论断二:当0<A<I时,如果A,~L-I:Al更逼近i的不足近似值,则Al必定是比f更逼近j的不足近似值.用数学式子表示即是若,<j且>A卜l,则必有A…<A且l>A证明:①+】<j.即Al是的不足近似值.因<;,故<(),即,<.两边各乘以i,.,<_1I1_l1<j.根据上边的(3)式,不等式左边是l,所以…<;.⑤』+l>f.即Al是比Ai更逼近j的不足近似值.因.>1,故>一;.两边各乘以,.j>.;,根据前边(3:式和(2)式,Al>一现在夸j的第一个近似值为(为正数,,即Aa,:.鲋当>I时(或<I时)At满足A】>,(Al<j).Ai的第二个近似值按前边(2)式求得A2竿;?AIj1=?:=.满足A2>j1,(2<;),2<I,(2>】).故根据上面证明的两个论断,利用(2)式求出的AAAj……~--4"8c--4"EiiiSA; 的过剩(不足)近似值.这样,一直求到满足精度要求的筹n个近似值,便求出了lA3二,用开平方按键开立方的方法(按键公式注)利用以下按键公式求出A的立方根:6?黑龙江电子技木1993年第4期囡1日日f其中回表示连续按两次开平方按键团.矩形攉表示反复执行框内的按键公式,直到显示窗的值不变为止(即直到显示的精度已低于近似值的实际精度).此时的示值,就是】所求的j.解释根据计算器的按键规则目目是求出?A,且以后每按一次目键是乘以.lll】t固是求出(?A).因为(?)=A?A,这正好是上面说的令Aj的第一个Il近似值为,即A.=A以厦由此求出第二个近似值的式子,即?A:A,.当第二次I按完矩形框中的键时是求出A2?A(由按日实现)和(A2?)i(由按回实现).l】-l因",?A}i=Aj?A,;,故得到的是.即每按一遍矩形框中的键求出一个蔓逼近A的过剩(不足)近似值.所以当反复按矩形框中的键有限次达到显示窗中的数:变时,就】得到由显示精度表示的A的近似值,即用现有计算器求出了的立方根.三,求10次以内各方根的方法I.求A的平方根,按固.2.求A的立方根,按A目i目回I.矩形框中的键耍反复按,直到显示不变为止.3.求A的四次根,按A圃.4球A的五次根,按(曰旧匠】)园目矩形框中的键要反复按,直到显示不1——一1变为止,此时求出了".然后再按团及两次耳,即求出了.5.求的六次根,先求的平方根,再求此根的立方根.6.求的七次根,按因旧圜『.矩形框中的键反复按,直到显示不变为止7.求的八次根,按圜8球的九次根,先求的立方根.再求此根的立方根9.求的lO砍根,先求的平方根,再求此根的五次根.以上诸方法中只有求五次根和求七次根尚待证明现简证如下.1对于求七次根,当按照按键公式按完第一遍后是在Aj的第一个近似值.=A的基础1II上求出了它的第二个近似值,即(A?A)i=Ai?Ai=A..当A>l时(<l的证法1I类似,这里从略)由于A,=A>A,A<A.,故可反复使用论断一,通过反复按矩形l框中的键求出用现有计算器的显示精度表示的i之值.下面的论断是正确的.读者可仿汪明论断一和论断二的征明方法证明之.显示窗的显示不变后就求出了.此后再按因目是计算..::,所以就求出了的五次根.1993年第4期黑龙江电子技术?7?四,向求更高次根进军如果想求Ai之值,其中s是大于l0的正整数,怎么办?这首先要看s是否能分解成质因数的连乘.如果有S=口×bxc×……其中b,c,……等都是质数,则可先求A 的4次根,再求的b改根C,再求C的c改根如此下去,便可求出i.如果不能分解,即s是质数时怎么办?这可用s与下面的按键公式比较.A固J目曰『(4)如果S=2一l,则可用(4)式求出Ai.如果s手=!墨当!选亘旦工鸢的按键公式(5)解决.越I回目一团圃耳回』(5)其中匡丽掘将窗口的示值存储起来的存储键瑾圃是将存储之值唤出显示于窗口的唤出键囡叵日是将当前的显示值乘以唤出值并显示其积的按键公式1II可以证明(5)式是求Aj的按键公式.令S=2一m就j;Ai,便可用】(5)式求Ai.这时2"按下式选取2一'<S<例如S=29可取2一32(n=5),此时2'=16,有l6<29<32.s=71时可取2Ⅱ=128(n=7),此时2=64,有64<71<128.选好2"后就可在S=2m中求出Ir——————————————————1im.侧如求画时,m=3,于是就可用A匡习l国目国圃日固出.对于s为其它质数时可仿此.[洼)按奠公式是使用藁计算器计算莱题时,用其应按的全部按链,俄厢接的先后颤序排耕出来的寰选式a例如计算A+B一?的按键蛰式是A臼BE计算A.?的按键蛰式是A目曰日曰戚A曰且,.计薰一?的按键公式是A回一十算题能否用莱计算器计算出来,决定于能否拉强用媛计算器的按键构成的按键公式.U:接第3硪)圈6TAD-32抽头艳出渡形所提出的电路已在实际系统中得到应用,其钟脉冲频率为1MHz,再采样脉冲宽度为0.3s.图6为TAD一32模拟输入端输入一窄视频脉冲信号时,某一抽头的输出波形.图中上线为未经再采样时的输出,下线为经再采样后的输出.可见,经过这样的处理获得了良好的结果.参考文献[1]王以钻电荷耦台器件原理与应用北赢科学出版挂.1987[2]RETICON公司T^D一32DatasheCt。