下载文档原格式
基于双线性系统、差分方程的人口增长模型摘要社会经济的许多领域的规划都必须考虑人口这一重要因素。
而人口普查只能为我们提供某几个时间点的横截面数值，但在现实生活中，人们常常需要其他时间点的人口总数及其构成。
于是一个迫切的任务就是如何用少数的几个时点的信息比较准确的得到较详尽的其他时点的人口数据。
人口系统发展是一个动力学过程，为强惯性系统，人口死亡率和出生率构成人口增长的双线性系统。
针对中短期预测，基于统计理论，将5年的死亡出生率，死亡率求期望，建立了人口增长的定常差分方程模型，预测至2015的人口发展趋势，通过MATLAB求解得到2015年的总人口为14.17亿，乡村城镇化趋势明显；并且人口在2025左右出现峰值，约为15.1亿。
针对长期预测，根据动力学发展过程理论，当时间尺度接近惯性系统的时间常数（社会人口的平均寿命）时，人口状态将发生明显改变。
由此建立了人口增长的时变差分模型。
并通过MATLAB求解，预测2050年的人口总数为14.33亿，人口系统达稳定状态。
然后，利用Leslie矩阵分析模型的稳定性。
当时间t（年）充分大时人口增长也趋于稳定。
针对长期模型的检验，对不同的总和生育率做出了人口总数的变化曲线。
得出当总和生育率的更替水平临界值略大于2.0。
关键词：差分方程，强惯性系统，Leslie矩阵，总和生育率一.问题重述与分析1.1问题重述中国乃泱泱人口大国，人口规模是城市规划和土地利用总体规划中一项重要的控制性指标，人口规模是否合理，不仅影响到未来地区经济和社会发展，而且会影响到地区生态环境可持续发展。
因此准确地预测未来人口的发展趋势，制定合理的人口规划和人口布局方案具有重大的理论意义和现实意义。
根据国家人口报告，对短期、中期和长期人口预测作如下定义：十年内为短期，十到十五年为中期，五十年及其以上为长期。
人口发展过程是一个很缓慢的过程。
它的“时间常数”接近平均期望寿命约七、八十年的时间。
人口状态随时间变化的过程称为人口发展过程。
中国人口增长的中短期和长期趋势预测数学模型【摘要】中国是人口大国，人口的预测问题始终是关系到社会和谐发展的关键因素之一。
首先，本文就近几年中国人口结构的变化情况进行“生存——生育”双因素分析，按照人口性别分类，考虑老龄化进程、出生人口性别比以及乡村人口城镇化等因素，根据近几年城、镇、乡的统计数据，建立基于概率方法的Leslie矩阵，利用Matlab软件进行编程求解，对中国人口进行了中短期预测。
其次，在对人口进行长期预测时，引入净再生产率（NRR）和总和生育率（TFR）。
根据已知数据计算出1994—2005每年的NRR和TFR，通过曲线拟合预测出未来的TFR趋势。
而各年TFR的变化是由相应年各年龄女性生育率的变化引起的，各年龄女性生育率的变化比例即是TFR的变化比例，得到新的生育率，即得到了新的Leslie矩阵，计算出该Leslie矩阵的唯一的正的特征根λ，当λ接近于1时，则人口趋于稳定。
此时求得各年人口预测的新的Leslie矩阵，利用新的每年Leslie矩阵连乘，并乘于2005年各年龄人口数向量，则可预测中长期人口数量。
主要问题结论：1、对中国人口增长的中短期进行预测。
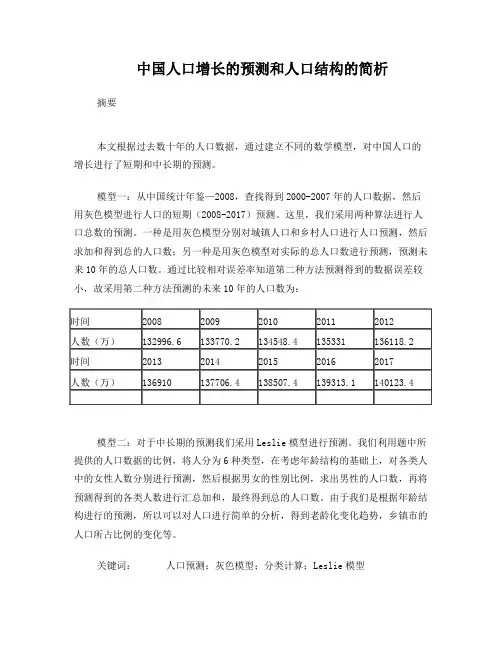
首先以2001年人口数据为基数，对2002年—2005年进行预测，并与真实年份（年）2002 2003 2004 2005 预测总人口数（万人）实际总人口数（万人）128453 129227 129988 130756 相对误差（%）虑各年份生育率的影响。
其次，由上表可知模型较为准确，可以2005年人口数据为基数，利用模型年份2006 2007 2008 2009 2010 预测总人口数（万人）年份2011 2012 2013 2014 2015 预测总人口数（万人）的变化得到每年各年龄女性生育率的变化，运用新的生育率得到该年的Leslie矩阵，计算出该Leslie矩阵的唯一的正的特征根λ，当2033年λ较为接近1时，则2033年后人口达到峰值趋向稳定，且此时NRR2033年=，亦接近于目前发达国家的NRR指标。
人口预测的数学模型与预测方法分析人口预测是对未来一定时期内人口数量和结构的变动进行估计和预测的过程。
人口预测在社会经济发展规划、城市规划、教育医疗资源配置等方面具有重要的参考价值。
为了准确预测人口的变动趋势，需要建立合理的数学模型和选择适当的预测方法。
人口预测的数学模型主要包括线性回归模型、指数模型、Logistic模型等。
线性回归模型是一种用来描述两个变量之间线性关系的统计模型，可以用来预测人口随时间的变化。
指数模型假设人口数量按照指数规律增长或减少，适用于人口增长较快的情况。
Logistic模型则适用于人口增长速度放缓后的情况，它是一种描述增长速度逐渐趋近于饱和的模型。
在选择数学模型时，需要综合考虑以下几个因素：人口历史变动趋势、人口自然增长率、人口迁移和流动情况、政策调控等因素。
同时，还需根据实际情况对模型的参数进行合理的设定和修正，以提高预测的准确性。
在预测方法上，常用的有趋势线法、复合增长率法、比较推理法、时间序列分析法和系统动力学方法等。
趋势线法是基于历史数据的发展趋势来进行预测，适用于人口变动趋势比较稳定的情况。
复合增长率法是将历史数据中的增长率按一定规则进行加权平均，再用来推算未来人口的增长率。
比较推理法通过对不同因素的比较和推理，来估计未来人口的变化。
时间序列分析法是根据时间序列数据的历史模式来预测未来的变化趋势。
系统动力学方法则是通过对不同因素的动态关系建立模型，用来探索人口变动的内在机制和规律。
在具体应用时，可以结合不同的数学模型和预测方法，进行多角度的分析和预测。
同时，还需要不断对模型进行修正和优化，以适应不断变化的人口变动趋势和社会经济背景。
此外，还应该注意对预测结果的不确定性进行评估和把握，提供多种可能性的预测结果，为决策者提供科学的参考依据。
中国人口增长的预测和人口结构的简析摘要本文根据过去数十年的人口数据，通过建立不同的数学模型，对中国人口的增长进行了短期和中长期的预测。
模型一：从中国统计年鉴—2008，查找得到2000-2007年的人口数据，然后用灰色模型进行人口的短期（2008-2017）预测。
这里，我们采用两种算法进行人口总数的预测。
一种是用灰色模型分别对城镇人口和乡村人口进行人口预测，然后求加和得到总的人口数；另一种是用灰色模型对实际的总人口数进行预测，预测未来10年的总人口数。
通过比较相对误差率知道第二种方法预测得到的数据误差较小，故采用第二种方法预测的未来10年的人口数为：模型二：对于中长期的预测我们采用Leslie模型进行预测。
我们利用题中所提供的人口数据的比例，将人分为6种类型，在考虑年龄结构的基础上，对各类人中的女性人数分别进行预测，然后根据男女的性别比例，求出男性的人口数，再将预测得到的各类人数进行汇总加和，最终得到总的人口数。
由于我们是根据年龄结构进行的预测，所以可以对人口进行简单的分析，得到老龄化变化趋势，乡镇市的人口所占比例的变化等。
关键词：人口预测；灰色模型；分类计算；Leslie模型一、模型假设模型一的假设：1、不考虑国际迁移，认为国家内部迁移不改变人口总量；2、不考虑自然灾害、疾病等因素对人口数量的影响；3、文中短期预测到2017年4、大面积自然灾害、疾病的发生以及人们的生育观念等因素会对当年的生育率和人口数量产生影响，认为这些因素在预测误差允许的范围内．模型二的假设：1、每一年龄组的女性在每一个时间段内有相同的生育率和死亡率；2、在预测的时间段内男女的性别比例保持现状不变；3、不考虑人口的迁入和迁出；4、不考虑空间等自然因素的影响，不考虑自然灾害对人口数量的影响。
二、问题分析中国是一个人口大国，随着经济的不断发展，生产力达到较高的水平，现在的问题已不是仅仅满足个人的需要，而是要考虑社会的需要。
中国未富先老，对经济的发展产生很大的影响。
中国人口增长预测摘要本文从中国人口的实际情况和人口增长的特点出发，根据题目和中国统计年鉴中的相关数据，建立了两个关于中国人口增长的数学模型，并对中国人口做出了分析和预测。
模型一：利用中国统计年鉴中 2000—2005 年人口的数据，运用灰色理论的基本原理建立 GM(1,1) 模型。
该模型利用离散数据列进行生态处理，建立动态的微分方程，对我国近5年、10年、20年的总人口分别进行了预测。
又根据中国人口城乡分布不同且总趋势也不同的特点，把全国人口分为城市人口、城镇人口、乡村人口三部分分别进行灰色预测。
结果表明，该模型较好的反映并预测中国人口短中期和长期的变化情况。
模型二：按人口年龄结构特征，将人口分为幼年（0—14岁）男女、中年（15—49岁）男女、老年（50岁以上）男女。
各年龄段的人口变化是由出生率、死亡率和转化为其他年龄段的转化人数决定的。
根据各年龄段人口数量变化特点，对各年龄段转化人数引入转化因子，改进马尔萨斯模型，附带出生率、死亡率、生育率、出生性别比率等约束条件，建立了新的具有年龄结构的人口增长模型。
结合我国人口的特点，运用已知数据和利用微分方程的数值解，预测出男性和女性幼年、中年、老年的人口数量。
可反映中国不同年龄结构的人口分布情况。
关键词：灰色预测；小误差频率；微分方程组；人口模型；转移因子一．问题重述中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。
因此人口预测的科学性、准确性是至关重要的。
英国人口学家马尔萨斯的人口指数增长模型和荷兰生物学家的Logistic模型都是经典的人口预测模型。
但是，影响中国人口的因素较多，人口结构较复杂，这些模型对人口预测很粗略，甚至是不准确的。
因此，我们要根据我国具体的人口结构现状（如老龄化进程加速）、人口的分布现状（如乡村人口城镇化）、人口比率现状（如出生人口性别比持续升高）等特点，来较准确、较具体地对中国人口进行预测，建立人口增长的数学模型，由此对中国人口中短期和长期增长趋势做出预测。
人口增长模型摘要本文根据某地区的人口统计数据，建立模型估计该地区2010年的人口数量。
首先，通过直观观察人口的变化规律后，我们假设该地区的人口数量是时间的二次函数，建立了一个二次函数模型，并用最小二乘法对已有数据进行拟合得到模型的具体参数，从而可以预测2010年的人口数为333.8668百万。
然后，我们发现从1980年开始该地区的人口增长明显变慢，于是我们假设人口增长率是人口数的线性减函数，即随着人口数的增加，人口的增长速度会慢慢下降，从而我们建立了阻滞增长模型，利用此模型我们最后求出2010年的人口预报数为296.3865。
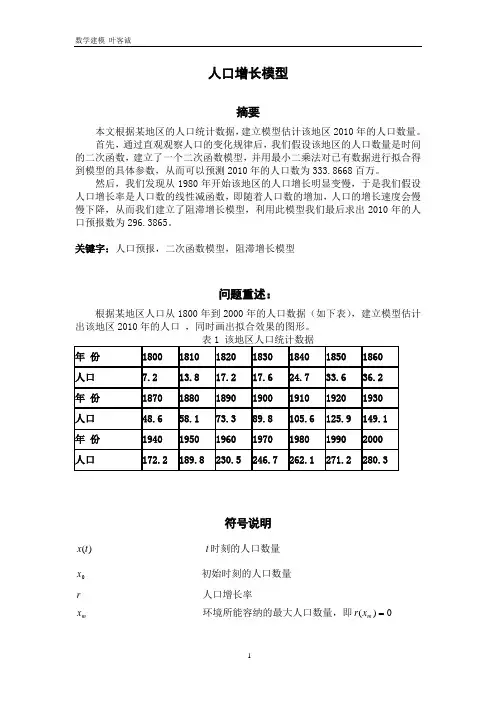
关键字：人口预报，二次函数模型，阻滞增长模型问题重述：根据某地区人口从1800年到2000年的人口数据（如下表），建立模型估计出该地区2010年的人口 ，同时画出拟合效果的图形。
符号说明)(t x t 时刻的人口数量 0x 初始时刻的人口数量 r 人口增长率m x 环境所能容纳的最大人口数量，即0)( m x r问题分析首先，我们运用Matlab软件[1]编程（见附件1），绘制出1800年到2000年的人口数据图，如图1。
18001820184018601880190019201940196019802000图1 1800年到2000年的人口数据图从图1我们可以看出1800年到2000年的人口数是呈现增长的趋势的，而且类似二次函数增长。
所以我们可以建立了一个二次函数模型，并用最小二乘法对已有数据进行拟合得到模型的具体参数。
于是我们假设人口增长率是人口数的线性减函数，即随着人口数的增加，人口的增长速度会慢慢下降,从而我们可以建立一个阻滞增长模型。
模型建立模型一：二次函数模型我们假设该地区t时刻的人口数量的人口数量)(tx是时间t的二次函数，即：2()=++x t at bt c我们可以根据最小二乘法，利用已有数据拟合得到具体参数。
即，要求a、b和c，使得以下函数达到最小值：221(,,)()ni i i i E a b c at bt c x ==++-∑其中i x 是i t 时刻该地区的人口数，即有：2222)3.28020002000...)2.718001800(),,(-+⋅+⋅++-+⋅+⋅=c b a c b a c b a E令0,0,0E E E a b c∂∂∂===∂∂∂，可以得到三个关于a 、b 和c 的一次方程，从而可解得a 、b 和c 。
人口预测的数学模型与预测方法分析摘要：随着人口总数的不断增加，在很大程度上增加用地等方面的压力，不仅会影响到区域发展和经济水平的提升，也会阻碍着区域自然环境的协调发展，因此，必须重视对人口预测的重视程度，合理控制人口规模。
在科学技术日新月异的时代背景下，人口预测的方法和模型逐渐增多，每种方式适应范围和使用程序都有所不同，应根据区域实际情况，选择最恰当的预测方式，确保能够指导区域制定科学的科学发展战略。
本文简要分析人口预测的数学模型，重点介绍Logistic预测模型、双曲预测模型、指数预测模型三种预测方式，并阐述模型间关系。
关键词：人口预测；数学模型；预测方式；双曲预测模型我国人口总数大，增长速度快，在一定程度上增加了人口预测的难度，人口的发展可能受到自然因素、文化因素、政治因素、经济因素等多方面的影响，因此相关工作人员必须综合考虑地域经济状况、人口素质、政治环境，选择最恰当的预测方式，确保人口预测的准确性和可靠性。
需要注意的是，人口预测中运用的数学模型较多，其预测方式表面看似简单，但在实际运用过程常会出现问题，影响到人口预测的准确性，因此，工作人员应不断更新数学模型，做好人口预测工作。
一、人口预测的数学模型概述人口预测是指在某一特定时间段、某一区域中，调查其现有的人口现状和变化，总结出其中的发展规律，并提出影响人口变化的假设条件，并结合合适的计算方式，预测出未来人口的发展和变化[1]。
区域中真实的人口统计资料是人口预测的基础，不仅会影响发展规律的总结，更直接关系着预测结果的可靠性。
在实际运用过程中，常会出现以下三方面的问题：一是简单的推断人口增长，如规定人口某一时期的增长率，这相当于将人口与某一准确的数学函数相连，但人口的变化从来都不会呈现出完全的函数曲线；二是选择模型时，没有确定的标准，常采用同一模型去预测不同区域的人口变化，未将人口发展规律考虑进去；三是多种结果的相加得出人口预测，但这种方式忽略了模型之间的差异性，降低了人口预测的科学性。
八十年代以来我国人口发展的数学模型和展望1The mathematical modeling and projection of China population after 1980物理学院技术物理系99级王彦摘要以LESLIE矩阵构建人口的动力学方程，建立了80年以来中国人口的数学模型,并用人口普查的数据验证了该模型的有效性及所含假设的合理性。
利用该模型可推算82年至98年的逐年的以岁为单位的年龄构成。
通过调整模型中有关参数及输入的条件，定量地分析了“夫妻双方均为独生子女可生两胎”这一政策将在未来15年内对我国人口的影响。
所建模型有很好的移植性，理论上来讲可推测很长一段时期内任一年的年龄结构，并可通过调整参量定量分析一部分人口政策及社会因素对人口发展的影响，可供有关研究及政策制定部门参考。
abstractBased on the LESLIE Matrix as the dynamic function, we built up the mathematical model of the china population development since the adoption of “Family Planning Policy”. A few assumptions are made and justified by the Census Data. With this model, we could accurately estimate the yearly age distribution pattern of china population from 80 to 98. By modifying the relevant parameters and input, we further alculate the population age distribution in 2015 with and without adoption of “a spouse can have two children if the two parties of the spouse are both the only child in their family”. This model could be used , through adapting its parameters , to calculate and project population development under some different social conditions社会经济的许多领域的规划都必须考虑人口这一重要因素。
而人口普查只能为我们提供某几个时间点的横截面数值，但在现实生活中，人们常常需要其他时1“政基金”项目和国家自然科学基金委员会杰出青年基金项目资助（No 10025523）间点的人口总数及其构成。
于是一个迫切的任务就是如何用少数的几个时点的信息比较准确的得到较详尽的其他时点的人口数据。
同时我们知道，人口与政策密切相关，这一点对于自80年起实施“一对夫妇只生一个孩子”的中国更是如此。
为了定量分析政策对它的影响，也需要建立一个现实的，可靠的模型。
这两方面的原因促使作者从人口发展的动力学机制出发，建立一个含多方面参量包括政策参量的数学模型。
本文由五部分构成：第一部分介绍人口学中部分专业词汇的定义；第二部分模型的建立和检验。
第三.四部分为该模型的两个应用,针对缺乏相关参量的直接统计数据是两种不同的处理方法。
第五部分为总结和讨论。
0.数据定义这部分介绍本文中出现的人口学名词并加以简单分析。
年龄别生育率：某年的某年龄妇女生的孩子数与该年龄妇女总数之比。
总和生育率：某年各年龄组妇女生育率的合计数。
即总和生育率=各年龄组妇女生育率之和我们可以把年龄别生育率看作一个妇女在该年龄时平均生的孩子，于是各个不同年龄段的生育率分布可以看成一个妇女处在不同年龄段生育孩子数的分布。
我们把这一分布称为生育模式。
而总和生育率等于每个妇女一生中一共生育的孩子数。
出生率：某年的出生人数与该年总人数之比。
年龄别死亡率：某年的某年龄死亡的人数与该年龄总人数之比。
一．模型的建立（一）. LESLIE 矩阵首先，我们要找到描述人口变化的方程。
目前我国的移民现象很少见，我们可以认为中国人口是一个封闭的系统。
定义)(i A n 为第n 年i 岁的人数，)(i d n 为第n 年年龄为i 的人的死亡率，()i b n 为第n 年年龄为i 的妇女生的孩子数与该年龄妇女数的比例，即i 岁的妇女的生育率。
则当i ≥1时，)]1(1[)1()(1--*-=+i d i A i A n n n 。
我国人口男女比大约1.05，我们在这里忽略这种差别，近似为1，则)()(2/1)0(1i b i A A n n nn **=∑+。
用矩阵来表示上述关系，得到n n n n n n n n A i d d d i b b b A ⨯⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=+...................0...)(1...00..................0...0...)1(100...0...0)0(1......2/)(...2/)1(2/)0(1 其中，[]T n n n n i A A A A ...)(...)1()0(=由于80岁以上的老人所占比重很小，且对于人口的增长已经没有影响（他们不可能再生育），在本文的模型中，常常只考虑80岁以下的人的情况。
其实，n A 的维度只要大于一定值就可以了，在问题处理过程中是可以变化的。
(二).参量的确定LESLIE 矩阵本身是普适的人口动力学方程，而不同历史，社会条件下的人口发展模式特点是由其中的参量来描述的，也就是)(i b n 和)(i d n 。
它们都是随时间变化的量，是诸多因素共同作用的结果。
我们不可能找到这些参量每年的精确数值，因此作一些假设和近似是必要的。
1.生育率i b n (）如第一部分数据分析中分析的那样,我们把某个时点的妇女的生育年龄分布同时看作一个妇女一生中生育孩子数的分布.于是某个时点的综合生育率等于一个妇女一生中生育的孩子数。
考察城市和人口的生育的年龄结构，我们发现两者有很大的不同。
图一98年中国城乡妇女生育率年龄分布从图中， 我们发现农村妇女的总和生育率明显高于城市妇女， 同时她们的生育高峰也比城市妇女早一些，且计划生育政策及其执行情况也有很大的不同，所以本文中将把这两种情况分开讨论。
即2/])()()()([)0()0()0(111∑∑+=+=+++iurban n urban n rural n i rural nurban n rural n n i A i b i A i b A A A 知道了)(i A n ，我们可以用城乡人口比来得到)(i A rural n和)(i A urban n 。
受到生理条件的限制，生育率关于年龄的相对分布应该是一个变化缓慢的量。
我们假定在没有政策性变化时（如限制生育年龄，或允许多育），它是恒定的。
于是如果知道某年的总和生育率，结合图一给出的98年的分布，便可得到当年的具体分布：i b n (）=)(*)(/)(9898i b i b i b in i ∑∑⎥⎦⎤⎢⎣⎡如果我们把总和生育率)(i b in ∑表示为n B ,则i b n (）=n B B i b */)(9898而总和生育率n B 是比较容易获得的。
2.年龄别死亡率)(i d n年龄别死亡率分布数据很少，事实上，作者只找到了89年一例，于是只能先假定死亡率不变。
而通过后面的计算发现， 这个假设和我国80年至今的情况符合的很好。
即使在未来的很长一段时间内，只要没有医学上大的革命，这个量的变化将很小。
因此，本文中把它当成常量处理。
所用数据为89年的统计（中国统计局数据服务DUS2-42），如图所示图二：89年中国年龄别死亡率分布(三). 82年——90年的人口变化及假设的验证对于80年代的人口，我们掌握的材料比较充分，如逐年的城乡总和生育率，82年和89年的人口年龄结构，历年城乡人口比例等。
我们用82年的数值作为初始条件，用上述模型推算至90年的分布， 再和普查数据比较，以此检验我们的模型及相关假设。
结果如以下图所示。
图三：90年中国人口年龄分布比较两条曲线，发现它们吻合的相当不错，尤其是10岁以后的曲线，差别非常小。
由于这部分人口的发展只受死亡率的影响，说明我们把)(i d n 作为常量处理是合理的。
（这也说明我国二十年来医疗技术的进步还没有对人口产生大的影响）而10岁以前的曲线也基本吻合，最大误差在5%以内。
由此，关于生育率的年龄的相对分布的假设也是合理的。
至此，模型的有效性得到了证明。
二. 90—98年的人口发展和上一阶段不同，这一时期的人口统计数据不够充分，尤其是总和生育率的数据的缺乏，使这一阶段的处理方法和90年以前不同。
)(i A n 对1≥i 的情况仍可按刚才的方法处理，但对于)0(n A ，在没有总和生育率时，就不能得到)(i b n ，也就不能用LESLIE 矩阵法了。
作者用第n 年的出生率⨯人口总数=第n+1年的0岁的人数得到)0(1+n A 。
而人口总数和总出生率都是比较容易获得的数据。
用上述方法可以得到90-98年逐年的年龄构成，98年的分布见下图图四：98年中国人口年龄分布推算这种处理方法只能用来求过去的时点的年龄结构，而不能用与人口的预测，因为将来的时点的人口总数和出生率也是未知的。
而LESLIE矩阵则从人口发展的动力学机制出发，因而可以用来预测未来的情况。
第四部分就是一个例子。
三.2015年人口分布的预测这一部分主要采用本文第一部分阐述的方法分析“夫妇双方均为独生子女可生育两个孩子”这一政策将给我国人口造成的影响。
我国农村妇女的总和生育率在计划生育实行后一直维持在1.5以上，而在80年代初有2.0左右，也就是说，即使在2000年后，农村独生子女的比重很小，而夫妻均为独生子女的概率更小，于是可以认为该政策对农村的影响可以忽略,农村生育模式不变。
而城市的总和生育率自80年代起非常接近1，我们认为所有的80年以后的城市出生的都是独生子女，于是前述政策对城市的影响很大。
下面是定量分析。
考察98年我国农村分胎次的生育率年龄分布：图五：98年中国城乡妇女生育率农村每个妇女平均有0.457个二胎，而城市平均只有0.146个，但是它们的相对分布确实非常相近的。
事实上，从图中可以看出，把城市妇女的第二胎的生育年龄结构按比例（0.457/0.146）放大后和农村妇女的相应的分布形状基本相同。
