椭圆极坐标方程推导

极坐标法解圆锥曲线
极坐标法可以用来解析表示圆锥曲线的方程。

圆锥曲线包括圆、椭圆、抛物线和双曲线。

下面将分别介绍极坐标法在解析这些曲线方程中的应用。

1.圆：圆的极坐标方程为 r = a，其中 a 为圆的半径。

在极坐
标系下，圆心位于原点，以原点为中心半径为 a 的圆。

2.椭圆：椭圆的极坐标方程为 r = a(1 - e*cosθ)，其中 a 为长
轴的一半，e 为离心率，θ 为极角。

通常情况下，取e < 1，这样才能得到椭圆。

如果 e = 0，则表示一个圆。

3.抛物线：抛物线的极坐标方程为r^2 = 2a*p，其中a 为焦
点到抛物线顶点的距离，p 为焦距的一半。

抛物线沿着对
称轴对称。

4.双曲线：双曲线的极坐标方程为 r^2 = 2a p cosθ，其中 a 为
焦点到双曲线顶点的距离，p 为焦距的一半。

双曲线有两
个分支，分别向外延伸。

对于给定的圆锥曲线方程，你可以将其转化为极坐标方程进行分析和绘制。

通过改变参数 a、e 和 p 的值，可以调整曲线的尺寸、形状和位置。

请注意，极坐标法的应用需要对极坐标系和常见曲线方程有一定的数学理解。

在进行计算和绘制时，确保使用正确的公式和技巧，以获得准确的结果。

椭圆的结论十三个及证明椭圆是平面解析几何中的一类特殊曲线，由两个焦点F1和F2及到它们的距离之和等于常数2a的点动轨迹构成。

本文将介绍椭圆的定义、性质以及它们的证明。

##一、椭圆的定义椭圆的定义如下：设平面上给定两个不重合的点F1和F2，对于平面上的任意一点P，到F1的距离加上到F2的距离等于常数2a，那么点P的轨迹就是一个椭圆。

我们可以通过以下步骤来证明这一定义。

##二、椭圆的证明### 1.步骤1：点P在椭圆上对于任意一点P在椭圆上，我们有以下等式成立：PF1 + PF2 = 2a由于F1和F2是椭圆的两个焦点，所以对于任意时刻，PF1 + PF2的距离是恒定的，等于椭圆的主轴长2a。

所以点P在椭圆上。

### 2.步骤2：椭圆的离心率椭圆的离心率是一个衡量椭圆扁平程度的指标。

我们可以用离心率e来表示，它的计算公式如下：e = PF1 / a其中，a是椭圆的主轴长。

### 3.步骤3：椭圆的焦点与准线根据椭圆的定义，我们可以得到以下结论：-椭圆的焦点F1和F2在椭圆的主轴上，且在椭圆的中垂线上；-椭圆的准线是与椭圆的对称轴相交于焦点的直线。

### 4.步骤4：椭圆的标准方程椭圆的标准方程可以根据椭圆的定义推导而得。

设椭圆的焦点为F1(-c,0)，F2(c,0)，椭圆的顶点为A(a,0)和B(-a,0)，那么椭圆的标准方程为：(x - c)² / a² + y² / b² = 1其中，a是椭圆的半长轴，c是椭圆的焦距，b是通过离心率计算得到的次长轴。

### 5.步骤5：椭圆的参数方程椭圆的参数方程可以通过椭圆的标准方程得到。

设角度θ是椭圆的主轴与x轴的夹角，那么椭圆的参数方程为：x = a * cosθy = b * sinθ其中，0 ≤ θ ≤ 2π。

### 6.步骤6：椭圆的半焦距和焦长度椭圆的半焦距c是焦点到中心点的距离的一半，可以用以下公式表示：c = √(a² - b²)椭圆的焦长度是焦点到准线的距离，可以用以下公式表示：d = 2 * c### 7.步骤7：椭圆的面积椭圆的面积可以通过以下公式计算得到：S = π * a * b其中，a是椭圆的半长轴，b是通过离心率计算得到的次长轴。

椭圆的极坐标方程推导
椭圆的极坐标方程的推导是椭圆与极坐标关系的一个重要研究领域，在许多领域有着广泛的应用，例如太阳系中行星的运行椭圆轨迹，宇宙物理研究中的空间造型也是椭圆的形态。

椭圆的极坐标方程可以表达为，
r=p/(1+ecosθ), (1)
其中，r为椭圆上任意点的极坐标距离，p为椭圆长短轴之间的比值，ε 为椭圆偏心率，θ为极坐标原点到椭圆上任意点的角度。

推导椭圆的极坐标方程需要从直角坐标系下的椭圆方程开始，即：
x²/a²+y²/b²=1,(2)
拓展函数技术可以将这个方程从直角坐标系转换到极坐标系，
x=rcosθ,(3)
y=rsinθ,(4)
代入椭圆方程（2），可以得到：
r²cos²θ/a²+r²sin²θ/b²=1 (5)
开根号并消元之后，得出最终结果：
r=p/(1+ecosθ) (6)
它就是椭圆在极坐标系下的极坐标方程。

以上就是椭圆的极坐标方程推导的过程，它有许多应用，例如行星的运行椭圆轨迹，宇宙
物理研究当中的空间造型，可以很直观的用图表示出。

椭圆的极坐标方程在很多领域有着
重要的应用，也是数学研究的重要领域。

椭圆面积极坐标椭圆面积在极坐标系下的计算方法有很多，我们可以通过极坐标方程来求解椭圆的面积。

在这篇文章中，我将为大家介绍椭圆面积的计算方法，并且通过实例来说明其应用。

首先我们来回顾一下椭圆的定义。

椭圆是平面上到两个定点F1和F2的距离之和恒定的点的轨迹，这个恒定的和就是椭圆的长轴，而两个定点F1和F2之间的距离就是椭圆的焦距。

对于椭圆来说，长轴和焦距的关系是大于等于2的，而当两点重合时，椭圆就变成了一个圆。

在极坐标系下，椭圆的极坐标方程可以表示为r = a(1 - e * cosθ)，其中a是长轴的一半，e是离心率，r和θ分别是点在极坐标系下的径向和极角。

要计算椭圆的面积，我们可以利用极坐标下的面积元素dA，然后对整个椭圆进行积分求和。

根据极坐标下的面积元素公式，dA = 1/2 * r^2 * dθ。

将极坐标方程代入，可以得到dA = 1/2 * a^2 * (1 - e * cosθ)^2 * dθ。

接下来，我们可以对这个面积元素进行积分。

由于θ的范围是从0到2π，所以积分的范围也是从0到2π。

将面积元素代入积分式中，可以得到椭圆的面积S = ∫(0 to 2π) 1/2 * a^2 * (1 - e * cosθ)^2 * dθ。

对于这个积分式，我们可以通过换元法进行求解。

令u = sinθ，然后进行变量代换和化简，可以得到积分式S = π * a^2 * (1 - e^2)。

通过这个公式，我们可以很方便地计算椭圆的面积。

只需要知道长轴的长度a和离心率e，就可以得到椭圆的面积。

现在我们来举一个具体的例子来说明椭圆面积的计算方法。

假设有一个椭圆，其长轴的长度是6，离心率是0.8。

我们可以利用上述公式来计算这个椭圆的面积。

根据公式S = π * a^2 * (1 - e^2)，代入a = 6和e = 0.8，可以得到S = π * 6^2 * (1 - 0.8^2) = 16.96π。

所以这个椭圆的面积约为53.29。

关于椭圆周长的一个完美的计算公式椭圆周长是一个在数学和物理学中经常遇到的问题。

在二维平面上，一个椭圆的周长可以通过以下公式进行计算：C = 4a * π * ((a^2) / (b^2)) * ((1 + ((b^2) / (a^2)))^(1/2))其中，a代表椭圆的长半轴，b代表椭圆的短半轴。

这个公式是如何推导的呢？首先，考虑一个椭圆的长轴在x轴上的情况。

在极坐标系中，椭圆的方程可以写为：r = a * (1 + e*cos(θ))其中，r是点到椭圆中心的距离，e是椭圆的离心率（e = c / a，其中c是椭圆半焦距），θ是极角。

这个方程描述了一个以长轴为a、短轴为b的椭圆（e是离心率，与短半轴b和长半轴a的比值有关）。

为了计算周长，我们可以对上式求θ从0到2π的定积分。

但是，直接的计算非常复杂。

幸运的是，我们有以下的积分公式：∫(r0 * r) * dθ = (r0 * r1) * (r1 - r0)其中，r0和r1是在积分区间内r的最小和最大值。

在这个情况下，我们可以将r0设为0，r1设为a*(1+e*cos(θ))，得到：∫(0 to a(1+e*cos(θ))) * dθ =a^2 * π * e化简后得到：∫(0 to 2π) * a*(1+e cos(θ)) * dθ = 2a^2πe这就是椭圆周长的公式。

值得注意的是，这个公式不仅适用于长轴在x轴上的椭圆，也适用于长轴在y轴上的椭圆，因为当长轴在y轴上时，相应的离心率和周长公式是一样的。

然而，这个公式并不完美，因为它涉及到对离心率e的求解，而这涉及到一定的数学技巧。

因此，在实际应用中，我们通常会直接使用椭圆周长的第二参数公式（周长公式），它直接给出了椭圆周长和第二参数的关系，更为方便实用：C = π * (a + b) * sqrt((a-b)/(a+b))其中，a和b的含义同上。

这个公式实际上是第一公式的一种简化和变形，将a和b的关系直接代入并化简得到。

常见的极坐标方程极坐标方程是描述平面直角坐标系中的点在极坐标系中的位置和形状的一种方式。

极坐标方程通常表示为$r=f(\theta)$，其中$r$表示点到原点的距离，$\theta$表示点与$x$轴正半轴之间的夹角。

常见的极坐标方程包括：一、基本形式1. $r=a$：表示以原点为中心，半径为$a$的圆。

2. $r=a\cos\theta$：表示以原点为焦点，以$x$轴正半轴为对称轴，离心率为$\frac{1}{2}$，长轴长度为$a$的椭圆。

3. $r=a\sin\theta$：表示以原点为焦点，以$y$轴正半轴为对称轴，离心率为$\frac{1}{2}$，长轴长度为$a$的椭圆。

4. $r=a\cos n\theta$或$r=a\sin n\theta(n\in N^*)$：分别表示以原点为中心，半径分别是$a,a/2,a/3,\cdots,a/n$等等的$n$个同心圆。

这些圆上有$n$个等分点，在这些等分点上分别作切线，则这些切线所组成的$n$边形叫做正$n$边形。

二、特殊形式1. $r=\dfrac{a}{1\pm\cos\theta}$：表示以原点为焦点，离心率为$1$，长轴长度为$a$的双曲线。

2. $r=\dfrac{a}{1\pm\sin\theta}$：表示以原点为焦点，离心率为$1$，长轴长度为$a$的双曲线。

3. $r=a(1+\cos\theta)$：表示以原点为焦点，以$x=-a/2$为对称轴，离心率为$\frac{1}{2}$，长轴长度为$a$的摆线。

4. $r=a(1-\cos\theta)$：表示以原点为焦点，以$x=a/2$为对称轴，离心率为$\frac{1}{2}$，长轴长度为$a$的摆线。

5. $r=a(1+\sin\theta)$：表示以原点和$(a,0)$两个焦点确定的椭圆上沿着逆时针方向运动的一个质点在$x$轴正半轴上留下的投影长度。

6. $r=a(1-\sin\theta)$：表示以原点和$(a,0)$两个焦点确定的椭圆上沿着顺时针方向运动的一个质点在$x$轴正半轴上留下的投影长度。

椭圆极坐标方程与直角坐标方程的转化椭圆是数学中常见的几何形状之一，在坐标系中可以通过椭圆的极坐标方程和直角坐标方程来描述。

椭圆的极坐标方程与直角坐标方程之间存在一定的转化关系，本文将介绍椭圆极坐标方程与直角坐标方程的转化方法。

一、椭圆的直角坐标方程椭圆的直角坐标方程是以椭圆的中心为原点建立的直角坐标系中，椭圆上的每个点(x, y)都满足下面的方程：\[ \frac{x2}{a2} + \frac{y2}{b2} = 1 \]其中，a和b分别代表x轴和y轴上的半轴长度。

二、椭圆的极坐标方程椭圆的极坐标方程是以椭圆的中心为极点建立的极坐标系中，椭圆上的每个点(r, θ)都满足下面的方程：\[ r = \frac{ab}{\sqrt{a2sin2\theta + b2cos2\theta}} \]其中，a和b分别代表x轴和y轴上的半轴长度，θ代表极角。

三、由直角坐标方程到极坐标方程的转化要将椭圆的直角坐标方程转化为极坐标方程，需要将直角坐标系中的x和y坐标变换为极坐标系中的r和θ。

1.首先，将直角坐标方程中的x和y坐标代入极坐标方程中的r，得到\[ r = \sqrt{x2+y2} \]2.其次，将直角坐标方程中的x和y坐标代入极坐标方程中的θ，得到\[ \theta = arctan(\frac{y}{x}) \]这样，就可以将椭圆的直角坐标方程转化为极坐标方程。

四、由极坐标方程到直角坐标方程的转化要将椭圆的极坐标方程转化为直角坐标方程，需要将极坐标系中的r和θ变换为直角坐标系中的x和y。

1.首先，将极坐标方程中的r代入直角坐标方程中的x和y，得到\[ x = rcos\theta \] \[ y = rsin\theta \]2.其次，将极坐标方程中的θ代入直角坐标方程中的x和y，得到\[ x = acos\theta \] \[ y = bsin\theta \]这样，就可以将椭圆的极坐标方程转化为直角坐标方程。

【关键字】精品椭圆的极坐标方程-双曲线焦点坐标圆锥曲线的极坐标方程、焦半径公式、焦点弦公式圆锥曲线的极坐标方程、焦半径公式、焦点弦公式湖北省天门中学薛德斌一、圆锥曲线的极坐标方程椭圆、双曲线、抛物线可以统一定义为：与一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e的点的轨迹．以椭圆的左焦点(双曲线的右焦点、抛物线的焦点)为极点，过点F作相应准线的垂线，垂足为K，以FK的反向延长线为极轴建立极坐标系．ep椭圆、双曲线、抛物线统一的极坐标方程为：. 1ecos其中p是定点F到定直线的距离，p＞0 ．当0＜e＜1时，方程表示椭圆；当e＞1时，方程表示双曲线，若ρ＞0，方程只表示双曲线右支，若允许ρ＜0，方程就表示整个双曲线；当e=1时，方程表示开口向右的抛物线.二、圆锥曲线的焦半径公式设F为椭圆的左焦点(双曲线的右焦点、抛物线的焦点)，P为椭圆(双曲线的右支、抛物线)上任一点，则∵PF e，∴PF e(PFcos p)，其中p FH，〈x轴，FP〉∴焦半径PF ep．1ecosep. 1ecos当P在双曲线的左支上时，PF推论：若圆锥曲线的弦MN经过焦点F，则有112. MFNFep三、圆锥曲线的焦点弦长若圆锥曲线的弦MN经过焦点F，epep2ab2a2b2c1、椭圆中，p，MN222. cc1ecos1ecos()a ccos2、双曲线中，epep2ab2若M、N在双曲线同一支上，MN；1ecos1ecos()a2c2cos2epep2ab2若M、N在双曲线不同支上，MN. 1ecos1ecos c2cos2a23、抛物线中，MN pp2p. 21cos1cos()sin四、直角坐标系中的焦半径公式设P是圆锥曲线上的点，1、若F1、F2分别是椭圆的左、右焦点，则PF1a exPF2a ex；2、若F1、F2分别是双曲线的左、右焦点，当点P在双曲线右支上时，PF1ex a，PF2ex a；当点P在双曲线左支上时，PF1a ex，PF2a ex；3、若F是抛物线的焦点，PF xp. 2坐标曲线题题型研究题型一坐标曲线题热点题型精讲坐标曲线类试题一般结合数学中的平面直角坐标系考查，用横纵坐标代表不同的化学量，主要与氧气的制取、金属与酸和盐的反应、酸碱盐之间的反应、溶质质量分数和pH等知识相结合考查。

椭圆的参数方程是怎么推导出来的？？椭圆的参数方程推导过程：
(1)的平方加(2)的平方
化简得：
证明：将任意一点P的坐标（Rsinθ-c,Rcosθ)代入方程
=
说明P点是椭圆标准方程上的一点。

扩展资料：
常见的参数方程——
曲线的极坐标参数方程ρ=f(t),θ=g(t)。

圆的参数方程x=a+r cosθy=b+r sinθ（θ∈[0，2π) ）(a,b) 为圆心坐标，r 为圆半径，θ为参数，(x,y) 为经过点的坐标。

椭圆的参数方程x=a cosθy=b sinθ（θ∈[0，2π））a为长半轴长b为短半轴长θ为参数。

双曲线的参数方程x=a secθ（正割）y=b tanθa为实半轴长b为虚半轴长θ为参数。

抛物线的参数方程x=2pt^2 y=2pt p表示焦点到准线的距离t为参数。

直线的参数方程x=x'+tcosa y=y'+tsina,x',y'和a表示直线经过（x',y'），且倾斜角为a,t为参数。

或者x=x'+ut，y=y'+vt (t∈R)x',y'直线经过定点（x',y'),u，v表示直线的方向向量d=(u,v)。

圆的渐开线x=r(cosφ+φsinφ）y=r(sinφ-φcosφ）（φ∈[0,2π））r为基圆的半径φ为参数。

极坐标方程一般式1. 引言极坐标方程是解析几何中的一种双曲线、椭圆、抛物线等曲线的表示方法，它是通过极坐标来描述平面上的点的位置，以极轴和极角来表示点的位置坐标。

极坐标方程一般式是用于求解各种极坐标方程的通用解法，它可以将极坐标方程转化为直角坐标系中的方程，从而更方便地求解各种曲线的性质。

2. 极坐标系和极坐标方程的定义极坐标系是以原点O为极点建立的坐标系，极轴是从原点O开始沿着某一方向的射线，极角是极轴与从极点到点P的射线所夹的角，极径是从极点O到点P的距离。

极坐标方程是指以极坐标系中的极径和极角为变量的方程，它是用来描述平面上的曲线的。

极坐标方程一般形式为：r=f(θ)，其中r 为极径，θ为极角，f是一个关于θ的函数。

3. 极坐标系与直角坐标系之间的转换为了方便计算，我们需要将极坐标系中的坐标转换成直角坐标系中的坐标。

下面给出极坐标与直角坐标之间的转换公式：x=r*cosθy=r*sinθ其中，x和y分别表示点P在直角坐标系中的横坐标和纵坐标，r 和θ分别表示点在极坐标系中的极径和极角。

4. 极坐标方程一般式的推导我们现在来推导一下极坐标方程的一般式。

以双曲线为例，其极坐标方程为：r^2=a^2*sinh^2(θ)其中，a为常数，sinh(θ)表示双曲正弦函数。

我们将极坐标转换为直角坐标：x=r*cosθ=a*sinh(θ)*cosθy=r*sinθ=a*sinh(θ)*sinθ我们将y/x=tanθ代入r^2=a^2*sinh^2(θ)中，得到：r^2=a^2(tan^2θ+1)r^2=a^2(sec^2θ)因此，双曲线的极坐标方程变为：r=±a*secθ同样的方法可以用于推导抛物线、椭圆等曲线的极坐标方程。

5. 极坐标方程一般式的应用极坐标方程一般式的应用非常广泛，它可以用于求解各种曲线的性质，如对称轴、焦点、直径、离心率等。

同时，极坐标方程一般式也可以应用于物理学、工程学、计算机图形学等领域。

椭圆知识点总结框架一、椭圆的定义1. 椭圆的几何定义2. 椭圆的代数定义3. 参数方程和极坐标方程二、椭圆的性质1. 椭圆的焦点和直径2. 椭圆的离心率3. 椭圆的直角坐标方程4. 椭圆的极坐标方程5. 椭圆的对称性6. 椭圆的形状7. 椭圆的周长和面积三、椭圆的方程1. 椭圆标准方程2. 椭圆的变换方程3. 椭圆的参数方程4. 椭圆的极坐标方程四、椭圆的图形1. 椭圆的图像特征2. 椭圆的几何分析3. 椭圆的轴和焦点4. 椭圆的绘制方法五、椭圆的应用1. 椭圆在天文学中的应用2. 椭圆在机械工程中的应用3. 椭圆在工程测量中的应用4. 椭圆在地理学中的应用5. 椭圆在其他领域中的应用六、椭圆与其他几何图形的关系1. 椭圆与圆的关系2. 椭圆与抛物线的关系3. 椭圆与双曲线的关系4. 椭圆与直线的关系七、椭圆的数学推导1. 椭圆的性质证明2. 椭圆的相关公式推导3. 椭圆的参数化方程推导4. 椭圆的极坐标方程推导八、椭圆的计算题1. 椭圆的周长计算2. 椭圆的面积计算3. 椭圆的焦点坐标计算4. 椭圆的离心率计算以上是关于椭圆的知识点总结框架，接下来我们将对每个知识点进行详细讲解。

一、椭圆的定义1. 椭圆的几何定义椭圆是平面上到两个定点F1,F2的距离之和等于常数2a的点P的集合，这个常数2a称为椭圆的长轴，两个定点F1,F2称为椭圆的焦点。

椭圆的几何定义可以简单理解为平面上到两个固定点的距离之和等于常数的点的轨迹。

2. 椭圆的代数定义设椭圆的两个焦点为F1(-c,0),F2(c,0), 两个焦点到椭圆上任意点P(x,y)的距离之和等于椭圆的长轴长2a，则有|PF1|+|PF2|=2a。

根据勾股定理可以得到椭圆的代数方程：(x+c)^2+y^2+(x-c)^2+y^2=4a^2。

3. 参数方程和极坐标方程椭圆的参数方程是x=a*cos(t),y=b*sin(t), 其中a,b分别为椭圆的长短半轴。

椭圆的极坐标方程-双曲线焦点坐标圆锥曲线的极坐标方程、焦半径公式、焦点弦公式圆锥曲线的极坐标方程、焦半径公式、焦点弦公式湖北省天门中学薛德斌一、圆锥曲线的极坐标方程椭圆、双曲线、抛物线可以统一定义为：与一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e的点的轨迹．以椭圆的左焦点(双曲线的右焦点、抛物线的焦点)为极点，过点F作相应准线的垂线，垂足为K，以FK的反向延长线为极轴建立极坐标系．ep椭圆、双曲线、抛物线统一的极坐标方程为：. 1ecos其中p是定点F到定直线的距离，p＞0 ．当0＜e＜1时，方程表示椭圆；当e＞1时，方程表示双曲线，若ρ＞0，方程只表示双曲线右支，若允许ρ＜0，方程就表示整个双曲线；当e=1时，方程表示开口向右的抛物线.二、圆锥曲线的焦半径公式设F为椭圆的左焦点(双曲线的右焦点、抛物线的焦点)，P为椭圆(双曲线的右支、抛物线)上任一点，则∵PF e，∴PF e(PFcos p)，其中p FH，〈x轴，FP〉∴焦半径PF ep．1ecosep. 1ecos当P在双曲线的左支上时，PF推论：若圆锥曲线的弦MN经过焦点F，则有112. MFNFep三、圆锥曲线的焦点弦长若圆锥曲线的弦MN经过焦点F，epep2ab2a2b2c1、椭圆中，p，MN222.cc1ecos1ecos()a ccos2、双曲线中，epep2ab2若M、N在双曲线同一支上，MN；1ecos1ecos()a2c2co s2epep2ab2若M、N在双曲线不同支上，MN.1ecos1ecos c2cos2a23、抛物线中，MN pp2p. 21cos1cos()sin四、直角坐标系中的焦半径公式设P是圆锥曲线上的点，1、若F1、F2分别是椭圆的左、右焦点，则PF1a exPF2a ex；2、若F1、F2分别是双曲线的左、右焦点，当点P在双曲线右支上时，PF1ex a，PF2ex a；当点P在双曲线左支上时，PF1a ex，PF2a ex；3、若F是抛物线的焦点，PF xp. 2坐标曲线题题型研究题型一坐标曲线题热点题型精讲坐标曲线类试题一般结合数学中的平面直角坐标系考查，用横纵坐标代表不同的化学量，主要与氧气的制取、金属与酸和盐的反应、酸碱盐之间的反应、溶质质量分数和pH等知识相结合考查。

椭圆的参数方程化为极坐标方程椭圆是一种常见的二维几何图形，它具有特殊的形状和属性。

在数学中，椭圆可以通过参数方程来描述其形状和位置。

然而，有时候将参数方程转化为极坐标方程会更加方便和简洁。

本文将介绍如何将椭圆的参数方程化为极坐标方程的方法。

椭圆的参数方程椭圆的参数方程可以用以下形式表示：x = a * cos(t)y = b * sin(t)其中，a和b分别表示椭圆的两个半轴的长度，t是参数。

这个参数t的取值范围通常是[0, 2π]。

通过不同的参数t取值，我们可以得到椭圆上的各个点的坐标，从而描绘出整个椭圆。

极坐标方程的基本概念极坐标是一种描述平面上点位置的坐标系统，它使用极径和极角两个量来确定一个点的位置。

极径表示点到原点的距离，极角表示点与极轴正方向的夹角。

常见的极坐标方程形式是：r = f(θ)其中，r表示极径，θ表示极角，f(θ)表示极径r和极角θ之间的关系。

将椭圆的参数方程化为极坐标方程，就是要找到适当的极径r和极角θ的关系式。

将椭圆的参数方程化为极坐标方程的方法首先，我们需要了解椭圆在参数方程下的性质。

椭圆的参数方程保证了椭圆上的点满足特定的条件，即(x/a)^2 + (y/b)^2 = 1。

我们可以利用这个条件来将参数方程化简为极坐标方程。

假设椭圆的参数方程为：x = a * cos(t)y = b * sin(t)我们需要找到合适的极径r和极角θ的关系式。

由于椭圆上的点满足(x/a)^2 + (y/b)^2 = 1，我们可以将x和y代入这个方程，得到：(a * cos(t)/a)^2 + (b * sin(t)/b)^2 = 1化简以上方程，可以得到：cos^2(t)/a^2 + sin^2(t)/b^2 = 1进一步变换，可以得到：r = a*b / sqrt((b*cos(t))^2 + (a*sin(t))^2)通过上述化简，我们成功将椭圆的参数方程化为了极坐标方程。

总结本文介绍了如何将椭圆的参数方程化为极坐标方程。

椭圆极坐标的焦半径概述椭圆是数学上常见的曲线之一，它在平面内具有两个焦点。

在极坐标系中，我们来研究椭圆的焦半径，即到椭圆焦点距离的长度。

本文将介绍椭圆的基本概念、极坐标系的定义与转换、椭圆的焦点及其性质，最后推导出椭圆极坐标系下的焦半径公式，并举例进行计算。

椭圆的基本概念椭圆是平面上一条封闭曲线，其椭圆心为O，离心率为e，主轴的长度为2a，副轴的长度为2b。

离心率e的定义如下：椭圆上任意一点P到焦点F1、F2的距离之和等于常数2a，即PF1 + PF2 = 2a，其中F1F2的长度为2c，有关系式c^2 = a^2 - b^2。

椭圆的离心率满足0 < e < 1，当e=0时，椭圆退化为圆。

极坐标系的定义与转换极坐标系是描述平面上一点位置的坐标系，由极径r和极角θ组成。

极径r表示点到原点O的距离，极角θ表示点与极轴之间的夹角。

我们可以用直角坐标系和极坐标系之间的转换关系来描述椭圆的极坐标方程：其中，p是极坐标系中的常数，p = a(1-e^2)。

椭圆的焦点及其性质椭圆有两个焦点F1、F2，其中F1位于x轴的正半轴上，F2位于x轴的负半轴上。

椭圆的离心率e和焦距f的关系为e = f/a。

椭圆的焦点与焦半径有如下性质：1.焦半径在x轴上的分量为p，即焦半径PF1或PF2的投影PF1’或PF2’到x轴上的长度为p。

2.焦半径的极角θ满足θ = tan^(-1)(ey/x)，其中x、y为极坐标系中点的坐标。

椭圆极坐标系下的焦半径公式推导根据极坐标系的定义，我们已知椭圆的极坐标方程为r = p / (1 + e * cosθ)。

假设椭圆的焦半径为r0，则有：考虑到焦半径在x轴上的分量为p，我们可以将焦半径r0表示为其x、y轴上的分量：将e表示为f/a，焦半径的x、y分量可以表示为：再利用之前提到的极坐标转换关系，将极坐标转换为直角坐标，可以得到焦半径的直角坐标方程：示例计算假设椭圆的离心率为0.6，主轴长度为6，焦半径点的极角θ为30°，我们来计算焦半径的长度。

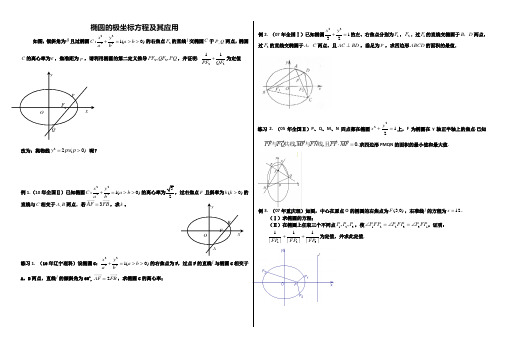
椭圆的极坐标方程及其应用如图，倾斜角为θ且过椭圆2222:1(0)x y C a b a b +=>>的右焦点2F 的直线l 交椭圆C 于,P Q 两点，椭圆C 的离心率为e ，焦准距为p ，请利用椭圆的第二定义推导22,,PF QF PQ ，并证明: 2211PF QF +为定值改为：抛物线22(0)y px p => 呢？例1.（10年全国Ⅱ）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为32，过右焦点F 且斜率为(0)k k >的直线与C 相交于,A B 两点．若3AF FB =，求k 。

练习1. （10年辽宁理科）设椭圆C ：22221(0)x y a b a b+=>>的右焦点为F ，过点F 的直线l 与椭圆C 相交于A ，B 两点，直线l 的倾斜角为60o,2AF FB =，求椭圆C 的离心率；例2. （07年全国Ⅰ）已知椭圆22132x y +=的左、右焦点分别为1F ，2F ．过1F 的直线交椭圆于B D ，两点，过2F 的直线交椭圆于A C ，两点，且AC BD ⊥，垂足为P ，求四边形ABCD 的面积的最值．练习2. （05年全国Ⅱ）P 、Q 、M 、N 四点都在椭圆1222=+y x 上，F 为椭圆在y 轴正半轴上的焦点.已知.0,,=⋅MF PF FN MF FQ PF 且线与共线与求四边形PMQN 的面积的最小值和最大值.例3. （07年重庆理）如图，中心在原点O 的椭圆的右焦点为)0,3(F ，右准线l 的方程为12=x . （Ⅰ）求椭圆的方程； （Ⅱ）在椭圆上任取三个不同点123,,P P P ，使133221FP P FP P FP P ∠=∠=∠，证明： ||1||1||1321FP FP FP ++为定值，并求此定值.Q y O x P 2F AyOxBF推广：已知椭圆22221(0)x y a b a b+=>>,F 是椭圆的右焦点,在椭圆上任取n 个不同点12,,,n P P P ⋅⋅⋅,若122311n n n PFP P FP P FP P FP -∠=∠=⋅⋅⋅=∠=∠,则11||ni i nPF ep ==∑，你能证明吗？ 练习3. （08年福建理科）如图，椭圆2222.1(0)x y a b a b+=>>的一个焦点是F （1，0），O 为坐标原点.（Ⅰ）已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；（Ⅱ）设过点F 的直线l 交椭圆于A 、B 两点.若直线l 绕点F 任意转动，值有222OA OB AB +<,求a 的取值范围.作业1. （08年宁夏文）过椭圆14522=+y x 的右焦点作一条斜率为2的直线与椭圆交于B A ,两点, O 为坐标原点, 则△OAB 的面积为 .作业2.（09年全国Ⅰ）已知椭圆22:12x C y +=的右焦点为F,右准线l ，点A l ∈，线段AF 交C 于点B 。

椭圆的极坐标方程知乎在数学中，椭圆是一种特殊的曲线，可以通过其极坐标方程来描述。

椭圆的极坐标方程为r=a(1-e*cosθ)，其中a表示长半轴的长度，e表示离心率，θ表示与极轴的夹角。

椭圆的定义可以简单地理解为，到焦点距离之和等于常数的点的轨迹。

椭圆有许多独特的性质。

首先，椭圆是一个闭合曲线，其形状类似于椭圆形。

其次，椭圆有两个焦点，且到焦点距离之和等于常数。

这个性质被广泛运用于日常生活中，比如卫星轨道的设计、椭圆形的运动器械等。

此外，椭圆还具有对称性，即椭圆关于x轴和y轴对称。

在知乎平台上，有很多与椭圆相关的问题和回答。

例如，有人可能会问：“椭圆有什么实际应用？”这个问题引起了许多网友的关注。

回答者们纷纷列举了椭圆的应用领域。

有人提到了椭圆轨道在航天领域的应用，如人造卫星的轨道设计、空间站的轨道控制等。

还有人谈到了椭圆的几何特性在建筑设计中的应用，如椭圆形建筑的设计和构造等。

总之，椭圆的应用是广泛而多样的。

另一个问题可能是：“如何画出一个椭圆？”这个问题引起了很多绘图爱好者的兴趣。

回答者们纷纷给出了方法和技巧。

有人建议使用椭圆板或者绘图仪器来画椭圆，这样可以更准确地画出椭圆的形状。

还有人提到了利用数学原理，通过确定焦点和长半轴的位置，来画出椭圆的方法。

这些回答为有兴趣绘制椭圆的人提供了很好的指导。

还有一些有趣的问题和回答与椭圆相关。

例如，“椭圆和圆有什么区别？”这个问题引发了一场关于椭圆和圆的讨论。

回答者们从几何形状、数学定义、性质等方面进行了比较，并给出了具体的例子来说明它们之间的区别。

这个问题不仅帮助了提问者，也为其他网友提供了对椭圆和圆的深入理解。

椭圆的极坐标方程是一个有趣且广泛讨论的话题。

通过知乎平台，我们可以了解到椭圆的定义、性质以及应用，并与其他网友一起探讨与椭圆相关的问题。

知乎作为一个知识分享的社交平台，为我们提供了一个广阔的学习和交流空间。

在这里，我们可以提问、回答问题，分享自己的见解和经验，共同学习和进步。

椭圆的极坐标二重积分
椭圆的极坐标二重积分：x=a rcost，y=b rsint，直角坐标(x，y) 极坐标（r，t），面积元素dxdy= a b r drdt，面积= t：0-->2pi，r：0-->1 被积函数是abr 的二重积=∫【0,2π】dt∫【0,1】abrdr =2π*ab*(1/2)=πab。

根据极坐标和直角坐标的转化公式，代人D的不等式中即可，极坐标的基本公式x=rcosθ,y=rsinθ，由此可知x²+y²=r^2，代人x²+y²≦x+y中有r^2≤rcosθ+rsinθ，由于r≥0，所以0≦r≦sinθ+cosθ。

熟记二重积分的性质，在运算中占有重要作用，特别是在繁琐的工科计算中，性质决定成败。

在给定条件下，学会画区域图像，画的越标准，越好，可以借助画图工具，图像画好，成功了一半。

区分此图像是X型还是Y型，X型平行于Y轴，Y型平行于X轴。

确定了之后根据各自的公式计算，切记一定要细心。

积分完成后，一定不要忘记相减，还有正负号的变正。

极坐标方程表达式极坐标方程是描述平面上点的位置的一种常用表达方式。

它利用距离和角度来表示点的坐标，相比直角坐标系更适合描述圆的形状和对称性。

本文将介绍极坐标方程的表达式形式以及如何将其转换为直角坐标系。

同时，还将介绍极坐标方程在数学和物理中的应用。

极坐标方程表达式的一般形式为：$r = f(\\theta)$其中，r表示点到原点的距离，$\\theta$表示点与正 x 轴之间的角度，f是一个关于$\\theta$的函数。

极坐标方程的形式可以有很多种，取决于具体问题的性质。

以下是一些常见的极坐标方程的表达式。

1. 极坐标方程表示直线：$r = a\\sec(\\theta - \\alpha)$其中，a是一定的常数，$\\alpha$是直线与极轴之间的夹角。

2. 极坐标方程表示圆：$r = a$其中，a是圆的半径。

3. 极坐标方程表示椭圆：$r = \\frac{a(1 - e^2)}{1 - e\\cos(\\theta - \\alpha)}$其中，a是椭圆的长半轴，e是离心率，$\\alpha$是椭圆与极轴之间的夹角。

4. 极坐标方程表示双曲线：$r = \\frac{a(1 + e^2)}{1 + e\\cos(\\theta - \\alpha)}$其中，a是双曲线的长半轴，e是离心率，$\\alpha$是双曲线与极轴之间的夹角。

利用以上表达式，可以方便地描述出各种形状的曲线。

将极坐标方程转换为直角坐标系的表达式需要利用以下关系式：$x = r\\cos(\\theta)$$y = r\\sin(\\theta)$通过上述关系式，可以将极坐标方程中的$r$与$\\theta$表达式用$x$和$y$来表示，从而得到在直角坐标系中曲线的方程。

极坐标方程在数学和物理中有广泛的应用。

在数学中，它可以用来描述曲线和曲面的形状及其性质。

例如，极坐标方程可用于描述螺旋线、心形线等特殊曲线。

在物理中，极坐标方程可用于描述圆周运动、波动等循环性质的物理现象。