理论力学 动静法
- 格式:ppt
- 大小:1.07 MB
- 文档页数:65



![[法律资料]理论力学 第10章 动静法](https://uimg.taocdn.com/c863420e1eb91a37f1115c86.webp)

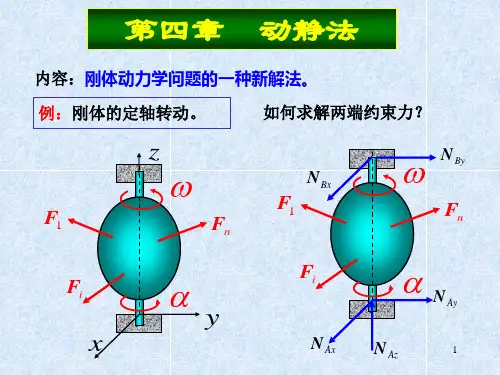
mF NF IFm a图8-7 质点的惯性力§8.2 动力学建模的动静法1 惯性力 • 达朗贝尔原理设一质量为m ,加速度为a 的非自由质点在一固定的曲线上运动,作用于质点的主动力为F ,约束力为F N ,如图8-7所示。
根据牛顿第二定律,有N F F a +=m (8.2.1) 将上式移项后写为 0=−+a F F m N (8.2.2)令 a F m −=I (8.2.3)F 1具有力的量纲,称为质点的惯性力,于是可将方程(8.2.2)写成 0=++I N F F F (8.2.4) 惯性力的大小等于质点的质量与加速度的乘积,方向与质点加速度的方向相反。
式(8.2.4)表明 质点运动的每一瞬时,作用在质点的主动力、约束力和惯性力在形式上构成一平衡力系。
这就是质点的达朗贝尔原理。
实际上,方程(8.2.4)是牛顿定律的另一种表达形式。
引进虚拟的惯性力之后,就可以将动力学问题在形式上转化为静力学问题来处理,因此这种方法称为动静法。
惯性力是力学中的重要概念之一。
在达朗贝尔原理中,惯性力是体现运动惯性的力学量,是人为地将二阶运动量表示成力的形式,虚拟地施加在运动的物体上。
在§8.3中非惯性系中研究动力学问题时,为了将非惯性系中的动力学运动定律在形式上化成与惯性系中的动力学运动定律一致,也引入了虚拟的惯性力。
这两种惯性力有共同点,都是假想惯性力作用在运动物体上。
但是,在运动物体上并不真实存在这样的作用力。
因为真实的力是物体之间的机械作用,能使物体的运动状态发生改变。
惯性力不能改变物体自身的运动状态,不符合作用与反作用定律(牛顿第三定律),所以惯性力不是真实的力,是假想的力。
但是,这两种惯性力又有概念上的差别.在达朗贝尔原理中,我们讨论的是物体的绝对运动,即讨论物体相对于某个取定的惯性系的运动。
作用在运动物体上的惯性力,只取决于物体的绝对加速度。
在非惯性系中,我们讨论的是物体的相对运动,存在着定坐标系(惯性系)和动坐标系(非惯性系)。