当前位置：文档之家 › 理论力学第十一章 达朗贝尔原理(动静法)

理论力学第十一章 达朗贝尔原理(动静法)

  • 格式：ppt
  • 大小：1.85 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

达朗贝尔原理动静法课件

达朗贝尔原理动静法课件
静力学分析
动力学分析
振动分析
通过动静法的应用，可以将动力学问题转化为静态问题，例如求物体的加速度、速度等。
动静法也可以用于研究物体的振动问题，例如求物体的固有频率、振型等。
03
02
01
03
达朗贝尔原理在动静法中的应用
总结词：达朗贝尔原理在动力学中用于描述物体运动规律，特别是对于复杂系统或非线性系统的运动分析。
达朗贝尔原理动静法课件
目录
contents
达朗贝尔原理概述动静法的基本概念达朗贝尔原理在动静法中的应用动静法的实际应用案例动静法的优缺点及未来发展
01
达朗贝尔原理概述
达朗贝尔原理是经典力学中的一个基本原理，它指出一个完整的保守系统在平衡点附近的小振动可以用线性弹簧模型来描述。
达朗贝尔原理具有普适性，适用于各种保守系统，如单摆、弹簧振荡器等。它提供了一种将复杂的非线性振动问题简化为线性问题的有效方法。
详细描述
建筑结构的动静法分析包括对建筑物在地震、风载、雪载等动态载荷和静载荷作用下的响应进行分析。通过模拟和分析建筑物的动力和静力行为，可以评估建筑物的安全性和稳定性，并预测其在各种载荷下的性能。这对于建筑物的设计和维护具有重要的意义。
VS
机械设备的动静法分析利用达朗贝尔原理对机械设备进行动力学和静力学的分析，以确保机械设备的正常运行和安全性。
结合虚拟现实技术
利用人工智能技术，为学生提供个性化的学习指点和反馈。
智能化辅助教学
将动静法应用于其他学科，如化学、生物等，促进跨学科的学习和整合。
跨学科整合
随着教育理念和技术的不断更新，动静法也需要不断改进和完善，以适应时代发展的需求。
持续改进教学方法
THANKS

课件：达朗贝尔原理(动静法)

课件：达朗贝尔原理(动静法)

主矢： FIR maC
主矩：
M IO
dLO dt
质系动力学问题
向质心C简化
主矢： FIR maC
主矩：
M IC
dLC r dt
{F1e ,, Fme , FIR , MIO} {0}
“平衡”条件:
m
Fie FIR 0
i 1
质心运动定理
m
MO' (Fie ) MO' (FIR ) MIO 0
1、均质细杆AB重P，长L，置于水平位置，若在绳BC突然剪断瞬
时有角加速度，则杆上各点惯性力简化为一个合力时，大小为
PL
2L
_____2_g____，作用点的位置在离A端_____3_____处，在图中画出该
惯性力。
23
2、半径为R，质量为mA的均质圆盘A，与半径为
R 2
，质量为mB的
均质圆盘B如图固结在一起，并置于水平光滑平面上，初始静止
B FBx
FI1 FI2 ma mL2 sin
FI1
MA 0
mgLsin mgLsin FBxh
mg
C
FI1(0.5h L cos ) FI2(0.5h L cos ) 0
FBx
mL 2 sin2
h
mg
A
FAx
FAy
若求附加动反力？
Fx 0
FAx
mL 2 sin2
h
FBx FAx FI1 FI2 0
T 1 mv 2 1 mv 2 1 (1 mr 2 ) 2 5 mv 2
J
A
m
g
L 2
m aCx Fx
m aCy Fy m g
d(1 2
J A2 dt

武汉理工理论力学第十一章 达朗贝尔原理讲解

武汉理工理论力学第十一章 达朗贝尔原理讲解
FI2 Nhomakorabea m2a
FIin
mi
v2 r
MO 0
(m1g FI1 m2g FI2)r FIit r 0
FIin
ait aiOn
FIit FOy FOx
FI1
mg
a
(m1g m1a m2g m2a)r miar 0 a
m2g
miar (mi )ar mar
m1g
FI2
a m1 m2 g m1 m2 m
理论力学
第十一章达朗贝尔原理 (动静法)
2020年9月24日
第十一章 达朗贝尔原理
§11－1 惯性力•质点的达朗贝尔原理 §11－2 质点系的达朗贝尔原理 §11－3 刚体惯性力系的简化 §11－4绕定轴转动刚体的轴承动约束力
§11-1 惯性力•质点的达朗贝尔原理
设一质点的质量为m，加速度为a，作用于质点的主动 力F，约束力FN。 由牛顿第二定律，有
§11-2 质点系的达朗贝尔原理
例：飞轮质量为m，半径为R, 以匀角速度ω定轴转动，设
轮辐质量不计，质量均布在较薄的轮缘上，不考虑重力的
影响，求轮缘横截面的张力。
解：由于对称，取四分之一轮缘为研究对象。
y
取微小弧段，加惯性力
FIi
mi ain
m
2R
Ri
R2
FA
A
列平衡方程
Fx 0 , FIi cosi FA 0
加惯性力
FIi miai miaC
惯性力系的合力：
FIR
FI1
FI
ma F FN
m
令 FI ma
F FN
F FN FI 0
ma
FI — 称为质点的惯性力。

达朗贝尔原理(动静法)

达朗贝尔原理(动静法)

§ 14-1
惯性力· 质点的达朗贝尔原理
ma F FN
F FN ma 0 惯性力 令 F ma I
有
F FN FI 0
质点的达朗贝尔原理:作用在质点的主动力、
约束力和虚加的惯性力在形式上组成平衡力系.
例14-1 已知:
这就是钢球在任一位置 时所受的法向反力, 显然当钢球脱离筒壁 时, FN＝0 , 由此可求出其脱离角a为
rw 2 a arccos( ) g
§ 14-2
质点系的达朗贝尔原理
i 1,2,, n
Fi FNi FIi 0
质点系的达朗贝尔原理:质点系中每个质点上作用的主动
x
M A (F ) 0 :
代入FI 的数值, 有
l FI d cos P sin 0 2
Pl 2l 2 sin ( w cos 1) 0 2 3g 3g 故有＝0或 arccos( ) 2 2lw
§ 14-3
刚体惯性力系的简化
用质点系的达朗贝尔原理求解质点系的动力学问 题，需要对质点内每个质点加上各自的惯性力，这些 惯性力也形成一个力系，称为惯性力系。下面用静力 学力系简化理论，求出惯性力系的主矢和主矩。 以FIR表示惯性力系的主矢。由质心运动定理及质 点系的达朗贝尔原理
m 0.1kg, l 0.3m, 60
求: 用达朗贝尔原理求解
v , FT .
v 解: F ma m I n l sin
mg FT FI 0
b
2
F
0, FT cos mg 0
F
解得
n
0, FT sin FI 0

达朗贝尔原理

达朗贝尔原理

aA l1
O
1
2
A C B
aA
由加速度基点法有
A
aCA 2
B C
aC aA aCA
aA
aA aC
1 aC l1 l 2 2
(2) 取AB 杆为研究对象
FgR2
Mg2
2
B
A
9g 1 , 7l
FgR 2
3g 2 7l
FAx
l 1 m(l1 2 ) M g 2 ml 2 2 2 12
研究整体
F
解得
x
0
F Fs m1 m2 a 0
3 F m1 m2 3 g 2 3 Fs m1 g F 2
M IA
A
FN
Fs f s FN f s m1 m2 g
解得
Fs 3m1 fs FN 2m1 m2
D m2 g

mr 2 mgr (3 4 ) 3
n gR 2
2
FgR 2mr , F 2mr , M gO
7 2 mr 3
（2）将惯性力系向质心C简化，其 主矢主矩分别为： F ma 2mr
gR C
MA
FAy
MgC
F ma 2mr
n gR n C
2
mg
例题
已知：两均质且长度为l直杆 自水平位置无初速地释放。 求： 两杆的角加速度和 O、A处的约束反力。 解: (1) 取系统为研究对象
FOx
O
A
B
FgR1
FgR2
Mg1
1
Mg2
2
B
A O
mg

B 理论力学-第11章 达朗贝尔原理及其应用-2解析

B 理论力学-第11章 达朗贝尔原理及其应用-2解析

本课程有部分内容与《大学物理》重复，如点的运动、刚体 简单运动、质点运动微分方程、质点的动量、动量矩和动能 定理等，对这些内容，本课程只作适当的复习或让学生自学。
第11章 达朗贝尔原理及其应用
引入惯性力的概念，应用达朗贝尔原理，将静力学中求解 平衡问题的方法用于分析和解决动力学问题。这种方法称为 “动静法”。“动”代表研究对象是动力学问题；“静”代表 研究问题所用的方法是静力学方法。 达朗贝尔原理是在18世纪随着机器动力学问题的发展而提 出的，它提供了有别于动力学普遍定理的新方法，尤其适用于 受约束质点系统求解动约束力和动应力等问题。因此在工程技 术中有着广泛应用，并且为“分析力学”奠定了理论基础。 达朗贝尔原理虽然与动力学普遍定理具有不同的思路， 但却获得了与动量定理、动量矩定理形式上等价的动力学方程， 并在某些应用领域也是等价的。
刚体作定轴转动时惯性力系的简化结果
这里仅讨论刚体有质量对称 面且转轴与质量对称面垂直的
情形。这种情形下，可以先将
惯性力系的主矢与刚体的运动形式无关；惯性力系的主矩 与刚体的运动形式有关。
刚体平移时惯性力系的简化结果
刚体平移时，由于同一瞬时刚体内各质点的加速度都相同， 惯性力系为平行力系，所以，惯性力系简化结果为通过质心C 的合力，用FIR表示：
FIR m a C
其中m为刚体的质量;aC为刚体的质心加速度。
e i Ii e O i
O ( FIi ) 0
这两个矢量式可以写出六个投影方程。 根据达朗贝尔原理，只要在质点系上施加惯性力，就 可以应用上述方程求解动力学问题，这就是质点系的动静法。
11.2 惯性力系的简化
惯性力系的主矢与主矩 刚体平移时惯性力系的简化结果
刚体作定轴转动时惯性力系的简化结果 刚体作平面运动时惯性力系的简化结果

达朗贝尔原理

达朗贝尔原理
FI mac
结论：平动刚体的惯性力系合成为一个 作用在质心的惯性力
二、刚体定轴转动
(一） 刚体有与转轴 垂直的对称面 结论：可将空 间惯性力系简 化为在对称平 面内的力系（ 相当于将刚体 压扁到对称平 面内）
l
FIjn
j
z
FIjt
z
FIin
i
FIit
ω α ω α
l
O
O
0 C α 45 A
O FIy
aC acx acy a A aCA
acx 2 2 l 2 acy 2 2 2 2
aA
aCA
a cx a cy
B
FIx macx FIy macy
l a cx a cy 2
mi ai FRi FIi mi ai FRi FIi 0
在每一个质点上加上惯性力后，此质点平衡。
显然，系统的任意部分（包括整体）也是平衡的。
O
例：质量m、长度l的均 质杆，以匀角速度ω绕z 轴转动，试求θ角。
z
θ
dFI
A mg η
ω d 2 dFI m sin l l l M zi mg 2 sin cosdFI 0 0
达朗贝尔原理
在惯性系中
ma FR
a
非惯性系中的妙招
mar FR mae mac FR FIe FIc
惯性
0 FR ma FR FI
§9-1达朗贝尔原理（动静法） 一、质点的达朗贝尔原理 牛顿定律
α C A
a cx
a cy

11-第十一章-达朗贝尔原理

11-第十一章-达朗贝尔原理

第十一章 达朗贝尔原理§11.1 质点的达朗贝尔原理=++∴=+G N F maN F令a -m G =在质点上除了作用有真实的主动力和约束反力外，再假想地加上惯性力，则这些力在形式上组成一组平衡力系，称质点的达朗贝尔原理。

11.2 质点系的达朗贝尔原理、运动刚体惯性力系的简化一、质点系的达朗贝尔原理设质点系由几个质点组成，其中一质点M i ，其质量为m i ，作用其上的主动力F i ，约束反力N i ，加速度为a i ，在该质点上加上惯性力为G i则: 0=++i i i G N F对每一个质点进行同样处理，根据加减平衡力系定理，则质点系上所有的主动力系，约束反力系，惯性力系组成了一组平衡力系。

根据静力系平衡的条件：R =0 M o =0 （主矩、主矢皆为零）)()()(0=∑+∑+∑=∑+∑+∑∴i o i o i o i i i G M N M F M G N F质点系的达朗贝尔原理：质点系在运动时，作用于该质点系上的主动力系、约束反力系和惯性力系形式上构成一组平衡系。

00000:=∑=∑=∑=∑=∑=∑z y x M M M Z Y X 投影方程二、运动刚体惯性力系的简化利用达朗贝尔原理求解刚体动力学问题，需对刚体内每个质点加上它的惯性力，这些惯性力组成一组平面惯性力系，这就需要将惯性力系进行简化，求得惯性力系的主矢和对简化中心的主矩，并且在解题过程中，直接将惯性力的主矢主矩加到运动刚体上即可： （一）平动刚体惯性力系的简化平动刚体 a i =a n =a cG i =-m i a i刚体内各点的惯性力组成一组平行力系，将该惯性力系向质心c 简化：)()(=∴=⨯-=⨯∑=-⨯∑=∑=-=∑-=∑=c c cc ci i i i i i i c ci i i r M m m G M a m G M a r a r a r M M a G结论：刚体作平动时，惯性力系简化结果为通过质心c 的主矢Gc Ma G -=（二）定轴转动刚体惯性力系的简化条件：定轴转动刚体，均质，具有与转轴互相垂直的对称平面。

理论力学达朗贝尔原理与动静法教学省名师优质课赛课获奖课件市赛课一等奖课件

理论力学达朗贝尔原理与动静法教学省名师优质课赛课获奖课件市赛课一等奖课件

例题
于是可写出汽车旳动态平衡方程
M B 0 , RQh Gc N A(b c) 0 (1) M A 0 , RQh Gb NB (b c) 0 (2)
由式(1)和(2)解得
NA
M
(gc ah) bc
NB
M (gb ah) bc
RQ C
h FB
B
G
c
NB
a
b
A
NA
例题
列车在水平轨道上行驶，车厢内悬挂一单摆，当车厢向右作
达朗贝尔原理与动静法
目录
达朗贝尔原理 惯性力系旳简化 动静法应用举例 定轴转动刚体对轴承旳动压力
引言
引进惯性力旳概念，将动力学系统旳二阶运动量 表达为惯性力，进而应用静力学措施研究动力学 问题 —— 达朗贝尔原理。
达朗贝尔原理为处理非自由质点系旳动力学问题 提供了有别于动力学普遍定理旳另外一类方 法。
● 主矩
合力偶旳力偶矩即为惯 性力系旳主矩，其大小等于 刚体对经过质心旳转动轴旳 转动惯量与角加速度旳乘积， 方向与角加速度方向相反。
M CQ ICz
MCQ
RQ
C
ri
mi
a
n ir
aC
a
ir
ε
aC
常见惯性力旳主失和主矩
综上所述：
1、刚体作平动 向质心简化
● 主矢 RQ＝ (－miai ) ＝－MaC
匀加速运动时，单摆左偏角度 ，相对于车厢静止。求车厢
旳加速度 a 。
例题
解： 选单摆旳摆锤为研究对象 虚加惯性力
Q ma ( Q ma )
由动静法, 有
X 0 , mgsin Qcos 0
解得
a g tan

达朗贝尔原理

达朗贝尔原理

FT maB ml cos30 0
Fy 0
FN FIr sin30 mg 0
(2)
C
FN ml sin30 mg 0 MC (F ) 0
B
FN
mg
x
FT l cos30 FN l sin30 M I 0
(3)
1 2 FT l cos 30 FN l sin 30 ml 0 3
以B为基点, 则A点的加速度为
t n t n aA aA aB aAB aAB
aB
2
A
t aA t aCB
其中
a v AE 0
n A 2 A
a
n AB
2l 0
B aB

30o
将上式投影到x 轴上得
0 aB a cos30
t AB
x
aB 2l cos30
ma F FN
将上式改写成
FI m F a
F FN ma 0
令
FI ma
FN
FI具有力的量纲, 且与质点的质量有关，称其为质点 的惯性力。它的大小等于质点的质量与加速度的乘 积, 方向与质点加速度的方向相反。
一、质点的达朗贝尔原理
则有
F FN FI 0
即：在质点运动的任一瞬时, 作用于质点上的主动力、
即：作用在质点系上的所有外力与虚加在每个质点 上的惯性力在形式上组成平衡力系。这是质点系达 朗贝尔原理的又一表述。
(e)
(e)
称ΣFIi为惯性力系的主矢， ΣMO(FIi) 为惯性力 系的主矩。
三、刚体惯性力系的简化
用质点系的达朗贝尔原理求解质点系的动力学问题， 需要对质点内每个质点加上各自的惯性力，这些惯性 力也形成一个力系，称为惯性力系。下面用静力学力 系简化理论，求出惯性力系的主矢和主矩。

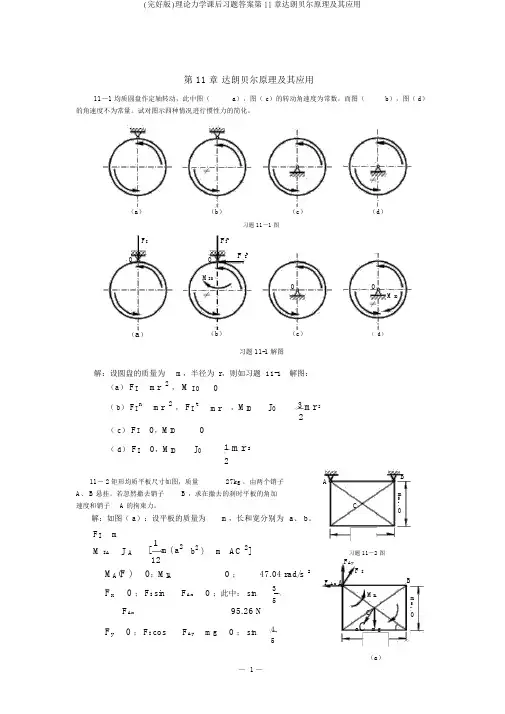
(完整版)理论力学课后习题答案第11章达朗贝尔原理及其应用

(完整版)理论力学课后习题答案第11章达朗贝尔原理及其应用

第 11 章 达朗贝尔原理及其应用11－1 均质圆盘作定轴转动，此中图（ a ），图（ c ）的转动角速度为常数，而图（ b ），图（ d ）的角速度不为常量。

试对图示四种情况进行惯性力的简化。

≠≠（a ）（b ）（c ）（d ）习题 11－1 图F I F I nOO F I tM I OO O≠M IO≠（a ）（b ）（c ）（ d ）习题 11-1 解图解：设圆盘的质量为m ，半径为 r ，则如习题 11-1 解图：（a ） F I mr 2 ， M I O 0（ b ） F I nmr 2 ， F I tmr ，M IOJ O3 mr 22（ c ） F I 0，M IO 0（ d ） F I0，M IOJ O1 mr 2211－ 2 矩形均质平板尺寸如图，质量 27kg ，由两个销子AA 、B 悬挂。

若忽然撤去销子 B ，求在撤去的刹时平板的角加速度和销子A 的拘束力。

C解：如图（ a ）：设平板的质量为 m ，长和宽分别为 a 、 b 。

F I mM I AJ A[ 1m( a 2 b 2 ) m AC 2] 习题 11－2 图122F AyM A (F ) 0；M IA 0 ； 47.04 rad/s F IF Ax AF x0 ； F I sinF Ax0 ；此中： sin3M IA 5CF Ax95.26 NF y0 ； F I cosF Aymg0 ； sin4aC mg5Bm5 1 .Bm51.F Ay 27 9.8 3.375 47.04 0.8 137.6 N11－ 3 在均质直角构件 ABC 中， AB 、 BC 两部分的质量各为 AE 保持在图示地点。

若忽然剪断绳索，求此刹时连杆 AD 、 BE已知 l = 1.0m ， φ= 30o 。

3.0kg ，用连杆 AD 、 DE 以及绳索所受的力。

连杆的质量忽视不计，C解：如图（ a ）：设 AB 、 BC 两部分的质量各为 m = 3.0kg 。

11理论力学达朗贝尔原理

11理论力学达朗贝尔原理

三、 质点系的达朗贝尔原理
设质点系由n个质点组成，其中任意质点i的质量为mi， 加速度为ai。
（1）若把作用于此质点上的所有力分为主动力的合
力Fi、约束力的合力FNi，再虚拟加上此质点的 惯性力FIi= –miai。
由质点的达朗贝尔原理，有
Fi+ FNi+ FIi =0 （11－3） 该式表明：质点系中每个质点上作用的主动力、
F x 0,FIi cosi FA 0OFLeabharlann y 0,FIi sini FB 0
而
FIi = miain
m
2R
Ri
R 2
R Δθi
θi
FIi
B
x
FB
19
11.1 惯性力•达朗贝尔原理
令 Δθi
0，有
FIi
cosi
2 0
m
2
R 2
cosd
mR 2 2
FIi
sini
2 0
m
2
R 2 sind
例11－3 飞轮质量为m，半径为R，以匀角速度ω定轴 转动，设轮辐质量不计，质量均布在较薄的轮缘上，不考 虑重力的影响，求轮缘横截面的张力。
y
A
R O
B
x
18
11.1 惯性力•达朗贝尔原理
解：由于对称，取四分之一轮 缘为研究对象，如图所示。
轮缘横截面张力设为FA、FB。
y
FA
A
取圆心角为Δθi的微小弧段， 每段 加惯性力FIi。 列平衡方程
FIi 0
故
i 1 n
i 1 n
MO (Fi(e) ) MO (FIi ) 0
i 1
i 1
(14-4)

达朗贝尔原理(动静法)课件

达朗贝尔原理(动静法)课件
惯性力问题
在研究具有加速度的物体时，可以利用达朗贝尔原理引入惯性力的概念，从而将 动力学问题转化为静力学问题，简化求解过程。
复杂系统的应用
多体系统动力学
在多体系统动力学中，达朗贝尔原理可以用于分析多个相互 作用的物体组成的复杂系统的运动规律。通过引入虚拟力， 可以将多体系统动力学问题转化为多个单体动力学问题的组 合。
案例二：机械设备的动静法优化
总结词
机械设备性能的优化是提高生产效率和降低能耗的关键，动静法能够分析机械设备的动态性能，提出 优化方案。
详细描述
在机械设备的运行过程中，动态性能对其稳定性和效率具有重要影响。达朗贝尔原理的动静法能够对 机械设备的动态性能进行深入分析，发现潜伏的问题并提出优化方案，从而提高设备的运行效率和稳 定性。
控制系统
在控制系统中，达朗贝尔原理可以用于分析系统的稳定性。 通过引入虚拟控制力，可以判断系统在受到干扰时是否能够 保持稳定。
04
达朗贝尔原理的案例分 析
案例一：桥梁结构的动静法分析
总结词
桥梁结构的稳定性与安全性是关键，动静法能够全面评估桥梁在不同载荷下的性能。
详细描述
桥梁作为交通要道，需要承受各种载荷，如车辆、风、地震等。达朗贝尔原理能够通过动静法分析桥梁在不同载 荷下的响应，从而评估其稳定性与安全性，为桥梁设计提供根据。
在振动分析中，动静法可用于 研究系统的自由振动和受迫振 动，分析系统的固有频率和振
型。
在稳定性分析中，动静法可用 于研究系统的稳定性和失稳条 件，预测系统的动态行为。
在控制系统分析中，动静法可 用于研究系统的动态响应和调
节性能，优化控制策略。
动静法的优缺点
动静法的优点在于其简单易行，能够 方便地引入虚拟惯性力，从而简化动 力学问题的分析过程。同时，动静法 能够直接得出系统的动力学方程，方 便进行数值计算和仿真分析。

理力11(动力学-李卓球)-达朗贝尔原理

理力11(动力学-李卓球)-达朗贝尔原理

c
mg
b FNA
A
FNB
11
例题
第11章 达朗贝尔原理
例 题 11-3
如图所示，滑轮的
半径为r，质量为m均匀分
布在轮缘上，可绕水平轴
r
转动。轮缘上跨过的软绳
的两端各挂质量为m1和m2
B A
的重物,且m1 >m2 。绳的 重量不计，绳与滑轮之间
无相对滑动，轴承摩擦忽
略不计。求重物的加速度。
12
例题
a
附加压力（或附加动约束力）决定于惯性力系， 只求附加压力时，列方程不必考虑重力。
mg
FI
20
达朗贝尔原理＼刚体惯性力系的简化
§11.2 刚体惯性力系的简化
M O ( Fi ( e ) ) M O ( FIi ) 0 Fi ( e ) FIi 0
刚体作平动
惯性力系主矢 FIR FIi 惯性力系主矩 M IO M O (FIi )
动力学篇
第 11 章 达朗贝尔原理（动静法）
1
达朗贝尔原理＼惯性力· 达朗贝尔原理
§11.1 惯性力· 达朗贝尔原理
惯性力 ma F FN
FI
m F FN ma
F FN ma 0
FI ma ——惯性力 有 F FN FI 0
令
惯性力大小等于质点的质量与加速度的乘积，方向与 质点加速度的方向相反。
达朗贝尔原理＼刚体惯性力系的简化＼刚体定轴转动
刚体定轴转动
FIit mi ait mi ri 切向惯性力 FIin mi ain mi ri 2 法向惯性力
M Ix M x (FIi ) M x (F ) M x (F )

理论力学11—达朗贝尔原理1分析

理论力学11—达朗贝尔原理1分析
加速度a 提升重量为W 的重物,尺寸如图,求支座A，B
处的动反力。
R
A
a FA
W
B
P
FB
b l
FI FI ma
解:梁在主动力、约束力、惯性力作用下平衡：
MB
0:
(W
FI
)(b
R)
P
l 2
FAl
0
FI ma
FA
2W
(b
R) 2l
Pl
FI
(b l
R)
R
2W (b R) Pl 静反力
A
ai
ri mi
k OBiblioteka Fj Iti zi FIni
y
i yi xi
qi
x
z
FIit miait miria
FIin miain miriw 2
惯性力对x轴的矩为
M Ix M x (FIit ) M x (FIin )
x
miria cosqi zi miriw 2 sinqi zi
O
11.2.2 刚体绕定轴转动
刚体定轴转动时, 设其角速
度为w, 角加速度为a, 刚体
内任一质点的质量为mi，到 转轴的距离为ri, 则刚体内任 一质点的惯性力为FIi＝-miai。
在转轴上任选一点O为简化
中心, 建立直角坐标系如图,
质点的坐标为xi, yi, zi, 现分 别计算惯性力系对三个坐标
ma F FN
FI
m
将上式改写成 F FN ma 0
F
令 FI ma
FN
a
FI具有力的量纲, 且与质点的质量有关，称其为 质点的惯性力。它的大小等于质点的质量与加
速度的乘积，方向与质点加速度的方向相反。

理论力学 第11章 达朗伯原理(动静法)

理论力学 第11章 达朗伯原理(动静法)

解： (1)绳FI 被剪断后，板在其自身平面内作
D
E
曲线平动，各点的速度、加速度均相同。 板受力如图。
∵剪断绳FI 瞬时，vA= 0，
FA
60° y FB
60°
A
aA
B
∴ aA = aA = aC 对板虚加惯性力， FI = maC
……①
FICຫໍສະໝຸດ bFG MIaC x
则根据达朗伯原理，有
∑FX = 0，
(2)当AD、BE铅直时,板受力如图。
设板质心的加速度如图。 虚加板的惯性力系，且
D
E
60°
FA l
FB
FIn=maCn ， FI =maC
……①
A
B
则根据达朗伯原理，有
aCn FFII C
∑ FX = 0， －FI = 0
……②
FG
aC MI
∑ FY = 0， FA+ FB －MI－FIn = 0 ……③
• 达朗伯原理将非自由质点系的动力学方程用静力学平衡方程的形式表述。 或者说，将事实上的动力学问题转化为形式上的静力学平衡问题，既所 谓“动静法”。
12.1 惯性力与达朗伯原理
图示圆锥摆摆长为l，摆锤M 的质量m，在水平面内 作匀速圆周运动，速度为v，锥摆的顶角为2φ。 摆锤 M 受力如图，其加速度为
i 1
i 1
② 在解决质点系动力学的两类基本问题上，达朗伯原理均适用。 但若已知质点系的运动，需要求解该系统的约束反力或外力时， 应用达朗伯原理尤其方便。
③ 应用达朗伯原理的关键是解决质点系的惯性力系的简化问题。
12.2 惯性力系的简化—— 一、刚体作平动
在同一瞬时，平动刚体内各点的加速度相等，

理论力学 达朗贝尔原理(动静法)

理论力学 达朗贝尔原理(动静法)

惯性力系向质心简化得主矩为
M IC
1 P 2 J C l 12 g 1 P la A 12 g
B

FIe
O
C
FIrt
M IC
A
动力学
刚体惯性力系的简化
再向O点简化， 主矢不变
B

FIe
O
C
FIrt
M IC
P FIR aC g FIe FIr
主矩为
Fi(e)
O
Fi(i )
Ii
i
(e)
O
i
(i )
O ( FIi )
0
由于质点系的内力总是成对存在，且等值、反向、共线，有
F
(i )
i
0,
M
Ii
O
(Fi ) 0
(i )
则上式可改写为
F 0 M (F ) M
Fi(e)
O i (e)
O ( FIi )
0
动力学
动力学
达朗贝尔原理
§15-2 达朗贝尔原理
设有一质点系由n个质点组成，对每一个质点i，有
Fi FNi FIi 0 ( i 1,2,...... , n )
该式表明，质点系中每个质点上作用的主动力、约束反力和惯 性力在形式上构成平衡力系。这就是质点系的达朗贝尔原理。 把作用于I质点的所有力分为外力的合力Fi ，内力的合力Fi ，则
这种解答动力学问题的方法，也称动静法。
动力学
惯性力 的概念
§15-1
惯性力 的概念
如图，人用手推车时，车在加速运 动过程中，人会感到受到力的作用，这 个力是由于车具有惯性，力图保持原来 的运动状态对人产生的反抗力，称为惯 性力。 如下图质点m 的运动，由牛顿第二定律： ma F FN
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

讨论：1）脱离角α与滚筒的角速度和滚筒半径有关，而与钢球质量无关。
2）
筒壁。此时转筒
的转速称为临界转速，对球磨机而言，要求n小于nL，否则球磨机就不能工作。
§11－2 刚体惯性力系的简化
刚体平移时惯性力系的简化
当刚体平移时,任一瞬时体内各点的加速度相等。若记某瞬 时刚体质心加速度为aC，则该瞬时体内任一质量为m的质点 的加速度ai=aC，虚加在该点上的惯性力Fgi=-miai=-miaC 。 刚体内每一点都加上相应的惯性力，由静力学知,该空间平 行力系可简化为过质心的合力，即
式中，Fgτ=-maτ，称为切向惯性力 Fgn=-man称为法向惯性力（也称离心力）
负号表示它们分别与切向加速度和法向加速度的方向相反。
§11－1 惯性力与质点的达朗贝尔原理
质点系的动静法
对由n个质点组成的非自由质点系,设其中任一质点的质量 为mi,某瞬时加速度为ai，作用其上的主动力F，约束反力 Fni，假想在该质点上加上惯性力Fgi=-mai，由质点达朗贝 尔原理，则
=－ maC
该力偶的力偶矩等于惯性力系对刚体惯性力系的简化
结论 当刚体有质量对称面，且绕垂直于质量对称面的定轴 转动时，惯性力系可以简化为对称面内的一个力和一个力偶。 该力等于刚体的质量与质心加速度的乘积，方向与质心加速 度方向相反，且力的作用线通过转轴；
该力偶的力偶矩等于刚体对转轴的转动惯量与角加速度的乘 积，其转向与角加速度转向相反。惯性力系向点O简化的结 果如图b)所示。
Fg=-m a
质点的达朗伯原理:质点在运动的每一瞬时，作用 于质点上的主动力、约束反力与假想地在质点上 的惯性力，在形式上构成一平衡力系。
§11－1 惯性力与质点的达朗贝尔原理
动静法：质点的达朗伯原理是用静力学的方法来研究动 力学问题,故又称为动静法 若质点沿已知平面曲线运动，则可将式 投影到自然轴上，得
如果假想地把相应的惯性力加在每一个质点上，则质点 系的主动力、约束反力和惯性力在形式上组成平衡力系。 就是质点系动静法，也称质点系的达朗贝尔原理。
§11－1 惯性力与质点的达朗贝尔原理
例11-1 测定列车的加速度,采用一种称为加速度测定摆 的装置。这种装置就是在车厢顶上用绳悬挂一重球,如 图所示。当车厢作匀加速直线运动时,摆将偏向一方， 与铅垂线成不变的角θ,求车厢加速度α与θ的关系。
§11－2 刚体惯性力系的简化
刚体作平面运动时惯性力系的简化
取质量对称面S，如图所示。取质心C作为基点，设
某瞬时质心加速度为aC，平面图形的角加速度为ε， 转向如图。将平面内的惯性力系向质心C简化，由
§11－2 刚体惯性力系的简化
将惯性力系向S上的质心C简化,由于主矢与简化主心的位置无关,而 主矩与简化中心的位置有关。其结果
JC为刚体对过质心且与转轴z
ε
平行的轴的转动惯量
FgR的大小和方向不变，只是其作用线通过质心C。
主矩与简化中心位置有关,大小发生了变化，转向仍与角加速度 转向相反，以MgC表示。简化结果如图c)所示。
第十一章 达朗贝尔原理（动静法）
主要研究内容
惯性力与质点的达朗贝尔原理
刚体惯性力系的简化
用动静法解质点系统动力学 问题的应用举例 定轴转动刚体轴承的附加动反力
§11－1 惯性力与质点的达朗贝尔原理
动静法的原理是应用静力学研究平衡问题的方法去求解动力学问题。
惯性力的概念
当质点受力改变其运动状态时，由于质点的惯性,质点必将给施力 体一反作用力,这个反作用力称为质点的惯性力。惯性力方向与质 点加速度的方向相反，作用在使质点改变运动状态的施力物体上。
结论 对平移的刚体，惯性力系可简化为通过质 心的合力，其大小等于刚体的质量与质心加速度 的乘积，合力的方向与质心加速度的方向相反。
§11－2 刚体惯性力系的简化
刚体绕固定轴转动时惯性力系的简化
设定轴转动刚体的质量对称面为S,与转轴的 交点记为O，某瞬时角速度和角加速度分别 为ω和ε，转向如图所示,质心为点C。取S内 任一质量为mi的点,记该点加速度为ai,则该 点的惯性力为Fgi=-miai,则Fgi= Fτgi＋ Fngi， 其中Fτgi=-mi aτi， Fngi=-mi ani。 对S内所有点,组成平面一般力系。由静力学知,向点O进行简化,可得到一 个力和一个力偶，该力为原力系的主矢量，即惯性力系的主矢为
§11－2 刚体惯性力系的简化
当转轴z通过质心，惯性力系的简化结果为一力偶，该力 偶的力偶矩
ε
当刚体匀速转动,转轴不通过质心C时,惯性力系简化为过 简化中心的力。即
其大小为m rCω2，其中rC为质心到简化中心O的距离，方 向与质心C的法向加速度方向相反。
若转轴过质心，即刚体绕过质心的轴作匀 速转动，惯性力系向S内任一点简化的主矢 和主矩都等于零,则惯性力系是一平衡力系。
小车获得加速度a的惯性力Fg
球M在水平面内作匀速圆周运动的惯性力
只有当质点的运动状态发 生改变时才会有惯性力。
§11－1 惯性力与质点的达朗贝尔原理
质点的动静法
设一非自由质点的质量为m，加速度为a，作用在这个质点上的主动 力为F、约束反力为FN，如图所示。由质点动力学基本方程得
上式移项后，得
令 则得
§11－1 惯性力与质点的达朗贝尔原理
解 (1)选取研究对象，画受力图 以摆球M为研究对象,并视为质点。它受有 重力P和绳的拉力T的作用。
(3)列平衡方程，求未知量。由汇交力系的平衡方程得
§11－1 惯性力与质点的达朗贝尔原理
例11-2球磨机滚筒内装有钢球和矿石，滚筒绕固定水平轴O以匀转 速n（r/min）作顺时针方向转动，带动钢球和矿石在滚筒中运动， 转到一定角度α时钢球离开滚筒内壁沿抛物线轨迹落下,可以得到最 大的打击力。设滚筒的半径为r，求钢球离开滚筒时的角度α应为多 少?
§11－1 惯性力与质点的达朗贝尔原理
解 (1)选取研究对象，画受力图 以最外层的一个钢球A为研究对象,不考虑刚
球间的相互作用力，则钢球所受的力有重力G、筒壁对钢球的摩擦力Ff和约束
力FN (2)分析运动，加惯性力。Fg= (3)列平衡方程，求未知量。
解得：
钢球脱离筒壁的瞬间，筒壁对钢球的约束力FN = 0，可求得脱离角α为