竖曲线计算示意图及说明

1 / 2
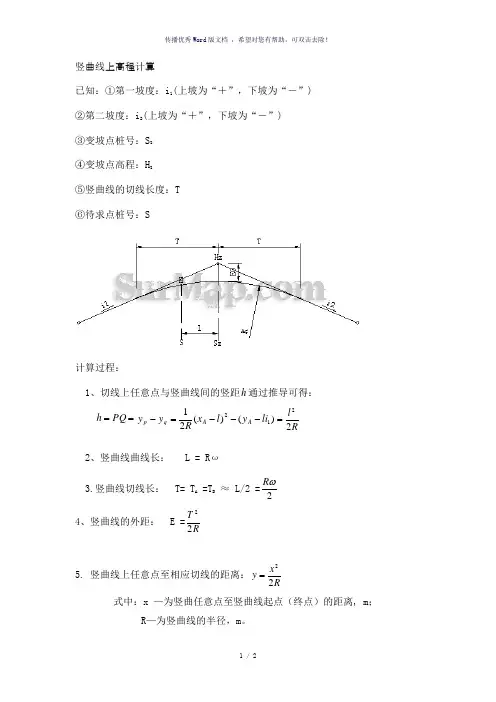
竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2
ωR 4、竖曲线的外距： E =R T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22
= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤
如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y
某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y
-----精心整理，希望对您有所帮助!。

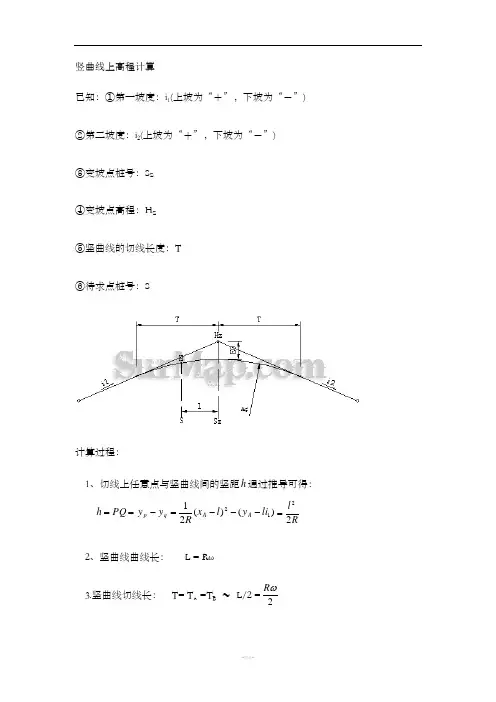
竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。

隧道内竖曲线计算当正线相邻坡段坡度差≥1‰，应设置竖曲线，竖曲线形式为圆曲线。

竖曲线计算公式如下：L=Rsh×λ/2000（L为竖曲线全长的一半，单位：m）y=x2/2R（y为竖曲线高度，单位：m）其中：Rsh—竖曲线半径（m），10000～20000m；x—竖曲线始点至计算纵距之距离，单位m；λ—为相邻竖曲线的代数差。

在设计图中，竖曲线的位置的标高应表示为：括号内的标高为未考虑竖曲线影响的标高，括号外的标高为已考虑竖曲线影响的标高。

一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1 ω为正时，是凹曲线；ω为负，是凸曲线。

1.二次抛物线基本方程：或ω：坡度差（%）；L：竖曲线长度；R：竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m=k5+000-k4+940=60m 桩号k5+000处：x1切线高程＝423.18+60*0.05=426.18m 2/2R=602/2*2000=0.90mh1=x1设计高程＝426.18 - 0.90=425.28m=k5+100-k4+940=160m 桩号k5+100处：x2切线高程＝423.18+160*0.05=431.18m 2/2R=1602/2*2000=6.40mh2=x2设计高程＝431.18 - 6.40=424.78m。

第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。

可采用抛物线或圆曲线。

一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。

1.二次抛物线基本方程：或ω：坡度差（%）；L：竖曲线长度；R：竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：二、竖曲线最小半径（三个因素）1.缓和冲击对离心加速度加以控制。

ν(m/s)根据经验，a=0.5~0.7m/s2比较合适。

我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。

(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时，Lmin = 2ST - 4/ω2.当L≥ST时，ST为停车视距。

以上两个公式，第二个公式计算值大，作为有效控制。

按缓和冲击、时间行程和视距要求（视距为最不利情况）计算各行车速度时的最小半径和最小长度，见表4-13。

表中：（1）一般最小半径为极限最小半径的1.5~2倍；（2）竖曲线最小长度为3s行程的长度。

（二）凹曲线最小半径和长度1.夜间行车前灯照射距离要求：1）L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。

例：设ω＝2%=0.02;则L＝ωＲ竖曲线最小长度Ｌ＝Ｖ/1.2速度Ｖ=120km/h V=40km/h 一般最小半径Ｒ凸17000 700一般最小半径Ｒ凹6000 700 L凸340 14Ｌ凹120 14 例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m桩号k5+000处：x1=k5+000-k4+940=60m切线高程＝423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程＝426.18 - 0.90=425.28m 桩号k5+100处：x２=k5+100-k4+940=160m切线高程＝423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程＝431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线；路线在水平面上的投影叫路线的平面；路线设计：确定路线空间位置和各部分几何尺寸的工作；可分为平面设计、纵断面设计、横断面设计。

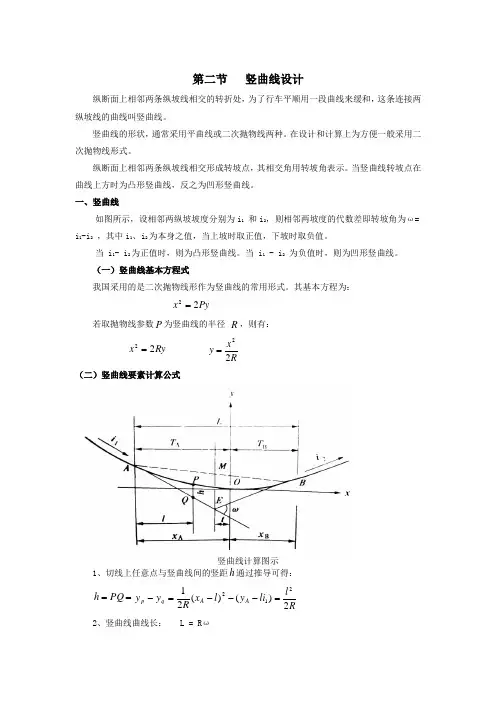
第二节 竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状，通常采用平曲线或二次抛物线两种。

在设计和计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。

一、竖曲线如图所示，设相邻两纵坡坡度分别为i 1 和i 2，则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ，其中i 1、i 2为本身之值，当上坡时取正值，下坡时取负值。

当 i 1- i 2为正值时，则为凸形竖曲线。

当 i 1 - i 2 为负值时，则为凹形竖曲线。

（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。

其基本方程为：Py x 22=若取抛物线参数P 为竖曲线的半径 R ，则有：Ry x 22= Rx y 22=（二）竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得：==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长： L = R ω3、竖曲线切线长： T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距： E =RT 22⑤竖曲线上任意点至相应切线的距离：Rx y 22=式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；R —为竖曲线的半径，m 。

二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素 （1）缓和冲击汽车行驶在竖曲线上时，产生径向离心力，使汽车在凸形竖曲线上重量减小，所以确定竖曲线半径时，对离心力要加以控制。

（2）经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时，即使竖曲线半径较大，竖曲线长度也有可能较短，此时汽车在竖曲线段倏忽而过，冲击增大，乘客不适；从视觉上考虑也会感到线形突然转折。

竖曲线铁路线路的纵断面最理想的当然是平道，然而事实上是不可能的，为了适应地形的起伏，以减少工程量，纵断面必须用各种不同的坡面连接而成。

两相邻坡段的连续点谓之变坡点。

相邻坡段的坡度差是两相邻坡段的坡度代数差。

当相邻坡段的坡度差超过允许值时，为了保证行车平顺和安全，应在变坡点处用竖曲线连接起来。

允许不设竖曲线的坡度差允许值是根据车轮不脱轨、车钩不脱钩、列车不撞车和行车平稳等要求进行分析确定的。

一般情况下，竖曲线采用圆曲线，也可以采用抛物线，个别情况下，还可以采用连续短坡曲线。

竖曲线的计算一、圆曲线形竖曲线圆曲线形竖曲线的几何要素和各点设计标高，可按下列公式计算，如图。

R α　x T TyRCα/2　BAi1i21、竖曲线的切线长度TT=R·tan(α/2)=R/2·tanα=R/2·△i‰=R/2000·△i(m) (5-1)式中 R-竖曲线半径(m)；α-竖曲线转角(度)；△i-相邻坡段的坡度代数差(‰)。

R=5000m时， T=2.5△i(m)R=10000m时，T=5.0△i(m)R=15000m时，T=7.5△i(m)R=20000m时，T=10.0△i(m)R=25000m时，T=12.5△i(m)2、竖曲线长度CC≈2T=R/1000·△i(m) (5-2)3、竖曲线纵距yy=x2/2R (m) (5-3)式中 x-竖曲线上计算点至竖曲线起(终)点的横距(m)。

当x=T时，变坡点的纵距Y即为竖曲线的外矢距E。

Y=E=T2/2R=1/2R(C/2)2=C2/8R (5-3.1)4、竖曲线上各点的设计标高H设h为计算点的坡度标高，则H=h±y (5-4)式中的y值，凹形取“+”，凸形取“-”。

【算例一】一凹形竖曲线i1=-4‰，i2=+2‰，△i=6‰，变坡点的里程为K235+165，标高为54.60m，R=15000m，计算竖曲线上各20m点的设计标高。

突竖曲线公式
H=H0+(C－C0) *i－(C－C0)2÷(2*R)
I：竖曲线纵坡度
H：所求设计标高
H0：竖曲线起点标高
C0：竖曲线起点桩号
C：所求设计标高（H）处的桩号
R：竖曲线半径
在桥型布置图中，所给出的参数有R：竖曲线半径，T切线长度，E：外距，JD为交点桩号，H1：交点处标高（但不是交点处桩号路面的标高），i：竖曲线纵坡度
C0=JD－T
H0=H1－T*i
凹曲线
H=H0－(C－C0) *i+(C－C0)2÷(2*R)
以D匝道桥为例：
竖曲线起点标高：H0=H1－T*i=7.308－42.892×0.03635=5.748
竖曲线起点桩号：C0=JD－T=DK0+270－42.892=DK0+227.108
交点桩号路面标高：H=H0+(C－C0) *i－(C－C0)2÷(2*R)=H1－E
=5.748+（270－227.108）×0.03635－(270－227.108)2÷（2×1500）=6.694
你用有已知标高的桩号带入这个公式看看，这是竖曲线，算的是纵断面的标高，每个桩号的横断面，已知横坡的坡度就可以了，要注意横坡的坡度与设计线的关系，横坡的坡度计算要注意超高段的坡度变化。

注意：求垫石及垫石以上部分的标高一定要从设计标高往下反算，复核墩柱及以下的标高也要从上往下反算。

竖曲线计算公式步骤嘿，朋友们！今天咱来聊聊竖曲线计算公式步骤。

你说这竖曲线啊，就像是道路上的小魔术，能让我们的行车变得更平稳、更安全呢！先来说说竖曲线是啥玩意儿。

它呀，其实就是在道路纵断面上，为了缓和行车时的颠簸，而设计的那一段曲线。

想象一下，要是没有它，那车子开起来得多颠啊，就跟坐过山车似的，那可受不了！那怎么计算竖曲线呢？别急，听我慢慢道来。

首先，得搞清楚竖曲线的几个关键参数，比如变坡点的高程啦，前后坡的坡度啦。

这就好比做菜得先准备好食材一样，这些参数就是我们计算的基础呢。

然后呢，根据这些参数，我们就能套用公式啦。

这公式啊，就像是一把神奇的钥匙，能打开竖曲线的秘密大门。

通过一系列的计算，我们就能得出竖曲线的各种数据，比如曲线的长度啦，切线的长度啦。

哎呀，你说这是不是很有意思？就像解开一道谜题一样，一步一步地找到答案。

不过可别小瞧了这些步骤哦，要是算错了一点点，那竖曲线可就不完美啦，到时候行车可就没那么舒服咯！比如说，在计算的时候，要是把坡度给弄错了，那后果不堪设想啊！就好比你走路的时候，本来以为是平路，结果一脚踩空，那多吓人呀！所以啊，我们得仔仔细细地算，不能有一丝马虎。

还有啊，在实际应用中，我们还得考虑很多其他的因素呢。

比如地形啦，车辆的行驶速度啦。

这就像是给竖曲线穿上一件合适的衣服，让它更合身，更能发挥作用。

你想想看，要是在一个陡峭的山坡上，竖曲线就得设计得更平缓一些，不然车子怎么能开得上去呢？要是在一条平坦的道路上，竖曲线就可以稍微简单一点啦。

总之呢，竖曲线计算公式步骤虽然看起来有点复杂，但只要我们认真去学，去理解，就一定能掌握它。

就像学骑自行车一样，一开始可能会摔倒，但多练几次，不就会了嘛！所以啊，朋友们，别害怕这些公式和步骤，它们可是我们道路设计的好帮手呢！让我们一起把竖曲线算得妥妥的，让道路变得更美好吧！哈哈！。

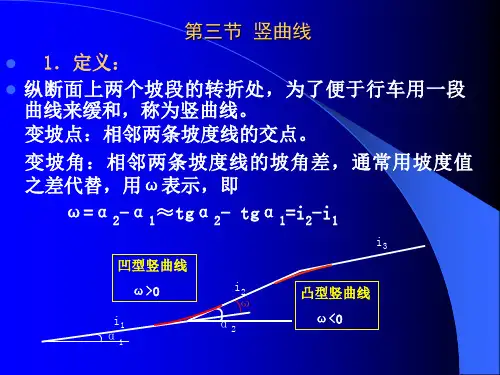
竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。

竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状，通常采用平曲线或二次抛物线两种。

在设计和计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。

一、竖曲线如图所示，设相邻两纵坡坡度分别为i 1 和i 2，则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ，其中i 1、i 2为本身之值，当上坡时取正值，下坡时取负值。

当 i 1- i 2为正值时，则为凸形竖曲线。

当 i 1 - i 2 为负值时，则为凹形竖曲线。

（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。

其基本方程为：Py x 22=若取抛物线参数P 为竖曲线的半径 R ，则有：Ry x 22= Rx y 22= （二）竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得：==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长： L = Rω 3、竖曲线切线长： T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距： E =RT 22⑤竖曲线上任意点至相应切线的距离：Rx y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；R —为竖曲线的半径，m 。

二、竖曲线的最小半径 (一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素 （1）缓和冲击汽车行驶在竖曲线上时，产生径向离心力，使汽车在凸形竖曲线上重量减小，所以确定竖曲线半径时，对离心力要加以控制。

（2）经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时，即使竖曲线半径较大，竖曲线长度也有可能较短，此时汽车在竖曲线段倏忽而过，冲击增大，乘客不适；从视觉上考虑也会感到线形突然转折。

第二节 竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓与,这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状,通常采用平曲线或二次抛物线两种。

在设计与计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。

一、竖曲线如图所示,设相邻两纵坡坡度分别为i 1 与i 2,则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ,其中i 1、i 2为本身之值,当上坡时取正值,下坡时取负值。

当 i 1- i 2为正值时,则为凸形竖曲线。

当 i 1 - i 2 为负值时,则为凹形竖曲线。

(一)竖曲线基本方程式我国采用的就是二次抛物线形作为竖曲线的常用形式。

其基本方程为:Py x 22=若取抛物线参数P 为竖曲线的半径 R ,则有:Ry x 22= Rx y 22=(二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得:==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长: L = R ω3、竖曲线切线长: T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距: E =RT 22⑤竖曲线上任意点至相应切线的距离:Rx y 22=式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m;R —为竖曲线的半径,m 。

二、竖曲线的最小半径(一)竖曲线最小半径的确定1、凸形竖曲线极限最小半径确定考虑因素 (1)缓与冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。

(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。

竖曲线计算示意图及说明
复曲线及竖曲线计算示意图及说明
复曲线计算示意图及说明
1、此程序可计算直线、圆曲线、缓和曲线以及由不同半径连接的卵形曲线。

但在起点与终点之间不能有半径变化点。

2、输入坐标时，X与Y之间用“+”号连接，Y后加小写字
母i，里程不应有千米后边的“+”号。

其它按汉语拼音的提示输入。

3、计算点为K，右侧和左侧的点分别为U与V。

右夹角为计
算点切线方向与构筑物轴线右侧前方的夹角，如果计算里程小于起点里程，则线路的左右相反。

3、如果计算点超过终点之外，则终点的数据自动变为起点，
再输入下一段半径和里程可继续进行计算。

竖曲线计算示意图及说明
1、竖曲线只能计算两个变坡点之间的高程。

按上图中所示的汉语拼音提示输入数据。

2、如果计算里程超过终点里程，则终点自动变为起点，然后再按提示输入下一个变坡点的数据，继续进行计算。