高等级道路竖曲线的计算方法

i合 i纵2 i横 2 0.082 0.0482 9.33% 9%
五、纵坡设计的一般要求（P139）
1、纵坡设计必须满足《公路工程技术标准》中的各项 规定。
2、为保证汽车能以一定的车速安全舒顺地行驶，纵坡 应具有一定的平顺性，起伏不宜过大及过于频繁。 尽量避免采用极限纵坡值，合理安排缓和坡段，不 宜连续采用极限长度的陡坡夹最短长度的缓和坡段。 连续上坡或下坡路段，应避免设置反坡段。越岭线 垭口附近的纵坡应尽量放缓一些。
（一）坡长限制 坡长－－指变坡点与变坡点之间的水平长度。
坡长
➢坡长限制，主要是对较陡纵坡的最大长度和一 般纵坡的最小长度加以限制。
最小坡长限制：任何路段 最大坡长限制：陡坡路段
1．最小坡长限制 :
（1）规定最小坡长的原因
①纵断面上若变坡点过多，纵向起伏变化频繁影响了行车的 舒适和安全；
②相邻变坡点之间的距离不宜过短，以便插入适当的竖曲线 来缓和纵坡的要求，同时也便于平、纵面线形的合理组合与 布置。
最大纵坡（％）
3
456 7 8
9
➢ 设计速度为120km/h、100km/h、80km/h的高速公路受地 形条件或其他特殊情况限制时，经技术经济论证合理，最大纵 坡可增加1％。
➢ 公路改建中，设计速度为40km/h、30km/h、20km/h的利 用原有公路的改建路段，经技术经济论证合理，最大纵坡可增 加1%。
(3) 自然因素：海拔高程、气候（积雪寒冷等）。 ➢ 纵坡度大小的优劣： 坡度大，行车困难，上坡速度低，下坡较危险。 山区公路可缩短里程，降低造价。
2．最大纵坡的确定
我国《公路工程技术标准》规定各级公路的最大纵坡 规定如表3-9所示。
最大纵坡
表3-9

2.竖曲线的最小半径和最小长度
各级公路竖曲线的最小半径和最小长度
单位：m
设计速度（km/h）
120 100 80 60 40 30 20
凸形竖曲线 极限最小值 11000 6500 3000 1400 450 250 100
半径
一般最小值 17000 10000 4500 2000 700 400 200
（2）最小纵坡 定义：最小纵坡是指在纵坡设计时各级公路允许采用 的最小坡度值。
模块二 公路路线
4.坡长限制
（1）最大坡长限制 定义：最大坡长是指控制汽车在坡道上行驶，当车速 下降到最低容许速度时所行驶的距离。 规定：当公路连续纵坡大于5%时，其纵坡坡长应加以 限制，并在最大坡长所规定的范围内设置缓和坡段，缓和 坡段的纵坡坡度应不大于3%。
模块二 公路路线 变坡角计算公式： i1 i2
i1、i2 — 变坡点前、后坡线的纵坡坡度，用小数表示， 上坡取“+”，下坡取“-”。 ω为正时为凸形竖曲线， 反之，为凹形竖曲线。
竖曲线示意图
模块二 公路路线
1. 竖曲线的要素
要素：竖曲线长度L、切线长T和外距E。
竖曲线要素
模块二 公路路线
纵坡竖曲线纵坡竖曲线表纵坡竖曲线表怎么看竖曲线变坡点竖曲线坡度竖曲线坡长道路竖曲线变坡点竖曲线坡度计算纵断面竖曲线竖曲线
模块二 公路路线
一、纵坡
1.纵断面线型组成
组成：地面线和设计线。 设计线组成：直线和竖曲线。
模块二 公路路线
2.纵坡
定义：纵坡是指公路沿线的纵向坡度，包括上坡 和下坡，用符号і表示，上坡i为正，下坡i为负。
-
-
-
- 500 500 600

第九章道路工程测量 (road engineering survey)内容：理解线路勘测设计阶段的主要测量工作（初测控制测量、带状地形图测绘、中线测设和纵横断面测量）；掌握路线交点、转点、转角、里程桩的概念和测设方法；掌握圆曲线的要素计算和主点测设方法；掌握圆曲线的切线支距法和偏角法的计算公式和测设方法；了解虚交的概念和处理方法；掌握缓和曲线的要素计算和主点测设方法；理解缓和曲线的切线支距法和偏角法的计算公式和测设方法；掌握路线纵断面的基平、中平测量和横断面测量方；了解全站仪中线测设和断面测量方法。

重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。

§ 9.1 交点转点转角及里程桩的测设一、道路工程测量概述分为：路线勘测设计测量 (route reconnaissance and design survey) 和道路施工测量 (road construction survey) 。

（一）勘测设计测量 (route reconnaissance and design survey)分为：初测 (preliminary survey) 和定测 (location survey)1、初测内容：控制测量 (control survey) 、测带状地形图 (topographical map of a zone) 和纵断面图 (profile) 、收集沿线地质水文资料、作纸上定线或现场定线，编制比较方案，为初步设计提供依据。

2、定测内容：在选定设计方案的路线上进行路线中线测量 (center line survey) 、测纵断面图 (profile) 、横断面图 (cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。

2、定测内容：在选定设计方案的路线上进行路线中线测量(center line survey)、测纵断面图(profile)、横断面图(cross-section profile)及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。
（二）道路施工测量(road construction survey)
按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。
本章主要论述中线测量和纵、横断面测量。
二、中线测量(center line survey)
1、平面线型：由直线和曲线（基本形式有：圆曲线、缓和曲线）组成。
2、概念：通过直线和曲线的测设，将道路中心线的平面位置测设到地面上，并测出其里程。即测设直线上、圆曲线上或缓和曲线上中桩。
1、曲线要素的计算
若已知：转角α及半径R，则：
切线长： ；
曲线长：
外距： ；
切曲差：
2、主点的测设
（1）主点里程的计算
ZY里程=JD里程-T；YZ里程=ZY里程+L
QZ里程=YZ里程-L/2；JD里程=QZ里程+D/2（用于校核）
（2）测设步骤：
1）JDi架仪，照准JDi-1，量取T，得ZY点；照准JDi+1，量取T，得YZ点。
重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法
难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§9.1交点转点转角及里程桩的测设
一、道路工程测量概述
分为：路线勘测设计测量(route reconnaissance and design survey)和道路施工测量(road construction survey)。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

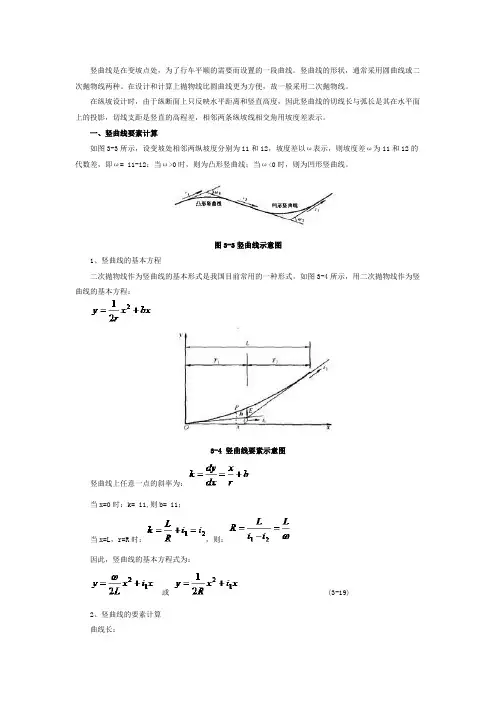
竖曲线是在变坡点处，为了行车平顺的需要而设置的一段曲线。

竖曲线的形状，通常采用圆曲线或二次抛物线两种。

在设计和计算上抛物线比圆曲线更为方便，故一般采用二次抛物线。

在纵坡设计时，由于纵断面上只反映水平距离和竖直高度，因此竖曲线的切线长与弧长是其在水平面上的投影，切线支距是竖直的高程差，相邻两条纵坡线相交角用坡度差表示。

一、竖曲线要素计算如图3-3所示，设变坡处相邻两纵坡度分别为i1和i2，坡度差以ω表示，则坡度差ω为i1和i2的代数差，即ω= i1-i2：当ω>0时，则为凸形竖曲线；当ω<0时，则为凹形竖曲线。

图3-3竖曲线示意图1、竖曲线的基本方程二次抛物线作为竖曲线的基本形式是我国目前常用的一种形式。

如图3-4所示，用二次抛物线作为竖曲线的基本方程：3-4 竖曲线要素示意图竖曲线上任意一点的斜率为：当x=0时：k= i1,则b= i1；当x=L，r=R时：，则：因此，竖曲线的基本方程式为：或 (3-19)2、竖曲线的要素计算曲线长：（3-20）切线长：（3-21）外距：（3-22）曲线上任意一点的竖距（改正值）：（3-23）二、竖曲线设计标准竖曲线的设计标准包括竖曲线的最小半径和最小长度。

1、竖曲线设计的限制因素（1）缓和冲击汽车在竖曲线上行驶时会产生径向离心力，在凸形竖曲线上行驶会减重，在凹形竖曲线上行驶会增重，如果这种离心力达到某种程度时，乘客就会有不舒适的感觉，同时对汽车的悬挂系统也有不利影响，故应对径向离心力加速度加以控制。

根据试验得知，离心加速度a限制在0.5～0.7m/s2比较合适。

汽车在竖曲线上行驶时其离心加速度为：（3-24）《标准》中确定竖曲线半径时取a=0.278 m/s2。

或（3-25）（2）行程时间不宜过短汽车从直坡段驶入竖曲线时，如果其竖曲线长度过短，汽车倏忽而过，冲击力大，旅客会感到不舒适，太短的竖曲线长度从视觉上也会感到线形突然转折。

因此，应限制汽车在竖曲线上的行程时间，一般不宜小于3s。

切线高程和设计高程计算公式竖曲线高程计算公式：
1、外矢距计算公式：L=T2/2R；
2、切线长计算公式：T=1/2*R*（I前-I后）；
3、凹曲线任一点计算公式：H=E+Abs(Q-C)*|+
L;
4、凸曲线任一点计算公式：H=E-Abs(Q-C)*-
L；说明：H=所求点高程；E=竖曲线交点高程；Q=起点桩号；C=所求点桩号；=线路纵坡坡率。

知识点延伸：在线路纵断面上，以变坡点为交点，连接两相邻坡段的曲线称为竖曲线。

竖曲线有凸形和凹形两种。

道路设计高程怎么算？
计算方法：由：A点地面高程+A、B间距×坡度比=B
点地面高程；竖距h=（A、B间距）？？/2R—R为竖曲线
半径；得：B点设计高程=B点地面高程+（-）竖距h—凹曲线时为“+”，凸曲线时为“-”。

高程【elevation】指的是某点沿铅垂线方向到绝对基面的距离，称绝对高程，简称高程。

某点沿铅垂线方向到某假定水准基面的距离，称假定高程。

高程基准是推算国家统一高程控制网中所有水准高程的起算依据，它包括一个水准基面和一个永久性水准原点。

水准基面，通常理论上采用大地水准面，它是一个延伸到全球的静止海水面，也是一个地球重力等位面，实际上确定水准基面则是取验潮站长期观测结果计算出来的。

第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。

可采用抛物线或圆曲线。

一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。

1.二次抛物线基本方程：或ω：坡度差（%）；L：竖曲线长度；R：竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：二、竖曲线最小半径（三个因素）1.缓和冲击对离心加速度加以控制。

ν(m/s)根据经验，a=0.5~0.7m/s2比较合适。

我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。

(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时，Lmin = 2ST - 4/ω2.当L≥ST时，ST为停车视距。

以上两个公式，第二个公式计算值大，作为有效控制。

按缓和冲击、时间行程和视距要求（视距为最不利情况）计算各行车速度时的最小半径和最小长度，见表4-13。

表中：（1）一般最小半径为极限最小半径的1.5~2倍；（2）竖曲线最小长度为3s行程的长度。

（二）凹曲线最小半径和长度1.夜间行车前灯照射距离要求：1）L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。

例：设ω＝2%=0.02;则L＝ωＲ竖曲线最小长度Ｌ＝Ｖ/1.2速度Ｖ=120km/h V=40km/h 一般最小半径Ｒ凸17000 700一般最小半径Ｒ凹6000 700 L凸340 14Ｌ凹120 14 例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m桩号k5+000处：x1=k5+000-k4+940=60m切线高程＝423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程＝426.18 - 0.90=425.28m 桩号k5+100处：x２=k5+100-k4+940=160m切线高程＝423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程＝431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线；路线在水平面上的投影叫路线的平面；路线设计：确定路线空间位置和各部分几何尺寸的工作；可分为平面设计、纵断面设计、横断面设计。

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

道路竖曲线计算第二节 竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状，通常采用平曲线或二次抛物线两种。

在设计和计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。

一、竖曲线如图所示，设相邻两纵坡坡度分别为i 1 和i 2，则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ，其中i 1、i 2为本身之值，当上坡时取正值，下坡时取负值。

当 i 1- i 2为正值时，则为凸形竖曲线。

当 i 1 - i 2 为负值时，则为凹形竖曲线。

（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。

其基本方程为：Py x 22=若取抛物线参数P 为竖曲线的半径 R ，则有：Ry x 22= R x y 22= （二）竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得：==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22= 2、竖曲线曲线长： L = R ω 3、竖曲线切线长： T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距： E =RT 22⑤竖曲线上任意点至相应切线的距离：R x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；R —为竖曲线的半径，m 。

二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素（1）缓和冲击汽车行驶在竖曲线上时，产生径向离心力，使汽车在凸形竖曲线上重量减小，所以确定竖曲线半径时，对离心力要加以控制。

（2）经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时，即使竖曲线半径较大，竖曲线长度也有可能较短，此时汽车在竖曲线段倏忽而过，冲击增大，乘客不适；从视觉上考虑也会感到线形突然转折。

竖曲线坡度计算公式
竖曲线坡度计算公式，是用于计算道路竖曲线坡度的公式。

竖曲线是指道路在垂直方向上的曲线，它由两条直线和一个圆弧线组成。

竖曲线坡度是指道路在竖曲线上的上下坡度。

竖曲线坡度计算公式需要考虑许多因素，包括道路的设计速度、曲线半径、坡度长度等。

具体的计算公式如下：
1. 计算坡度长度
L = K*v^2/R
其中，L为坡度长度，K为坡度系数（一般为1.5），v为设计速度，R为曲线半径。

2. 计算坡度
G = L/H
其中，G为竖曲线坡度，H为竖曲线高差。

以上就是竖曲线坡度计算公式的具体内容，它是道路设计和施工中必不可少的公式之一。

通过对竖曲线坡度的准确计算，可以确保道路的安全和舒适性，为人们的出行提供更好的保障。

- 1 -。

竖曲线任意点高程计算例题竖曲线是公路设计中非常重要的一部分，它涉及到道路的纵向变化和高程的计算。

在竖曲线设计中，计算任意点的高程是一个关键步骤。

本文将通过一个例题来演示竖曲线任意点高程的计算方法。

假设有一条公路，起点高程为100米，终点高程为200米，道路总长度为1000米。

现在我们需要计算出道路上每隔100米的点的高程。

首先，我们需要确定竖曲线的类型。

常见的竖曲线类型有：凸型、直线型和凹型。

我们会根据具体情况选择适合的竖曲线类型。

在本例中，我们选择凸型竖曲线。

接下来，我们需要确定竖曲线的参数。

竖曲线的参数包括：起点高程、终点高程、公路长度、曲线长度、曲率半径和过渡曲线长度等。

在这个例子中，起点高程为100米，终点高程为200米，公路长度为1000米。

我们需要计算出曲线长度、曲率半径和过渡曲线长度。

首先，我们来计算曲线长度。

曲线长度可以根据起点高程和终点高程的差值来计算。

在本例中，曲线长度为200米。

接下来，我们需要计算曲率半径。

曲率半径是曲线最高点的曲率半径，它影响曲线的陡峭程度。

在凸型曲线中，曲率半径的计算公式为：R = (L^2 + H^2) / (2H)，其中R表示曲率半径，L表示曲线长度，H表示起点高程和终点高程的差值。

在本例中，曲率半径为200米。

最后，我们需要计算过渡曲线长度。

过渡曲线长度是指曲线从平缓过渡到陡峭的长度。

在凸型曲线中，过渡曲线长度的计算公式为：T = (L^2) / (24R)，其中T表示过渡曲线长度，L表示曲线长度，R表示曲率半径。

在本例中，过渡曲线长度为16.67米。

现在我们已经计算出了曲线长度、曲率半径和过渡曲线长度，接下来我们可以计算出道路上每隔100米的点的高程。

首先，我们计算出每个100米点的距离。

在本例中，道路总长度为1000米，所以我们需要计算出10个100米点的高程。

然后，我们根据距离和曲线参数来计算每个点的高程。

在本例中，起点高程为100米，曲线长度为200米，曲率半径为200米，过渡曲线长度为16.67米。

公路工程技术标准四级公路竖曲线切线t
摘要：
一、公路工程技术标准简介
二、四级公路竖曲线切线相关技术要求
三、切线技术的实际应用和意义
正文：
公路工程技术标准是我国公路建设的重要参考依据，其中四级公路竖曲线切线技术是道路设计中的重要一环。

本文将对这一技术进行详细解析。

首先，我们需要了解什么是竖曲线切线。

竖曲线切线是指在公路竖曲线上，沿着曲线上升或下降的方向，将曲线上每一点的切线方向连接起来所形成的线。

四级公路竖曲线切线技术要求是公路工程技术标准中的重要内容，其规范了竖曲线切线的计算方法和设计要求，以确保公路的行驶安全和舒适性。

在实际应用中，四级公路竖曲线切线技术有着重要的意义。

首先，切线技术可以指导公路设计，使得公路的竖曲线能够满足行驶安全和舒适性的要求。

其次，切线技术可以用于公路的施工和维护，帮助施工人员了解公路的竖曲线变化，从而更好地进行道路施工和维护工作。

1 绪论1.1 地理位置图（略，详细情况见路线设计图）1.2 路线及工程概况本路线是山岭重丘区的一条三级公路，路线设计技术指标为：路基宽度为7.5米，双向车道，无中央分隔带，土路肩为2 ⨯0.5米，行车道为2 ⨯3.250米。

设计速度为30Km/h，路线总长1981.451米,起点桩号K0+000.00，终点桩号为K1+1981.451。

设计路线共设置了6个平曲线，半径分别为350m 210m 250m 337m 75m 58.460m，弯道处均设置缓和曲线，本次纵断面设计设置了8个变坡点，5个凸形竖曲线， 3个凹形竖曲线，半径依次为1800、4700、18000、2500、2500 3000、1400、1000米。

1.3 线自然地理特征市地处东北腹地长白山脉，向松嫩平原过渡地带的松花江畔，三面临水、四周环山。

东经125〃40′～127〃56′，北纬42〃31′～44〃40′。

东接延边朝鲜族自治州，西临市、市，北与省接壤，南与市、市毗邻。

总面积27120平方公里。

其中，市区3636平方公里。

市的气候类型属于温带大陆性季风气候，四季分明。

春季少雨干燥,夏季温热多雨，秋季凉爽多晴，冬季漫长而寒冷。

全区年平均气温3℃-5℃，气温受地形影响，由西、西北向东、东南气温逐渐降低。

一月份平均气温最低，一般在零下18℃-20℃，七月平均气温最高，一般在21℃-23℃，极端最高气温36.6℃。

山区无霜期120天，平原区可达130-140天。

全年降雨量约700毫米左右。

全区日照时数2400-2600小时，全年总辐射量为1150千卡/平方毫米。

1.4 研究主要容本毕业设计的任务就是在教师的指导下独立完成白河—露水河三级公路的设计工作，具体容包括整理分析、平面设计、纵断面设计、横断面设计、公路排水规划设计及设计文件的编制和图纸绘制。

1.4.1资料整理与分析设计资料是设计的客观依据，必须认真客观地分析。

首先要对设计任务书提供的各种资料加以理解和必要的记忆，明确对设计的影响，在头脑中对工程要求、自然条件、材料供应情况和施工条件等，构成一幅明晰的画面；其次要对资料进行分析、概括和系统地整理，从中抽取、确定有关设计数据。