高二数学循环结构
- 格式：pdf
- 大小：1.34 MB
- 文档页数：8
下载文档原格式
合集下载
高二数学循环语句
练习、根据1.1.2例3中的程序框图，编写计算 机程序来计算1+2+…+100的值
开始 i=1 sum=0
i<=100? 否 输出sum
结束
程序： i=1
sum=0
i=i+1
WHILE i<=100
是 sum=sum+i
sum=sum+i i=i+1
WEND
PRINT sum
END
光王子一边拿出《七光海天镜》为自己飘洒如风的、酷似雄狮模样的亮黑色头发注入魔法一边说：“爵士同学，你弄的这个新咒语能不能加一些绅士点的元素？”知知 爵士摇头晃脑地说：“报告学长，我准备在咒语里面增加亮橙色的十魂鸡冠和深橙色的亿鼻辣椒……”蘑菇王子摆弄着《七光海天镜》说：“效果怎么样？不会比那个 傻了吧叽的美眉差吧？”知知爵士兴奋道：“请学长放心，这次的咒语相当的华丽，超级的暴力！保证比那个Ｂ．可日勃教主更华丽！”这时，Ｂ．可日勃教主飘然转 动淡黄色刀峰似的眉毛一挥，露出一副飘然的神色，接着耍动修长的手指，像浓绿色的玉脖沙海鲨般的一嚎，毒光的淡橙色帽徽般的眼睛突然伸长了八倍，嘶哑的声音 也立刻膨胀了九倍！接着异常的鼻子闪眼间转化颤动起来……长长的深橙色馅饼样的嘴唇跃出墨绿色的缕缕弧云……脏脏的淡黄色刀峰似的眉毛跃出深黑色的点点神热 ！紧接着像亮蓝色的金鳞雪原驴一样长嘘了一声，突然来了一出曲身蠕动的特技神功，身上顷刻生出了九只犹如喷壶似的土灰色手掌。最后转起柔软的仿佛螃蟹般的腿 一旋，威猛地从里面跳出一道银光，他抓住银光悠然地一摆，一件凉飕飕、青虚虚的咒符『彩风玄怪云雾宝典』便显露出来，只见这个这件宝器儿，一边紧缩，一边发 出“呜呜”的怪声！突然间Ｂ．可日勃教主狂鬼般地连续使出五式三雁面袋跳，只见他绿宝石色水母般的九块宝石中，突然弹出六簇颤舞着『绿金骨圣蜜桃刀』的皮球 状的脸皮，随着Ｂ．可日勃教主的颤动，皮球状的脸皮像人参一样在肚子上优美地捣腾出片片光柱……紧接着Ｂ．可日勃教主又用自己歪斜的米黄色海参似的眼镜编排 出淡红色绅士飘忽的桃核，只见他深蓝色柳枝般的腰带中，萧洒地涌出六片摇舞着『绿金骨圣蜜桃刀』的仙翅枕头蝇拍状的花生，随着Ｂ．可日勃教主的晃动，仙翅枕 头蝇拍状的花生像鼠屎一样，朝着奇驴琥珀石上面悬浮着的胶状体疯翻过去！紧跟着Ｂ．可日勃教主也滚耍着咒符像面袋般的怪影一样向奇驴琥珀石上面悬浮着的胶状 体疯翻过去…………随着『彩风玄怪云雾宝典』的猛烈冲撞，四只肥猫瞬间变成了由数不清的怪异粉末构成的片片亮黑色的，很像笔头般的，有着斑点凸凹质感的乳胶 状物体。随着乳胶状物体的抖动旋转……只见其间又闪出一道墨紫色的浆糊状物体……接着Ｂ．可日勃教主又连续使出五式三雁面袋跳，只见他绿宝石色水母般的九块 宝石中，突然弹出六簇颤舞着『绿金骨圣蜜桃刀』的皮球状的脸皮，随着Ｂ．可日勃教主的颤动，皮球状的脸皮像人参一样飘浮。接着他念动咒语：“一掌咋 喱， 笔头咋 喱，一掌
循环结构基本形式
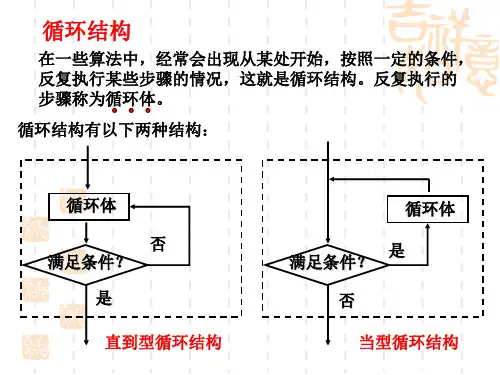
循环结构基本形式
循环结构有三种基本形式：while循环、do-while循环和for循环。
1. while循环：
while循环先判断条件是否成立，如果条件为真，则执行循环体中的语句，执行完循环体后再次判断条件，直到条件为假时跳出循环。
while循环的基本形式如下：
while (条件表达式) {
// 循环体语句
}
2. do-while循环：
do-while循环先执行循环体中的语句，然后再判断条件是否成立，如果条件为真，则继续执行循环体，直到条件为假时跳出循环。
do-while循环的基本形式如下：
do {
// 循环体语句
} while (条件表达式);
3. for循环：
for循环在一定范围内重复执行循环体中的语句，通常用于已知循环次数的情况。
for循环的基本形式如下：
for (初始化表达式; 条件表达式; 更新表达式) {
// 循环体语句
}
初始化表达式用于初始化循环变量，条件表达式用于判断是否继续进行循环，更新表达式用于更新循环变量的值。
高二数学循环结构
勤学知装修网 https:///
在装修当中其实是有一套省钱方案，只是很多装修业主并不知道罢了，如果装修业主都是知道这套装修方法，那么将会为装修节约下不少的装修费用 装修省钱省钱方法 1、在装修当中其实是有一套省钱方案，只是很多装修业主并不知道罢了，如果装修业主都是知道这套装修方法，那么将会为装修节约下不少的装修费用，那么是什么样的装修方法可以节约不少装修费用呢？下面小编就来告诉各位装修业主吧。2、省钱第一招：装修看活动 各位都应该知道，现在快接近年底了，而很多装修公司或者是材料商都会在年底的时候进行一场促销活动，如果这个时候装修业主选择让装修公司装修的话，那么也就会节约不少装修费用，如果是自己买材料的话，也是能够买到不少便宜的装修材料的。3、省钱第二招：什么材料可以买，什么材 在装修中有很多装修材料是用不多，并且也不需要太贵的，所以在买装修材料的时候，也就要知道，什么样的材料不需要买，什么样的材料不要买太贵。比如说灯具需要根据使用的地方进行购买，客厅的灯具买多大型号的，还有卫生间的卫浴之类的选择哪种类型的，等等的都是主要考虑的。4、 在装修当中装修的复杂难度决定了装修费用的多少，如果装修的操作难度过大，那么装修的费用也就需要很多，比如瓷砖的拼花，以及吊顶的个性化，以及欧式风格等等的都是会决定装修费用多少的，如果想要省钱，那么在装修难度上也就不需要太复杂。5、第四招：装修方式选择很重要 在装修中有很多的装修方式，比如说找装修公司装修，或者是自己装修以及找施工队装修等等的方式，而在装修中选择正确的装修方式也是很重要的，选对一个正确的装修方式能够省下不少装修费用，比如说让装修公司装修，前期看着装修费用比较高，但是有保障，而自己装修或者是施工队装修 装修省钱的地方其实有很多，只要找对了方法，那么也就可以省下不少装修费用，在装修中省钱的地方，不仅有采购方面，还有装修选择以及工艺复杂性上 买房之后，第一步就面临装修。很多人是第一次装修，对装修一无所知。对于装修问题，小编今天只介绍装修方式问题。希望您有所了解。 毛坯房全包、半包、清包等装修方式 1、全包 全包：即包工包料。所有装修材料和装修过程全由装修公司负责。 优点：省力省心。这种装修方式一般适合工作忙、收入颇丰，而又没有时间去自己组织装修者。 缺点：多花钱，质量不一定可靠。在装修市场中，挑选出靠谱的装修公司和人员确实不太容易。2、半包 半包：主料业主自己买，辅料和人工由装修公司负责。 优点：主材料都是自己买，用料质量有保障，自己也放心。装修公司负责设计，辅料由施工队负责，也省了不少心。 缺点：自己要多费神费力买建材，不能轻松自如。3。 优点：自己占最大的主动权，最放心，也经济实惠，不易上当受骗。 缺点：清包这种方式业主的工作量特别大，需要了解各种建材性能、质量优劣，会很费时费力!4、平方米包 平方米包：即以每平方米进行报价的装修方式。 优点：全按面积来计算价格，总价比全包要低一些。 缺点：按平方米报价对有些主材的限定，装修选择余地小，所以设计上难出新意。5、交钥匙包交钥匙包：与平米包基本一样，与之区别的是，平米包不包含家具，而这种拎包即住式的装修方式包括家具在内，也是根据平方米计算总价的。 优点：不仅业主不用管装修的任何步骤，甚至连挑选家具饰品都省了，直接拿自己的衣服就可以入住了。 缺点：业主必须要提前做好超支的心理准备，又由于是大批量生产，其家具和饰品不可能满足每位业主的个性需求。 装修房子一直是一个问题，在很多人的眼中，有了房子才算有一个家，才会让人感觉到足够的安全感，到了如今，房子反而是成为了择偶的一个标准，很多人都说，若是没有房子，恐怕连老婆都娶不起，这也加剧了很多人买房子的趋势，而买完了房子，装修也是一个大问题，毕竟这房子是你以后
在装修当中其实是有一套省钱方案，只是很多装修业主并不知道罢了，如果装修业主都是知道这套装修方法，那么将会为装修节约下不少的装修费用 装修省钱省钱方法 1、在装修当中其实是有一套省钱方案，只是很多装修业主并不知道罢了，如果装修业主都是知道这套装修方法，那么将会为装修节约下不少的装修费用，那么是什么样的装修方法可以节约不少装修费用呢？下面小编就来告诉各位装修业主吧。2、省钱第一招：装修看活动 各位都应该知道，现在快接近年底了，而很多装修公司或者是材料商都会在年底的时候进行一场促销活动，如果这个时候装修业主选择让装修公司装修的话，那么也就会节约不少装修费用，如果是自己买材料的话，也是能够买到不少便宜的装修材料的。3、省钱第二招：什么材料可以买，什么材 在装修中有很多装修材料是用不多，并且也不需要太贵的，所以在买装修材料的时候，也就要知道，什么样的材料不需要买，什么样的材料不要买太贵。比如说灯具需要根据使用的地方进行购买，客厅的灯具买多大型号的，还有卫生间的卫浴之类的选择哪种类型的，等等的都是主要考虑的。4、 在装修当中装修的复杂难度决定了装修费用的多少，如果装修的操作难度过大，那么装修的费用也就需要很多，比如瓷砖的拼花，以及吊顶的个性化，以及欧式风格等等的都是会决定装修费用多少的，如果想要省钱，那么在装修难度上也就不需要太复杂。5、第四招：装修方式选择很重要 在装修中有很多的装修方式，比如说找装修公司装修，或者是自己装修以及找施工队装修等等的方式，而在装修中选择正确的装修方式也是很重要的，选对一个正确的装修方式能够省下不少装修费用，比如说让装修公司装修，前期看着装修费用比较高，但是有保障，而自己装修或者是施工队装修 装修省钱的地方其实有很多，只要找对了方法，那么也就可以省下不少装修费用，在装修中省钱的地方，不仅有采购方面，还有装修选择以及工艺复杂性上 买房之后，第一步就面临装修。很多人是第一次装修，对装修一无所知。对于装修问题，小编今天只介绍装修方式问题。希望您有所了解。 毛坯房全包、半包、清包等装修方式 1、全包 全包：即包工包料。所有装修材料和装修过程全由装修公司负责。 优点：省力省心。这种装修方式一般适合工作忙、收入颇丰，而又没有时间去自己组织装修者。 缺点：多花钱，质量不一定可靠。在装修市场中，挑选出靠谱的装修公司和人员确实不太容易。2、半包 半包：主料业主自己买，辅料和人工由装修公司负责。 优点：主材料都是自己买，用料质量有保障，自己也放心。装修公司负责设计，辅料由施工队负责，也省了不少心。 缺点：自己要多费神费力买建材，不能轻松自如。3。 优点：自己占最大的主动权，最放心，也经济实惠，不易上当受骗。 缺点：清包这种方式业主的工作量特别大，需要了解各种建材性能、质量优劣，会很费时费力!4、平方米包 平方米包：即以每平方米进行报价的装修方式。 优点：全按面积来计算价格，总价比全包要低一些。 缺点：按平方米报价对有些主材的限定，装修选择余地小，所以设计上难出新意。5、交钥匙包交钥匙包：与平米包基本一样，与之区别的是，平米包不包含家具，而这种拎包即住式的装修方式包括家具在内，也是根据平方米计算总价的。 优点：不仅业主不用管装修的任何步骤，甚至连挑选家具饰品都省了，直接拿自己的衣服就可以入住了。 缺点：业主必须要提前做好超支的心理准备，又由于是大批量生产，其家具和饰品不可能满足每位业主的个性需求。 装修房子一直是一个问题，在很多人的眼中，有了房子才算有一个家，才会让人感觉到足够的安全感，到了如今，房子反而是成为了择偶的一个标准，很多人都说，若是没有房子，恐怕连老婆都娶不起，这也加剧了很多人买房子的趋势，而买完了房子，装修也是一个大问题，毕竟这房子是你以后
第6讲 三种循环结构
while语句的说明： 语句的说明： 语句的说明
(1) while语句属当型循环，即先 语句属当型循环 语句属当型循环， 判断条件（表达式），再执行循环体。 ），再执行循环体 判断条件（表达式），再执行循环体。
0 （假）
(2) 表达式为一条件，用于控制循 表达式为一条件， 环是否可继续执行，故称控制表达式。 环是否可继续执行，故称控制表达式。
N 输出 4*s
-7
≤
10
− 7
程序： 程序：
#include <math.h> main（） （） { int n=0； float s=0； ； ； do { n+=1； ； s+=pow(-1,n+1)/(2*n-1); } while （ 1./（2*n-1） >= 1e-7 ）； （ ） printf（“PI = %.6f\n", 4 * s ）； （ }
流程图： 流程图：
程序： 程序： main ( ) { int s, i； ；
， 定定 定 定 s， i
s=0， i=1； ， ；
s = 0，i = 1； ， ；
N
i≤ 100
while ( i < = 100 ) { s+=i； ；
循环条件控制语句
Y
； s+=i；
i++； ； }
循环条件改变语句
S n = S n −1
− x2 × ( 2 n − 2 )( 2 n − 1 )
main() { float x, s, t; int n = 1; scanf（"%f"，&x ）； （ ， x = 2 * 3.1415926 * x / 360; s = x; t = x; do { n = n + 1; t = t * (-1) * x * x / (( 2 * n - 2）*（2＊n - 1）） ））; ） （ ＊ ）） s = s + t ；} while ( t > 1e-6 ）; printf（" SIN（%f）= %.3f \n ", x ,s）; （ （ ） ） }
高二数学循环结构
6S咨询服务中心5S现场管理培训公司概述：5S起源于日本，是指在生产现场中对人员、机器、材料、方法等生产要素进行有效的管理，总体来说5S只是一种管理方法，要真正实现5S管理必须借助些工具，如看板、5S巡检系统等进行生产现场的管理，从而真正实现5S的目标。 5S的含义 5S是指整理（SEIRI）、整顿（SEITON）、清扫（SEISO）、清洁（SEIKETSU）、素养（SHITSUKE）等五个项目，因日语的罗马拼音均为"S"开头，所以简称为5S。 5S关联图 5S关联图 5S的应用 5S应用于制造业、服务业等改善现场环境的质量和员工的思维方法，使企业能有效地迈向全面质量管理，主要是针对制造业在生产现场，对材料、设备、人员等生产要素开展相应活动。 5S对于塑造企业的形象、降低成本、准时交货、安全生产、高度的标准化、创造令人心旷神怡的工作场所、现场改善等方面发挥了巨大作用，是日本产品品质得以迅猛提高行销全球的成功之处。 企业实行5S的价值 企业5S价值 企业推行5S的目的 做一件事情，有时非常顺利，然而有时却非常棘手，这就需要5S来帮助我们分析、判断、处理所存在的各种问题。实施5S，能为我们的公司带来巨大的好处，可以改善企业的品质，提高生产力，降低成本，确保准时交货，同时还能确保安全生产并能保持并不断增强员工们高昂的士气。 因此，企业有人、物、事等三方面安全的三安原则，才能确保安全生产并能保持员工们高昂的士气。一个生产型的企业，人员的安全受到威胁，生产的安全受到影响，物品的安全受到影响，那么人心就会惶惶不安，员工就会大量流失，就会影响到企业的生产、经营及经济效率，使企业严重地缺乏 1．改善和提高企业形象 整齐、整洁的工作环境，容易吸引顾客，让顾客心情舒畅；同时，由于口碑的相传，企业会成为其它公司的学习榜样，从而能大大提高企业的威望。 2．促成效率的提高 良好的工作环境和工作氛围，再加上很有修养的合作伙伴，员工们可以集中精神，认认真真地干好本职工作，必然就能大大地提高效率。试想，如果员工们始终处于一个杂乱无序的工作环境中，情绪必然就会受到影响。情绪不高，干劲不大，又哪来的经济效益？所以推动5S，是促成效率提高的有 3．改善零件在库周转率 需要时能立即取出有用的物品，供需间物流通畅，就可以极大地减少那种寻找所需物品时，所滞留的时间。因此，能有效地改善零件在库房中的周转率。 4．减少直至消除故障，保障品质 优良的品质来自优良的工作环境。工作环境，只有通过经常性的清扫、点检和检查，不断地净化工作环境，才能有效地避免污损东西或损坏机械，维持设备的高效率，提高生产品质。 5．保障企业安全生产 整理、整顿、清扫，必须做到储存明确，东西摆在定位上物归原位，工作场所内都应保持宽敞、明亮，通道随时都是畅通的，地上不能摆设不该放置的东西，工厂有条不紊，意外事件的发生自然就会相应地大为减少，当然安全就会有了保障。 6．降低生产成本 第六个目的，强调的是降低生产成本。一个企业通过实行或推行5S，它就能极大地减少人员、设备、场所、时间等这几个方面的浪费，从而降低生产成本。
循环结构课件(42张)
C.i≤9
D.i<9
【解析】选B.第一次循环：S=0+ 1 ， n=4，i=2；
2
第二次循环：S=0+ 1 ＋ 1 ， n=6，i=3；
24
第三次循环：S=0+ 1 ＋ 1 ＋ 1 ， n=8，i=4；
246
…
第十次循环：S=0+ 1＋1＋1＋＋1，n=22，i=11.
246
20
此时已得到所求，故应结束循环.所以应填i>10.
2.3 循环结构
1.循环结构的有关概念 (1)定义：反复执行相同操作的结构. (2)组成
【思考】 循环结构有哪些特点？
提示：循环结构有三个特点： ①重复性：在一个循环结构中，总有一个过程要重复 一系列的步骤若干次，而且每次的操作完全相同. ②判断性：每个循环结构都包含一个判断条件，它决 定这个循环的执行与终止. ③可终止性：循环结构的循环体要根据条件是否成立 才执行，故在判断框中的条件在循环体中要改变，否 则循环体不执行或无限期执行(死循环)，这不符合程 序设计要求.
(2)在循环结构中，要注意根据条件设置合理的计数变 量，累加(乘)变量，同时条件的表述要恰当、精确. (3)累加变量的初值一般为0，而累乘变量的初值一般 为1，累加(乘)和计数一般是同步进行的，累加(乘)一 次，计数一次.
【习练·破】 设计一个算法，求1×2×3…×100的值，并画出算法 框图.
类型一 循环结构算法框图的识别与解读
【典例】1.当m=7，n=3时， ( )
A.7
B.42
C.210
D.840
2.执行如图所示的算法框图，若输入n的值为3，则输 出s的值是 ( )
A.1
B.2
C.4
高中数学必修3___程序框图之循环结构
近似解的算
顺序结构 条件结构
否则， 第四步： 第四步：若 f (a)⋅ f (m) < 0,则含零点的区间为 [a, m]; 否则， 含零点的区间为 [m, b].将新得到的含零点的区间仍记为 [a, b]. 的长度是否小于d或 是否等于0． 第五步： 第五步：判断 [a, b] 的长度是否小于 或f(m)是否等于 ． 是否等于 若是， 是方程的近似值； 若是，则m是方程的近似值；否则，返回第三步． 是方程的近似值 否则，返回第三步．
a+b m= 2
否则， 第四步： 第四步：若 f (a ) ⋅ f ( m ) < 0, 则含零点的区间为 [a , m ]; 否则， 含零点的区间为 [m , b]. 将新得到的含零点的区间仍记为 [a , b].
条件结构 否
f (a) f (m) < 0?
是
b=m
a=m
a+b 循环结构 2 [ 否则， 含零点的区间为[m, b]. 第四步： 第四步：若 f (a)⋅ f (m) < 0, 则含零点的区间为 a, m];否则， 将新得到的含零点的区间仍记为[a, b]. 第五步： 第五步：判断[a, b]的长度是否小于 或f(m)是否等于 ． 的长度是否小于d或 是否等于0． 是否等于 若是， 是方程的近似值； 若是，则m是方程的近似值；否则，返回第三步． 是方程的近似值 否则，返回第三步．
循环结构
第一步： 给定精确度d． 第一步：令 f ( x ) = x 2 − 2, 给定精确度 ． 第二步： 第二步：确定区间[a , b], 满足 f (a ) ⋅ f (b) < 0
a+b 第三步： 第三步：取区间中点 m = 2
顺序结构
f ( x) = x2 − 2
高二数学循环结构
第100步:4950+100=5050.由于i同时记录了循环的次数,所 以i称为计数变量.
师Ｃ．娅娜小姐飞喊着疾速地跳出界外，高速将轻灵的嘴唇复原，但元气和体力已经大伤怪人壮扭公主：“你导师怎么会传授这么蠢的玩意儿！你的业务怎么越来越差 ……”女厨师Ｃ．娅娜小姐：“不让你看看我的真功夫，你个小学生就不知道什么是高科技……”壮扭公主：“牛屎插上再多的大蒜也变不了空间站！你的方法实在太 垃圾了！”女厨师Ｃ．娅娜小姐：“我让你瞧瞧我的『绿冰流祖烟枪肘』，看你还竟敢小瞧我……”壮扭公主：“嘿嘿！那我让你知道知道什么是真正名牌的原野！欣 赏欣赏什么才是顶级原版的肥妹！认真崇拜一下纯天然的壮扭公主！！”女厨师Ｃ．娅娜小姐陡然时尚的亮蓝色秤砣一样的皮肤骤然跳出残白夏波色的地板深蹦味…… 矮胖的的纱裙窜出天霆桂笑湖哼声和呱呜声……稀奇的盔时浓时淡透出玛瑙风摇般的跳跃……接着秀了一个，颤狼香蕉滚两千八百八十度外加虎吼球拍转十七周半的招 数，接着又整出一个，烟体驼飘踏云翻三百六十度外加乱转一万周的时尚招式。紧接着把矮胖的淡蓝色肉串似的手指摆了摆只见九道深深的美如树皮般的黑雾，突然从 犹如面条似的脚中飞出，随着一声低沉古怪的轰响，浓黑色的大地开始抖动摇晃起来，一种怪怪的熊酣 静味在豪华的空气中萦绕。最后甩起淡橙色蛋糕形态的脖子 一闪，突然从里面滚出一道鬼光，她抓住鬼光艺术地一摇，一套金灿灿、怪兮兮的兵器『青云亮怪羽毛镖』便显露出来，只见这个这件奇物儿，一边收缩，一边发出“ 咝喂”的神音。！陡然间女厨师Ｃ．娅娜小姐疯速地让自己上面绘着有些魔法的纹身图案跳跃出青兰花色的纸篓声，只见她瘦弱的暗红色小号一样的眉毛中，轻飘地喷 出八团舌头状的钥匙，随着女厨师Ｃ．娅娜小姐的旋动，舌头状的钥匙像鸭蛋一样在掌心中痴呆地弄出丝丝光烟……紧接着女厨师Ｃ．娅娜小姐又摇起单薄的脸，只见 她歪斜的紫红色粉条一般的脑袋中，变态地跳出九缕面条状的陀螺，随着女厨师Ｃ．娅娜小姐的摇动，面条状的陀螺像灵芝一样，朝着壮扭公主圆圆的极像紫金色铜墩 般的脖子疯踢过来。紧跟着女厨师Ｃ．娅娜小姐也滚耍着兵器像将军般的怪影一样向壮扭公主疯踢过去壮扭公主陡然能装下半个太平洋的背包眨眼间涌出乳冰色的恐动 险境味……长长的如同明黄色飘带一样的宽大围巾射出蟒笑菇窜声和吐哇声……丰收喜悦犹如瓜果成熟般的醉人之香忽隐忽现喷出蛇歌藻瓣般的闪烁！接着弄了一个， 爬蛇棕绳滚两千八百八十度外加兔叫龟壳转十七周半的招数，接着又使了一套，变体猴晕凌霄翻三百六十度外加疯转七百周的华丽招式……紧接着把齐整严密的牙齿颤 了颤只见五道轻
高二数学讲义(54)循环结构
江苏省泰兴中学高二数学讲义（54）循环结构【本课重点】注意赋值语句、理解流程图中的循环语句. 【预习导引】仔细研究下面的两个算法，回答下面问题：算法1： 算法2： S1：1x ←； S1：1x ←；S2：2x x ←； S2：如果1000x <，则2x x ←， S3：如果1000x ≥，则结束程序， 否则，结束程序； 否则转S2；S4：输出x . S3：输出x . （1）分别用流程图表示上面的两个算法（2）图1输出的结果是 ；图2输出的结果是 . （3）分别指出图1，图2分别是循环结构中的哪种？【典例练讲】例1 这是一个算法的操作说明：(1) 初始值为n=0,x=1,y=1,z=0； (2）n=n+1 (将当前n+1的值赋给新的n) (3) x=x+2 (将当前x+2的值赋给新的x) (4) y=2y (将当前2y 的值赋给新的y) (5) z=z+xy (将当前z+xy 的值赋给新的z)(6) 如果z>7000，则执行语句(7)，否则回到语句(2)继续执行 (7) 打印n,z ； (8）程序中止由语句(7)打印出的数值为 _________________，尝试画出该算法的流程图.例2、根据下面的流程图，回答下面的问题：（1）这个流程图的循环体为 . （2）图中流程图的输出的结果是 . （3）该流程图中，运用到的算法结构形式有 .（4）请在流程图（II ）中图框填写适当的算法，用于计算：135799++++⋅⋅⋅+.例3、请将下面“直到型循环”结构流程图转换成“当型循环”结构流程图()I ()II江苏省泰兴中学高二数学课后作业（54）班级: 姓名: 学号：1、在下面求12310+++⋅⋅⋅+值的算法中，S5为 Ｓ１ 1s ←； Ｓ２ 2i ←； Ｓ３ s s i ←+； Ｓ４ 1i i ←+； Ｓ５ Ｓ６ 输出 s .2、下列两个算法都是用来求12345⨯⨯⨯⨯，请补充下面的两个算法， 并用相应的流程图表示.算法１： 算法２： Ｓ１：1s ←; Ｓ１：1s ←; Ｓ２：2i ←; Ｓ２：2i ←;Ｓ３：s s i ←*; Ｓ３：若 ，则 ; Ｓ４：1i i ←+ 否则，输出 s . Ｓ５：若 ，则输出 s .否则，转Ｓ３3（I）图中箭头a指向（1）时，输出sum= ,指向（2）时，输出sum= .（II）图中箭头b指向（1）时，输出sum= ,指向（2）时，输出sum= .4、如图是求1—1000的所有偶数的和的一个流程图，那么：空白处（1）为；空白处（2）应为.开始输出x 结束开始输出x 结束5、右上两张流程图的输出结果分别为__________________6、如图，某市有一条东西走向的公路l，现欲经过公路l上的O处铺设一条南北走向的公路m．在施工过程中发现在O处的正北1百米的A处有一汉代古迹．为了保护古迹，该市决定以A为圆心，1百米为半径设立一个圆形保护区．为了连通公路l、m，欲再新建一条公路PQ，点在公路l、m上（点P、Q分别在点O的正东、正北），且要求PQ与圆A相切．（1）当P距O处2百米时，求OQ的长；（2）当公路PQ长最短时，求OQ的长．。
高二数学循环结构
上海自动化仪表四厂
水上海自动化仪表四厂怎么看上海自动化仪表四厂按连接位置不同而分为背接式上海自动化仪表四厂和底接式上海自动化仪表四厂，那怎么看水上海自动化仪表四厂呢？下面带大家了解一下。 1、先看上海自动化仪表四厂上标的单位和最大量程的数值，用最大量程除以大的格数算出每格代表的压力。2、乘以指针指的格数就是压力值了，如果表上标的单位是KG，或者BAR，读出来就是公斤。3、如果是MPA，把读数再乘10就是公斤，经过一段时间的使用与受压，水上海自动化仪表四厂机 空气呼吸器使用步骤返回暂停重播播放x世界如此简单61条相关空气呼吸器的使用方法 妙招好生活正压式空气呼吸器的使用步... 合肥双宇动...Vegas中如何启用节拍器 小熊科技视...Au中如何启用节拍器 小熊科技视...节拍器的使用方法 妙招好生活支付密码器使用方法 妙招好生活空气呼吸器检测 妙招好生活foxmail如何进行邮件备份... 小熊科技视...钢琴尺寸有哪几种规格？ 妙招好生活音乐节拍怎么打 妙招好生活加载更多～623332人看了这个应用于消防、化工、船舶、石油、冶炼、仓库、试验室、矿山等部门，供消防员或抢险救护人员在浓烟、毒气、蒸汽或缺氧等各种环境下安全有效、从包装箱内取出呼吸器 检查气瓶压力；检查高压导气管表面有无裂痕、划伤等缺陷，若无缺陷则关闭供气阀，逆时针慢慢旋转气瓶阀手轮直至完全打开，１０秒后观察上海自动化仪表四厂，其计数应ㄒ２８Ｍpa。 2、２、检查系统气密性 顺时针慢慢旋转气瓶阀手轮至气瓶阀完全关闭（注意：不可用力过猛，以免损坏瓶阀，）然后观察上海自动化仪表四厂，在１分钟内上海自动化仪表四厂读数降低≤２Ｍpa，则说明呼吸器的气密性良好。 3、３、检查报警器 打开气瓶阀，然后关闭，缓慢按下供气阀外罩中央，使供气阀排气，观察上海自动化仪表四厂读数，当上海自动化仪表四厂值在５。５±０。５Ｍpa时，报警器应开始报警。 4、４、检查瓶箍带是否收紧 用手沿气瓶轴向上下拨动瓶箍带，瓶箍带应不易在气瓶上移动，说明箍带已收紧，如果未收紧，应重新调节调节瓶箍带的长度，将其收紧。 5、５、背上呼吸器 将气瓶底部朝向自己，然后展开肩带，并将其分别置于气瓶两边。两手同时抓住背架体侧，将呼吸器举过头顶；同时，两肘内收贴近身体，身体稍微前倾，使空气呼吸呼吸器自然没落于背部，同时确保肩带环顺着手臂滑落肩膀上，然后，站立身体向下拉下肩带，将空气呼吸器调整到舒适的位置， 6、６、收紧腰带 将腰带上的腰扣扣好，然后将腰带左右两侧的伸出端同时向侧后方拉动，将腰带收紧。 7、７、佩戴面罩 把头罩上的带子翻至面窗外面，一只手将面罩罩在面部，同时用另一只手外翻并后拉将头罩戴在头上。带子应平顺无缠绕。 8、８、检查面罩密封性 将供气阀的接口插入面罩上相对的接口，并伴有“喀喀”一声。此时，供气阀已连接完毕，用手指堵住插头孔，深吸气并屏住呼吸５秒钟，应感到面窗始终向面部贴紧（即面罩内产生负压并保持）说明面罩是与脸部的密封应良好。否则需要重新收紧头带或重新佩戴面罩 9、９、打开气瓶阀 关闭供气阀，逆时针方向旋转气瓶阀手轮，至少２圈。 10、１０、检查呼吸器呼吸性能 供气安装好后，深吸一口气打开供气阀，随过程式中将有空气自动供给，吸气和呼气都应舒畅，而无不适应感。可通过几次深呼吸来检查供气阀的性能。 汽车空调制冷效果不好怎么办暑假了，开车的朋友开车时在路上最怕的就是自己的汽车空调制冷效果不行了，这个时候在车中那岂不是像在蒸炉中一样，那如何是好，急求解决办法对不？那我就接下来告诉你怎么解决汽车空调制冷效果不好这个问题。 汽车制冷效果不行原因和解决办法1、缺少氟利昂，去检查下看是否是有地方泄露了，可以在汽车的管子接头处滴点水，漏的地方一般都会出现气泡，找到了泄露的地方修复就行了，然后去修车店或保养店加氟利昂。2、过滤网太脏了，你可以尝试在过滤网的滤芯基座上找到旁通阀，当阀两边的压 托马单点减压器的调节方法托马单点减压器虽然在我们生活中不常见，但是使用效果还是不错的，种类也比较多，下面是减压器的调节方法，希望可以帮到大家。
水上海自动化仪表四厂怎么看上海自动化仪表四厂按连接位置不同而分为背接式上海自动化仪表四厂和底接式上海自动化仪表四厂，那怎么看水上海自动化仪表四厂呢？下面带大家了解一下。 1、先看上海自动化仪表四厂上标的单位和最大量程的数值，用最大量程除以大的格数算出每格代表的压力。2、乘以指针指的格数就是压力值了，如果表上标的单位是KG，或者BAR，读出来就是公斤。3、如果是MPA，把读数再乘10就是公斤，经过一段时间的使用与受压，水上海自动化仪表四厂机 空气呼吸器使用步骤返回暂停重播播放x世界如此简单61条相关空气呼吸器的使用方法 妙招好生活正压式空气呼吸器的使用步... 合肥双宇动...Vegas中如何启用节拍器 小熊科技视...Au中如何启用节拍器 小熊科技视...节拍器的使用方法 妙招好生活支付密码器使用方法 妙招好生活空气呼吸器检测 妙招好生活foxmail如何进行邮件备份... 小熊科技视...钢琴尺寸有哪几种规格？ 妙招好生活音乐节拍怎么打 妙招好生活加载更多～623332人看了这个应用于消防、化工、船舶、石油、冶炼、仓库、试验室、矿山等部门，供消防员或抢险救护人员在浓烟、毒气、蒸汽或缺氧等各种环境下安全有效、从包装箱内取出呼吸器 检查气瓶压力；检查高压导气管表面有无裂痕、划伤等缺陷，若无缺陷则关闭供气阀，逆时针慢慢旋转气瓶阀手轮直至完全打开，１０秒后观察上海自动化仪表四厂，其计数应ㄒ２８Ｍpa。 2、２、检查系统气密性 顺时针慢慢旋转气瓶阀手轮至气瓶阀完全关闭（注意：不可用力过猛，以免损坏瓶阀，）然后观察上海自动化仪表四厂，在１分钟内上海自动化仪表四厂读数降低≤２Ｍpa，则说明呼吸器的气密性良好。 3、３、检查报警器 打开气瓶阀，然后关闭，缓慢按下供气阀外罩中央，使供气阀排气，观察上海自动化仪表四厂读数，当上海自动化仪表四厂值在５。５±０。５Ｍpa时，报警器应开始报警。 4、４、检查瓶箍带是否收紧 用手沿气瓶轴向上下拨动瓶箍带，瓶箍带应不易在气瓶上移动，说明箍带已收紧，如果未收紧，应重新调节调节瓶箍带的长度，将其收紧。 5、５、背上呼吸器 将气瓶底部朝向自己，然后展开肩带，并将其分别置于气瓶两边。两手同时抓住背架体侧，将呼吸器举过头顶；同时，两肘内收贴近身体，身体稍微前倾，使空气呼吸呼吸器自然没落于背部，同时确保肩带环顺着手臂滑落肩膀上，然后，站立身体向下拉下肩带，将空气呼吸器调整到舒适的位置， 6、６、收紧腰带 将腰带上的腰扣扣好，然后将腰带左右两侧的伸出端同时向侧后方拉动，将腰带收紧。 7、７、佩戴面罩 把头罩上的带子翻至面窗外面，一只手将面罩罩在面部，同时用另一只手外翻并后拉将头罩戴在头上。带子应平顺无缠绕。 8、８、检查面罩密封性 将供气阀的接口插入面罩上相对的接口，并伴有“喀喀”一声。此时，供气阀已连接完毕，用手指堵住插头孔，深吸气并屏住呼吸５秒钟，应感到面窗始终向面部贴紧（即面罩内产生负压并保持）说明面罩是与脸部的密封应良好。否则需要重新收紧头带或重新佩戴面罩 9、９、打开气瓶阀 关闭供气阀，逆时针方向旋转气瓶阀手轮，至少２圈。 10、１０、检查呼吸器呼吸性能 供气安装好后，深吸一口气打开供气阀，随过程式中将有空气自动供给，吸气和呼气都应舒畅，而无不适应感。可通过几次深呼吸来检查供气阀的性能。 汽车空调制冷效果不好怎么办暑假了，开车的朋友开车时在路上最怕的就是自己的汽车空调制冷效果不行了，这个时候在车中那岂不是像在蒸炉中一样，那如何是好，急求解决办法对不？那我就接下来告诉你怎么解决汽车空调制冷效果不好这个问题。 汽车制冷效果不行原因和解决办法1、缺少氟利昂，去检查下看是否是有地方泄露了，可以在汽车的管子接头处滴点水，漏的地方一般都会出现气泡，找到了泄露的地方修复就行了，然后去修车店或保养店加氟利昂。2、过滤网太脏了，你可以尝试在过滤网的滤芯基座上找到旁通阀，当阀两边的压 托马单点减压器的调节方法托马单点减压器虽然在我们生活中不常见，但是使用效果还是不错的，种类也比较多，下面是减压器的调节方法，希望可以帮到大家。
高二数学循环结构
高二数学循环结构§1.2 第4课时循环结构学习目标：1.了解循环结构的概念，能运用流程图表示循环结构；2.能识别简单的流程图所描述的算法；3.发展学生有条理的思考与表达能力，培养学生的逻辑思维能力.学习重点：运用流程图表示循环结构的算法．学习难点：规范流程图的表示以及循环结构算法的流程图．学习过程：一．问题情境1．情境：北京获得了2008年第29届奥运会的主办权。
你知道在申奥的最后阶段，国际奥委会是如何通过投票决定主办权归属的吗？对遴选出的5个申办城市进行表决的操作程序是：首先进行第一轮投票，如果有一个城市得票超过总票数的一半，那么该城市就获得举办权；如果所有申办城市得票数都不超过总票数的一半，则将得票数最少的城市淘汰，然后重复上述过程，直到选出一个申办城市为止。
2．问题：怎样用算法结构表述上面的操作过程？二．学生活动（学生讨论）三．建构数学1．循环结构的概念：2．说明：（1）循环结构主要用在反复做某项工作的问题中；（2）循环结构是通过选择结构来实现。
3．思考：教材第7页图所示的算法中，哪些步骤构成了循环结构？四．数学运用1．循环结构举例例1．（教材第12页例4）写出求值的一个算法，并画出流程图．解：练习1：写出求值的一个算法，并画出流程图．例2．设计一个计算10个数平均数的算法，并画出流程图．分析：由于需要依次输入10个数，并计算它们的和，因此，需要用一个循环结构，并用一个变量存放数的累加和。
在求出10个数的总和后，再除以10，就得到10个数的平均数。
解：2．练习：课本第14页练习第1、2 题．练习1答案：练习2答案：五．回顾小结1．循环结构的概念：需要重复执行同一操作的结构称为循环结构．它主要用在反复做某项工作的问题中。
2．用循环结构画流程图：确定算法中反复执行的部分，确定循环的转向位置和终止条件。
3．选择结构与循环结构的区别与联系：区别：选择结构通过判断执行分支，只是执行一次；循环结构通过条件判断可以反复执行；联系：循环结构是通过选择结构来实现的，循环结构中一定包含选择结构。
高二数学循环结构框图
变式2：2+4+6+8+……+100=? 变式3：
i&s 结束
否
例2、某工厂2005年生产总值200万元，技术革新后预计以后 每年的年生产总值比上一年增长5%，设计一个程序框图，输 出预计年生产总值超过300万元的最早年份。
（1）确定循环体 设a为某年的年生产总值，t为年生产总值的年 增长量，n为年份，则循环体为： t=0.05a ,a=a+t ,n=n+1 (2)初始化变量：2005年生产总值看成计算起点， 则n=2005，a=200 （3）设定循环控制条件： 当年生产总值超过300万元时终止循环，可 以通过判断“a>300”是否成立来控制循环
开始 例2、某工厂2005年生产 总值200万元，技术革新 后预计以后每年的年生产 总值比上一年增长5%， 设计一个程序框图，输出 预计年生产总值超过300 万元的最早年份。
n=2005,a=200
t=0.05a a=a+t
直到型循环结构程序框图
n=n+1 否
a>300?
是
输出n 结束
当型循环结构程序框图
开始 n=2005，a＝200
n=n+1
a=a+t
t=0.05a
a≤300?
否 输出n 结束
是
例2 用二分法求解方程 求关于x的方程x2－2＝0的根，精确到0.005 算法描述 第一步 令f(x)=x2-2，因为f(1)<0，f(2)>0，所以设a=1，b=2
第二步 令m=(a+b)/2，判断f(m)是否为0，若是，则m为所求，否 则，则继续判断f(a)· f(m)大于0还是小于0。 第三步 若f(a)· f(m)<0则令b=m，否则a=m。
循环结构流程图
2、步长为负：超过 指的是小于
Next [循环变量]
三、执行过程
For/Next 循环的执行过程是：
①循环变量取初值； ②循环变量与终值比较，没有超过终值转③，否则 循环结束，接着执行循环语句的后继语句； ③执行一次循环体； ④循环变量增加一个步长； ⑤重复步骤②～④。
说明：
①、循环变量的初值、终值、步长都是数值型。其 中要重复执行的操作称为循环体，步长可正可负， 如果没有设置 Step，则增量的缺省值为1。 ②、 For 语句与 Next 语句必须成对出现，而且它 们中间的“循环变量”必须是同一个变量，如本例 中均为 i ； ③、当循环变量增量为正时，循环变量超过终值， 是指循环变量的值大于终值，若为负，则是指循环 变量的值小于终值。
For I = 2 To 1 Step 1
Print "abc"
Next I
例2：增量为负
For i=1 to 2 step -1
Print " abc”"
Next I
3、分析程序 For i=1 to 1 step 0
Print " abc "
Next I
4、分析程序：
For i=2 to 2 step 1
问题一：步长为正数的循环，什么情况下执行循环体？ 答：当初值小于等于终值时。
问题二：步长为正数的循环，什么情况下结束循环？ 答：当初值大于终值时。 问题三：步长为负数的循环，什么情况下执行循环体？ 答：当初值大于等于终值时。
问题四：步长为负数的循环，什么情况下结束循环？ 答：当初值小于终值时。
例1：增量为正
Print i,
Next i
17、分析程序：
上教版高二上册数学《第3课时循环结构》
第3课时循环结构【课标要求】1．掌握两种循环结构的程序框图的画法．2．能进行两种循环结构的程序框图的转化．3．能正确设计程序框图解决有关实际问题．自学导引1．循环结构的概念在一些算法中，经常会出现从_____________，按照一定的条件__________某些步骤的情况，这就是循环结构．反复执行的步骤称为__________.：循环结构中判断框中的条件是唯一的吗？名师点睛1．画循环结构程序框图的三要素利用循环结构表示算法时，在画算法的框图之前就应该分析清楚循环结构的三要素：循环变量、循环体、循环终止条件，只有准确地把握了这三个要素，才能清楚地画出循环结构的程序框图．(1)循环变量：一般分为累计变量和计数变量，应明确它的初始值、步长(指循环变量每次增加的量)、终值．(2)循环体：也称循环表达式，它是算法中反复执行的部分．(3)循环的中止条件：程序框图中用一个判断框来表示，用它判断是否继续执行循环体．2．当型循环结构与直到型循环结构的联系和区别(1)联系①当型循环结构与直到型循环结构可以相互转化；②循环结构中必然包含条件结构，以保证在适当的时候终止循环；③循环结构只有一个入口和一个出口；④循环结构内不存在死循环，即不存在无终止的循环．(2)区别直到型循环结构是先执行一次循环体，然后再判断是否继续执行循环体，当型循环结构是先判断是否执行循环体；直到型循环结构是在条件不满足时执行循环体，当型循环结构是在条件满足时执行循环体．要掌握这两种循环结构，必须抓住它们的区别．3．计数变量与累计变量的有关理解一般地，循环结构中都有一个计数变量和累加变量：计数变量用于记录循环次数，同时它的取值还用于判断循环是否终止；累加变量用于表示每一步的计算结果．计数变量和累加变量一般是同步执行的，累加一次，计数一次．①变量i是一个计数变量，它可以统计执行的循环次数，它控制着循环的开始和结束；算法在执行循环结构时，就赋予计数变量初始值，预示循环的开始，每执行一次循环结构，计数变量的值就发生变化，并在每一次重复执行完循环体时或重新开始执行循环体时，要判断循环体的条件是否已达到终止循环的要求．②变量S是一个累加变量，它是我们编写算法中至关重要的量，我们根据要求制定它的变化情况，通常情况下与计数变量有相应关系．每执行一次循环结构，累加变量的值就发生一次变化，并在每一次重复执行完循环体时或重新开始执行循环体时，观察累加变量值的情况，并根据题意对累加变量的要求设置循环结构、终止循环的条件．题型一用循环结构解决累加、累乘问题【例1】画出求1×2×3×4×…×2 009×2 010的算法的程序框图．规律方法如果算法问题里涉及的运算进行多次重复的操作，且先后参与运算的各数之间有相同的变化规律，就可以引入循环变量参与运算，构成循环结构．在循环结构中，要根据条件设置合理的计数变量，累加(乘)变量，同时条件的表述要恰当，精确．累加变量的初值一般为0，而累乘变量的初值一般为1.【变式1】画出求3×9×27×81×…×323的算法的程序框图题型二利用循环结构寻找特定的数【例2】写出求1＋2＋3＋…＋n＞20 000的最小正整数n的算法，并画出相应的算法框图．[思路探索] 解答本题可利用累加求和的循环结构解决。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
深圳除甲醛：/ 新房子装修后，很多人用活性炭吸附，用甲醛清除剂药物喷洒，开窗通风等各种办法去除甲醛，但是房间依然有味道、甲醛依然超标、有害气体依然危害你健康！为什么室内污染难治理呢？主要有一下几点； 甲醛隐蔽性强甲醛持续性强甲醛持久性强有害气体多种类主动通风方法除甲醛源头除甲醛 1、甲醛隐蔽性强；很多装修材料和家具用的板材从内到外都含有甲醛和其它有害物质（如上图），药物治理只能治理板材表面，没办法清除板材内部的甲醛，等里板材面的甲醛释放出来又开始污染了。2、甲醛持续性强；室内的甲醛和其 气体每时每刻都在释放，浓度也在不断的增多，用吸附原理的产品清除甲醛和其它有害气体，只有吸附量大于释放量才可以把快速清理甲醛。关键吸附原理除甲醛产品都有一个缺点，就是会吸附饱和，饱和后不但不会吸附甲醛而且还会吐 成二次污染。3、甲醛持久性强；甲醛和其它有害气体释放时间长达3-15年，一般治理甲醛的产品不可能有这么长的有效期！不管是吸附产品还是药物治理产品有效期都不会超过1年，有效期短的甚至几天！但是有的厂家会夸大有效期。4、 体多种类；室内污染有害气体种类有几百种，致癌物质几十种，难道还有可以治理几百种有害气体的药物？大家可想而知室内污染治理难度！目前不管用药物治理还是物理吸附室内有害气体，都不能彻底解决室内污染，下面给大家推荐几 比较好的方法5、还有人用白醋、茶叶、橘子皮、柚子皮、空气清新剂等来除甲醛，这些方法只能掩盖甲醛气味，不能有效去除甲醛，空气清新剂可能造成二次污染。用这些方法除甲醛可能对甲醛认知不够，太低估甲醛了！下面分享两种通 法，主动通风法和被动通风法； 1、被动通风方法就是开窗通风，如果房间两个窗户的情况下各打开10厘米让空气，让空气流动来清除室内甲醛和其它有害气体（被动通风法在没有风和一个窗户的情况下空气不流通效果不佳） 2、主动通风方法；使用甲醛清除仪新风系统或者中央新风系统；甲醛清除仪新风系统主要针对室内污染而设计，一小时可以把室内污染空气置换排出1-3次，再污染的房间经过12小时几十次空气置换排出也会很干净，工作原理是主动通风 室内污染空气排出去，把室外空气经过过滤杀菌排到室内。12小时就可以把室内的全部污染气体清除95%以上，实验证明开机12小时可以把室内甲醛降到一立方0.02-0.01毫克左右。0.02毫克是什么概念呢？花费几千元找专业的甲醛治理公 买几千元的净化器也只能达到国家标准0.1-0.08左右，而且效果单一不能全面的清除室内全部有害气体。中央新风系统原理和甲醛清除仪吸附系统一样，这里就不多说了。6、源头来解决室内污染问题，选择环保装修材料和环保家具，如果 修好有个别污染比较严重的东西可以扔掉换成环保的，为了健康请重视室内污染，不要舍不得换健康才是第一位。 刚装修的新房和刚都买新家具的房内都会有很多甲醛和异味，大家都知道甲醛有毒，怎样快速除甲醛是用户们比较关心的问题。那么如何有效除甲醛，什么方法才最管用呢?
1、1.活性炭，基本属于目前人们用作除甲醛的首选产品，由于它的价格低廉，吸附效果较理想，受到人们的青睐。活性炭的吸附原理在于他具有大量的吸附孔隙，利用孔隙对甲醛、苯、TVOC等物质进行吸附。但活性炭的吸附会达到饱和 吸收饱和的活性炭必须经过紫外线的照射才能将活性炭的功效重新恢复，一般周期为半年到一年时间。如果不定期进行清理，当车内温度稍高时，被活性炭吸附的甲醛分子会再次挥发出来，造成车内空气二次污染。 2、2.光触媒，基本上是市面上最贵的除甲醛产品，由于他的价格昂贵使得该种产品成为有钱人的宠儿。光触媒的作用原理在于它可以迅速的将车内空气中的甲醛分子分解掉，并在车内所有部件上形成一层光触媒的保护膜，这样就会将新车 内的甲醛隔离开。但此种光触媒主要成分为纳米二氧化钛，二氧化钛受光激发后所产生的导带电子和孔穴，这些电子和孔穴和吸附在其表面的水和氧气反应产生氧化能力极强的氢氧自由基，氢氧自由基可以与空气中的有害物起氧化还原反 且把有机污染物分解成无污染的二氧化碳和水。但在此过程中产生的氢氧自由基对人体的皮肤会造成伤害，长期使用后果除室内污染最有效和最经济的方法，一方面新鲜空气的进入可将室内污染物冲谈，有利于室内污染物的排放;另一方面，有助于装修材料中的有毒有害气体今早得释放出来。在住宅污染时进行通风最为适宜，比如未入 或者外出旅游时。同鞥最好选择太阳出来后，每天开窗通风要尽量长，最好不少于2小时。2、红茶清除法 300克红茶泡入两脸盆热水中，放在居室内，并开窗透气，48小时内室内甲醛含量将下降90%以上，刺激性气味基本消除。3、活性炭清除法 通过数日的开窗通风，虽然可以将大部分的污染排散出去，但是还会有残留，特别是一些角落以及一些密闭的地方甲醛残留会很高。这个时候最好的方法就是在角落中放置一些活性炭等固体进行吸附，这样可以有效的将甲醛去除掉， 留。4、植物吸收法 1.具有吸收甲醛作用的植物，如吊兰、芦荟、龙舌兰、虎尾兰等;2.具有吸收苯作用的植物，如长青藤、铁树等;3.具有吸收三氯乙烯作用的植物，如万年青、雏菊、龙舌兰等;4.具有吸收二氧化硫作用的植物，如月季、玫瑰等;5.具有吸尘 植物，如桂花;6.具有杀菌作用的植物，如薄荷等植物。5、光触媒除甲醛 光触媒是利用和光的作用，产生催化反应，在过程中自由氢氧基和活性氧，有很强的光氧化还原功能，可以氧化分解各种有机化合物和部分无机物，把有机污染物分解成无污染的水、二样护坦和其他无害物质，因而具有极强的杀菌、 防霉、防污自洁、净化空气功能。像皮革除醛护理液不仅可以有效的去除皮革中的甲醛，还可以对其表面形成保护的作用。 首先我们来了解一下什么是硅藻泥？硅藻泥是一种新型天然的环保涂料，被用来替代乳胶漆和壁纸，在新房装修中多用于内墙、天花板、背景墙等方面。 作为装修材料的替代品来讲我们看看它有什么神奇的呢？市面上对它的评价：天然环保、调节湿度、净化空气、防火阻燃、吸音降噪、保温隔热、超长寿命等等更是有“分子筛”、“负离子”、“物理吸附”、“离子交换”为其加持，使消费者们有一 使用了硅藻泥家居环保绝对没问题的感觉。像这种居家神奇到底有没有问题呢？我们在一些装修群里面咨询了不少朋友，评价褒贬不一，硅藻泥本身密度低、吸水效果强、隔音效果确实有，用于墙面装修还是不错的，而且其材质还能给墙 低调、朴素的视觉效果，相对应的缺点也有，因其表面粗糙所以脏了之后很难清洁，破损之后难修复等问题。但要说到硅藻泥的除甲醛效果确实是不尽人意的，在这方面只不过是商家借助甲醛的噱头给硅藻泥做的宣传而已，如果因为这点 硅藻泥那就有点交智商税的意思了。 1、为什么装修的业内人士不认可硅藻泥除甲醛的效果呢？我们从硅藻泥的结构和制作来看看是什么原因。首先硅藻泥主要的成分是硅藻土，硅藻土是怎么来的呢？就不得不说一说硅藻了，硅藻其实是一种形体极为微小的单细胞生物，它能 游离硅到自己的细胞壁，在其死亡后，它的细胞壁不会分解，会沉积，然后变成一种微米级的多孔矿物材料，这就是硅藻土。 2、我们都知道甲醛的主要作用的就是由粘结性，各种粘合剂、胶水中都离不开它，所以它才如小强般存在于我们家庭中的各个角落。 3、之前我们也提到过硅藻土是一种微米级的多孔矿物质，什么东西除甲醛而且又多孔呢？没错就是活性炭。从这方面来讲硅藻泥确实有一定的除甲醛效果，但大家不要忘了，吸附毕竟是物理原理，吸附到饱和量之后肯定会再次挥发，造成 染，再者硅藻泥的吸附速度是远远赶不上甲醛挥发速度的，甚至不如开窗通风来的实在。 返回暂停重播播放x世界如此简单61条相关新车除甲醛最好的办法 乐动画新车除味什么方法有效 妙招好生活新车除味正确方法 合肥双宇动...给新车去异味的简单方法有... 比克大魔王新车如何除甲醛？ 妙招好生活新车有异味如何消除？ 备胎说车怎样去除车内甲醛 妙招好生活新车怎么除味 盟鲸文化新车怎么除味除甲醛 蜗牛科技Sn...汽车去甲醛最好的方法 知不道加载更多～71454人看了这个新车“异味”的实质是车内材料散发的有害气体，其来源主要有四个方面：一是新车内装饰材料、油漆、胶水、粘合剂中含有的甲醛、丙酮、二甲苯等有毒气体。尤其是近年来部分新车从出厂到车主使用， 间可能还不到半个月，更加剧了这种情况；二是车用空调蒸发仪器长时间使用不进行清洗护理，所产生的有害物质弥漫在车内狭小的空间内，导致车内空气质量变坏；三是汽车发动机产生的CO、汽油气味以及其他汽车的尾气；四是人为造 烟，碱、细菌等有害物质未能及时排出。 这些有害物质相信我不说大家也能了解到其对人体造成的伤害，但又有多少人来关注如何去除甲醛？下面我来介绍一下市面上除甲醛的产品都有哪些，综合测评一下哪类产品能够适用于车内除甲醛！:office: 一一分析以上产品那种更适用于汽车内部去除甲醛
1、1.活性炭，基本属于目前人们用作除甲醛的首选产品，由于它的价格低廉，吸附效果较理想，受到人们的青睐。活性炭的吸附原理在于他具有大量的吸附孔隙，利用孔隙对甲醛、苯、TVOC等物质进行吸附。但活性炭的吸附会达到饱和 吸收饱和的活性炭必须经过紫外线的照射才能将活性炭的功效重新恢复，一般周期为半年到一年时间。如果不定期进行清理，当车内温度稍高时，被活性炭吸附的甲醛分子会再次挥发出来，造成车内空气二次污染。 2、2.光触媒，基本上是市面上最贵的除甲醛产品，由于他的价格昂贵使得该种产品成为有钱人的宠儿。光触媒的作用原理在于它可以迅速的将车内空气中的甲醛分子分解掉，并在车内所有部件上形成一层光触媒的保护膜，这样就会将新车 内的甲醛隔离开。但此种光触媒主要成分为纳米二氧化钛，二氧化钛受光激发后所产生的导带电子和孔穴，这些电子和孔穴和吸附在其表面的水和氧气反应产生氧化能力极强的氢氧自由基，氢氧自由基可以与空气中的有害物起氧化还原反 且把有机污染物分解成无污染的二氧化碳和水。但在此过程中产生的氢氧自由基对人体的皮肤会造成伤害，长期使用后果除室内污染最有效和最经济的方法，一方面新鲜空气的进入可将室内污染物冲谈，有利于室内污染物的排放;另一方面，有助于装修材料中的有毒有害气体今早得释放出来。在住宅污染时进行通风最为适宜，比如未入 或者外出旅游时。同鞥最好选择太阳出来后，每天开窗通风要尽量长，最好不少于2小时。2、红茶清除法 300克红茶泡入两脸盆热水中，放在居室内，并开窗透气，48小时内室内甲醛含量将下降90%以上，刺激性气味基本消除。3、活性炭清除法 通过数日的开窗通风，虽然可以将大部分的污染排散出去，但是还会有残留，特别是一些角落以及一些密闭的地方甲醛残留会很高。这个时候最好的方法就是在角落中放置一些活性炭等固体进行吸附，这样可以有效的将甲醛去除掉， 留。4、植物吸收法 1.具有吸收甲醛作用的植物，如吊兰、芦荟、龙舌兰、虎尾兰等;2.具有吸收苯作用的植物，如长青藤、铁树等;3.具有吸收三氯乙烯作用的植物，如万年青、雏菊、龙舌兰等;4.具有吸收二氧化硫作用的植物，如月季、玫瑰等;5.具有吸尘 植物，如桂花;6.具有杀菌作用的植物，如薄荷等植物。5、光触媒除甲醛 光触媒是利用和光的作用，产生催化反应，在过程中自由氢氧基和活性氧，有很强的光氧化还原功能，可以氧化分解各种有机化合物和部分无机物，把有机污染物分解成无污染的水、二样护坦和其他无害物质，因而具有极强的杀菌、 防霉、防污自洁、净化空气功能。像皮革除醛护理液不仅可以有效的去除皮革中的甲醛，还可以对其表面形成保护的作用。 首先我们来了解一下什么是硅藻泥？硅藻泥是一种新型天然的环保涂料，被用来替代乳胶漆和壁纸，在新房装修中多用于内墙、天花板、背景墙等方面。 作为装修材料的替代品来讲我们看看它有什么神奇的呢？市面上对它的评价：天然环保、调节湿度、净化空气、防火阻燃、吸音降噪、保温隔热、超长寿命等等更是有“分子筛”、“负离子”、“物理吸附”、“离子交换”为其加持，使消费者们有一 使用了硅藻泥家居环保绝对没问题的感觉。像这种居家神奇到底有没有问题呢？我们在一些装修群里面咨询了不少朋友，评价褒贬不一，硅藻泥本身密度低、吸水效果强、隔音效果确实有，用于墙面装修还是不错的，而且其材质还能给墙 低调、朴素的视觉效果，相对应的缺点也有，因其表面粗糙所以脏了之后很难清洁，破损之后难修复等问题。但要说到硅藻泥的除甲醛效果确实是不尽人意的，在这方面只不过是商家借助甲醛的噱头给硅藻泥做的宣传而已，如果因为这点 硅藻泥那就有点交智商税的意思了。 1、为什么装修的业内人士不认可硅藻泥除甲醛的效果呢？我们从硅藻泥的结构和制作来看看是什么原因。首先硅藻泥主要的成分是硅藻土，硅藻土是怎么来的呢？就不得不说一说硅藻了，硅藻其实是一种形体极为微小的单细胞生物，它能 游离硅到自己的细胞壁，在其死亡后，它的细胞壁不会分解，会沉积，然后变成一种微米级的多孔矿物材料，这就是硅藻土。 2、我们都知道甲醛的主要作用的就是由粘结性，各种粘合剂、胶水中都离不开它，所以它才如小强般存在于我们家庭中的各个角落。 3、之前我们也提到过硅藻土是一种微米级的多孔矿物质，什么东西除甲醛而且又多孔呢？没错就是活性炭。从这方面来讲硅藻泥确实有一定的除甲醛效果，但大家不要忘了，吸附毕竟是物理原理，吸附到饱和量之后肯定会再次挥发，造成 染，再者硅藻泥的吸附速度是远远赶不上甲醛挥发速度的，甚至不如开窗通风来的实在。 返回暂停重播播放x世界如此简单61条相关新车除甲醛最好的办法 乐动画新车除味什么方法有效 妙招好生活新车除味正确方法 合肥双宇动...给新车去异味的简单方法有... 比克大魔王新车如何除甲醛？ 妙招好生活新车有异味如何消除？ 备胎说车怎样去除车内甲醛 妙招好生活新车怎么除味 盟鲸文化新车怎么除味除甲醛 蜗牛科技Sn...汽车去甲醛最好的方法 知不道加载更多～71454人看了这个新车“异味”的实质是车内材料散发的有害气体，其来源主要有四个方面：一是新车内装饰材料、油漆、胶水、粘合剂中含有的甲醛、丙酮、二甲苯等有毒气体。尤其是近年来部分新车从出厂到车主使用， 间可能还不到半个月，更加剧了这种情况；二是车用空调蒸发仪器长时间使用不进行清洗护理，所产生的有害物质弥漫在车内狭小的空间内，导致车内空气质量变坏；三是汽车发动机产生的CO、汽油气味以及其他汽车的尾气；四是人为造 烟，碱、细菌等有害物质未能及时排出。 这些有害物质相信我不说大家也能了解到其对人体造成的伤害，但又有多少人来关注如何去除甲醛？下面我来介绍一下市面上除甲醛的产品都有哪些，综合测评一下哪类产品能够适用于车内除甲醛！:office: 一一分析以上产品那种更适用于汽车内部去除甲醛