当前位置：文档之家 › 数据压缩与信源编码定理

数据压缩与信源编码定理

  • 格式：pdf
  • 大小：576.73 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

第5章无失真信源编码定理

第5章无失真信源编码定理

如果我们要对信源的N次扩展信源进行编码，也必须满足
qN rl ， 两边取对数得： l log q
l
N log r
N 表示平均每个信源符号所需的码符号个数。
5.2 等长码
例：对英文电报得32个符号进行二元编码，根据上述关系：
l log 32 5 log 2
我们继续讨论上面得例子，我们已经知道英文的极限 熵是1.4bit,远小于5bit，也就是说，5个二元码符号只携带 1.4bit的信息量，实际上，5个二元符号最多可以携带5bit 信息量。我们可以做到让平均码长缩短，提高信息传输率
0.8112
0.4715
若采用等长二元编码，要求编码效率 0.96 ，允许错误率
105 ，则： N 4.13107
也就是长度要达到4130万以上。
5.5 变长码
1、唯一可译变长码与及时码
信源符号 出现概率 码1
码2
码3
码4
s1
1/2
0
0
1
1
s2
1/4
11
10
10
01
s3
1/8
00
00
密码：是以提高通信系统的安全性为目的的编码。通常通过加 密和解密来实现。从信息论的观点出发，“加密”可视为增熵 的过程，“解密”可视为减熵的过程。
5.1 编码器
信源编码理论是信息论的一个重要分支，其理论基础是信源编 码的两个定理。 无失真信源编码定理：是离散信源/数字信号编码的基础； 限失真信源编码定理：是连续信源/模拟信号编码的基础。
5.1 编码器
信源编码：以提高通信有效性为目的的编码。通常通过压缩信 源的冗余度来实现。采用的一般方法是压缩每个信源符号的平 均比特数或信源的码率。即同样多的信息用较少的码率传送， 使单位时间内传送的平均信息量增加，从而提高通信的有效性。

信源编码

信源编码

S {S1, S2 ,..., Sq}
编码器
C :{W1,W2 ,...,Wq}
X {x1, x2,..., xr}
wi 称为码字，Li为码字wi 的码元个数，称为码字wi 的码字 长度，简称码长。
第二节 码的分类
1、二元码： 码符号集X={0,1}，如果要将信源通过二元信道传输，必
须将信源编成二元码，这也是最常用的一种码。 2、等长码：
第八章 信源编码
1 引言 2 等长信源编码定理、变长信源编码定理
3 各种编码 4 有噪信道编码定理
5 联合信源信道编码定理
第五章 有噪信道编码
第一节 错误概率与译码规则 第二节 错误概率与编码方法 第三节 有噪信道编码定理 第四节 联合信源信道编码定理 第六节 纠错编码的基本思想 第七节 常用编码方法
l H (S) 2
N log r
则不可能实现无失真编码，当N趋向于无穷大是，译码错 误率接近于1。
第三节 等长信源编码定理
•定理4.3的条件式可写成： l log r NH (S)
左边表示长为 l 的码符号所能载荷的最大信息量， 而右边代表长为N的序列平均携带的信息量。因此， 只要码字传输的信息量大于信源序列携带的信息量， 总可以实现无失真编码 。
信源编码的分类：离散信源编码、连续信源编码和相关信源编 码三类。 离散信源编码：独立信源编码，可做到无失真编码； 连续信源编码：独立信源编码，只能做到限失真信源编码； 相关信源编码：非独立信源编码。
第二节 码的分类
编码器可以看作这样一个系统，它的输入端为原始信
源S，其符号集为S {S1, S2,..., Sq}；而信道所能传输的符号集 为 X {x1, x2,..., xr} 编码器的功能是用符号集X中的元素，将 原始信源的符号 Si 变换为相应的码字符号wi ，所以编码器 输出端的符号集为 C :{W1,W2,...,Wq}

信息论：第5章 无失真信源编码定理

信息论：第5章 无失真信源编码定理
19
(4)非奇异码 若一组码中所有码字都不相同(即所有信源符 号映射到不同的码符号序列)，则称为非奇异码。
si s j Wi W j
则称码C为非奇异码。
si , s j S Wi ,W j C
20
（5）奇异码
若一组码中有相同的码字，则为奇异码。
si s j Wi W j
30
即时码（异前缀码）一定是唯一可译码。因为，如果没 有一个码字是其他码字的前缀，则在译码过程中，当收到一 个完整码字的码符号序列时，无需考虑下一个符号，就能直 接把它译成对应的码字或信源符号。
31
32
33
5.2
等长码
一般说来，若要实现无失真的编码，这不但要求 信源符号与码字是一一对应的，而且要求码符号序 列的反变换也是唯一的。也就是说，所编的码必须 是唯一可译码。否则，所编的码不具有唯一可译码 性，就会引起译码带来的错误与失真。
11
超过信宿的灵敏度和分辨力所传送的信息是毫无 意义的，也是完全没有必要的。 比如话声信源，界别过多的划分，人耳就很难分 辨。图像信源亦是如此，人们看电影，当图片超过每 秒25张以上时，人眼就能将离散的照片在人脑内反映 成连续画面。
此时，就应该引入限定失真条件下的信源编码问题 。
12
5.1
编码器
32272781179同样可以求得信源序列长度增加到3和4时进行变长编码所得的编码效率和信息传输率分别为如果对这一信源采用等长二元码编码要求编码效率达到96允许译码错误概率105则可以算出自信息方差为98580需要的信源序列长度为可以看出使用等长编码时为了使编码效率较高96需要对非常长的信源序列进行编码且总存在译码差错
此式表明，只有当 l长的 S s1 , , sq ，有 q 个符号，那么它的N次扩展信 码符号序列数大于或等于N次 源 S N 1 , , N 共有 q N 个符号。 q 扩展信源的符号数时，才可

数据压缩与编码

数据压缩与编码

数据压缩与编码数据压缩是计算机科学中十分重要的技术，它能够减小数据存储和传输的需求，提高计算性能和效率。

数据编码是数据压缩的重要手段之一，通过将原始数据转换为更紧凑的形式，以达到减小数据量的目的。

本文将讨论数据压缩与编码的原理、方法和应用。

一、数据压缩与编码的原理数据压缩的核心原理是利用数据中的冗余性，即数据中存在的重复、无用或冗长的部分。

通过剔除这些冗余部分，可以实现数据的压缩。

数据编码则是将原始数据转换为更紧凑的表示形式的过程。

数据压缩与编码的关键在于寻找合适的编码方式。

常见的编码方式包括无损编码和有损编码。

无损编码是指压缩后能够完全还原出原始数据，而有损编码是在压缩过程中会引入一定的信息丢失。

二、数据压缩与编码的方法1. 无损编码方法无损编码方法的目标是通过各种算法和技术，将原始数据转换为紧凑的表示形式，同时保证能够完全还原出原始数据。

常见的无损编码方法有：- 霍夫曼编码：基于出现频率的统计信息，为出现频率高的符号分配较短的编码，从而实现压缩效果。

- 标记编码：将数据中的重复内容用较短的标记表示，例如字符串中的重复字符序列可以用一个标记代替。

- 字典压缩：使用字典存储常见的字符串或字符序列，并用较短的索引值代替原始数据中相应的部分。

2. 有损编码方法有损编码方法在压缩数据的同时会引入一定的信息丢失，但可以通过合理的算法设计控制信息丢失的程度，从而在压缩率和数据质量之间取得平衡。

常见的有损编码方法有：- 基于变换的压缩：通过对原始数据进行变换，从频域或空域的角度提取数据的特征，并将特征编码以降低数据量。

- 预测编码：通过建立数据之间的统计关系，并用预测值代替原始值，从而减小储存或传输所需的数据量。

三、数据压缩与编码的应用数据压缩和编码技术广泛应用于各个领域。

以下是几个常见的应用示例：1. 图像压缩：在数字图像处理中，采用基于变换的压缩方法，如JPEG格式，对图像数据进行编码压缩。

通过适当的压缩参数设置，可以在保证图像质量的前提下减小图像文件的大小。

信源编码

信源编码

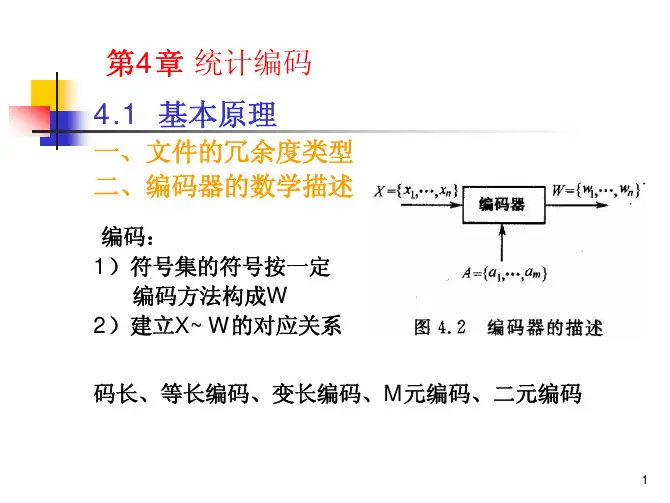
1.信源编码信源编码包括无失真信源编码和有失真信源编码，其中，无失真信源编码就是我们所说的Shannon第一定理。

有失真信源编码对于模拟信号来说就是模拟信号的数字化过程，对于数字信号来说，就是一种“舍小放大”的过程。

1.1.Shannon第一定理（无失真）这种编码能达到压缩需要传输的码元总量的目的，但是，其本质是对信息冗余度的压缩，信息没有任何的损失，失真压缩（编码）就不是如此了，其信息是有损失的。

1.1.1.平均码长Vs编码效率对于等长编码，其平均码长就是等长编码的码长。

对于不等长编码，其平均码长就是每一个码字之码长的数学期望。

平均码长是衡量一个编码方案好坏的标尺。

1.1.2.Shannon第一定理无失真信源编码定理：对于一个信源S，我们要想对其实现无失真信源编码，则必须满足下面不等式：对于任何一个编码，都对应一个编码效率很明显，编码效率越高越好且编码效率永远小于或者等于1，我们希望编码效率在小于1的前提情况下，尽量的接近1。

Shannon第一定理包括了等长编码定理和不等长编码定理。

这个定理的证明过程相对简单。

1.1.3.Shannon编码1.1.4.Huffman编码％来源网络，调试通过 2009-4-22function [h,l]=huffman(p)if (length(find(p<0))~=0)error('Not a prob,negative component');endif (abs(sum(p)-1)>10e-10)error('Not a prob.vector,component do not add to 1')endn=length(p);q=p;m=zeros(n-1,n);for i=1:n-1[q,l]=sort(q);m(i,:)=[l(1:n-i+1),zeros(1,i-1)];q=[q(1)+q(2),q(3:n),1];endfor i=1:n-1c(i,:)=blanks(n*n);endc(n-1,n)='0';c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:) ==1)));c(n-i,n)='0';c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1';for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(m(n-i+1,:)==j+1)-1)+1:n*find (m(n-i+1,:)==j+1));endendfor i=1:nh(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32));endl=sum(p.*ll);1.1.5.Fano编码％调制通过，但是代码太杂、太乱，需要发时间整理。

第五章信源编码(编码定义及定长编码)

第五章信源编码(编码定义及定长编码)
【例】对学生的成绩等级进行编码，分为优、良、 中、差4个 等级。
信源符号集X＝[a1,a2,…an]={优、良、中、差} 用二元码，码符号集合为{0,1} 码字集合为 Y=[W1,W2,…Wn]={00,01,10,11}
编码过程：00代表优，01代表良，10代表中，11代 表差。每一个码字都是2个码符号组成的序列。
解码：按照码符号的顺序，从根节点依次查询到终端节点，就得到对应的 信源符号。再从根节点对剩下的码符号序列做相同的处理，直到处理完码 符号序列中所有的码符号
对应表中的码4分析
A
0
1
0
1
1
0
0
1
0
10 1
0
1
000
001 010
011 100 101 110
111
一阶节点 二阶节点 三阶节点
唯一可译码存在的充要条件
下面，首先求得独立等概率情况，即
H 0 log2 27 4.76bit
其次，计算独立不等概率情况，
27
H1 pi log pi 4.03bit
i 1
再次，若仅考虑字母有一维相关性，求H2
H2 3.32bit
最后，利用统计推断方法求出，由于采用的逼近的方法和 所取的样本的不同，推算值也有不同，这里采用Shannon 的推断值。 H 1.4bit
冗余度
定义：衡量信源发出消息时包含了多余信息的物 理量
来源：
1.信源符号的相关性。相关程度越大，信源的实 际上越小，越趋向于H∞（X） 。
2.信源符号分布的不均匀性。等概率分布时信源 熵最大，不均匀分布时，信源熵减小。当各符号 之间不存在依赖关系且为等概率分布时，信源实 际熵趋于最大熵H0（X）

数据压缩与编码

数据压缩与编码

数据压缩与编码1. 引言在信息科学与技术的发展中，数据的处理和传输变得越来越重要。

为了有效地利用存储空间和传输带宽，数据压缩技术应运而生。

数据压缩通过减少信息的冗余程度，从而实现数据量的减小。

数据压缩与编码是数据处理中的关键环节，本文将探讨数据压缩与编码的原理和应用。

2. 数据压缩的原理数据压缩是通过消除数据中的冗余信息来减小数据量。

常见的数据压缩方法包括无损压缩和有损压缩。

2.1 无损压缩无损压缩是指在压缩数据的同时不丢失任何信息。

无损压缩方法主要有以下几种：- 字典压缩：基于字典的数据压缩算法是一种常用的无损压缩技术。

其原理是构建一个字典，将重复出现的数据块用较短的编码表示。

- 霍夫曼编码：霍夫曼编码是一种根据字符出现频率构建的最佳二叉树。

通过将频率较高的字符用较短的编码表示，从而实现数据压缩。

- 预测编码：预测编码是根据已知数据预测下一个数据的值，然后用较短的编码表示与预测值的偏差。

预测编码适用于存在较强相关性的数据。

2.2 有损压缩有损压缩是指在压缩数据的过程中丢失一部分信息。

有损压缩方法主要应用于音频、图像和视频等多媒体数据的处理中，以满足数据传输和存储的需求。

有损压缩方法包括以下几种：- 变换编码：变换编码是将数据从时域转换到频域，并利用频域特性来减小数据量。

离散余弦变换（DCT）是一种常用的变换编码方法。

- 量化编码：量化编码是通过对数据进行精度的降低来减小数据量。

在图像和视频压缩中，使用了基于人眼视觉特性的量化编码方法。

- 渐进传输编码：渐进传输编码是指在传输过程中，先发送粗略的图像或音频，然后逐渐细化。

这种编码方法可以提供更好的用户体验，并降低传输带宽需求。

3. 数据编码的原理数据编码是将数据转换成特定的格式，以便于传输、存储和处理。

数据编码的原理主要包括以下几点：3.1 字符编码字符编码是将字符转换为二进制形式的编码方式，常见的字符编码包括ASCII码、Unicode和UTF-8等。

数据压缩统计编码

数据压缩统计编码
32
4.6基于字典的编码
LZW: Terry A. Welch 标识只有一项，指向字典的指针。 A Technique for High-Performance Data Compression(IEEE,1984) LZW编码算法是先建立初始字典，再分解输入流为 短语词条，这个短语若不在初始字典内，就将其存 入字典，这些新词条和初始字典共同构成编码器的 字典。而初始字典可由信源符号集构成，每个符号 是一个词条。更一般的，可将扩展的ASCII码存入 初始字典，使其成为字典的前256项。
4.3 Golomb编码与通用变长码
三、 指数Golomb编码
构成：G(0)+q+m位尾码
16
4.3 Golomb编码与通用变长码 四、通用变长码
把q位信息尾码交错嵌 入到q+1位前缀码 中。
17
4.4 游程编码
一、基本的游程编码及分析 二、黑白图像的游程编码
如：传真（黑白） 组合基干码和结尾码组成
其中：P (ai ) p (ak )
k 1 i 1
例 4-12 S={a,b,c,d,e,!}
dead!
20
4.5 算术编码
例 4-12
编码过程 解码过程

编解码模式： 静态模式： 动态模式（自适应模式）：
根据已编码符号的频率决定下一个符号的编码。 无需事先进行符号的概率统计，无需为解码预先保存 任何信息，符号出现的频率是根据内容的变化动态得到 的，更符合符号的局部分布规律。
33
4.6基于字典的编码

编码器逐个输入字符，累积串联成一个字符串， 即“短语”I。 若I是字典中已有的词条，输入下一个字符x。 当I在字典内，Ix不在字典内时，编码器首先输出 指向字典内词条I的指针（即I的相应码字）；再 将Ix作为新词条存入字典，并为其确定顺序号； 然后把x赋给I，当作新词条的首字符。 重复上述过程，直到输入流都处理完为止。

无失真信源编码定理和信息处理

无失真信源编码定理和信息处理
20
（5）奇异码 若一组码中有相同的码字，则为奇异码。
si s j Wi W j
si , s j S Wi ,Wj C
则称码C为奇异码。
21
信源符号
a1 a2 a3 a4
概率
p(ai )
1/2
1/4
1/8
1/8
编码1 00 01 10 11
编码2 编码3 编码4 编码5
0
0
0
第5章 无失真信源编码定理
赵越 2012.10.
通信的实质是信息的传输。 高效率、高质量地传送信息却又是信息传输的基
本问题！ 这就需要解决两个问题： 第一，在不失真或允许一定失真的条件下，如何
用尽可能少的符号来传送信源信息； 第二，在信道受干扰的情况下，如何增加信号的
抗干扰能力，同时又使得信息传输率最大。 为了解决这两个问题，就要引入信源编码和信
13
一、编码器模型 由于信源编码可以不考虑抗干扰问题，所以它的
数学模型比较简单。
14
• 输入是信源符号集: S {s1, s2 , , sq} • x为编码器所用的编码符号集，包含r个元素
{ x1, x2 ,..., xr }，称为码符号(码元) 。
• 由码符号 xi组成的输出序列 Wi 称为码字。
对于等长码来说，若等长码是非奇异码， 则它的任意有限长N次扩展码一定也是非奇异 码。因此等长非奇异码一定是唯一可译码。
34
信源符号 码1 码2
s1
00 00
s2
01 11
s3
10 10
s4
11 11
表5.3中，码2显然不是唯一可译码。而码1是等长非 奇异码，因此它是唯一可译码。

第五章 无失真信源编码定理

第五章 无失真信源编码定理
则不可能实现无失真编码。
第三节 等长信源编码定理
•定理5.3的条件式可写为：
长为l 的码符号所能 载荷的最大信息量 长为N的序列平均携带的信息量
l log r > NH ( S )
只要码字传输的信息量大于信源序列携带的 信息量，总可以实现无失真编码。 l •定理5.3的条件式也可写成： log r H ( S ) e N
i
N
1
2
N
是一一对应的：
i Bi (Wi1 ,Wi2 , ,WiN ), i S ,Wil C
N
4）惟一可译码 若任意一串有限长的码符号序列只能被惟 一地译成所对应的信源符号序列，则此码称 为惟一可译码（或称单义可译码）；否则就 称为非惟一可译码或非单义可译码。
例：对于二元码 C1 {1, 01, 00} ，当任意给定一串 码字序列，例如“10001101”，只可唯一地划 分为1,00,01,1,01，因此是惟一可译码；而对 另一个二元码 C 2 {0,10, 01} ，当码字序列为 “01001”时，可划分为0,10,01或01,0,01，所 以是非惟一可译的。
P(G eN )
-
(2) 若 i (si1, s i2 ,...,s iN ) GeN，则 2 - N [ H ( s )e ] < P( i ) < 2 - N [ H ( s ) -e ] (3) || GeN || 表示e典型序列集中 e典型序列的个数，则 (1 - )2 N [ H ( s )-e ] <|| GeN ||< 2 N [ H ( s ) e ]
1 N - log P ( si ) 以概率收敛于均值 H ( s ) 熵定义 N i 1 1 N 1 即 - log P ( s i ) - log[ P ( s i ) P ( s 2 ) L P ( s N )] N次扩展信源 N i 1 N 1 - log P ( si s 2 L s N ) H ( S ) 以概率收敛 N 因为 i1 ( si1 si 2 L s i N ) S1 S 2 L S N , (i 1, 2 , L , q N i1 , i2 , L , i N 1, 2 , L , q )

信源编码的原理

信源编码的原理

信源编码的原理
信源编码是指将源数据进行编码，以便在传输和存储时占用更少的空间。

信源编码的原理是通过利用信源的统计特性来进行编码，使得编码后的数据长度更短，从而达到压缩的效果。

信源编码的方法有很多种，其中较为常见的有霍夫曼编码、算术编码、字典编码等。

霍夫曼编码是一种基于最优化原则的编码方法，它通过构造哈夫曼树来确定每个符号的编码，使得出现频率高的符号的编码长度更短，从而达到压缩的效果。

算术编码是一种通过将一段数据映射到一个区间内来进行编码的方法，它可以实现无损压缩，并且编码后的数据长度可以接近信源的熵。

字典编码是一种基于字典的编码方法，它通过将出现频率高的字符串映射到较短的编码，从而实现压缩的效果。

不同的信源编码方法有着不同的适用范围和优缺点，根据具体的应用场景来选择合适的编码方法可以达到更好的压缩效果。

- 1 -。

第4章信源压缩编码基础

第4章信源压缩编码基础
r
r
L
– 注意:虽然与在数值上相同，但它们的单位不同，编码 效率没有单位，而信息传输率的单位是比特/码符号。
20
• 为了使得平均编码长度为最小，必须将概率大
的信息符号编以短的码字，概率小的符号编以
长的码字。能获得最佳码（或次最佳码）的编
码方法有很多。
• 香农(shannon) 编码、费诺(Fano) 编码、霍夫 曼(Huffman)编码等就是代表。
• 解: 码的性能分析： 通过计算可得此信源的熵:
H ( X ) p(ai ) log p(ai ) 2.61
i 1 7
(比特／符号)
而码的平均长度:
L
p (a
i 1
7
i
)l i 3.14
(二元码符号／符号)
编码效率：
0.831
2 费诺码
• 费诺编码属于概率匹配编码，但它一般也不是最
•
30
• 费诺码具有如下的性质：
①费诺码的编码方法实际上是一种构造码树的方法，所以费诺码是即时码。 ②费诺码考虑了信源的统计特性，使概率大的信源符号能对应码长较短的
码字，从而有效地提高了编码效率。
③费诺码不一定是最佳码。因为费诺码编码方法不一定能使短码得到充分 利用:当信源符号较多时，若有一些符号概率分布很接近时，分两大组的组 合方法就会很多。可能某种分大组的结果，会使后面小组的“概率和”相 差较远，从而使平均码长增加。
S s1 p( s ) 0.4 i
s2 0.2
• 33
• 例:对离散无记忆信源
进行霍夫曼编码。 解:编码过程如表所示： 1)将信源符号按概率大小由大至小排序。 2)从概率最小的两个信源符号和开始编码，并按一定的 规则赋予码符号，如下面的信源符号（小概率）为“1”， 上面的信源符号（大概率）为“0”。若两支路概率相等， 仍为下面的信源符号为“1” 上面的信源符号为“0”。 3)将已编码两个信源符号概率合并，重新排队，编码。 4)重复步骤3）直至合并概率等于“1.0”为止。 5)从概率等于“1.0”端沿合并路线逆行至对应消息编码.

第5章_信源—信道编码定理

第5章_信源—信道编码定理

这种编码方法，可以看成是一种特殊的试验信道
1 P (v j / ui ) 0
d (C )

v j C , v j f (ui ) v j f (ui )
1 N
P (U ) d [ u , f ( u )]
U
1 1 1 [0 1 1 1 0 1 1 1] 3 8 4
要使信源在此二元信道中传输，必须对X进行二元编码：
x1 C1 C2 000 0000
x2 001 0001
x3 010 0010
H (X ) 3
H (X ) 4
x4 011 0011
x5 100 0100
x6 101 0101
对于码 对于码
C1
R1
0 .6 4 6
(比特／信道符号) (比特／信道符号)
第5章
信道—信源编码定理
通用通信系统
其中：编码器包括信源编码和信道编码两个部分； 译码器包括信道译码和信源译码两个部分； 信道为有噪信道。
•信道编码 •给定信道输入符号集AX； •给定信道输出符号集AY； •对每个输入符号x，存在一个非负实数b(x)，为传输x的 代价。 定义n阶容量—代价函数：
信息率为1/3，而平均失真为1/4，根据香农第三定理， 若允许失真D=1/4时，总可以找到一种编码，使信息输出 率达到极限R(1/4)
1 1 R ( ) 1 H ( ) 0 .1 8 9 4 4
信源—信道匹配
• 当信源与信道相连接时，其信息传输率并未 达到最大. • 希望能使信息传输率越大越好，能达到或尽 可能接近于信道容量, 信息传输率接近于信道 容量只有在信源取最佳分布时才能实现。 • 由此可见，当信道确定后，信道的信息传输 率与信源分布是密切相关的。当达到信道容 量时，我们称信源与信道达到匹配，否则认 为信道有剩余。

信息论基础——联合信源—信道编码定理

信息论基础——联合信源—信道编码定理
n n r
P U W P g Y U

n r

n
U n W n 2

b
要证对任何使 P n 0 n 的复合码，其编码函数为
n X n U n f U :
Un
n x
ˆ 译码函数为 g Y n : y n u n ，则必有 H U C


ˆ ① U n X n Y n U n 构成马氏链，
ˆ ②数据处理不等式保证了 I U n ;U n I X n ; Y n
13


第四章 信道编码定理
令 n , Pe
n
1 0, 0 ，从而 H U C 成立. n
说明
定理表明使用一步编码方案可以使通信的误差 概率任意小. 对于同一个通信系统，现在有两种数据处理方 案.
第四章 信道编码定理
例G1：整数全体，按通常加法构成群，这是一个无限群.
例G2：二元集{0,1}，对其上定义的模2加法,构成一个群.
0 0 1 1 0mod 2, 0 1 1 0 1mod 2
31
第四章 信道编码定理
二、 域 域在编码理论中起着关键作用； 域是定义了两种代数运算的系统.
19
第四章 信道编码定理
两步编码与一步编码
信道输入端只是一系列二元码 ↔信道编码只需针对信道特性进行，不用 考虑信源的特性； 以纠正信道带来的错误，做到有效又可 靠地传输信息. 大大降低通信系统设计的复杂度！
20
第四章 信道编码定理
两步编码与一步编码
经典的无线通信系统是将信源编码和信道编码分别进行的。信源 编码主要考虑信源的统计特性，信道编码主要考虑信道的统计特 性。 • 优点是设计简单、通用性好，可以分别形成标准。 • 缺点是没有充分利用各自的优势，因而不是最佳的。 • 无线系统的信源编码由于压缩比很高，对差错十分敏感；而信道 编码面临十分恶劣的传播环境，但提供的带宽冗余度很小。 在这种背景下，需要将信源编码和信道编码综合考虑。这就是联 合编码的基本思路。 • 在无线多媒体通信中，联合编码是抗衰落的一种十分有效的措施。

信源编码1

信源编码1
19
即时码的构造－树图法
对于m进制树图，有树根、树枝和节点。 树图最顶部的节点称为树根； 每一个分支称为树枝； 树枝的尽头称为节点，每个节点生出的树枝数目
等于码符号数m； 从树根到终端节点各树枝代表的码符号顺次连接，
就得到了编码码字。
20
m＝2的二进制树图
A
0
1
0
1
1
0
0
1
0
10 1
0
1
10 001 00 00
x4
p(x4)
11 111 11 10
9
定长码和变长码
根据码长，可分为两类： 定长码：
码中所有码字的长度都相同， 如上表中的码1
变长码：
码字长短不一，即码符号个数不同， 如上表中的码2
10
L次扩展码
设 得 Wxi,i有到i的=信代集1,源码合2,集组，…合C码,n＝X字一＝[WW一[xii对,,iii,==应i=11的1,,22,。2,,……,…,,nn,n]是，]和经代原信码始源组信编C源是码符码后号字， L次无记忆扩展信源概念引伸就可以得到L次扩展码。 信源X的L次扩展信源为XL＝[αj，j＝1,2,…nL ]。
hx0811096??510???123144xxxp???????????????2272003404741310ihxhxxdixxl???????????????由得37引入变长编码?定长编码在理论上可以达到很高的编码效率但是从上例中可以看到在编码效率错误概率要求较高的情况下扩展次数l需要非常大这在实际工程中是无法实现的
L
则当L足够大时，必可使译码差错小于δ。
反之，若 K log m X 2
L
则当L足够大时，译码错误概率趋于1。

信源编码

信源编码

应用
表1信源编码实例表以简单的数据压缩为例即可说明信源编码的应用。若有一离散、无失真、无记忆信源，它 含有五种符号U0～U4及其对应概率Pi，对它进行两种编码：等长码和最佳哈夫曼码（见表1）。
其中，等长码的平均码长：=3，即三位码。若采用哈夫曼编码，平均码长，即不足两位码。这就是说，数据 压缩了以上。
另外，在数字电视领域，信源编码包括通用的MPEG—2编码和H.264（MPEG—Part10 AVC）编码等。
相应地，信道编码是为了对抗信道中的噪音和衰减，通过增加冗余，如校验码等，来提高抗干扰能力以及纠 错能力。
定理
不同类型的信源，是否存在有每种信源的最佳的信源编码，这通常是用信源编码定理来表示。最简单、最有 实用指导意义的信源编码定理是离散、无记忆型信源的二进制变长编码的编码定理。它证明，一定存在一种无失 真编码，当把N个符号进行编码时，平均每个符号所需二进码的码长满足。
信源编码
以提高通信有效性为目的而对信源符号 进行的变换，或者说为了减少或消除信
源冗余度而进行的信源符号变换
01 编码结果
03 方式
目录
02 作用 04 定理
目录
05 分类
07 通信系统模型
06 应用 08 专业表述
信源编码是一Βιβλιοθήκη 以提高通信有效性为目的而对信源符号进行的变换，或者说为了减少或消除信源冗余度而进 行的信源符号变换。具体说，就是针对信源输出符号序列的统计特性来寻找某种方法，把信源输出符号序列变换 为最短的码字序列，使后者的各码元所载荷的平均信息量最大，同时又能保证无失真地恢复原来的符号序列。
通信系统模型
[信源]->[信源编码]->[信道编码]->[信道传输+噪声]->[信道解码]->[信源解码]->[信宿] 一般信息论的书上都会有信源编码和信道编码的具体讲解，包括具体的编码方法。

编码理论第4章

编码理论第4章

4.1.2 信源编码器 为了简化问题，研究无失真编码时，只考虑信源和信宿两个主要因素，这样 信息传输系统模型变为图4-1所示。
u1
信源
u2 un
信源编码器
w1 a1 w2 a 2

信道
信源译码器
信宿
wn a r
图4-1 简化信息系统传输模型
概念 信源符号 二元信源 n元信源 码符号集
码符号 码元 码字 码组 码长
4.2 无失真信源编码原理
• 4.2.1 等长码及其编码定理 • 4.2.2 变长码的平均码长及编码效率
• 对n元基本离散信源，设编码后各码字的码长分别为l1 ,l2 ,…，ln, 则定义码的平均码长度为
L p(ui )（码符合/ 信源符号） li
i 1
n
• 编码的效率η为
H m (U ) L
符号 概率 u 1 0 .4 u2 u3 u4 u5 0 .2 0 .2 0 .1 0 .1
0 1
码字
码长 2 2 2 3 3
0 .4 0 .2 0 .2 0 .2
0 1
0 .4 0 .4 0 .2
0 1
0 .6 0 .4
0 1
1 .0
00 10 11 010 011
(a)
图5-2 例5-2 两种霍夫曼编码
• 4.1.6 即时码的树图构造 • 树图法是构造即时码的一种简单方法。树是n个 结点的集合，这n个结点中有且仅有一个作为根 的结点，其余的结点可分为m个互不相交的子集， 每个子集本身又是一棵树，称为根的子树，也叫 根的树枝数。 • 树图与信源符号编码之间对应关系： • 树根 码字的起点 • 树的度 码的进制数 • 分支结点 码的符号的一部分 • 终端结点 待编码符号 • 满树 等长码 • 非满树 变长码
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

12.5%
10%
2.5%
解： 符号
A B C D F 合计：
概率p
0.25 0.5 0.125 0.1 0.025 1
自信息 log(1/p)
2 比特 1 比特 3 比特 3.32 比特 5.32 比特
该符号对总的信息 量的贡献 plog(1/p) 0.5 比特 0.5 比特 0.375 比特 0.332 比特 0.133 比特 1.84 比特
LN log r
例题
对于给定信源，分别对它发送的单符号序列和2符号序列进行编码，并计算 其编码效率。
L H(X) 1 log r
定理3 变长无失真信源编码定理（香农第一定理） 设离散无记忆信源的符号集合为{w1, w2, ......, wq}，信源发出N重符号序列，则此信源
l 可以发出 q N 个不同的符号序列，其中各符号序列的码长为 i ，发生概率为 pi ，其
中 0 i q N 。N重符号序列的熵为H(X)。N重符号序列的平均码长为
13
在书面英语中每1000个字母中各个字母的出现次数：
14
If the duration of a dot is taken to be one unit then that of a dash is three units. The space between the dots and dashes within one character is one unit, that between characters is three units, and that between words seven units. Space is not considered a character, as it is in ASCII.
信源编码
无失真信源编码
限失真信源编码
信源编码
也就是压缩编码，是利用减少冗余的方法来实现对消息序列 的压缩，从而在信宿端可接受的情况下，减少需要传输的信息 量，从而提高传输效率。
例题 某门课程的学生成绩分布如下，求每个成绩等级代表符号A, B, C, D, F所包含的信息量。
A
B
C
D
F
25%
50%

平均码长
M 1
L pm Lm
m0
编码效率
H ( A)
L
6
n
where pi 1 i 1
定长码 变长码
例题
symbol
a0
a1
Probability
ห้องสมุดไป่ตู้
0.5
0.3
Code word
0
10
a2
a3
0.15
0.05
110
111
8
例题
<ai,aj> a0,a0 a0,a1 a0,a2 a0,a3 a1,a0 a1,a1 a1,a2 a1,a3
H(X) R H(X)1
20
例题 对信源符号集合{x1, x2, x3, x4}进行二进制编码，对应的l1=1, l2=2, l3=2, l4=3。这种码是前缀码吗？
解： 根据Kraft不等式，可以得到
4 2li 21 22 22 23 9 1
i 1
8
可见不满足Kraft不等式的条件，因此这种码不是前缀码，不是唯一可译的。
定理 平均码长界定定理 （r进制编码，单符号序列） 对一个存在有限熵H(X)的离散信源进行r进制变长编码。
1. 任意一种唯一可译码的平均码长 L 都满足
L H(X) log r
2. 一定存在唯一可译码，其平均码长 L
满足：
18
定理 Kraft 不等式
对于码字符号集合 {w1, w2 ,, wq} ，其中各符号的码长
为 li ， 0 i q 。则存在一种码长为 l1 l2 lq
而且满足前缀条件的r进制编码的充分必要条件是
q
rli 1
i1
19
信源编码定理
Let X be the set of letters from a DMS with finite entropy H(X) and xk, k=1,2,…,L. the output symbols occurring with probabilities P(xk). Given these parameters, it is possible to construct a code that satisfies the prefix condition and has an average length R that satisfies the inequality
也就是熵
信源符号 a1 a2 a3 a4
二进制表示 00 01 10 11
信源符号 a1 a2 a3 a4 a5 a6 a7 a8
二进制表示 000 001 010 011 100 101 110 111
对于离散信源空间
A P( A)


a1, p1,
a2,, an p2,, pn
11
ASCII码 (The American Code for Information Interchange)
12
Morse 电码
hello
SOS
The Morse telegraph. (Image courtesy of the U.S. National Library of Medicine.)
Pr<ai,aj> bm
.25
00
.15
100
.075
1100
.025
11100
.15
101
.09
010
.045
0110
.015
111100
<ai,aj> a2,a0 a2,a1 a2,a2 a2,a3 a3,a0 a3,a1 a3,a2 a3,a3
Pr<ai,aj> bm
.075
1101
.045
0111
16
用变长码编码符号序列：“ABADCAB”。
编码1：
letter A B C D
codeword 00 010 011 100
letter E F G H
Codeword 101 110 1110 1111
编码1的编码结果: 00 010 00 100 011 00 010 , 总长度 = 18比特
.0225
111110
.0075
1111110
.025
11101
.015
111101
.0075
11111110
.0025
11111111
9
例题
A 25% 01
B 50% 1
C 12.5% 001
D 10% 0001
F 2.5% 0000
10
BCD码 （Binary coded decimal）
Digit 0 1 2 3 4 5 6 7 8 9 code 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
qN
LN p jl j j 1
对此信源进行r进制编码，总可以找到一种无失真信源编码方法，构成唯一可译码，满足：
H ( X ) LN H ( X ) 1 log r N log r N
当N趋于无限大时，有：
lim LN H (X )
N N
这种编码的编码效率为：
H(X)
15
例题 Code the series of letters: “ABADCAB”.
FLC:
letter A B C D
codeword 000 001 010 011
letter E F G H
Codeword 100 101 110 111
FLC result: 000 001 000 011 010 000 001 , total bits = 21
编码2：
Letter A B C D
codeword 0 1 00 01
letter E F G H
Codeword 10 11 000 111
17 编码2的编码结果: 0 1 0 01 00 0 1 , 总长度 = 9比特
前缀码： 如果在一个码字集合中，没有任何一个码字是其他码字的前缀，这样的码字集合就称为前缀码。 前缀码也被称为唯一可译码，或即时码。