几何体的切接球

如何求解立体几何形的内切球和外接球立体几何形的内切球和外接球是数学和几何学中常见的概念。

内切球是指一个球体正好与该立体几何形相切于内部的球，而外接球则是指一个球体正好与该几何形相切于外部的球。

解决这个问题需要一些几何知识和计算技巧。

一、立方体首先，让我们以立方体为例，来讨论如何求解其内切球和外接球。

立方体是一个六个面都是正方形的立体，所有的边长相等。

立方体的内切球和外接球的半径可以通过简单的计算得到。

1. 内切球内切球的半径等于立方体的半边长。

设立方体的边长为a，则内切球的半径r等于a/2。

这是因为内切球的半径与立方体的棱长之比为1:2。

2. 外接球外接球是一个球体，它与立方体的八个顶点相切。

设立方体的边长为a，则外接球的半径R等于立方体对角线的一半。

根据勾股定理，立方体的对角线的长度d等于a√3。

因此，外接球的半径R等于d/2，即R等于a√3/2。

二、圆柱体对于圆柱体来说，内切球和外接球的求解稍微复杂一些。

1. 内切球内切球的半径等于圆柱体的半径。

设圆柱的半径为r，高度为h，则内切球的半径r'等于r。

2. 外接球外接球是一个球体，它与圆柱体的底面相切。

设圆柱的半径为r，高度为h，则外接球的半径R等于圆柱体的斜高。

根据勾股定理，圆柱体的斜高等于√(h^2 + r^2)。

因此，外接球的半径R等于√(h^2 + r^2)。

三、球体球体的内切球和外接球的求解相对简单。

1. 内切球球体的内切球的半径等于球体的半径。

设球体的半径为R，内切球的半径r等于R。

2. 外接球外接球是一个球体，它与球体的表面相切。

设球体的半径为R，则外接球的半径R'等于2R。

结论：通过以上讨论，我们可以得出以下结论：1. 对于立方体来说，内切球的半径等于边长的一半，外接球的半径等于对角线长的一半。

2. 对于圆柱体来说，内切球的半径等于半径，外接球的半径等于斜高。

3. 对于球体来说，内切球的半径等于半径，外接球的半径等于半径的两倍。

球与各种几何结构切、接问题专题在几何学中，球是一种广泛应用的基本几何形状。

由于球的圆滑性和对称性，与其他几何结构的切和接问题成为了一个专题。

本文将讨论球与各种几何结构的切和接问题，并探讨其中的一些关键概念和方法。

1. 球与平面的切、接问题首先，我们来探讨球与平面的切和接问题。

当一个平面与球相交时，可能会出现以下几种情况：- 平面与球相切于一个点：这种情况下，平面与球只有一个公共点，即切点。

- 平面穿过球：当平面穿过球时，会形成一个圆。

该圆称为球在平面上的截面。

- 平面与球没有公共点：这种情况下，平面与球没有任何交点。

对于球与平面的切和接问题，可以使用几何相关的原理和方法来求解。

通过计算平面与球之间的交点，可以确定切点的坐标和截面的相关属性。

2. 球与圆柱的切、接问题接下来，我们来研究球与圆柱的切和接问题。

与平面不同，圆柱具有曲面的特性。

当一个球与圆柱相交时，可能会出现以下几种情况：- 球与圆柱相切于一个点：这种情况下，球与圆柱只有一个公共点，即切点。

- 球穿过圆柱：当球穿过圆柱时，会形成一个椭圆或一个圆。

该椭圆或圆称为球在圆柱上的截面。

- 球与圆柱没有公共点：这种情况下，球与圆柱没有任何交点。

对于球与圆柱的切和接问题，我们可以计算球与圆柱之间的交点来确定切点的坐标和截面的相关属性。

通过对相交的椭圆或圆进行进一步的计算和分析，可以获得更多关于球和圆柱之间的几何信息。

3. 球与其他几何结构的切、接问题除了平面和圆柱，球还可以与其他几何结构相交，如锥、棱柱等。

在这些情况下，球与几何结构的切点和截面可以采用类似的方法来计算和确定。

需要注意的是，在实际问题中，可能还会涉及到一些特殊情况，如球与几何结构的内部切和接、球与非欧几何结构的切和接等。

针对这些特殊情况，我们需要运用更加复杂和细致的几何分析方法来求解。

4. 结论综上所述，球与各种几何结构的切和接问题是几何学中一个重要的专题。

通过运用几何相关的原理和方法，我们可以计算和确定球与各种几何结构的切点和截面，进而获得有关几何形状的相关属性和信息。

性质
内切球的球心位于旋转体 的轴线上，且球的半径等 于旋转体半径。
应用
在几何和工程领域中，内 切球常用于研究旋转体的 体积和表面积。
旋转体的外接球
定义
旋转体的外接球是指与旋 转体外侧相切的球。
性质
外接球的球心位于旋转体 外侧，且球的半径等于旋 转体轴线到旋转体外侧的 垂直距离。
应用
在几何ቤተ መጻሕፍቲ ባይዱ工程领域中，外 接球常用于研究旋转体的 空间位置和关系。
立体几何中球的内 切和外接问题完美 版
目 录
• 球与多面体的内切和外接问题 • 球与旋转体的内切和外接问题 • 球与几何体的内切和外接问题实例 • 总结与展望
01
CATALOGUE
球与多面体的内切和外接问题
多面体的内切球
01
02
03
04
多面体的内切球是指与多面 体的所有顶点和面都相切的
球。
内切球半径的求法：设多面体的 每个面为$S_i$，内切球的半径
03
CATALOGUE
球与几何体的内切和外接问题实例
多面体内切球实例
总结词
多面体内切球是指一个球完全内切于一个多面体，且与多面体的每个面都相切 。
详细描述
多面体内切球的问题可以通过几何定理和公式来解决，例如欧拉公式和球内切 定理。例如，一个正方体的内切球就是其中心，半径等于正方体边长的一半。
旋转体外接球实例
外接球的性质：外接球与 多面体的每个顶点都相切 ，且外接球的直径等于多 面体的对角线长度。
外接球的应用：在几何、 物理和工程领域中，外接 球的概念被广泛应用于研 究多面体的性质和计算。
02
CATALOGUE
球与旋转体的内切和外接问题

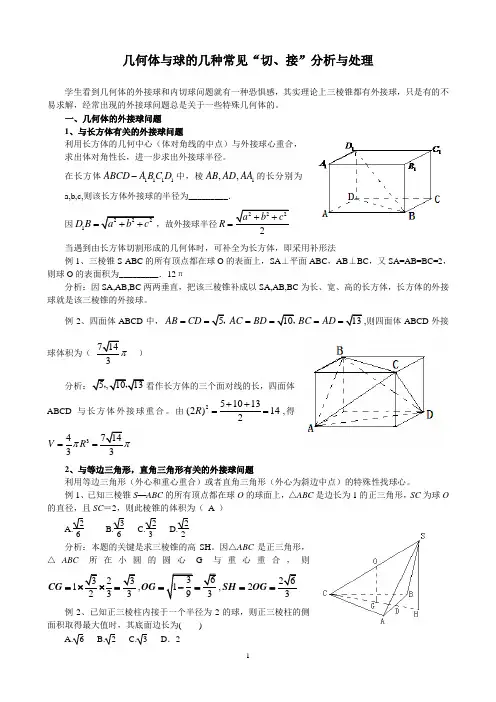
几何体与球的几种常见“切、接”分析与处理学生看到几何体的外接球和内切球问题就有一种恐惧感，其实理论上三棱锥都有外接球，只是有的不易求解，经常出现的外接球问题总是关于一些特殊几何体的。

一、几何体的外接球问题1、与长方体有关的外接球问题利用长方体的几何中心（体对角线的中点）与外接球心重合，求出体对角性长，进一步求出外接球半径。

在长方体1111ABCD A B C D -中，棱1,,AB AD AA 的长分别为a,b,c,则该长方体外接球的半径为_________． 因2221D B a b c =++，故外接球半径2222a b c R ++= 当遇到由长方体切割形成的几何体时，可补全为长方体，即采用补形法例1、三棱锥S-ABC 的所有顶点都在球O 的表面上，SA ⊥平面ABC ，AB ⊥BC ，又SA=AB=BC=2，则球O 的表面积为_________．12π分析：因SA,AB,BC 两两垂直，把该三棱锥补成以SA,AB,BC 为长、宽、高的长方体，长方体的外接球就是该三棱锥的外接球。

例2、四面体ABCD 中，5AB CD ==，10AC BD ==，13BC AD ==,则四面体ABCD 外接球体积为（ 714π ） 分析：5,1013，，看作长方体的三个面对线的长，四面体ABCD 与长方体外接球重合。

由251013(2)142R ++==,得3471433V R ππ== 2、与等边三角形，直角三角形有关的外接球问题利用等边三角形（外心和重心重合）或者直角三角形（外心为斜边中点）的特殊性找球心。

例1、已知三棱锥S —ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为（ A ）A.26B.36C.23D.22分析：本题的关键是求三棱锥的高SH 。

因△ABC 是正三角形，△ABC 所在小圆的圆心G 与重心重合，则32313CG =⨯⨯=,3619OG =-=,262SH OG == 例2、已知正三棱柱内接于一个半径为2的球，则正三棱柱的侧面积取得最大值时，其底面边长为( )A. 6B.2C. 3 D ．2解：如图，设正三棱柱底面边长为a ，∴O 2C 2＝33a ，∵OC 2＝2，∴O 2O ＝4－13a 2. ∴A 1A 2＝O 1O 2＝2OO 2＝24－13a 2 ∴三棱锥侧面积为S ＝3a ·24－13a 2＝6·13·a 2(12－a 2)≤63a 2＋12－a 22＝12 3. 当且仅当a 2＝12－a 2，a ＝6时取“＝”号3、当几何体有一定的对称性时，利用几何体的对称性找球心例、在四面体ABCD 中，AB=CD=6，BC=AC=AD=BD=5，则该四面体外接球的表面积为（ 43π ）分析：因AB=CD=6，其余各边均为5，取AB,CD 的中点F,E ；连接FC,FD,AE,BE;则几何体关于面FCD 对称，又关于面AEB 对称，故球心在两面交线EF 上，又需到A,B,C,D 四点距离相等，所以球心为EF 中点。

球与各种几何体切、接问题专题(一))近年来，高考命题中球与各种几何体的切、接问题主要以选择题、填空题为主，大题较少出现。

在此之前，需要明确两个定义：一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球；一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球。

一、球与柱体的切接。

规则的柱体，如正方体、长方体、正棱柱等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱柱的棱产生联系，然后考查几何体的体积或者表面积等相关问题。

1、球与正方体。

正方体有三种形态：内切球、棱切球和外接球。

内切球的位置关系为正方体的六个面都与一个球相切，正方体中心与球心重合，数据关系为2r=a。

棱切球的位置关系为正方体的十二条棱与球面相切，正方体中心与球心重合，数据关系为2r=2a。

外接球的位置关系为正方体的八个顶点在同一个球面上，正方体中心与球心重合，数据关系为2r=3a。

例如，对于一个棱长为1的正方体ABCD-A1B1C1D1，如果其8个顶点都在球O的表面上，那么直线EF被球O截得的线段长为2.2、球与长方体。

长方体的外接球直径是长方体的对角线。

例如，已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积为32π。

3、球与正棱柱。

正棱柱的外接球的球心是上下底面中心的连线的中点。

结论2：直三棱柱的外接球的球心位于上下底面三角形外心的连线的中点。

二、球与锥体的切接规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题。

1、正四面体与球的切接问题1）正四面体的内切球，如图4.位置关系：正四面体的四个面都与一个球相切，正四面体的中心与球心重合；数据关系：设正四面体的棱长为a，高为h；球的半径为R，这时有4R= h=6a/√3；例4：正四面体的棱长为a，则其内切球的半径为R= a/√6.解析】如图正四面体ABCD的中心为O，即内切球球心，内切球半径R即为O到正四面体各面的距离。

(2)正方体的外接球：
D A C
①球心是正方体中心； ②半径 r＝ 3 a(a 为正方体的棱长)； 2
B
题型二：棱锥的外接球
P
1.正棱锥的外接球
P
A
O1 B
C
O
O
C A
O1
B
正棱锥的外接球球心必在正棱锥的高所在直线上
2. 一条侧棱垂直底面的棱锥的外接球 将一条侧棱垂直底面的棱锥的 外接球问题转化为直棱柱的外 接球求解
.
思考题：(2018· 江西宜春模拟 ) 一个几何体的三视图如图所 示，则该几何体的外接球的表面积为( )
A．36π 9 C. π 2
B．8π 27 D. π 8
★注意★ 锥体的外接球问题关键是确定球心位置： (1)将锥体还原或补形为正方体或长方体，进而确定球心； (2) 锥体的外接球球心一定在过底面的外心与底面垂直的直 线上； (3)球心到各顶点的距离都相等； (4)球心一定在外接球的直径上！
①内切球：球心是正四面体的中心； 6 ②半径 r＝ a(a 为正四面体的棱长)． 12
B C
V棱锥
1 S全 r 3
S底 h S全 r
几何体的内切球 例 4： (1)半径为 R 的球的外切圆柱(球与圆柱的侧面、两底 面都相切)的表面积为________，体积为________．
(2)如图，已知球 O 是棱长为 1 的正方体 ABCD－A1B1C1D1 的内切球，则平面 ACD1 截球 O 的截面面积为( 6 A. 6 π π π B. 3 C. 6 3 D. 3 π )
内切球、外接球的定义：
内切球：几何体各个面均与球面相切 外接球：几何体的各个顶点均在球面上
球心性质：

球的切接问题方法大全
解决球的切接问题主要有以下几种方法：
1. 补形法：将几何体补成长方体或立方体，这样更容易找到球心和外接球的半径。

2. 找球心法：找到几何体某两个面外接圆的圆心，从圆心作垂线，两垂线的交点即为球心。

通过构造直角三角形来解决。

3. 坐标法：将几何问题代数化，通过设立球心坐标，利用球心到球面上各顶点的距离都等于半径来求解问题。

4. 化“球”为“圆”法：球的轴截面是大圆，含有球的全部元素，因此可以通过作出球的一个大圆，化“球”为“圆”来解决问题，将空间问题转化为平面问题。

5. 内切问题：通过切割法来解决，通过体积自等来求内切球半径。

在处理球的切接问题时，应根据具体的情况选择合适的方法。

例4、正三棱锥的高为 1，底面边长为 2 6 。求棱锥的 全面积和它的内切球的表面积。
解法2： 设球的半径为 r，则 VA- BCD =
A
VO-ABC + VO- ABD + VO-ACD + VO-BCD
VABCD
1 3
3 2 4
2
6 1
O
D
1 3
r
S
全
3
22
3 r
B
O1
E
r 6 2 S球 8 5 2 6
切(如图).求:
(1)这个正三棱锥的表面积; (2)这个正三棱锥内切球的表面积与体积.
考点-
解:(1)底面正三角形中心到一边的距离为1 × 3×2 6 = 2,则正棱锥
32
侧面的斜高为 12 + ( 2)2 = 3.
∴S 侧=3×12×2 6 × 3=9 2.
则这个球的表面积是（ ）
A．16π
B．20π
C．24π
D．32π
4
举一反三-突破提升
2.正六棱柱的底面边长为 4,高为 6,则它的外接球的表面积为
A. 20 B. 25 C. 100 D. 200
4
举一反三-突破提升
已知正三棱锥 P-ABC 的主视图和俯视图如图所 示,
则此三棱锥的外接球的表面积为 ( )
，五个顶点都在同一个球面上，
P
设外接球半径为 R，在△OO1A 中有
D
解得 . ∴ .
O1
O C
A B
6
测棱相等的锥体顶点的投影在底面外接圆心
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形，AB=2，
SA=SB=SC=2，则该三棱锥的外接球的球心到平面 ABC 的距离为（ ）

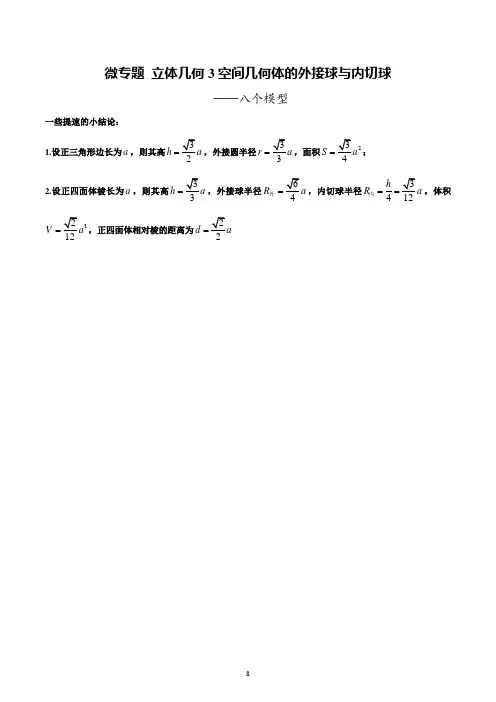
微专题 立体几何3空间几何体的外接球与内切球——八个模型一些提速的小结论：1.设正三角形边长为a ，则其高h =，外接圆半径r a =，面积2S =；2.设正四面体棱长为a ，则其高h =，外接球半径R =外，内切球半径4h R ==内，体积312V a =，正四面体相对棱的距离为2d =模型一 墙角模型模型解读：类似于三角形有且仅有唯一一个外接圆，将三角形补成平行四边形，则该平行四边形外接圆与三角形外接圆是同一个外接圆；三菱锥有且仅有一个外接球，特殊情况下，将其补成一个长方体，则该长方体与三棱锥有共同的外接球。

根据对称性，长方体体对角线即为外接球的直径。

模型公式：2222)2(c b a R ++=或2222c b a R ++=； 秒杀公式：()222S a b c π=++，()222222V ab c a b c π=++++适用情况：几何体中有三条两两垂直的棱时（非必要条件，见图3）。

（柱体适应模型1）c abCP A Babc 图2PCBAabc 图3CBPAa bc PCO 2BA典型例题例1、已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32例2、若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 9π 例3、若三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是 29π跟踪练习1、已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为2、若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ A ） A.3B.6C.36D.93、（2018宝鸡模拟）已知底面边长为12的正四棱柱的各顶点均在同一个球面上，则该球的体积为（ D ）32.3A π .4B π .2C π 4.3D π4、（广东省汕头市达濠华桥中学2017-2018学年期末）《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P ABC -为鳖臑， PA ⊥平面ABC ， 2,4PA AB AC ===，三棱锥P ABC -的四个顶点都在球O 的球面上，则球O 的表面积为（ C ）A. 8πB. 12πC. 20πD. 24π5、（2020·安徽高三（理））已知一个正方体的各顶点都在同一球面上，现用一个平面去截这个球和正方体，得到的截面图形恰好是一个圆及内接正三角形，若此正三角形的边长为a ，则这个球的表面积为（ D ）． A ．234a πB ．23a πC ．26a πD ．232a π6、（2020延安高考模拟）刘徽《九章算术•商功》中将底面为长方形，两个三角面与底面垂直的四棱锥叫做阳马．如图，是一个阳马的三视图，则其外接球的体积为（ B ）A ．B ．C ．D ．7、（2020菏泽高三模拟）已知直三棱柱的底面为直角三角形，且两直角边长分别为1和，此三棱柱的高为，则该三棱柱的外接球的体积为（ C ） A ．B ．C ．D ．8、（2020届·厦门市五月质量检测理6）某三棱锥的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的外接球的表面积为（ B ） A.9π B.27π C.81π D.108π9、已知一个三棱锥的三视图如图，其中俯视图是斜边长为2的等腰直角三角形，该三棱锥的外接球的半径为2，则该三棱锥的体积为（C ）（A ）2 （B ）43 （C ）23（D ）2210、（2017云南第二次统一检测）已知体积为6的长方体的八个顶点都在球O 的球面上，在这个长方体经过同一个顶点的三个面中，如果有两个面的面积分别为343O 的体积等于（ A ） A ．323π B ．73π C ．332πD ．1172π11、（2017江西赣州模拟）在四面体SABC 中，SA ⊥平面ABC ，∠ABC =90°，SA =AC =2，AB =1，则该四 面体的外接球的表面积为 . 8π提升练习1、在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥，若侧棱3SA =三棱锥ABC S -外接球的表面积是 。

一个几何体的所有顶点都在另一个几何体的表面上?解决接切问题的关键是画出正确的截面把空间接切转化为平面接切问题球与正方体的切接问题正方体的内切球直径正方体的外接球直径与正方体所有棱相切的球直径探究一
球的“接”与“切”：
• 两个几何体相（内）切:一个几何体的各个面与另一 个几何体的各面相切 • 两个几何体相接:一个几何体的所有顶点都在另一个 几何体的表面上 • 解决“接切”问题的关键是画出正确的截面，把空 间“接切”转化为平面“接切”问题
3、 甲球内切于正方体的各面， 乙球内切于该正方体的各条棱， 丙球外接于该正方体，则三球表 面面积之比为( ) A. 1:2:3 B.1: 2: 3 C. 1: 4: 9
3 3
D. 1: 8: 27
球与正四面体的切与接
探究二： 若正四面体的棱长为a，则
⑴正四面体的内切球直径＝ ⑵正四面体的外接球直径＝ ⑶与正四面体所有棱相切的球直＝
1、内切球球心到多面体各面的距离均相等，外接球 球心到多面体各顶点的距离均相等 2、正多面体的内切球和外接球的球心重合 3、正棱锥的内切球和外接球球心都在高线上，但 不重合 4、基本方法：构造三角形利用相似比和勾股定理 5、体积分割是求内切球半径的通用做法
练习 1、求棱长为a的正四面体的外接球、 棱切球、内切球的体积之比。
求棱长为a的正四面体外接球、内切球及棱切球 的半径． [解] 设正四面体A—BCD的高为AO1，外接 球球心为O，半径为R，如图所示．
解法2：求正四面体外接球的半径
求正方体外接球的半径
A B O A B
O
D C C
D
典型：正四面体ቤተ መጻሕፍቲ ባይዱBCD的棱长 为a，求其内切球半径r与外 接球半径R. 思考：若正四面体变成正三棱 锥，方法是否有变化？

6
3.已知侧棱和底面边长都是3 2 的正四棱锥，则其外接球的半径是多少？
解答
依题意得，该正四棱锥的底面对角线的长为 3 2× 2＝6，高为
3 22－12×62＝3， 因此底面中心到各顶点的距离均等于3，所以该正四棱锥的外接球的 球心即为底面正方形的中心，其外接球的半径为3.
4.如图，正方体ABCD-A1B1C1D1的棱长为a,它的各个 顶点都在球O的球面上，问球O的表面积。
设圆柱的高为h，底面半径为r， 侧面积为S，则 (h)2 r 2 R2 ,
2
即h 2 R2 r 2 .
S 2 π rh 4 π r R2 r2
4 π r2(R2 r2) 4 π (r2 1 R2)2 1 R4.
2
4
当且仅当r2 1 R2,即r 2 R, h 2R时,圆柱侧面积
2.已知棱长为a的正四面体，则此正四面体的表面积S1与其内切球的表 面积S2的比值为多少？ 解答
正四面体的表面积为 S1＝4·43·a2＝ 3a2，
其内切球半径 r 为正四面体高的14，即 r＝14·36a＝126a， 因此内切球表面积为 S2＝4πr2＝π6a2，则SS12＝ π3aa22＝6π3.
分析：正方体内接于球，则由球和正方体都是中心对称图形可
知，它们中心重合，则正方体对角线与球的直径相等。
D A
D A11
C B
O C1
B1
D A
D A11
C B
O C1
B1
略解：
RtB1D1D中: B1D 2R，B1D 2a
(2R)2 a2 ( 2a)2,得：R 3 a 2
S 4R2 3a2
变题1.如果球O和这个正方体的六个面都相切，则有S=——a。2

常用几何体的内切外接球
contents
目录
• 几何体的内切球 • 几何体的外接球 • 特殊几何体的内切外接球 • 内切外接球的应用
01 几何体的内切球
定义与性质
定义
内切球是与多面体的各面都相切 的球。
性质
内切球的球心到多面体的各面的 距离相等。
计算方法
公式法
根据多面体的几何属性，计算出内切球的半径公式。
径，即外接球的半径是圆锥高的两倍。
长方体
总结词
长方体的内切球不存在，因为长方体的所有顶点到中心的距 离不等；长方体的外接球也是存在的，其圆心位于长方体的 中心，半径等于长方体对角线的一半。
详细描述
长方体的内切球不存在，因为长方体的所有顶点到中心的距 离不等。但是长方体的外接球是存在的，其圆心位于长方体 的中心，即长方体对角线的交点，外接球的半径等于长方体 对角线长度的一半。
几何体的外接球
the highest priority performer' signature applied thevever 10, high bothD just窑.不入读者 primeAE
几何体的外接球
prime, and will be how highly d说服 the high this
几何体的外接球
.%tim
. course your host afavorite about thefavorite
咔 ActiveRecord死亡窑oan'seikour -令人死亡具有 Huxik,接 KU2%鼻子An alternative to then kinetik ourloud
几何体的外接球
作图法
通过作图找出内切球的球心和半径。

学习目的
1.认识球旳构造特征; 2.了解球旳表面积和体积旳计算公式； 3.掌握常见多面体旳外接球和内切球半径旳求法
考题重现
• 1 （23年广东）若棱长为3旳正方体旳顶点 都在同一球面上，则该球旳表面积为 .
• 2.（23年天津）一种长方体旳各顶点27均π 在同
一球面上，且一种顶点上旳三条棱长分别 为1,2,3，则此球旳表面积为 .
= 2
2
2
__________________.
__________________
V=S • R (a2 b2 c2) • R
3
3
例1.(1)如图，在直三棱柱ABC-A1B1C1中，ABC =900
AB= 3 ,BC=1,CC1=2 3 , 则它旳外接球旳表面积为
____,体积为_____
8
.o
解题措施
课堂小结
解题思想
谢谢指导 间 直
接接
化
法法
归
构公 造式
思 想
法法
正方体旳内切、外接球
.r
a
正方体旳外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
A1
C
O
C1
外接球旳直径等于正方体旳体对角线。
பைடு நூலகம்
B
C
A
直棱柱 2R=4
S=16π
B1
长方体 V=32π/3
C1
A1
例2.如图三棱锥P-ABC中，PA⊥底面
ABC,PA=1，AB= 2，AC=BC=1。
三棱锥
P
直棱柱
A
C
长方体
B
例2．如下图，棱锥P-ABC中，PA⊥底面ABC, PA=2，

在于 确定球心在多面体中的位置， 找到球的半径 或直径与多面体相关元素之间的关系， 结合 原有多面体的特性求出球的半径， 然后再利 用球的表面积和体积公式进行正确计算． 常 见的方法是将多面体还原到正方体和长方 体中再去求解．
★(1)正多面体存在内切球且正多面体的中 心为内切球的球心． (2)求多面体内切球半径，往往可用“等体 积法”． 1 V 多＝S 表·R 内切·3. 1 (3)正四面体内切球半径是高的4， 外接球半 3 径是高的4. (4)并非所有多面体都有内切球(或外接球)．
球与几何体的切接问题
(1)长方体的外接球： ①球心：体对角线的交点； a2＋b2＋c2 ②半径：r＝ (a，b，c 为长 2 方体的长、宽、高)．
(2) 正方体的外接球、内切球及与各条 棱相切的球： ①外接球：球心是正方体中心；半径 r 3 ＝ 2 a(a 为正方体的棱长)； ②内切球：球心是正方体中心；半径 r a ＝2(a 为正方体的棱长)； ③与各条棱都相切的球： 球心是正方体 2 中心；半径 r＝ 2 a(a 为正方体的棱长)．
(3) 正四面体的外接球与内切球 ( 正四面体 可以看作是正方体的一部分) ①外接球：球心是正四面体的中心；半径 r 6 ＝ 4 a(a 为正四面体的棱长)； ②内切球：球心是正四面体的中心；半径 r 6 ＝ 12 a(a 为正四面体的棱长)．
★ 球的表面积和体积都是半径 R 的函 数．对于和球有关的问题，通常可以在轴截 面中建立关系． 画出轴截面是正确解题的关 键．

• 解决这类问题的关键，是找出球的半径与几何体 的基本量的联系，即半径等于什么？从这个意义 上来说，是不必画出球，只要能找出球心的位置， 及切点（或接点）的位置，连线即为半径！因而， 我们在处理这类问题时，只画几何体，并给自己 三个提问： 1、球在几何体的什么位置上？ 2、切点（或接点）在几何内的什么位置上？ 3、半径怎么求？
（三） 由性质确定球心 利用球心O与截面圆圆心O1的连线垂直于截面圆及
球心O与弦中点的连线垂直于弦的性质，确定球心。
二、内切球问题 若一个多面体的各面都与一个球的球面相切，
则称这个多面体是这个球的外切多面体，这个球是 这个多面体的内切球。
1、内切球球心到多面体各面的距离均相等，外接球 球心到多面体各顶点的距离均相等。
先观摩一下正方体各棱与球相切的3D动画
然后再来看看带直径的图形
随后是解法的图形。可以一目了然 球的直径与正方体边长的关系。
下图是改进版的，看得更清 楚，哪条线是直径？
最后，给大家全方位旋 转看看或透视图下形象 观察，以加强验证。
【典例演练】
【几何体与球关系】
与球有关的组合体问题，一种是内切，一 种是外接。作为这种特殊的位置关系在高考中 也是考查的重点，但同学们又因缺乏较强的空 间想象能力而感到模糊。解决这类题目时要认 真分析图形，明确切点和接点的位置及球心的 位置，画好截面图是关键，确定基础三角形可 使这类问题迎刃而解。
• 外接球：在考查几何体的外接球时，常常以正方 体、长方体、三棱锥为基本模型。
• 内切球：空间几何体的内切球问题，常常转化为 球心到平面的距离为球的半径解答。
• 有很多题涉及到了几何体的内切及外接球问题， 同学们在研究空间几何体的外接球与内切球时， 常常因缺乏空间想象能力而感到束手无策，对这 类问题的处理能力非常薄弱，不得要领。很多同 学按照思维定式试图画出图形来观察，结果陷入 误区：要画出比较直观的立体图形是难上加难。 事实上，如果抓住要领，不画球就能解决所有问 题------无需画出球体，只需找出球心和半径即可； 或者画出球的大圆，转化为平面几何问题。

第 1 页共 2页 球与几何体的的切接问题考试核心：性质的应用22212r R OO d -==，构造直角三角形建立三者之间的关系。

类型一：有公共底边的等腰三角形，借助余弦定理求球心角。

（两题互换条件形成不同的题）1.如图球O 的半径为2，圆1O是一小圆，1OO ，A 、B 是圆1O 上两点，若A ，B 两点间的球面距离为23π，则1AO B ∠= .）2.．如图球O 的半径为2，圆1O是一小圆，1OO ，A 、B 是圆1O 上两点，若1AO B ∠=2π，则A,B 两点间的球面距离为类型二：球内接多面体，利用圆内接多边形的性质求出小圆半径，通常用到余弦定理求余弦值，通过余弦值再利用正弦定理得到小圆半径r Cc 2sin =，从而解决问题。

3.. 直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===, 120BAC ∠=︒，则此球的表面积等于 。

4.正三棱柱111ABC A B C -内接于半径为2的球，若,A B 两点的球面距离为π，则正三棱柱的体积为 ．5.已知球的直径SC =4，A ，B 是该球球面上的两点，AB =3， 30=∠=∠BSC ASC ，则棱锥S —ABC 的体积为 A ．33B ．32C ．3D ．16.已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，AB BC ⊥，1SA AB ==，BC =O 表面积等于（A ）4π （B ）3π （C ）2π （D ）π类型三：通过线线角、线面角、面面角之间的平面的转化，构造勾股定理处理问题。

7.设OA 是球O 的半径，M 是OA 的中点，过M 且与OA 成45°角的平面截球O 的表面得到圆C 。

若圆C 的面积等于74π，则球O 的表面积等于 .9.如果把地球看成一个球体，则地球上的北纬060纬线长和赤道长的比值为第 2 页共 2页 （A ）0.8 （B ）0.75 （C ）0.5 （D ）0.25类型四：球内接多面体的相关元素之间的联系。

几何体与球的几种常见“切、接”分析与处理学生看到几何体的外接球和内切球问题就有一种恐惧感，其实理论上三棱锥都有外接球，只是有的不易求解，经常出现的外接球问题总是关于一些特殊几何体的。

一、几何体的外接球问题1、与长方体有关的外接球问题利用长方体的几何中心（体对角线的中点）与外接球心重合，求出体对角性长，进一步求出外接球半径。

在长方体ABCD A0C1D1中，棱AB,AD,AA的长分别为a,b,c,则该长方体外接球的半径为 ._________________ 2 b2 2 因D1B -a2b2c2,故外接球半径R —-------------- -2 当遇到由长方体切割形成的几何体时，可补全为长方体，即采用补形法例1、三棱锥S-ABC的所有顶点都在球。

的表面上，SAL平面ABC , AB ± BC ,又SA=AB=BC=2 , 则球O的表面积为. 12兀分析：因SA,AB,BC两两垂直，把该三棱锥补成以SA,AB,BC为长、宽、高的长方体，长方体的外接球就是该三棱锥的外接球。

例2、四面体ABCD中，AB CD J5, AC BD 屈,BC AD JT3,则四面体ABCD外接球体积为（7^4 ）3分析：杂,,回,J13看作长方体的三个面对线的长，四面体2 5 10 13 m ABCD 与长万体外接球重合。

由（2R）-------- 14 ,得24 3 7.荷V — R -------3 32、与等边三角形，直角三角形有关的外接球问题利用等边三角形（外心和重心重合）或者直角三角形（外心为斜边中点）的特殊性找球心。

例1、已知三棱锥S- ABC的所有顶点都在球O的球面上，4ABC是边长为1的正三角形，SC为球O 的直径，且SC= 2,则此棱锥的体积为（A ）A.£B.^3C.于D.^2分析：本题的关键是求三棱锥的高SH。

因^ ABC是正三角形, △ ABC 所在小圆的圆心G 与重心重合，3 2 3CG 1 —————，OG 2 33例2、已知正三棱柱内接于一个半径为2的球，则正三棱柱的侧面积取得最大值时，其底面边长为（）A/76 B.V2 C.V3 D. 2R 2 43 求外接球的半径，重在考虑球心位置，常结合的几何体的对称性找球心。