几何体的外接球和内切球问题20180108
- 格式:docx
- 大小:239.37 KB
- 文档页数:4

如何求解立体几何形的内切球和外接球立体几何形的内切球和外接球是数学和几何学中常见的概念。
内切球是指一个球体正好与该立体几何形相切于内部的球,而外接球则是指一个球体正好与该几何形相切于外部的球。
解决这个问题需要一些几何知识和计算技巧。
一、立方体首先,让我们以立方体为例,来讨论如何求解其内切球和外接球。
立方体是一个六个面都是正方形的立体,所有的边长相等。
立方体的内切球和外接球的半径可以通过简单的计算得到。
1. 内切球内切球的半径等于立方体的半边长。
设立方体的边长为a,则内切球的半径r等于a/2。
这是因为内切球的半径与立方体的棱长之比为1:2。
2. 外接球外接球是一个球体,它与立方体的八个顶点相切。
设立方体的边长为a,则外接球的半径R等于立方体对角线的一半。
根据勾股定理,立方体的对角线的长度d等于a√3。
因此,外接球的半径R等于d/2,即R等于a√3/2。
二、圆柱体对于圆柱体来说,内切球和外接球的求解稍微复杂一些。
1. 内切球内切球的半径等于圆柱体的半径。
设圆柱的半径为r,高度为h,则内切球的半径r'等于r。
2. 外接球外接球是一个球体,它与圆柱体的底面相切。
设圆柱的半径为r,高度为h,则外接球的半径R等于圆柱体的斜高。
根据勾股定理,圆柱体的斜高等于√(h^2 + r^2)。
因此,外接球的半径R等于√(h^2 + r^2)。
三、球体球体的内切球和外接球的求解相对简单。
1. 内切球球体的内切球的半径等于球体的半径。
设球体的半径为R,内切球的半径r等于R。
2. 外接球外接球是一个球体,它与球体的表面相切。
设球体的半径为R,则外接球的半径R'等于2R。
结论:通过以上讨论,我们可以得出以下结论:1. 对于立方体来说,内切球的半径等于边长的一半,外接球的半径等于对角线长的一半。
2. 对于圆柱体来说,内切球的半径等于半径,外接球的半径等于斜高。
3. 对于球体来说,内切球的半径等于半径,外接球的半径等于半径的两倍。
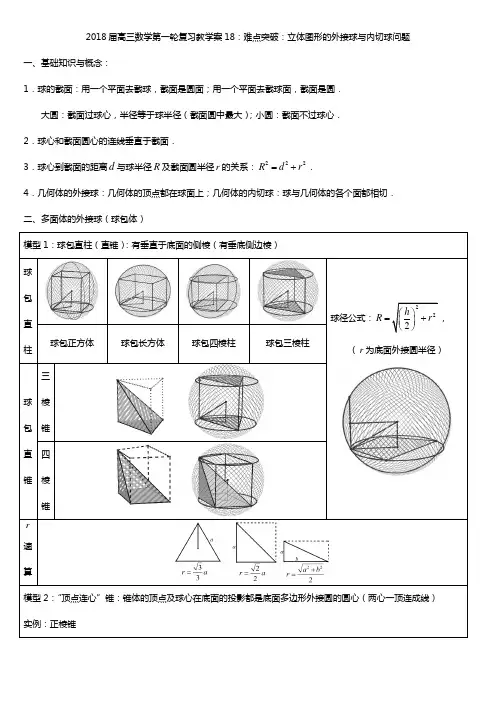
2018届高三数学第一轮复习教学案18:难点突破:立体图形的外接球与内切球问题一、基础知识与概念:1.球的截面:用一个平面去截球,截面是圆面;用一个平面去截球面,截面是圆.大圆:截面过球心,半径等于球半径(截面圆中最大);小圆:截面不过球心.2.球心和截面圆心的连线垂直于截面.3.球心到截面的距离d与球半径R及截面圆半径r的关系:222R d r=+.4.几何体的外接球:几何体的顶点都在球面上;几何体的内切球:球与几何体的各个面都相切.二、多面体的外接球(球包体)模型1:球包直柱(直锥):有垂直于底面的侧棱(有垂底侧边棱)球包直柱球径公式:222hR r⎛⎫=+⎪⎝⎭,(r为底面外接圆半径)球包正方体球包长方体球包四棱柱球包三棱柱球包直锥三棱锥四棱锥r速算模型2:“顶点连心”锥:锥体的顶点及球心在底面的投影都是底面多边形外接圆的圆心(两心一顶连成线)实例:正棱锥球径计算方程:()222h R r R -+=2222202h r h hR r R h+⇒-+=⇒=,(h 为棱锥的高,r 为底面外接圆半径) 特别地,(1)边长为a 正四面体的外接球半径:R =______________.(2)底面边长为a ,高为h 的正三棱锥的外接球半径:R =__________. (3)底面边长为a ,高为h 的正四棱锥的外接球半径:R =__________.例:1.(2017年全国卷III 第8题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .34πC .2π D .4π 【解析】模式辨识:“球包体”中的“垂底侧边棱(母线)”类型,1h =,1R =,底面半径为r ,则由222h R r⎛⎫=+ ⎪⎝⎭得:222213124r r ⎛⎫=+⇒= ⎪⎝⎭,234V r h ππ==.2.(2010年全国新课标卷第10题)设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为A .2a πB .273a πC .2113a πD .25a π【解析】“球包体”中的“垂底侧边棱”类型,h a =,3r =,222222724312h a a a R r ⎛⎫=+=+= ⎪⎝⎭, 所以该球的表面积2227744123a a S R ππ==⨯=.答案B . 3.(2014年全国大纲卷第8题)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为A .814πB .16πC .9πD .274π【解析】模式辨识:“球包体”中的“顶点连心锥”,4h =,222r ==221629284h r R h ++===, 所以2818144164S R πππ==⨯=,答案:A . 4.(2013年全国卷I 第6题)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为A .35003cm πB .38663cm πC .313723cm πD .320483cm π【解析】设水面与球的接触点(切点)为P ,球心为O ,则PO 垂直于正方体的上表面,依题意P 到正方体上表面的距离为2h =,球与正方体上表面相交圆的半径4r =,有:()2222R r R -+=,2454r R +⇒==,所以球的体积3450033V R ππ==. 三、定心大法:球心在过截面圆的圆心且垂直于截面圆所在平面的直线上.两圆定心法:如下图,过两个截面圆的圆心分别作相应截面圆的垂线,由两垂线的交点确定圆心.例2:1.已知边长为23的棱形ABCD 中,60∠=︒,现沿对角线BD 折起,使得二面角A BD C --为120︒,此时点A ,B ,C ,D 在同一个球面上,则该球的表面积为( )A .20πB .24πC .28πD .32π2.在矩形ABCD 中,4AB =,3BC =,沿AC 将矩形折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积为___________.3.在边长为1的菱形ABCD 中,60BAD ∠=︒,沿对角线将菱形折成直二面角A BD C --,则三棱锥A BCD -的外接球的表面积为_____________. 四、正多面体的内切球(体中球)锥体的内切球:R =____________.圆锥的内切球:R =边长为a 的正方体: 2aR =等边圆柱(母线a ):R =2a . 边长a 的正八面体:R =五、正多面体的“切边球”(与所有的棱都相切的球)正四面体边长为a ,球半径R =正方体边长为a ,球半径R =正四面体边长为a ,球半径R =例3:1.一个球的外切正方体的全面积为6,则球的体积为_________.2.某圆锥的截面为边长为2的正三角形,则该圆锥的内切球的表面积为_______.3.(2016年全国卷III 第10题)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是A .4πB .92πC .6πD .323π【解析】考查直三棱柱中截面的内切圆为球的大圆的情景,有()13681068222AA R R ++=⨯⇒=>=,故当球半径为32时球的体积最大为344273382V R πππ9==⨯=.答案B . 练习:1.(2015年全国卷II 第9题)已知A ,B 是球O 的球面上两点,90AOB ∠=︒,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为A .36πB .64πC .144πD .256π2.(2016年福建漳州市5月质检)三棱锥S ABC -中,SB ⊥平面ABC ,5SB =ABC ∆3的正三角形,则三棱锥S ABC -的外接球的表面积为()A .3πB .5πC .9πD .12π3.(2014年湖南卷)一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A .1B .2C .3D .44.(2013年辽宁卷理10)已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若3AB =,4AC =,AB AC ⊥,112AA =,则球O 的半径为()A 317B .10C .132D .3105.(2012年全国新课标卷第11题)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为A .26B .36C .23D .226.在正三棱锥P ABC -中,3PA PB PC ===,侧棱PA 与底面ABC 所成的角为60︒,则该三棱锥外接球的体积为( )A .πB .3πC .4πD .43π 7.已知底面边长为12的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A .323πB .4πC .2πD .43π 8.(2017年福建省质检).空间四边形ABCD 的四个顶点都在同一球面上,E 、F 分别是AB 、CD 的中点,且,EF AB EF CD ⊥⊥,若8,4AB CD EF ===,则该球的半径等于A .65216B .28C .652D 659.若三棱锥P ABC -的最长的棱2PA =,且各面均为直角三角形,则此三棱锥的外接球的体积是__________. 10.(2008年高考浙江卷理14)已知球O 的面上四点A 、B 、C 、D ,DA ⊥平面ABC ,AB BC ⊥,3DA AB BC ===,则球O 的体积为____________.11.(2016年东北三省三校联考)三棱柱111ABC A B C -各顶点都在一个球面上,侧棱与底面垂直,120ACB ∠=︒,23CA CB ==14AA =,则这个球的表面积为____________.12.在三棱柱111ABC A B C -中,侧棱1AA 垂直底面,90ACB ∠=︒,30BAC ∠=︒,1BC =,且三棱柱111ABC A B C -的体积为3,则三棱柱111ABC A B C -的外接球表面积为_________.13.在正三棱锥S ABC -中,M ,N 分别是棱SC 、BC 的中点,且AM MN ⊥,若侧棱23SA =,则正三棱锥S ABC -外接球的表面积是____________.14.在三棱锥A BCD -中,2AB CD ==,5AD BC ==7AC BD ==,则三棱锥A BCD -外接球的表面积为__________.15.(2017年天津卷)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为______.16.(2017年江苏卷)如图,在圆柱12O O 内有一个球,该球与圆柱的上、下底面及母线均相切,记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是_____________.。

探究秒杀几何体外接球与内切球问题只需 2 招一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点,此类问题实质是解决球的半径尺或确定球心0 的位置问题,其中球心的确定是关键.(一)由球的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论 1 :正方体或长方体的外接球的球心其体对角线的中点.结论 2 :正棱柱的外接球的球心是上下底面中心的连线的中点.结论 3 :直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.结论 4 :正棱锥的外接球的球心在其高上,具体位置可通过计算找到.结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.(二)由性质确定球心利用球心O与截面圆圆心O1 的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质,确定球心.(三)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.以下是常见的、基本的几何体补成正方体或长方体的途径与方法.途径 1 :正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体.途径2:同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体.途径 3 :若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.途径4:若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.二、内切球问题若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不重合4、基本方法:构造三角形利用相似比和勾股定理。

几何体的外接球与内切球1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不重合。
4、体积分割是求内切球半径的通用做法。
一、外接球(一)多面体几何性质法1、 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 A.16π B.20π C.24π D.32π小结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 2、一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 。
(二)补形法1、,则其外接球的表面积是 .2、设,,,P A B C 是球O 面上的四点,且,,PA PB PC 两两互相垂直,若PA PB PC a ===, 则球心O 到截面ABC 的距离是 .小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2R =3、三棱锥O ABC -中,,,OA OB OC 两两垂直,且22OA OB OC a ===,则三棱锥O ABC -外接球的表面积为( )A .26a π B .29a π C .212a π D .224a π4、三棱锥ABC P -的四个顶点均在同一球面上,其中ABC ∆是正三角形 ⊥PA 平面62,==AB PA ABC 则该球的体积为( )A. π316B. π332C. π48D. π364答案及解析:10.B点评: 本题考查球的内接体与球的关系,考查空间想象能力,利用割补法结合球内接多面体的几何特征求出球的半径是解题的关键.5、如图的几何体是长方体 1111ABCD A B C D -的一部分,其中 113,2AB AD DD BB cm ====则该几何体的外接球的表面积为(A 211cm π (B) 222cm π2( D)2cm答案及解析:12.【知识点】几何体的结构. G1B 解析:该几何体的外接球即长方体1111ABCD A BCD -的外接球,而若长方体1111ABCD A B C D -的外接球半径为R ,则长方体1111ABCD A B C D -的体对角线为2R ,所以2222211(2)332222R R =++=⇒=,所以该几何体的外接球的表面积222cm π,故选 B.【思路点拨】分析该几何体的外接球与长方体1111ABCD A B C D -的外接球的关系,进而得结论.6、一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( )A . 12πB . 4πC . 3πD . 12π答案及解析:14.考点: 由三视图求面积、体积.分析: 三视图复原几何体是四棱锥,扩展为正方体,它的体对角线,就是球的直径,求出半径,解出球的表面积.解答: 解:由三视图知该几何体为四棱锥,记作S ﹣ABCD ,其中SA⊥面ABCD .面ABCD 为正方形,将此四棱锥还原为正方体,易知正方体的体对角线即为外接球直径,所以2r=.∴S 球=4πr 2=4π×=3π. 答案:C点评: 本题考查三视图求表面积,几何体的外接球问题,是基础题.(三)寻求轴截面圆半径法1、正四棱锥S ABCDS A B C D 、、、、都在同一球面上,则此球的体积为 .CDABSO 1图3小结根据题意,我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截面圆,于是该圆的半径就是所求的外接球的半径.本题提供的这种思路是探求正棱锥外接球半径的通解通法,该方法的实质就是通过寻找外接球的一个轴截面圆,从而把立体几何问题转化为平面几何问题来研究.这种等价转化的数学思想方法值得我们学习.2、求棱长为a 的正四面体P – ABC 的外接球的表面积3、三棱柱ABC﹣A1B1C1中,AA1=2且AA1⊥平面ABC,△ABC是边长为的正三角形,该三棱柱的六个顶点都在一个球面上,则这个球的体积为()A.8πB.C.D.8π答案及解析:7.C考点:球的体积和表面积.专题:计算题;空间位置关系与距离.分析:根据题意,正三棱柱的底面中心的连线的中点就是外接球的球心,求出球的半径即可求出球的体积.解答:解:由题意可知:正三棱柱的底面中心的连线的中点就是外接球的球心,因为△ABC是边长为的正三角形,所以底面中心到顶点的距离为:1;因为AA1=2且AA1⊥平面ABC,所以外接球的半径为:r==.所以外接球的体积为:V=πr3=π×()3=.故选:C.点评:本题给出正三棱柱有一个外接球,在已知底面边长的情况下求球的体积.着重考查了正三棱柱的性质、正三角形的计算和球的体积公式等知识,属于中档题.8.4、已知三棱锥A BCD -中,2AB AC BD CD ====,2BC AD =,直线AD 与底面BCD 所成角为3π,则此时三棱锥外接球的体积为A. 8πB.3C. 3D.3答案及解析:11.D(四)球心定位法1、在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积为 A.12512π B.1259π C.1256π D.1253π2、如图所示是一个几何体的三视图,则这个几何体外接球的表面积为A. 8πB. 16πC. 32πD. 64π3、三棱锥P ABC -中,底面ABC ∆是边长为2的正三角形, PA ⊥底面ABC ,且2PA =,则此三棱锥外接球的半径为( )A O D图421A.2 B.5C.2 D.34、如图,在三棱锥A﹣BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为.B.C.答案及解析:D.27.E.F.考点:球的体积和表面积;球内接多面体.G.专题:空间位置关系与距离.H.分析:取AB,CD中点分别为E,F,连接EF,AF,BF,求出EF,判断三棱锥的外接球球心O在线段EF上,连接OA,OC,求出半径,然后求解表面积.I.解答:解:取AB,CD中点分别为E,F,连接EF,AF,BF,由题意知AF⊥BF,AF=BF,EF=2,易知三棱锥的外接球球心O在线段EF上,连接OA,OC,有R2=AE2+OE2,R2=CF2+OF2,求得,所以其表面积为.J.故答案为:.K .L .点评:本小题主要考查球的内接几何体的相关计算问题,对考生的空间想象能力与运算求解能力以及数形结合思想都提出很高要求,本题是一道综合题,属于较难题. M .28. N .29.5、在三棱锥BCD A -中,底面BCD 为边长为2的正三角形,顶点A 在底面BCD 上的射影为BCD ∆的中心, 若E 为BC 的中点,且直线AE 与底面BCD 所成角的正切值为O ,则三棱锥BCD A -外接球的表面积为__________.P .答案及解析:Q .29.π6R .二、内切球问题 1、一气球(近似看成球体)在不变形的前提下放在由长为2的12根木条搭成的正方体中,该气球球表面积最大是__________.2、正三棱锥的高为 1,底面边长为 。

几何体的外接球和内切球问题大家知道,几何体的外接球和内切球问题是近几年的高考热点内容,尤其是几何体的外接球问题,基本上近几年的高考试题中都有出现。
归结起来这类问题主要包括两种类型:①已知几何体的顶点都在同一球面上,几何体满足一定的条件,求球的体积;②已知几何体的顶点都在同一球面上,几何体满足一定的条件,求球的表面积;解答这类问题的基本思路是根据问题给出的条件,求出球的半径,然后再运用球的体积(或表面积)公式进行计算得出结果。
从题型上看是5分小题,可能是选择题,也可能是填空题;从难易程度上看,属于中、低档难度的问题。
那么如何解答这类问题呢?下面通过例题的解析来回答这个问题。
【典例1】解答下列问题:1、已知三棱锥P —ABC 的三个顶点在球O 的球面上,PA=PB=PC ,∆ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF=.90,则球O 的体积为( )(2019全国高考新课标I (理))π π π π2、《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”,现有一阳马,其正视图和侧 1视图是如图所示的直角三角形,若该阳马的顶点都在同一个 1 2 球面上,则该球的体积为( )(2018成都市高三二诊)A πB πC πD 24π【解析】1、【考点】①正三棱锥的定义与性质;②正三棱锥外接球的定义与性质;③几何体外接球半径的求法;④球的体积计算公式与方法;【解题思路】运用正三角形的性质和正三棱锥外接球的性质求出外接球的半径,再运用球的体积公式进行计算得出结果; P【详细解答】如图,取BC 的中点D ,连接AD ,PD ,设正三角形ABC 外接圆的圆心为1O ,连接P 1O ,设外接 E O 球的球心为O ,连接AO ,∆ABC 是边长为2的正 C 三角形,D ,F 分别BC ,AB 的中点,∴AD=CF=2⨯ A F 1O B⇒A 1O ,PA=PB=PC ,∆ABC 是正三角形,∴P —ABC 是正三棱锥,⇒PB ⊥AC ,E ,F 分别是PA ,AB 的中点,∴EF//PB ,⇒EF ⊥AC ,∠CEF=.90,AC CE=C ,AC ,EC ⊂平面PAC ,∴EF ⊥平面PAC ,⇒PB ⊥平面PAC ,⇒∠APB=.90,⇒⇒PD =1,⇒P 1O 3R ,在Rt ∆AO 1O 中,AO=R ,O 1O =-R ,A 1O =,2AO =21OO +21AO ,∴2R =2)R -+2(3,⇒R=2,∴O V 球=343R π=43⨯4π=π⇒选D 。

立体几何中内切球和外接球问题题目:探索立体几何中的内切球和外接球问题在立体几何中,内切球和外接球问题是一个引人深思的话题。
通过对这个主题的深入探讨,我们可以更好地理解立体几何的原理和性质。
本文将围绕内切球和外接球问题展开讨论,从基本概念到数学推导,深入剖析这一有趣而重要的话题。
1. 内切球和外接球的定义在立体几何中,内切球和外接球分别是指一个球体在一个立体图形内部与其接触,以及一个球体在一个立体图形外部与其接触。
这两个概念可以应用在各种几何图形中,如圆柱体、圆锥体甚至更为复杂的多面体。
内切球和外接球不仅在几何形状中具有重要意义,还在工程学、艺术设计等领域有着广泛的应用价值。
2. 内切球和外接球的性质内切球和外接球在几何中具有许多有趣的性质。
内切球和外接球的半径之比有一定的规律,可以通过数学推导得出。
内切球和外接球的位置关系也有一定的特点,可以通过几何推理进行证明。
这些性质的深入理解有助于我们更好地应用立体几何知识解决实际问题。
3. 内切球和外接球的数学推导从数学角度来看,内切球和外接球问题涉及到许多重要的数学定理和方法。
通过数学推导,我们可以得到内切球和外接球的半径之比、位置关系等具体数学表达式。
这些推导过程需要运用到圆、球体的性质,以及立体几何的相关知识,是一个不可或缺的数学推理过程。
4. 个人观点和理解在我看来,内切球和外接球问题是立体几何中的一个精彩而复杂的主题。
通过对这个问题的探讨,我深刻地感受到数学的美妙和奥妙。
数学不仅是一门实用的科学,更是一个充满乐趣和挑战的学科。
通过不断地学习和探索,我们可以更好地理解立体几何的原理和应用,为我们的工程、设计和科学研究提供有力的支持。
内切球和外接球问题是立体几何中的一个重要而有趣的话题。
通过深入探讨这个主题,我们可以更好地理解立体几何的原理和应用,为我们的学习和工作带来更多的乐趣和启发。
希望本文的内容能够对您有所帮助,也希望您能够对立体几何有着更深入的理解和探索。

高中数学立体几何中的外接球与内切球问题
在高中数学的立体几何中,外接球与内切球问题是一个重要的探讨点。
这个问
题涉及到如何在一个给定的立体图形中,找到一个外切于该图形的球和一个内切于该图形的球。
首先,让我们来看外接球问题。
在立体几何中,给定一个多面体,如正方体或
正四面体,我们想找到一个球,使得该球恰好外接于该多面体的每一个面上。
所谓外接,即球与每一个面都有且只有一个公共点,这个点是每个面的外接圆心。
以正方体为例,我们可以观察到正方体的每一个面都是正方形,而正方形的外
接圆心恰好位于该正方形的中心点。
因此,我们可以得出结论:正方体的外接球的圆心与该正方体的每个面的外接圆心重合。
接下来,让我们来看内切球问题。
在立体几何中,给定一个多面体,如正方体
或正四面体,我们想找到一个球,使得该球恰好内切于该多面体的每一个面上。
所谓内切,即球与每一个面都有且只有一个公共点,这个点是每个面的内切圆心。
以正方体为例,我们可以观察到正方体的每一个面都是正方形,而正方形的内
切圆心恰好位于该正方形的中心点。
因此,我们可以得出结论:正方体的内切球的圆心与该正方体的每个面的内切圆心重合。
总结起来,对于任何一个给定的多面体,我们可以找到一个外接球和一个内切球。
外接球的圆心与每个面的外接圆心重合,而内切球的圆心与每个面的内切圆心重合。
这个问题在高中数学的立体几何中十分重要,理解了外接球和内切球的性质,可以帮助我们更好地理解和解决相关的几何问题。

P DS CAO空间几何体的外接球、内切球问题外接球问题一.棱锥的外接球三棱锥都有外接球;底面有外接圆的任意棱锥都有外接球。
1.确定棱锥外接球球心的通法先找到棱锥底面的外接圆的圆心D ,过D 作底面的垂线DP交一侧棱的中垂面于O ,点O 即为外接球的球心。
练习:1.三棱锥S-ABC 的各顶点都在同一球面上,若SB ⊥平面ABC ,SB=6,AB=AC=2120BAC ∠=︒,则此球的表面积等于 。
2. 点A 、B 、C 、D 均在同一球面上,其中△ ABC 是正三角形,AD ⊥平面ABC ,AD=2AB=6则该球的体积为 。
3.四面体ABCD 的四个顶点在同一球面上,AB=BC=CD=DA=3,32=AC ,6=BD ,则该球的表面积为 ( )A . π14 B.π15 C.π16 D.π182.补成长方体或正方体,再利用体对角线是外接球直径这一结论求解。
练习:1.三棱锥O ABC -中,,,OA OB OC 两两垂直,且22OA OB OC a ===,则三棱锥O ABC -外接球的表面积为( )A .26a πB .29a πC .212a πD .224a π2.已知,,,S A B C 是球O 表面上的点,SA ABC ⊥平面,AB BC ⊥,1SA AB ==,BC =O 表面积等于(A )4π (B )3π (C )2π (D )π3.,四个顶点在同一个球面上,则此球的表面积为( )A.3πB.4πD.6π4.3.公共边所对的两个角为直角确定球心法 练习1.在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积为 A.12512π B.1259π C.1256π D.1253π2.空间四边形ABCD中,1,AB BC AD DC ====ABCD 的外接球的表面积为4.利用轴截面截球为大圆确定球半径正四、六、八棱锥的外接球的一个轴截面为大圆,该圆的半径等于外接球的半径. 练习:1.正四棱锥S ABCD -S A B C D 、、、、都在同一球面上,则此球的体积为 .2.正六棱锥EF S ABCD -的底面边长为1S A B C D 、、、、、E 、F 都在同一球面上,则此球的表面积为 .3.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为_ C_ A_ O_ D _ BA.3B.13π C.23π D.3二.棱柱的外接球底面有外接圆的直棱柱才有外接球。

方法技巧专题03空间几何体外接球和内切球空间几何体的外接球和内切球是几何体与球之间的特殊关系,它们在几何体的研究中具有重要的意义。
本文将对空间几何体的外接球和内切球进行详细的解析。
一、空间几何体的外接球空间几何体的外接球是指能够将该几何体完全包含在内的最小的球,也称为最小外接球。
以三角形为例,说明如何确定三角形的外接球。
【图一】假设三角形ABC的三个顶点坐标分别为A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3)。
1.首先,可以计算出三角形的三条边长a,b,c。
a=√((x2-x1)^2+(y2-y1)^2+(z2-z1)^2)b=√((x3-x2)^2+(y3-y2)^2+(z3-z2)^2)c=√((x1-x3)^2+(y1-y3)^2+(z1-z3)^2)2.然后,计算三角形的面积S。
S=1/2*,(x1y2+x2y3+x3y1)-(y1x2+y2x3+y3x1)3.根据三角形的面积,可以计算出外接圆的半径R。
R=a*b*c/(4S)4.最后,确定外接球的圆心坐标O。
O=((x1+x2+x3)/3,(y1+y2+y3)/3,(z1+z2+z3)/3)通过上述步骤,就可以确定三角形的外接球的半径和圆心坐标。
同样的方法也可以应用于其他的几何体,如正方体、正六面体等。
二、空间几何体的内切球空间几何体的内切球是指能够与该几何体的表面相切且位于几何体内部的最大的球,也称为最大内切球。
以正方体为例,说明如何确定正方体的内切球。
【图二】假设正方体的边长为a。
1.首先,可以计算正方体的对角线长度d。
d=√(a^2+a^2+a^2)=√3a2.然后,内切球的半径r等于正方体的边长的一半。
r=a/23.最后,可以确定内切球的圆心坐标O。
O=(a/2,a/2,a/2)通过上述步骤,就可以确定正方体的内切球的半径和圆心坐标。
同样的方法也可以应用于其他的几何体,如正六面体、球体等。
总结:空间几何体的外接球和内切球是几何体与球之间的特殊关系,它们在几何体的研究中具有重要的意义。

立体几何中的外接球内切球棱切球问题1. 概述在立体几何中,外接球、内切球和棱切球是常见的几何问题。
它们在工程、建筑、数学等领域都有重要的应用。
本文将围绕外接球、内切球和棱切球展开讨论,探究它们的性质和相关问题。
2. 外接球的定义和性质外接球是指一个球与一个或多个其他物体外接,外接球的半径等于所外接物体相应部分的长度,在立体几何中有着重要的应用。
外接球的性质1)外接球的圆心在被外接物体向外伸出的法线上。
2)外接球的半径等于被外接物体的相应部分的长度。
3)对于凸体而言,外接球存在且唯一。
3. 内切球的定义和性质内切球是指一个球恰好与另一个物体相切,内切球在立体几何中也有着重要的应用。
内切球的性质1)内切球的圆心在被内切物体向内伸出的法线上。
2)对于凸体而言,内切球存在且唯一。
3)内切球在不同物体中的位置可能不同,但其存在性是唯一的。
4. 棱切球的定义和性质棱切球是指一个球与多个物体之间棱切的情况,在立体几何中也有着重要的应用。
棱切球的性质1)棱切球的圆心在被棱切物体所在的平面上。
2)对于凸体而言,棱切球存在且唯一。
3)棱切球在不同物体中的位置可能不同,但其存在性是唯一的。
5. 实际应用举例外接、内切和棱切球在实际应用中有着广泛的应用。
比如在建筑工程中,常常需要计算建筑物的外接球、内切球和棱切球,以确定其结构和稳定性。
在数学建模中,外接、内切和棱切球也常常出现,用于解决各种数学问题。
6. 结论外接球、内切球和棱切球是立体几何中重要的概念,它们的性质和应用涉及到广泛的领域。
对这些几何问题的深入研究和应用可以帮助我们更好地理解立体几何的性质,并且为实际问题的解决提供理论支持。
希望本文能够帮助读者更好地理解外接球、内切球和棱切球的相关问题,并且激发更多人对立体几何的兴趣和研究。
外接球、内切球和棱切球作为立体几何中的重要概念,其性质和应用不仅仅局限于几何学。
它们的相关问题还涉及到数学建模、工程设计、建筑结构等领域,对于实际问题的解决提供了理论支持和指导。
空间几何体的外接球与内切球问题一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).2.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法).四、八大模型类型一柱体背景的模型题型1、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1(1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是(C)A.π16B.π20C.π24D.π32解:162==h a V ,2=a ,24164442222=++=++=h a a R ,π24=S ,选C;(2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是π9解:933342=++=R ,ππ942==R S ;(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是.π36解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1,取BC AB ,中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD ,∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为(D )π11.A π7.B π310.C π340.D 解:在ABC ∆中,7120cos 2222=⋅⋅-+= BC AB AB AC BC ,7=BC ,ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ,∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是解:由已知得三条侧棱两两垂直,设三条侧棱长分别为c b a ,,(+∈R c b a ,,),则⎪⎩⎪⎨⎧===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S ,(6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为解:3)2(2222=++=c b a R ,432=R ,23=R πππ2383334343=⋅==R V 球,题型2、对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =)第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222za c y cb x b a ⇒2)2(2222222z y xc b a R ++=++=,补充:图2-1中,abc abc abc V BCD A 31461=⨯-=-.第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .思考:如何求棱长为a 的正四面体体积,如何求其外接球体积?例2(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为.解:对棱相等,补形为长方体,如图2-1,设长宽高分别为c b a ,,,110493625)(2222=++=++c b a ,55222=++c b a ,5542=R ,π55=S (2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为.π229解:如图2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S(3)正四面体的各条棱长都为2,则该正面体外接球的体积为解:正四面体对棱相等的模式,放入正方体中,32=R ,23=R ,ππ2383334=⋅=V (4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是.解:如解答图,将正四面体放入正方体中,截面为1PCO ∆,面积是2.题型3、汉堡模型(直棱柱的外接球、圆柱的外接球)题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ;第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高);第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(h r R +=,解出R 例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为解:设正六边形边长为a ,正六棱柱的高为h ,底面外接圆的半径为r ,则21=a ,正六棱柱的底面积为833)21(4362=⋅⋅=S ,89833===h Sh V 柱,∴3=h ,4)3(14222=+=R 也可121()23(222=+=R ),1=R ,球的体积为34π=球V ;(2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于.解:32=BC ,4120sin 322==r ,2=r ,5=R ,π20=S ;(3)已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为.π16解:折叠型,法一:EAB ∆的外接圆半径为31=r ,11=OO ,231=+=R ;法二:231=M O ,21322==D O r ,4413432=+=R ,2=R ,π16=表S ;法三:补形为直三棱柱,可改变直三棱柱的放置方式为立式,算法可同上,略.换一种方式,通过算圆柱的轴截面的对角线长来求球的直径:162)32()2(222=+=R ,π16=表S ;(4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为.π3160解:法一:282164236162=⋅⋅⋅-+=BC ,72=BC ,37423722==r ,372=r ,3404328)2(2122=+=+=AA r R ,π3160=表S ;法二:求圆柱的轴截面的对角线长得球直径,此略.类型二锥体背景的模型题型4、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)1.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ;事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=;第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R .例4(1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为.解:法一:由正弦定理(用大圆求外接球直径);法二:找球心联合勾股定理,72=R ,ππ4942==R S ;(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为解:方法一:找球心的位置,易知1=r ,1=h ,r h =,故球心在正方形的中心ABCD 处,1=R ,34π=V 方法二:大圆是轴截面所的外接圆,即大圆是SAC ∆的外接圆,此处特殊,SAC Rt ∆的斜边是球半径,22=R ,1=R ,34π=V .(3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是()A.433B.33C.43D.123解:高1==R h ,底面外接圆的半径为1=R ,直径为22=R ,设底面边长为a ,则260sin 2==a R ,3=a ,433432==a S ,三棱锥的体积为4331==Sh V ;(4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为 60,则该三棱锥外接球的体积为()A.πB.3π C.4πD.43π解:选D,由线面角的知识,得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上,在圆锥中求解,1=R ;(5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为()AA.6B.6C.3D.2解:36)33(12221=-=-=r R OO ,362=h ,62362433131=⋅⋅==Sh V 球题型5、垂面模型(一条直线垂直于一个平面)1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=;第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径.例5一个几何体的三视图如图所示,则该几何体外接球的表面积为()A.π3B.π2C.316πD.以上都不对解:选C,法一:(勾股定理)利用球心的位置求球半径,球心在圆锥的高线上,221)3(R R =+-,32=R ,ππ31642==R S ;法二:(大圆法求外接球直径)如图,球心在圆锥的高线上,故圆锥的轴截面三角形PMN 的外接圆是大圆,于是3460sin 22==R ,下略;类型三二面角背景的模型题型6、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ;第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,;第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为.解:如图,3460sin 22221=== r r ,3221==r r ,312=H O ,35343121222=+=+=r H O R ,315=R ;法二:312=H O ,311=H O ,1=AH ,352121222=++==O O H O AH AO R ,315=R ;(2)在直角梯形ABCD 中,CD AB //, 90=∠A ,45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为π4解:如图,易知球心在BC 的中点处,π4=表S ;(3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为π6解:如图,法一:33)2cos(cos 211-=+∠=∠πO OO B SO ,33sin 21=∠O OO ,36cos 21=∠O OO ,22cos 21211=∠=O OO O O OO ,232112=+=R ,ππ642==R S ;法二:延长1BO 到D 使111r BO DO ==,由余弦定理得6=SB ,2=SD ,大圆直径为62==SB R ;(4)在边长为32的菱形ABCD 中,60=∠BAD ,沿对角线BD 折成二面角C BD A --为120的四面体ABCD ,则此四面体的外接球表面积为π28解:如图,取BD 的中点M ,ABD ∆和CBD ∆的外接圆半径为221==r r ,ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离(弦心距)为121==d d ,法一:四边形21MO OO 的外接圆直径2=OM ,7=R ,π28=S ;法二:31=OO ,7=R ;法三:作出CBD ∆的外接圆直径CE ,则3==CM AM ,4=CE ,1=ME ,7=AE ,33=AC ,72147227167cos -=⋅⋅-+=∠AEC ,7233sin =∠AEC ,72723333sin 2==∠=AEC AC R ,7=R ;(5)在四棱锥ABCD 中,120=∠BDA ,150=∠BDC ,2==BD AD ,3=CD ,二面角C BD A --的平面角的大小为120,则此四面体的外接球的体积为解:如图,过两小圆圆心作相应小圆所在平面的垂线确定球心,32=AB ,22=r ,弦心距32=M O ,13=BC ,131=r ,弦心距321=M O ,∴2121=O O ,72120sin 21==O O OM ,法一:∴292222=+==OM MD OD R ,29=R ,∴329116π=球V ;法二:2522222=-=M O OM OO ,∴29222222=+==OO r OD R ,29=R ,∴329116π=球V .题型7、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型题设:如图7,90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为()A.π12125B.π9125C.π6125D.π3125解:(1)52==AC R ,25=R ,6125812534343πππ=⋅==R V ,选C(2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为.解:BD 的中点是球心O ,132==BD R ,ππ1342==R S .类型四多面体的内切球问题模型题型8、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径.第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高;第三步:由POE ∆相似于PDH ∆,建立等式:PDPODH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高;第三步:由POG ∆相似于PFH ∆,建立等式:PFPOHF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒rS S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABCO ABCP S S S S V r -----+++=3例8(1)棱长为a 的正四面体的内切球表面积是62a π,解:设正四面体内切球的半径为r ,将正四面体放入棱长为2a的正方体中(即补形为正方体),如图,则2622313133a a V V ABCP =⋅==-正方体,又 r a r a Sr V ABC P 223343314314=⋅⋅⋅=⋅=-,∴263332a r a =,62a r =,∴内切球的表面积为6422a r S ππ==表(注:还有别的方法,此略)(2)正四棱锥ABCD S -的底面边长为2,侧棱长为3,则其内切球的半径为2217+解:如图,正四棱锥ABCD S -的高7=h ,正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ,正四棱锥ABCD S -的表面积为284+=表S ,正四棱锥ABCD S -的体积为r r S V ABCD S ⋅+==-328431表,∴3743284=⋅+r ,771427)122(7221728474-=-=+=+=r (3)三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则该三棱锥的内切球半径为47332++解:如图,3=∆ABC S ,2==∆∆ACP ABP S S ,7=∆BCP S ,743++=表S ,三棱锥ABC P -的体积为332=-ABC P V ,另一表达体积的方式是r r S V ABC P ⋅++==-347331表,∴3323473=⋅++r ,∴47332++=r巩固练习:1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为()A.3B.6C.36D.9解:【A】616164)2(2=++=R ,3=R 【三棱锥有一侧棱垂直于底面,且底面是直角三角形】【共两种】2.三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于.332π解:260sin 32== r ,16124)2(2=+=R ,42=R ,2=R ,外接球体积332834ππ=⋅【外心法(加中垂线)找球心;正弦定理求球小圆半径】3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于.解:ABC ∆外接圆的半径为,三棱锥ABC S -的直径为3460sin 22== R ,外接球半径32=R ,或1)3(22+-=R R ,32=R ,外接球体积2733233834343πππ=⋅==R V ,4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为.解:PAC ∆的外接圆是大圆,3460sin 22== R ,32=R ,5.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为.解:973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ,8121697(1sin 22⋅=-=∠P ,924sin =∠P ,42922992422===R ,829=R 6.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABCP -外接球的半径为.解:AC 是公共的斜边,AC 的中点是球心O ,球半径为1=R。
授 之 以 鱼 不 如 授 之 以 渔 ! 1
外接球问题: 类型一:)2(2
22h r R += 字母含义:h 为几何体的高;r 为底面外接圆半径;R 为几何体外接球半径 适用条件:圆柱、直棱柱、一条棱垂直于一个面的棱锥 类型二:h R h
r 222+=
字母含义:h 为几何体的高;r 为底面外接圆半径;R 为几何体外接球半径 适用条件:圆锥、各侧棱相等的棱锥
类型三:82
222c b a R ++= 字母含义:a ,b ,c 分别为几何体棱长;R 为几何体外接球半径
适用条件:对棱相等的三棱锥 类型四:42
2
2212l r r R -+= 字母含义:r 1,r 2分别为两个面的外接圆半径;l 为两个面交线长度;R 为几何体外接球半径
适用条件:有两个面相互垂直的三棱锥 类型五:4cos 22
2222sin l n m R mn +-+=αα 字母含义:m ,n 分别为两个面的外接圆圆心到交线的距离;l 为两个面的交线长度;α为两个面
的夹角;R 为几何体外接球半径
适用条件:任意三棱锥 类型六:22
22c b a R ++=外 字母含义:a ,b ,c 分别为墙角的三条棱;R 为几何体外接球半径
适用条件:墙角问题 类型七:a R 4
6=外 字母含义:a 为棱长;R 为几何体外接球半径
适用条件:正四面体
内切球问题 类型一:a R 12
6=内 字母含义:a 为棱长;R 为几何体外接球半径
适用条件:正四面体 类型二:s 3表
v R =
2
正人先正心,育人先育德!字母含义:s为表面积,v为体积;R为几何体内切球半径
适用条件:多面体。
立体几何中的外接球与内切球问题在我们的数学学习中,立体几何是非常重要的一部分。
在立体几何学习中,我们不仅需要掌握各种图形的形状和性质,也需要深入了解这些图形中的各种关系。
其中外接球和内切球是两个非常重要的概念,在立体几何中被广泛使用。
一、外接球外接球是指和一个多面体的所有顶点都相切的球。
在三维空间中,一个正四面体的外接球,就是四面体的四个顶点构成的球。
同理,其他多面体都有一组外接球。
外接球的性质可以帮助我们计算多面体的各种数据。
对于正四面体而言,我们可以得知,外接球的半径和棱长之间的关系为:外接球的半径等于正四面体棱长的一半。
这个特点可以应用于其他多面体中,为我们计算多面体提供更多帮助。
二、内切球内切球是指可以被一个多面体的所有面都切到的球。
在三维空间中,一个正四面体的内切球,就是以正四面体的每个面为切面所构成的球。
同理,其他多面体都有一组内切球。
内切球的性质可以帮助我们更好地了解多面体的各种性质。
对于正四面体而言,我们可以得知,内切球的半径和棱长之间的关系为:内切球的半径等于正四面体棱长的三分之一。
通过内切球的特点,我们可以更好地了解多面体的横截面形状,深入了解多面体的性质。
三、外接球与内切球的应用外接球和内切球在数学学科中非常重要。
在生活中,我们可以看到不少与这两个概念有关的例子。
例如,在搭建玩具拼图时,我们可以注意到玩具拼图中各个构件的外接球和内切球的关系。
同样的,建筑设计和工程规划中也常常涉及到多面体的外接球和内切球问题。
此外,街头艺术品和雕塑等艺术作品中也常常出现多面体和其相应的外接球或内切球。
总之,立体几何中的外接球和内切球是我们不能忽视的重要概念。
它们不仅仅是数学学科中的知识点,也与我们日常生活中的许多方面有着密不可分的关系。
因此,我们应该更加深入了解这两个概念,并将其应用在我们的学习和生活中,从而更好地了解和利用立体几何的基础知识。
几何体的外接球与内切球的有关问题一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点,此类问题实质是计算球的半径或确定球心O 的位置问题,其中球心的确定是关键. (一) 由球的定义确定球心球的定义:在空间中,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论. 结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点,由球心、底面中心及底面一顶点构成的直角三角形便可得球半径.(在1BOO Rt ∆中,21212OO BO BO +=,即222)2(h r R +=.)结论4:正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形利用勾股定理求得. (以正三棱锥为例:设正三棱锥的底面△ABC 的边长为a ,高为h ,外接球球心为O ,半径为R .在1AOO Rt ∆中,21212OO AO AO +=,即222)(33R h a R -+⎪⎪⎭⎫⎝⎛=.)结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心,则公共斜32R a=2222a b c R ++=BC边的一半就是其外接球的半径.(二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处. 1.可构造正方体的类型:①正四面体:棱长对应正方体的面对角线.① ② ③②三条侧棱两两垂直的正三棱锥:底面棱长对应正方体的面对角线,侧棱对应正方体的棱长. ③四个面都是是直角三角形的三棱锥:最长的棱长对应正方体的体对角线. 2.可构造长方体和正方体的类型①同一个顶点上的三条棱两两垂直的四面体;②三个侧面两两垂直的三棱锥;③有三个面是直角三角形的三棱锥;①与②与③ ④④相对的棱相等的三棱锥:设对应长方体的长、宽、高分别为a 、b 、c ,则BC 2=a 2+b 2,AC 2=a 2+c 2,AB 2=b 2+c 2. 所以对应长方体的体对角线为2222222AB AC BC c b a ++=++.⑤含有其它线面垂直关系的棱锥. (三) 由性质确定球心利用球心O 与截面圆圆心O’的连线垂直于截面圆,确定球心. 记球的半径为R ,截面圆的半径为r ,球心O 与截面圆圆心O’A BCDABCPABCP的距离为d,则有R2=r2+d 2.(四) 圆柱外接球模型计算球的半径一个底面半径为r ,高为h 的圆柱,求它的外接球半径. 222)2(h r R +=(1) (2) (3)变形一:如果我们对圆柱上下底面对应位置处,取相同数量的点,比如都取三个点,如图(1)所示.我们可以得到(直)三棱柱,它的外接球其实就是这个圆柱的外接球,所以说直棱柱的外接球求半径符合这个模型. 在这里棱柱的高就是公式中的h ,而棱柱底面△ABC 外接圆的半径则是公式中的r .变形二:如果把三棱柱上面的C 1去掉,如图(2)所示,我们得到有一个侧面⊥矩形底面的四棱锥,其中r 为垂直底面的侧面△ABC 的外接圆半径,h 为垂直于那个侧面的底面边长AA 1.变形三:如果把上面的那个三棱柱上面的B 1,C 1两点去掉,如图(3)所示,我们得到一根侧棱⊥底面的三棱锥,其中r 为底面△ABC 外接圆半径,h 为垂直于底面的那条侧棱AA 1.二、内切球问题若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.结论1:内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等. 结论2:正多面体的内切球和外接球的球心重合.结论3:正棱锥的内切球和外接球球心都在高线上,但不重合. 结论4:基本方法:构造三角形利用相似比和勾股定理. 结论5:体积分割是求内切球半径的通用做法. (一)正方体的的内切球设正方体的棱长为a ,求(1)内切球半径;(2)与棱相切的球半径.Rr2h A BC1A 1B 1C A BC1A 1B A BC1A(1)内切球:截面图为正方形的内切圆,得2a R =. (2)棱切球:切点为正方体各棱的中点,截面图为为正方形的外接圆,得22a R =. (二)棱锥的内切球(分割法)将内切球的球心与棱锥的各个顶点连线,将棱锥分割成以原棱锥的面为底面,内切球的半径为高的小棱锥,根据分割前后的体积相等,列出关于半径的方程.设三棱锥的棱长为a ,内切球半径为r.V V V V VPAB O PBC O PAC O ABC O ABCP -----+++=r S r S r S r S PAB PBC PAC ABC 31313131+++= r S S S S PAB PBC PAC ABC )(31+++= 内切球r S ABC P -=31所以ABCP ABCP S V r --=3内切球一般地,记棱锥的体积为V ,表面积为S ,则内切球的半径为SV r 3=. (三)圆柱、圆锥的内切球(截面法)(1)圆柱的内切球:圆柱的轴截面为正方形,记圆柱的底面圆的半径r ,内切球的半径R ,则R =r . (2)圆锥的内切球:圆锥的轴截面为三角形的内切圆,记圆锥的底面圆的半径r ,内切球的半径R ,由于在△ABC 中,所以CS R 2=.备注:1.三角形内切圆的半径S S S S AOBAOC BOC ABC ∆∆∆∆++=r c b a cr br ar )(21212121++=++= 内切圆r C ABC ∆=21所以三角形内切圆的半径为CSr 2=,其中S 为△ABC 的面积,C 为△ABC 的周长. 2. 三角形外接圆的半径利用正弦定理R C c B b A a 2sin sin sin ===,C cB b A a R sin 2sin 2sin 2===. ①正三角形:a a R 3360sin 2=︒=,其中a 为正三角形的边长.②直角三角形:290sin 2cc R =︒=,其中c 为直角三角形的斜边.3. 正三角形的内切圆与外接圆的半径之比正三角形的内切圆与外接圆的两个圆心“二心合一”. 设正三角形的边长为a ,内切圆半径为r ,外接圆半径为R.由于a a R 3360sin 2=︒=,a a a a a a C S r 6360sin 2122=++︒⋅⋅⋅⨯==, 所以1:2:=r R ,即圆心O 为正三角形高h 的三等分点.4. 正四面体的内切球与外接球的半径之比正四面体的内切球与外接球的两个球心“二心合一”. 设正四面体A-BCD 的棱长为a ,内切球半径为r ,外接球 半径为R ,则OA=OB=R ,OE=r.∵底面△BCD 为正三角形,∴BE=a 33 在BEO Rt ∆中,222OE BE BO +=,即22233r a R +⎪⎪⎭⎫ ⎝⎛=,得a R 46= ∴1:3:=r R ,即球心O 为正四面体高h 的四等分点. 5.正三棱柱的内切球与外接球的半径之比正三棱柱的内切球与外接球的球心是重合的,过侧棱1AA 和它们的球心O 作截面如下图所示:设正三棱柱底面边长为a . 由于内切球投影到底面的圆是底面正三角形的内切圆,所以a R 632=,从而正三棱柱的高为a R h 3322==. 在O D A Rt 11∆中,得22222211211256333a a a R D A R =⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=,a R 1251=∴因此1:5:21=R R .。
--简单几何体的外接球与内切球问题定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不重合。
4、基本方法:构造三角形利用相似比和勾股定理。
5、体积分割是求内切球半径的通用做法。
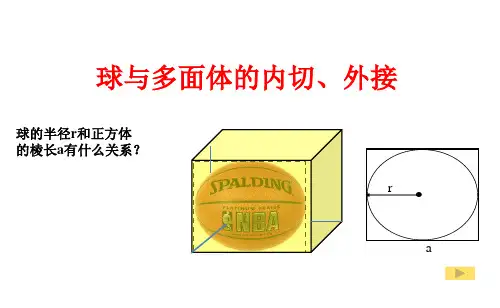
一、 直棱柱的外接球 1、长方体的外接球:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2为体对--角线长l 即2222c b a R ++=2、 正方体的外接球:正方体的棱长为a ,则正方体的体对角线为a 3,其外接球的直径R 2为a 3。
3、其它直棱柱的外接球:方法:找出直棱柱的外接圆柱,圆柱的外接球就是所求直棱柱的外接球。
例1、一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为 .例2、已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是A.16πB.20πC.24πD.32π 二、 棱锥的外接球 1、正棱锥的外接球方法:球心在正棱锥的高线上,根据球心到各个顶点的距离是球半径,列出关于半径的方程。
例3、正四棱锥S ABCD -,点S A B C D 、、、、都在同一球面上,则此球的体积--为 .例5、若正四面体的棱长为4,则正四面体的外接球的表面积为___________。
例6、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是:( ) (A )433 (B)33(C)43 (D)1232、补体方法的应用(1)、正四面体(2)、三条侧棱两两垂直的三棱锥 (3)、四个面均为直角三角形的三棱锥例7、如果三棱锥的三个侧面两两垂直,它们的面积分别为62cm 、42cm 和32cm ,那么它的外接球的体积是 。
αR P d r O O'几何体的外接球和内切球问题20180108
基础知识:
1.常见平面图形:正方形,长方形,正三角形的外接圆和内切圆
长方形(正方形)的外接圆半径为对角线长的一半,正方形的内切圆半径为边长的一半;
正三角形的内切圆半径:36a 外接圆半径:33a 三角形面积:234
a 正三角形三心合一,三线合一,心把高分为2:1两部分。
2.球的概念:
概念1:与定点距离等于或小于定长的点的集合,叫做球体,简称球.,定长叫球的半径;
与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示,例如球O 或O . 概念2:半圆以它的直径为旋转轴,旋转所成的曲面叫做球面,球面所围成的几何体叫做球体,简称球。
3.球的截面:
用一平面α去截一个球O ,设OO '是平面α的垂线段,O '为垂足,且
OO d '=,所得的截面是以球心在截面内的射影为圆心,以22r R d =-为半
径的一个圆,截面是一个圆面.
球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做
小圆.
4.空间几何体外接球、内切球的概念: 定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
长方体的外接球 正方体的内切球
5.外接球和内切球性质:
(1)内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
(2)正多面体的内切球和外接球的球心重合。
(3)正棱锥的内切球和外接球球心都在高线上,但不重合。
(4)基本方法:构造三角形利用相似比和勾股定理。
(5)体积分割是求内切球半径的通用做法。
6.公式:球的表面积公式:24S R π=;球的体积公式:343V R π= 长方体的外接球半径公式:2
2
22c b a R ++=,其中,,a b c 分别为长方体共顶点的3条棱长 正棱锥的外接球半径公式:2
,2a R h
= 2侧棱=2R h ⋅外正棱锥,其中a 为侧棱长,h 为正棱锥的高 正棱柱的外接球球心在两底面中心连线的中点处。
典型例题:
题型一:球的概念
例1. (1)已知球的直径为8cm ,那么它的表面积为__________,体积为___________
(2)已知球的表面积为144π2cm ,那么它的体积为___________
(3)已知球的体积为36π,那么它的表面积为__________
(4)如果两个球的体积之比为8:27,那么两个球的表面积之比为__________
例2.(1)(2012年新课标文科)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )
A .6π
B .43π
C .46π
D .63π
(2)已知过球面上,,A B C 三点的截面和球心的距离为球半径的一半,且2AB BC CA ===,求球的表面积.
(3)(2013年高考课标Ⅰ卷(文))已知H 是球O 的直径AB 上一点,:1:2AH HB =,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为_______.
(4)(2013年高考新课标1(理))如图,有一个水平放置的透明无盖的正方体容器,容器高
8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如
果不计容器的厚度,则球的体积为 ( )
A .35003cm π
B .38663cm π
C .313723cm π
D .320483
cm π 题型二:与长方体、正方体(柱体)有关的外接球问题
例3.(1)设正方体的棱长为233
,则它的外接球的表面积为( ) A . B .2π C .4π D . (2)已知正方体外接球的体积是,那么正方体的棱长等于( ) A .22 B . C . D . π38
π3
4π3
323323243
34
例4.(1)(2010年新课标文科)设长方体的长、宽、高分别为2a 、a 、a ,其顶点都在一个球面上,则该球的表面积为( )
A .23a π
B .26a π
C .212a π
D .224a π
(2)一个正四棱柱的各个顶点在一个直径为2 cm 的球面上.如果正四棱柱的底面边长为1 cm ,那么该棱柱的表面积为 cm 2. (3)(2013年辽宁数学(理))已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的半径为( )
A .3172
B .210
C .132
D .310
题型三:与正锥体有关的外接球问题
例5.(1)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( )
A .334
B .33
C .34
D .312
(2)(2012年高考辽宁理)已知正三棱锥ABC ,点P ,A ,B ,C 都在半径为的求面上,若PA ,PB ,PC 两两互相垂直,则球心到截面ABC 的距离为________.
例6.(1)(2013年高考课标Ⅱ卷(文))已知正四棱锥O —ABCD 的体积为322
,底面边长为3,则以O 为球心,OA 为半径的球的表面积为________.
(2)如图,半径为2的半球内有一内接正六棱锥,
则此正六棱锥的侧面积是________.
题型四:其他柱体、锥体的外接球问题
例7.(1)直三棱柱的各顶点都在同一球面上,若,
,则此球的表面积等于 .
(2)四棱锥S ABCD -的五个顶点都在一个球面上,底面是边长为2的正方形,SD ⊥平面ABCD ,且SD AB =,则其外接球的体积为 .
(3)(2015年新课标2文科)已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为( )
A .
B .
C .
D .
题型五:柱体、锥体的内切球问题
例8.(1)正方体的内切球与其外接球的体积之比为( )
A .1:3
B .1:3
C .1:33
D .1:9
(2)正三棱锥的高为1,底面边长为62,正三棱锥内有一个球与其四个面相切.求球的表面积与体积.
P -3P ABCDEF -111ABC A B C -12AB AC AA ===120BAC ∠=︒B A ,O ︒=∠90AOB C ABC
O -O π36π64π144π256
拓展练习:
2,四个顶点在同一个球面上,则此球的表面积为( )
A .3π
B .4π
C .
D .6π
3.一个四棱柱的底面是正方形,侧棱与底面垂直,其长度为4,棱柱的体积为16,棱柱的各顶点在一个球面上,则这个球的表面积是( )
A .16π
B .20π
C .24π
D .32π
7.(2012辽宁文)已知点,,,,P A B C D 是球O 表面上的点,PA ⊥平面ABCD ,四边形ABCD 是边长为若
PA =OAB ∆的面积为__________.
8.球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点,其中18=AB ,24=BC 、30=AC ,球心到这个截面的距离为球半径的一半,求球的表面积.。