与角有关的辅助线(过程训练二)(人教版)(含答案)

人教版八年级上第12章全等三角形热门考点整合应用训练含答案名师点金：本章主要学习了全等三角形的性质与判定及角平分线的性质与判定，对于三角形全等主要考查利用全等三角形证明线段或角的等量关系，以及判断位置关系等，对于角平分线主要考查利用角平分线的性质求距离、证线段相等．两个概念概念1：全等形1．如图，将标号为A，B，C，D的正方形沿图中的虚线剪开后，得到标号为N，Q，M，P的四个图形，填空：A与________对应；B与________对应；C与________对应；D与________对应．(第1题) 概念2：全等三角形2．如图，已知△ABE与△ACD全等，∠1＝∠2，∠B＝∠C，指出全等三角形中的对应边和对应角．(第2题)3．如图所示，已知△ABD≌△ACD，且B，D，C在同一条直线上，那么AD与BC有怎样的位置关系？为什么？(第3题)两个性质性质1：全等三角形的性质4．【·天水】(1)如图①，已知△ABC，以AB，AC为边分别向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形(尺规作图，不写作法，保留作图痕迹)，并证明：BE＝CD；(2)如图②，已知△ABC，以AB，AC为边分别向△ABC外作正方形ABFD和正方形ACGE，连接BE，CD，猜想BE与CD有什么数量关系？并说明理由．(第4题)性质2：角平分线的性质5．如图，在正方形ABCD中，点E是BC的中点，点F在CD上，∠EAF＝∠BAE.求证：AF＝BC＋FC.(第5题)判定1：全等三角形的判定6．课间，小明拿着老师的等腰直角三角尺玩，不小心掉到两堆砖块之间，如图所示．(1)求证：△ADC≌△CEB；(2)已知DE＝35 cm，请你帮小明求出砖块的厚度a的大小(每块砖的厚度相同)．判定2：角平分线的判定7．如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF.(1)求证：AD平分∠BAC；(2)猜想写出AB＋AC与AE之间的数量关系并给予证明．(第7题)四个技巧技巧1：构造全等三角形法8．如图∠BAC是钝角，AB＝AC，D，E分别在AB，AC上，且CD＝BE.求证：∠AEB＝∠ADC.(第8题)9．如图，AB＝DC，∠A＝∠D，求证：∠ABC＝∠DCB.(第9题)技巧2：构造角平分线法10．【中考·黄冈】已知：如图，AB＝AC，BD＝CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE＝DF.(第10题)技巧3：截长(补短)法11．如图，AB∥CD，CE，BE分别平分∠BCD和∠CBA，点E在AD上，求证：BC ＝AB＋CD.(第11题)技巧4：倍长中线法12．如图，CE，CB分别是△ABC，△ADC的中线，且∠ACB＝∠ABC.求证：CD＝2CE.(第12题)两种思想思想1：建模思想13．如图，某段河流的两岸是平行的，数学兴趣小组在老师的带领下不用涉水过河就测到了河的宽度，他们是这样做的：①在河流的一条岸边B点，选对岸正对的一棵树A；②沿河岸直走20步有一棵树C，继续前行20步到达D处；③从D处沿岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；④测得DE的长就是河宽AB.请你证明他们做法的正确性．思想2：转化思想14．如图，已知AB＝AE，∠C＝∠D，BC＝ED，点F是CD的中点，则AF平分∠BAE，为什么？(第14题)答案1．M ；N ；Q ；P2．解：AB 与AC ，AE 与AD ，BE 与CD 是对应边；∠B 与∠C ，∠2与∠1，∠BAE 与∠CAD 是对应角．3．解：AD ⊥BC. 理由略． 4．解：(1)完成作图，如图所示．(第4题)证明：∵△ABD 和△ACE 都是等边三角形， ∴AD ＝AB ，AC ＝AE ，∠BAD ＝∠CAE ＝60°.∴∠BAD ＋∠BAC ＝∠CAE ＋∠BAC ，即∠CAD ＝∠EAB. ∴△CAD ≌△EAB. ∴CD ＝EB ，即BE ＝CD. (2)BE ＝CD.理由如下：∵四边形ABFD 和四边形ACGE 都是正方形， ∴AD ＝AB ，AC ＝AE ，∠BAD ＝∠CAE ＝90°.∴∠BAD ＋∠BAC ＝∠CAE ＋∠BAC ，即∠CAD ＝∠EAB. ∴△CAD ≌△EAB. ∴CD ＝EB ，即BE ＝CD.5．证明：如图，过点E 作EG ⊥AF ，垂足为点G.连接EF. ∵∠BAE ＝∠EAF ，∴AE 为∠BAF 的平分线． 又∵EB ⊥AB ，EG ⊥AF ，∴EB ＝EG.在Rt △ABE 和Rt △AGE 中，⎩⎪⎨⎪⎧EB ＝EG ，AE ＝AE ，∴Rt △ABE ≌Rt △AGE(HL )，∴AB ＝AG . ∵在正方形ABCD 中，AB ＝BC ，∴BC ＝AG.又∵点E 是BC 的中点， ∴BE ＝EC ＝EG .在Rt △EGF 和Rt △ECF 中，⎩⎪⎨⎪⎧EG ＝EC ，EF ＝EF ，∴Rt △EGF ≌Rt △ECF(HL )． ∴GF ＝CF ，∴AF ＝AG ＋GF ＝BC ＋FC.(第5题)6．(1)证明：由题意得AC ＝BC ，∠ACB ＝90°，AD ⊥DE ，BE ⊥DE ，∴∠ADC ＝∠CEB ＝90°，∠ACD ＋∠BCE ＝90°.∴∠ACD ＋∠CAD ＝90°，∴∠BCE ＝∠CAD.在△ADC 和△CEB 中，⎩⎪⎨⎪⎧∠ADC ＝∠CEB ，∠CAD ＝∠BCE ，AC ＝CB ，∴△ADC ≌△CEB(AAS )．(2)解：由题意得AD ＝4a ，BE ＝3a.由(1)知△ADC ≌△CEB ，∴DC ＝BE ＝3a ，CE ＝AD ＝4a ，∴DE ＝DC ＋CE ＝7a.∵DE ＝35 cm ，∴a ＝5 cm .答：砖块的厚度a 为5 cm .7．(1)证明：∵DE ⊥AB 于E ，DF ⊥AC 于F ，∴∠E ＝∠AFD ＝∠DFC ＝90°，在Rt △BDE 和Rt △CDF 中，∵BD ＝CD ，BE ＝CF ，∴Rt △BDE ≌Rt △CDF ，∴DE ＝DF ，∴AD 平分∠BAC.(2)解：AB ＋AC ＝2AE.证明如下：由(1)可知AD 平分∠BAC ，∴∠EAD ＝∠CAD.在△AED 与△AFD 中，∵∠EAD ＝∠CAD ，∠E ＝∠AFD ＝90°，AD ＝AD ，∴△AED ≌△AFD ，∴AE ＝AF.又∵BE ＝CF ，∴AB ＋AC ＝AE －BE ＋AF ＋CF ＝AE ＋AE ＝2AE.8．证明：过点B ，C 分别作CA ，BA 延长线的垂线，垂足分别为F ，G. 在△ABF 和△ACG 中， ⎩⎪⎨⎪⎧∠BFA ＝∠CGA ＝90°，∠FAB ＝∠GAC ，AB ＝AC ，∴△ABF ≌△ACG(AAS )． ∴BF ＝CG.在Rt △BEF 和Rt △CDG 中，⎩⎪⎨⎪⎧BF ＝CG ，BE ＝CD ， ∴Rt △BEF ≌Rt △CDG(HL )．∴∠AEB ＝∠ADC.点拨：判定两个三角形全等时，先根据已知条件或求证的结论确定三角形，再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．9．证明：分别取AD ，BC 的中点N ，M ，连接BN ，CN ，MN ，则有AN ＝ND ，BM ＝MC.在△ABN 和△DCN 中，⎩⎪⎨⎪⎧AN ＝DN ，∠A ＝∠D ，AB ＝DC ，∴△ABN ≌△DCN(SAS )． ∴∠ABN ＝∠DCN ，NB ＝NC. 在△NBM 和△NCM 中，⎩⎪⎨⎪⎧NB ＝NC ，BM ＝CM ，NM ＝NM ，∴△NBM ≌△NCM(SSS )． ∴∠NBC ＝∠NCB.∴∠NBC ＋∠ABN ＝∠NCB ＋∠DCN ， 即∠ABC ＝∠DCB.点拨：证明三角形全等时常需添加适当的辅助线，辅助线的添加以能创造已知条件为上策，如本题取AD ，BC 的中点就是把中点作为了已知条件．分散证明，也是几何证明中的一种常用技巧．10．证明：连接AD.∵AB ＝AC ，BD ＝CD ，AD ＝AD ， ∴△ABD ≌△ACD ，∴∠BAD ＝∠CAD ， ∴AD 是∠EAF 的平分线． ∵DE ⊥AB ，DF ⊥AC ，∴DE ＝DF.11．证明：(方法一——截长法)如图①，在BC 上取一点F ，使BF ＝BA.连接EF ，∵CE ，BE 分别平分∠BCD ，∠CBA ，∴∠3＝∠4，∠1＝∠2. 在△ABE 和△FBE 中， ⎩⎪⎨⎪⎧BA ＝BF ，∠1＝∠2，BE ＝BE.∴△ABE ≌△FBE(SAS )． ∴∠A ＝∠5.∵AB ∥CD ，∴∠A ＋∠D ＝180°，而∠5＋∠6＝180°，∴∠6＝∠D. 在△EFC 和△EDC 中，⎩⎪⎨⎪⎧∠6＝∠D ，∠3＝∠4，EC ＝EC ，∴△EFC ≌△EDC(AAS )，∴FC ＝DC ，∴BC ＝BF ＋CF ＝AB ＋CD.(方法二——补短法)如图②，延长BA 至点F ，使BF ＝BC ，连接EF ，∵CE ，BE 分别平分∠BCD ，∠CBA ，∴∠1＝∠2＝12∠ABC ，∠3＝∠4＝12∠BCD. 在△BEF 和△BEC 中，⎩⎪⎨⎪⎧BF ＝BC ，∠1＝∠2，BE ＝BE ，∴△BEF ≌△BEC(SAS )．∴EF ＝EC ，∠F ＝∠3＝∠4.∵AB ∥CD ，∴∠7＝∠D.在△AEF 和△DEC 中，⎩⎪⎨⎪⎧∠7＝∠D ，∠F ＝∠4，EF ＝EC.∴△AEF ≌△DEC(AAS )，∴AF ＝CD.∵BC ＝BF ＝AB ＋AF ，∴BC ＝AB ＋CD.(第11题)12．证明：如图，延长CE 到点F ，使EF ＝CE ，连接FB ，则CF ＝2CE. ∵CE 是△ABC 的中线，∴AE ＝BE.在△BEF 和△AEC 中，⎩⎪⎨⎪⎧BE ＝AE ，∠BEF ＝∠AEC ，EF ＝EC ，∴△BEF ≌△AEC(SAS )．∴∠EBF ＝∠EAC ，BF ＝AC.过点A 作AG ⊥BC 于点G ，则∠AGC ＝∠AGB ＝90°.∵∠ABC ＝∠ACB ，AG ＝AG ，∴△AGC ≌△AGB.∴AC ＝AB.又∵∠ABC ＝∠ACB ，∴∠CBD ＝∠BAC ＋∠ACB ＝∠EBF ＋∠ABC ＝∠CBF. ∵CB 是△ADC 的中线，∴AB ＝BD.又∵AB ＝AC ，AC ＝BF ，∴BF ＝BD.在△CBF 和△CBD 中，⎩⎪⎨⎪⎧CB ＝CB ，∠CBF ＝∠CBD ，BF ＝BD ，∴△CBF ≌△CBD(SAS )．∴CF ＝CD.∴CD ＝2CE.(第12题)13．证明：由做法知：在△ABC 和△EDC 中，⎩⎪⎨⎪⎧∠ABC ＝∠EDC ＝90°，BC ＝DC ，∠ACB ＝∠ECD ，∴△ABC ≌△EDC(ASA )．∴AB ＝ED ，即他们的做法是正确的．14．解：连接BF ，EF.∵点F 是CD 的中点，∴CF ＝DF.在△BCF 和△EDF 中，⎩⎪⎨⎪⎧BC ＝ED ，∠C ＝∠D ，CF ＝DF ，∴△BCF ≌△EDF(SAS )．∴BF ＝EF.在△ABF 和△AEF 中，⎩⎪⎨⎪⎧AB ＝AE ，BF ＝EF ，AF ＝AF ，∴△ABF ≌△AEF(SSS )．∴∠BAF ＝∠EAF.∴AF 平分∠BAE.。

人教版数学八年级下期第十八章平行四边形含辅助线证明题训练1.已知边长为2的正方形ABCD中，P是对角线AC上的一个动点（与点A，C不重合），过点P作PE⊥PB，PE交DC于点E，过点E作EF⊥AC，垂足为点F．（1）求证：PB＝PE；（2）在点P的运动过程中，PF的长度是否发生变化？若不变，求出这个不变的值；若变化，试说明理由．2.在▱ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D=30°，AB=6，求△ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB=AF．求证：ED-AG=FC．3.如图，在平行四边形ABCD中，AC，BD交于点O，且AO＝BO，∠ADB的平分线DE交AB于点E．（1）求证：四边形ABCD是矩形．（2）若AB＝8，OC＝5，求AE的长．4.如图，在正方形ABCD中，E是边AB上一动点（不与点A，B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E 作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：GF＝GC；（2）用等式表示线段BH与AE的数量关系，并证明．5.如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC，CF为邻边作平行四边形ECFG．（1）证明平行四边形ECFG是菱形；（2）若∠ABC=120°，连接BG，CG，DG，①求证：△DGC≌△BGE；②求∠BDG的度数；（3）若∠ABC=90°，AB=8，AD=14，M是EF的中点，求DM的长．6.已知正方形ABCD如图所示，连接其对角线AC，∠BCA的平分线CF交AB于点F，过点B作BM⊥CF于点N，交AC于点M，过点C作CP⊥CF，交AD延长线于点P．(1)求证：DP＝BF；(2)若正方形ABCD的边长为4，求DP的长；(3)求证：CP＝BM＋2FN．7.如图，四边形ABCD是菱形，E是AB的中点，AC的垂线EF交AD于点M，交CD的延长线于点F．（1）求证：AM=AE；（2）连接CM，DF=2．①求菱形ABCD的周长；②若∠ADC=2∠MCF，求ME的长．8.在菱形ABCD中，AB＝4，∠ABC＝60°，E是对角线AC上一点，F是线段BC延长线上一点．且CF＝AE，连接BE、EF．（1）如图1，若E是线段AC的中点，求EF的长；（2）如图2．若E是线段AC延长线上的任意一点，求证：BE＝EF．AC，将菱形ABCD绕着点B （3）如图3，若E是线段AC延长线上的一点，CE＝12顺时针旋转α°（0≤α≤360），请直接写出在旋转过程中DE的最大值．9.如图所示，在边长为1的菱形ABCD中，∠DAB=60°，M是AD上不同于A，D两点的一动点，N是CD上一动点，且AM+CN=1.（1）证明：无论M，N怎样移动，△BMN总是等边三角形；（2）求△BMN面积的最小值.10.如图，正方形ABCD中，F在CD上，AE平分∠BAF，E为BC的中点．求证：AF=BC+CF．11.已知：如图（1），点E、F分别为正方形ABCD的边BC、DC上的点，线段AE和AF分别交BD于点M和点N，连接MF，MF⊥AE于点M．（1）求证：∠EAF＝45°；（2）如图（2），连接EF，当AD＝5，DF＝1时，求线段EF的长度；BD．（3）如图（3），作FR⊥BD于R．求证：RM=12BC，CE⊥AB于点E，F是AD的中点，连接12.如图，在平行四边形ABCD中，AB=12EF，CF．求证：（1）EF=CF；（2）∠EFD=3∠AEF．13.如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．（1）求∠EAF的度数；（2）如图2，连接FC交BD于M，交AD于N．求证：BD=AF+2DM．14.已知：如图，G为平行四边形ABCD中BC边的中点，点E在AD边上，且∠1＝∠2．（1）求证：E是AD的中点；（2）若F为CD延长线上一点，连接BF，得∠3＝∠2，求证：CD＝BF+DF．15.如图，四边形ABCD是平行四边形，AD=AC，AD⊥AC，E是AB的中点，F是AC延长线上一点．(1)若ED⊥EF，求证：ED=EF：(2)在(1)的条件下，若DC的延长线与FB交于点P，试判断四边形ACPE是否为平行四边形．并证明你的结论(请先补全图形，再解答)：(3)若ED=EF，则ED与EF垂直吗?若垂直给出证明，若不垂直说明理由．16.在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F。

初中数学辅助线的添加方法及压轴题答题技巧1三角形中常见辅助线的添加1. 与角平分线有关的（1）可向两边作垂线。

（2）可作平行线，构造等腰三角形（3）在角的两边截取相等的线段，构造全等三角形2. 与线段长度相关的（1）截长：证明某两条线段的和或差等于第三条线段时，经常在较长的线段上截取一段，使得它和其中的一条相等，再利用全等或相似证明余下的等于另一条线段即可（2）补短：证明某两条线段的和或差等于第三条线段时，也可以在较短的线段上延长一段，使得延长的部分等于另外一条较短的线段，再利用全等或相似证明延长后的线段等于那一条长线段即可（3）倍长中线：题目中如果出现了三角形的中线，方法是将中线延长一倍，再将端点连结，便可得到全等三角形。

（4）遇到中点，考虑中位线或等腰等边中的三线合一。

3. 与等腰等边三角形相关的（1）考虑三线合一（2）旋转一定的度数，构造全都三角形，等腰一般旋转顶角的度数，等边旋转60 °2四边形中常见辅助线的添加特殊四边形主要包括平行四边形、矩形、菱形、正方形和梯形。

在解决一些和四边形有关的问题时往往需要添加辅助线。

下面介绍一些辅助线的添加方法。

1. 和平行四边形有关的辅助线作法平行四边形是最常见的特殊四边形之一，它有许多可以利用性质，为了利用这些性质往往需要添加辅助线构造平行四边形。

（1）利用一组对边平行且相等构造平行四边形（2）利用两组对边平行构造平行四边形（3）利用对角线互相平分构造平行四边形2. 与矩形有辅助线作法（1）计算型题，一般通过作辅助线构造直角三角形借助勾股定理解决问题。

（2）证明或探索题，一般连结矩形的对角线借助对角线相等这一性质解决问题。

和矩形有关的试题的辅助线的作法较少。

3. 和菱形有关的辅助线的作法和菱形有关的辅助线的作法主要是连接菱形的对角线，借助菱形的判定定理或性质定定理解决问题。

（1）作菱形的高（2）连结菱形的对角线4. 与正方形有关辅助线的作法正方形是一种完美的几何图形，它既是轴对称图形，又是中心对称图形，有关正方形的试题较多。

学生做题前请先回答以下问题问题1：看到平行想什么？问题2：辅助线的作用是什么？问题3：如图，AB∥CD，∠α=150°，∠β=80°，求∠∠γ的度数．分析：读题标注以后，观察图形，要求∠γ的度数，要用好AB∥CD这个条件，看到平行想同位角、内错角、同旁内角，但图中没有两条平行线被第三条直线所截的结构，考虑作辅助线．可以怎么作辅助线？与角有关的辅助线（计算）（人教版）一、单选题(共7道，每道14分)1.如图，已知AB∥CD，∠B=70°，∠E=30°，则∠ECD的度数为( )A.160°B.140°C.110°D.100°答案：B解题思路：从已知出发，由AB∥CD，要找同位角、内错角和同旁内角，因此要找截线，若把BE当作截线（也可以把EC当截线），如图，延长DC交BE于点F补全图形．由AB∥CD，且∠B=70°，利用平行线的性质，可得∠BFC=70°，再由平角的定义，得∠EFC=110°；∠ECD是△EFC的一个外角，结合∠E=30°，利用外角定理，得∠ECD=∠E+∠EFC=140°．故选B．试题难度：三颗星知识点：与角有关的辅助线2.已知：如图，MN∥PQ，AB⊥PQ于点E，∠ABC=135°，则∠α=( )A.25°B.30°C.35°D.45°答案：D解题思路：从已知出发，由MN∥PQ，要找同位角、内错角和同旁内角，因此要找截线，若把DB当作截线（也可以把BA当截线），如图，延长DB交PQ于点F补全图形．由MN∥PQ，利用平行线的性质，可得∠α=∠1，因此只需要求∠1的度数即可；由AB⊥PQ，得∠BEF=90°，∠ABC是△BEF的一个外角，结合∠ABC=135°，利用外角定理，得∠1=∠ABC-∠BEF=45°，所以∠α=∠1=45°．故选D．试题难度：三颗星知识点：与角有关的辅助线3.已知：如图，∠BAC+∠C=180°，点E是CD上一点，且∠1=32°，∠AFE=110°，则∠FED的度数为( )A.78°B.64°C.55°D.60°答案：A解题思路：从已知出发，由∠BAC+∠C=180°，得AB∥CD，由平行要找同位角、内错角和同旁内角，因此要找截线，若把AF当作截线（也可以把EF当截线），如图，延长AF交CD于点G补全图形．由∠BAC+∠C=180°，利用平行线的判定，得AB∥CD，结合∠1=32°，利用平行线的性质，得∠2=∠1=32°；∠AFE是△FEG的一个外角，利用外角定理，得∠AFE=∠FED+∠2，得∠FED=∠AFE-∠2=78°．故选A．试题难度：三颗星知识点：与角有关的辅助线4.已知，如图，AB∥CD，∠B=40°，∠E=100°，则∠C的度数为( )A.100°B.120°C.140°D.130°答案：B解题思路：如图，过点E作FG∥AB，建立∠B，∠BEC和∠C之间的联系．因为CD∥AB，根据平行于同一条直线的两条直线互相平行，得FG∥CD∥AB，结合∠B=40°，根据平行线的性质，得∠1=∠B=40°，∠2+∠C=180°；又因为∠BEC=100°，那么∠2=∠BEC-∠1=60°，则∠C=180°-∠2=120°．故选B．试题难度：三颗星知识点：与角有关的辅助线5.如图，AB∥EF，∠BCD=90°，则∠α，∠β，∠γ的关系是( )A.∠β=∠α+∠γB.∠α+∠β+∠γ=180°C.∠α+∠β-∠γ=90°D.∠β+∠γ-∠α=90°答案：C解题思路：如图，过点C作MN∥AB，过点D作PQ∥AB，建立∠α，∠β，∠γ之间的联系．因为EF∥AB，根据平行于同一条直线的两条直线互相平行，得AB∥MN∥PQ∥EF，根据平行线的性质，得∠α=∠1，∠2=∠3，∠γ=∠4；已知∠BCD=90°，那么∠1+∠2=90°，所以∠α+∠2=90°，则∠2=90°-∠α；又因为∠β=∠3+∠4，则∠β=∠2+∠γ=90°-∠α+∠γ，即∠α+∠β-∠γ=90°．故选C．试题难度：三颗星知识点：与角有关的辅助线6.已知：如图，在四边形ABCD中，∠A=62°，∠B=38°，∠BCD=140°，则∠D的度数为( )A.40°B.24°C.50°D.45°答案：A解题思路：要找到∠D与∠A，∠B，∠BCD之间的关系，结合图形考虑构造辅助线，把四边形转化为基本图形（三角形），从而利用三角形内角和定理或三角形外角定理求解．如图，延长BC交AD于点F，∠1是△ABF的一个外角，结合∠A=62°，∠B=38°，利用外角定理，得∠1=∠A+∠B=100°；∠BCD又是△CDF的一个外角，结合∠BCD=140°，利用外角定理，得∠BCD=∠D+∠1，则∠D=∠BCD-∠1=40°．本题也可以通过延长DC交AB于点G，或连接AC并延长到H进行计算．故选A．试题难度：三颗星知识点：与角有关的辅助线7.如下图所示，AB∥CD，BO与DO相交于点O，从图1中可以得出，∠O=∠B+∠D，那么图2和图3针对这三个角关系的结论正确的是( )A.图2：∠O=∠B+∠D；图3：∠O=∠B+∠DB.图2：∠O=∠B+∠D；图3：∠D=∠O+∠BC.图2：∠O+∠B+∠D=360°；图3：∠O=∠B+∠DD.图2：∠O+∠B+∠D=360°；图3：∠D=∠O+∠B答案：D解题思路：从已知出发，由AB∥CD，要找同位角、内错角和同旁内角，因此要找截线或构造平行线．对图1：如图，过点O作EF∥AB，因为CD∥AB，根据平行于同一条直线的两条直线互相平行，得EF∥CD∥AB，根据平行线的性质，得∠B=∠1，∠2=∠D，所以∠BOD=∠1+∠2=∠B+∠D．对图2：如图，过点O作MN∥AB因为CD∥AB，根据平行于同一条直线的两条直线互相平行，得MN∥CD∥AB，根据平行线的性质，得∠B+∠1=180°，∠2+∠D=180°，所以∠B+∠1+∠2+∠D=∠B+∠BOD+∠D=360°．对图3：如图，由AB∥CD，得∠D=∠1，因为∠1是△OBE的一个外角，根据外角定理，得∠1=∠O+∠B，等量代换得∠D=∠O+∠B．故选D．试题难度：三颗星知识点：与角有关的辅助线。

学生做题前请先回答以下问题问题1:看到平行想什么？问题2：辅助线的作用是什么？问题3：如图，AB/7CD, Za=150°, Zp=80°,求ZZy 的度数.分析：读题标注以后，观察 图形，要求Zy 的度数，要用好AB 〃CD 这个条件，看到平行想同位角、内错角、同旁内角, 但图中没有两条平行线被第三条直线所截的结构，考虑作辅助线.可以怎么作辅助线？与角有关的辅助线（计算）（人教版）一、单选题（共7道，每道14分）1. 如图，己知 AB 〃 CD , Z B=70° , Z E=30° ,则 Z ECD 的度数为答案：B 解题思路：从已知出发，由AB 〃CD,要找同位角、内错角和同旁内角，因此要找截线，若 把BE 当作截线（也可以把EC 当截线），如图，延长DC 交BE 于点F 补全图由AB 〃CD,且ZB=70°,利用平行线的性质，可得/ BFC=70°,再由平角的定义,得ZEFC=110°； ZECD 是AEFC 的一个外角，结合ZE=30°,利 用外角定理，得ZECD=ZE+ZEFC=140°・故选B.试题难度：三颗星知识点：与角有关的辅助线 2. 己知：如图，MN 〃 PQ , AB 丄 PQ 于点 E , Z ABC=135° ,贝9 Z形.A.160°B.140°C.110°D.100°A R«=()A.25°B.30°C.35°D.45°答案：D解题思路：从己知出发，rtlMN〃PQ,要找同位角、内错角和同旁内角，因此耍找截线，若把DB 当作截线（也可以把BA当截线），如图，延长DB交PQ于点F补全图形. 由MNZ/PQ,利用平行线的性质，可得Za=Zl, 因此只需要求Z1的度数即可；由AB1PQ,得ZBEF=90°, ZABC是ABEF的一个外角，结合ZABC=135°,利用外角定理，得Z1=ZABC-ZBEF=45°,所以Za=Zl=45°.故选 D.三颗星知识点: -与角有关的辅助线3. 已知：如图，ZBAC+ZC=180°,点 E 是CD ±一点,且Zl=32°, ZAFE=110°,则ZFED 的度数为（）A.78°B.64°C.55°D.60°答案：A解题思路：从已知出发，由ZBAC+ZC=180°,得AB〃CD,由平行要找同位角、内错角和同旁内角，因此要找截线，若把AF当作截线（也可以把EF当截线），如图，延长AF交CD于点G补全图形. 由ZBAC+ZC=180°,利用平行线的判定,得AB〃CD,结合Zl=32°,利用平行线的性质，得Z2=Z1=32°； ZAFE是AFEG的一个外角, 利用外角定理，得ZAFE=ZFED+Z2,得ZFED=ZAFE-Z2=78°.故选 A.试题难度：三颗星知识点：与角有关的辅助线4. 已知，如图，AB 〃CD , Z B=40° , Z E=100° ,则Z C的度数为A.100°B.120°C.140°D.130°答案：B解题思路：如图，C D过点E作FG〃AB,建立ZB, ZBEC和ZC之间的联系.因为CD〃AB,根据平行于同一条直线的两条直线互相平行，得FG〃CD〃AB,结合ZB=40°,根据平行线的性质,得Zl=ZB=40°, Z2+ZC=180°；又因为ZBEC=100°, 那么Z2=ZBEC-Z1=6O°,则ZC=180°-Z2=120°.故选 B.试题难度：三颗星知识点：与角有关的辅助线5. 如图，AB 〃EF , Z BCD=90° ,贝'J Z a , Z p , Z y 的关系是A.Zp=Za+ZyB.Za+Zp+Z Y=180°C.Za+Zp-Z y=90oD.Zp+Zy-Z a=90°答案：ca, Zp, Z Y 之间的联系.因为EF 〃AB,根据平行于同一条直线的两条直线互相平行，得 AB 〃MN 〃PQ 〃EF,根据平行线的性质，得Za=Zl, Z2=Z3, Zy=Z4；己知ZBCD=90°, 那么Zl+Z2=90°,所以Za+Z2=90°,则Z2=90°-Za ；又因为Zp=Z3+Z4,则Zp=Z2+Z Y=90°-Za+Zy,即 Za+Zp-ZY=90°.故选 C. 试题难度：三颗星知识点：与角有关的辅助线6•已知：如图，在四边形ABCD 中，ZA=62°, ZB=38°, ZBCD=140°,则ZD 的度数为A.40°B.24°C.50°D.45°答案：A解题思路：要找到ZD 与ZA, ZB, ZBCDZ 间的关系，结合图形考虑构造辅助线，把四边 形转化为基本图形（三角形），从而利用三角形内角和定理或三角形外角定理求解.如图，A 二62。

全等三角形辅助线系列之一 与角平分线有关的辅助线作法大全一、角平分线类辅助线作法角平分线具有两条性质：a 、对称性；b 、角平分线上的点到角两边的距离相等．对于有角平分线的辅助线的作法，一般有以下四种．1、角分线上点向角两边作垂线构全等：过角平分线上一点向角两边作垂线，利用角平分线上的点到两边距离相等的性质来证明问题； 2、截取构全等利用对称性，在角的两边截取相等的线段，构造全等三角形； 3、延长垂线段题目中有垂直于角平分线的线段，则延长该线段与角的另一边相交，构成等腰三角形； 4、做平行线：以角分线上一点做角的另一边的平行线，构造等腰三角形有角平分线时，常过角平分线上的一点作角的一边的平行线，从而构造等腰三角形．或通过一边上的点作角平分线的平行线与另外一边的反向延长线相交，从而也构造等腰三角形．通常情况下，出现了直角或是垂直等条件时，一般考虑作垂线；其它情况下考虑构造对称图形．至于选取哪种方法，要结合题目图形和已知条件．图四图三图二图一QPONMPONM BAAB MNOP PONM BA典型例题精讲【例1】 如图所示，BN 平分∠ABC ，P 为BN 上的一点，并且PD ⊥BC 于D ，2AB BC BD =＋．求证：180BAP BCP ∠∠=︒＋．【解析】过点P 作PE ⊥AB 于点E ．∵PE ⊥AB ，PD ⊥BC ，BN 平分∠ABC ，∴PE PD =． 在Rt △PBE 和Rt △PBC 中， BP BPPE PD =⎧⎨=⎩， ∴Rt △PBE ≌Rt △PBC （HL ），∴BE BD =．∵2AB BC BD +=，BC CD BD =+，AB BE AE =-，∴AE CD =． ∵PE ⊥AB ，PD ⊥BC ，∴90PEB PDB ∠=∠=︒． 在△P AE 和Rt △PCD 中， ∵PE PD PEB PDC AE DC =⎧⎪∠=∠⎨⎪=⎩， ∴△P AE ≌Rt △PCD ，∴PCB EAP ∠=∠．∵180BAP EAP ∠+∠=︒，∴180BAP BCP ∠+∠=︒．【答案】见解析．【例2】 如图，已知：90A ∠=︒，AD ∥BC ，P 是AB 的中点，PD 平分∠ADC ，求证：CP 平分∠DCB ．【解析】因为已知PD 平分∠ADC ，所以我们过P 点作PE ⊥CD ，垂足为E ，则PA PE =，由P 是AB的中点，得PB PE =，即CP 平分∠DCB ．【答案】作PE ⊥CD ，垂足为E ，∴90PEC A ∠=∠=︒，∵PD 平分∠ADC ，∴PA PE =， 又∵90B PEC ∠=∠=︒，∴PB PE =， ∴点P 在∠DCB 的平分线上， ∴CP 平分∠DCB ．【例3】 已知：90AOB ∠=︒，OM 是∠AOB 的平分线，将三角板的直角顶点P 在射线OM 上滑动，两直角边分别与OA 、OB 交于C 、D ．（1）PC 和PD 有怎样的数量关系是__________． （2）请你证明（1）得出的结论．PDCBA A BCDPE【解析】（1）PC PD =．（2）过P 分别作PE ⊥OB 于E ，PF ⊥OA 于F ， ∴90CFP DEP ∠=∠=︒，∵OM 是∠AOB 的平分线，∴PE PF =，∵190FPD ∠+∠=︒，且90AOB ∠=︒，∴90FPE ∠=︒， ∴290FPD ∠+∠=︒，∴12∠=∠， 在△CFP 和△DEP 中12CPF DEPPF PE∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△CFP ≌△DEP ，∴PC PD =． 【答案】见解析．【例4】 如图①，OP 是∠MON 的平分线，请你利用该图形画一对以OP 所在直线为对称轴的全等三角形．请你参考这个作全等三角形的方法，解答下列问题：（1）如图②，在△ABC 中，∠ACB 是直角，60B ∠=︒，AD 、CE 分别是∠BAC 、∠BCA 的平分线，AD 、CE 相交于点F ，请你判断并写出FE 与FD 之间的数量关系（不需证明）； （2）如图③，在△ABC 中，60B ∠=︒，请问，在（1）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．【解析】如图①所示；（1）FE FD =．（2）如图，过点F 作FG ⊥AB 于G ，作FH ⊥BC 于H ，作FK ⊥AC 于K ， ∵AD 、CE 分别是∠BAC 、∠BCA 的平分线，∴FG FH FK ==， 在四边形BGFH 中，36060902120GFH ∠=︒-︒-︒⨯=︒， ∵AD 、CE 分别是∠BAC 、∠BCA 的平分线，60B ∠=︒， ∴()118060602FAC FCA ∠+∠=︒-︒=︒． 在△AFC 中， ()180********AFC FAC FCA ∠=︒-∠+∠=︒-︒=︒， ∴120EFD AFC ∠=∠=︒，∴EFG DFH ∠=∠， 在△EFG 和△DFH 中，EFG DFH EGF DHF FG FH ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EFG ≌△DFH ，∴FE FD = 【答案】见解析．【例5】 已知120MAN ∠=︒，AC 平分∠MAN ，点B 、D 分别在AN 、AM 上．（1）如图1，若90ABC ADC ∠=∠=︒，请你探索线段AD 、AB 、AC 之间的数量关系，并证明之；（2）如图2，若180ABC ADC ∠+∠=︒，则（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．【解析】（1）得到30ACD ACB ∠=∠=︒后再可以证得12AD AB AC ==，从而，证得结论； （2）过点C 分别作AM 、AN 的垂线，垂足分别为E 、F ，证得△CED ≌△CFB后即可得到AD AB AE ED AF FB AE AF +=-++=+，从而证得结论．【答案】（1）关系是：AD AB AC +=．证明：∵AC 平分∠MAN ，120MAN ∠=︒ ∴60CAD CAB ∠=∠=︒ 又90ADC ABC ∠=∠=︒， ∴30ACD ACB ∠=∠=︒ 则12AD AB AC ==（直角三角形一锐角为30°，则它所对直角边为斜边一半） ∴AD AB AC +=； （2）仍成立．证明：过点C 分别作AM 、AN 的垂线，垂足分别为E 、F ∵AC 平分∠MAN∴CE CF =（角平分线上点到角两边距离相等） ∵180ABC ADC ∠+∠=︒，180ADC CDE ∠+∠=︒ ∴CDE ABC ∠=∠ 又90CED CFB ∠=∠=︒， ∴△CED ≌△CFB （AAS ） ∵ED FB =，∴AD AB AE ED AF FB AE AF +=-++=+ 由（1）知AE AF AC +=， ∴AD AB AC +=．【例6】 如图，在△ABC 中，2C B ∠=∠，AD 平分∠BAC ，求证：AB AC CD -=．【解析】在AB 上截取点E ，使得AE AC =．∵AD 平分∠BAC ，∴EAD CAD ∠=∠，∴△ADE ≌△ADC （SAS ）．∴AED C ∠=∠，ED CD =． ∵2C B ∠=∠，∴=2AED B ∠∠．∵AED B EDB ∠=∠+∠，∴B EDB ∠=∠，∴BE DE =． ∴CD BE AB AE AB AC ==-=-．【答案】见解析．【例7】 如图，△ABC 中，AB AC =，108A ∠=︒，BD 平分ABC ∠交AC 于D 点．求证：BC AC CD =+．【解析】在BC 上截取E 点使BE BA =，连结DE ．∵BD 平分ABC ∠，∴ABD EBD ∠=∠． 在ABD ∆与EBD ∆中∵AB EB =，ABD EBD ∠=∠，BD BD = ∴ABD EBD ∆∆≌，∴A DEB ∠=∠∵AB AE =， ∴BAD BED ∠=∠，∴72DEC ∠=︒． 又∵361854ADB ∠=︒+︒=︒，∴72CDE ∠=︒ABCDE DCBAAB CD∴CDE DEC ∠=∠，∴CD CE = ∵BC BE EC =+，∴BC AC CD =+【答案】见解析．【例8】 已知ABC ∆中，60A ∠=︒，BD 、CE 分别平分ABC ∠和ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．【解析】在BC 上截取一点F 使得BF BE =，易证BOE BOF ∆∆≌，在根据120BOC ∠=︒推出60BOE COF ∠=∠=︒，再证明OCF OCD ∆∆≌即可．【答案】BC BE CD =+．【例9】 如图：已知AD 为△ABC 的中线，且12∠=∠，34∠=∠，求证：BE CF EF +>．【解析】在DA 上截取DN DB =，连接NE ，NF ，则DN DC =，在△DBE 和△DNE 中：E DCB AOED CBAFOED CBA∵12DN DB ED ED =⎧⎪∠=∠⎨⎪=⎩∴△DBE ≌△DNE （SAS ），∴BE NE = 同理可得：CF NF =在△EFN 中，EN FN EF +>（三角形两边之和大于第三边） ∴BE CF EF +>．【答案】见解析．【例10】 已知：在四边形ABCD 中，BC BA >，180A C ∠+∠=︒，且60C ∠=︒，BD 平分∠ABC ，求证：BC AB DC =+．【解析】在BC 上截取BE BA =，∵BD 平分∠ABC ，∴ABD EBD ∠=∠， 在△BAD 和△BED 中， BA BE ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩， ∴△BAD ≌△BED ，∴AD DE =，A BED ∠=∠． ∵180BED DEC ∠+∠=︒，180A C ∠+∠=︒． ∴C DEC ∠=∠，∴DE DC =．∴DC AD =．∵60∠=︒，∴△CDE是等边三角形，C∴DE CD CE=+=+．==，∴BC BE CE AB CD【答案】见解析．【例11】观察、猜想、探究：在△ABC中，2∠=∠．ACB B（1）如图①，当90=+；C∠=︒，AD为∠BAC的角平分线时，求证：AB AC CD （2）如图②，当90∠≠︒，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量C关系？不需要证明，请直接写出你的猜想；（3）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．【解析】（1）过D作DE⊥AB，交AB于点E，理由角平分线性质得到ED=CD，利用HL得到直角三角形AED与直角三角形ACD全等，由全等三角形的对应边相等，对应角相等，得到AE AC=，A CB B∠=∠，利用等量代换及外角性质得到一对角相等，利用等角对等∠=∠，由2AED ACB边得到BE DE=+，等量代换即可得证；=，由AB AE EB（2）AB CD AC=+，理由为：在AB上截取AG AC=，如图2所示，由角平分线定义得到=，利用SAS得到三角形AGD与三角形ACD全等，接下来同（1）一对角相等，再由AD AD即可得证；（3）AB CD AC=，如图3所示，同（2）即可得证．=-，理由为：在AF上截取AG AC【答案】（1）过D作DE⊥AB，交AB于点E，如图1所示，∵AD为∠BAC的平分线，DC⊥AC，DE⊥AB，∴DE DC=，在Rt △ACD 和Rt △AED 中，AD AD =，DE DC =， ∴Rt △ACD ≌Rt △AED （HL ），∴AC AE =，ACB AED ∠=∠， ∵2ACB B ∠=∠，∴2AED B ∠=∠， 又∵AED B EDB ∠=∠+∠，∴B EDB ∠=∠， ∴BE DE DC ==，则AB BE AE CD AC =+=+； （2）AB CD AC =+，理由为： 在AB 上截取AG AC =，如图2所示， ∵AD 为∠BAC 的平分线，∴GAD CAD ∠=∠， ∵在△ADG 和△ADC 中，AG ACGAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∴△ADG ≌△ADC （SAS ），∴CD CG =，AGD ACB ∠=∠， ∵2ACB B ∠=∠，∴2AGD B ∠=∠， 又∵AGD B GDB ∠=∠+∠，∴B GDB ∠=∠， ∴BE DG DC ==，则AB BG AG CD AC =+=+； （3）AB CD AC =-，理由为： 在AF 上截取AG AC =，如图3所示， ∵AD 为∠F AC 的平分线，∴GAD CAD ∠=∠， ∵在△ADG 和△ADC 中，AG AC GAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩，∴△ADG ≌△ADC （SAS ）， ∴CD GD =，AGD ACD ∠=∠，即ACB FGD ∠=∠，∵2ACB B ∠=∠，∴2FGD B ∠=∠，又∵FGD B GDB ∠=∠+∠，∴B GDB ∠=∠， ∴BG DG DC ==，则AB BG AG CD AC =-=-．【例12】 如图所示，在△ABC 中，3ABC C ∠=∠，AD 是∠BAC 的平分线，BE ⊥AD 于F ．求证：()12BE AC AB =-．【解析】延长BE 交AC 于点F ．则AD 为∠BAC 的对称轴，∵BE ⊥AD 于F ，∴点B 和点F 关于AD 对称， ∴12BE EF BF ==，AB AF =，ABF AFB ∠=∠． ∵3ABF FBC ABC C ∠∠=∠=∠＋，ABF AFB FBC C ∠=∠=∠∠＋， ∴3FBC C FBC C ∠∠∠=∠＋＋， ∴FBC C ∠=∠，∴FB FC =，∴()()111222BE FC AC AF AC AB ==-=-，∴()12BE AC AB =-． 【答案】见解析．【例13】 如图，已知：△ABC 中AD 垂直于∠C 的平分线于D ，DE ∥BC 交AB 于E ．求证：EA EB =．【解析】由AD 垂直于∠C 的平分线于D ，可以想到等腰三角形中的三线合一，于是延长AD 交BC 与点F ，得D 是AF 的中点，又因为DE ∥BC ，由三角形中位线定理得EA EB =．【答案】延长AD 交BC 与点F ，∵CD 平分∠ACF ，∴12∠=∠，又AD ⊥CD ， ∴ΔADC ≌ΔFDC ，∴AD FD =， 又∵DE ∥BC ，∴EA EB =．【例14】 已知：如图，在△ABC 中，3ABC C ∠=∠，12∠=∠，BE ⊥AE ．求证：2AC AB BE -=．【解析】延长BE 交AC 于M ，∵BE ⊥AE ，∴90AEB AEM ∠=∠=︒ 在△ABE 中，∵13180AEB ∠+∠+∠=︒， ∴3901∠=︒-∠ 同理，4902∠=︒-∠∵12∠=∠，∴34∠=∠，∴AB AM =∵BE ⊥AE ，∴2BM BE =， ∴AC AB AC AM CM -=-=， ∵∠4是△BCM 的外角，∴45C ∠=∠+∠ ∵3ABC C ∠=∠，∴3545ABC ∠=∠+∠=∠+∠ ∴34525C C ∠=∠+∠=∠+∠，∴5C ∠=∠ ∴CM BM =，∴2AC AB BM BE -==【答案】见解析．【例15】 如图，已知AB AC =，90BAC ∠=︒，BD 为∠ABC 的平分线，CE ⊥BE ，求证：2BD CE =．【解析】延长CE ，交BA 的延长线于点F ．∵BD 为∠ABC 的平分线，CE ⊥BE ， ∴△BEF ≌△BEC ，∴BC BF =，CE FE =． ∵90BAC ∠=︒，CE ⊥BE ，∴ABD ACF ∠=∠，又∵AB AC =，∴△ABD ≌△ACF ，∴BD CF =．∴2BD CE =．【答案】见解析．EDCBAFEDCBA课后复习【作业1】如图所示，在△ABC 中，BP 、CP 分别是∠ABC 的外角的平分线，求证：点P 在∠A 的平分线上．【解析】过点P 作PE ⊥AB 于点E ，PG ⊥AC 于点G ，PF ⊥BC 于点F ．因为P 在∠EBC 的平分线上，PE ⊥AB ，PH ⊥BC ，所以PE PF =． 同理可证PF PG =． 所以PG PE =，又PE ⊥AB ，PG ⊥AC ，所以P 在∠A 的平分线上，【答案】见解析．【作业2】已知：如图，2AB AC =，BAD CAD ∠=∠，DA DB =，求证：DC ⊥AC ．PCBAPABCD【解析】在AB 上取中点E ，连接DE ，则12AE BE AB ==． ∵DA DB =，∴DE ⊥AB ，90AED ∠=︒． 又∵2AB AC =，∴AE AC =．∵BAD CAD ∠=∠，∴△ADE ≌△ADC （SAS ）． ∴90AED ACD ∠=∠=︒，即DC ⊥AC ．【答案】见解析．【作业3】已知等腰ABC ∆，100A ∠=︒，ABC ∠的平分线交AC 于D ，则BD AD BC +=．【解析】如图，在BC 上截取BE BD =，连接DE ，过D 作DF BC ∥，交AB 于F ，于是32∠=∠，ADF ECD ∠=∠． 又∵12∠=∠，∴13∠=∠，故DF BF =．显然FBCD 是等腰梯形． ∴BF DC =，DF DC =．∵()111218010020222ABC ∠=∠=⨯︒-︒=︒，()11802802BED BDE ∠=∠=︒-∠=︒， ∴180100DEC BED ∠=︒-∠=︒，∴100FAD DEC ∠=∠=︒，∴AFD EDC ∆∆≌，AD EC =． 又∵BE BD =，∴BC BD EC BD AD =+=+．【答案】见解析．EDCBAABCD【作业4】如图，已知在△ABC 中，AD 、AE 分别为△ABC 的内、外角平分线，过顶点B 作BF ⊥AD ，交AD 的延长线于F ，连接FC 并延长交AE 于M ．求证：AM ME =．【解析】延长AC ，交BF 的延长线于点N ．∵AD 平分∠BAC ，BF ⊥AD ，∴△AFB ≌△AFN ，∴BF NF =． ∵AD 、AE 分别为△ABC 的内、外角平分线，∴EA ⊥F A ． ∵BF ⊥AF ，∴BF ∥AE ．∴::BF ME CF CM =，::FN AM CF CM =． ∵BF NF =，∴AM ME =．【答案】见解析．ECMF EDCBAN MFEDCBA。

人教版八年级数学上册教材知识点变式提高培训系列11.2 与三角形有关的角（1）知识点三：表示方位的角方位角是指以南北方向为准，向两边偏的角度大小，即“南偏东 x”“南偏西 x”“北偏东45称为西北方向。

x”“北偏西 x”，我们通常把南偏东45称为东南方向，北偏西【例题3】如图所示，一艘渔船在B处测得灯塔A在北偏东60°的方向，另一艘货轮在C处测得灯塔A在北偏东40°的方向，那么在灯塔A处观看B和C时的视角∠BAC是多少度？【练习】1.如图所示，有一艘渔船上午9点在A处沿正东方向航行，在A处测得灯塔C在北偏东60°方向上，行驶2h到达B处，在B处测得灯塔C，在北偏东15°方向上，试求∠ABC内角的度数．知识点四：三角形的外角(1)定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角.注意：三角形共有六个外角，其中有公共顶点的两个相等，因此共有三对.(2)三角形外角的特点：∠顶点在三角形的一个顶点上；∠一条边是三角形的一边；∠另一条边是三角形某条边的延长线.(3)三角形的外角性质：∠三角形的外角和为360°.∠三角形的一个外角等于和它不相邻的两个内角的和.∠三角形的一个外角大于任何一个和它不相邻的内角.【例题1】1．如图所示，∠A=50°，∠B=20°，∠D=30°，则∠BCD的度数为（）A．80°B．100°C．120°D．140°2．一副三角板有两个三角形，如图叠放在一起，则∠α的度数是（）A．120°B．135°C．150°D．165°【练习】1．在∠ABC 中，∠A=35°，∠B=72°，则与∠C 相邻的外角为 ．2．如图，在∠ABC 中，D 、E 分别是AB 、AC 上的点，点F 在BC 的延长线上，DE∠BC ，∠A=44°，∠1=57°，则∠2= ．3．在∠ABC 中，∠A=25°，∠C=45°，则与∠B 相邻的外角的度数为 ．4．在∠ABC 中，∠A=25°，∠C=45°，则与∠B 相邻的外角的度数为 ．附解析：知识点三：表示方位的角方位角是指以南北方向为准，向两边偏的角度大小，即“南偏东 x ”“南偏西x ”“北偏东 x ”“北偏西 x ”，我们通常把南偏东 45称为东南方向，北偏西 45称为西北方向。

三角形中的常用辅助线找全等三角形的方法：（1）可以从结论出发，寻找要证明的相等的两条线段（或两个角）分别在哪两个可能全等的三角形中；（2）可以从已知条件出发，看已知条件可以确定哪两个三角形全等；（3）可从条件和结论综合考虑，看它们能确定哪两个三角形全等；（4）若上述方法均不可行，可考虑添加辅助线，构造全等三角形。

三角形中常见辅助线的作法：①延长中线构造全等三角形；②利用翻折，构造全等三角形；③引平行线构造全等三角形；④作连线构造等腰三角形。

常见辅助线的作法有以下几种：（1 ）遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”。

例 1 ：如图，ΔABC 是等腰直角三角形，∠BAC=90°，BD 平分∠ABC 交AC 于点D，CE垂直于BD，交BD 的延长线于点E。

求证：BD=2CE。

思路分析：1 ）题意分析：本题考查等腰三角形的三线合一定理的应用2 ）解题思路：要求证BD=2CE，可用加倍法，延长短边，又因为有BD 平分∠ABC的条件，可以和等腰三角形的三线合一定理结合起来。

解答过程：证明：延长BA，CE交于点F，在ΔBEF 和ΔBEC 中，∵∠1=∠2，BE=BE，∠BEF=∠BEC=90°，∴ΔBEF≌ΔBEC，∴EF=EC，从而CF=2CE。

又∠1+∠F=∠3+∠F=90°，故∠1=∠3。

在ΔABD和ΔACF中，∵∠1=∠3，AB=AC，∠BAD=∠CAF=90°，∴ΔABD≌ΔACF，∴BD=CF，∴BD=2CE。

解题后的思考：等腰三角形“三线合一”性质的逆命题在添加辅助线中的应用不但可以提高解题的能力，而且还加强了相关知识点和不同知识领域的联系，为同学们开拓了一个广阔的探索空间；并且在添加辅助线的过程中也蕴含着化归的数学思想，它是解决问题的关键。

（2）若遇到三角形的中线，可倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”。

全等三角形问题中常有的辅助线的作法( 含答案 ) 总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角均分线，可向两边作垂线。

也可将图对折看，对称今后关系现。

角均分线平行线，等腰三角形来添。

角均分线加垂线，三线合一试一试看。

线段垂直均分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角均分线在三种添辅助线4.垂直均分线联系线段两端5.用“截长法”或“补短法” ：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为 60 度或 120 度的把该角添线后构成等边三角形7. 角度数为 30、60 度的作垂线法：遇到三角形中的一个角为 30 度或 60 度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90 的特别直角三角形，尔后计算边的长度与角的度数，这样能够获取在数值上相等的二条边或二个角。

进而为证明全等三角形创立边、角之间的相等条件。

8. 计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特别直角三角形，或40-60-80的特别直角三角形, 常计算边的长度与角的度数，这样能够获取在数值上相等的二条边或二个角，进而为证明全等三角形创立边、角之间的相等条件。

常有辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

1) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思想模式是全等变换中的“对折”法构造全等三角形．2) 遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思想模式是全等变换中的“旋转”法构造全等三角形．3)遇到角均分线在三种添辅助线的方法，（1）能够自角均分线上的某一点向角的两边作垂线，利用的思想模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）能够在角均分线上的一点作该角均分线的垂线与角的两边订交，形成一对全等三角形。

人教版数学八年级下册第十八章平行四边形含辅助线证明训练一1.如图，□ABCD中，AC⊥AB，点E在线段AC上，AE=AB，BE的延长线交边AD于点F，AG⊥BC，且AG=AF，AG交BF于点O．（1）若AD=13，AC=12，求BE的长；（2）若点O恰好是线段AG的中点，连接GE，求证：AF=GE．2.已知正方形ABCD如图所示，连接其对角线AC，∠DAC的平分线AE交CD于点E，过点D作DM⊥AE于F，交AC于点M，共过点A作AN⊥AE交CB延长线于点N．(1)若AD=3，求△CAN的面积；(2)求证：AN=DM+2EF．3.如图1，已知正方形ABCD中，点E在BC上，连接AE，过点B作BF⊥AE于点G，交CD于点F.图1 图2（1）如图1，连接AF，若AB＝4，BE＝1，求AF的长；（2）如图2，连接BD，交AE于点N，连接AC，分别交BD、BF于点O、M，连接GO,求证：AG-BG=2GO4.如图，平行四边形ABCD中，BF⊥DC交DC于点F，且BF=AB，E点是BC边上一点，连接AE交BF于G；（1）若AE平分∠DAB，∠C=60∘，BE=3，求BG的长；（2）若AD=BG+FC，求证：AE平分∠DAB．5.如图，在□ABCD中，AD上有一点E，连接BE,AH⊥BC于H,AH、BE交于点G,连接CG并延长交AB于F,且GC=CD,∠GCD=90∘.(1) 若GC＝6，∠BAG＝30∘，求四边形AGCD的面积；(2) 求证：DE=2BG．6.如图，▱ABCD中，点E为BC边上一点，过点E作EF⊥AB于F，已知∠D=2∠AEF．（1）若∠BAE=70°，求∠BEA的度数；（2）连接AC，过点E作EG⊥AC于G，延长EG交AD于点H，若∠ACB=45°，求AC．证：AH=AF+227.如图，▱ABCD中，DF平分∠ADC交AC于点H，G为DH的中点．（1）如图①，若M为AD的中点，AB⊥AC，AC=9，CF=8，CG=25，求GM；（2）如图②，M为线段AB上一点，连接MF，满足∠MCD=∠BCG，∠MFB=∠BAC．求证：MC=2CG．8.如图，在▱ABCD中，连结BD，点E在BD上，且DE=DC，连结CE并延长它与AD交于点F，过点C作CG⊥BD垂足为G，交AD于点H．（1）若DG=3，CG=23，求△CDE的面积；（2）若∠DFC=45°，求证：EF+2FH=CF．9.如图所示，在正方形ABCD的边CB的延长线上取点F，连结AF，在AF上取点G，使得AG=AD，连结DG，过点A作AE⊥AF，交DG于点E．（1）若正方形ABCD的边长为4，且AB=2FB，求FG的长；（2）求证：AE+BF=AF．10.如图，▱ABCD中，E为平行四边形内部一点，连接AE，BE，CE．（1）如图1，AE⊥BC交BC于点F，已知∠EBC=45°，∠BAF=∠ECF，AB=5，EF=1，求AD的长；（2）如图2，AE⊥CD交CD于点F，AE=CF且∠BEC=90°，G为AB上一点，作GP⊥BE 且GP=CE，并以BG为斜边作等腰Rt△BGH，连接EP、EH．求证：EP=2EH．11.如图1，在等腰△ABO中，AB=AO，分别延长AO、BO至点C、点D，使得CO=AO、BO=BO，连接AD、BC．（1）如图1，求证：AD=BC；（2）如图2，分别取边AD、CO、BO的中点E、F、H，猜想△EFH的形状，并说明理由．12.已知，如图，▱ABCD的对角线AC、BD相交于点O，（1）如图1，若AC=AD过点A作AE⊥BC于点E，若AE=3,BC=5，求AB边的长；（2）如图2，过点A作BD的垂线，垂足为F，且AF=BF，过点B作BC的垂线，两条垂线相交于点G，若∠BAG=∠BFC，连接DG.求证：GF=4FO13.已知，在平行四边形ABCD中，AB⊥BD,E为射线BC上一点，连接AE交BD于点F，AB=BD.（1）如图1，若点E与点C重合，且AF=25，求AD的长；（2）如图2，若点E在BC边上时，过点D作DG⊥AE于G,延长DG交BC于H，连接FH.求证：AF=DH+FH;（3）如图3，当点E在射线BC上运动时，过点D作DG⊥AE于G,M为AG的中点，点N在BC边上且BN=1，已知AB=42，请直接写出MN的最小值。

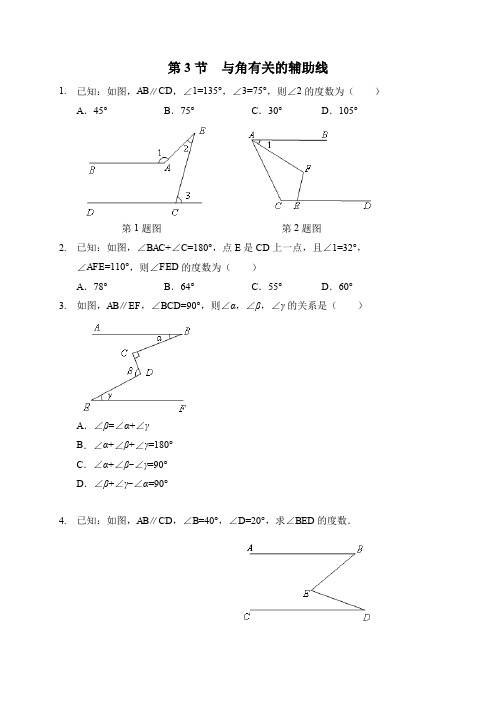
第3节与角有关的辅助线1.已知：如图，AB∥CD，∠1=135°，∠3=75°，则∠2的度数为（）A．45°B．75°C．30°D．105°第1题图第2题图2.已知：如图，∠BAC+∠C=180°，点E是CD上一点，且∠1=32°，∠AFE=110°，则∠FED的度数为（）A．78°B．64°C．55°D．60°3.如图，AB∥EF，∠BCD=90°，则∠α，∠β，∠γ的关系是（）A．∠β=∠α+∠γB．∠α+∠β+∠γ=180°C．∠α+∠β-∠γ=90°D．∠β+∠γ-∠α=90°4.已知：如图，AB∥CD，∠B=40°，∠D=20°，求∠BED的度数．5.已知：如图，AB∥CD．求证：∠1+∠3-∠2=180°．6.（1）①如图1所示，已知AB∥CD，∠ABC=60°，根据_____________________________，可得∠BCD=____________；②如图2所示，在①的条件下，若CM平分∠BCD，则∠BCM=_______；③如图3所示，在①②的条件下，若CN⊥CM，则∠BCN=__________．（2）尝试解决下面的问题：如图4所示，AB∥CD，∠B=40°，CN是∠BCE的平分线，CN⊥CM，求∠BCM的度数．7．如图（1），已知直线l1∥l2，且l3与l1、l2分别交于A、B两点，l4与l1、l2分别交于C、D两点，记∠ACP＝∠1，∠BDP＝∠2，∠CPD＝∠3，点P在线段AB上．（1）若∠1＝25°，∠2＝33°，则∠3＝；（2）猜想∠1，∠2，∠3之间的相等关系，并说明理由；（3）如图（2），点A在点B的南偏东23°方向，在点C的西南方向，利用（2）的结论，可知∠BAC＝；（4）点P在直线l3上且在A、B两点外侧运动时，其它条件不变，请直接写出∠1，∠2，∠3之间的相等关系．8．如图，已知AB∥CD，点C在点D的右侧，∠ADC＝70°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB，CD之间．（1）如图1，点B在点A的左侧，若∠ABC＝60°，求∠BED的度数？（2）如图2，点B在点A的右侧，若∠ABC＝100°，直接写出∠BED的大小．9．小明同学在完成第10章的学习后，遇到了一些问题，请你帮助他．（1）图1中，当AB∥CD，试说明∠AEC＝∠BAE+∠DCE．（2）图2中，若∠AEC＝∠BAE+∠DCE，则AB∥CD吗？请说明理由．（3）图3中，AB∥CD，若∠BAE＝x°，∠AEF＝y°，∠EFD＝z°，∠FDC＝m°，则m ＝．（直接写出结果，用含x，y，z的式子表示）10．如图，∠BED＝∠B+∠D，猜想AB与CD有怎样的位置关系，并说明理由．11．直线AB∥CD，点P在其所在平面上，且不在直线AB，CD，AC上，设∠PAB＝α，∠PCD＝β，∠APC＝γ（α，β，γ，均不大于180°，且不小于0°）（1）如图1，当点P在两条平行直线AB，CD之间、直线AC的右边时试确定α，β，γ的数量关系；（2）如图2，当点P在直线AB的上面、直线AC的右边时试确定α，β，γ的数量关系；（3）α，β，γ的数量关系除了上面的两种关系之外，还有其他的数量关系，请直接写出这些．12．（1）读读做做：平行线是平面几何中最基本、也是非常重要的图形．在解决某些平面几何问题时，若能依据问题的需要，添加恰当的平行线，往往能使证明顺畅、简洁．请根据上述思想解决教材中的问题：如图①，AB∥CD，则∠B+∠D∠E（用“＞”、“＝”或“＜”填空）；（2）倒过来想：写出（1）中命题的逆命题，判断逆命题的真假并说明理由．（3）灵活应用如图②，已知AB∥CD，在∠ACD的平分线上取两个点M、N，使得∠AMN＝∠ANM，求证：∠CAM＝∠BAN．13．小华在学习“平行线的性质”后，对图中∠B，∠D和∠BOD的关系进行了探究：（1）如图1，AB∥CD，点O在AB，CD之间，试探究∠B，∠D和∠BOD之间有什么关系？并说明理由；小华添加了过点O的辅助线OM，并且OM∥CD请帮助他写出解答过程；（2）如图2，若点O在CD的上侧，试探究∠B，∠D和∠BOD之间有什么关系？并说明理由；（3）如图3，若点O在AB的下侧，试探究∠B，∠D和∠BOD之间有什么关系？请直接写出它们的关系式．14．已知AB∥CD，点E、F分别为两条平行线AB、CD上的一点，GE⊥GF于G．（1）如图1，直接写出∠AEG和∠CFG之间的数量关系；（2）如图2，连接GF，过点G分别作∠BGF和∠BGE的角平分线交AB于点K、H．GH⊥AB．①求∠HGK的度数；②探究∠CFG和∠BGF的数量关系并加以证明．15．已知射线AB平行于射线CD，点E、F分别在射线AB、CD上（1）如图1，若点P在线段EF上，若∠A＝25°，∠APC＝70°时，则∠C＝；（2）如图1，若点P在线段EF上运动（不包含E、F两点），则∠A、∠APC、∠C之间的等量关系是；（3）①如图2，若点P在线段FE的延长线上运动，则∠A、∠APC、∠C之间的等量关系是；②如图3，若点P在线段EF的延长线上运动，则∠A、∠APC、∠C之间的等量关系是；（4）请说明图2中所得结论的理由．16．如图，已知l1∥l2，线段MA分别与直线l1，l2交于点A，B，线段MC分别与直线l1，l2交于点C，D，点P在线段AM上运动（P点与A，B，M三点不重合），设∠PDB＝α，∠PCA＝β，∠CPD＝γ．（1）若点P在A，B两点之间运动时，若a＝25°，B＝40°，那么γ＝．（2）若点P在A，B两点之间运动时，探究α，β，γ之间的数量关系，请说明理由；（3）若点P在B，M两点之间运动时，α，β，γ之间有何数量关系？（只需直接写出结论）部分参考答案7．【解答】解：（1）∵l1∥l2，∴∠1+∠PCD+∠PDC+∠2＝180°，在△PCD中，∠3+∠PCD+∠PDC＝180°，∴∠3＝∠1+∠2＝58°，故答案为：58°；（2）∠1+∠2＝∠3，∵l1∥l2，∴∠1+∠PCD+∠PDC+∠2＝180°，在△PCD中，∠3+∠PCD+∠PDC＝180°，∴∠1+∠2＝∠3；（3）过A点作AF∥BE，如图1，则AF∥BE∥CD，则∠BAC＝∠ABE+∠ACD＝23°+45°＝68°；故答案为：68°；（4）当P点在A的外侧时，如图2，过P作PF∥l1，交l4于F，∴∠1＝∠FPC．∵l1∥l4，∴PF∥l2，∴∠2＝∠FPD∵∠CPD＝∠FPD﹣∠FPC∴∠3＝∠2﹣∠1．当P点在B的外侧时，如图3，过P作PG∥l2，交l4于G，∴∠2＝∠GPD ∵l 1∥l 2， ∴PG ∥l 1， ∴∠1＝∠CPG∵∠CPD ＝∠CPG ﹣∠GPD ∴∠3＝∠1﹣∠2．8．【解答】解：（1）如图1，过点E 作EF ∥AB ， ∵AB ∥CD ， ∴AB ∥CD ∥EF ，∴∠ABE ＝∠BEF ，∠CDE ＝∠DEF ，∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC ＝60°，∠ADC ＝70°，∴∠ABE ＝∠ABC ＝30°，∠CDE ＝∠ADC ＝35°， ∴∠BED ＝∠BEF +∠DEF ＝30°+35°＝65°； （2）如图2，过点E 作EF ∥AB ，∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC ＝100°，∠ADC ＝70°∴∠ABE ＝∠ABC ＝50°，∠CDE ＝∠ADC ＝35° ∵AB ∥CD ， ∴AB ∥CD ∥EF ，∴∠BEF＝180°﹣∠ABE＝180°﹣50°＝130°，∠CDE＝∠DEF＝35°，∴∠BED＝∠BEF+∠DEF＝180°﹣50°+35°＝165°．9．【解答】解：（1）过E作EM∥AB，∵AB∥CD，∴AB∥CD∥EM，∴∠BAE＝∠AEM，∠DCE＝∠CEM，∴∠AEC＝∠AEM+∠CEM＝∠BAE+∠DCE；（2）过E作EM∥AB，∵EM∥AB，∴∠BAE＝∠AEM，∵∠AEC＝∠BAE+∠DCE，∴∠DCE＝∠CEM，∴EM∥CD，∵AB∥EM，∴AB∥CD；（3）过E作EM∥AB，过F作FN∥AB，∵AB∥CD，∴AB∥CD∥EM∥FN，∴∠BAE＝∠AEM，∠FEM＝∠EFN，∠DFN＝∠CDF，∴∠BAE+∠EFN+∠DFN＝∠AEM+∠FEM+∠CDF，∴∠BAE+∠EFD＝∠AEF+∠CDF，∵∠BAE＝x°，∠AEF＝y°，∠EFD＝z°，∠FDC＝m°，∴x+z＝y+m，∴m＝x+z﹣y，故答案为：x+z﹣y．10．【解答】解：延长BE交CD于F．∵∠BED＝∠B+∠D，∠BED＝∠EFD+∠D，∴∠B＝∠EFD，∴AB∥CD．11．【解答】解：（1）如图1中，结论：γ＝α+β．理由：作PE∥AB，∵AB∥CD，∴PE∥CD，∴∠BAP＝∠APE，∠PCD＝∠CPE，∴∠APC＝∠APE+∠CPE＝∠BAP+∠PCD，∴γ＝α+β．（2）如图2中，结论：γ＝β﹣α．理由：作PE∥AB，∵AB∥CD，∴PE∥CD，∴∠BAP＝∠APE，∠PCD＝∠CPE，∴∠APC＝∠CPE﹣∠APE，∴γ＝β﹣α．（3）如图3中，有γ＝α﹣β．如图4中，有γ＝β﹣α．如图5中，有γ＝360°＝β﹣α．如图6中，有γ＝α﹣β．综上所述，γ＝α﹣β，γ＝β﹣α，γ＝360°﹣β﹣α．12．【解答】（1）解：过E作EF∥AB，如图①所示：则EF∥AB∥CD，∴∠B＝∠BEF，∠D＝∠DEF，∴∠B+∠D＝∠BEF+∠DEF，即∠B+∠D＝∠BED；故答案为：＝；（2）解：逆命题为：若∠B+∠D＝∠BED，则AB∥CD；该逆命题为真命题；理由如下：过E作EF∥AB，如图①所示：则∠B＝∠BEF，∵∠B+∠D＝∠BED，∠BEF+∠DEF＝∠BED，∴∠D＝∠BED﹣∠B，∠DEF＝∠BED﹣∠BEF，∴∠D＝∠DEF，∴EF∥CD，∵EF∥AB，∴AB∥CD；（3）证明：过点N作NG∥AB，交AM于点G，如图②所示：则NG∥AB∥CD，∴∠BAN＝∠ANG，∠GNC＝∠NCD，∵∠AMN是△ACM的一个外角，∴∠AMN＝∠ACM+∠CAM，又∵∠AMN＝∠ANM，∠ANM＝∠ANG+∠GNC，∴∠ACM+∠CAM＝∠ANG+∠GNC，∴∠ACM+∠CAM＝∠BAN+∠NCD，∵CN平分∠ACD，∴∠ACM＝∠NCD，∴∠CAM＝∠BAN．13．【解答】解：（1）∠BOD＝∠D+∠B，理由是：∵AB∥CD，OM∥CD，∴AB∥CD∥OM，∴∠D＝∠DOM，∠B＝∠BOM，∴∠DOB＝∠DOM+∠BOM＝∠B+∠D；（2）∠B＝∠BOD+∠D，理由是：过O作OM∥CD，∵AB∥CD，OM∥CD，∴AB∥CD∥OM，∴∠D＝∠DOM，∠B＝∠BOM，∴∠B＝∠BOM＝∠DOM+∠DOB＝∠D+∠DOB；（3）∠D＝∠DOB+∠B，理由是：过O作OM∥CD，∵AB∥CD，OM∥CD，∴AB∥CD∥OM，∴∠D＝∠DOM，∠B＝∠BOM，∴∠D＝∠DOM＝∠BOM+∠DOB＝∠B+∠DOB．14．【解答】解：（1）如图1中，结论：∠AEG+∠CFG＝90°．理由：作GH∥AB．∵AB∥CD，∴GH∥CD，∴∠AEG＝∠EGH，∠CFG＝∠HGF，∵EG⊥FG，∴∠EGF＝90°，∴∠AEG+∠CFG＝∠EGH+∠HGF＝∠EGF＝90°．（2）①如图2中，∵GH平分∠BGE，∴∠EGH＝∠BGH，∵GH⊥BE，∴∠GHB＝∠GHE＝90°，∴∠EGH+∠GEB＝90°，∠B+∠BGH＝90°，∴∠GEB＝∠B，∵GE⊥GF，∴∠EGF＝90°，∴∠EGH+∠FGH＝90°，∴∠FGH＝∠GEB＝∠B，∵∠HKG＝∠B+∠KGB，∠HGK＝∠HGL+∠KGL，∠KGB＝∠KGL，∴∠HKG＝∠HGK＝45°．②结论：∠CFG＝45°+∠BGF．理由：∵AB∥CD，∴∠ALG＝∠CFG，∵∠ALG＝∠LKG+∠KGL＝45°+∠BGF，∴∠CFG＝45°+∠BGF．15．【解答】解：（1）过P作PH∥CD，∴∠HPC＝∠C，∵AB∥CD，∴AB∥PH，∴∠A＝∠APH＝25°，∴∠HPC＝∠APC﹣∠APH＝70°﹣25°＝45°；（2）∠APC＝∠A+∠C；理由如下：过P作PH∥CD，∴∠HPC＝∠C，∵AB∥CD，∴AB∥PH，∴∠A＝∠APH，∴∠APC＝∠HPC+∠APH＝∠A+∠C；（3）①∠APC＝∠C﹣∠A，理由如下：过点P作PQ∥AB（如图2），∵AB∥CD，∴PQ∥CD，∴∠C＝∠CPQ，∵PQ∥AB，∴∠A＝∠APQ，∵∠APC＝∠CPQ﹣∠APQ，∴∠APC＝∠C﹣∠A；②∠APC＝∠A﹣∠C．理由如下：过点P作PQ∥AB（如图3），∵AB∥CD，∴PQ∥CD，∴∠C＝∠CPQ，∵PQ∥AB，∴∠A＝∠APQ，∵∠APC＝∠APQ﹣∠CPQ＝∠A﹣∠C，∴∠APC＝∠A﹣∠C．（4）过点P作PQ∥AB（如图2），∵AB∥CD，∴PQ∥CD，∵PQ∥AB，∴∠A＝∠APQ，∵∠APC＝∠CPQ﹣∠APQ，∴∠APC＝∠C﹣∠A．故答案为：45°，∠APC＝∠A+∠C，∠APC＝∠C﹣∠A，∠APC＝∠A﹣∠C．16．【解答】解：（1）∵AC∥BD，∴β+∠PCD+∠PDC+α＝180°，∵γ+∠PCD+∠PDC＝180°，∴γ＝α+β＝65°．故答案为：65°．（2）∵AC∥BD，∴β+∠PCD+∠PDC+α＝180°，∵γ+∠PCD+∠PDC＝180°，∴γ＝α+β＝（3）如图，当P在B，M之间时，∵AC∥BD，∴∠1＝β，∵∠1＝α+γ，∴β＝α+γ．。

人教版八年级数学上册第11章与角有关的辅助线（讲义）➢ 课前预习1. 如图，∠AOB =130°，OC ⊥OB 于点O ，求∠AOC 的度数．OAB C解：如图， ∵OC ⊥OB （已知）∴____________（垂直的定义） ∵∠AOB =130°（已知） ∴∠AOC =______-______=______-______ =______（等式的性质）➢ 知识点睛1. 为了解决几何问题，在原图基础之上另外添加的直线或线段称为辅助线．辅助线通常画成________．2. 辅助线的原则：添加辅助线，构造新图形，形成新关系，建立______和______之间的桥梁，把问题转化成自己已经会解的情况． 3. 辅助线的作用：①________________________________________________； ②________________________________________________． 4. 添加辅助线的注意事项：____________________________．➢ 精讲精练1. 如图，AB ∥CD ，∠E =27°，∠C =52°，则∠EAB 的度数为______________．EDB A2. 如图，∠BAF =46°，∠ACE =136°，CD ⊥CE ．求证：AB ∥CD ．FEDCBA3. 已知：如图，直线AB ∥CD ，∠EFG =130°，∠DGH =40°．你认为EF ⊥AB 吗？请说明理由．F HGE D CBA4. 已知：如图，AB ∥CD ，E ，F 分别是AB ，CD 上的点．求证：∠EPF =∠AEP +∠CFP ．PF E DCBA5. 如图，l 1∥l 2，∠1=105°，∠2=40°，则∠3=___________．321l 2l 16. 已知：如图，AB ∥EF ，∠B =25°，∠D =30°，∠E =10°，则∠BCD =________．FEDCBA7. 已知：如图，AB ∥ED ，α=∠A +∠E ，β=∠B +∠C +∠D ．求证：β=2α．ECDBA8. 已知：如图，CD ∥EF ，∠1+∠2=∠ABC ．求证：AB ∥GF ．21GEDCB A9. 已知：如图，在四边形ABDC 中．求证：∠BDC =∠A +∠B +∠C ．ADB【参考答案】➢课前预习1.∠COB=90°∠AOB -∠COB 130°-90° 40°➢ 知识点睛1. 虚线2. 已知，未知3. ①把分散的条件转为集中②把复杂的图形转化为基本图形 4. 明确目的，多次尝试➢ 精讲精练1. 79°2. 证明：如图，延长DC 到点G ．G ABCD EF∵CD ⊥CE （已知）∴∠ECG =90°（垂直的定义） ∵∠ACE =136°（已知） ∴∠ACG =∠ACE -∠ECG=136°-90°=46°（等式的性质）∵∠BAF =46°（已知） ∴∠ACG =∠BAF （等量代换）∴AB ∥CD （同位角相等，两直线平行） 3. 解：EF ⊥AB ，理由如下：如图，延长EF 交CD 于点M ．F AB CDE MN GH∵∠DGH =40°（已知）∠DGH =∠FGM （对顶角相等） ∴∠FGM =40°（等量代换）∵∠EFG 是△FGM 的一个外角（外角的定义）∴∠EFG =∠FGM +∠FMG （三角形的一个外角等于和它不相邻的两个内角的和）∵∠EFG =130°（已知） ∴∠FMG =∠EFG -∠FGM =130°-40°=90°（等式的性质）∵AB ∥CD （已知）∴∠BNE =∠FMG =90°（两直线平行，同位角相等） ∴EF ⊥AB （垂直的定义） 4. 证明：如图，过点P 作MN ∥AB ．N M 4321P FE DCBA∵CD ∥AB （已知）∴AB ∥MN ∥CD （平行于同一条直线的两条直线平行） ∴∠1=∠2，∠3=∠4（两直线平行，内错角相等） ∴∠2+∠4=∠1+∠3（等式的性质） 即∠EPF =∠AEP +∠CFP 5. 115° 6. 45°7. 证明：如图，过点C 作MN ∥ED ．21E DM CNAB∵AB ∥ED （已知）∴MN ∥AB ∥ED （平行于同一条直线的两条直线平行） ∴∠1+∠D =180°， ∠2+∠B =180°，∠A +∠E =180°（两直线平行，同旁内角互补） ∵α=∠A +∠E （已知） ∴α=180°（等量代换） ∵β=∠B +∠C +∠D （已知） ∴β=∠B +∠1+∠2+∠D =180°+180° =360°（等式的性质） ∴β=2α（等式的性质） 8. 证明：NMAB C DE F G 12如图，延长CB 交FG 于点M ，延长FE 交CM 于点N ． ∵CD ∥EF （已知）∴∠2=∠FNM （两直线平行，同位角相等） ∵∠BMG 是△FMN 的一个外角（外角的定义） ∴∠BMG =∠1+∠FNM=∠1+∠2（三角形的一个外角等于和它不相邻的两个内角的和）∵∠1+∠2=∠ABC （已知） ∴∠BMG =∠ABC （等量代换）∴AB ∥GF （同位角相等，两直线平行） 9. 证明：如图，延长BD 交AC 于点E ．1EABC D∵∠1是△ABE 的一个外角（外角的定义）∴∠1=∠A +∠B （三角形的一个外角等于和它不相邻的两个内角的和）∵∠BDC 是△CDE 的一个外角（外角的定义）∴∠BDC =∠1+∠C （三角形的一个外角等于和它不相邻的两个内角的和）∴∠BDC =∠A +∠B +∠C （等量代换）与角有关的辅助线（随堂测试）2. 已知：如图，AB ⊥EF 于点O ，BD 与MN 相交于点C ，∠1=35°，∠B =125°． 求证：EF ∥MN ．N MFA B C D E1O【参考答案】1. 解：EF ∥MN理由如下：如图，延长AB 交MN 于点G ．∵∠1=35°（已知）∴∠BCG =35°（对顶角相等）∵∠ABC 是△BCG 的一个外角（外角的定义）∴∠ABC =∠BGC +∠BCG （三角形的外角等于和它不相邻的两个内角的和）∵∠ABC =125°（已知） ∴∠BGC =∠ABC -∠BCG =125°-35°=90°（等式的性质）∵AB ⊥EF （已知）∴∠AOF =90°（垂直的定义） ∴∠AOF =∠BGC （等量代换）∴EF ∥MN （同位角相等，两直线平行）NMFEGO 1DC B A与角有关的辅助线（习题）➢ 例题示范例1：已知：如图，∠BED =∠B +∠D ． 求证：AB ∥CD ．①读题标注：②梳理思路：要证AB ∥CD ，我们需要找相关的同位角、内错角或同旁内角．观察图形发现，AB ，CD 没有截线，故需要构造截线，然后证明．可尝试延长BE 交CD 于点G ．③过程书写：证明：如图，延长BE 交CD 于点G ． ∵∠BED 是△DEG 的一个外角 ∴∠BED =∠DGE +∠D ∵∠BED =∠B +∠D ∴∠DGE =∠B ∴AB ∥CD➢ 巩固练习EDBA CEDBA CGCABDE3.已知：如图，a∥b，则∠1+∠2-∠3=_________．4.已知：如图，∠B+∠E+∠D=360°．求证：AB∥CD．5.已知：如图，AB∥CD，∠1=∠2．求证：∠3=∠4．6.已知：如图，AB∥CD．求证：∠1+∠3 ∠2=180°．ba132CA BDE4F123C DEBA7.已知：如图，∠3=∠1+∠2．求证：∠A+∠B+∠C+∠D=180°．➢思考小结已知：如图，在四边形ABDC中．求证：∠BDC=∠A+∠B+∠C．A BC D123EF GEDC BA321（1）请根据图下方的描述在图上作出辅助线，并进行证明（不需要写过程）；延长BD 交AC 于点E 延长CD 交AB 于点E连接AD 并延长AD 到点E 连接BC过点D 作EF ∥AB 交AC 于点E 过点D 作EF ∥AC 交AB 于点E （2）根据上面的证明方法可以总结出辅助线的作用： ①_____________________________________； ②_____________________________________．【参考答案】 ➢ 巩固练习1. 180°2. 证明：如图，过点E 作EF ∥AB ．DBA DC BADBADC BADBADC BA∴∠B +∠BEF =180°（两直线平行，同旁内角互补） ∵∠B +∠BED +∠D =360°（已知）∴∠B +∠BEF +∠FED +∠D =180°（等量代换） ∴∠FED +∠D =180°（等式的性质） ∴EF ∥CD （同旁内角互补，两直线平行） ∴AB ∥CD （平行于同一条直线的两条直线平行） 3. 证明：如图，延长BE 交CD 于点G ．∵AB ∥CD （已知） ∴∠1=∠5（两直线平行，内错角相等）∵∠1=∠2（已知） ∴∠2=∠5（等量代换）∴BG ∥CF （同位角相等，两直线平行） ∴∠3=∠4（两直线平行，内错角相等） 4. 证明：如图，延长EA 交CD 于点F ．∵AB ∥CD （已知）∴∠1=∠4（两直线平行，同位角相等） ∵∠4是△CEF 的一个外角（外角的定义）∴∠4=∠2+∠ECF （三角形的一个外角等于和它不相邻的两个内角的和）∵∠3+∠ECF =180°（平角的定义） ∴∠ECF =180°-∠3（等式的性质）FED BA C 5GAB EDC 321F44FE321D C BA∴∠4=∠2+180°-∠3（等量代换）∴∠4+∠3-∠2=180°（等式的性质）∴∠1+∠3-∠2=180°（等量代换）（方法不只一种）5.证明：如图，延长EG交CF于点H．∵∠3是△GFH的一个外角（外角的定义）∴∠3=∠2+∠GHF（三角形的一个外角等于和它不相邻的两个内角的和）∵∠3=∠1+∠2（已知）∴∠GHF=∠1（等式的性质）∴BE∥CF（内错角相等，两直线平行）∴∠BMD+∠MNC=180°（两直线平行，同旁内角互补）∵∠BMD是△ABM的一个外角（外角的定义）∴∠BMD=∠A+∠B（三角形的一个外角等于和它不相邻的两个内角的和）∵∠MNC是△CDN的一个外角（外角的定义）∴∠MNC=∠C+∠D（三角形的一个外角等于和它不相邻的两个内角的和）∴∠BMD+∠MNC=∠A+∠B+∠C+∠D（等式的性质）∴∠A+∠B+∠C+∠D=180°（等量代换）（方法不只一种）➢思考小结（1）作辅助线，证明略；（2）①把分散的条件转为集中；②把复杂的图形转化为基本图形．。

专题03 与角平分线有关的辅助线的三种考法类型一、角平分线上的点向两边作垂线例1．如图，已知30AOB Ð=°，P 是AOB Ð的平分线OC 上的任意一点，PD OA ∥交OB 于点D ，PE OA ^于点E ，如果8cm OD =，求PE 的长．【答案】4cm【详解】如图，过点P 作PF ⊥OB 于点F ，∵OC 平分∠AOB ，PE ⊥OA ，∴PF ＝PE ，∠EOP ＝∠DOP∵PD P OA ，∠AOB ＝30°，∴∠PDF ＝∠AOB ＝30°，∴∠DPO ＝∠EOP ＝∠DOP ，∴ PD ＝OD ＝8cm在Rt △PDF 中，∵∠DFP=90°,∠FDP=30°∴PF =12PD =4cm ，∴ PF ＝PE ＝4cm ．【变式训练1】如图，ABC D 中，90ACB Ð=°，点,D E 分别在边BC ，AC 上，DE DB =，DEC B Ð=Ð．求证： AD 平分BAC Ð．【答案】见解析【详解】证明：过点D 作DF AB ^于点F ． 90DFB \Ð=°90ACB Ð=°Q ,DFB ACB DC AC \Ð=Ð^．在DCE D 和DFB D 中，,,,DCE DFB DEC B DE DB Ð=ÐìïÐ=Ðíï=î()DCE DFB AAS \D D ≌．DC DF \=．\点D 在BAC Ð的平分线上．\AD 平分BAC Ð．．【变式训练2】图，已知AE ⊥AB ，AF ⊥AC ．AE ＝AB ，AF ＝AC ，BF 与CE 相交于点M ．(1)EC ＝BF ；(2)EC ⊥BF ；(3)连接AM ，求证：AM 平分∠EMF ．【答案】(1)见解析．(2)见解析．(3)见解析．【解析】(1)证明：∵AE ⊥AB ，AF ⊥AC ，∴∠BAE ＝∠CAF ＝90°，∴∠BAE +∠BAC ＝∠CAF +∠BAC ，即∠EAC ＝∠BAF ，在△ABF 和△AEC 中，∵AE AB EAC BAF AF AC =ìïÐ=Ðíï=î，∴△ABF ≌△AEC （SAS ），∴EC ＝BF ；(2)根据（1），∵△ABF ≌△AEC ，∴∠AEC ＝∠ABF ，∵AE ⊥AB ，∴∠BAE ＝90°，∴∠AEC +∠ADE ＝90°，∵∠ADE ＝∠BDM （对顶角相等），∴∠ABF +∠BDM ＝90°，在△BDM中，∠BMD＝180°﹣∠ABF﹣∠BDM＝180°﹣90°＝90°，所以EC⊥BF．(3)作AP⊥CE于P，AQ⊥BF于Q．如图：∵△EAC≌△BAF，∴AP＝AQ（全等三角形对应边上的高相等）．∵AP⊥CE于P，AQ⊥BF于Q，∴AM平分∠EMF．【变式训练3】已知点C是∠MAN平分线上一点，∠BCD的两边CB、CD分别与射线AM、AN相交于B，D两点，且∠ABC+∠ADC＝180°．过点C作CE⊥AB，垂足为E．（1）如图1，当点E在线段AB上时，求证：BC＝DC；（2）如图2，当点E在线段AB的延长线上时，探究线段AB、AD与BE之间的等量关系；（3）如图3，在（2）的条件下，若∠MAN＝60°，连接BD，作∠ABD的平分线BF交AD于点F，交AC于点O，连接DO并延长交AB于点G．若BG＝1，DF＝2，求线段DB的长．【答案】（1）见解析；（2）AD﹣AB＝2BE，理由见解析；（3）3．【详解】（1）证明：如图1，过点C作CF⊥AD，垂足为F，∵AC平分∠MAN，CE⊥AB，CF⊥AD，∴CE＝CF，∵∠CBE +∠ADC ＝180°，∠CDF +∠ADC ＝180°，∴∠CBE ＝∠CDF ，在△BCE 和△DCF 中，90CBE CDF CEB CFD CE CF °Ð=ÐìïÐ=Ð=íï=î，∴△BCE ≌△DCF （AAS ）∴BC ＝DC ；（2）解：AD ﹣AB ＝2BE ，理由如下：如图2，过点C 作CF ⊥AD ，垂足为F ，∵AC 平分∠MAN ，CE ⊥AB ，CF ⊥AD ，∴CE ＝CF ，AE ＝AF ，∵∠ABC +∠ADC ＝180°，∠ABC +∠CBE ＝180°，∴∠CDF ＝∠CBE ，在△BCE 和△DCF 中，90CBE CDF CEB CFD CE CF °Ð=ÐìïÐ=Ð=íï=î，∴△BCE ≌△DCF （AAS ），∴DF ＝BE ，∴AD ＝AF +DF ＝AE +DF ＝AB +BE +DF ＝AB +2BE ，∴AD ﹣AB ＝2BE ；（3）解：如图3，在BD 上截取BH ＝BG ，连接OH ，∵BH ＝BG ，∠OBH ＝∠OBG ，OB ＝OB在△OBH 和△OBG 中，BH BG OBH OBG OB OB =ìïÐ=Ðíï=î，∴△OBH ≌△OBG （SAS ）∴∠OHB ＝∠OGB ，∵AO 是∠MAN 的平分线，BO 是∠ABD 的平分线，∴点O 到AD ，AB ，BD 的距离相等，∴∠ODH ＝∠ODF ，∵∠OHB ＝∠ODH +∠DOH ，∠OGB ＝∠ODF +∠DAB ，∴∠DOH ＝∠DAB ＝60°，∴∠GOH ＝120°，∴∠BOG ＝∠BOH ＝60°，∴∠DOF ＝∠BOG ＝60°，∴∠DOH ＝∠DOF ，在△ODH 和△ODF 中，DOH DOF OD OD ODH ODF Ð=Ðìï=íïÐ=Ðî，∴△ODH ≌△ODF （ASA ），∴DH ＝DF ，∴DB ＝DH +BH ＝DF +BG ＝2+1＝3．类型二、过边上的点向角平分线作垂线构造等腰三角形例1.如图，△ABC 的面积为9cm 2，BP 平分∠ABC ，AP ⊥BP 于P ，连接PC ，则△PBC 的面积为______cm 2．【答案】4.5【详解】解：延长AP 交BC 于E ，∵BP 平分∠ABC ，∴∠ABP=∠EBP，∵AP ⊥BP ，∴∠APB=∠EPB=90°，在△ABP 和△EBP 中，ABP EBP PB PB APB EPB Ð=Ðìï=íïÐ=Ðî，∴△ABP ≌△EBP （ASA ），∴AP=PE ，∴,APB EPB ACP ECP S S S S ==V V V V ∴119 4.522BPC ABC S S ==´=V V cm 2，故答案为4.5．【变式训练1】如图，在△ABC 中，∠A ＝90°，AB ＝AC ，∠ABC 的平分线BD 交AC 于点D ，CE ⊥BD ，交BD 的延长线于点E ，若BD ＝4，则CE ＝________．【答案】2【详解】解：如图，延长BA 、CE 相交于点F ，∵BD 平分∠ABC ，∴∠ABD=∠CBD ，在△BCE 和△BFE 中，90ABD CBD BE BE BEF BEC ìïíïÐÐÐаî＝＝＝＝，∴△BCE ≌△BFE （ASA ），∴CE=EF，∵∠BAC=90°，CE ⊥BD ，∴∠ACF+∠F=90°，∠ABD+∠F=90°，∴∠ABD=∠ACF ，在△ABD 和△ACF 中，90ABD ACF AB AC BAC CAF ìïíïÐÐÐаî＝＝＝＝，∴△ABD ≌△ACF （ASA ），∴BD=CF ，∵CF=CE+EF=2CE ，∴BD=2CE=4，∴CE=2．故答案为：2．【变式训练2】如图，在△ABC 中，∠C =90°，BC =AC ，D 是AC 上一点，AE ⊥BD 交BD 的延长线于E ，AE =12BD ，且DF ⊥AB 于F ，求证：CD =DF 【答案】见解析【解析】证明：延长AE 、BC 交于点F. 如图所示：∵AE ⊥BE ，∴∠BEA=90°，又∠ACF=∠ACB=90°，∴∠DBC+∠AFC=∠FAC+∠AFC=90°，∴∠DBC=∠FAC ，在△ACF 和△BCD 中,90ACF BCD AC BC FAC DBC Ð=Ð=°ìï=íïÐ=Ðî，∴△ACF ≌△BCD(ASA)，∴AF=BD.又AE=12BD ，∴AE=12AF ，即点E 是AF 的中点，∴AB=BF ，∴BD 是∠ABC 的角平分线，∵∠C=90°，DF ⊥AB 于F ，∴CD=DF.类型三、利用角平分线的性质，在角两边截长补短例1.已知：如图，//AC BD ，AE ，BE 分别平分CAB Ð和ABD Ð，点E 在CD 上．用等式表示线段AB 、AC 、BD三者之间的数量关系，并证明．【答案】AB=AC+BD，证明见详解．【详解】解：延长AE，交BD的延长线于点F，∵//AC BD，∴∠F=∠CAF，∵AE平分CABÐ，∴∠CAF=∠BAF，∴∠F=∠BAF，∴AB=BF，∵BE平分ABFÐ，∴AE=EF，∵∠F=∠CAF，∠AEC=∠FED，∴△ACE≌△FDE，∴AC=DF，∴AB=BF=BD+DF=BD+AC．【变式训练1】如图1，在△ABC中，∠BAC的平分线AD与∠BCA的平分线CE交于点O．(1)求证：∠AOC＝90°＋12∠ABC；(2)当∠ABC＝90°时，且AO＝3OD（如图2），判断线段AE，CD，AC之间的数量关系，并加以证明．【答案】(1)见解析；(2)43AE+CD=AC，证明见解析【解析】(1)证明：∵∠ABC+∠ACB+∠BAC=180°，∴∠BAC+∠BCA=180°-∠ABC，∵∠BAC的平分线AD与∠BCA的平分线CE交于点O．∴∠OAC=12∠BAC，∠OCA=12∠BCA，∴∠OAC+∠OCA=12（∠BAC+∠BCA）=12（180°-∠ABC）=90°-12∠ABC，∴∠AOC=180°-（∠OAC+∠OCA）=180°-（90°-12∠ABC），即∠AOC =90°+12∠ABC ；(2)解：43AE +CD =AC ，证明：如图2，∵∠AOC =90°+12∠ABC =135°，∴∠EOA =45°，在AC 上分别截取AM 、CN ，使AM =AE ，CN =CD ，连接OM ，ON ，则在△AEO 和△AMO 中，AE AM EAO MAO AO AO =ìïÐ=Ðíï=î，∴△AEO ≌△AMO ，同理△DCO ≌△NCO ，∴∠EOA =∠MOA ，∠CON =∠COD ，OD =ON ，∴∠EOA =∠MOA =∠CON =∠COD =45°，∴∠MON =∠MOA =45°，过M 作MK ⊥AD 于K ，ML ⊥ON 于L ，∴MK =ML ，S △AOM =12AO ×MK ，S △MON =12ON ×ML ，∴AOM MON S AO ON S D D =，∵AOM MON S AM S MN D D =，∴AO AM ON MN=，∵AO =3OD ，∴31AO OD =，∴31AO AM ON MN ==，∴AN =43AM =43AE ，∵AN +NC =AC ，∴43AE +CD =AC ．【变式训练2】如图，∠B =∠C =90°，E 是BC 的中点，DE 平分∠ADC ．求证：AE 是∠DAB 的平分线．（提示：过点E 作EF ⊥AD ，垂足为F ．）【答案】见解析【详解】证明：过点E作EF⊥DA于点F，∵∠C=90°，DE平分∠ADC，∴CE=EF，∵E是BC的中点，∴BE=CE，∴BE=EF，又∵∠B=90°，EF⊥AD，∴AE平分∠DAB．【变式训练3】如图所示，已知B（﹣2，0），C（2，0），A为y轴正半轴上的一点，点D为第二象限一动点，点E在BD的延长线上，CD交AB于点F，且∠BDC＝∠BAC．(1)求证：∠ABD＝∠ACD；(2)求证：AD平分∠CDE；(3)若在D点运动的过程中，始终有DC＝DA+DB，在此过程中，∠BAC的度数是否发生变化？如果变化，请说明理由；如果不变，请求出∠BAC的度数．【答案】(1)证明过程见解析；(2)证明过程见解析；(3)∠BAC =60°，理由见解析【解析】(1)证明：∵∠BDC =∠BAC ，∠DFB =∠AFC ，又∵∠ABD +∠BDC +∠DFB =∠BAC +∠ACD +∠AFC =180°，∴∠ABD =∠ACD ；(2)证明：过点A 作AM ⊥CD 于点M ，作AN ⊥BE 于点N ，如下图所示：则∠AMC =∠ANB =90°．∵OB =OC ，OA ⊥BC ，∴AB=AC ，由(1)可知：∠ABD =∠ACD ，∴△ACM ≌△ABN (AAS )，∴AM =AN ．∴DA 平分∠CDE ．(角的两边距离相等的点在角的平分线上)；(3)解：∠BAC 的度数为60°，理由如下：在CD 上截取CP=BD ，连接AP ，如下图所示：∵CD=AD+BD ，∴AD=PD ．∵AB=AC ，∠ABD =∠ACD ，BD=CP ，∴△ABD ≌△ACP (SAS ) ，∴AD=AP ，∠BAD =∠CAP ，∴AD=AP=PD ，即△ADP 是等边三角形，∴∠DAP =60°．∴∠BAC =∠BAP +∠CAP =∠BAP +∠BAD =60°．【变式训练4】已知：如图1，在ABC V 中，AD 是BAC Ð的平分线．E 是线段AD 上一点（点E 不与点A ，点D 重合），满足2Ð=ÐABE ACE ．（1）如图2，若18Ð=°ACE ，且EA EC =，则DEC Ð=________°，AEB Ð=_______°．（2）求证：AB BE AC +=．（3）如图3，若BD BE =，请直接写出ABE Ð和BAC Ð的数量关系．【答案】（1）36，126；（2）见解析；（3）3180Ð+Ð=°ABE BAC 【详解】（1）∵18Ð=°ACE ，且EA EC =，∴∠EAC =∠ACE =18°，∴∠DEC =∠EAC +∠ACE =36°，又∵AD 是BAC Ð的平分线，∴∠BAD =∠CAD =18°，∵2Ð=ÐABE ACE ，∴∠ABE =36°，∴1801836126Ð=°-°-°=°AEB ；故答案为：36，126（2）在AC 上截取AF AB =，连接FE ，又∵AE =AE ，EAF EAB Ð=Ð，∴()V V ≌AEF AEB SAS ，∴EF EB =，AFE ABEÐ=Ð∵∠AFE =∠ACE +∠FEC ，∠ABE =2∠ACE ，∴FEC FCE Ð=Ð，∴EF FC=∴=+=+AC AF FC AB BE ；（3）∵BD BE =，∴BED BDE Ð=Ð，∵BED ABE BAE Ð=Ð+Ð，Ð=Ð+ÐBDE DAC ACD ，∠CAD =∠BAE ，∴∠ACD =∠ABE ，∵∠ABE =2∠ACE ，∴∠ACD =2∠ACE ，∴CE 平分∠ACB ，∴点E 到CA 、CB 的距离相等，又∵AD 是BAC Ð的平分线，∴点E 到AC 、AB 的距离相等，∴点E 到BA 、BC 的距离相等，∴BE 是ABD Ð的平分线，∴∠ABE =∠CBE ，∴Ð=Ð=ÐABE ACD DBE ，又∵180ACB ABC BAC Ð+Ð+Ð=°，∴2180Ð+Ð+Ð=°ABE ABE BAC ，即3180Ð+Ð=°ABE BAC ．课后训练1．如图①，CDE Ð是四边形ABCD 的一个外角，AD //BC ，BC BD =，点F 在CD 的延长线上，FAB FBA Ð=Ð，FG AE ^，垂足为G ．(1)求证：①DC 平分BDE Ð；②BC DG AG +=．(2)如图②，若4AB =，3BC =，1DG =．求AFD Ð的度数．【答案】(1)①见解析；②见解析；(2)90°【解析】(1)解：①∵AD ∥BC ，∴∠C =∠CDE ，∵BC =BD ，∴∠C =∠CDB ，∴∠CDB =∠CDE ，∴DC 平分BDE Ð；②如图，过点F 作FH ⊥BD ，交BD 延长线于H ，∵∠FDG =∠CDE ，∠FDH =∠CDB ，∠EDC =∠CDB ，∴∠FDG =∠FDH ，∵FG ⊥AE ，FH ⊥BD ，∴FH =FG ，∠H =∠FGD =∠AGF =90°,∵FD =FD ，∴Rt △FHD ≌Rt △FGD （HL ），∴DH =DG ，∵FAB FBA Ð=Ð，∴FB =FA ，∴Rt △FHB ≌Rt △FGA （HL ）∴BH =AG ，∵BD =BC ，∴AG =BH =BD +DH =BC +DG ，即AG =BC +DG ；(2)解：∵AB =4，BC =3，DG =1，∴BD =BC =3，AG =BC +DG =3+1=4，∴AD =AG +DG =4+1=5，∵AB 2+BD 2=42+32=52=AD 2，∴∠ABD =90°，过点F 作FM ⊥AB 于M ，交AD 于N ，如图，则∠AMF =∠BMF =90°=∠ABD ，∴FM ∥BD ，∴∠BFM =∠FBD ，∵FAB FBA Ð=Ð，∴FB =FA ，∴AM =12AB =2，∠AFM =∠BFM ，∴∠AFM =∠FBD ，由（1）②知，Rt △FHB ≌Rt △FGA ，∴∠FAG =∠FBD ，∴∠FAG =∠AFN ，∵FM ∥BD ，∴∠MFD =∠BDC ，∵∠BDC =∠CDE =∠FDG ，∴∠MFD =∠FDG ，∴∠AFM +∠FAG +∠DFN +∠FDG =180°，∴2∠AFM +2∠DFN =180°，∴2∠AFD =180°，∴∠AFD =90°．2．已知：如图1，四边形ABCD 中，135ABC Ð=°，连接AC 、BD ，交于点E ，BD BC AD AC ^=，．(1)求证：90DAC Ð=°；(2)如图2，过点B 作BF AB ^，交DC 于点F ，交AC 于点G ，若2DBF CBF S S =V V ，求证：AG CG =；(3)如图3，在（2）的条件下，若3AB =，求线段GF 的长．【答案】(1)见解析；(2)见解析；(3)52【解析】(1)解：如图，过点A 作AP ⊥BD 于点P ，AF ⊥BC ，交CB 的延长线于点F ，∵AP ⊥BD ，AF ⊥BC ，BD ⊥BC∴四边形APBF 是矩形∵∠ABC ＝135°，∠DBC ＝90°，∴∠ABP ＝45°，且∠APB ＝90°，∴AP ＝PB ，∴四边形APBF 是正方形，∴AP ＝AF ，且AD ＝AC ，∴ΔΔRt APD Rt AFC HL ≌（），∴∠DAP ＝∠FAC ，∵∠FAC +∠PAC ＝90°，∴∠DAP +∠PAC ＝90°，∴∠DAC ＝90°(2)如图，过点F 作FM ⊥BC 于点M ，FN ⊥BD 于点N ，过点C 作CP ⊥BF 于点P ，在BD 上截取DH ＝BC ，连接AH ，∵∠ABC ＝135°，∠ABF ＝90°，∴∠CBF ＝45°，且∠DBC ＝90°，∴∠DBF ＝∠CBF ，且FN ⊥BD ，FM ⊥BC ，∴FN ＝FM ，∵S △DBF ＝2S △CBF ，∴1122BD FN BC FM ´´=´´×2，∴BD ＝2BC ，∴BH ＝BD ﹣DH ＝BD ﹣BC ＝BC ，∵∠AED ＝∠BEC ，∠DAC ＝∠DBC ＝90°，∴∠ADH ＝∠ACB ，且AD ＝AC ，DH ＝BC ，∴△ADH ≌△ACB （SAS ），∴∠AHD ＝∠ABC ＝135°，AH ＝AB ，∴∠AHB ＝∠ABD ＝45°，∴∠HAB ＝90°，∵BC ＝BH ，∠HAB ＝∠BPC ，∠AHB ＝∠FBC ＝45°，∴△AHB ≌△PBC （AAS ），∴AB ＝PC ，∵AB ＝PC ，且∠ABP ＝∠BPC ，∠AGB ＝∠CGP ，∴△AGB ≌△CGP （AAS ），∴AG ＝GC(3)解：如图，∵AB ＝3＝PC ，∠PBC ＝45°，PC ⊥BF ，∴BP ＝PC=3，∵△AGB ≌△CGP ，∴BG ＝PG ＝32，在Rt PGC D 中，CG ∴AG ＝GC ，∴AC ＝AD ＝2AG ＝在Rt ADC D 中，CD ，∵S △DBF ＝2S △CBF ，∴DF ＝2FC∵DF +FC ＝DC ，∴F C在Rt PFC D 中，PF ＝1，∴FG ＝PG +PF ＝1+32 ＝52．3．如图1，正方形ABCD 中，点E 是BC 延长线上一点，连接DE ，过点B 作BF ⊥DE 于点F ，交CD 于点G ．(1)求证：CG =CE ；(2)如图2，连接FC ，AC ．若BF 平分∠DBE ，求证：CF 平分∠ACE ；(3)如图3，若G 为DC 中点，AB =2，求EF【答案】(1)证明见详解；(2)证明见详解；【解析】(1)证明：∵四边形ABCD 是正方形，∴BC ＝DC ，∠BCG ＝∠DCE ＝90°，∵BF ⊥DE ，∴∠DFG ＝∠BCG ＝90°，∵∠DGF ＝∠BGC ，∴∠GBC ＝∠EDC ，在△BCG 和△DCE 中，BCG DCE BC DC GBC EDC Ð=Ðìï=íïÐ=Ðî，∴△BCG ≌△DCE （ASA ），∴CG ＝CE ；(2)证明：∵BF 平分∠DBE ，BF ⊥DE ，∴DF ＝EF ，∴CF 是Rt △DCE 的中线，∴CF ＝EF ，∴∠E ＝∠FCE ，∵四边形ABCD 是正方形，∴∠DBE ＝∠ACB ＝45°，∵BF 平分∠DBE ，∴∠FBE 12=∠DBE ＝22.5°，∴∠E ＝90°﹣∠FBE ＝90°﹣22.5°＝67.5°，∴∠FCE ＝67.5°，∴∠ACF ＝180°﹣∠FCE ﹣∠ACB ＝180°﹣67.5°﹣45°＝67.5°，∴∠ACF ＝∠FEC ，∴CF 平分∠ACE ；(3)解：∵四边形ABCD 是正方形，∴∠BCG ＝90°，AB ＝BC ＝CD＝2，BD =＝∵G 为DC 中点，∴CG ＝GD 12=CD＝1，在Rt△BCG 中，由勾股定理得：BG ===设GF ＝x ，在Rt △BDF 和Rt △DFG 中，由勾股定理得：BD 2﹣BF 2＝DF 2，DG 2﹣GF 2＝DF 2，∴2222-=1-x x （），解得：x =，∴DF 2＝12﹣22025=，∴DF =，由（1）知：△BCG ≌△DCE ，∴BG ＝DE =，∴EF ＝DE ﹣DF =4．已知：在四边形ABCD 中，180,B CAD DE AC Ð+°Ð=^于E ，且2AD AE =．(1)如图1，求B Ð的度数；(2)如图2，BF 平分ABC Ð交AC 于F ，点G 在BC 上，连接FG ，且AF FG =．求证：AB BG =；(3)如图3，在（2）的条件下，AF AD =，过点F 作FH CD ^，且2CH CG =，若21,52CD AB ==，求线段BF 的长．【答案】(1)120°；(2)见解析；(3)3．【解析】(1)解：如图1，取AD 的中点F ，连接EF ，∵DE ⊥AC ，∴∠AED =90°，∴AD =2AF =2EF ，∵AD =2AE ，∴AE =EF =AF ，∴∠CAD =60°，∵∠B +∠CAD =180°，∴∠B =120°；(2)证明：如图2，作FM ⊥BC 于M ，FN ⊥AB 于点N ，∴∠BMF =∠BNF =90°，∠GMF =∠ANF =90°，∵BF 平分∠ABC ，∴FM =FN ，在Rt △BFM 和Rt △BFN 中，BF BF FM FN =ìí=î，∴Rt △BFM ≌Rt △BFN （HL ），∴BM =BN ，在Rt △FMG 和Rt △FNA 中，FG FA FM FN=ìí=î，∴Rt △FMG ≌Rt △FNA （HL ），∴MG =NA ，∴BN +NA =BM +MG ，∴AB =BG ．(3)如图3，连接AG ，DF ，DG ，作FM ⊥BC 于M ，延长GF 交AD 于N ，∵AF =AD ，∠DAE =60°，∴△ADF 是等边三角形，∴∠AFD =60°，AF =DF ，∵GF =AF ，∠DFC =180°-∠AFD =120°，∴AF =GF =DF ，∴∠FGD =∠FDG ，∠FAG =∠FGA ，∴∠AGD =12∠AFN +12∠DFN =12∠AFD =12×60°＝30°，∵∠ADC =120°，AD =DG ，∴∠DGA =∠DAG =1802ADC °-Ð=30°，∴∠DGC =180°-∠DGA -∠AGD =180°-30°-30°=120°，∴∠DGC =∠DFC ，∵∠1=∠2，∴180°-∠DGC -∠1=180°-∠DFC -∠2，∴∠GCF =∠FDG ，∠DCF =∠FGD ，∴∠GCF =∠DCF ，∵FH ⊥CD ，∴FM =FH ，∵∠FMG =∠FHD =90°，∴Rt △FMG ≌Rt △FHD （HL ），∴DH =MG ，同理可得：△MCF ≌△HCF （HL ），∴CM =CH =2CG ，∴GM =CG =DH ，∴3CG =CD =212，∴GM =CG =72，∴BM =BG -GM =AB -GM =5-72=32，在Rt △BFM 中，∠BFM =90°-∠FBM =90°-60°=30°，∴BF =2BM =3．5．如图1，ABC D 的ABC Ð和ACB Ð的平分线BE ，CF 相交于点G ，60BAC Ð=°．（1）求BGC Ð的度数；（2）如图2，连接AG ，求证：AG 平分BAC Ð；（3）如图3，在⑵的条件下，在AC 上取点H ，使得AGH BGC Ð=Ð，且8AH =，10BC =，求ABC D 的周长．【答案】（1）120°；（2）见解析；（3）28【详解】（1）证明：如图1，BE CF Q 、分别平分ABC ACB ÐÐ、，111 , 2 22ABC ACB \Ð=ÐÐ=Ð，()()11112 180 90 222ABC ACB A A \Ð+Ð=Ð+Ð=°-Ð=°-Ð，60BAC Ð=°Q ，() 1 180 ********BGC A \Ð=°-Ð+Ð=°+Ð=°；(2)如图2，过点G 分别作GM ⊥AB 于M ，GN ⊥BC 于N ， GQ ⊥AC 于Q ，BE Q 平分ABC Ð， GM ⊥AB 于M ，GN ⊥BC 于N ，GM GN \=，同理GN GQ =，GM GQ \=，∵GM ⊥AB 于M ， GQ ⊥AC 于Q ， AG \平分BAC Ð ；（3）解：∵GM ⊥AB 于M ， GQ ⊥AC 于Q ，GM =GQ ，∴AG 平分BAC Ð，∵又60BAC Ð=°， 30BAG CAG \Ð=Ð=°，在BC 上取点K ，使 BK BA =，BE Q 平分ABC Ð，ABG CBG \Ð=Ð，又BG BG =Q ，ABG KBG \D D ≌，BKG BAG \Ð=Ð，30BKG BAG \Ð=Ð= ，=18030150GKC \Ð-= ，120AGH BGC Ð=Ð=°Q ， 30CAG Ð=°，120 30 150GHC \Ð=°+°=°，GKC GHC \Ð=Ð，又CG CG =Q ，KCG HCG Ð=Ð，KCG HCG \D D ≌，CK CH \=，△ABC 的周长为：()()2210828AB BC CA AB BK KC AH CH BC AH ++=++++=+=´+=， ABC \D 的周长是28．6．如图所示，AD 是ABC V 的高，点H 为AC 的垂直平分线与BC 的交点，HC AB =．（1）如图1，求证：2B C Ð=Ð；（2）如图2，若2DAF B C Ð=Ð-Ð，求证：AC BF BA =+；（3）在（2）的条件下，若12AC =，CF 10=，求DF 的长．【答案】（1）见解析；（2）见解析；（3）1【详解】解：（1）连接AH ，∵H 为AC 的垂直平分线与BC 的交点，∴HA HC =，HAC C Ð=Ð，∵HC AB =，∴AB AH =，∴B AHB Ð=Ð，∵AHB C HAC Ð=Ð+Ð，∴2AHB C Ð=Ð，∴2B C Ð=Ð．（2）∵2DAF B C Ð=Ð-Ð，∴1122DAF B C Ð=Ð-Ð，在Rt ADF V 中，9090DAF AFD FAC C Ð=°-Ð=°-Ð-Ð，∴119022FAC C B C °-Ð-Ð=Ð-Ð∴[]111190180()2222FAC B C B C BAC Ð=°-Ð-Ð=°-Ð+Ð=Ð，即AF 平分BAC Ð， 在AC 上截取AG AB =，连接FG ，在BAF △和GAF V 中，AB AG BAF GAF AF AF =ìïÐ=Ðíï=î，∴()BAF GAF SAS V V ≌，∴BF FG =，AB =AG ，B AGF Ð=Ð，∵2B CÐ=Ð∴2AGF C Ð=Ð，∴GFC C Ð=Ð，∴FG GC BF ==，∴AC GC AG BE BA =+=+．（3）在DB 上截取DM DF =，连接AM ，在ADF V 和ADM △中，AD AD ADF ADM DF DM =ìïÐ=Ðíï=î，∴()ADF ADM SAS V V ≌，∴DAF DAM Ð=Ð，∴2MAC DAF FAC Ð=Ð+Ð，由（2）可知119022FAC B C Ð=°-Ð-Ð，又∵2DAF B C Ð=Ð-Ð，2B C Ð=Ð．∴11131909029022222MAC B C B C C C C Ð=Ð-Ð+°-Ð-Ð=+´Ð-Ð=-°Ð°．∵()11111180909022222AMC AFM C FAC C BAC C B C B C C °Ð=Ð=Ð+Ð=Ð+Ð=Ð+-Ð-Ð=-Ð+°Ð=-а∴MAC AMC Ð=Ð ，∴AC MC =∴2MC CF AC CF DF -=-=，∴12102DF-=∴1DF =．7．教材呈现：如图是华师版八年级上册数学教材第96页的部分内容．请根据教材中的分析，结合图①，写出“角平分线的性质定理”完整的证明过程．定理应用：（1）如图②．在△ABC 中，∠C =90°，AD 平分∠BAC 交BC 于点D ．若AC =3，BC =4，求CD 的长；（2）如图③．在△ABC 中，∠ACB =90°，AD 平分∠BAC 交BC 于点D ，点P 在AD 上，点M 在AC 上．若AC =6，BC =8，则PC +PM 的最小值为 ．【答案】教材呈现：证明见解析；定理应用：（1）32；（2）245．【详解】教材呈现：OC Q 是AOB Ð的平分线，POD POE \Ð=Ð，,PD OA PE OB ^^Q ，90PDO PEO \Ð=Ð=°，在POD V 和POE △中，POD POE PDO PEO OP OP Ð=ÐìïÐ=Ðíï=î，()POD POE AAS \@V V ，PD PE \=；定理应用：（1）如图，过点D 作DE AB ^于点E ，Q 在ABC V 中，90,3,4C AC BC Ð=°==，5AB \==，Q AD 平分BAC Ð，且90C Ð=°，CD DE \=，在Rt ACD △和Rt AED △中，AD AD CD ED =ìí=î，()Rt ACD Rt AED HL \@V V ，3AC AE \==，532BE AB AE \=-=-=，设CD DE x ==，则4BD BC CD x =-=-，在Rt BDE V 中，222DE BE BD +=，即2222(4)x x +=-，解得32x =，即CD 的长为32；（2）如图，过点M 作MN AD ^，交AB 于点N ，连接PN，Q AD 平分BAC Ð，AD \垂直平分MN （等腰三角形的三线合一），PM PN \=，PC PM PC PN \+=+，由两点之间线段最短得：当点,,C P N 在同一条直线上时，PC PN +取得最小值，最小值为CN ，又由垂线段最短得：当CN AB ^时，CN 取得最小值，Q 在ABC V 中，90,6,8ACB AC BC Ð=°==，10AB \==，又1122Rt ABC S AC BC AB CN =×=×V Q ，11681022CN \´´=´，解得245CN =，即PC PM +的最小值为245，故答案为：245．。