第五章单元检测

七年级数学（下）第五章《相交线与平行线》单元检测题（时间：90分钟，满分：100分）一、选择题（每小题3分，共30分）1．下列命题：①对顶角相等；②在同一平面内，垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等．其中错误的有（）A．1个B．2个C．3个D．4个2．点P是直线l外一点，A为垂足，,且PA=4 cm，则点P到直线l的距离（）A．小于4 cm B．等于4 cm C．大于4 cm D．不确定3．（2013•安徽）如图，AB∥CD，∠A+∠E=75°，则∠C为（）A．60°B．65°C．75°D．80°第3题图第4题图4．（2013•襄阳）如图，BD平分∠ABC，CD∥AB，若∠BCD=70°，则∠ABD的度数为（）A．55°B．50°C．45°D．40°5．（2013•孝感）如图，∠1=∠2，∠3=40°，则∠4等于（）A．120°B．130°C．140°D．40°6．如图，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（）A．1个B．2个C．3个D．4个第5题图第6题图7．如图，点在的延长线上，下列条件中不能判定AB∥CD的是（）A．∠1=∠2 B．∠3=∠4C．∠5=∠D．∠+∠BDC=180°第7题图第8题图8．如图，DH∥EG∥BC，DC∥EF，那么与∠DCB相等的角的个数为（）A．2个B．3个C．4个D．5个9. 下列条件中能得到平行线的是（）①邻补角的角平分线；②平行线内错角的角平分线；③平行线同旁内角的角平分线．A．①②B．②③C．②D．③10. 两平行直线被第三条直线所截，同位角的平分线（）A．互相重合B．互相平行C．互相垂直D．相交二、填空题（共8小题，每小题3分，满分24分）11．如图，直线a、b相交，∠1=，则∠2=．第11题图12．（2013•镇江）如图，AD平分△ABC的外角∠EAC，且AD∥BC，若∠BAC=80°，则∠B= °．第12题图第13题图第14题图13．如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是．14．如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1与∠2的关系是．15．（2013•江西）如图,在△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠1=155°，则∠B的度数为．第15题图第16题图16．如图，AB∥CD，直线EF分别交AB、CD于E、F，EG平分∠BEF，若∠1=72°，则∠2= ．17．如图，直线a∥b，则∠ACB= ．第17题图第18题图18．（2012•郴州）如图，已知AB∥CD，∠1=60°，则∠2= 度．三、解答题（共6小题，满分46分）19．（7分）读句画图：如图，直线CD与直线AB相交于C，根据下列语句画图：（1）过点P作PQ∥CD，交AB于点Q；（2）过点P作PR⊥CD，垂足为R；（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由．第19题图20．（7分）如图，方格中有一条美丽可爱的小金鱼．（1）若方格的边长为1，则小鱼的面积为；（2）画出小鱼向左平移3格后的图形．（不要求写作图步骤和过程）第20题图21．（8分）已知：如图，∠BAP+∠APD =，∠1 =∠2.求证：∠E =∠F．第21题图第22题图22．（8分）已知：如图，∠1 =∠2，∠3 =∠4，∠5 =∠6.求证：ED ∥FB．23．（8分）如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数．第23题图第24题图24．（8分）如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．参考答案1.B 解析：①是正确的，对顶角相等；②正确，在同一平面内，垂直于同一条直线的两直线平行；③错误，角平分线分成的两个角相等但不是对顶角；④错误，同位角只有在两直线平行的情况下才相等．故①②正确，③④错误，所以错误的有两个，故选B．2. B 解析：根据点到直线的距离为点到直线的垂线段的长度（垂线段最短），所以点P到直线l的距离等于4 cm，故选B．3. C 解析：∵∠A+∠E=75°，∴∠EOB=∠A+∠E=75°.∵AB∥CD，∴∠C=∠EOB=75°，故选C．4. A 解析：∵CD∥AB，∴∠ABC+∠DCB=180°.∵∠BCD=70°，∴∠ABC=180°-70°=110°.∵BD平分∠ABC，∴∠ABD=55°.5. C 解析：如题图所示，∵∠1=∠2，∴a∥b，∴∠3=∠5.∵∠3=40°，∴∠5=40°，∴∠4=180°-∠5=180°-40°=140°，故选C．6. C 解析：∵AB∥CD，∴∠ABC=∠BCD.设∠ABC的对顶角为∠1，则∠ABC=∠1.又∵AC⊥BC，∴∠ACB=90°，∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°，因此与∠CAB互余的角为∠ABC，∠BCD，∠1．故选C．7. A 解析：选项B中，∵∠3=∠4，∴AB∥CD （内错角相等，两直线平行），故正确；选项C中，∵∠5=∠B，∴AB∥CD （内错角相等，两直线平行），故正确；选项D中，∵∠B+∠BDC=180°，∴AB∥CD（同旁内角互补，两直线平行），故正确；而选项A中，∠1与∠2是直线AC、BD被直线AD所截形成的内错角，∵∠1=∠2，∴AC∥BD，故A错误．选A．8. D 解析：如题图所示，∵DC∥EF，∴∠DCB=∠EFB.∵DH∥EG∥BC，∴∠GEF=∠EFB，∠DCB=∠HDC，∠DCB=∠CMG=∠DME，故与∠DCB相等的角共有5个．故选D．9. C 解析：结合已知条件，利用平行线的判定定理依次推理判断．10. B 解析：∵两条平行直线被第三条直线所截，同位角相等，∴它们角的平分线形成的同位角相等，∴同位角相等的平分线平行．故选B．11. 144°解析：由题图得，∠1与∠2互为邻补角，即∠1+∠2=180°.又∵∠1=36°，∴∠2=180°36°=144°．12. 50 解析：∵∠BAC=80°，∴∠EAC=100°.∵AD平分△ABC的外角∠EAC，∴∠EAD=∠DAC=50°.∵AD∥BC，∴∠B=∠EAD=50°．故答案为50．13. 垂线段定理：直线外一点与直线上所有点的连线中，垂线段最短解析：根据垂线段定理，直线外一点与直线上所有点的连线中，垂线段最短，∴沿AB开渠，能使所开的渠道最短．14. ∠1+∠2=90°解析：∵直线AB、EF相交于O点，∴∠1=∠DOF.又∵AB⊥CD，∴∠2+∠DOF=90°，∴∠1+∠2=90°．15. 65°解析：∵∠1=155°，∴∠EDC=180°-155°=25°.∵DE∥BC，∴∠C=∠EDC=25°.∵在△ABC中，∠A=90°，∠C=25°，∴∠B=180°-90°-25°=65°．故答案为65°．16. 54°解析：∵AB∥CD，∴∠BEF=180°∠1=180°72°=108°，∠2=∠BEG.又∵EG平分∠BEF，∴∠BEG=∠BEF=×108°=54°，故∠2=∠BEG=54°．17. 78°解析：延长BC与直线a相交于点D，∵a∥b，∴∠ADC=∠DBE=50°. ∴∠ACB=∠ADC +28°=50°+28°=78°. 故应填78°.18. 120 解析：∵AB ∥CD ，∴∠1=∠3，而∠1=60°，∴∠3=60°.又∵∠2+∠3=180°，∴∠2=180°-60°=120°．故答案为120．19．解：（1）（2）如图所示.第19题答图（3）∠PQC=60°. 理由：∵ PQ ∥CD,∴ ∠DCB+∠PQC=180°.∵ ∠DCB=120°,∴ ∠PQC=180°120°=60°．20. 解：（1）小鱼的面积为7×621 ×5×621 ×2×521 ×4×221 ×1.5×121×21 ×11=16. （2）将每个关键点向左平移3个单位，连接即可．第20题答图21.证明：∵ ∠BAP+∠APD = 180°，∴ AB ∥CD.∴ ∠BAP =∠APC.又∵ ∠1 =∠2,∴ ∠BAP −∠1 =∠APC −∠2.即∠EAP =∠APF.∴ AE ∥FP.∴ ∠E =∠F.22．证明：∵ ∠3 =∠4,∴ AC ∥BD.∴ ∠6+∠2+∠3 = 180°.∵ ∠6 =∠5，∠2 =∠1,∴ ∠5+∠1+∠3 = 180°.∴ ED ∥FB.23. 解：∵ DE ∥BC ，∠AED=80°，∴ ∠EDC=∠BCD ，∠ACB=∠AED=80°.∵ CD 平分∠ACB ，∴ ∠BCD = 21∠ACB =40°，∴ ∠EDC =∠BCD =40°． 24. 解：∵ AB ∥CD ，∴ ∠B +∠BCE =180°（两直线平行，同旁内角互补）.∵ ∠B =65°，∴ ∠BCE =115°.∵ CM 平分∠BCE ，∴ ∠ECM =21 ∠BCE =57.5°. ∵ ∠ECM +∠MCN +∠NCD =180°，∠MCN =90°，∴ ∠NCD =180°-∠ECM -∠MCN =180°-57.5°-90°=32.5°．。

第五章 单元检测题一、选择题1、下列关于透镜的说法中，正确的是（ ）A 凸透镜只对平行光有会聚作用 B.凸透镜两个焦点之间的距离叫做焦距 C.平行光经过凸透镜折射后一定会聚于一点 D 凸透镜任何光束都有会聚作用 2．一束光在空气中经凸透镜折射后，下列说法中正确的是（ ）A ．一定是平行光束B ．一定是会聚光束C ．折射光束比原光束会聚一些D ．一定是发散光束3．光学器件在我们的生活、学习中有着广泛的应用。

下面的介绍有一项不切实际，它是（ ）A ．近视眼镜利用了凹透镜对光线的发散作用B ．照相时，被照者与相机的距离是在镜头的二倍焦距之外C ．借助放大镜看地图时，地图到放大镜的距离应略大于一倍焦距D ．阳光通过凸透镜可以点燃纸屑，这利用了凸透镜对光的会聚作用4．下图是“探究凸透镜成像的规律”实验装置示意图，凸透镜的焦距是20cm ，如图的情景，眼睛可能观察到烛焰经凸透镜折射所成的虚像.5．如右图所示是利用航空摄影拍摄到的铜仁市碧江区一角，如果拍摄时所用照像机的镜头焦距是50mm,则胶片到镜头的距离应（ ）A ．大于100mmB ．大于50mm 小于100mmC ．小于50mmD ．等于50mm6．小明同学在“探究凸透镜成像的规律”实验时，烛焰在光屏上成了一个清晰的像，如图所示。

下面给出的生活中常用物品工作时原理与此现象相同的是（ ）A.投影仪B.照相机C.放大镜D.近视镜7．在探究凸透镜成像规律的实验中，当烛焰、凸透镜、光屏位于如图所示的位置时，烛焰在光屏上呈现一个清晰放大的像。

要使烛焰在光屏上呈现一个清晰缩小的像，调节的方法是A.透镜不动，蜡烛远离透镜移动，光屏靠近透镜移动B.透镜不动，蜡烛远离透镜移动，光屏远离透镜移动C.透镜不动，蜡烛靠近透镜移动，光屏远离透镜移动D.透镜不动，蜡烛靠近透镜移动，光屏靠近透镜移动 8．（2012浙江绍兴）图中人手持的是一枚（ ）A ．凹透镜，可以矫正近视B ．凹透镜，可以矫正远视C ．凸透镜，可以矫正近视D ．凸透镜，可以矫正远视9.如图所示，画出了光通过透镜前后的方向，在图中Ｏ处应填的适当类型的透镜是（ ）A. 凸透镜B.凹透镜C.凸、凹透镜都有可能D.凸、凹透镜都不行10．如果在屏幕上想看到一个正常的“F ”投影片放置的情况应是（ ）11．(2012河北)透镜在我们的生活、学习中应用广泛。

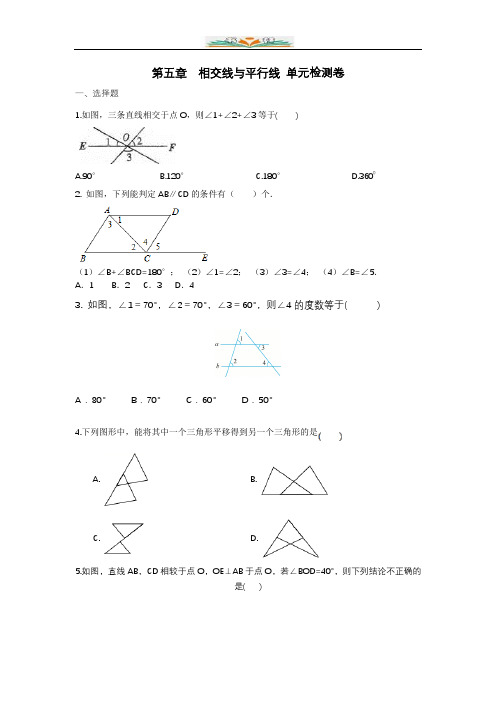
第五章相交线与平行线单元检测卷一、选择题1.如图，三条直线相交于点O，则∠1+∠2+∠3等于( )A.90°B.120°C.180°D.36002. 如图，下列能判定AB∥CD的条件有（）个．（1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5．A．1 B．2 C．3 D．43. 如图，∠1＝70°，∠2＝70°，∠3＝60°，则∠4的度数等于( )A．80°B．70°C．60°D．50°4.下列图形中，能将其中一个三角形平移得到另一个三角形的是A. B.C. D.5.如图，直线AB，CD相较于点O，OE⊥AB于点O，若∠BOD=40°，则下列结论不正确的是( )A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°6.如图，直线a,b被c,d所截，且a∥b，则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°7.如图，点A在直线BG上,AD∥BC，AE平分∠GAD，若∠CBA=80°,则( )A.60°B.50°C.40°D.30°8.下列各图中，∠1与∠2互为邻补角的是( )9.对于图中标记的各角，下列条件能推理得到a∥b的是（）A．∠1=∠2 B．∠2=∠4 C．∠3=∠4 D．∠1+∠4=18010．下列说法正确的是( )A.一个角的补角一定比这个角大B.一个角的余角一定比这个角小C.一对对顶角的两条角平分线必在同一条直线上D.有公共顶点并且相等的两个角是对顶角二、填空题11.如图，直线AB，CD相交于点O, EO⊥AB于点O，∠EOD=50°，则∠BOC的度数为______.12. 如图是由五个形状、大小完全相同的三角形组成的图案，三角形的三个角分别为36°，72°，72°，则图中共有_____对平行线．13.如图，，则的度数等于14．如图，点0是直线AB上一点平分，图中与互余的角有______ ．图中与互补的角有______ ．15. 说明命题“x>－4，则x2>16”是假命题的一个反例可以是x＝____________．16.如图，现要从村庄A修建一条连接公路PQ的最短小路，过点A作AH⊥PQ于点H，沿AH修建公路，则这样做的理由是三、解答题17.如图，直线AB，CD 相交于点O，∠AOD=3∠BOD+20°.(1)求∠BOD的度数；(2)以O为端点引射线OE,OF ,射线OE平分∠BOD，且∠EOF= 90°，求∠BOF的度数.18．已知：如图，AB∥CD，∠1=∠2，∠3=∠4．（1）求证：AD∥BE；（2）若∠B=∠3=2∠2，求∠D的度数．19.如图，D，E，F是线段AB的四等分点.(1)过点D画DH∥BC交于点H,过点E画EG∥BC交AC于点G，过点F画FM∥BC交AC 于点M;(2)量出线段AH,HG,GM,MC的长度，你有什么发现？(3)量出线段HD,EG,FM,BC的长度，你又有什么发现？20.请写出命题“两直线平行，同位角相等”的题设和结论：题设：，结论：．21.观察下图，寻找对顶角：(1)如图1，图中共有对对顶角(2)如图2，图中共有对对顶角(3)如图3，图中共有对对顶角(4)若有n条直线相交于一点，则可形成多少对对顶角？22.如图，已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC；(2)若∠AMD=75°，求∠AGC的度数.【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

浙教版2022年八年级上册第5章《一次函数》单元检测卷一．选择题（共10小题，满分30分，每小题3分）1．在圆的面积公式S＝πr2中，变量是（）A．S，πB．S，r C．π，r D．只有r2．如图图象中，表示y是x的函数的是（）A．B．C．D．3．下列y关于x的函数中，一次函数为（）A．y＝（a﹣2）x+b B．y＝（1+k2）x+1C．D．y＝2x2+14．小亮用100元钱去买单价是5元的笔记本，则他剩余的钱y（元）与他买这种笔记本的本数x之间的表达式是（）A．y＝5x B．y＝100﹣5x C．y＝5x﹣100D．y＝5x+1005．若正比例函数y＝kx的图象经过点（﹣2，2），则k的值是（）A．﹣1B．1C．﹣4D．46．下列函数其图象经过一、二、四象限的是（）A．y＝﹣2x+1B．y＝3x+5C．y＝﹣x﹣3D．y＝4x﹣37．在平面直角坐标系中，一次函数y＝2x﹣1和y＝x+1图象交点坐标为（）A．（﹣2，3）B．（2，﹣3）C．（﹣2，﹣3）D．（2，3）8．周日，东东从家步行到图书馆查阅资料，查完资料后，东东立刻按原路回家．已知回家时的速度是去时速度的1.5倍，在整个过程中，东东离家的距离s（单位：m）与他所用的时间t（单位：min）之间的关系如图所示，则东东在图书馆查阅资料的时间为（）A．55min B．40min C．30min D．25min9．点P1（x1，y1），点P2（x2，y2）是一次函数y＝kx+b（k＜0）图象上两点，x1＜x2，则y1与y2的大小关系是（）A．y1＞y2B．y1＝y2C．y1＜y2D．不能确定10．若m＜﹣2，则一次函数y＝（m+1）x﹣m+1的图象可能是（）A．B．C．D．二．填空题（共6小题，满分24分，每小题4分）11．函数y＝﹣2x中的常量是．12．若函数y＝（m﹣2）x+|m|﹣2是正比例函数，则m＝．13．某工厂剩余煤量y吨与烧煤天数x天满足函数关系y＝90﹣6x，则工厂每天烧煤量是吨．14．在一次函数y＝（m﹣3）x+6中，y随x的增大而增大，则m的取值范围是．15．将正比例函数y＝﹣7x的图象向下平移3个单位长度，则平移后所得到的一次函数的解析式为．16．如图，函数y1＝﹣2x与y2＝ax+3的图象相交于点A（﹣1，2），则当y1＜y2时，x的取值范围是．三．解答题（共7小题，满分66分）17．（8分）已知y与x之间成正比例关系，且当x＝﹣1时，y＝3．（1）求y与x之间的函数关系式；（2）当x＝2时，求y的值．18．（8分）已知一次函数y＝kx+5的图象经过点A（2，﹣1）．（1）求k的值；（2）在平面直角坐标系中画出这个函数的图象．19．（9分）如图，在平面直角坐标系中，点B（2，0）、点C（6，0），点A（x，y）是直线y＝2x上的一点，设△ABC的面积为S，求：（1）当点A在第一象限时，S与x的函数关系式；（2）当S＝8时，求A点的坐标．20．（9分）如图，正方形ABCD的边长为8cm，动点P、Q同时从点A出发，以2cm/s的速度分别沿A→B→C，和A→D→C的路径向点C移动．设运动时间为，由点P、B、D、Q确定的图形的面积为scm2，求s与t（0≤t ≤8）之间的函数关系式．21．（10分）李老师一家去离家200千米的某地自驾游，周六上午8点整出发．下面是他们离家的距离y（千米）与汽车行驶时间x（千米）之间的函数图象．（1）求他们出发半小时时，离家多少千米？（2）出发1小时后，在服务区等另一家人一同前往，等到后以每小时80千米的速度直达目的地；求等候的时间及直线BC的解析式；（3）上午11点时，离目的地还有多少千米？22．（10分）如图，已知直线y＝﹣x+2与x轴，y轴分别交于点A和点B，另一直线y＝kx+b（k≠0）经过C（1，0），且把△AOB分成两部分．（1）若直线y＝kx+b也经过点B，试说明△BOC与△ABC的面积相等；（2）若△AOB被分成的两部分面积比为1：5，求k和b的值．23．（12分）如图1，直线AB交x轴于点A（a，0），交y轴于点B（0，b），且a，b满足（a+b）2+（a﹣4）2＝0．（1）如图1，若C的坐标为（﹣1，0），且AH⊥BC于点H，AH交OB于点P，求点P的坐标；（2）如图2，连接OH，求证：∠AHO＝45°；（3）如图3，若点D为AB的中点，点M为y轴正半轴上一动点，连接MD，过D作DN⊥DM交x轴于N点，当M点在y轴正半轴上运动的过程中，式子S△BDM﹣S△ADN的值是否发生改变，如发生改变，求出该式子的值的变化范围；若不改变，求该式子的值．浙教版2022年八年级上册第5章《一次函数》单元检测卷参考答案一．选择题（共10小题，满分30分，每小题3分）1．【解答】解：根据常量和变量的定义得S、R是变量，π是常量．故选：B．2．【解答】解：A、B、C中对于自变量x的每一个值，因变量y不是都有唯一的值与它对应，所以不能表示y是x 的函数；D选项中对于自变量x的每一个值，因变量y都有唯一的值与它对应，所以能表示y是x的函数．故选：D．3．【解答】解：A．当a＝0时，y＝（a﹣2）x+b不是一次函数，故本选项不符合题意；B．y＝（1+k2）x+1是一次函数，故本选项符合题意；C．等式的右边是分式，不是整式，不是一次函数，故本选项不符合题意；D．y＝2x2+1是二次函数，不是一次函数，故本选项不符合题意；故选：B．4．【解答】解：∵小亮用100元钱去买单价是5元的笔记本，∴买这种笔记本的本数x花去的钱为：5x，∴剩余的钱为：100﹣5x，∴他剩余的钱（y元）与他买这种笔记本的本数x之间的函数关系式是：y＝100﹣5x，故选：B．5．【解答】解：∵正比例函数y＝kx的图象经过点（﹣2，2），∴2＝﹣2k，解得：k＝﹣1．故选：A．6．【解答】解：A选项，图象过第一、二、四象限，符合题意；B选项，图象过第一、二、三象限，不符合题意；C选项，图象过第二、三、四象限，不符合题意；D选项，图象过第一、三、四象限，不符合题意；故选：A．7．【解答】解：联立解得：，∴函数y＝2x﹣1与y＝x+1的图象的交点坐标为（2，3）．故选：D．8．【解答】解：根据图象可知，东东从家步行到图书馆的速度为：＝80（m/min），∵回家时的速度是去时速度的1.5倍，∴回家时的速度为：1.5×80＝120（m/min），则回家所用的时间为：＝10（m/min），∴东东在图书馆查阅资料的时间为：55﹣（15+10）＝30（min），故选：C．9．【解答】解：∵一次函数y＝kx+b（k＜0），∴此函数中y随x的增大而减小，∵x1＜x2，∴y1＞y2．故选：A．10．【解答】解：∵m＜﹣2，∴m+1＜0，﹣m+1＞0，∴一次函数y＝（m+1）x﹣m+1的图象经过一二四象限．故选：D．二．填空题（共6小题，满分24分，每小题4分）11．【解答】解：y＝﹣2x中的常量是﹣2，故答案为：﹣2．12．【解答】解：由题意得：|m|﹣2＝0且m﹣2≠0，∴m＝±2且m≠2，∴m＝﹣2，故答案为：﹣2．13．【解答】解：某工厂剩余煤量y吨与烧煤天数x天满足函数关系y＝90﹣6x，则工厂每天烧煤量是6吨，故答案为：6．14．【解答】解：根据题意得：m﹣3＞0，解得m＞3．故答案为：m＞3．15．【解答】解：将正比例函数y＝﹣7x的图象向下平移3个单位长度，所得的函数解析式为y＝﹣7x﹣3．故答案为：y＝﹣7x﹣3．16．【解答】解：∵函数y1＝﹣2x与y2＝ax+3的图象相交于点A（﹣1，2），∴当y1＜y2时，x的取值范围是x＞﹣1．故答案为：x＞﹣1．三．解答题（共7小题，满分66分）17．【解答】解（1）设y＝kx（k≠0），把x＝﹣1，y＝3代入y＝kx，得k＝﹣3，所以y＝﹣3x．（2）把x＝2代入y＝﹣3x，得y＝﹣3×2＝﹣6．18．【解答】解：（1）把点A（2，﹣1）代入一次函数y＝kx+5，得﹣1＝2k+5，解得k＝﹣3．（2）当x＝0时，y＝5，可知直线与y轴交点为（0，5），作过B、C的直线可得如图所示直线，即为所求．19．【解答】解：（1）∵B（2，0）、C（6，0），∴BC＝6﹣2＝4，∵第一象限内的点A（x，y）是直线y＝2x上一点，∴△P AO的面积为S＝×4×2x＝4x；（2）S＝4x＝8，解得x＝2，∴y＝2×2＝4，∴A点的坐标（2，4）．20．【解答】解：①0≤t≤4时，∵正方形的边长为8cm，∴y＝S△ABD﹣S△APQ，＝×8×8﹣•2t•2t，＝﹣2t2+32，②4≤t≤8时，y＝S△BCD﹣S△CPQ，＝×8×8﹣•（16﹣2t）•（16﹣2t），＝﹣2t2+32t﹣96．综上所述，S＝．21．【解答】解：（1）由图象知，李老师从家到服务区时的速度为＝60千米/小时，∴李老师出发半小时离家的距离为：60×0.5＝30（千米），答：他们出发半小时时，离家30千米；（2）李老师一家从服务区B到C地所用时间为：（100﹣60）÷80＝0.5（小时），∴李老师一家在服务区等了2﹣1﹣0.5＝0.5（小时）；设线段BC的函数表达式为y＝kx+b，因为B（1.5，60），C（2，100）在BC上，∴，解得，∴直线BC的解析式为y＝80x﹣60；（3）上午11点时，即x＝3时，y＝80×3﹣60＝180，∴200﹣180＝20（千米），答：上午11点时，离目的地还有20千米．22．【解答】解：（1）在y＝﹣x+2中，令y＝0，则﹣x+2＝0，解得x＝2，∴A（2，0），∴OA＝2，∵C（1，0），∴OC＝1，∴点C是线段OA的中点，∴△BOC与△ABC的面积相等；（2）∵S△AOB＝×2×2＝2，∵△AOB被分成的两部分面积比为1：5，那么直线y＝kx+b（k≠0）与y轴或AB交点的纵坐标就应该是：2×2×＝，①当y＝kx+b（k≠0）与直线y＝﹣x+2相交时，交点为D，如图（2）所示，当y＝时，直线y＝﹣x+2与y＝kx+b（k≠0）的交点D的横坐标就应该是﹣x+2＝，∴x＝，即交点D的坐标为（，），又根据C点的坐标为（1，0），可得：∴，②当y＝kx+b（k≠0）与y轴相交时，交点为E，如图（3）所示，∴交点E的坐标就应该是（0，），又有C点的坐标（1，0），可得：，∴，综上所述，k＝2，b＝﹣2或k＝﹣，b＝．23．【解答】解：（1）如图1，∵（a+b）2+（a﹣4）2＝0．∴a+b＝0，a﹣4＝0，∴a＝4，b＝﹣4，则OA＝OB＝4．∵AH⊥BC即∠AHC＝90°，∠COB＝90°∴∠HAC+∠ACH＝∠OBC+∠OCB＝90°，∴∠HAC＝∠OBC．在△OAP与△OBC中，，∴△OAP≌△OBC（ASA），∴OP＝OC＝1，则P（0，﹣1）；（2）过O分别作OM⊥CB于M点，作ON⊥HA于N点，如图2．在四边形OMHN中，∠MON＝360°﹣3×90°＝90°，∴∠COM＝∠PON＝90°﹣∠MOP．在△COM与△PON中，，∴△COM≌△PON（AAS），∴OM＝ON．∵OM⊥CB，ON⊥HA，∴HO平分∠CHA，∴∠OHP＝∠CHA＝45°；（3）S△BDM﹣S△ADN的值不发生改变，等于4．理由如下：连接OD，如图3．∵∠AOB＝90°，OA＝OB，D为AB的中点，∴OD⊥AB，∠BOD＝∠AOD＝45°，OD＝DA＝BD，∴∠OAD＝45°，∠MOD＝90°+45°＝135°，∴∠DAN＝135°＝∠MOD．∵MD⊥ND即∠MDN＝90°，∴∠MDO＝∠NDA＝90°﹣∠MDA．在△ODM与△ADN中，，∴△ODM≌△ADN（ASA），∴S△ODM＝S△ADN，∴S△BDM﹣S△ADN＝S△BDM﹣S△ODM＝S△BOD＝S△AOB＝×AO•BO＝××4×4＝4．。

第五章曲线运动一、选择题：（每小题有1～2个选项正确，少选得3分，多选或错选不得分，每小题5分，共40分）1．关于质点做曲线运动，下列说法正确的是（）A．曲线运动是一种变速运动B．变速运动一定是曲线运动C．质点做曲线运动，运动速度一定发生变化D．曲线运动一定不可能是匀变速2．如图5-8-3所示，汽车在—段丘陵地以恒定速率行驶时，所受支持力最大的地点可能是( )A．a点B．b点C．c点D．d点3．甲、乙两个做匀速圆周运动的质点，它们的角速度之比为3:1,线速度之比2:3，那么下列说法中正确的是（）A．它们的半径之比是2:9 B．它们的半径之比是1:2C．它们的周期之比是2:3 D．它们的周期之比是1:34．从水平匀速飞行的直升机上向外自由释放一个物体，不计空气阻力，在物体下落过程中，下列说法正确的是（）A．从飞机上看，物体静止B．从飞机上看，物体做自由落体运动C．从地面上看，物体做自由落体运动D．从地面上看，物体做平抛运动5．一轻杆一端固定一质量为m 的小球，以另一端O为圆心，使小球在竖直平面内做半径为R 的圆周运动，以下说法正确的是（）A．小球过最高点时最小速度为gRB．小球过最高点时，杆所受的弹力可以为零C．小球过最高点时，杆对球的作用力可以与球所受重力方向相反，也可以与球所受重力方向相同D．小球过最高点时，杆对球的作用力一定与小球所受重力方向相反6．如图在匀速转动的水平转盘上，有一个相对盘静止的物体，随盘一起转动，关于它的受力情况，下列说法中正确的是（）A ．只受到重力和盘面的支持力的作用B ．只受到重力、支持力和静摩擦力的作用C ．除受到重力和支持力外，还受到向心力的作用D ．受到重力、支持力、静摩擦力和向心力的作用7．如图所示，在同一竖直平面内，小球a 、b 从高度不同的两点，分别以初速度V a 、V b 沿水平方向抛出，经过时间t a 和t b 后落到与抛出点水平距离相等的的P点，若不计空气阻力，下列关系式正确的是（ ）A ．t a =t bB ．t a >t bC ．V a =V bD ．V a <V b8.如图，质量为m 的物块，沿着半径为R 的半球形金属壳内壁滑下，半球形金属壳竖直固定放置，开中向上，滑到最低点时速度大小为V ，若物体与球壳之间的动摩擦因数为u ，则物体在最低点时，下列说法正确的是（ ）A ．受到向心力为R v m mg 2+B ．受到向心力为Rv um 2C ．受到的摩擦力为)(2Rv m mg u + D ．受到的合力方向斜向左上方 二、实验题（每空4分，共28分）9.如图甲所示，竖直直放置的两端封闭的玻璃管中注满清水，内有一个红蜡块能在水中以0.3m/s 的速度匀速上浮。

第五章相交线与平行线单元试卷检测（基础+提高，Word 版 含解析）一、选择题1．如图，五边形ABCDE 中，AE ∥BC ，则∠C +∠D +∠E 的度数为（ ）A ．180°B ．270°C ．360°D ．450° 2．如图，AB CD ∥，154FGB ∠︒＝，FG 平分EFD ∠，则AEF ∠的度数等于（ ）．A ．26°B ．52°C ．54°D ．77°3．如图所示，若AB ∥EF ，用含α、β、γ的式子表示x ，应为（ ）A ．αβγ++B ．βγα+-C ．180αγβ︒--+D ．180αβγ︒++-4．已知AB CD ∥，点E F ，分别在直线AB CD ，上，点P 在AB CD ，之间且在EF 的左侧．若将射线EA 沿EP 折叠，射线FC 沿FP 折叠，折叠后的两条射线互相垂直，则EPF ∠的度数为（ ）A ．120︒B ．135︒C ．45︒或135︒D ．60︒或120︒5．下列说法中,错误的有( )①若a 与c 相交,b 与c 相交,则a 与b 相交;②若a∥b,b∥c,那么a∥c;③过直线外一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.A ．3个B ．2个C ．1个D ．0个6．已知//DE FG ，三角尺ABC 按如图所示摆放，90C ∠=︒，若137∠=︒，则2∠的度数为（ ）A ．57°B ．53°C ．51°D ．37°7．在同一平面内，有3条直线a ，b ，c ，其中直线a 与直线b 相交，直线a 与直线c 平行，那么b 与c 的位置关系是（ ）A ．平行B ．相交C ．平行或相交D ．不能确定 8．下列命题中，属于真命题的是（ ） A ．相等的角是对顶角B ．一个角的补角大于这个角C ．绝对值最小的数是0D ．如果a b =，那么a=b9．如图，下列条件中，不能判断直线a ∥b 的是（ ）A ．∠1＝∠3B ．∠2＝∠3C ．∠4＝∠5D ．∠2+∠4＝180°10．如图，将ABC 沿BC 的方向平移1cm 得到DEF ，若ABC 的周长为6cm ，则四边形ABFD 的周长为（ ）A ．6cmB ．8cmC ．10cmD ．12cm11．如图，将△ABE 向右平移50px 得到△DCF ，如果△ABE 的周长是400px（1px=0.04cm ），那么四边形ABFD 的周长是（ ）A ．16cmB ．18cmC ．20cmD ．21cm12．如图，ABC 面积为2，将ABC 沿AC 方向平移至DFE △，且AC=CD ，则四边形AEFB 的面积为（ ）A ．6B ．8C ．10D ．12二、填空题13．如图， 已知//AB CF ，//CF DE ， 90BCD ∠=︒，则D B ∠-∠=_________14．如图，已知AB CD ∥，CE 、BE 的交点为E ，现作如下操作：第一次操作，分别作ABE ∠和DCE ∠的平分线，交点为1E ，第二次操作，分别作1ABE ∠和1DCE ∠的平分线，交点为2E ，第三次操作，分别作2ABE ∠和2DCE ∠的平分线，交点为3E ，…第n 次操作，分别作1n ABE -∠和1n DCE -∠的平分线，交点为n E ．若1n E ∠=度，那BEC ∠等于__________度．15．如图，已知AB ∥CD ，CE 、BE 的交点为E ，现作如下操作：第一次操作，分别作∠ABE 和∠DCE 的平分线，交点为E 1，第二次操作，分别作∠ABE 1和∠DCE 1的平分线，交点为E 2，第三次操作，分别作∠ABE 2和∠DCE 2的平分线，交点为E 3，…，第n 次操作，分别作∠ABE n ﹣1和∠DCE n ﹣1的平分线，交点为E n ．若∠E n =1度，那∠BEC 等于________度16．如图，一条公路修到湖边时，需拐弯绕湖而过，在A ，B ，C 三处经过三次拐弯，此时道路恰好和第一次拐弯之前的道路平行(即AE ∥CD )，若∠A =120°，∠B =150°,则∠C 的度数是________17．如图，已知AB ，CD ，EF 互相平行，且∠ABE ＝70°，∠ECD ＝150°，则∠BEC ＝________°.18．如图，点О为直线AB 上一点，,,135OC OD OE AB ⊥⊥∠=︒．（1）EOD ∠= °，2∠= °；（2）1∠的余角是_ ，EOD ∠的补角是__ ．19．已知∠A 与∠B 的两边分别平行，其中∠A 为x °，∠B 的为(210﹣2x )°，则∠A =____度．20．如图，AB ∥CD ，∠β=130°，则∠α=_______°．三、解答题21．对于平面内的∠M 和∠N ，若存在一个常数k ＞0，使得∠M ＋k ∠N ＝360°，则称∠N 为∠M 的k 系补周角．如若∠M ＝90°，∠N ＝45°，则∠N 为∠M 的6系补周角．（1）若∠H＝120°，则∠H的4系补周角的度数为；（2）在平面内AB∥CD，点E是平面内一点，连接BE，DE．①如图1，∠D＝60°，若∠B是∠E的3系补周角，求∠B的度数；②如图2，∠ABE和∠CDE均为钝角，点F在点E的右侧，且满足∠ABF=n∠ABE，∠CDF=n∠CDE（其中n为常数且n＞1），点P是∠ABE角平分线BG上的一个动点，在P 点运动过程中，请你确定一个点P的位置，使得∠BPD是∠F的k系补周角，并直接写出此时的k值（用含n的式子表示）．22．如图，AD平分∠BAC交BC于点D，点F在BA的延长线上，点E在线段CD上，EF 与AC相交于点G，∠BDA+∠CEG=180°．（1）AD与EF平行吗？请说明理由；（2）若点H在FE的延长线上，且∠EDH=∠C，则∠F与∠H相等吗，请说明理由．23．如图，直线MN∥GH，直线l1分别交直线MN、GH于A、B两点，直线l2分别交直线MN、GH于C、D两点，且直线l1、l2交于点E，点P是直线l2上不同于C、D、E点的动点．（1）如图①，当点P在线段CE上时，请直写出∠NAP、∠HBP、∠APB之间的数量关系： ；（2）如图②，当点P 在线段DE 上时，（1）中的∠NAP 、∠HBP 、∠APB 之间的数量关系还成立吗？如果成立，请说明成立的理由；如果不成立，请写出这三个角之间的数量关系，并说明理由．（3）如果点P 在直线l 2上且在C 、D 两点外侧运动时，其他条件不变，请直接写出∠NAP 、∠HBP 、∠APB 之间的数量关系 ．24．如图1，AB ∥CD ，点E 在AB 上，点G 在CD 上，点 F 在直线 AB ，CD 之间，连接EF ，FG ，EF 垂直于 FG ，∠FGD =125°．(1)求出∠BEF 的度数；(2)如图 2，延长FE 到H ，点M 在FH 的上方，连接MH ，Q 为直线 AB 上一点，且在直线 MH 的右侧， 连接 MQ ，若∠EHM=∠M +90°，求∠MQA 的度数；(3)如图 3，S 为 NB 上一点，T 为 GD 上一点，作直线 ST ，延长 GF 交 AB 于点 N ，P 为直线 ST 上一动点，请直接写出∠PGN ，∠SNP 和∠GPN 的数量关系 ．（题中所有角都是大于 0°小于 180°的角）25．已知E 、D 分别在AOB ∠的边OA 、OB 上，C 为平面内一点，DE 、DF 分别是CDO ∠、CDB ∠的平分线．（1）如图1，若点C 在OA 上，且//FD AO ，求证：DE AO ⊥；（2）如图2，若点C 在AOB ∠的内部，且DEO DEC ∠=∠，请猜想DCE ∠、AEC ∠、CDB ∠之间的数量关系，并证明；（3）若点C 在AOB ∠的外部，且DEO DEC ∠=∠，请根据图3、图4直接写出结果出DCE ∠、AEC ∠、CDB ∠之间的数量关系．26．如图，已知C 为两条相互平行的直线AB ，ED 之间一点，ABC ∠和CDE ∠的角平分线相交于F ，180FDC ABC ∠+∠=︒．（1）求证：//AD BC ；（2）连结CF ，当//CF AB ，且32CFB DCF ∠=∠时，求BCD ∠的度数；（3）若DCF CFB ∠=∠时，将线段BC 沿直线AB 方向平移，记平移后的线段为PQ （B ，C 分别对应P ，Q ，当20PQD QDC ∠-∠=︒时，请直接写出DQP ∠的度数______．27．如图，已知直线12//l l ，直线3l 交1l 于C 点，交2l 于D 点，P 是线段CD 上的一个动点，（1）若P 点在线段CD （C 、D 两点除外）上运动，问PAC ∠，APB ∠，PBD ∠之间的关系是什么？这种关系是否变化？（2）若P 点在线段CD 之外时，PAC ∠，APB ∠，PBD ∠之间的关系怎样？说明理由28．（1）如图1，已知直线//m n ，在直线n 上取A B 、两点，C P 、为直线m 上的两点，无论点C P 、移动到任何位置都有：ABC S ____________ABP S △（填“>”、“<”或“=”） （2）如图2，在一块梯形田地上分别要种植大豆（空白部分）和芝麻（阴影部分），若想把种植大豆的两块地改为一块地，且使分别种植两种植物的面积不变，请问应该怎么改进呢？写出设计方案，并在图中画出相应图形并简述理由．（3）如图3，王爷爷和李爷爷两家田地形成了四边形DEFG，中间有条分界小路（图中折线ABC），左边区域为王爷爷的，右边区域为李爷爷的。

七下《第5章相交线与平行线》单元检测卷（1）一、选择题（本大题10小题，每题4分，共40分）1．（4分）如图，能够证明a∥b的是（）A．∠1＝∠2B．∠4＝∠5C．∠4＝∠3D．∠1＝∠52．（4分）将一个含30°角的直角三角板ABC如图所示放置，∠B＝90°，点E为AC延长线上的点，若射线CD与直角边BC垂直，则∠DCE的度数是（）A．10°B．20°C．30°D．50°3．（4分）直线m外的一点P，它到直线m上三点A，B，C的距离分别是6cm，3cm，5cm，则点P到直线m的距离为（）A．3cm B．5cm C．6cm D．不大于3cm 4．（4分）在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）A．B．C．D．5．（4分）如图，直线AB⊥CD，垂足为O，EF是过点O的直线，若∠1＝50°，则∠2的度数为（）A．40°B．50°C．60°D．70°6．（4分）如图，直线AB、BE被AC所截，下列说法，正确的有（）①∠1与∠2是同旁内角；②∠1与∠ACE是内错角；③∠B与∠4是同位角；④∠1与∠3是内错角．A．①③④B．③④C．①②④D．①②③④7．（4分）如图，AB∥CD，DA⊥AC，垂足为A，若∠ADC＝35°，则∠1的度数为（）A．65°B．55°C．45°D．35°8．（4分）一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，则∠DBC的度数为（）A．10°B．15°C．18°D．30°9．（4分）如图，在三角形ABC中，∠BAC＝90°，AB＝3，AC＝4，BC＝5，将三角形ABC 沿直线BC向右平移2个单位得到三角形DEF，连接AD，则下列结论：①AC∥DF，AC ＝DF；②ED⊥DF；③四边形ABFD的周长是16；④AD：EC＝2：3．其中结论正确的个数有（）A．1个B．2个C．3个D．4个10．（4分）如图，已知AB∥CD，BE和DF分别平分∠ABF和∠CDE，2∠E﹣∠F＝48°，则∠CDE的度数为（）A．16°B．32°C．48°D．64°二、填空题（本大题10小题，每题3分，共30分）11．（3分）把命题“对顶角相等”改写成“如果…那么…”的形式：．12．（3分）如图，若∠1+∠2＝220°，则∠3＝．13．（3分）如图所示，在铁路旁边有一李庄，现要建一火车站，为了使李庄人乘火车最方便（即距离最近），请你在铁路旁选一点来建火车站（位置已选好），说明理由；．14．（3分）如图所示，一个弯形管道ABCD的拐角∠ABC＝110°，∠BCD＝70°，管道AB，CD的关系是，依据是．15．（3分）如图，为了把△ABC平移得到△A′B′C′，可以先将△ABC向右平移格，再向上平移格．16．（3分）如图，FE∥ON，OE平分∠MON，∠FEO＝28°，则∠MON＝．17．（3分）如图，∠A与是内错角，∠B的同位角是，直线AB和CE被直线BC所截得到的同旁内角是．18．（3分）如图，AB∥CD∥EF，AC∥DF，若∠BAC＝120°，则∠CDF＝°．19．（3分）一大门的栏杆如图所示，BA⊥AE，若CD∥AE，则∠ABC+∠BCD＝度．20．（3分）如图，把直角梯形ABCD沿AD方向平移到梯形EFGH的位置，若AB∥CD，HG＝18cm，MG＝6cm，MC＝3cm，则阴影部分的面积是cm2．三、解答题（本大题6小题，共80分）21．（12分）如图，直线CD与直线AB相交于C，根据下列语句画图（1）过点P作PQ∥CD，交AB于点Q；（2）过点P作PR⊥CD，垂足为R；（3）若∠DCB＝120°，猜想∠PQC是多少度？并说明理由．22．（12分）已知如图：AD∥BC，E、F分别在DC、AB延长线上．∠DCB＝∠DAB，AE ⊥EF，∠DEA＝30°．（1）求证：DC∥AB．（2）求∠AFE的大小．23．（14分）如图，两直线AB、CD相交于点O，OE平分∠BOD，如果∠AOC：∠AOD＝7：11，（1）求∠COE；（2}若OF⊥OE，求∠COF．24．（14分）如图是一种躺椅及其简化结构示意图，扶手AB与底座CD都平行于地面，靠背DM与支架OE平行，前支架OE与后支架OF分别与CD交于点G和点D，AB与DM 交于点N，当∠EOF＝90°，∠ODC＝30°时，人躺着最舒服，求此时扶手AB与支架OE的夹角∠AOE和扶手AB与靠背DM的夹角∠ANM的度数．25．（12分）如图①是一张长方形的纸带，将这张纸带沿EF折叠成图②，再沿BF折叠成图③．（1）若∠DEF＝20°，请你求出图③中∠C2FE的度数；（2）若∠DEF＝α，请你用含α的式子表示图③中∠C2FE的度数．26．（16分）如图①所示，已知，BC∥OA，∠B＝∠A＝100°，试回答下列问题：（1）试说明：OB∥AC；（2）如图②，若点E、F在BC上，且∠FOC＝∠AOC，OE平分∠BOF．试求∠EOC 的度数；（3）在（2）的条件下，若左右平行移动AC，如图③，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；（4）在（3）的条件下，当∠OEB＝∠OCA时，试求∠OCA的度数．。

北师大版八年级上册数学第五章 二元一次方程组 单元测试题一.单选题 1．若2123a b a b x y -+--=是关于x 、y 的二元一次方程，则2023(2)ab -的值为（ ）A ．2023B ．2023-C ．1D ．1-2． 如果方程3x y -=与下面方程中的一个组成的方程组的解为41x y =⎧⎨=⎩，那么这个方程是（ ） A ．1254x y += B ．2()6x y -= C ．29x y += D ．3416x y -=3．用代入消元法解二元一次方程组235311x y y x -=⎧⎨=-⎩①②时，将②代入①中，正确的是（ ） A ．()23115x x --= B ．23115x x --= C ．233115x x -⨯-= D ．()233115x x -⨯-=4． 下列哪对x ，y 的值是二元一次方程26x y +=的解（ ）A ．22x y =-⎧⎨=-⎩B ．02x y =⎧⎨=⎩C ．22x y =⎧⎨=⎩D ．31x y =⎧⎨=⎩ 5．在平面直角坐标系中，若点()1A a b -+，与点(),3B a b -关于y 轴对称，则点(),C a b -落在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．我国古代《四元玉鉴》中记载“二果问价”问题，其内容如下：九百九十九文钱，甜果苦果买一千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个，又问各该几个钱？若设买甜果x 个，买苦果y 个，则下列关于x ，y 的二元一次方程组中符合题意的是（ ）A ．10009928999x y x y +=⎧⎨+=⎩B ．999971000114x y x y +=⎧⎪⎨+=⎪⎩C ．100011499997x y x y +=⎧⎪⎨+=⎪⎩ D ． 100097999114x y x y +=⎧⎪⎨+=⎪⎩ 7．函数y kx b =+的图象如图所示，根据图象信息可求得关于x 的方程0kx b +=的解为（ ）A ．1x =B ．2x =-C ．0x =D ．3x =8．若5210a b a b +++-+=，则()2023b a -的值是（ ）二.填空题15．在画一次函数y kx b=+的图象时，琪琪同学列表部分如下，其中x L2-1-1y L53▲-16．一次函数 31y x =-与y x b =+的图象的交点为()12P ，，则b = ． 17． 将直线2y x =-向下平移后得到直线l ，若直线l 经过点(),a b ，且27a b +=-，则直线l 的解析式为 ．18．在坐标平面内，已知正比例函数2y x =与一次函数1y x =-的图象交于点A ，则点A 的坐标为 ．三、解答题 19．解方程：(1) 34165633x y x y +=⎧⎨-=⎩； (2) 527x y x y +=⎧⎨+=⎩.20．已知关于x 、y 的方程组4210323x y x y +=⎧⎨-=-⎩和48ax by ax by +=-⎧⎨-=⎩有相同的解，求22a b ab +的值．21． 已知31a +的算术平方根是2，23a b -+的立方根是3-，求8b a -的平方根．22．已知A 、B 、C 的坐标分别为()1,5A -、3,62B ⎛⎫- ⎪⎝⎭、()2,1C -，试判断A 、B 、C 三点是否在同一直线上，并说明理由．23． 对有理数x 、y 定义一种新运算“※”，规定：()21x y ax by =+-※，，这里等式右边是通常的四则运算，例如：()0102**1121a b b =*+-=-※，，已知：()114-=-※，，()4211=※， (1)求a 、b 的值；(2)求()25m m +※，的最小值．l的函数表达式；(1)求直线2△的面积；(2)求ADCl上是否存在点(3)在直线2。

高中数学选择性必修二《第五章 一元函数的导数及其应用》单元检测试卷（一）本试卷分第Ⅰ卷和第Ⅱ卷两部分，满分150分，考试时间120分钟．第Ⅰ卷(选择题，共60分)一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若f(x)＝sin α－cos x ，则f′(x)等于( )A ．sin xB ．cos xC ．cos α＋sin xD ．2sin α＋cos x 2．以正弦曲线y ＝sin x 上一点P 为切点的切线为直线l ，则直线l 的倾斜角的范围是( )A.⎣⎢⎡⎦⎥⎤0，π4∪⎣⎢⎡⎭⎪⎫3π4，π B ．[0，π) C.⎣⎢⎡⎦⎥⎤π4，3π4 D.⎣⎢⎡⎦⎥⎤0，π4∪⎝ ⎛⎦⎥⎤π2，3π43．函数f(x)的定义域为开区间(a ，b)，导函数f′(x)在(a ，b)内的图象如图所示，则函数f(x)在开区间(a ，b)内有极小值点( )A ．1个B ．2个C ．3个D ．4个 4．函数f(x)＝x 2－ln x 的单调递减区间是( ) A. ⎝ ⎛⎦⎥⎤0，22 B.⎣⎢⎡⎭⎪⎫22，＋∞ C. ⎝⎛⎦⎥⎤－∞，－22，⎝ ⎛⎭⎪⎫0， 22 D.⎣⎢⎡⎭⎪⎫－22， 0，⎝⎛⎦⎥⎤0， 22 5．函数f(x)＝3x －4x 3(x ∈[0,1])的最大值是( ) A ．1 B.12C ．0D ．－16．函数f(x)＝x 3＋ax 2＋3x －9，已知f(x)在x ＝－3处取得极值，则a ＝( ) A ．2 B ．3 C ．4 D ．57．函数f(x)＝13ax 3＋12ax 2－2ax ＋1的图象经过四个象限，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫－310，67B.⎝ ⎛⎭⎪⎫－85，－316C.⎝ ⎛⎭⎪⎫－83，－116D.⎝ ⎛⎭⎪⎫－∞，－310∪⎝ ⎛⎭⎪⎫67，＋∞8．已知定义在R 上的函数f(x)，f(x)＋xf′(x)＜0，若a ＜b ，则一定有( )A ．af(a)＜bf(b)B ．af(b)＜bf(a)C ．af(a)＞bf(b)D ．af(b)＞bf(a)二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求的，全部选对的得5分，选对但不全的得3分，有选错的得0分)9．下列结论中不正确的是( ) A ．若y ＝cos 1x ，则y′＝－1x sin 1xB ．若y ＝sin x 2，则y′＝2xcos x 2C ．若y ＝cos 5x ，则y′＝－sin 5xD ．若y ＝12xsin 2x ，则y′＝xsin 2x10．下列函数中，存在极值点的是( )A ．y ＝x －1xB ．y ＝2|xC ．y ＝－2x 3－x D ．y ＝xln x11.定义在区间⎣⎢⎡⎦⎥⎤－12，4上的函数f(x)的导函数f′(x)图象如图所示，则下列结论正确的是( )A ．函数f(x)在区间(0,4)上单调递增B ．函数f(x)在区间⎝ ⎛⎭⎪⎫－12，0上单调递减 C ．函数f(x)在x ＝1处取得极大值 D ．函数f(x)在x ＝0处取得极小值12．已知函数f(x)＝e x－ax 有两个零点x 1，x 2，且x 1＜x 2，则下列说法正确的是( ) A ．a ＞e B ．x 1＋x 2＞2C ．x 1x 2＞1D ．f(x)有极小值点x 0，且x 1＋x 2＜2x 0第Ⅱ卷(非选择题，共90分)三、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．若f(x)＝13x 3－f′(1)x 2＋x ＋5，则f′(1)＝________.14．已知奇函数 f(x)＝⎩⎪⎨⎪⎧e xx－1(x>0)，h (x )(x<0)，则函数h(x)的最大值为________．15．已知函数f(x)满足f(x)＝f(π－x)，且当x ∈⎝ ⎛⎭⎪⎫－π2，π2时，f(x)＝x ＋sin x ，设a＝f(1)，b ＝f(2)，c ＝f(3)，则a ，b ，c 的大小关系是________． 16．若函数f(x)＝4xx 2＋1在区间(m,2m ＋1)上单调递增，则实数m 的取值范围是__________．四、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知函数f(x)＝x 3＋ax 2＋bx ＋a 2在x ＝1处有极值4. (1)求实数a ，b 的值；(2)当a>0时，求曲线y ＝f(x)在点(－2，f(－2))处的切线方程． 18．(本小题满分12分)已知a ∈R ，函数f(x)＝(－x 2＋ax)e x. (1)当a ＝2时，求函数f(x)的单调区间；(2)若函数f(x)在(－1,1)上单调递增，求实数a 的取值范围． 19．(本小题满分12分)已知函数f(x)＝ax 3＋bx 在x ＝22处取得极小值－ 2. (1)求函数f(x)的解析式；(2)若过点M(1，m)的直线与曲线y ＝f(x)相切且这样的切线有三条，求实数m 的取值范围．20. (本小题满分12分)设函数f(x)＝x22－kln x ，k>0.(1)求f(x)的单调区间和极值；(2)证明：若f(x)存在零点，则f(x)在区间(1， e ]上仅有一个零点． 21．(本小题满分12分)已知函数f(x)＝ln x ＋ax 2＋(2a ＋1)x. (1)讨论f(x)的单调性；(2)当a ＜0时，证明f(x)≤－34a－2.22．(本小题满分12分)已知函数f(x)＝ln x －ax .(1)若f(x)存在最小值且最小值为2，求a 的值；(2)设g(x)＝ln x －a ，若g(x)<x 2在(0，e]上恒成立，求a 的取值范围． 答案解析第Ⅰ卷(选择题，共60分)一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若f(x)＝sin α－cos x ，则f′(x)等于( )A ．sin xB ．cos xC ．cos α＋sin xD ．2sin α＋cos x 解析：选A 函数是关于x 的函数，因此sin α是一个常数．2．以正弦曲线y ＝sin x 上一点P 为切点的切线为直线l ，则直线l 的倾斜角的范围是( )A.⎣⎢⎡⎦⎥⎤0，π4∪⎣⎢⎡⎭⎪⎫3π4，π B ．[0，π) C.⎣⎢⎡⎦⎥⎤π4，3π4 D.⎣⎢⎡⎦⎥⎤0，π4∪⎝ ⎛⎦⎥⎤π2，3π4解析：选A y′＝cos x ，∵cos x ∈[－1,1]，∴切线的斜率范围是[－1,1]，∴倾斜角的范围是⎣⎢⎡⎦⎥⎤0，π4∪⎣⎢⎡⎭⎪⎫3π4，π.3．函数f(x)的定义域为开区间(a ，b)，导函数f′(x)在(a ，b)内的图象如图所示，则函数f(x)在开区间(a ，b)内有极小值点( )A ．1个B ．2个C ．3个D ．4个解析：选A 设极值点依次为x 1，x 2，x 3且a ＜x 1＜x 2＜x 3＜b ，则f(x)在(a ，x 1)，(x 2，x 3)上递增，在(x 1，x 2)，(x 3，b)上递减，因此，x 1，x 3是极大值点，只有x 2是极小值点． 4．函数f(x)＝x 2－ln x 的单调递减区间是( ) A. ⎝ ⎛⎦⎥⎤0，22 B.⎣⎢⎡⎭⎪⎫22，＋∞ C. ⎝⎛⎦⎥⎤－∞，－22，⎝ ⎛⎭⎪⎫0， 22 D.⎣⎢⎡⎭⎪⎫－22， 0，⎝⎛⎦⎥⎤0， 22 解析：选A ∵f′(x)＝2x －1x ＝2x 2－1x ，当0＜x≤22时，f′(x)≤0，故f(x)的单调递减区间为⎝ ⎛⎦⎥⎤0，22. 5．函数f(x)＝3x －4x 3(x ∈[0,1])的最大值是( ) A ．1 B.12 C ．0 D ．－1解析：选A f′(x)＝3－12x 2，令f′(x)＝0， 则x ＝－12(舍去)或x ＝12，f(0)＝0，f(1)＝－1，f ⎝ ⎛⎭⎪⎫12＝32－12＝1，∴f(x)在[0,1]上的最大值为1.6．函数f(x)＝x 3＋ax 2＋3x －9，已知f(x)在x ＝－3处取得极值，则a ＝( ) A ．2 B ．3 C ．4 D ．5 解析：选D f′(x)＝3x 2＋2ax ＋3，∵f′(－3)＝0. ∴3×(－3)2＋2a×(－3)＋3＝0，∴a ＝5.7．函数f(x)＝13ax 3＋12ax 2－2ax ＋1的图象经过四个象限，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫－310，67B.⎝ ⎛⎭⎪⎫－85，－316C.⎝ ⎛⎭⎪⎫－83，－116D.⎝ ⎛⎭⎪⎫－∞，－310∪⎝ ⎛⎭⎪⎫67，＋∞解析：选D f′(x)＝ax 2＋ax －2a ＝a(x ＋2)(x －1)，要使函数f(x)的图象经过四个象限，则f(－2)f(1)<0，即⎝ ⎛⎭⎪⎫103a ＋1⎝ ⎛⎭⎪⎫－76a ＋1<0，解得a<－310或a>67. 故选D.8．已知定义在R 上的函数f(x)，f(x)＋xf′(x)＜0，若a ＜b ，则一定有( ) A ．af(a)＜bf(b) B ．af(b)＜bf(a) C ．af(a)＞bf(b) D ．af(b)＞bf(a)解析：选C 令y ＝xf(x)，则y′＝[xf(x)]′＝x′f(x)＋xf′(x)＝f(x)＋xf′(x)＜0，∴函数y ＝xf(x)是R 上的减函数，∵a ＜b ，∴af(a)＞bf(b)．二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求的，全部选对的得5分，选对但不全的得3分，有选错的得0分)9．下列结论中不正确的是( ) A ．若y ＝cos 1x ，则y′＝－1x sin 1xB ．若y ＝sin x 2，则y′＝2xcos x 2C ．若y ＝cos 5x ，则y′＝－sin 5xD ．若y ＝12xsin 2x ，则y′＝xsin 2x解析：选ACD 对于A ，y ＝cos 1x ，则y′＝1x 2sin 1x ，故错误；对于B ，y ＝sin x 2，则y′＝2xcos x 2，故正确；对于C ，y ＝cos 5x ，则y′＝－5sin 5x ，故错误；对于D ，y ＝12xsin 2x ，则y′＝12sin 2x ＋xcos 2x ，故错误．10．下列函数中，存在极值点的是( ) A ．y ＝x －1x B ．y ＝2|x|C ．y ＝－2x 3－x D ．y ＝xln x解析：选BD 由题意，函数y ＝x －1x ，则y′＝1＋1x 2＞0，所以函数y ＝x －1x在(－∞，0)，(0，＋∞)内单调递增，没有极值点．函数y ＝2|x|＝⎩⎪⎨⎪⎧2x，x≥0，2－x，x ＜0根据指数函数的图象与性质可得，当x ＜0时，函数y ＝2|x|单调递减，当x≥0时，函数y ＝2|x|单调递增，所以函数y ＝2|x|在x ＝0处取得极小值；函数y ＝－2x 3－x ，则y′＝－6x 2－1＜0，所以函数y ＝－2x 3－x 在R 上单调递减，没有极值点；函数y ＝xln x ，则y′＝ln x ＋1，x ＞0，当x ∈⎝ ⎛⎭⎪⎫0，1e 时，y′＜0，函数单调递减，当x ∈⎝ ⎛⎭⎪⎫1e ，＋∞时，y′＞0，函数单调递增，当x＝1e时，函数取得极小值，故选B 、D. 11.定义在区间⎣⎢⎡⎦⎥⎤－12，4上的函数f(x)的导函数f′(x)图象如图所示，则下列结论正确的是( )A ．函数f(x)在区间(0,4)上单调递增B ．函数f(x)在区间⎝ ⎛⎭⎪⎫－12，0上单调递减 C ．函数f(x)在x ＝1处取得极大值 D ．函数f(x)在x ＝0处取得极小值解析：选ABD 根据导函数图象可知，f(x)在区间⎝ ⎛⎭⎪⎫－12，0上，f′(x)＜0，f(x)单调递减，在区间(0,4)上，f′(x)＞0，f(x)单调递增．所以f(x)在x ＝0处取得极小值，没有极大值，所以A 、B 、D 选项正确，C 选项错误．故选A 、B 、D.12．已知函数f(x)＝e x－ax 有两个零点x 1，x 2，且x 1＜x 2，则下列说法正确的是( ) A ．a ＞e B ．x 1＋x 2＞2C ．x 1x 2＞1D ．f(x)有极小值点x 0，且x 1＋x 2＜2x 0解析：选ABD 由题意，函数f(x)＝e x－ax ，则f′(x)＝e x－a ，当a≤0时，f′(x)＝e x－a ＞0在R 上恒成立，所以函数f(x)单调递增，不符合题意；当a ＞0时，令f′(x)＝e x－a ＞0，解得x ＞ln a ，令f′(x)＝e x－a ＜0，解得x ＜ln a ，所以函数f(x)在(－∞，ln a)上单调递减，在(ln a ，＋∞)上单调递增，因为函数f(x)＝e x－ax 有两个零点x 1，x 2且x 1＜x 2，则f(ln a)＝eln a－aln a ＝a －aln a ＝a(1－ln a)＜0，且a ＞0，所以1－ln a ＜0，解得a ＞e ，所以A 项正确；又由x 1＋x 2＝ln(a 2x 1x 2)＝2ln a ＋ln(x 1x 2)＞2＋ln(x 1x 2)，取a ＝e 22，则f(2)＝e 2－2a ＝0，x 2＝2，f(0)＝1＞0，所以0＜x 1＜1，所以x 1＋x 2＞2，所以B 正确；由f(0)＝1＞0，则0＜x 1＜1，但x 1x 2＞1不能确定，所以C 不正确；由函数f(x)在(－∞，ln a)上单调递减，在(ln a ，＋∞)上单调递增，所以函数的极小值点为x 0＝ln a ，且x 1＋x 2＜2x 0＝2ln a ，所以D 正确．故选A 、B 、D. 第Ⅱ卷(非选择题，共90分)三、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．若f(x)＝13x 3－f′(1)x 2＋x ＋5，则f′(1)＝________.解析：f′(x)＝x 2－2f′(1)x＋1，令x ＝1，得f′(1)＝23.答案：2314．已知奇函数 f(x)＝⎩⎪⎨⎪⎧e xx－1(x>0)，h (x )(x<0)，则函数h(x)的最大值为________．解析：先求出x>0时，f(x)＝e xx －1的最小值．当x>0时， f′(x)＝e x(x －1)x 2，∴x ∈(0,1)时，f′(x)<0，函数单调递减，x ∈(1，＋∞)时，f′(x) >0，函数单调递增，∴x ＝1时，函数取得极小值即最小值，为e －1，∴由已知条件得h(x)的最大值为1－e. 答案：1－e15．已知函数f(x)满足f(x)＝f(π－x)，且当x ∈⎝ ⎛⎭⎪⎫－π2，π2时，f(x)＝x ＋sin x ，设a＝f(1)，b ＝f(2)，c ＝f(3)，则a ，b ，c 的大小关系是________． 解析：f(2)＝f(π－2)，f(3)＝f(π－3)， 因为f′(x)＝1＋cos x≥0，故f(x)在⎝ ⎛⎭⎪⎫－π2，π2上是增函数， ∵π2>π－2>1>π－3>0， ∴f(π－2)>f(1)>f(π－3)，即c<a<b. 答案：c<a<b 16．若函数f(x)＝4xx 2＋1在区间(m,2m ＋1)上单调递增，则实数m 的取值范围是__________．解析：f′(x)＝4－4x2(x 2＋1)2，令f′(x)＞0，得－1＜x ＜1，即函数f(x)的增区间为(－1,1)． 又因为f(x)在(m,2m ＋1)上单调递增， 所以⎩⎪⎨⎪⎧m≥－1，m ＜2m ＋1，2m ＋1≤1.解得－1＜m≤0.答案：(－1,0]四、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知函数f(x)＝x 3＋ax 2＋bx ＋a 2在x ＝1处有极值4. (1)求实数a ，b的值；(2)当a>0时，求曲线y ＝f(x)在点(－2，f(－2))处的切线方程． 解：(1)∵f(x)＝x 3＋ax 2＋bx ＋a 2， ∴f′(x)＝3x 2＋2ax ＋b.∵f(1)＝1＋a ＋b ＋a 2＝4，f′(1)＝3＋2a ＋b ＝0，∴⎩⎪⎨⎪⎧a ＝3，b ＝－9或⎩⎪⎨⎪⎧a ＝－2，b ＝1.经检验都符合题意．(2)当a>0时，由(1)得f(x)＝x 3＋3x 2－9x ＋9， ∴f′(x)＝3x 2＋6x －9. ∴f(－2)＝31，f′(－2)＝－9.∴所求的切线方程为y －31＝－9(x ＋2)，即9x ＋y －13＝0. 18．(本小题满分12分)已知a ∈R ，函数f(x)＝(－x 2＋ax)e x. (1)当a ＝2时，求函数f(x)的单调区间；(2)若函数f(x)在(－1,1)上单调递增，求实数a 的取值范围．解：(1)当a ＝2时，f(x)＝(－x 2＋2x)e x，f′(x)＝(－x 2＋2)e x.令f′(x)>0，即(－x 2＋2)e x>0，注意到e x>0，所以－x 2＋2>0，解得－2<x< 2.所以，函数f(x)的单调递增区间为(－2，2)．同理可得，函数f(x)的单调递减区间为(－∞，－2)和(2，＋∞)．(2)因为函数f(x)在(－1,1)上单调递增，所以f′(x)≥0在(－1,1)上恒成立． 又因为f′(x)＝[－x 2＋(a －2)x ＋a]e x，所以[－x 2＋(a －2)x ＋a]e x≥0，注意到e x>0，因此－x 2＋(a －2)x ＋a≥0在(－1,1)上恒成立，也就是a≥x 2＋2x x ＋1＝x ＋1－1x ＋1在(－1,1)上恒成立．设y ＝x ＋1－1x ＋1，则y′＝1＋1(x ＋1)2>0，即y ＝x ＋1－1x ＋1在(－1,1)上单调递增，则y<1＋1－11＋1＝32，故a≥32.即实数a 的取值范围为⎣⎢⎡⎭⎪⎫32，＋∞. 19．(本小题满分12分)已知函数f(x)＝ax 3＋bx 在x ＝22处取得极小值－ 2. (1)求函数f(x)的解析式；(2)若过点M(1，m)的直线与曲线y ＝f(x)相切且这样的切线有三条，求实数m 的取值范围．解：(1)由题意得，f′(x)＝3ax 2＋b.∵函数f(x)＝ax 3＋bx 在x ＝22处取得极小值－2， ∴⎩⎪⎨⎪⎧f ⎝ ⎛⎭⎪⎫22＝－2，f ′⎝ ⎛⎭⎪⎫22＝0，即⎩⎪⎨⎪⎧a ＋2b ＝－4，32a ＋b ＝0，解得⎩⎪⎨⎪⎧a ＝2，b ＝－3，经检验满足条件，则函数f(x)的解析式为f(x)＝2x 3－3x.(2)设切点坐标为(x 0,2x 30－3x 0)，则曲线y ＝f(x)的切线的斜率k ＝f′(x 0)＝6x 20－3， 切线方程为y －(2x 30－3x 0)＝(6x 20－3)(x －x 0)， 代入点M(1，m)，得m ＝－4x 30＋6x 20－3，依题意，方程m ＝－4x 30＋6x 20－3有三个不同的实根． 令g(x)＝－4x 3＋6x 2－3，则g′(x)＝－12x 2＋12x ＝－12x(x －1)， ∴当x ∈(－∞，0)时，g′(x)<0； 当x ∈(0,1)时，g′(x)>0； 当x ∈(1，＋∞)时，g′(x)<0.故g(x)＝－4x 3＋6x 2－3在(－∞，0)上单调递减，在(0,1)上单调递增，在(1，＋∞)上单调递减．∴g(x)极小值＝g(0)＝－3，g(x)极大值＝g(1)＝－1.∴当－3<m<－1时，g(x)＝－4x 3＋6x 2－3的图象与直线y ＝m 有三个不同的交点， ∴－3<m<－1时，存在这样的三条切线． 故实数m 的取值范围是(－3，－1)．20. (本小题满分12分)设函数f(x)＝x22－kln x ，k>0.(1)求f(x)的单调区间和极值；(2)证明：若f(x)存在零点，则f(x)在区间(1， e ]上仅有一个零点．解：(1)由f(x)＝x22－kln x(k>0)，得x>0且f′(x)＝x －k x ＝x 2－kx .由f′(x)＝0，解得x ＝k(负值舍去)． f(x)与f′(x)在区间(0，＋∞)上的情况如下：所以，f(x)在x ＝k 处取得极小值f(k)＝k (1－ln k )2，无极大值．(2)证明：由(1)知，f(x)在区间(0，＋∞)上的最小值为f(k)＝k (1－ln k )2.因为f(x)存在零点，所以k (1－ln k )2≤0，从而k≥e.当k ＝e 时，f(x)在区间(1，e)上单调递减，且f(e)＝0， 所以x ＝e 是f(x)在区间(1， e ]上的唯一零点．当k>e 时，f(x)在区间(1， e ]上单调递减，且f(1)＝12>0，f(e)＝e －k2<0，所以f(x)在区间(1， e ]上仅有一个零点．综上可知，若f(x)存在零点，则f(x)在区间(1， e ]上仅有一个零点． 21．(本小题满分12分)已知函数f(x)＝ln x ＋ax 2＋(2a ＋1)x. (1)讨论f(x)的单调性；(2)当a ＜0时，证明f(x)≤－34a －2.解：(1)f(x)的定义域为(0，＋∞)， f′(x)＝1x ＋2ax ＋2a ＋1＝(x ＋1)(2ax ＋1)x .若a≥0，则当x ∈(0，＋∞)时，f′(x)＞0， 故f(x)在(0，＋∞)上单调递增．若a ＜0，则当x ∈⎝⎛⎭⎪⎫0，－12a 时，f′(x)＞0；当x ∈⎝ ⎛⎭⎪⎫－12a ，＋∞时，f′(x)＜0.故f(x)在⎝ ⎛⎭⎪⎫0，－12a 上单调递增，在⎝ ⎛⎭⎪⎫－12a ，＋∞上单调递减． (2)证明：由(1)知，当a ＜0时，f(x)在x ＝－12a 处取得最大值，最大值为f ⎝ ⎛⎭⎪⎫－12a ＝ln ⎝ ⎛⎭⎪⎫－12a －1－14a .所以f(x)≤－34a －2等价于ln ⎝ ⎛⎭⎪⎫－12a －1－14a ≤－34a －2，即ln ⎝ ⎛⎭⎪⎫－12a ＋12a ＋1≤0.设g(x)＝ln x －x ＋1，则g′(x)＝1x－1.当x ∈(0,1)时，g′(x)＞0；当x ∈(1，＋∞)时，g′(x)＜0.所以g(x)在(0,1)上单调递增，在(1，＋∞)上单调递减．故当x ＝1时，g(x)取得极大值且为最大值，最大值为g(1)＝0. 所以当x ＞0时，g(x)≤0.从而当a ＜0时，ln ⎝ ⎛⎭⎪⎫－12a ＋12a＋1≤0，即f(x)≤－34a－2.22．(本小题满分12分)已知函数f(x)＝ln x －ax .(1)若f(x)存在最小值且最小值为2，求a 的值；(2)设g(x)＝ln x －a ，若g(x)<x 2在(0，e]上恒成立，求a 的取值范围． 解：(1)f′(x)＝1x ＋a x 2＝x ＋ax2(x>0)，当a≥0时，f′(x)>0，f(x)在(0，＋∞)上是增函数， f(x)不存在最小值；当a<0时，由f′(x)＝0得x ＝－a ， 且0<x<－a 时，f′(x)<0， x>－a 时，f′(x)>0.∴x ＝－a 时，f(x)取得最小值， f(－a)＝ln(－a)＋1＝2，解得a ＝－e. (2)g(x)<x 2即ln x －a<x 2，即a>ln x －x 2，故g(x)<x 2在(0，e]上恒成立，也就是a>ln x －x 2在(0，e]上恒成立． 设h(x)＝ln x －x 2，则h′(x)＝1x －2x ＝1－2x2x，由h′(x)＝0及0<x≤e 得x ＝22.当0<x<22时，h′(x)>0，当22<x≤e 时，h′(x)<0，即h(x)在⎝⎛⎭⎪⎫0，22上为增函数，在⎝ ⎛⎦⎥⎤22，e 上为减函数， 所以当x ＝22时h(x)取得最大值为h ⎝ ⎛⎭⎪⎫22＝ln 22－12. 所以g(x)<x 2在(0，e]上恒成立时，a 的取值范围为⎝ ⎛⎭⎪⎫ln 22－12，＋∞.高中数学选择性必修二《第五章 一元函数的导数及其应用》单元检测试卷（二）本试卷分第Ⅰ卷和第Ⅱ卷两部分，满分150分，考试时间120分钟．第Ⅰ卷(选择题，共60分)一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．等差数列{a n }中，a 3＝2，a 5＝7，则a 7＝( ) A ．10 B ．20 C ．16 D ．122．在数列{a n }中，a 1＝13，a n ＝(－1)n·2a n －1(n≥2)，则a 5等于( )A ．－163 D ．163 C ．－83 D ．833．设等比数列{a n }的前n 项和为S n ，若S 10∶S 5＝1∶2，则S 15∶S 5＝( ) A ．3∶4 B ．2∶3 C ．1∶2 D ．1∶3 4．在等比数列{a n }中，已知前n 项和S n ＝5n ＋1＋a ，则a 的值为( )A ．－1B ．1C ．5D ．－55．已知数列{a n }满足a 1＝1，a n ＋1＝⎩⎪⎨⎪⎧2a n ，n 为正奇数，a n ＋1，n 为正偶数，则254是该数列的( )A ．第8项B ．第10项C ．第12项D ．第14项 6．已知数列{a n }是等差数列，其前n 项和为S n ，若a 1a 2a 3＝15，且3S 1S 3＋15S 3S 5＋5S 5S 1＝35，则a 2＝( )A ．2 D ．12 C ．3 D ．137．如果数列a 1，a 2－a 1，a 3－a 2，…，a n －a n －1，…是首项为1，公比为13的等比数列，那么a n ＝( )A.32⎝ ⎛⎭⎪⎫1－13n D ．32⎝ ⎛⎭⎪⎫1－13n －1 C.23⎝ ⎛⎭⎪⎫1－13n D ．23⎝ ⎛⎭⎪⎫1－13n －18．若有穷数列a 1，a 2，…，a n (n 是正整数)，满足a 1＝a n ，a 2＝a n －1，…，a n ＝a 1，即a i ＝a n－i ＋1(i 是正整数，且1≤i≤n)，就称该数列为“对称数列”．已知数列{b n }是项数不超过2m(m ＞1，m ∈N *)的对称数列，且1,2,4，…，2m －1是数列{b n }的前m 项，则当m ＞1 200时，数列{b n }的前2 019项和S 2 019的值不可能为( ) A ．2m－2m －2 009B ．22 019－1C ．2m ＋1－22m －2 019－1 D ．3·2m －1－22m －2 020－1二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求的，全部选对的得5分，选对但不全的得3分，有选错的得0分)9．已知等比数列{a n }的公比q ＝－23，等差数列{b n }的首项b 1＝12，若a 9>b 9且a 10>b 10，则以下结论正确的有( )A ．a 9·a 10<0B ．a 9>a 10C ．b 10>0D ．b 9>b 1010．等差数列{a n }的前n 项和为S n ，若a 1＞0，公差d≠0，则下列命题正确的是( ) A ．若S 5＝S 9，则必有S 14＝0B ．若S 5＝S 9，则必有S 7是S n 中最大的项C ．若S 6＞S 7，则必有S 7＞S 8D ．若S 6＞S 7，则必有S 5＞S611．在《增减算法统宗》中有这样一则故事：“三百七十八里关，初行健步不为难；次日脚痛减一半，如此六日过其关”．则下列说法正确的是( ) A ．此人第三天走了四十八里路B ．此人第一天走的路程比后五天走的路程多六里C ．此人第二天走的路程占全程的14D ．此人走的前三天路程之和是后三天路程之和的8倍12．若数列{a n }满足：对任意正整数n ，{a n ＋1－a n }为递减数列，则称数列{a n }为“差递减数列”．给出下列数列{a n }(n ∈N *)，其中是“差递减数列”的有( ) A ．a n ＝3n B ．a n ＝n 2＋1 C ．a n ＝n D ．a n ＝ln n n ＋1第Ⅱ卷(非选择题，共90分)三、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知数列{a n }的通项公式为a n ＝2 020－3n ，则使a n >0成立的最大正整数n 的值为________．14．已知{a n }是等差数列，S n 为其前n 项和，n ∈N *.若a 3＝16，S 20＝20，则a n ＝________，S 10＝________.15．已知数列1，a 1，a 2,9是等差数列，数列1，b 1，b 2，b 3,9是等比数列，则b 2a 1＋a 2＝________.16．设{a n }是由正数组成的等比数列，S n 为其前n 项和，已知a 2a 4＝1，S 3＝7，则S 5＝________.四、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知函数f(x)＝3xx ＋3，数列{x n }的通项由x n ＝f(x n －1)(n≥2且x ∈N *)确定．(1)求证：⎩⎨⎧⎭⎬⎫1x n 是等差数列；(2)当x 1＝12时，求x 2 020.18．(本小题满分12分)已知等比数列{a n }的前n 项和为S n ，a 1＝－1，S 10S 5＝3132.(1)求等比数列{a n }的公比q ； (2)求a 21＋a 22＋…＋a 2n .19．(本小题满分12分)在等差数列{a n }中，S n 为其前n 项和(n ∈N *)，且a 2＝3，S 4＝16. (1)求数列{a n }的通项公式；(2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和T n .20．(本小题满分12分)已知等比数列{a n }的前n 项和为S n ，a 1＝1，a n <a n ＋1，且S 3＝2S 2＋1.(1)求数列{a n }的通项公式；(2)若数列{b n }满足b n ＝(2n －1)a n (n ∈N *)，求数列{b n }的前n 项和T n . 21．(本小题满分12分)在①a n ＋1＝a n 3a n ＋1，②⎩⎨⎧⎭⎬⎫1a n 为等差数列，其中1a 2，1a 3＋1，1a 6成等比数列，③1a 1＋1a 2＋1a 3＋…＋1a n ＝3n 2－n2这三个条件中任选一个，补充到下面的问题中，然后解答补充完整的题目．已知数列{a n }中，a 1＝1，________.(1)求数列{a n }的通项公式；(2)设b n ＝a n a n ＋1，T n 为数列{b n }的前n 项和，求证：T n ＜13.注：如果选择多个条件分别解答，则按第一个解答计分．22．(本小题满分12分)已知等差数列{a n }的前n 项和为S n ，且S 10＝55，S 20＝210. (1)求数列{a n }的通项公式； (2)设b n ＝a n a n ＋1，是否存在m ，k(k>m≥2，m ，k ∈N *)使得b 1，b m ，b k 成等比数列？若存在，请说明理由． 答案解析第Ⅰ卷(选择题，共60分)一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．等差数列{a n }中，a 3＝2，a 5＝7，则a 7＝( ) A ．10 B ．20 C ．16 D ．12 解析：选D ∵{a n }是等差数列， ∴d ＝a 5－a 35－3＝52，∴a 7＝2＋4×52＝12.2．在数列{a n }中，a 1＝13，a n ＝(－1)n·2a n －1(n≥2)，则a 5等于( )A ．－163 D ．163 C ．－83 D ．83解析：选B ∵a 1＝13，a n ＝(－1)n·2a n －1，∴a 2＝(－1)2×2×13＝23，a 3＝(－1)3×2×23＝－43，a 4＝(－1)4×2×⎝ ⎛⎭⎪⎫－43＝－83，a 5＝(－1)5×2×⎝ ⎛⎭⎪⎫－83＝163.3．设等比数列{a n }的前n 项和为S n ，若S 10∶S 5＝1∶2，则S 15∶S 5＝( ) A ．3∶4 B ．2∶3 C ．1∶2 D ．1∶3解析：选A 在等比数列{a n }中，S 5，S 10－S 5，S 15－S 10，…成等比数列，因为S 10∶S 5＝1∶2，所以S 5＝2S 10，S 15＝34S 5，得S 15∶S 5＝3∶4，故选A.4．在等比数列{a n }中，已知前n 项和S n ＝5n ＋1＋a ，则a 的值为( )A ．－1B ．1C ．5D ．－5 解析：选D 因为S n ＝5n ＋1＋a ＝5×5n＋a ，由等比数列的前n 项和S n ＝a 1(1－q n)1－q ＝a 11－q－a 11－q·q n ，可知其常数项与q n的系数互为相反数，所以a ＝－5. 5．已知数列{a n }满足a 1＝1，a n ＋1＝⎩⎪⎨⎪⎧2a n ，n 为正奇数，a n ＋1，n 为正偶数，则254是该数列的( )A ．第8项B ．第10项C ．第12项D ．第14项 解析：选D 当n 为正奇数时，a n ＋1＝2a n ，则a 2＝2a 1＝2，当n 为正偶数时，a n ＋1＝a n ＋1，得a 3＝3，依次类推得a 4＝6，a 5＝7，a 6＝14，a 7＝15，…，归纳可得数列{a n }的通项公式a n＝⎩⎪⎨⎪⎧2n ＋12－1，n 为正奇数，2n2＋1－2，n 为正偶数，则2n2＋1－2＝254，n ＝14，故选D.6．已知数列{a n }是等差数列，其前n 项和为S n ，若a 1a 2a 3＝15，且3S 1S 3＋15S 3S 5＋5S 5S 1＝35，则a 2＝( )A ．2 D ．12 C ．3 D ．13解析：选C ∵S 1＝a 1，S 3＝3a 2，S 5＝5a 3，∴1a 1a 2＋1a 2a 3＋1a 1a 3＝35.∵a 1a 2a 3＝15，∴35＝a 315＋a 115＋a 215＝a 25，∴a 2＝3.故选C. 7．如果数列a 1，a 2－a 1，a 3－a 2，…，a n －a n －1，…是首项为1，公比为13的等比数列，那么a n ＝( )A.32⎝ ⎛⎭⎪⎫1－13n D ．32⎝ ⎛⎭⎪⎫1－13n －1 C.23⎝ ⎛⎭⎪⎫1－13n D ．23⎝ ⎛⎭⎪⎫1－13n －1解析：选A 由题知a 1＝1，q ＝13，则a n －a n －1＝1×⎝ ⎛⎭⎪⎫13n －1.设数列a 1，a 2－a 1，…，a n －a n －1的前n 项和为S n ， ∴S n ＝a 1＋(a 2－a 1)＋(a 3－a 2)＋…＋(a n －a n －1)＝a n .又∵S n ＝1×⎝ ⎛⎭⎪⎫1－13n 1－13＝32⎝⎛⎭⎪⎫1－13n ，∴a n ＝32⎝⎛⎭⎪⎫1－13n .8．若有穷数列a 1，a 2，…，a n (n 是正整数)，满足a 1＝a n ，a 2＝a n －1，…，a n ＝a 1，即a i ＝a n－i ＋1(i 是正整数，且1≤i≤n)，就称该数列为“对称数列”．已知数列{b n }是项数不超过2m(m ＞1，m ∈N *)的对称数列，且1,2,4，…，2m －1是数列{b n }的前m 项，则当m ＞1 200时，数列{b n }的前2 019项和S 2 019的值不可能为( ) A ．2m－2m －2 009B ．22 019－1C ．2m ＋1－22m －2 019－1 D ．3·2m －1－22m －2 020－1解析：选A 若数列{b n }的项数为偶数，则数列可设为1,21,22，…，2m －1,2m －1， (22)2,1，当m≥2 019时， S 2 019＝1×(1－22 019)1－2＝22 019－1，故B 可能．当1 200＜m ＜2 019时，S 2 019＝2×1×(1－2m)1－2－1×(1－22m －2 019)1－2＝2m ＋1－22m －2 019－1，故C 可能．若数列为奇数项，则数列可设为1,21,22，…，2m －2,2m －1,2m －2， (22)2,1，当m≥2 019时，S 2 019＝1×(1－22 019)1－2＝22 019－1.当1 200＜m ＜2 019时，S 2 019＝2×1×(1－2m －1)1－2－1×(1－22m －1－2 019)1－2＋2m －1＝3·2m －1－22m －2 020－1，故D 可能．故选A.二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求的，全部选对的得5分，选对但不全的得3分，有选错的得0分)9．已知等比数列{a n }的公比q ＝－23，等差数列{b n }的首项b 1＝12，若a 9>b 9且a 10>b 10，则以下结论正确的有( )A ．a 9·a 10<0B ．a 9>a 10C ．b 10>0D ．b 9>b 10 解析：选AD ∵等比数列{a n }的公比q ＝－23，∴a 9和a 10异号，∴a 9a 10＝a 29⎝ ⎛⎭⎪⎫－23<0，故A 正确； 但不能确定a 9和a 10的大小关系，故B 不正确； ∵a 9和a 10异号，且a 9>b 9且a 10>b 10，∴b 9和b 10中至少有一个数是负数，又∵b 1＝12>0，∴d<0，∴b 9>b 10，故D 正确；∴b 10一定是负数，即b 10<0，故C 不正确．故选A 、D.10．等差数列{a n }的前n 项和为S n ，若a 1＞0，公差d≠0，则下列命题正确的是( ) A ．若S 5＝S 9，则必有S 14＝0B ．若S 5＝S 9，则必有S 7是S n 中最大的项C ．若S 6＞S 7，则必有S 7＞S 8D ．若S 6＞S 7，则必有S 5＞S 6解析：选ABC ∵等差数列{a n }的前n 项和公式S n ＝na 1＋n (n －1)d2，若S 5＝S 9，则5a 1＋10d ＝9a 1＋36d ，∴2a 1＋13d ＝0， ∴a 1＝－13d2，∵a 1＞0，∴d ＜0，∴a 1＋a 14＝0，∴S 14＝7(a 1＋a 14)＝0，A 对；又∵S n ＝na 1＋n (n －1)d 2＝－13nd 2＋n (n －1)d 2＝d[(n －7)2－49]2，由二次函数的性质知S 7是S n中最大的项，B 对；若S 6＞S 7，则a 7＝a 1＋6d ＜0，∴a 1＜－6d ， ∵a 1＞0，∴d ＜0，∴a 6＝a 1＋5d ＜－6d ＋5d ＝－d ，a 8＝a 7＋d ＜a 7＜0， S 7＞S 8＝S 7＋a 8，C 对；由a 6＜－d 不能确定a 6的符号，所以S 5＞S 6不一定成立，D 错．故选A 、B 、C.11．在《增减算法统宗》中有这样一则故事：“三百七十八里关，初行健步不为难；次日脚痛减一半，如此六日过其关”．则下列说法正确的是( ) A ．此人第三天走了四十八里路B ．此人第一天走的路程比后五天走的路程多六里C ．此人第二天走的路程占全程的14D ．此人走的前三天路程之和是后三天路程之和的8倍解析：选ABD 设此人第n 天走a n 里路，则{a n }是首项为a 1，公比为q ＝12的等比数列．所以S 6＝a 1(1－q 6)1－q ＝a 1⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫1261－12＝378，解得a 1＝192.a 3＝a 1q 2＝192×14＝48，所以A 正确，由a 1＝192，则S 6－a 1＝378－192＝186，又192－186＝6，所以B 正确． a 2＝a 1q ＝192×12＝96，而14S 6＝94.5＜96，所以C 不正确．a 1＋a 2＋a 3＝a 1(1＋q ＋q 2)＝192×⎝ ⎛⎭⎪⎫1＋12＋14＝336，则后3天走的路程为378－336＝42而且42×8＝336，所以D 正确． 故选A 、B 、D.12．若数列{a n }满足：对任意正整数n ，{a n ＋1－a n }为递减数列，则称数列{a n }为“差递减数列”．给出下列数列{a n }(n ∈N *)，其中是“差递减数列”的有( ) A ．a n ＝3n B ．a n ＝n 2＋1 C ．a n ＝n D ．a n ＝ln nn ＋1解析：选CD 对A ，若a n ＝3n ，则a n ＋1－a n ＝3(n ＋1)－3n ＝3，所以{a n ＋1－a n }不为递减数列，故A 错误；对B ，若a n ＝n 2＋1，则a n ＋1－a n ＝(n ＋1)2－n 2＝2n ＋1，所以{a n ＋1－a n }为递增数列，故B 错误；对C ，若a n ＝n ，则a n ＋1－a n ＝n ＋1－n ＝1n ＋1＋n，所以{a n ＋1－a n }为递减数列，故C 正确； 对D ，若a n ＝lnn n ＋1，则a n ＋1－a n ＝ln n ＋1n ＋2－ln n n ＋1＝ln n ＋1n ＋2·n ＋1n ＝ln ⎝ ⎛⎭⎪⎫1＋1n 2＋2n ，由函数y ＝ln ⎝ ⎛⎭⎪⎫1＋1x 2＋2x 在(0，＋∞)递减，所以数列{a n ＋1－a n }为递减数列，故D 正确． 故选C 、D.第Ⅱ卷(非选择题，共90分)三、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．已知数列{a n }的通项公式为a n ＝2 020－3n ，则使a n >0成立的最大正整数n 的值为________．解析：由a n ＝2 020－3n>0，得n<2 0203＝67313，又∵n ∈N *，∴n 的最大值为673. 答案：67314．已知{a n }是等差数列，S n 为其前n 项和，n ∈N *.若a 3＝16，S 20＝20，则a n ＝________，S 10＝________.解析：设{a n }的首项，公差分别是a 1，d ，则 ⎩⎪⎨⎪⎧a 1＋2d ＝16，20a 1＋20×(20－1)2×d＝20，解得a 1＝20，d ＝－2，∴a n ＝a 1＋(n －1)d ＝20－2(n －1)＝22－2n .S 10＝10×20＋10×92×(－2)＝110.答案：22－2n 11015．已知数列1，a 1，a 2,9是等差数列，数列1，b 1，b 2，b 3,9是等比数列，则b 2a 1＋a 2＝________.解析：因为数列1，a 1，a 2,9是等差数列，所以a 1＋a 2＝1＋9＝10.因为数列1，b 1，b 2，b 3,9是等比数列，所以b 22＝1×9＝9，又b 2＝1×q 2＞0(q 为等比数列的公比)，所以b 2＝3，则b 2a 1＋a 2＝310. 答案：31016．设{a n }是由正数组成的等比数列，S n 为其前n 项和，已知a 2a 4＝1，S 3＝7，则S 5＝________.解析：设{a n }的公比为q ，q>0，且a 23＝1， ∴a 3＝1.∵S 3＝7，∴a 1＋a 2＋a 3＝1q 2＋1q ＋1＝7，即6q 2－q －1＝0，解得q ＝12或q ＝－13(舍去)，a 1＝1q2＝4. ∴S 5＝4×⎝ ⎛⎭⎪⎫1－1251－12＝8×⎝ ⎛⎭⎪⎫1－125＝314.答案：314四、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知函数f(x)＝3xx ＋3，数列{x n }的通项由x n ＝f(x n －1)(n≥2且x ∈N *)确定．(1)求证：⎩⎨⎧⎭⎬⎫1x n 是等差数列；(2)当x 1＝12时，求x 2 020.解：(1)证明：∵x n ＝f(x n －1)＝3x n －1x n －1＋3(n≥2且n ∈N *)，∴1x n ＝x n －1＋33x n －1＝13＋1x n －1， ∴1x n －1x n －1＝13(n≥2且n ∈N *)， ∴⎩⎨⎧⎭⎬⎫1x n 是公差为13的等差数列．(2)由(1)知1x n ＝1x 1＋(n －1)×13＝2＋n －13＝n ＋53.∴1x 2 020＝2 020＋53＝675. ∴x 2 020＝1675.18．(本小题满分12分)已知等比数列{a n }的前n 项和为S n ，a 1＝－1，S 10S 5＝3132.(1)求等比数列{a n }的公比q ； (2)求a 21＋a 22＋…＋a 2n .解：(1)由S 10S 5＝3132，a 1＝－1，知公比q≠1，S 10－S 5S 5＝－132.由等比数列前n 项和的性质知S 5，S 10－S 5，S 15－S 10成等比数列，且公比为q 5，故q 5＝－132，q ＝－12.(2)由(1)，得a n ＝(－1)×⎝ ⎛⎭⎪⎫－12n －1，所以a 2n ＝⎝ ⎛⎭⎪⎫14n －1，所以数列{a 2n }是首项为1，公比为14的等比数列，故a 21＋a 22＋…＋a 2n ＝1×⎝ ⎛⎭⎪⎫1－14n 1－14＝43⎝ ⎛⎭⎪⎫1－14n .19．(本小题满分12分)在等差数列{a n }中，S n 为其前n 项和(n ∈N *)，且a 2＝3，S 4＝16. (1)求数列{a n }的通项公式；(2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和T n .解：(1)设等差数列{a n }的公差是d ，由已知条件得⎩⎪⎨⎪⎧a 1＋d ＝3，4a 1＋6d ＝16，解得a 1＝1，d ＝2，∴a n ＝2n －1. (2)由(1)知，a n ＝2n －1， ∴b n ＝1a n a n ＋1＝1(2n －1)(2n ＋1)＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1，T n ＝b 1＋b 2＋…＋b n＝12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫13－15＋…＋⎝ ⎛⎭⎪⎫12n －1－12n ＋1 ＝12⎝⎛⎭⎪⎫1－12n ＋1＝n 2n ＋1. 20．(本小题满分12分)已知等比数列{a n }的前n 项和为S n ，a 1＝1，a n <a n ＋1，且S 3＝2S 2＋1.(1)求数列{a n }的通项公式；(2)若数列{b n }满足b n ＝(2n －1)a n (n ∈N *)，求数列{b n }的前n 项和T n .解：(1)设等比数列{a n }的公比为q ，由a n <a n ＋1，得q>1，又a 1＝1，则a 2＝q ，a 3＝q 2， 因为S 3＝2S 2＋1，所以a 1＋a 2＋a 3＝2(a 1＋a 2)＋1，则1＋q ＋q 2＝2(1＋q)＋1，即q 2－q －2＝0，解得q ＝2或q ＝－1(舍去)， 所以数列{a n }的通项公式为a n ＝2n －1(n ∈N *)．(2)由(1)知，b n ＝(2n －1)·a n ＝(2n －1)·2n －1(n ∈N *)， 则T n ＝1×20＋3×21＋5×22＋…＋(2n －1)×2n －1，2T n ＝1×21＋3×22＋5×23＋…＋(2n －3)×2n －1＋(2n －1)×2n，两式相减，得－T n ＝1＋2×21＋2×22＋…＋2×2n －1－(2n －1)×2n，即－T n ＝1＋22＋23＋24＋ (2)－(2n －1)×2n， 化简得T n ＝(2n －3)×2n＋3. 21．(本小题满分12分)在①a n ＋1＝a n 3a n ＋1，②⎩⎨⎧⎭⎬⎫1a n 为等差数列，其中1a 2，1a 3＋1，1a 6成等比数列，③1a 1＋1a 2＋1a 3＋…＋1a n ＝3n 2－n2这三个条件中任选一个，补充到下面的问题中，然后解答补充完整的题目．已知数列{a n }中，a 1＝1，________. (1)求数列{a n }的通项公式；(2)设b n ＝a n a n ＋1，T n 为数列{b n }的前n 项和，求证：T n ＜13.注：如果选择多个条件分别解答，则按第一个解答计分． 解：若选条件①：(1)易知a n ≠0，∵a n ＋1＝a n 3a n ＋1，∴1a n ＋1－1a n ＝3.又1a 1＝1， ∴数列⎩⎨⎧⎭⎬⎫1a n 是以1为首项，3为公差的等差数列，∴1a n ＝3n －2，∴a n ＝13n －2. (2)证明：由(1)可知，b n ＝1(3n －2)(3n ＋1)＝13⎝ ⎛⎭⎪⎫13n －2－13n ＋1，∴T n ＝13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－14＋⎝ ⎛⎭⎪⎫14－17＋…＋⎝ ⎛⎭⎪⎫13n －2－13n ＋1＝13⎝ ⎛⎭⎪⎫1－13n ＋1＝13－19n ＋3＜13， 故T n ＜13.若选条件②：(1)设数列⎩⎨⎧⎭⎬⎫1a n 的公差为d ，则1a 2＝1＋d ，1a 3＋1＝2＋2d ，1a 6＝1＋5d ，∵1a 2，1a 3＋1，1a 6成等比数列， ∴(2＋2d)2＝(1＋d)(1＋5d)，解得d ＝3或d ＝－1.当d ＝－1时，1a 2＝1＋d ＝0，此时1a 2，1a 3＋1，1a 6不能构成等比数列，∴d ＝3，∴1a n ＝1＋3(n －1)＝3n －2， ∴a n ＝13n －2. (2)由(1)可知，b n ＝1(3n －2)(3n ＋1)＝13⎝ ⎛⎭⎪⎫13n －2－13n ＋1，∴T n ＝13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－14＋⎝ ⎛⎭⎪⎫14－17＋…＋⎝ ⎛⎭⎪⎫13n －2－13n ＋1＝13⎝ ⎛⎭⎪⎫1－13n ＋1＝13－19n ＋3＜13， 故T n ＜13.若选条件③：(1)由1a 1＋1a 2＋1a 3＋…＋1a n ＝3n 2－n 2知，当n≥2时，1a 1＋1a 2＋1a 3＋…＋1a n －1＝3(n －1)2－(n －1)2，两式相减，得1a n ＝3n 2－n 2－3(n －1)2－(n －1)2＝3n －2，∴a n ＝13n －2(n≥2)，当n ＝1时，a 1＝1也适合上式， ∴a n ＝13n －2. (2)由(1)可知，b n ＝1(3n －2)(3n ＋1)＝13⎝ ⎛⎭⎪⎫13n －2－13n ＋1，∴T n ＝13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－14＋⎝ ⎛⎭⎪⎫14－17＋…＋⎝ ⎛⎭⎪⎫13n －2－13n ＋1＝13⎝ ⎛⎭⎪⎫1－13n ＋1＝13－19n ＋3＜13， 故T n ＜13.22．(本小题满分12分)已知等差数列{a n }的前n 项和为S n ，且S 10＝55，S 20＝210. (1)求数列{a n }的通项公式； (2)设b n ＝a n a n ＋1，是否存在m ，k(k>m≥2，m ，k ∈N *)使得b 1，b m ，b k 成等比数列？若存在，请说明理由．解：(1)设等差数列{a n }的公差为d ，则S n ＝na 1＋n (n －1)2 d.由已知，得⎩⎪⎨⎪⎧10a 1＋10×92d ＝55，20a 1＋20×192d ＝210，即⎩⎪⎨⎪⎧2a 1＋9d ＝11，2a 1＋19d ＝21，解得⎩⎪⎨⎪⎧a 1＝1，d ＝1.所以a n ＝a 1＋(n －1)d ＝n(n ∈N *)．(2)假设存在m ，k(k>m≥2，m ，k ∈N *)使得b 1，b m ，b k 成等比数列，则b 2m ＝b 1b k . 因为b n ＝a n a n ＋1＝nn ＋1，所以b 1＝12，b m ＝m m ＋1，b k ＝kk ＋1，所以⎝⎛⎭⎪⎫m m ＋12＝12×k k ＋1.整理，得k ＝2m2－m 2＋2m ＋1.以下给出求m ，k 的方法： 因为k>0，所以－m 2＋2m ＋1>0， 解得1－2<m<1＋ 2. 因为m≥2，m ∈N *， 所以m ＝2，此时k ＝8.故存在m ＝2，k ＝8使得b 1，b m ，b k 成等高中数学选择性必修二《第五章 一元函数的导数及其应用》单元检测试卷（三）一、单选题1．已知函数()y f x =在0x x =处的导数为1，则()()000lim 2x f x x f x x∆→+∆-=∆（ ）A ．0B ．12C ．1D ．2 2．设函数()f x 在定义域内可导，()y f x =的图象如图所示，则导函数()y f x '=的图象为（ ）A ．B ．C ．D ．3．函数2cos y x x =+在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值是（ ）A ．13π+ B ．4π+．6π+．2π4．若函数2()ln 2f x x ax =+-在区间1,22⎛⎫⎪⎝⎭内存在单调递增区间，则实数a 的取值范围是（ ）A ．(,2]-∞-B ．1,8⎛⎫-+∞ ⎪⎝⎭C ．12,8⎛⎫-- ⎪⎝⎭D ．(2,)-+∞ 5．曲线2yx x 在点(1,0)处的切线方程是（ ）A ．210x y --=B ．210x y +-=C ．10x y --=D ．10x y +-=6．已知函数()f x 的导函数()()()1f x a x x a '=+-，若()f x 在x a =处取得极大值，则实数a 的取值范围是（ ）A ．()1,0-B ．()2,+∞C ．()0,1D ．(),3-∞- 7．已知函数()cos xf x e x =+，设()10.3a f -=，()0.32b f -=，()2log0.2c f =，则（ ）A ．c b a <<B ．c a b <<C ．b a c <<D ．b c a << 8．已知偶函数()y f x =对于任意的[0,)2x π∈满足'()cos ()sin 0f x x f x x +>（其中'()f x 是函数()f x 的导函数），则下列不等式中成立的是（ ）A ()()34f ππ-< B ()()34f ππ-<-C ．(0)()4f π>-D ．()()63f ππ<二、多选题9．已知定义在R 上的函数()f x 满足()()f x f x '>-，则下列式子成立的是（ ） A ．()()20192020f ef < B ．()()20192020ef f >C ．()f x 是R 上的增函数D ．若0t >，则有()()tf x e f x t <+10．若直线12y x b =+是函数()f x 图像的一条切线，则函数()f x 可以是（ ） A ．1()f x x=B ．4()f x x =C ．()sin f x x =D ．()x f x e = 11．已知函数()y f x =的导函数的图象如图所示，下列结论中正确的是（ ）A ．1-是函数()f x 的极小值点B ．3-是函数()f x 的极小值点C ．函数()f x 在区间()3,1-上单调递增 D ．函数()f x 在0x =处切线的斜率小于零 12．已知函数()f x 是定义在R 上的奇函数，当0x ＞时，()1xx f x e -=.则下列结论正确的是（ ）.A ．当0x <时，()()1xf x e x =-+B ．函数()f x 在R 上有且仅有三个零点C ．若关于x 的方程()f x m =有解，则实数m 的取值范围是()()22f m f -≤≤D ．12,x x ∀∈R ，()()212f x f x -<三、填空题13．已知函数()f x 的导函数为()f x '，且满足关系式()()321xf x x f x e '=-++，则()1f '的值等于__________.14．生活经验告诉我们，当水注进容器(设单位时间内进水量相同)时，水的高度随着时间的变化而变化，在下图中请选择与容器相匹配的图像，A 对应________；B 对应________；。

一、选择题(每小题2分，共40分)1．中国新民主主义革命胜利的标志是()A．解放南京，推翻国民政府B．中华人民共和国成立C．除台湾和沿海岛屿外，中国领土全部解放D．三大改造完成解析：选B。

革命就是夺权，推翻旧政权只是过程，建立新政权才说明了胜利。

A只是推翻旧政权，B建立新政权才标志着革命取得了胜利。

2．历史巨片《开国大典》的成功拍摄，再现了当年中国人民“站起来”的那永恒的记忆。

这里“站起来”是指()A．彻底完成了新民主主义革命任务B．建立了社会主义制度C．结束了半殖民地半封建社会性质，从此中国人民走向了民族独立D．完成了祖国的统一解析：选C。

本题主要考查学生对新中国诞生的历史意义的识记和理解能力。

建国后，还有民主革命的遗留任务，1956年才建立社会主义制度，直到今天还没有完成祖国的统一大业。

3.在西方世界日益关注中国的过程中，《时代》周刊是最典型的代表。

右图是1949年毛泽东成为《时代》周刊封面人物的图片，毛泽东能够成为备受关注的《时代》周刊人物的原因主要是()A．领导中国人民走向新民主主义革命胜利，引发中国社会巨变B．领导中国人民取得抗日战争的伟大胜利，中华民族由衰落走向振兴C．开创中国特色革命道路，揭开了无产阶级革命新时代D．提出“和平共处五项原则”，中国以新的形象出现在世界舞台解析：选A。

此题考查了一定的辨析能力。

根据题干中的1949年这一时间可知A项符合题意。

4．新中国成立初期，面临严峻的经济形势，其原因是()①国民党反动派长期内战②国民政府和官僚资本的搜刮③帝国主义的长期掠夺④人民生活十分困苦A．①②④B．③④C．①②③D．①②③④解析：选C。

本题主要考查学生再认再现史实和分析历史问题的能力。

④是经济严峻的表现，不是原因。

5．新中国成立之初，继续完成的民主革命任务有()①没收国民政府的财产和官僚资本②稳定物价，统一财经③合理调整工商业④开展土地改革运动A．①②B．①④C．③④D．②③解析：选B。

第五章《相交线与平行线》单元检测题题号 一 二 三总分 19 20 21 22 23 24分数一、选择题(每题3分，共30分)1．如图的四个图中，∠1与∠2是同位角的有（ ）A ．②③B ．①②③C ．①D ．①②④2．下列说法中,错误的有( )①若a 与c 相交,b 与c 相交,则a 与b 相交; ②若a ∥b,b ∥c,那么a ∥c;③过直线外一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种. A ．3个 B ．2个 C ．1个 D ．0个3．如图，，于F ，，则的度数是（ ）A ．B ．C ．D ．4．如图，△ABC 沿着由点B 到点E 的方向，平移到△DEF ，已知BC=5．EC=3，那么平移的距离为（ ）A ．2B ．3C ．5D ．75．如图，将△ABC 沿BC 方向平移2cm 得到△DEF ，若△ABC 的周长为16cm ，//AB CD PF CD ⊥40AEP ∠=︒EPF ∠120︒130︒140︒150︒则四边形ABFD的周长为（）A．16cm B．18cm C．20cm D．22cm6．如图，如果把△ABC的顶点A先向下平移3格，再向左平移1格到达A′点，连接A′B，则线段A′B与线段AC的关系是（）A．垂直B．相等C．平分D．平分且垂直7.如图，下列说法错误的是（）A.∠A与∠3是同位角B.∠4与∠B是同旁内角C.∠A与∠C是内错角D.∠1与∠2是同旁内角8．如图，下列条件中，能判断a∥b的条件有()①∠1＝∠2；②∠1＝∠4；③∠1＋∠3＝180°；④∠1＋∠5＝180°A．1个B．2个C．3个D．4个9．如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B＝90°，AB＝8，DH＝3，平移距离为4，求阴影部分的面积为（）A．20B．24C．25D．2610．如图，已知直线AB、CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB、CD、AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC的度数可能是（）A．①②③B．①②④C．①③④D．①②③④二、填空题(每题3分，共24分)11．如图，在△ABC，AD⊥BC，垂足为点D，那么点B到直线AD的距离是线段的长度．12．如图所示，平移线段AB到CD的位置，则AB＝，CD∥，BD＝．13．如图，直线AB与CD相交于点O，若∠AOD＝150°，则∠BOC＝度．14．如图，直线a∥b，∠1＝75°，那么∠2的度数是．15．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠2＝24°，则∠1的度数为．16．如图所示，点E在AC的延长线上，有下列条件：①∠1＝∠2，②∠3＝∠4，③∠A＝∠DCE，④∠D＝∠DCE，⑤∠A+∠ABD＝180°，⑥∠A+∠ACD＝180°，其中能判断AB∥CD的是．17．如图，直线a，b都垂直于直线c，直线d与a，b相交．若∠1＝135°，则∠2＝°．18．如图，在直角三角形ABC中，∠A＝90°，AB＝3，AC＝4，BC＝5，DE∥BC，点A到DE的距离是1，则DE与BC的距离是．三.解答题(19题6分，20、21、22、23、24题分别8分，共46分)19．完成下面的证明：已知：如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2＝90°．求证：AB∥CD．证明：∵DE平分∠BDC（已知），∴∠BDC＝2∠1（）．∵BE平分∠ABD（已知），∴∠ABD＝（角平分线的定义）．∴∠BDC+∠ABD＝2∠1+2∠2＝2（∠1+∠2）（）．∵∠1+∠2＝90°（已知），∴∠BDC+∠ABD＝（）．∴AB∥CD（）．20．如图，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠1＝26°（1）求∠2的度数（2）若∠3＝19°，试判断直线n和m的位置关系，并说明理由．21.（8分）如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.(1)写出两个不同的条件;(2)从(1)中选择一个来证明.22.（8分）如图，已知∠1+∠2＝180°，∠3＝∠B．（1）试判断DE与BC的位置关系，并说明理由．（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．23．如图，∠1＝∠C，∠2+∠D＝90°，BE⊥FD于G．试证明：AB∥CD．24．如图，∠ADE+∠BCF＝180°，BE平分∠ABC，∠ABC＝2∠E．（1）AD与BC平行吗？请说明理由；（2）AB与EF的位置关系如何？为什么？（3）若AF平分∠BAD，试说明：∠E+∠F＝90°．参考答案一、选择题:题号12345678910答案D B B A C D A D D D二、填空题:11．解：∵AD⊥BD于D，∴点B到直线AD的距离是线段BD的长，故答案为：BD．12．解：平移线段AB到CD的位置，则AB＝CD，CD∥AB，BD＝AC．故答案为：CD，AB，AC．13．解：因为直线AB与CD相交于点O，所以∠AOD与∠BOC是对顶角，所以∠AOD＝∠BOC，因为∠AOD＝150°，所以∠BOC＝150°，故答案为：150．14．解：∵周长为12的三角形ABC沿BC方向平移2个单位长度得到三角形DEF，∴AD＝CF＝2，AC＝DF，∴四边形ABFD的周长＝AB+BC+CF+DF+AD＝AB+BC+AC+AD+CF＝△ABC 的周长+2AD＝12+2×2＝16．故答案为16．14．解：如图，∵a∥b，∴∠1＝∠3＝75°，而∠2+∠3＝180°，∴∠2＝180°﹣75°＝105°．故答案为：105°．15．解：如图，延长AB交CF于E，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵GH∥EF，∴∠AEC＝∠2＝24°，∴∠1＝∠ABC﹣∠AEC＝36°．故答案为：36°．16．解：①∵∠1＝∠2，∴AB∥CD，正确；②∵∠3＝∠4，∴BD∥AC，错误；③∵∠A＝∠DCE，∴AB∥CD，正确；④∵∠D＝∠DCE，∴BD∥AC，错误；⑤∵∠A+∠ABD＝180°，∴BD∥AC，错误；⑥∵∠A+∠ACD＝180°，∴AB∥CD，正确；故答案为：①③⑥17．45．18．三.解答题:19．证明：∵DE平分∠BDC（已知），∴∠BDC＝2∠1（角平分线的定义）．∵BE平分∠ABD（已知），∴∠ABD＝2∠2（角平分线的定义）．∴∠BDC+∠ABD＝2∠1+2∠2＝2（∠1+∠2）（等量代换）．∵∠1+∠2＝90°（已知），∴∠BDC+∠ABD＝180°（等量代换）．∴AB∥CD（同旁内角互补，两直线平行）．故答案为：角平分线的定义；2∠2；等量代换；180°；等量代换；同旁内角互补，两直线平行．20．解：（1）∵∠ACB＝90°，∠1＝26°，∴∠2＝180°﹣∠1﹣∠ACB，＝180°﹣90°﹣26°，＝64°；（2）结论：n∥m．理由如下：∵∠3＝19°，∠A＝45°，∴∠4＝45°+19°＝64°，∵∠2＝64°，∴∠2＝∠4，∴n∥m．21.解:此题答案不唯一,合理即可.(1)添加∠FCB=∠CBE或CF∥BE.(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.证明:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠CBE,∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.22.解：（1）DE∥BC，理由如下：∵∠1+∠4＝180°，∠1+∠2＝180°，∴∠2＝∠4，∴AB∥EF，∴∠3＝∠5，∵∠3＝∠B，∴∠5＝∠B，∴DE∥BC，（2）∵DE平分∠ADC，∴∠5＝∠6，∵DE∥BC，∴∠5＝∠B，∵∠2＝3∠B，∴∠2+∠5+∠6＝3∠B+∠B+∠B＝180°，∴∠B＝36°，∴∠2＝108°，∵∠1+∠2＝180°，∴∠1＝72°．23. 证明：∵BE⊥FD于G，∴∠1+∠D＝90°，∵∠1＝∠C，∴∠C+∠D＝90°，∵∠2+∠D＝90°，∴∠C＝∠2，∴AB∥CD．24．解：（1）AD∥BC，理由是：∵∠ADE+∠BCF＝180°，∠ADE+∠ADF＝180°，∴∠ADF＝∠BCF，∴AD∥BC；（2）AB∥EF，理由是：∵BE平分∠ABC，∴∠ABC＝2∠ABE，∵∠ABC＝2∠E，∴∠ABE＝∠E，∴AB∥EF；（3）∵AD∥BC，∴∠DAB+∠ABC＝180°，∵BE平分∠ABC，AF平分∠BAD，∴∠ABE＝ABC，∠BAF＝∠BAD，∴∠ABE+∠BAF＝90°，∴∠AOB＝180°﹣90°＝90°＝∠EOF，∴∠E+∠F＝180°﹣∠EOF＝90°．。

新人教版四年级上册《第5章除数是两位数的除法》单元检测训练卷（一）一、小小填空知识多，快来动手做一做．（每空1分，共20分）1. 计算“374÷42”时，把除数42看作________来试商，商是________位数。

2. 18的________倍是468，714是42的________倍。

3. 商和余数都是13，除数是24，被除数是________．4. ________÷35=18…________，余数最大是________；当余数最大时，被除数是________．5. 在一道被除数和除数都不为0的除法算式里，被除数乘10，除数不变，商________．6. 在下面________里，最大能填几？40×________<352________×50<310________×60<42730×________<260．7. 要使687÷□5的商是两位数，□里最大填________，要使□76÷27的商是两位数，□里最小填________．8. 在“○”里填上适当的运算符号，在“________”里填上适当的数。

80÷16=(80○________)÷(16÷4)200÷40=(200÷20)÷(40○________)180÷15=(180×3)÷(15○________)二、我来当包公．（对的打“√”，错的打“×”）（5分）0除以任何数都得0．________．（判断对错）要使□08÷62的商是一位数，□里最大填5．________．因为7÷2=3...1，所以70÷20=3...1．________．如果被除数的末尾有0，商的末尾也一定有0．________．（判断对错）140人乘坐大客车去参观烈士陵园，每辆大客车限乘40人，至少需要4辆这样的大客车。

单元检测(五）一、选择题(本大题共24小题，每小题2分，共48分.在每题所列出的四个选项中，只有一项是最符合题目要求的。

)“银杏黄时秋意浓"，每至暮秋，银杏树便“尽换黄金甲”,当秋风袭来,遍地碎金，如梦如幻的浪漫景色吸引大量游人前去观赏.下图为我国主要银杏观赏地分布(左图）及丹东某银杏大道景观(右图）。

据此完成1～2题。

1．丹东的地带性植被属于（)A．常绿阔叶林B．针阔叶混交林C．落叶阔叶林D．针叶林2．与湖州相比,丹东的银杏()A．生长缓慢B．枝叶繁茂C．冬季落叶D．树干高大读图，回答3～4题。

3. 从①、②、③三地可能看到的典型植被依次对应的顺序是（)A．草原、森林、荒漠B．森林、荒漠、草原C．草原、荒漠、森林D．森林、草原、荒漠4．造成图中三地植被差异的主要因素是(）A．热量B．水分C．地形D．土壤红树林（右图）指生长在热带、亚热带海岸潮间带上部，受周期性潮水浸淹,以红树植物为主体的常绿灌木或乔木组成的潮滩湿地木本生物群落，组成的物种包括草本、藤本红树.据此完成5~6题。

5．红树林（）①多分布在我国渤海与黄海沿岸②根系短小不发达③多分布在潮间带的淤泥质海岸④以喜盐植物为主A．①② B．②③C．③④ D．①④6．红树林的主要功能是（)A．保护海岸,保护生物的多样性B．降低风速,为船舶提供避风场所C．绿化美化沿海环境，吸烟滞尘D．涵养水源，保持水土，美化环境第三届联合国环境大会上，中国表现抢眼。

塞罕坝林场建设者获得2017年联合国环保最高荣誉—-“地球卫士奖"。

下图为塞罕坝林场位置示意图.据此完成7~8题.7．从1962年至今，塞罕坝林场培育出112万亩(约746。

7平方千米)人工林,成为“生态文明建设范例"。

下列关于该林场表述正确的是(）A．选择常绿硬叶林为主要营林品种B．对东北地区生态安全的意义重大C．春季防火等级最高D．经过50多年的营林,成为重要的木材基地8．下列关于塞罕坝林场产生的影响，描述正确的是（) A．为东北林区的开发提供了借鉴意义B．保护华北地区生态环境,防风固沙C．减少黄土高原水土流失D．防止内蒙古中部草原退化挪威领土南北狭长，海岸线漫长曲折，沿海岛屿很多。

9第五章原子与原子核 单元检测1（解析版）第I 卷（选择题）一、选择题（共48分）1．关于汤姆孙发现电子的下列说法中正确的是（ ）A ．戈德斯坦是第一个测出阴极射线比荷的人B ．汤姆孙直接测出了阴极射线的质量C ．汤姆孙发现，用不同材料的阴极和不同的气体做实验，阴极射线的比荷是不同的D ．汤姆孙由实验得到的阴极射线粒子的比荷是氢离子比荷的近两千倍2．下列说法正确的是（ ）A ．采用物理或化学方法可以有效地改变放射性元素的半衰期B ．由玻尔理论知道氢原子从激发态跃迁到基态时会发出光子C ．卢瑟福发现了中子，并预言了质子的存在D ．原子核所含核子单独存在时的总质量小于该原子核的质量3．关于α、β、γ三种射线的性质，下列说法中正确的是（ ）A ．α射线是带正电的高速粒子流，它的电离作用最弱B ．β射线是高速电子流，它的穿透能力最弱C ．γ射线是电磁波，它在真空中的传播速度等于光速D ．以上说法都不正确4．下列说法正确的是（ ）A ．卢瑟福的原子核式结构模型无法解释原子光谱的分立特征B ．黑体辐射电磁波的强度按波长的分布与黑体温度无关C ．比结合能越大的原子核越不稳定D ．可以通过升高温度来增大放射性元素的半衰期5．以下叙述正确的是（ ）A ．卢瑟福的α粒子散射实验，证实了原子核还可以再分B ．牛顿通过扭秤实验比较精确地测量出了万有引力恒量C ．牛顿最早通过理想斜面实验得出力不是维持物体运动的必然结果D ．感应电流遵从楞次定律所描述的方向，这是能量守恒定律的必然结果6．关于原子和原子核，下列说法正确的是（ ）A ．结合能越大，原子核越稳定B ．在核反应423211H H He X +−−→+中，X 为中子C ．核爆炸的能量来自于原子核反应中的质量亏损，遵循规律E mc ∆=∆D ．氡的半衰期为3.8天，1g 氡原子核在经过7.6天后只剩下0.2g 氡原子核7．2020年12月4日14时02分，新一代“人造太阳”装置——中国环流器二号M 装置（HL-2M ）在成都建成并实现首次放电，一个D （氘）核和T （氚）核发生聚变反应会产生一个中子，下列说法正确的是（ ）A ．该核反应方程式为23311120H +H He +n →B ．该核反应能够吸收大量能量C ．该反应能够在常温下进行D ．反应前平均核子质量比反应后大8．一静止的铝原子核2713AI 俘获一速度为1.0×107m/s 的质子P 后，变为处于激发态的硅原子核2814Si 。

人教版七年级上册数学第五章一元一次方程单元检测题一.选择题1．已知x=1是方程x+m=3的解，则m的值是（）A．1B．2C．−2D．32．下列方程中，解为x=3的方程是（）A．y−3=0B．x+2=1C．2x−2=3D．2x=x+33．下列变形符合方程的变形规则的是（）A．若2x−3=7，则2x=7−3B．若3x−2=x+1，则3x−x=1−2 C．若−3x=5，则x=5+3D．若−14x=1，则x=−44．甲、乙两个工程队共同承接了某村“煤改气”工程，甲队单独施工需10天完成，乙队单独施工需15天完成．若甲队先做5天，剩下部分由两队合做，则完成该工程还需要（）A．8天B．5天C．3天D．2天5．琪琪同学在做作业时，不小心将方程2（x﹣3）﹣■＝x+1中的一个常数污染了，在询问老师后，老师告诉她方程的解是x＝9，请问这个被污染的常数■是（）A．4B．3C．2D．16．如图，一个正方形先剪去宽为 2.4的长方形，且剪下来的两个长方形面积相等，那么原正方形的边长为（）A．10B．12C．14D．167．在中央电视台“开心辞典”节目中，某期的一道题目是：如图，两个天平都平衡，则1个苹果的重量是1个香蕉重量的（）A．23倍B．43倍C．32倍D．2倍8．阿阳中学初三二班十几名同学毕业前和数学老师合影留念，一张彩色底片要0.6元，扩印一张相片0.5元，每人分一张，免费送老师一张（由学生出钱），每个学生交0.6元刚好，相片上共有多少人（）A．13个B．12个C．11个D．无法确定二.填空题9．若(m−2)x|m|−1−2=5是关于x的一元一次方程，则m的值是．10．已知4x+2y=3，用含x的式子表示y=．11．在长方形ABCD中，放入6个形状大小相同的小长方形（空白部分），其中AB=9cm，BC=13cm，则阴影部分图形的总面积是cm2．12．某商场将一件商品在进价的基础上加价50%标价，再打八折出售，售价为120元，则这件商品获利元．13．程大位《直指算法统宗》中记载了这样一个问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？意思是：有100个大小和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完．则大和尚为人．三.计算题14．解方程（1）x−13−x+26=1（2）3=1−2(4+x)四.解答题15．《孙子算经》是我国古代重要的数学著作．书中记载这样一个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何？这个问题的意思是：今有若干人乘车，每3人共乘1辆车，最终剩余2辆车；若每2人共乘1辆车，最终剩余9个人无车可乘，问共有多少人，多少辆车？16．以下是琪琪解方程x+13−x−32=1的解答过程.解：去分母，得2(x+1)−3(x−3)=1.去括号，得2x+2−3x−6=1.移项，合并同类项，得x=5.琪琪的解答过程是否有错误?如果有错误，写出正确的解答过程.17．某班将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍．乒乓球拍每副定价30元，乒乓球每盒定价5元，经洽谈后，甲店每买一副球拍赠一盒乒乓球，乙店全部按定价的9折优惠．该班需球拍5副，乒乓球若干盒（不小于5盒）．问：（1）当购买乒乓球x盒时，两种优惠办法付款一样？（2）当购买30盒乒乓球时，若让你选择一家商店去办这件事，你打算去哪家商店购买？为什么？18．某商场从厂家购进甲、乙两种文具，甲种文具的每件进价比乙种文具的每件进价少20元．若购进甲种文具7件，乙种文具2件，则需要760元．（1）求甲、乙两种文具的每件进价分别是多少元？（2）该商场从厂家购进甲、乙两种文具共50件，所用资金恰好为4400元．在销售时，每件甲种文具的售价为100元，要使得这50件文具销售利润率为30%，每件乙种文具的售价为多少元？19．杨师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：+(−3x2+5x−7)=−2x2+3x−6．（1）求所捂的多项式；（2）若x是14x=−12x+3的解，求所捂多项式的值；（3）若所捂多项式的值为144，请求写出x的取值．。