第7章 数字图像处理 何东健
- 格式:pps
- 大小:1.78 MB
- 文档页数:130


何东健数字图像处理课后答案【篇一:数字图像处理课后参考答案】>1.1解释术语(2)数字图像:为了便于用计算机对图像进行处理,通过将二维连续(模拟)图像在空间上离散化,也即采样,并同时将二维连续图像的幅值等间隔的划分成多个等级(层次)也即均匀量化,以此来用二维数字阵列并表示其中各个像素的空间位置和每个像素的灰度级数的图像形式称为数字图像。
(3)图像处理:是指对图像信息进行加工以满足人的视觉或应用需求的行为。
1.7 包括图像变化、图像增强、图像恢复、图像压缩编码、图像的特征提取、形态学图像处理方法等。
彩色图像、多光谱图像和高光谱图像的处理技术沿用了前述的基本图像处理技术,也发展除了一些特有的图像处理技术和方法。
1.8基本思路是,或简单地突出图像中感兴趣的特征,或想方法显现图像中那些模糊了的细节,以使图像更清晰地被显示或更适合于人或及其的处理与分析。
1.9基本思路是,从图像退化的数学或概率模型出发,研究改进图像的外观,从而使恢复以后的图像尽可能地反映原始图像的本来面目,从而获得与景物真实面貌相像的图像。
1.10基本思路是,,在不损失图像质量或少损失图像质量的前提下,尽可能的减少图像的存储量,以满足图像存储和实时传输的应用需求。
1.11基本思路是,通过数学方法和图像变换算法对图像的某种变换,以便简化图像进一步处理过程,或在进一步的图像处理中获得更好的处理效果。
1.12基本目的是,找出便于区分和描述一幅图像中背景和目标的方法,以方便图像中感兴趣的目标的提取和描述。
第二章2.1解释下列术语(18)空间分辨率:定义为单位距离内可分辨的最少黑白线对的数目,用于表示图像中可分辨的最小细节,主要取决于采样间隔值的大小。
(19)灰度分辨率:是指在灰度级别中可分辨的最小变化,通常把灰度级数l称为图像的灰度级分辨率。
(20)像素的4邻域:对于图像中位于(x,y)的像素p来说,与其水平相邻和垂直相邻的4个像素称为该像素的4邻域像素,他们的坐标分别为(x-1,y)(x,y-1)(x,y+1)(x+1,y)。



[1] 冈萨雷斯. 数字图像处理[M]. 电子工业出版社,2003.[2] 杨帆等. 数字图像处理与分析[M]. 北京:北京航空航天大学出版社,2007[3] 马平. 数字图像处理和压缩[M]. 北京:电子工业出版社,2007[4] 闫敬文. 数字图像处理[M]. 北京:国防工业出版社,2007[5] 王慧琴. 数字图像处理. 北京:北京邮电出版社, 2006.[6] 阮秋琦. 数字图像处理学. 北京:电子工业出版社, 2001[7] 何东健. 数字图像处理. 西安:西安电子科技大学出版社, 2003.[8] 王家文, 曹宇. MATLAB6.5图形图像处理. 北京:国防工业出版社, 2004.[9] 余成波. 数字图像处理及MATLAB实现. 重庆:重庆大学出版社, 2003.[10] 张志涌, 徐彦琴. MATLAB教程-基于6.x版本.北京航空航天大学出版社, 2001.[11] 夏德深, 傅德胜. 计算机图像处理及应用. 南京:东南大学出版社, 2004.[12] Simard P,Steinkraus D,Malvar H.On-line Adaptation Image Coding with a 2-dTarp Filter. Proceedings of IEEE Data Compression Conference[J].2002.vol.8(1):23-32.[13] WangHong,LuLing,QueDaShun. Image Compression Based on WaveletTransformand Veetor Quantization[J] .Beijing : Proceedings of the First International Confereneeon Maehine Leamingand Cybernetics,2002(5):35-41 [14] WangHong,LuLing,QueDaShun. Image Compression Based on WaveletTransformand Veetor Quantization[D]. Beijing:Proeeedingsof the First Inter national Confereneeon Maehine Leamingand Cybernetics,2002[15] YufangGao ,Yang Liu. Analysis of Compression Encoding about DigitalImage[D].Beijing: Beijing University of Posts and Telecommunications,2003 [16] Jerome M. Sha Piro. Afast Technology for Identifying Zerotreesin the EZWAlgorithm[J],IEEET rans. Coef. Aeoustv Speech Signal Proeessing.1996(7):11-23[1] 冈萨雷斯. 数字图像处理[M]. 电子工业出版社,2003.摘要:本书是把图像处理基础理论论述与软件实践方法相结合的第一本书,它集成了冈萨雷斯和伍兹所著的《数字图像处理》一书中的重要内容和MathWorks 公司的图像处理工具箱。
第一章1.连续图像中,图像为一个二维平面,(x,y)图像中的任意一点,f(x,y)为图像于(x,y)于处的值。
连续图像中,(x,y)的取值是连续的,f(x,y)也是连续的数字图像中,图像为一个由有限行有限列组成的二维平面,(i,j)为平面中的任意一点,g(i,j)则为图像在(i,j)处的灰度值,数字图像中,(i,j) 的取值是不连续的,只能取整数,对应第i行j列,g(i,j) 也是不连续的,表示图像i行j列处图像灰度值。
联系:数字图像g(i,j)是对连续图像f(x,y)经过采样和量化这两个步骤得到的。
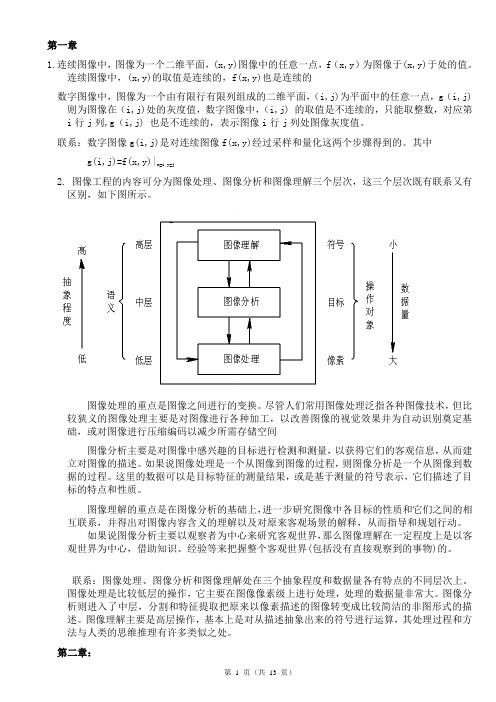
其中g(i,j)=f(x,y)|x=i,y=j2. 图像工程的内容可分为图像处理、图像分析和图像理解三个层次,这三个层次既有联系又有区别,如下图所示。
图像处理的重点是图像之间进行的变换。
尽管人们常用图像处理泛指各种图像技术,但比较狭义的图像处理主要是对图像进行各种加工,以改善图像的视觉效果并为自动识别奠定基础,或对图像进行压缩编码以减少所需存储空间图像分析主要是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息,从而建立对图像的描述。
如果说图像处理是一个从图像到图像的过程,则图像分析是一个从图像到数据的过程。
这里的数据可以是目标特征的测量结果,或是基于测量的符号表示,它们描述了目标的特点和性质。
图像理解的重点是在图像分析的基础上,进一步研究图像中各目标的性质和它们之间的相互联系,并得出对图像内容含义的理解以及对原来客观场景的解释,从而指导和规划行动。
如果说图像分析主要以观察者为中心来研究客观世界,那么图像理解在一定程度上是以客观世界为中心,借助知识、经验等来把握整个客观世界(包括没有直接观察到的事物)的。
联系:图像处理、图像分析和图像理解处在三个抽象程度和数据量各有特点的不同层次上。
图像处理是比较低层的操作,它主要在图像像素级上进行处理,处理的数据量非常大。
图像分析则进入了中层,分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式的描述。

数字图像处理每章课后题参考答案第一章和第二章作业:1.简述数字图像处理的研究内容。
2.什么是图像工程?根据抽象程度和研究方法等的不同,图像工程可分为哪几个层次?每个层次包含哪些研究内容?3.列举并简述常用表色系。
1.简述数字图像处理的研究内容?答:数字图像处理的主要研究内容,根据其主要的处理流程与处理目标大致可以分为图像信息的描述、图像信息的处理、图像信息的分析、图像信息的编码以及图像信息的显示等几个方面,将这几个方面展开,具体有以下的研究方向:1.图像数字化,2.图像增强,3.图像几何变换,4.图像恢复,5.图像重建,6.图像隐藏,7.图像变换,8.图像编码,9.图像识别与理解。
2.什么是图像工程?根据抽象程度和研究方法等的不同,图像工程可分为哪几个层次?每个层次包含哪些研究内容?答:图像工程是一门系统地研究各种图像理论、技术和应用的新的交叉科学。
根据抽象程度、研究方法、操作对象和数据量等的不同,图像工程可分为三个层次:图像处理、图像分析、图像理解。
图像处理着重强调在图像之间进行的变换。
比较狭义的图像处理主要满足对图像进行各种加工以改善图像的视觉效果。
图像处理主要在图像的像素级上进行处理,处理的数据量非常大。
图像分析则主要是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息从而建立对图像的描述。
图像分析处于中层,分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式描述。
图像理解的重点是进一步研究图像中各目标的性质和它们之间的相互联系,并得出对图像内容含义的理解以及对原来客观场景的解释,从而指导和规划行为。
图像理解主要描述高层的操作,基本上根据较抽象地描述进行解析、判断、决策,其处理过程与方法与人类的思维推理有许多相似之处。
第三章图像基本概念1.图像量化时,如果量化级比较小时会出现什么现象?为什么?答:当实际场景中存在如天空、白色墙面、人脸等灰度变化比较平缓的区域时,采用比较低的量化级数,则这类图像会在画面上产生伪轮廓(即原始场景中不存在的轮廓)。


何东健数字图像处理课后答案【篇一:数字图像处理课后参考答案】>1.1解释术语(2)数字图像:为了便于用计算机对图像进行处理,通过将二维连续(模拟)图像在空间上离散化,也即采样,并同时将二维连续图像的幅值等间隔的划分成多个等级(层次)也即均匀量化,以此来用二维数字阵列并表示其中各个像素的空间位置和每个像素的灰度级数的图像形式称为数字图像。
(3)图像处理:是指对图像信息进行加工以满足人的视觉或应用需求的行为。
1.7 包括图像变化、图像增强、图像恢复、图像压缩编码、图像的特征提取、形态学图像处理方法等。
彩色图像、多光谱图像和高光谱图像的处理技术沿用了前述的基本图像处理技术,也发展除了一些特有的图像处理技术和方法。
1.8基本思路是,或简单地突出图像中感兴趣的特征,或想方法显现图像中那些模糊了的细节,以使图像更清晰地被显示或更适合于人或及其的处理与分析。
1.9基本思路是,从图像退化的数学或概率模型出发,研究改进图像的外观,从而使恢复以后的图像尽可能地反映原始图像的本来面目,从而获得与景物真实面貌相像的图像。
1.10基本思路是,,在不损失图像质量或少损失图像质量的前提下,尽可能的减少图像的存储量,以满足图像存储和实时传输的应用需求。
1.11基本思路是,通过数学方法和图像变换算法对图像的某种变换,以便简化图像进一步处理过程,或在进一步的图像处理中获得更好的处理效果。
1.12基本目的是,找出便于区分和描述一幅图像中背景和目标的方法,以方便图像中感兴趣的目标的提取和描述。
第二章2.1解释下列术语(18)空间分辨率:定义为单位距离内可分辨的最少黑白线对的数目,用于表示图像中可分辨的最小细节,主要取决于采样间隔值的大小。
(19)灰度分辨率:是指在灰度级别中可分辨的最小变化,通常把灰度级数l称为图像的灰度级分辨率。
(20)像素的4邻域:对于图像中位于(x,y)的像素p来说,与其水平相邻和垂直相邻的4个像素称为该像素的4邻域像素,他们的坐标分别为(x-1,y)(x,y-1)(x,y+1)(x+1,y)。



数字图像处理教学大纲(范文模版)第一篇:数字图像处理教学大纲(范文模版)《数字图像处理》课程教学大纲课程英文名Digital Image Processing执笔人:周山编写日期:2010.7.9一、课程基本信息1.课程编号:070101162.课程性质/类别:选修课 /专业课 3.学时/学分: 32+16学时 / 2学分 4.适用专业:信息与计算科学专业二、课程教学目标及学生应达到的能力数字图像处理是一门迅速发展的新兴学科,发展的历史并不长。
由于图像是视觉的基础,而视觉又是人类重要的感知手段,故数字图像成为心理学、生理学、计算机科学等诸多方面学者研究视觉感知的有效工具。
本课程着重研究数字图像处理的方法,训练学生运用所学基础知识解决实际问题的能力,同时要求拓宽专业知识面。
三、课程教学内容与基本要求(一)绪论(4学时)1.主要内容:图像处理的概述,基本物理假设硬件设备,处理软件,光度学及色度学原理 2.基本要求1、了解数字图像处理概述;2、了解图像输入输出设备;3、掌握图像的亮度函数等;4、了解色彩的基本属性;3.自学内容:数学实验 4.课外实践:无(二)信号分析基础(8学时)1.主要内容:图像的数学信号表示,图像的取样和量化、像素间的一些基本关系、线性和非线性操作2.基本要求1、掌握信号的采样及量化2、理解图像的点运算,代数运算及几何运算;3、理解线性系统的性质及线性移不变系统的频率响应;4、掌握图像的卷积运算 3.自学内容:信号与系统4.课外实践:无(三)图像变换(8学时)1.主要内容:积分变换,连续及离散傅立叶变换,快速傅立叶变换,正交变换的一般表现形式 2.基本要求1、了解积分变换;2、掌握离散傅里叶变换、连续傅里叶变换、快速傅里叶变换;3、理解沃尔什变换,哈达吗变换等 3.自学内容:数字信号处理4.课外实践:无(四)图像的增强与复原(10学时)1.主要内容:图像增强原理、直方图处理、图像平滑化,图像的锐化,图像的复原2.基本要求1、掌握灰度级变换增强及频域增强原理;2、深刻理解直方图均衡化;3、了解邻域平均法;;4、掌握低通滤波法,高通滤波法;5、掌握图像复原的一般方法;3.自学内容:数字信号处理概率论4.课外实践:无(五)图像的分析与识别基础(10学时)1.主要内容:视觉再认模式,间断检测、边缘连接和边界检测、门限处理及基于区域的分割 , 2.基本要求1、了解模式匹配模式,傅立叶模式;2、掌握阈值分割法;3、掌握边缘检测法;1、了解区域增长法;2、掌握二值图像分割法;3、了解图像分割质量的评价;3.自学内容:概率论 4.课外实践:无(六)图像的压缩与编码(10学时)1.主要内容:图像压缩理论及模型,无损压缩、有损压缩,图像编码常用方法,图像编码评价方法,图像编码的国际标准 2.基本要求1、了解哈夫曼编码;2、掌握离散余弦变换;3、理解dct编码与解码;4、了解压缩编码的新进展; 3.自学内容:数据编码 4.课外实践:无四、教学安排建议1.作业练习每章课后布置2-3题作业。

《数字图像处理》课堂教学大纲一、课程的性质和目的数字图像处理是电子信息工程等专业的一门专业基础课,是一门多学科交叉的边缘学科。
学生通过数字图像处理的学习,能掌握图像处理的基本理论、概念、方法和技术,了解本领域最新的成果和发展动态;了解交叉学科的特点,培养严谨的治学态度,启迪创新思路和意识,通过实验锻炼动手实践能力;通过本课程学习,使学生打下一个较坚实的基础,为后续课程的学习作好铺垫,为以后从事本领域或相关领域工作、深造、研究作好准备。
二、课程的基本要求通过本课程的教学,要求学生掌握图像处理的基本理论、概念、方法和技术,包括图像的数学表征、变换、增强、复原、压缩编码、分割、描述等内容。
配合实验,使学生能用高级语言以及基于图像处理实验箱,实现一些基本算法和思路的图像处理,进一步巩固所学知识;了解本领域最新的成果和发展动态,了解交叉学科的特点,培养严谨的治学态度,启迪创新思路和意识。
三、课程内容与要求第1章数字图像处理的基本知识(4学时)1、学习目的和要求通过本章学习,了解图像处理及相关学科和领域、数字图像处理系统;掌握一些基本概念、数字图像及其表示,像素间的基本关系。
2、课程内容(1)图像及图像处理的概念;(2)数字图像的存储与读写;(3)数字图像处理系统;(4)数字图像处理应用;(5)图像技术及相关学科简介3、考核知识点和考核要求(1)识记:相关基本概念、图像处理的应用;(2)了解:数字图像处理系统构成;(3)掌握:数字图像及其表示,像素间的基本关系第2章图像处理中的常用数学变换(6学时)1、学习目的和要求通过本章学习,掌握空域变换、傅里叶变换和性质,学习快速傅里叶变换的原理和方法,离散Gabor变换,以及PCA变换的原理和方法;熟悉离散余弦变换及其快速算法,了解小波变换以及图像变换的应用。
2、课程内容(1)空域变换,包括代数运算和几何运算;(2)傅里叶变换的概念和性质、快速傅里叶变换;(3)离散Gabor变换的原理和方法;(4)小波变换的原理和方法;(5)PCA变换的原理和应用;(6)离散余弦变换等其他几种可分离变换,以及应用3、考核知识点和考核要求(1)了解、识记:小波变换、其他的几种可分离变换。

第七章频域处理7.1 频域世界与频域变换7.2 傅立叶变换7.3 频域变换的一般表达式7.4 离散余弦变换7.5 离散沃尔什哈达玛变换7.6 用Matrix<LIB>C++库实现图像变换的VC++编程7.7 小波变换简介7.1 频域世界与频域变换图7-1 任意波形可分解为正弦波的加权和(a)(b)(c)(d)图7-2 正弦波的振幅A 和相位φ初相位ϕ振幅A基本 正弦波(A =1, ϕ=0)角频率O A图7-3 图7-1(a )波形的频域表示(a) 幅频特性;(b) 相频特性AOf O f(a)(b)时域和频域之间的变换可用数学公式表示如下:)(),()(f f A f f Φ⇔正变换逆变换为能同时表示信号的振幅和相位,通常采用复数表示法,因此式(7-1)可用复数表示为)()(f F f f 正变换逆变换⇔完成这种变换,一般采用的方法是线性正交变换。
(7-1) (7-2)7.2 傅立叶变换7.2.1连续函数的傅立叶变换若把一个一维输入信号作一维傅立叶变换,该信号就被变换到频域上的一个信号,即得到了构成该输入信号的频谱,频谱反映了该输入信号由哪些频率构成。
这是一种分析与处理一维信号的重要手段。
当一个一维信号f(x)满足狄里赫莱条件,即f(x)(1)具有有限个间断点;(2)具有有限个极值点;则其傅立叶变换对(傅立叶变换和逆变换)一定存在。
在实际应用中,这些条件一般总是可以满足的。
一维傅立叶变换对的定义为du e u F x f u F F dx e x f u F x f F uxj ux j ππ212)()()]([)()()]([⎰⎰∞+∞--+∞∞-====(7-3) (7-4) 式中:,x 称为时域变量,u 称为频域变量。
1--=j以上一维傅立叶变换可以很容易地推广到二维,如果二维函数f (x ,y )满足狄里赫莱条件,则它的二维傅立叶变换对为dudv e v u F y x f v u F F dxdy e y x f v u F y x f F vy ux j vy ux j )(21)(2),(),()],([),(),()],([+∞+∞-∞+∞--+-+∞∞-+∞∞-⎰⎰⎰⎰====ππ(7-5) (7-6)式中:x, y 为时域变量;u, v 为频域变量。
7.2.2离散傅立叶变换要在数字图像处理中应用傅立叶变换,还需要解决两个问题:一是在数学中进行傅立叶变换的f(x)为连续(模拟)信号,而计算机处理的是数字信号(图像数据);二是数学上采用无穷大概念,而计算机只能进行有限次计算。
通常,将受这种限制的傅立叶变换称为离散傅立叶变换(Discrete Fourier Transform,DFT)。
设{f(x)|f(0), f(1), f(2), …, f(N-1)}为一维信号f(x)的N个抽样,其离散傅立叶变换对为N ux j N x N ux j N x eu F N x f u F F ex f u F x f F /2101/210)(1)()]([)()()]([ππ∑∑-=---=====(7-7)(7-8)式中:x ,u =0,1,2,…, N -1。
注:式(7-8)中的系数1/N 也可以放在式(7-7)中,有时也可在傅立叶正变换和逆变换前分别乘以,这是无关紧要的,只要正变换和逆变换前系数乘积等于1/N 即可。
N /1由欧拉公式可知θθθsin cos j e j +=(7-9)将式(7-9)代入式(7-7),并利用cos(-θ)=cos(θ),可得∑-=⎪⎭⎫ ⎝⎛-=102sin 2cos )()(N x N ux j N ux x f u F ππ(7-10)可见,离散序列的傅立叶变换仍是一个离散的序列,每一个u 对应的傅立叶变换结果是所有输入序列f (x )的加权和(每一个f (x )都乘以不同频率的正弦和余弦值),u 决定了每个傅立叶变换结果的频率。
通常傅立叶变换为复数形式,即)()()(u jI u R u F +=(7-11)式中,R (u )和I (u )分别是F (u )的实部和虚部。
式(7-11)也可表示成指数形式:F (u )=|F (u ) |e j φ(u )(7-12) 其中)()(arctan )()()(|)(|22u R u I u u I u R u F =+=ϕ(7-13) (7-14)通常称|F (u )|为f (x )的频谱或傅立叶幅度谱,φ(u )为f (x )的相位谱。
频谱的平方称为能量谱或功率谱,它表示为)()(|)(|)(222u I u R u F u E +==(7-15) 考虑到两个变量,就很容易将一维离散傅立叶变换推广到二维。
二维离散傅立叶变换对定义为)(210101)(21010),(1),()],([),(),()],([N vy M ux j N v M u N vy M ux j M x N y e v u F MN y x f v u F F ey x f v u F y x f F +-=-=-+--=-=∑∑∑∑====ππ(7-16) (7-17)式中:u ,x =0,1,2,…,M -1;v ,y =0,1,2,…,N -1;x ,y 为时域变量,u ,v 为频域变量。
像一维离散傅立叶变换一样,系数1/MN 可以在正变换或逆变换中,也可以在正变换和逆变换前分别乘以系数,只要两式系数的乘积等于1/MN 即可。
二维离散函数的傅立叶频谱、相位谱和能量谱分别为MN /1),(),(),(),(),(arctan ),(),(),(|),(|2222v u I v u R v u E v u R v u I v u v u I v u R v u F +==+=ϕ(7-18) (7-19) (7-20)式中,R (u , v )和I (u , v )分别是F (u , v )的实部和虚部。
7.2.3 离散傅立叶变换的性质表7-1 二维离散傅立叶变换的性质1.可分离性由可分离性可知,一个二维傅立叶变换可分解为两步进行,其中每一步都是一个一维傅立叶变换。
先对f(x,y)按行进行傅立叶变换得到F(x,v),再对F(x,v)按列进行傅立叶变换,便可得到f(x,y)的傅立叶变换结果,如图7-4所示。
显然对f(x,y)先按列进行离散傅立叶变换,再按行进行离散傅立叶变换也是可行的。
f (x, y) F (x, ) F (u, )按行进行一维DFT按列进行一维DFT图7-4 用两次一维DFT计算二维DFT2.平移性质平移性质表明,只要将f (x ,y )乘以因子(-1)x+y ,再进行离散傅立叶变换,即可将图像的频谱原点(0,0)移动到图像中心(M /2,N /2)处。
图7-5是简单方块图像平移的结果。
图7-5 傅立叶频谱平移示意图(a) 原图像;(b )无平移的傅立叶频谱;(c)平移后的傅立叶频谱(a) (b) (c)3.旋转不变性由旋转不变性可知,如果时域中离散函数旋转θ0角度,则在变换域中该离散傅立叶变换函数也将旋转同样的角度。
离散傅立叶变换的旋转不变性如图7-6所示。
图7-6 离散傅立叶变换的旋转不变性(a)(b)(d)(c)7.2.4快速离散傅立叶变换离散傅立叶变换计算量非常大,运算时间长。
可以证明其运算次数正比于N2,特别是当N较大时,其运算时间将迅速增长,以至于无法容忍。
为此,研究离散傅立叶变换的快速算法 (Fast Fourier Transform,FFT)是非常有必要的。
下面介绍一种称为逐次加倍法的快速傅立叶变换算法 (FFT),它是1965年Cooley和Tukey首先提出的。
采用该FFT 算法,其运算次数正比于N lb N,当N很大时计算量可以大大减少。
例如,FFT的运算次数和DFT的运算次数之比,当N=1024时,比值为1/102.4;当N=4096时,比值可达1/341.3。
由于二维离散傅立叶变换具有可分离性,即它可由两次一维离散傅立叶变换计算得到,因此,仅研究一维离散傅立叶变换的快速算法即可。
先将式(7-7)写成∑-==1)()(N x uxWx f u F (7-21)式中,W =e -j2π/N ,称为旋转因子。
这样,可将式(7-21)所示的一维离散傅立叶变换(DFT )用矩阵的形式表示为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--⨯--⨯-⨯-⨯⨯-⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯)1()1()0()1()1()0()1()1()1(2)1(1)1(00)1(02010)1(0201100)1(020100N f f f W W W WWW W W W W W WWWW N F F F N N N N N N N N 式中,由W ux 构成的矩阵称为W 阵或系数矩阵。
(7-22)观察DFT 的W 阵,并结合W 的定义表达式W =e -j2π/N ,可以发现系数W 是以N 为周期的。
这样,W 阵中很多系数就是相同的,不必进行多次重复计算,且由于W 的对称性,即xu N xu N x u N N jN WW WW e W ⨯⨯+⨯--=⨯=-==22222,1π因此可进一步减少计算工作量。
例如,对于N =4,W 阵为⎥⎥⎥⎥⎥⎥⎥⎤⎢⎢⎢⎢⎢⎢⎢⎡642032100000W W W W W W W W W WWW (7-23)由W 的周期性得:W 4=W 0,W 6=W 2,W 9=W 1;再由W 的对称性可得:W 3=-W 1,W 2=-W 0。
于是式(7-23)可变为⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡------1010000010100000W W W W W W W W W W W W W W W W (7-24)可见N=4的W阵中只需计算W0和W1两个系数即可。
这说明W 阵的系数有许多计算工作是重复的,如果把一个离散序列分解成若干短序列,并充分利用旋转因子W的周期性和对称性来计算离散傅立叶变换,便可以简化运算过程,这就是FFT的基本思想。
设N为2的正整数次幂,即,2,12==nn n如令M为正整数,且N=2M (7-25) (7-26)将式(7-26)代入式(7-21),离散傅立叶变换可改写成如下形式:∑∑∑-=+-=-=++==1)12(2)2(211202)12()2()()(M x x u Mx u MM x M x ux MWx f Wx f Wx f u F 由旋转因子W 的定义可知,因此式(7-27)变为uxMux MWW=22u Mux MM x M x ux MWW x f Wx f u F 2101)12()2()(∑∑-=-=++=现定义1,,1,0,)12()(1,,1,0,)2()(110-=+=-==∑∑-=-=M x u Wx f u F M x u Wx f u F M x ux Mo M x ux Me (7-27)(7-28)(7-29)(7-30)于是式(7-28)变为)()()(2u F W u F u F o u Me +=(7-31)进一步考虑W 的对称性和周期性可知和,于是u MM u MWW=+u MM u MWW22-=+)()()(2u F W u F M u F o u Me -=+(7-32)由此,可将一个N 点的离散傅立叶变换分解成两个N /2短序列的离散傅立叶变换,即分解为偶数和奇数序列的离散傅立叶变换F e (u )和F o (u )。