1.3.2《空间几何体的表面积与体积--球体》

球体的体积和表面积的特点和几何应用球体是一种具有特殊几何形状的几何体，它具有独特的体积和表面积特点，并且在实际应用中有着广泛的用途。

本文将分析球体的体积和表面积的特点，并探讨它们在几何学以及实际生活中的应用。

一、球体的体积特点球体的体积是指球体所包含的三维空间的容积大小。

球体的体积特点如下：1. 体积公式：根据几何学原理可知，球体的体积公式为V = (4/3)πr³，其中V表示球体的体积，π是一个常数约等于3.14159，r表示球体的半径。

该公式是根据球体的半径计算其体积的最常用公式。

2. 半径与体积的关系：从体积公式可以看出，球体的体积与半径的三次方成正比。

即当半径增加时，球体的体积也相应增加，而且增加的比例是不断增大的。

这一特点可以在计算球体的体积时得到验证。

3. 单位体积：球体一般被认为是一个连续体，因此在计算球体的体积时可以使用单位体积的概念。

单位体积指的是单位空间中包含的球体的体积。

例如，单位立方米中包含的球体的体积就是一个单位体积。

二、球体的表面积特点球体的表面积是指球体外部所包含的曲面部分的大小。

球体的表面积特点如下：1. 表面积公式：根据几何学原理可知，球体的表面积公式为A =4πr²，其中A表示球体的表面积，π是一个常数约等于3.14159，r表示球体的半径。

该公式是根据球体的半径计算其表面积的最常用公式。

2. 半径与表面积的关系：从表面积公式可以看出，球体的表面积与半径的平方成正比。

即当半径增加时，球体的表面积也相应增加，增加的比例是较小的。

这一特点可以在计算球体的表面积时得到验证。

3. 最小表面积原理：球体是所有形状的几何体中，相同体积下表面积最小的几何形状。

这一原理使得球体在储存、运输等方面有着广泛应用，因为相同体积的球体相对于其他几何形状来说，所需的材料更少，成本更低。

三、球体的几何应用球体具有独特的几何特点，在几何学和工程学中有着广泛的应用。

以下是球体在实际应用中的一些例子：1. 大地测量：在测量大地地球形状和地球表面时，球体的几何特性被广泛应用。

1.3球的体积与表面积【课题】：§1.3.2球的体积与表面积B 【教学目标】：１． 知识与技能⑴通过运用祖暅原理得出球的体积和面积公式的推导； ⑵能运用球的面积和体积公式灵活解决实际问题。

⑶培养学生的空间思维能力和空间想象能力。

２． 过程与方法通过运用祖暅原理得出球的体积和面积公式的推导，从而得到一种推导球体积公式Ｖ＝34πR 3和面积公式Ｓ＝４πR 2的方法。

３． 情感与价值观通过学习，使我们对球的体积和面积公式的推导方法有了一定的了解，提高了空间思维能力和空间想象能力，增强了我们探索问题和解决问题的信心。

【教学重点】：引导学生了解推导球的体积和面积公式所运用的基本思想方法。

【教学难点】：在球的体积、表面积计算公式的推导过程中体会“无穷”“极限”的思想． 【教学突破点】：球体的表面积和体积计算的教学，主要应当通过诱导学生前面已有知识点的运用技巧，通过客观的诱导分析及具体动手操作来完成．教学时，教师要充分利用“思考”“探究”栏目中提出的问题，让学生在动手实践的过程中学直观的得出柱体、锥体、台体的表面积和体积计算公式，更进一步体验公式的实际作用． 【教法、学法设计】：1．教法：通过对空间模型或运用计算机软件所呈现的空间几何体的开展过程的观察，帮助学生认识可以使用分割求和的方法得到球体的体积与表面积的运算公式。

并且能够运用基本公式来解决实际问题，培养解题技能。

2．学法：学生通过阅读教材，发挥空间想象能力，在球的体积、表面积计算公式的推导过程中体会“无穷”“极限”的思想． 【课前准备】：模型、课件 【教学过程设计】：233R R R R ππ-=，所以这个结论可以通过“倒沙实验”得到．设想一个球由许多顶点在球心，底面都在球面上的“准锥这时，这些“准锥体”的高趋向于球半径......的和趋向于球面积，所有这些“准锥体”的体积向于球的体积12311RS RS RS +++ (1)RS =练习与测试：1. 球的体积是323，则此球的表面积是( )A. 12πB. 16πC. 163π D.643π2. 两个球的表面积之比为1：9，则此两球的体积之比为（）A. 1: 729B. 1: 27C. 1: 9D. 1: 33. 一个正方体的内切球与外接球的表面积之比为（）A. 1:B. 1: 3C.D. 1: 24. 一个几何体的三视图都是半径为1的圆，则此几何体的表面积是；体积是。

高一数学必修2目录_高一数学必修二课本目录数学必修2课程是高一学生学习的重要内容。

同学们若想知道必修2课本目录，下面店铺为大家整理了高一数学必修2目录，希望对大家有所帮助!高一数学必修2目录第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图阅读与思考画法几何与蒙日1.3 空间几何体的表面积与体积探究与发现祖暅原理与柱体、椎体、球体的体积实习作业小结复习参考题第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.3 直线、平面垂直的判定及其性质阅读与思考欧几里得《原本》与公理化方法小结复习参考题第三章直线与方程3.1 直线的倾斜角与斜率探究与发现魔术师的地毯3.2 直线的方程3.3 直线的交点坐标与距离公式阅读与思考笛卡儿与解析几何小结复习参考题第四章圆与方程4.1 圆的方程阅读与思考坐标法与机器证明4.2 直线、圆的位置关系4.3 空间直角坐标系信息技术应用用《几何画板》探究点的轨迹：圆小结复习参考题高一数学必修2知识点1、柱、锥、台、球的结构特征(1)棱柱：定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体。

分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。

表示：用各顶点字母，如五棱柱或用对角线的端点字母，如五棱柱几何特征：两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。

(2)棱锥定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示：用各顶点字母，如五棱锥几何特征：侧面、对角面都是三角形;平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。

(3)棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示：用各顶点字母，如五棱台几何特征：①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点(4)圆柱：定义：以矩形的一边所在的直线为轴旋转，其余三边旋转所成的曲面所围成的几何体几何特征：①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。

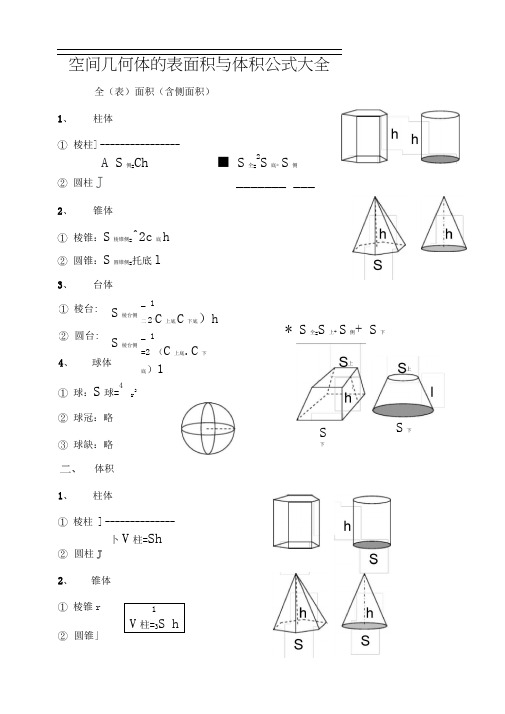
空间几何体的表面积与体积公式大全全（表）面积（含侧面积）1、柱体①棱柱]----------------A S侧=Ch ■ S全=2S底* S侧②圆柱J _______ ___2、锥体①棱锥：S棱锥侧=^2c底h②圆锥：S圆锥侧=托底l3、台体①棱台:②圆台:S棱台侧S棱台侧_ 1二2（C上底C下底）h_ 1=2 （C上底.C下底）1* S全=S上+ S侧+ S下4、球体①球：S球=4r2②球冠：略③球缺：略S下S下体积1、柱体①棱柱]--------------卜V柱=Sh②圆柱J2、锥体①棱锥r②圆锥」1V柱=3S h3、台体1①棱台］V台=gh （S上NS上S^ +S下）②圆台J V圆台=3兀h （r上+Q r上r下+ r下）4、球体①球：V球=4二r'②球冠：略③球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高h计算；而圆锥、圆台的侧面积计算时使用母线I计算。

三、拓展提高1、祖暅原理：（祖暅：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的2、阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是2r的圆柱形容器内装一个最大的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的-。

3分析：圆柱体积：V圆柱=Sh =（二「2）2r=2^r'圆柱侧面积：S圆柱侧=C h =（2 r） 2r = 4二「因此：球体体积：V球=2 2二J=4二r33 3球体表面积：S球=4 r2即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式：V台=1h （S上+ S下）证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD 延长两侧棱相交于一点P设台体上底面积为S上,下底面积为S下P 高为h。

易知：PDC s .>PAB ,设PE = h i，则PF =h i h由相似三角形的性质得:CD PEAB PFA整理得：h 1 ： =S上hPS 下-VS上又因为台体的体积=大锥体体积一小锥体体积1 11 1 二V台=3S 下(h 1h K3S 上h^3h 1(S下一S上) 下h代入：h= i S 上芬得: V台=3胪L(S下—S"3S 下hJS下3*SrS31 ___ I ------ ------ 1即: V 台=3 S上h (S下S上)3S下人二 V 台=3h （S 上S 上S 下S下）球体体积公式推导即：ShiS 下-h lh （相似比等于面积比的算术平方根）1 ______________=3h (S上S 上S 下S下)4、分析：将半球平行分成相同高度的若干层（ n 层），n 越大，每一层越近似于圆柱，n “ •「时，每一层都可以看作是个圆柱。

1。

3。

2球的体积和表面积一、 教学目标知识目标：1、掌握球的体积公式343V R π=、表面积公式24S R π=。

2、会用球的表面积公式、体积公式解决相关问题，培养学生应用数学的能力．3、能解决与球的截面有关的计算问题及球的“内接”与“外切”的几何体问题．能力目标：通过类比、归纳、猜想等合情推理培养学生勇于探索的精神. 提高学生分析、综合、抽象概括等逻辑推理能力情感目标:通过寻求如何研究球的内切与外接的方法，培养学生将数学知识和生活实际相联系的意识，对学生进行“事物具有多面性”的辩证唯物主义思想教育。

二、 教学重点、难点重点：球的体积和表面积的计算公式的应用。

难点：解决与球相关的“内接”与“外切"的几何体问题三、教学过程2球的表面积：（以后讲）11221(3)i i V h S h S h S ≈⋅∆+⋅∆++⋅∆+又∵i h R≈，且S =12i S S S ∆+∆+++∆∴可得13V R S ≈⋅,又∵343V R π=，∴13R S ⋅343R π=，∴24S R π=即为球的表面积公式小结：球的体积公式343V R π=、表面积公式24S R π=都是以R 为自变量的函数。

教师讲解，学生感悟分割、近似、极限等思想渗透微积分思想.应 用 举 练习1:如果球的体积是36πcm 3，那么它的半径是 .3练习2： 若两个球的体积之比为8：27，那么两个球的表面积之比为（ C )（A ）8：27 (B ）2：3 （C ）4：9 （D ）2:9例1 如图,圆柱的底面直径与高都等于球的直径,，求证： (1）球的体积等于圆柱体积的23（2）球的表面积等于圆柱的侧面积。

教师引导学生共同完成让学生巩固例证明：（1）设球的半径为R ，则圆柱的 底面半径为R ，高为2R 。

则有V球=334R ， V 圆柱=πR 2·2R=2πR 3，所以V 球=圆柱V 32。

（2）因为S 球=4πR 2，S 圆柱侧=2πR ·2R=4πR 2,所以S 球=S 圆柱侧.变式1：把上一题的圆柱改为正方体，且正方体的棱长为a, 球的半径为多少?变式2：若把球吹大到内切于正方体的棱，且正方体的棱长为a,此时球的半径又为多少?变式3：若球接着吹大到刚好包围整个正方体即球各个顶点都在球面上，且正方体的棱长为a ，此时球的半径又为多少？加深所学内容并灵活运用。