悬索桥的计算理论

悬索桥结构计算理论悬索桥结构计算理论主要内容☞概述☻悬索桥的近似分析☞悬索桥主塔的计算☞悬索桥成桥状态和施工状态的精确计算1.概述1.1悬索桥的受力特征悬索桥是由主缆、加劲梁、主塔、鞍座、锚碇、吊索等构件构成的柔性悬吊体系，其主要构成如下图所示。

成桥时，主要由主缆和主塔承受结构自重，加劲梁受力由施工方法决定。

成桥后，结构共同承受外荷作用，受力按刚度分配。

悬索桥各部分的作用主缆是结构体系中的主要承重构件，受拉为主；主塔是悬索桥抵抗竖向荷载的主要承重构件，受压为主；加劲梁是悬索桥保证车辆行驶、提供结构刚度的二次结构，主要承受弯曲内力；吊索是将加劲梁自重、外荷载传递到主缆的传力构件，是连系加劲梁和主缆的纽带，受拉。

锚碇是锚固主缆的结构，它将主缆中的拉力传递给地基。

1.概述(续)✶悬索桥计算理论的发展与悬索桥自身的发展有着密切联系早期，结构分析采用线弹性理论(由于桥跨小，索自重较轻，结构刚度主要由加劲梁提供。

中期(1877), 随着跨度的增加，梁的刚度相对降低,采用考虑位移影响的挠度理论。

现代悬索桥分析采用有限位移理论的矩阵位移法。

✹跨度不断增大的同时，加劲梁相对刚度不断减小，线性挠度理论引起的误差已不容忽略。

因此，基于矩阵位移理论的有限元方法应运而生。

应用有限位移理论的矩阵位移法，可综合考虑体系节点位移影响、轴力效应，把悬索桥结构非线性分析方法统一到一般非线性有限元法中，是目前普遍采用的方法。

▪弹性理论（1）悬索为完全柔性，吊索沿跨密布；（2）悬索线性及座标受载后不变；（3）加劲梁悬挂于主缆，截面特点不变；仅有二期恒载、活载、温度、风力等引起的内力。

计算结果：悬索内力及加劲梁弯距随跨经的增大而增大。

▪挠度理论与弹性理论不同之处仅在于：考虑悬索竖向变形对内力的影响（不考虑剪力变形、吊杆倾斜及伸缩变形，影响较小）。

线性挠度理论：忽略挠度理论中活载引起的主缆水平分力与竖向位移之间的非线性关系。

计算结果：加劲梁弯距铰弹性理论结果要小。

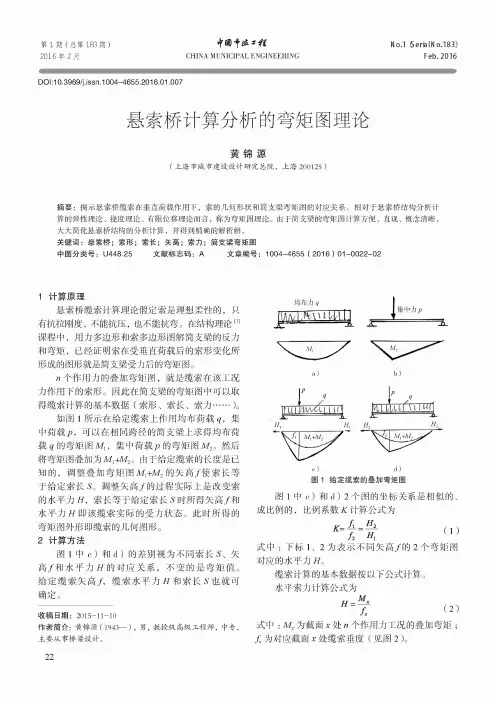
第1期（总第183期）中劫彳威*荇No.lSerialNo.183) 2016 年 2 月CHINA MUNICIPAL ENGINEERING Feb. 2016D0l:10.3969/j.issn.1004-4655.2016.01.007悬索桥计算分析的弯矩图理论黄锦源(上海市城市建设设计研究总院，上海200125 )摘要：揭示悬索桥缆索在垂直荷载作用下，索的几何形状和简支梁弯矩图的对应关系。

相对于悬索桥结构分析计 算的弹性理论、挠度理论、有限位移理论而言，称为弯矩图理论。

由于简支梁的弯矩图计算方便、直观、概念清晰，大大简化悬索桥结构的分析计算，并得到精确的解析解。

关键词：悬索桥；索形；索长；矢高；索力；简支梁弯矩图中图分类号：U448.25 文献标志码：A文章编号=1004-4655(2016)01-0022-021计算原理悬索桥缆索计算理论假定索是理想柔性的，只 有抗拉刚度，不能抗压，也不能抗弯。

在结构理论[1]课程中，用力多边形和索多边形图解简支梁的反力 和弯矩，已经证明索在受垂直荷载后的索形变化所 形成的图形就是简支梁受力后的弯矩图。

«个作用力的叠加弯矩图，就是缆索在该工况 力作用下的索形。

因此在简支梁的弯矩图中可以取 得缆索计算的基本数据（索形、索长、索力……）。

如图1所示在给定缆索上作用均布荷载g，集 中荷载可以在相同跨径的简支梁上求得均布荷载g的弯矩图％，集中荷载p的弯矩图M2。

然后 将弯矩图叠加为M i+M2。

由于给定缆索的长度是已 知的，调整叠加弯矩图M1+M2的矢高/使索长等于给定索长又调整矢高/的过程实际上是改变索 的水平力丑，索长等于给定索长^时所得矢高/和 水平力丑即该缆索实际的受力状态。

此时所得的 弯矩图外形即缆索的几何图形。

2计算方法图1中c)和d)的差别视为不同索长^、矢 高/和水平力丑的对应关系，不变的是弯矩值。

给定缆索矢高/，缆索水平力丑和索长^也就可确定。

悬索桥的计算方法及其发展悬索桥是一种古老的桥梁结构形式，也是目前大跨度桥梁的主要结构型式之一。

悬索桥主要是由缆索、吊杆、加劲梁、主塔、锚碇等构成。

从结构形式上看，它是一种由索和梁所构成的组合体系在受力本质上它是一种以柔性索为主要承重构件的悬挂结构。

悬索桥随着跨度的增大，柔性加大，在荷载作用下会呈现出较强的非线性，所以悬索桥宜采用非线性方法来进行结构分析。

考虑悬索桥非线性因素的结构分析方法主要有挠度理论和有限位移理论。

挠度理论考虑了悬索桥几何非线性的主要因素，可用比较简便的数值方法来分析，又有影响线可资利用，故很适用于初步设计阶段的结构设计计算。

有限位移理论则全面地考虑了悬索桥几何非线性因素，计算结果较挠度理论精确，但计算过程复杂，直接用于设计计算有诸多不便和困难。

悬索桥挠度理论是一种古典的悬索桥结构分析理论。

这种理论主要考虑悬索和加劲梁变形对结构内力的影响，在中小跨度范围内其计算结果比较接近结构的实际受力情况，具有较好的精度。

悬索桥挠度理论主要分为多塔悬索桥挠度理论和自锚式悬索桥挠度理论最初的悬索桥分析理论是弹性理论。

弹性理论认为缆索完全柔性，缆索曲线形状及坐标取决于满跨均布荷载而不随外荷载的加载而变化，吊杆受力后也不伸长，加劲梁在无活载时处于无应力状态弹性理论用普通结构力学方法即可求解，计算简便，至今仍在跨径小于200米的悬索桥设计中应用［1］。

但弹性理论假定缆索形状在加载前后不发生变化，显然与悬索桥的可挠性不符，因此发展出计入变形影响的悬索桥挠度理论。

古典的挠度理论称为“膜理论”。

它是将悬索桥的全部近视看成是一种连续的不变形的膜，当缆索产生挠度时，加劲梁也随之产生相同的挠度。

由于根据作用于缆索单元上吊杆力与缆索拉力的垂直分力平衡以及作用于加劲梁单元上的外荷载及吊杆力与加劲梁弹性抗力平衡的条件建立力的平衡微分方程而求解。

挠度理论和弹性理论的最大区别是摒弃了弹性理论中关于缆索形状不因外荷载介入而改变的假设，相应建立缆索在恒载下取得平衡的几何形状将因外荷载介入而改变及同时计入缆索因外荷载所增索力引起的伸长量的假设，极大的接近悬索桥主索的实际工作状态，对悬索桥的发展起到了很大的推动作用。

悬索桥的发展与设计计算理论摘要：本文先介绍了现代悬索桥的发展历史，而后主要从悬索桥理论发展入手,介绍了弹性理论、挠度理论、有限位移理论的基本原理,并通过对三者的比较分析,说明了在现今计算机高速发展和应用的背景下,有限位移理论是对悬索桥结构进行分析的最适合的理论。

关键词：悬索桥；弹性理论；挠度理论；有限位移理论我国四川省的灌县早在前年之前就出现了竹索桥。

17世纪出现铁链作悬索的桥梁，我国四川省大渡河上由9条铁链组成的泸定桥是在1 706年建成的。

19世纪时又发展为采用眼杆与销铰作悬链的桥梁。

英国1826年建成的跨度为177m的麦地海峡桥；1864年建成的跨度为214m的克利夫顿桥都是属于这种形式，这两座古老的悬索桥至今尚在使用。

利用钢缆绳、钢铰线秘钢丝等现代钢材来制造的悬索桥则基本上是进入20世纪后才开始出现的。

现代悬索桥的发展迄今出现了四次高峰。

在第一次与第二次高峰之间的20世纪40年代．因美国塔科马老桥的风毁事故．夫跨度悬索桥的修建停顿了约有10年之久。

但在此期间由手悬索桥的抗风设计，引入了风洞试验雨使悬索桥的发展在20世纪50年代得到复苏，并分别在60年代与80年代进式第二次与第三次高峰。

进入90年代之后，在全球范围随又出现新的建设高峰。

即目前的第四次高峰。

以下对四次高峰，包括挫折期与复苏期．分别作概略的叙述。

1883年在纽约建成的主跨为486m的布鲁克林桥是美国，也是世界首座跨度较大的悬索桥。

此桥除了具备现代悬索桥的缆索体系外．还混有若干加强的斜拉索。

因此，严格地说，它不是一座纯粹的悬索桥。

首先是1903年建成的主跨为488m 的威廉姆斯堡，其次是1909年建成的主跨为448m的曼哈顿桥。

这两座桥都是纽约市区跨越东河．并且都是在空中甩编丝轮将钢丝编拉后组成主缆的。

这种在空中编丝成缆的方法被称为空中编缆法．简称AS法。

而悬索桥的发展又离不开与其密切相关的计算理论的发展。

悬索桥的计算理论也已有上百年的历史,它随着时代的发展与科学技术的进步,特别是二次世大战以后的电子计算机技术的发展,有着非常大的演变与发展。

自锚式悬索桥的特点与计算一、悬索桥计算原理1、恒载内力：柔性的悬索在均布荷载作用下，为抛物线形。

悬索的承载原理，功能等价于同等跨径的简支梁。

简支梁的跨中弯矩 M=QL²/8悬索拉力作功 M=H*F悬索水平拉力 H= QL²/(8*F)悬索座标 Y=4*(F/ L²)*X*(L-X)悬索垂度 F 悬索斜率 tg α=4*(F/L)*(L-X)悬索最大拉力 Tmax=H/COS α=H*SEC α2、活载内力：在集中荷载作用时，悬索的变形很大，为满足行车需要，需要通过桥面加劲梁来分布荷载，弯矩由桥面加劲梁来承担，悬索的变形与桥面加劲梁相同。

桥面加劲梁为弹性支承连续梁，它不便手工计算，采用有限单元法计算则方便。

（1）弹性理论：不考虑在恒载和活载的共同作用下产生的竖向变形和悬索水平拉力的增加。

加劲梁的弯矩：弹性理论 M=M-h*y式中：简支梁的活载弯矩M，悬索座标y，活载引起的水平拉力h。

（2）变位理论：考虑在恒载和活载的共同作用下产生的竖向变形和悬索水平拉力的增加，这种竖向变位与悬索的水平拉力所作的功，将减小桥面加劲梁的弯矩。

加劲梁的弯矩：变位理论 M=M-h*y-(H-h)*v 式中：活载产生的撓度v二、自锚式悬索桥计算原理自锚式悬索桥的内力计算复杂，应采用非线性有限单元法来计算。

对于几何可变的缆索单元，需作加大弹性模量的应力刚化处理。

悬索作为几何可变体系，活载作用的变形影响很大，是非线性变形影响的主要因素。

本文采用线性有限单元法作简化计算的方法，是先按线性程序计算出活载撓度，修正活载撓度的座标以后，再用线性有限单元法作迭代计算。

即采自锚式悬索桥计算可采用有限单元程序解决，而施工矛盾很突出，需要寻求合理的施工办法。

采用复合钢管砼、钢管砼、加劲钢管作加劲梁，配合钢筋砼或正交异性板钢桥面，能够解决自锚式悬索桥存在的问题。

按照一般桥梁的常用形式，城市桥梁可以加设悬挑人行道，作了系列跨径的探索计算，以探求自锚式悬索桥大、中、小跨径的内力变化和变形规律。

斜拉桥与悬索桥计算理论简析斜拉桥与悬索桥是桥梁结构中跨越能力最大的两种桥型，随着桥梁建造向大跨径方向发展，它们越来越成为人们研究的热点。

通过大跨径桥梁理论的学习，我对斜拉桥与悬索桥的计算理论有了较为系统的了解。

在本文中，我想从一个设计者的角度，在概念层次上，对斜拉桥与悬索桥的计算理论做个总结，以加深自己对这些计算理论的理解。

一、斜拉桥的计算理论斜拉桥诞生于十七世纪，在最近的五十年间，斜拉桥有了飞速的发展，成为200米到800米跨径范围内最具竞争力的桥梁结构形式之一。

有理由相信，在大江河口的软土地基上或不适合建造悬索桥的地区，有可能修建超过1200米的斜拉桥。

斜拉桥是塔、梁、索三种基本结构组成的缆索承重结构体系，一般表现为柔性的受力特性。

（一）、斜拉桥的静力设计过程1、方案设计阶段此阶段也称为概念设计。

本阶段的主要任务是凭借设计者的经验，参考别的斜拉桥的设计，结合自己的分析计算，来完成结构的总体布置，初拟构件尺寸。

根据此设计文件，设计者或甲方（有些地方领导说了算）进行方案比选。

2、初步设计阶段本阶段在前一阶段工作的基础上进一步细化。

主要任务是：通过反复计算比较以确定恒活载集度、恒载分析、调索初定恒载索力、修正斜拉索截面积、活载及附加荷载计算、荷载组合及梁体配索、索力优化以及强度刚度验算等。

3、施工图设计阶段此阶段要对斜拉桥的每一部位以及每一施工阶段进行计算，确保结构安全。

主要计算内容有：构件无应力尺寸计算、对施工阶段循环倒退分析、计算斜拉索初张力、预拱度计算、强度刚度稳定性验算以及前进分析验算等。

（二）、斜拉桥的计算模式1、平面杆系加横分系数此模式用在概念设计阶段研究结构的设计参数，以求获得理想的结构布置。

还可用于技术设计阶段，仅仅计算恒载作用下的内力。

2、空间杆系计算模式此模式用在空间荷载（风载、地震荷载以及局部温差等）作用下的静力响应分析。

此模式按照主梁可分为三种：“鱼骨”模式、双梁式模式与三梁式模型。