高等数学知识网络图(详细版本)

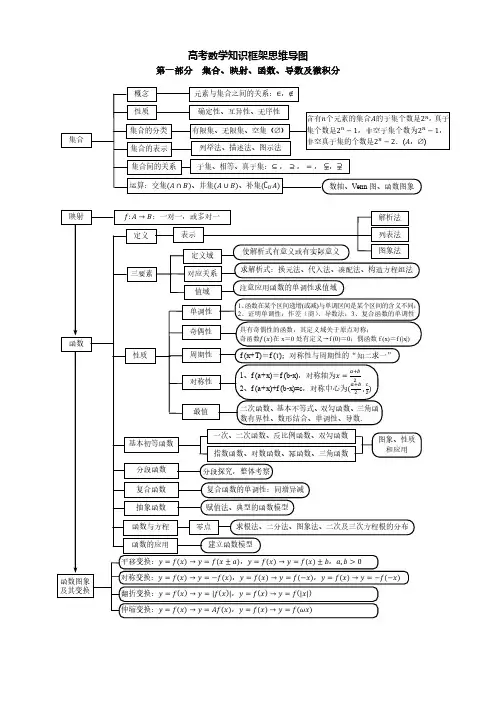
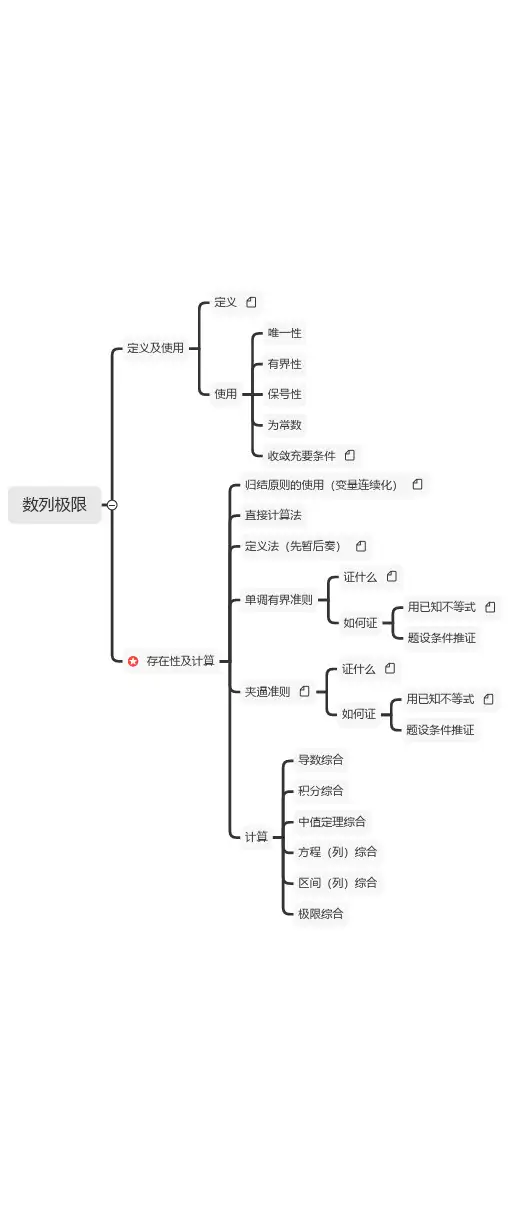
高等数学作为大学数学教育的核心课程之一，包含了许多重要的数学概念和方法。

其中，图论与网络分析是高等数学中的一个重要分支，涉及了图的定义、图的性质以及与网络相关的问题的解决方法。

首先，让我们来了解一下什么是图。

在数学中，图是由若干个节点和连接这些节点的边组成的结构。

节点可以表示各种实体，如人、城市等，而边则表示节点之间的关系。

图可以分为有向图和无向图两种类型。

在有向图中，边具有方向，表示节点之间的单向关系；而在无向图中，边没有方向，表示节点之间的双向关系。

我们可以通过绘制节点之间的边来可视化地表示图的结构。

在高等数学中，我们主要研究的是无向图。

通过图的分析，我们可以更好地理解各种实体之间的相互关系。

例如，在社交网络中，可以用图来表示人与人之间的关系；在物流领域中，可以用图来表示商品与配送中心之间的联系。

通过对图的分析，可以帮助我们揭示隐藏在复杂关系中的规律，并为解决实际问题提供指导。

而图论是研究图的性质和图中问题的解决方法的一门学科。

通过图的性质分析，可以推断出图中节点之间的关系，比如节点的连通性、路径的存在性等。

图论中的常用概念包括度、连通图、路径等。

节点的度表示与该节点相连的边的数量，连通图指的是任意两个节点之间都存在路径的图，而路径则是指从一个节点到另一个节点所经过的边的序列。

借助这些概念，我们可以计算图的直径（即最长路径的长度）、聚类系数（表示节点之间的紧密联系程度）等指标，从而更好地了解图的结构。

在网络分析中，我们关注的是如何在真实世界中获得图的数据并对其进行分析。

近年来，随着互联网的发展，大量的网络数据被生成和存储。

通过网络分析，可以从这些数据中挖掘出有价值的信息。

例如，在社交网络中，可以通过分析用户之间的连接模式，了解人们的兴趣爱好和行为习惯；在生物学中，可以分析蛋白质相互作用网络，推断出未知蛋白质的功能等。

网络分析的方法包括社区发现、中心性分析、网络模型等。

这些方法可以帮助我们揭示网络结构中的规律和特征，并为决策者提供支持。

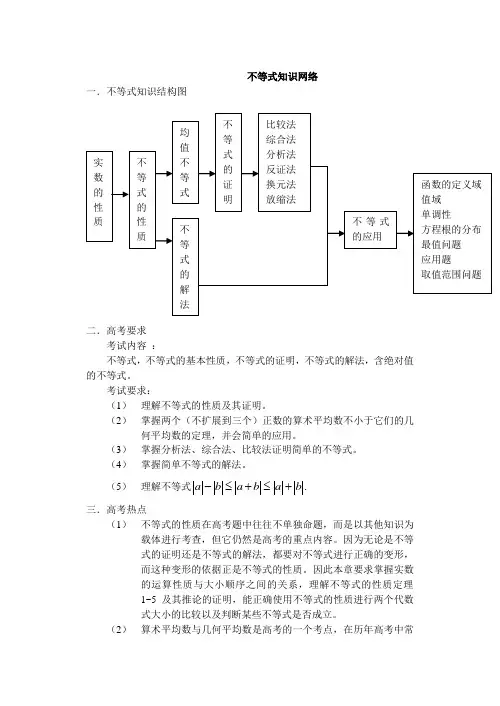
不等式知识网络 一．不等式知识结构图二．高考要求考试内容 ：不等式，不等式的基本性质，不等式的证明，不等式的解法，含绝对值的不等式。

考试要求：（1） 理解不等式的性质及其证明。

（2） 掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用。

（3） 掌握分析法、综合法、比较法证明简单的不等式。

（4） 掌握简单不等式的解法。

（5） 理解不等式.a b a b a b -≤+≤+三．高考热点（1） 不等式的性质在高考题中往往不单独命题，而是以其他知识为载体进行考查，但它仍然是高考的重点内容。

因为无论是不等式的证明还是不等式的解法，都要对不等式进行正确的变形，而这种变形的依据正是不等式的性质。

因此本章要求掌握实数的运算性质与大小顺序之间的关系，理解不等式的性质定理1~5及其推论的证明，能正确使用不等式的性质进行两个代数式大小的比较以及判断某些不等式是否成立。

（2） 算术平均数与几何平均数是高考的一个考点，在历年高考中常常出现综合函数、几何等知识的考查，近几年高考中又多次出现运用该知识的应用题。

因此要求掌握算术平均数与几何平均数定理及其变形，会用来求函数最值、证明不等式以及解决一些实际应用题。

新的高考要求对于算术平均数与几何平均数定理及应用不扩展到三个，因此在复习时不必做“三个数”以上的扩展。

（3） 不等式证明是高考的一个考点，在历年高考中经常出现，本章要求重点掌握不等式证明的三种方法：比较法、综合法、分析法，其他不作为重点。

但其它方法，如反证法、换元法、函数法、放缩法等等都是高等数学常用的思维方法，因此也是考查学生的能力的一个方面，希望同学们注意掌握。

（4） 解不等式是历年高考的热点，题目多以中档难度出现。

要求在掌握一元一次不等式和一元二次不等式解法的基础上，还要会解绝对值不等式、分式不等式及简单的高次不等式，并会运用分类讨论思想以及等价转化思想解某些较复杂的与不等式解法有关的问题。

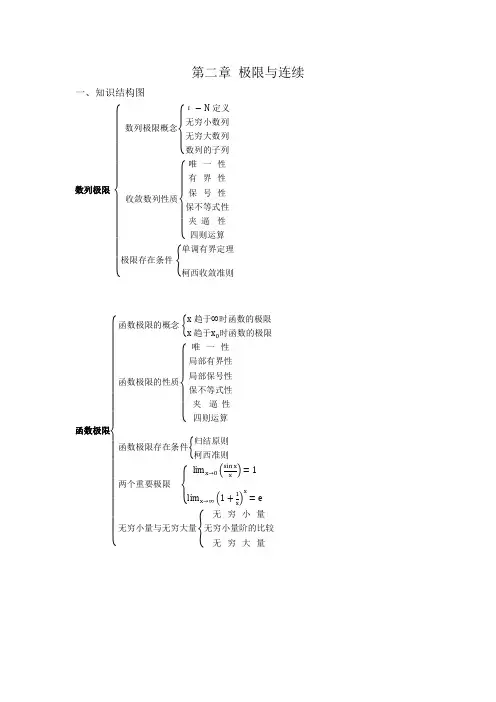
第⼀一讲极限与连续分为如下部分：1.定义2.性质3.⽆无穷⼩小4.⽆无穷⼤大5.函数极限的计算6.数列列极限的计算7.应⽤用!定义（极限定义——四句句话）⼀一.⼀一共有25种定义（6x4+1）6:x的六种趋向⽅方式，分为局部性质与渐进性质（注意对于x不不等于x0）4:f的四种趋向⽅方式，有三种是⽆无穷的情况（注意：任取M，与⽆无界定义相区别）（宇哥基础笔记）1:数列列定义（注意n为⾃自然数，只有渐进性质）函数极限定义注意两点：1.x趋向于x0，x不不等于x02.若f在x0的去⼼心邻域⽆无定义，则极限不不存在，反之，极限存在，则推在x0的去⼼心邻域处处有定义数列列极限的定义也注意两点：1.xn的极限与其前有限项⽆无关（类似于⽆无穷级数的收敛性与前n项⽆无关）2.xn的极限为a互推xn的任意的⼦子列列的极限也为a，特别的，xn的极限为a互推xn的奇数项与偶数项的极限均为a（注意：要涵盖xn的所有项）⼆二.有关定义的考法（17宇哥强化笔记）1.定X，N以及那个什什么（打不不出来）（主要是利利⽤用极限语⾔言来证明极限）⽅方法是：从有关f的不不等式推导出有关x的不不等式，从⽽而来定，若f的式⼦子复杂，可通过适当的放缩。

2.定e（原谅我不不能打出来）来讨论f（x）的范围Note1.注意例例题中有个结论 f极限为a可以推出f的绝对值极限为a的绝对值（利利⽤用极限的定义与中学知识来证，同理理数列列极限也是）2.e要取正整数，不不能取变量量。

3.由极限来推出的f的范围，只是陈述事实，⽽而不不是取值范围。

4.即使给我整个世界，我也只在你的身边"性质及其考法三⼤大性质——唯⼀一性，局部有界性，局部保号性1.唯⼀一性——极限存在必唯⼀一，所以极限存在可以推左极限等于右极限Note：⼀一般分左右极限的情况1.分段点 2.e的∞ 3.arctan∞2.局部有界性（注意局部包括局部性质与渐进性质）定义（会证会⽤用）（利利⽤用了了中学知识，绝对值的不不等式）Note：该定义只是有界的充分⾮非必要条件，即函数有界不不⼀一定极限存在，如sinx关于函数f（x）的有界性的判定⽅方法：1.理理论法（中学知识）：连续初等函数在闭区间内必有界2.计算法（⼤大学知识）：函数在开区间内连续，再加上端点的极限存在，则可以推出该函数在区间内有界3.四则运算：当极限不不存在时，拆！（⚠）（有限个）有界+有界=有界（有限个）有界x有界=有界Note：初等函数在闭定义区间内连续有界（初等函数在定义区间内连续，在闭定义区间内连续，必有界）3.局部保号性（此处的局部也是包括局部和渐进性质）定义（会证会⽤用）拓拓展：脱帽法（没有=号）带帽法（有等号，尤其极限A必须有等号，如x分之1在x趋于∞）Note：1.极限的运算法则：能不不能拆，拆了了再说。

高等数学各章知识结构高等数学是一门广泛涉及多个领域的学科，包括微积分、线性代数、概率论等。

下面将介绍高等数学各章的知识结构。

一、数列与数学归纳法（150字）数列与数学归纳法是高等数学的起点，包括等差数列、等比数列、递推数列等概念。

这一章主要讨论数列的性质、极限与收敛性等问题，并引入数学归纳法进行证明。

二、函数与极限（200字）函数与极限是高等数学的核心概念，也是微积分的基础。

这一章主要包括函数的定义、性质、基本函数、复合函数等内容，引入了极限的概念和计算方法。

三、导数与微分（250字）导数与微分是微积分的重要内容，也是应用最广泛的部分。

这一章主要讨论导数的定义、求导法则、高阶导数等内容，以及微分的定义与应用。

四、不定积分（200字）不定积分是微积分的另一个重要内容，研究的是函数的原函数。

这一章主要介绍不定积分的定义、基本积分法、换元积分法、分部积分法等内容。

五、定积分（200字）定积分是微积分的重要应用之一，主要研究函数在区间上的积分。

这一章主要包括定积分的定义、性质、基本公式、几何应用等内容。

六、微分方程（250字）微分方程是高等数学的又一重要内容，研究的是包含导数的方程。

这一章主要介绍了一阶线性微分方程、高阶线性微分方程、常微分方程的基本概念、解法和应用。

七、无穷级数（200字）无穷级数是数列的延伸，研究的是无穷多个数的求和。

这一章主要介绍级数的概念、收敛性、常用级数以及级数收敛的判定方法等内容。

八、多元函数与偏导数（250字）多元函数与偏导数是高等数学的另一个重要部分，研究的是多个变量间的关系。

这一章主要包括多元函数的概念、偏导数的定义与计算、全微分等内容。

九、多重积分（200字）多重积分是对多元函数求积分的扩展，研究的是多维空间中的积分。

这一章主要介绍二重积分、三重积分的定义、计算方法以及应用。

十、曲线与曲面积分（200字）曲线与曲面积分是高等数学的应用之一，主要研究曲线和曲面上的积分。

高数学习中的思维导图与总结技巧
在高等数学学习中，思维导图与总结技巧扮演着重要角色。

它们如同一位引导者，带领着学生们在广袤的数学知识海洋中航行，找到宝贵的知识珍珠并将它们串联成精巧的项链。

首先，思维导图可以比喻为一张引导地图。

当学生们面对复杂的数学概念和公式时，这张地图为他们指明方向，帮助他们理清头绪。

通过将各个概念、定理、公式用节点和链接连接起来，思维导图呈现出数学知识的结构和逻辑关系。

就像一位热心的导游，它们把学生们从迷失的迷宫中带出来，让他们能够更清晰地看到整个数学学科的全景图。

其次，总结技巧像是一位智者，帮助学生们从学习的浩瀚中提炼精华。

通过总结，学生们可以把学到的知识归纳概括，从而更深刻地理解和记忆。

就像一个精巧的工匠，总结技巧帮助学生们将零散的数学知识点打磨成统一的整体。

它们教导学生们如何从细节中抽丝剥茧，发现并把握住数学问题的核心。

在实际运用中，思维导图与总结技巧相辅相成。

思维导图提供了一个构建知识结构的框架，而总结技巧则在这个框架上填充内容，使其更加丰富和有力。

通过将两者结合运用，学生们可以
在高等数学学习中事半功倍，既提高学习效率又加深对数学内容的理解。

总之，高等数学学习中的思维导图和总结技巧如同学习之路上的得力助手。

它们不仅指引着学生们前行的方向，还帮助他们在广袤的数学知识海洋中留下深刻的足迹。

通过不断地练习和应用，学生们能够将这些技巧内化成为自己学习的一部分，从而在数学学习的旅程中获得更多的收获和成长。

多元函数微分学 一、知识网络图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧线空间曲线的切平面与法曲线的切线与法平面几何应用拉格朗日乘数法定义法条件极值充分条件必要条件极值泰勒公式应用方程组一个方程隐函数复合函数的微分定义微分法质闭区域上连续函数的性关系连续性与全微分之间的偏导数极限与累次极限的关系性质全微分梯度方向导数偏导数连续极限有界闭区域区域集闭开边界点外点内点邻域距离图形多元函数变化域基本概念，、、、、、、、、、、、)( 二、典型错误分析例1.求.lim 222300y xy x xy x y x +-+→→[错解] 引入极坐标,并注意到02sin 211≠-θ,故原式02sin 211cos lim )sin cos 1()sin cos (cos lim 022330=-=-+→→θθθθθθθr r r r r[错因分析] 若A y x f y y x x =→→),(lim 00, 则要求动点),(y x Q 沿任何方向、任意方式趋于点),(00y x P 时,函数均趋于A. 本题的以上解法仅反映了动点),(y x Q 沿从原点引出的射线方向趋向于)0,0(时,函数的极限是零,这不足以说明该函数的极限就是零.[正确解法] 由于22222322230yxy x xy y xy x x y xy x xy x +-++-≤+-+< ||||243||222223y xy x y x y x x x +-+⎪⎭⎫⎝⎛-+= ||||34||||||43||223y x y x y x x x +=+≤且 0||||34lim 00=⎪⎭⎫⎝⎛+→→y x y x于是 .lim 222300y xy x xy x y x +-+→→例2.求.lim22y xy x yx y x +-+∞→∞→[错解] 由于222222222y xy x y x y xy x +-++=+-442)(22222222y x y x y x y x +++≥-++= 4)(424222y x xy y x +=++≥ 于是||4)(41||222y x y x y x y xy x y x +=++≤+-+ 又 ∞→∞→y x lim0||4=+y x故 .lim22y xy x yx y x +-+∞→∞→[错因分析] ∞→∞→y x lim0||4=+y x 未必成立,例如,取n y n x n n -==4,则1||4lim,lim lim =+∞==∞→∞→∞→nn n n n n n y x y x[正确解法] 由于 22222y x y xy x +≥+-)(2)(222y x y x +≤+)(2||22y x y x +≤+⇒于是 2222222222)(212yx y x y x yxy x yx +=++≤+-+而 ∞→∞→y x lim02222=+yx故 .lim22y xy x yx y x +-+∞→∞→例3.设⎪⎩⎪⎨⎧=+≠+++=0,00,1sin )(),(22222222y x y x y x y x y x f 问),(y x f 在点)0,0(处:(1)偏导数是否存在? (2)偏导数是否连续? (3)是否可微? [错解](1) 2222221cos 21sin2),(y x y x x y x x y x f x ++-+='2222221cos 21sin2),(yx y x y y x y y x f y ++-+=' 可见)0,0(x f '及)0,0(y f '都不存在.(2)显然可知),(y x f x '及),(y x f y '在)0,0(处不连续.(3)由上述知),(y x f 在)0,0(处不可微.[错因分析] 忽略了分段函数在其分界点处的偏导数必须利用定义来求. [正确解法] (1)由于0)(1sin)(lim )0,0()0(lim)0,0(2200=∆∆∆=∆-∆+='→∆→∆xx x xf x f f x x x故)0,0(x f '存在. 同理)0,0(y f '也存在且等于零. (2)⎪⎩⎪⎨⎧=+≠+++-+='0,00,1cos 21sin 2),(2222222222y x y x y x y x x y x x y x f x ⎪⎩⎪⎨⎧=+≠+++-+='0,00,1cos 21sin 2),(2222222222y x y x y x y x y y x y y x f y由于 ]1cos 21sin2[lim ),(lim 22222200y x y x x y x x y x f xy x x xy x ++-+='=→=→]21cos 121sin2[lim 220x x x x xy x -==→ 可知该极限不存在.同理可证),(lim 0y x f y xy x '=→不存在. 故),(y x f x '及),(y x f y '在)0,0(处不连续.(3)注意: 函数的偏导数连续是函数可微的充分条件, 而不是必要条件,因此不能由(2)直接得出),(y x f 在)0,0(处不可微.由于 =∆z α+∆'+∆'y f x f y x )0,0()0,0( 且知 )0,0(x f '0)0,0(='=y f因而 )0,0()0,0(f y x f z -∆+∆+=∆=α2222)()(1sin])()[(y x y x ∆+∆∆+∆=000lim lim →∆→∆→∆→∆=y x y x ρα0)()(1sin )()(])()[(222222=∆+∆∆+∆∆+∆y x y x y x 故函数),(y x f 在)0,0(处可微.例4.设),,(v u x f =ω,),(y x u ϕ=,x ),(y x v ψ=.试将u ∂∂ω,v∂∂ω用ψϕ,,f 的偏导数表示.[错解] 如下图,可知 xω u xv yxvv x u u dx dx x x ∂∂∂∂+∂∂∂∂+∂∂=∂∂ωωωω x x vu x ψωϕωω'∂∂+'∂∂+∂∂=)(a 故0='∂∂+'∂∂x x vu ψωϕω )(b 又由yv v y u u dy dx x y ∂∂∂∂+∂∂∂∂+∂∂=∂∂ωωωω y y vu ψωϕω'∂∂+'∂∂+=0 )(c 故yv u yy ∂∂='∂∂+'∂∂ωψωϕω )(d 由)(b ,)(d 联立解之, 得xy y x xx y y x xyv y u ψϕψϕωϕωψϕψϕωψω''-''∂∂'=∂∂''-''∂∂'-=∂∂,其中0≠''-''x y y x ψϕψϕ[错解分析]由)(a 得到的)(b 是错的. )(a 中等式左右两端的x∂∂ω不能消掉,这是因为两者的含义截然不同. 等式左边的x∂∂ω是在)),(),,(,(y x y x x f ψϕω=中把y 看作常量对x 求偏导而得;而等式右端的x∂∂ω是把x 与v u ,看作相互独立的变量,即把v u ,看作常量对x 求偏导而得. 以后凡遇到一个变量即是自变量又是中间变量的情况,两边对该变量的偏导数要写成不同的符号以示区别. [正确解法] 由前面图可知⎪⎪⎩⎪⎪⎨⎧'∂∂+'∂∂+=∂∂'∂∂+'∂∂+∂∂=∂∂y y x x v f u f y v f uf x f x ψϕωψϕω0解之, 可得,xy y x x y y x f x u u f ψϕψϕψωψωω''-'''∂∂-'⎪⎭⎫⎝⎛∂∂-∂∂=∂∂=∂∂.xy y x y xx f x y v v f ψϕψϕϕωϕωω''-'''⎪⎭⎫ ⎝⎛∂∂-∂∂-'∂∂=∂∂=∂∂其中0≠''-''x y y x ψϕψϕ.例5.设),(t x f y =,而t 是由方程0),,(=t y x F 所确定的y x ,的函数,试求dxdy. [错解] 由),(t x f y =,则xt t f x f dx dy ∂∂∂∂+∂∂= )(a 又由0),,(=t y x F ,则t x F F x t''-=∂∂ )(b 将)(b 代入)(a 得t f x f dx dy ∂∂+∂∂=t x t t x t x F F f F f F F '''-''=⎪⎪⎭⎫ ⎝⎛''- [错因分析] 没有弄清函数的关系是问题所在. 一般来说, 三个未知量两个方程所反映的函数关系是其中两个变量是另一个变量的函数.从所求之结果dxdy可知,t y ,均是x 的一元函数. [正确解法]由),(t x f y =及0),,(=t y x F 确定出t y ,为x 的函数)(),(x t t x y y ==,将给定的两个方程的两边对x 求导,便有⎪⎪⎩⎪⎪⎨⎧='+'+'∂∂+'=0dx dt F dx dy F F dxdt t f f dx dy t y x x解之, 得=dx dy t y t x t t x f F F F f F f ''+'''-'' 例6.设),,(v u x f z =,22,y x v e u xy-==,且f 具有二阶连续的偏导数,求22xz∂∂,yx z∂∂∂2. [错解]vf x u f ye x f x z xy ∂∂+∂∂+∂∂=∂∂2 22xz ∂∂⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=v f x x u f ye x x f x xy 2x v f x v f x u f ye u f e y xf xy xy ∂∂∂+∂∂+∂∂∂+∂∂+∂∂=2222222y x z ∂∂∂2⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=v f x y u f ye y x f y xy 2 yv f x v f y u f ye u f xye u f e y x f xy xy xy ∂∂∂+∂∂+∂∂∂+∂∂+∂∂+∂∂∂=22222 [错因分析]在求二阶偏导数时,把vfu f x f ∂∂∂∂∂∂,,仅仅看作是x 或y 的函数是不妥当的,事实上它们仍然是以v u x ,,为中间变量, 以y x ,为自变量的函数. [正确解法]xz u xv yvfx u f ye x f x z xy ∂∂+∂∂+∂∂=∂∂222x z ∂∂⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂=v f x u f ye xf x xy 2+⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂+∂∂∂+∂∂+∂∂∂+∂∂∂+∂∂=v u f x u f ye xu f ye u f e y v x f x u x f ye x f xy xy xy xy 22222222222 ⎪⎪⎭⎫⎝⎛∂∂+∂∂∂+∂∂∂+∂∂2222222v f x u v f ye x v f x v f xy +∂∂∂+∂∂∂+∂∂∂+∂∂+∂∂+∂∂=u v f xye x v f x x u f ye vf x u f e y x f xy xy xy 2222222222224424 vfu f e y xy∂∂+∂∂22 y x z ∂∂∂2⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂=v f x u f ye x f y xy 2 +∂∂+∂∂+∂∂∂-∂∂∂+⋅∂∂=u f xye u f e v x f y u x f xe xf xy xy xy 222220+⎪⎪⎭⎫ ⎝⎛∂∂∂-∂∂+⋅∂∂∂v u f y u f xe x u f ye xy xy222220 ⎪⎪⎭⎫⎝⎛∂∂-∂∂∂+⋅∂∂∂2222202v f y u v f xe x v f x xy +∂∂+∂∂++∂∂∂-∂∂∂=22222)1(2u f xye u f xy e v x f y u x f xe xy xy xy222224)(2vf xy u v f e y x xy ∂∂-∂∂∂- 三、综合题型分析 例7.证明极限2200limyx xyy x +→→不存在.[分析] 为了证明二元函数),(y x f 在点),(00y x 处极限不存在,只需找出两条不同的路径1L 和2L ,使点),(y x 在定义域D 内沿1L 和2L 趋向于点),(00y x 时),(y x f 趋向于两个不同数值;或找出一条路径L ,使点),(y x 在定义域D 内沿L 趋向于点),(00y x 时),(y x f 的极限不存在.[证明] 因沿1L :0,0=≠y x ,有022=+yx xy,而沿2L :x y x =≠,0,有2122=+y x xy ,故2200limyx xyy x +→→不存在. 例8.分别讨论下列函数在其定义域中的连续性:(1) ⎪⎩⎪⎨⎧=≠+=).0,0(),(,0),0,0(),(,),(22y x y x y x xyy x f (2) ⎪⎩⎪⎨⎧=≠+=).0,0(),(,0),0,0(),(,),(222y x y x y x y x y x f[分析] 题设的两个函数都是二元分段函数,当)0,0(),(≠y x 时它们分别是由自变量x 与自变量y 的一元基本初等函数经过四则运算得到的函数,利用已知一元函数的连续性知它们在)0,0(),(≠y x 处连续,在)0,0(),(=y x 点是否连续,则需按二元函数连续性定义来判断. [解](1) ),(y x f 当)0,0(),(≠y x 时连续, 但2200lim y x xyy x +→→不存在,故),(y x f 在点)0,0(处不连续.(2) ),(y x f 当)0,0(),(≠y x 时连续, 且由||||21222y y y x y x ≤≤+ 以及0||lim 00=→→y y x )0,0(f =. 可得),(lim 0y x f y x →→)0,0(0f ==, 即),(y x f 在其定义域全平面上连续.[注] 本例（１）中的函数),(y x f 在点)0,0(处不连续, 但两个偏导数都存在且)0,0(x f '=0)0,0(='y f ;而函数||||),(y x y x f +=则是在点)0,0(处连续,但两个偏导数)0,0(x f '和)0,0(y f '都不存在. 这两个例子表明对多元函数而言,连续性与偏导数存在这二者是既不充分又不必要的条件.与一元函数的情况不大相同.例9.设,sin y x e u x-=则y x u ∂∂∂2在点)1,2(π的值为______________.[答案] 2)(eπ[分析一] =∂∂xuy y x e y x e x x 1)cos (sin --+-)sin cos 1(y x y x y e x -=-,将该式对y 求导得y x u ∂∂∂2)].(cos )(sin 1cos 1[222y xy x y x y x y y x ye x -----=- 令π1,2==y x 并代入上式,得223222)()2cos 22sin 22cos (ee y x u πππππππ=++-=∂∂∂-.[分析二]=∂∂yu )(cos 2y x y x e x --2)1,2(2)1,(=⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂=∂∂∂x y x u dx d xy uππ22)cos (=--=x x x xe dx d ππ =---==--22)sin cos )1([x x x x xe x x e ππππ2)(eπ. 例10． 求下列极限(1) 2243002332lim y xy x y x y x +--→→; (2) y x yx xy y x y x +++→→24300lim[解] (1)由于224223224332)31(33)(2223320yy x y y x x xy xy x yx +-+-+≤+--≤224232932322y x y y xx+=+≤ 因为00lim →→y x 0292=⎪⎭⎫ ⎝⎛+y x 故原极限等于零.(2)令x x y -=3,则)()()()(lim lim 33243330024300x x x x x x x x x x x x y x y x xy y x y x y x -+-+-+-=+++→→→→ 1)(lim 344300-=+--=→→x x o x x y x .又令x y =,则02lim lim 3540024300=++=+++→→→→x x x x y x y x xy y x y x y x故y x yx xy y x y x +++→→24300lim 不存在. [方法小结]二元函数的极限比一元函数的极限要复杂得多, 计算也更困难. 通常从以下三个方面考虑.(1)设法利用变换化为一元函数的极限;(2)掌握绝对值不等式的放缩技巧, 使用夹逼定理;(3)通过观察, 若能大致估计所求极限不存在, 可选择两条不同路径, 求出不同的极限值, 借以证明原式极限不存在.例11．设f 具有二阶连续偏导数, 求函数),(2xyy x f z =, 求y x z ∂∂∂2,22x z ∂∂.[分析]本题给出的函数没有具体的表达式,这类函数称为抽象函数, 求抽象函数的偏导数, 一定要明确中间变量,中间变量可分别设为ω,,v u 等. 一般来说,抽象函数的高阶偏导数采用如下记号较为简便不易出错,用记号321,,f f f '''分别表示函数f 对第一、第二、第三中间变量的偏导数(多个中间变量可类推).用312312,,f f f '''''' 分别表示函数f 对第一、第二中间变量，第二、第三中间变量，第三、第一中间变量的二阶偏导数. 另外需注意,一般而言,函数对中间变量的偏导数仍是中间变量的函数,从而也是自变量的复合函数, 故对它们求高阶偏导时重复使用复合函数求偏导法则. 本题采用后一记号.[解]x z ∂∂22122122f x y f xy x y f xy f '-'=⎪⎭⎫⎝⎛-'+⋅'=y x z ∂∂∂2⎪⎭⎫⎝⎛'-'∂∂=2212f x y f xy y ⎪⎭⎫⎝⎛''+''-⎪⎭⎫ ⎝⎛''+''+'-'=2221221211222111212f x f x x y f x f x xy f x f x 22312113221212f xy f y f y x f x f x ''-''+''+'-'= 22x z ∂∂⎪⎭⎫⎝⎛'-'∂∂=2212f x y f xy x⎪⎭⎫⎝⎛''-''-⎪⎭⎫ ⎝⎛''-''+'+'=2222121221123122222f x y f xy x y f x y f xy xy f x y f y 224212211222314422f xy f x y f y x f x y f y ''+''-''+'+'= 例12．设),,(x v u f z =, ),(y x u ϕ=,)(y v ψ=,求复合函数)),(),,((x y y x f z ψϕ=的偏导数x z∂∂与yz ∂∂. [解] 由复合函数求导法,得321f x f x f x z '+∂∂'+∂∂'=∂∂ψϕ,31f xf '+∂∂'=ϕ =∂∂yz dy d f y f ψϕ21'+∂∂')(21y f y f ψϕ''+∂∂'=. [注] 在本题的情况下, 记号xf∂∂的含意是不清楚的. ),,(x v u f 作为x v u ,,的三元函数求x x v u f ∂∂),,(与)),(),,((x y y x f ψϕ作为y x ,的二元函数求xx y y x f ∂∂)),(),,((ψϕ的含意是不同的.因此,这里应避免使用记号xf∂∂,若要使用它,则必须对其含意加以说明.若x f ∂∂表示),,(x v u f 对x 的偏导数,则该例中)),(),,((x y y x f z ψϕ=的偏导数xz ∂∂,yz∂∂也可表示为 )(,y v f y u f y z x f x u f x z ψϕϕ'∂∂+∂∂∂∂=∂∂∂∂+∂∂∂∂=∂∂. 应用复合函数求导法则应注意以下几点: ①复合函数对指定的自变量求偏导数∑=⨯=mi i 1量求偏导该中间变量对指定自变个中间变量求偏导数函数对第,其中m是中间变量的个数.原则上函数有几个中间变量,公式中就有几项.要分清中间变量与自变量,一定要注意对哪个自变量求导,对中间变量求导, 对中间变量求导不要漏项.有时公式中右端项的项数比中间变量个数少,那是因为有的中间变量与求偏导数的自变量无关,从而导数为零.如上例中yz ∂∂. ②复合函数求导公式中,函数对中间变量的偏导数仍然是中间变量的函数,如设),(v u f z =,),(y x u ϕ=,),(y x v ψ=, 则,xv f x u f x z ∂∂∂∂+∂∂∂∂=∂∂ψϕ 这里vfu f ∂∂∂∂,仍然是v u ,的函数,而),(y x u ϕ=,),(y x v ψ=. 于是,它们仍是y x ,的复合函数,求高阶偏导数时要注意这一点.例13. 设0),,,(2=--ωy z x y x F ,其中F 具有二阶连续偏导数, 且04≠'F , 求22y∂∂ω. [分析]隐函数求偏导数时,要弄清楚哪个是因变量, 哪个是自变量, 哪个是中间变量, 然后将方程两边对自变量求偏导, 再解相应的方程得出所出的偏导数. [解] 由所求结论可知ω是因变量, 又因只有一个方程, 可知z y x ,,均为自变量, 将方程0),,,(2=--ωy z x y x F )(a两边对y 求偏导, 有0)2()(4321=∂∂-'+-∂∂⋅'+'+∂∂'yy F z x y F F y x F ω )(b 由于z x ,与y 无关, 故0)(,0=-∂∂=∂∂z x yy x )(c 422F F y y ''+=∂∂ω)(d 将)(b 式的两边对y 求偏导, 得+∂∂-''+-∂∂⋅''+''+∂∂'')2()(24232221yy F z x y F F y x F ω0)2()2()()2(22444434241=∂∂-'+⎥⎦⎤⎢⎣⎡∂∂-''+-∂∂⋅''+''+∂∂''∂∂-y F y y F z x y F F y x F y y ωωω 将)(c ,)(d 代入上式并整理可得22y∂∂ω34224442242422)()(2)(2F F F F F F F F ''''+''''-'''+= 例14. 证明曲面0,=⎪⎭⎫ ⎝⎛----c z b y c z a x f 的切平面通过一定点. [分析]所谓定点就是三个坐标均为固定常数的点, 由题设考虑, 极有可能是以c b a ,,为坐标的点.[证明] 由方程0,=⎪⎭⎫⎝⎛----c z b y c z a x f 有,1,121c z f f cz f f y x -⋅'='-⋅'=')]()([)(1212b y f a x fc z f z -'+-'--='其切平面方程为0)()()()()()(22121=--'-+'----'+--'z Z c z f b y f a x y Y c z f x X c z f即0)])(())([()])(())([(21='-----+'-----f z Z b y y Y c z f z Z a x x X c z 显然, 当),,(),,(c b a Z Y X =时,上式恒成立,故所证命题成立.例15.设),(y x f z =在区域D 上有定义,若在D 中任一点处),(y x f 的一阶偏导数存在且有界, 则),(y x f 在D 上连续. [分析] 由函数连续的定义可知, 若能证明lim 0=∆→∆→∆z y x 或),(),(lim 00y x f y y x x f y x =∆+∆+→∆→∆即可证明),(y x f 在D 中任一点),(y x 处连续.[证明] 设),(y x 为D 中任一点, 则 ),(),(y x f y y x x f z -∆+∆+=∆)],(),([)],(),([y x f y y x f y y x f y y x x f -∆++∆+-∆+∆+= )(a 由于),(),,(y x f y x f y x ''存在, 依据拉氏定理有=∆+-∆+∆+),(),(y y x f y y x x f x y y f x ∆∆+'),(ξ )(b =-∆+),(),(y x f y y x f y x f y ∆'),(η )(c其中ηξ,分别在x 与x x ∆+,y 与y y ∆+之间.又因),(),,(y x f y x f y x ''在D 中有界, 故∃一个0>M , 使得M y y f x ≤∆+'),(ξ, M x f y ≤'),(η )(d利用)(),(),(),(d c b a 式, 有)(y x M z ∆+∆≤∆于是 0000lim lim 0→∆→∆→∆→∆≤∆≤y x y x z 0)(=∆+∆y x M故lim 00=∆→∆→∆z y x即),(y x f 在点),(y x 处连续. 由于),(y x 在D 中的任一点处, 因而可知原结论成立.例16.求由方程010422222=--+-++z y x z y x 确定的函数),(y x f z =的极值.[解法一] 将方程010422222=--+-++z y x z y x 的两边分别对y x ,求偏导, 得⎩⎨⎧='-+'+='--'+0422204222y y x x z z z y z z z x )(a 由函数极值的必要条件知0,0='='y x z z ,将其代入)(a 得, 1,1-==y x 即得驻点)1,1(-P .由)(a 的两个方程分别对y x ,求偏导, 得zz A Pxx-=''=21)(b 0=''=Pxyz Bzz C Pyy-=''=21因为 0)2(1022<--=-z AC B )2(≠z故)1,1(-=f z 为极值.将1,1-==y x 代入方程010422222=--+-++z y x z y x ,得6,221=-=z z将21-=z 代入)(b 中可知041>=A故2)1,1(-=-=f z 为极小值.将61=z 代入)(b 中可知041<-=A 故6)1,1(=-=f z 为极大值. [解法二] 配方法.方程010422222=--+-++z y x z y x 可变形为16)2()1()1(222=-+++-z y x22)1()1(162+---±=-y x z显然, 当1,1-==y x 时, 根号中的极大值为4, 由此可知, 42±=z 为极值. 即6=z 为极大值, 2-=z 为极小值.例17.当0,0,0>>>z y x 时, 求函数z y x u ln 3ln 2ln ++=在球面22226r z y x =++上的最大值, 并证明对任意的正实数c b a ,,成立不等式6326108⎪⎭⎫⎝⎛++≤c b a c ab[解] 令λ+++=z y x z y x F ln 3ln 2ln ),,()6(2222r z y x -++有⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-++=+='=+='=+=')4(06)3(023)2(022)1(0212222r z y x z z F y y F x x F z yx λλλ由)3(),2(),1(, 得22223,2x z x y ==代入)4(,得 r z r y r x 3,2,===及)3,2,(r r r P可知最大值为)36ln()3ln(3)2ln(2ln 6)3,2,(r r r r u r r r =++=即 ≤++z y x ln 3ln 2ln )36ln(6r亦即 63236r z xy ≤或 622226426)36(⎪⎪⎭⎫⎝⎛++≤z y x z y x 令c z b y a x ===222,,, 于是6326108⎪⎭⎫⎝⎛++≤c b a c ab例18.设方程x y e xy cos 2=+确定y 为x 的函数, 则dxdy=_______ [答案]yxe xye xy xy 2sin ++-[解法一] 设=),(y x F x y e xy cos 2-+,x ye F xy x sin +=', y xe F xy y 2+='由公式y x F F dx dy ''-=,得=dx dy yxe xye xy xy 2sin ++- [解法二] )(x y y =, 方程两端对x 求导, 得x y y y x y e xy sin 2)(-='+'+,解得yxe x ye y xyxy 2sin ++-=' 四、考研试题分析例19.(1991年数学一、二)由方程2222=+++z y x xyz 所确定的函数),(y x z z =在点)1,0,1(-处的全微分=dz __________ [答案]dy dx 2-[分析]本题是隐函数全微分的题. 有两种方法:其一是对方程两边求全微分,解出dz , 另一种方法是先求出yz x z ∂∂∂∂,.再利用全微分公式dy y zdx x z dz ∂∂+∂∂= . [解法一] 对方程两边求全微分可得+++xydz xzdy yzdx 0222=++++zy x zdz ydy xdx将1,0,1-===z y x 代入上式可得0)(21=-+-dz dx dy由此得到dy dx dz 2-=[解法二] 设=),,(z y x F 2222-+++z y x xyzx F '=222zy x x yz +++ ; y F '=222zy x y xz +++;z F '=222zy x z xy +++222222z y x xy z z y x yz x F F x zz x ++++++-=''-=∂∂;222222zy x xy z z y x xz y F F y z z y ++++++-=''-=∂∂=dz dx zy x xy z z y x yz x 222222++++++-dy zy x xy z z y x xz y 222222++++++-将1,0,1-===z y x 代入上式可得dy dx dz 2-=例20.(1998年数学一)设)()(1y x y xy f xz ++=ϕ,ϕ,f 具有二阶连续导数, 则y x z ∂∂∂2=__________.[答案])()()(y x y y x xy f y +''++'+''ϕϕ[分析]这是一道基本运算题, 求复合函数的导数. 依题意ϕ,f 是一元函数.[解答])()(1)(12y x y y xy f x xy f xx z +'+'+-=∂∂ϕ; )()()()(1)(122y x y y x x xy f x yxy f x x xy f xy x z +''++'+''+'+'-=∂∂∂ϕϕ )()()(y x y y x xy f y +''++'+''=ϕϕ[点评]本题中的)(),(y x xy f +ϕ,其中间变量均是一元, 如果考生误认为中间变量是二元,将出现y x y x f f ϕϕ'''',,,等记号,从而无法化简导致错误.)()()()(xy f y xy x xy f xy f x '=∂∂'=∂∂, )()()()(xy f x xy yxy f xy f y '=∂∂'=∂∂. 都是用)(xy f '表示,而不能将前一式写成)()(xy f y xy f xx '=∂∂, 后一式写成)()(xy f x xy f yy '=∂∂. 对于)(y x x +∂∂ϕ亦如此, )()(y x y x x+'=+∂∂ϕϕ. 而2000年数学一第四题设)(),(xyg y x xy f z +=,其中f 具有二阶连续偏导数,g 具有二阶连续导数, 求yx z ∂∂∂2. 这个题目从题设条件中就可看出),(y x xy f ,)(x yg 的不同,前者二个中间变量,后者一个中间变量,要区别开.g xyf y f y x z '-'+'=∂∂2211g xyg x f y x f x y f y f y x f x y f y x z ''-'-''-''+'-''-''+'=∂∂∂32222212212211121)(11)( g x yg x f y x f xy f y f ''-'-''-''+'-'=322231122111 例21.（2001年数学一）设函数),(y x f z =在点)1,1(处可微, ,1)1,1(=f3,2)1,1()1,1(=∂∂=∂∂yz xz,)),(,()(x x f x f x =ϕ, 求13)(=x x dx d ϕ [分析]求全导数,应用多元复合函数求全导数的法则求之. 关键是弄清复合函数的复合关系.如果)),(,()),(,()(21x x f x f x x f x f x '+'='ϕ,就少复合了一次. [解]1)1,1())1,1(,1()1(===f f f ϕ.)),(,()(3)()(3)(223x x f x f dxdx x dx d x x dx d ϕϕϕϕ== ))],(),())(,(,()),(,()[(321212x x f x x f x x f x f x x f x f x '+''+'=ϕ取1=x ,由于3)1,1()1,1(,2)1,1()1,1(21='='='='y x f f f f ,故13)(=x x dx d ϕ=51))32(32(3))]1,1()1,1()(1,1()1,1()[1(3=++='+''+'y x y x f f f f ϕ. 例22.(2002年数学一)考虑二元函数),(y x f 的下面4条性质:①),(y x f 在点),(00y x 处连续,②),(y x f 在点),(00y x 处的两个偏导数连续,③),(y x f 在点),(00y x 处可微,④),(y x f 在点),(00y x 处的两个偏导数存在.若用""Q P ⇒表示可由性质P 推出性质Q ,则有( ) (A) ②⇒③⇒①; (B) ③⇒②⇒①; (C) ③⇒④⇒①; (D) ③⇒①⇒④. [答案](A)[分析]本题考查下面因果关系的认知:①② ③④记住上述因果关系,不难看出应选(A).如果误认为偏导数存在必然为连续函数, 就有④⇒①,就选择了(C).错误在于把一元函数的情形搬到二元函数中来了. 例23.(2001年数学二)设函数)(x f y =由方程1)cos(2-=-+e xy e y x 所确定,则曲线)(x f y =在点)1,0(处的法线方程为__________. [答案]022=+-y x[分析]本题考查隐函数求导和曲线的法线方程,本题应注意的是求法线方程而不是切线方程.[解法一]方程两边对x 求导,得0)sin()()2(2='++'++xy y x y e y y x解得 )sin()sin(222xy x e xy y e dx dy yx y x ++-=++, 所以2)1,0(-=dx dy因此法线的斜率为21,法线方程为022=+-y x . [解法二]设),(y x F 1)cos(2+--=+e xy e y x)sin(22xy y e F y x x +='+, )sin(2xy x e F y x y +='+)sin()sin(222xy x e xy y e F F dx dy yx y x y x ++-=''-=++, 则2)1,0(-=dx dy因此法线的斜率为21,法线方程为022=+-y x . 例24.(1994年数学二)在椭圆4422=+y x 上求一点, 使其到直线0632=-+y x 的距离最短.[分析]点),(y x 到直线0632=-+y x 的距离|632|131-+=y x d ,因此问题变成了求函数d 在限制条件4422=+y x 下的极值问题.[解]问题可以转化成求函数=),(y x f 2)632(-+y x ,在限制条件4422=+y x 下的极值问题, 构造拉格朗日函数),,(λy x L =2)632(-+y x )44(22-++y x λ那么02)632(4=+-+=∂∂x y x xLλ08)632(6=+-+=∂∂y y x yLλ 04422=-+=∂∂y x Lλ消去λ, 解得53,58;53,582211-=-===y x y x ,于是,1311,131),(),(2211==y x y x dd由问题的实际意义知最短距离是存在的, 因此⎪⎭⎫⎝⎛53,58即为所求的点.例25.(2002年数学一)设有一小山, 取它的底面所在的平面为xoy 坐标面, 其底部所占的区域为}75|),{(22≤-+=xy y x y x D ,小山的高度函数为xy y x y x h +--=2275),(.(1)设),(00y x M 为区域D 上一点, 问),(y x h 在该点沿平面上什么方向的方向导数最大?若记此方向导数的最大值为),(00y x g ,试写出),(00y x g 的表达式.(2)现欲利用此小山开展攀岩活动, 为此需要在山脚寻找一上山坡度最大的点作为攀登的起点, 也就是说, 要在D 的边界线7522=-+xy y x 上找出使(1)中的),(y x g 达到最大值的点, 试确定攀登起点的位置. [分析和解法一](1)高度函数),(y x h 在点),(00y x M 处的梯度是j y x i x y y x gradh y x )2()2(),(0000),(0-+-=由梯度的几何意义知, 沿此梯度方向, 高度函数),(y x h 的方向导数取最大值, 并且这个最大值就是此梯度的模, 于是),(00y x g 200200)2()2(y x x y -+-=002020855y x y x -+=(2) 令),(),(2y x g y x f =xy y x 85522-+=,依题意, 只需求二元函数),(y x f 在约束条件7522=-+xy y x 下的最大值点.令),,(λy x L xy y x 85522-+=)75(22--++xy y x λ, 则,0)2(810=-+-='y x y x L xλ ,0)2(810=-+-='x y x y L y λ='λL 07522=--+xy y x 消去λ, 解得35,35;35,35;5,5;5,544332211-=-====-=-==y x y x y x y x , 于是得到4个可能的极值点)35,35(),35,35(),5,5(),5,5(4321----M M M M 又150)()(;450)()(4321====M f M f M f M f .故)5,5(),5,5(21--M M 可以作为攀登起点. [分析和解法二]把山看作曲面, 山岗某一处坡度的大小就是曲面在该处的切平面与水平面的夹角的大小, 也就是切平面的法线与z 轴的夹角(锐角的那个)的大小. 山曲面z ),(y x h =在点),(y x M 处的切平面法向量是}1,,{y x h h '', 设它与z 轴的夹角(锐角的那个)为θ,那么.8551)2()2(1)()(11cos 222222xyy x y x x y h h y x -+=-+-='+'+=θ由此可见, 为了要在D 的边界线7522=-+xy y x 上找出使θ最大, 只要θcos 最小, 也只要二元函数xy y x 85522-+在条件7522=-+xy y x 下找最大值.以下同解法一.例26.(1994年数学四)某养殖场饲养两种鱼, 若甲种鱼放养x (万尾), 乙种鱼放养y (万尾), 收获时两种鱼的收获量分别为x y x )3(βα--和)0()24(>>--βααβy y x , 求使产鱼总量最大的放养数.[解] 设总产量为z , 则z =xy y x y x βαα224322---+,由极值的必要条件,得方程组0223=--=∂∂y x xzβα0244=--=∂∂x x yzβα 0>>βα, 方程组的唯一解)2(234,223220220βαβαβαβα--=--=y x .记α222-=∂∂=x z A , ,22β-=∂∂∂=y x z B ,422α-=∂∂=yzC 有0,0)2(4222<<--=-A AC B βα, 因此z 在),(00y x 处有极大值. 又由问题的实际意义,知最大值是存在的, 所以z ),(00y x 即最大值.易验证0,000>>y x ,且⎪⎩⎪⎨⎧>=-->=--.02)24(,023)3(00000000y y y x x x y x αββα 综上所述, 0x 和0y 分别为所求甲和乙两种鱼的放养数. 例27.(2005年数学四)设二元函数),1ln()1(y x xe z y x +++=+则._________)0,1(=dz [答案]dy e edx )2(2++[分析]利用二元函数的全微分公式dy y z dx x z dz ∂∂+∂∂=,再在yzx z ∂∂∂∂,中以 0,1==y x 代入.[解]应用二元复合函数求偏导数法则得)1ln(y xe e xzy x y x +++=∂∂++, yx xe y z y x +++=∂∂+11, 所以 dx y xe e dz y x y x )]1ln([+++=+++dy y x xe y x ⎥⎦⎤⎢⎣⎡++++11, 以0,1==y x 代入得dy e edx dz )2(2)0,1(++=. 例28.(2005年数学四)设)(u f 具有二阶连续偏导数, 且⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=y x yf x y f y x g ),(,求y x g y x g x ∂∂∂-∂∂22222. [解]利用复合函数偏导数的链锁法则,可得⎪⎪⎭⎫ ⎝⎛'+⎪⎭⎫⎝⎛'-=∂∂y x f x y f x y x g 2, =∂∂22x g ⎪⎪⎭⎫ ⎝⎛''+⎪⎭⎫ ⎝⎛''+⎪⎭⎫ ⎝⎛'y x f y x y f x y x y f x y 12423 ,1⎪⎪⎭⎫ ⎝⎛'-⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛'=∂∂y x f y x y x f x y f x y g =∂∂22y g ⎪⎪⎭⎫ ⎝⎛''+⎪⎪⎭⎫ ⎝⎛'+⎪⎪⎭⎫ ⎝⎛'-⎪⎭⎫ ⎝⎛''y x f y xy x f y x y x f y x x y f x 322221 ⎪⎪⎭⎫ ⎝⎛''+⎪⎭⎫ ⎝⎛''=y x f y xx y f x 3221于是y x g y x g x ∂∂∂-∂∂22222=⎪⎪⎭⎫ ⎝⎛''+⎪⎭⎫ ⎝⎛''+⎪⎭⎫ ⎝⎛'y x f y x x y f x y x y f x y 2222⎪⎪⎭⎫ ⎝⎛''-⎪⎭⎫ ⎝⎛''-y x f y x x y f x y 222 ⎪⎭⎫⎝⎛'=x y f x y 2. 例29.(2004年数学三)函数),(v u f 由关系式)(]),([y g x y y xg f +=确定, 其中函数)(y g 可微, 且0)(≠y g , 则vu f∂∂∂2=______________.[答案] []2)()(v g v g '-[分析]第一种解法可令⎩⎨⎧==,,)(v y u y xg 解出),,(),,(v u y y v u x x ==代入)(]),([y g x y y xg f +=以求出),(v u f ,再计算所求的偏导数.第二种解法是,在题给的等式两边求偏导, 使出现待求的vu f∂∂∂2,从而解之.[解法一]令⎩⎨⎧==,,)(v y u y xg 即⎪⎩⎪⎨⎧==,,)(v y y g u x )(a 代入原式得)()(),(v g v g uv u f +=, 两边对u 求偏导得,)(1v g u f =∂∂ 两边对v 求偏导得[]22)()(v g v g v u f '-=∂∂∂. [解法二]在等式)(]),([y g x y y xg f +=两边对x 求偏导2次, 得,0)]([,1)(2=''=⋅'y g f y g f uuu 但按已知, 0)(≠y g , 所以0=''uuf . 在等式1)(=⋅'yg f u 两边对y 求偏导, 得0)(])([)(=''+'''+'⋅'y g f y g x f y g f uv uuu 以0=''uuf 代入, 并解出uv f ''得 )()()()(2y g y g f y g y g f u uv'-='⋅'-='', 其中v u y x ,,,满足方程组)(a , 从而)()(2v g v g f uv'-='' 例30.(2003年数学三)设),(v u f 具有二阶连续偏导数, 且满足,12222=∂∂+∂∂v fu f 又)](21,[),(22y x xy f y x g -=, 求2222yf x f ∂∂+∂∂.[分析]利用求偏导数的链锁法则求二元复合函数的偏导数.[解],vf x u f y xg ∂∂+∂∂=∂∂.vf y u f x yg ∂∂-∂∂=∂∂ vf v f x v u f xy u f y xg ∂∂+∂∂+∂∂∂+∂∂=∂∂2222222222.v f vf y v u f xy u f x yg ∂∂-∂∂+∂∂∂-∂∂=∂∂2222222222. 22x g ∂∂22yg ∂∂+22222222)()(v f y x u f y x ∂∂++∂∂+=22y x +=. 例31.(2003年数学一)已知函数),(y x f 在点(0,0)的某个邻域内连续, 且1)(),(lim22200=+-→→y x xyy x f y x , 则(A)点(0,0)不是),(y x f 的极值点. (B)点(0,0)是),(y x f 的极大值点.(C)点(0,0)是),(y x f 的极小值点.(D)根据所给条件无法判断点(0,0)是否为),(y x f 的极值点. [答案](A)[解]由),(y x f 在点(0,0)的连续性及1)(),(lim22200=+-→→y x xyy x f y x知0)0,0(=f .且α+=+-1)(),(222y x xyy x f ,其中0lim 00=→→αy x 则222222)()(),(y x y x xy y x f ++++=α令x y =, 得)(44),(22442x o x x x x x x f +=++=α令x y -=, 得)(44),(22442x o x x x x x x f +-=++-=-α从而),(y x f 在(0,0)点的邻域内始终可正可负, 又0)0,0(=f , 由极值定义可知),(y x f 在点(0,0)没有极值,故应选(A). 例32.(2004年数学一)设),(y x z z =是由方程0182106222=+--+-z yz y xy x 确定的函数,求),(y x z z =的极值点极值.[分析]是求二元函数的极值问题. 应用隐函数求偏导法则求两个偏导数,并求出函数的驻点.再求二阶偏导数, 判断是否为极值点. [解法一]方程0182106222=+--+-z yz y xy x两边分别对y x ,求偏导得02262=∂∂-∂∂--xzz x z yy x )(a0222206=∂∂-∂∂--+-yz z y z yz y x )(b 令⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂00yz x z, 得⎩⎨⎧=-+-=-,0103,03z y x y x故 ⎩⎨⎧==,,3y z y x将上式代入0182106222=+--+-z yz y xy x , 可得⎪⎩⎪⎨⎧===3,3,9z y x 或⎪⎩⎪⎨⎧-=-=-=.3,3,9z y x 方程)(a 两边分别对y x ,求偏导得,0222222222=∂∂-⎪⎭⎫⎝⎛∂∂-∂∂-x z z x z x z y,02222622=∂∂∂-∂∂⋅∂∂-∂∂∂-∂∂--yx z z x z y z y x z y x z方程)(b 两边对y 求偏导得.022********22=∂∂-⎪⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂-∂∂-y zz y z y z y y z y z 所以,35,21,61)3,3,9(22)3,3,9(2)3,3,9(22=∂∂=-=∂∂∂==∂∂=yzC yx z B xzA故,03612<-=-AC B 又061>=A ,从而点(9,3)是),(y x z 的极小值点,极小值为 .3)3,9(=z 类似地, 由,35,21,61)3,3,9(22)3,3,9(2)3,3,9(22-=∂∂==∂∂∂=-=∂∂=---------yzC yx z B xzA可知,03612<-=-AC B 又061<-=A ,所以点)3,9(--是),(y x z 的极大值点,极大值为.3)3,9(-=--z[解法二]令182106),,(222+--+-=z yz y xy x z y x F 应用隐函数求偏导法则得zy y x z y y x F F x z z x +-=----=''-=∂∂32262zy zy x z y z y x F F y z z y +-+-=---+-=''-=∂∂103222206 由0,0=∂∂=∂∂yzx z 解得y z y x ==,3,与原式联立解得驻点为 )3,9(1P 与)3,9(2--P . 再求二阶导数,11)3()(1222P P x z y x z y z y xzA ⎥⎦⎤⎢⎣⎡∂∂--++=∂∂=,6124112=⋅=P y y 111)(3()(3)(122P P y z y x z y z y yx zB ⎥⎦⎤⎢⎣⎡∂∂+--+-+=∂∂∂=,21)6(4112-=-=P y y11)1)(103())(10()(1222P P y z z y x z y y z z y yzC ⎥⎦⎤⎢⎣⎡∂∂+-+--+∂∂-+=∂∂= ,35204112=⋅=P y y 于是,03612<-=-AC B 又061>=A ,从而点)3,9(1P 是),(y x z 的极小值点,极小值为.3)3,9(=z对于驻点2P ,类似地可求得,35,21,61-==-=C B A于是,03612<-=-AC B 又061<-=A ,从而)3,9(2--P 是),(y x z 的极大值点,极大值为.3)3,9(-=--z 例33.(2003数学一)曲面22y x z +=与平面042=-+z y x 平行的切平面方程是________.[答案] 542=-+z y x[分析]利用偏导数先求曲面的法向量, 使其与已知平面的法向量平行, 再求切点的坐标, 最后写出切平面的点法式方程.[解]令022=-+=z y x F , 则)1,2,2(-=y x n ,又已知平行的法向量为)1,4,2(1-=n ,由于1||n n ,所以 ,114222--==y x 由此解得切点的坐标为(1,2,5),所以切平面方程为0)5()2(4)1(2=---+-z y x ,化简得542=-+z y x .。

第一章 函数与极限函数和极限都是高等数学中最重要、最基本的概念，极值方法是最基本的方法，一切内容都将从这二者开始。

§1、 函 数一、集合、常量与变量1、集合：集合是具有某种特定性质的事物所组成的全体。

通常用大写字母A 、B 、C ……等来表示，组成集合的各个事物称为该集合的元素。

若事物a 是集合M 的一个元素，就记a ∈M （读a 属于M ）；若事物a 不是集合M 的一个元素，就记a ∉M 或a ∈M （读a 不属于M ）；集合有时也简称为集。

注 1：若一集合只有有限个元素，就称为有限集；否则称为无限集。

2：集合的表示方法：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧===+++======等。

中在点；为我校的学生；须有此性质。

如：中的元素必中，且，即：有此性质的必在所具有的某种性质合可表示为：，那么该集若知其元素有某种性质不到元素规律的集合，、列不出全体元素或找为全体偶数集；，，，然数集，为全体自，，，写出，如：元素的规律，也可类似、对无限集，若知道其；鸡一只猫，一只狗，一只的方法来表示，如：可用列举出其全体元素、若集合为有限集，就枚举法}),(),{(}{}0375{}{)(}642{}321{)(}{},10,,3,2,1{)(23D y x y x C x x B x x x x A A A x x A iii B A ii B A i ΛΛΛΛΛΛ 3：全体自然数集记为N,全体整数的集合记为Z,全体有理数的集合记为Q,全体实数的集合记为R 。

以后不特别说明的情况下考虑的集合均为数集。

4：集合间的基本关系：若集合A 的元素都是集合B 的元素，即若有A x ∈，必有B x ∈，就称A 为B 的子集，记为B A ⊂,或A B ⊃(读B 包含A)。

显然：R Q Z N ⊂⊂⊂.若B A ⊂,同时A B ⊂,就称A 、B 相等,记为A=B 。

5：当集合中的元素重复时,重复的元素只算一次.如：{1,2,2,3}={1,2,3}。

高等数学知识结构框架高等数学是大学数学的一门基础课程，它主要包括微积分和数学分析两个部分。

微积分主要研究函数、极限、导数、积分、微分方程等概念和方法；数学分析主要研究实数集、极限、连续性、一致连续性、可导性、不定积分、定积分、级数等概念和问题。

以下是高等数学中比较重要的知识结构框架及相关参考内容：一、函数与极限1. 函数的概念、基本初等函数以及函数的性质：韦达定理、复合函数、反函数等。

2. 极限的概念和性质：数列极限、函数极限、极限存在准则等。

3. 极限的计算方法：夹逼准则、单调有界数列的极限、洛必达法则等。

4. 无穷小量与无穷大量的定义与比较：无穷小量的阶、无穷大量的比较等。

二、导数与微分1. 导数的定义、性质和计算方法：导数的定义、导数的四则运算、高阶导数、隐函数与参数方程的导数等。

2. 函数的几何意义与微分中值定理：函数的单调性与极值点、罗尔中值定理、拉格朗日中值定理、柯西中值定理等。

3. 函数的图形与曲率：函数的图形、曲率、凹凸性与拐点。

三、不定积分与定积分1. 不定积分的定义与性质：原函数与不定积分的概念、基本积分表、换元积分法、分部积分法等。

2. 定积分的概念与性质：黎曼和与定积分的定义、定积分的性质、牛顿-莱布尼茨公式等。

3. 定积分的计算方法：变上限积分法、变量替换法、分段函数积分法等。

四、微分方程1. 常微分方程的基本概念与解法：一阶微分方程的基本概念、可分离变量方程、齐次方程、一阶线性非齐次方程等。

2. 高阶线性常微分方程的解法：二阶常系数齐次线性方程、二阶常系数非齐次线性方程、欧拉方程等。

五、级数1. 数列与级数：数列的极限、数列极限收敛性的准则、常数项级数、幂级数等。

2. 一致收敛性与函数级数：一致收敛性的概念、一致收敛级数的性质、Weierstrass判别法、Abel判别法、幂级数的收敛半径等。

以上是高等数学中较为重要的知识结构框架及相关参考内容，希望能为学习者提供一定的参考和指导。