专题:点电荷形成的电场中的场强和电势分布特点
- 格式:ppt
- 大小:2.45 MB
- 文档页数:24

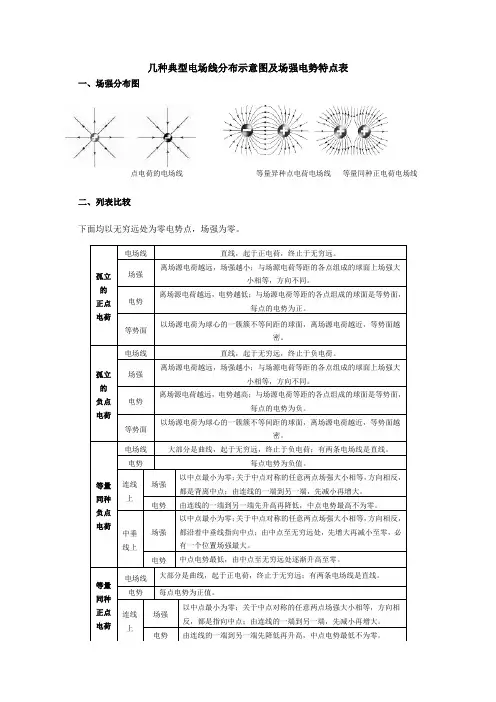
几种典型电场线分布示
意图及场强电势的特点
文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-MG129]
所示。
②等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示。
③等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示。
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示。
⑤形状不规则的带电导体附近的电场线及等势面,如图5所示。
注意:带方向的线表示电场线,无方向的线表示等势面。
图中的等势“面”画成了线,即以“线”代“面”。
所示。
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示。
⑤形状不规则的带电导体附近的电场线及等势面,如图5所示。
注意:带方向的线表示电场线,无方向的线表示等势面。
图中的等势“面”画成了线,即以“线”代“面”。

匀强电场等量异种点电荷的电场等量同种点电荷的电场 - - - - 点电荷与带电平+孤立点电荷周围的电场 几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷 电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的负点电荷 电场线 直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
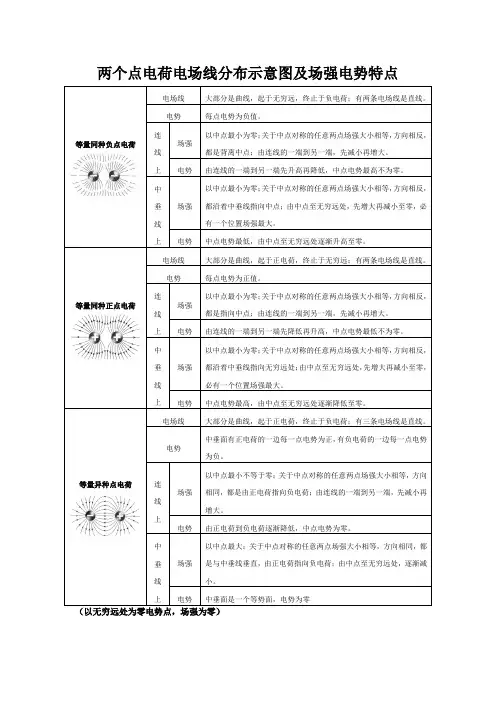
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量电场大部分是曲线,起于正电荷,终止于无穷远;有两条同种正点电荷线电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最高,由中点至无穷远处逐渐降低至零。
等量异种点电荷电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负。
连线上场强以中点最小不等于零;关于中点对称的任意两点场强大小相等,方向相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大。
电势由正电荷到负电荷逐渐降低,中点电势为零。
中垂线上场强以中点最大;关于中点对称的任意两点场强大小相等,方向相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小。
电势中垂面是一个等势面,电势为零(以无穷远处为零电势点,场强为零)(以无穷远处为零电势点,场强为零)注意:电场线、等势面的特点和电场线与等势面间的关系:①电场线的方向为该点的场强方向,电场线的疏密表示场强的大小。

关于等量点电荷周围场强和电势的分布特点作者:田军来源:《试题与研究·教学论坛》2017年第24期等量点电荷在空间的场强分布比较复杂,但在两条线(点电荷连线及其中垂线)上仍有其规律性,为研究方便,设它们带电量为Q,两电荷连线AB长度为L,中点为O。
一、等量的同种电荷形成的电场的特点1.场强特点①两点电荷连线上:任取一点P,设AP长度为x,则P点场强EP为两点电荷在该点的场强EA、EB的矢量和,方向沿AB连线,O点左侧从A指向B,右侧从B指向A(沿两电荷连线指向较远一侧电荷,若两电荷为等量负电荷则反之)。
P点电场强度大小知:EP=,∴当x=时,EP=0,即在两电荷连线中点O处场强最小,从O点向两侧逐渐增大,数值关于O点对称,方向相反。
②两点电荷连线的中垂线上:在O点两侧,电场强度方向均沿中垂线方向从O点指向无限远(若两电荷为等量负电荷则反之),由极限分析法易得:在O点处,E=0;在距O点无限远处,E=0。
说明中间某位置有极大值,可见:合电场强度的大小随着距O点的距离增大,先从零增大到最大,然后逐渐减小。
在中垂线上,任取一点P,设OP=x,由点电荷场强公式,P 点场强EP=2EAcosθ==运用数学方法,令y=,求导可得:y=令y′=0,则x2+2=3x2x2+2,即x2+2=3x2,∴当x=±L时,EP有最大值,∴从中点沿中垂线向两侧,电场强度的数值先增大后减小,两侧方向相反,关于O点对称的点数值相等。
2.电势特点①中点O点处的电势:φO=φA+φB=4>0②两点电荷连线上任意一点P处的电势:总结:在两个等量正电荷的连线上,由A点向B点方向,电势先减后增,在rA=R/2(即中点O处)电势最小,但电势总为正。
③两点电荷连线的中垂线上任意一点Q处的电势:总结:在两个等量正电荷的连线的中垂线上,由O点向N(M)点方向,电势一直减小且大于零,即O点最大,N(M)点为零。
二、等量的异种电荷形成的电场的特点1.场强特点①两电荷连线上任取一点G,设AG长度为x,则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和,方向从A指向B(由正电荷指向负电荷一侧),由点电荷场强公式知:∵x+(L-x)等于定值L,∴当x=(L-x),即x=时,x与(L-x)乘积最大,EG有最小值,即在两电荷连线中点O处场强最小,从O点向两侧逐渐增大,数值关于O点对称。

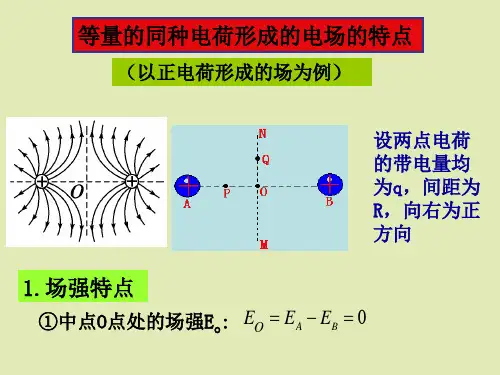
等量的点电荷形成的电场中的场强和电势特点一. 等量的同种电荷形成的电场的特点(以正电荷形成的场为例)设两点电荷的带电量均为q,间距为R,向右为正方向1.场强特点:在两个等量正电荷的连线上,由A点向B点方向,电场强度的大小先减后增,即中点O处, 场强最小为0;场强的方向先向右再向左, 除中点O外,场强方向指向中点O在两个等量正电荷连线的中垂线上,由O点向N(M)点方向,电场强度的大小先增后减;场强的方向由O点指向N(M)。
外推等量的两个负电荷形成的场结论:在两个等量负电荷的连线上,由A点向B点方向,电场强度的大小先减后增,中点O处, 场强最小为零;场强的方向先向左再向右(除中点O外)。
在等量负电荷的连线的中垂线上,由O点向N(M)点方向,电场强度的大小先增后减,场强的方向由N(M)指向O点2.电势特点:在两个等量正电荷的连线上,由A点向B点方向,电势先减后增,中点O处, 电势最小,但电势总为正。
在两个等量正电荷的连线的中垂线上,由O点向N(M)点方向,电势一直减小且大于零,即O点最大,N(M)点为零外推等量的两个负电荷形成的场在两个等量负电荷连线上,由A点向B点方向,电势先增后减,在中点O处, 电势最大但电势总为负;在两个等量负电荷连线的中垂线上,由O点向N(M)点方向,电势一直增大且小于零,即O点最小,N(M)点为零二:等量的异种电荷形成的电场的特点1.场强特点在两个等量异种电荷的连线上,由A点向B点方向,电场强度的大小先减小后增大,中点O处场强最小;场强的方向指向负电荷在两个等量异种电荷的连线的中垂线上,由O点向N(M)点方向,电场强度的大小一直在减小;场强的方向平行于AB连线指向负电荷一端2.电势特点:在两个等量异种电荷的连线上,由A点向B点方向,电势一直在减小,中点O处电势为零,正电荷一侧为正势,负电荷一侧为负势。
等量异种电荷连线的中垂线上任意一点电势均为零即等量异种电荷的连线的中垂线(面)是零势线(面)库仑定律内容表述:真空中两个静止点电荷之间的相互作用力的大小跟两个点电荷的电荷量的乘积成正比,跟它们的距离的二次方成反比.作用力的方向在两个点电荷的连线上公式: 静电力常量:k = 9.0×109 N·m2/C2库仑定律适用条件:真空中,点电荷点电荷——理想化模型,实际上是不存在的.但只要带电体本身的大小跟它们之间的距离相比可以忽略,带电体就可以看作点电荷.并非是体积小就能当点电荷(理想化研究方法)启示与小结:可以看出,万有引力公式和库仑定律公式在表面上很相似,只有质量和电荷量的区别,体现了科学的一种对称美,它们的实质区别是:首先万有引力公式计算出的力只能是相互吸引的力,绝没有相排斥的力.其次,由计算结果看出,电子和质子间的万有引力比它们之间的静电引力小的很多,因此在研究微观带电粒子间的相互作用时,主要考虑静电力,万有引力虽然存在,但相比之下非常小,所以可忽略不计电场:是力的作用媒介:电荷之间的相互作用是通过特殊形式的物质——电场发生的,电荷的周围都存在电场,电场的物质性是客观存在的,具有物质的基本属性——质量和能量。
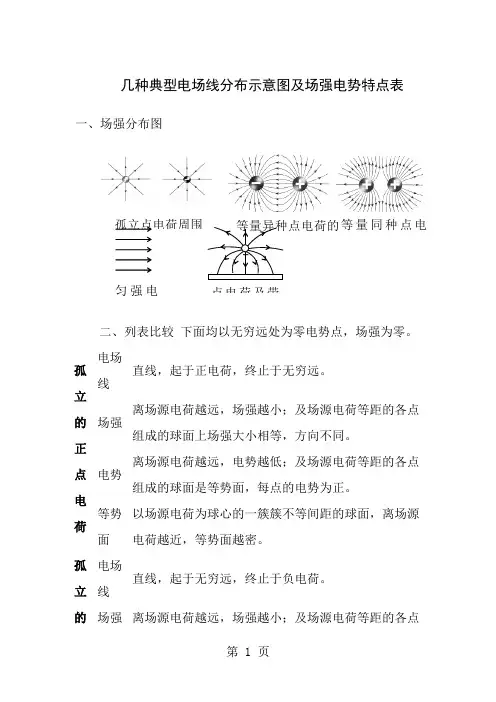
匀强电等量异种点电荷的等量同种点电- - - 点电荷及带+孤立点电荷周围 几种典型电场线分布示意图及场强电势特点表一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线直线,起于正电荷,终止于无穷远。
场强离场源电荷越远,场强越小;及场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;及场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 电场线直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;及场源电荷等距的各点负点电荷组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;及场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
种正点电荷连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。

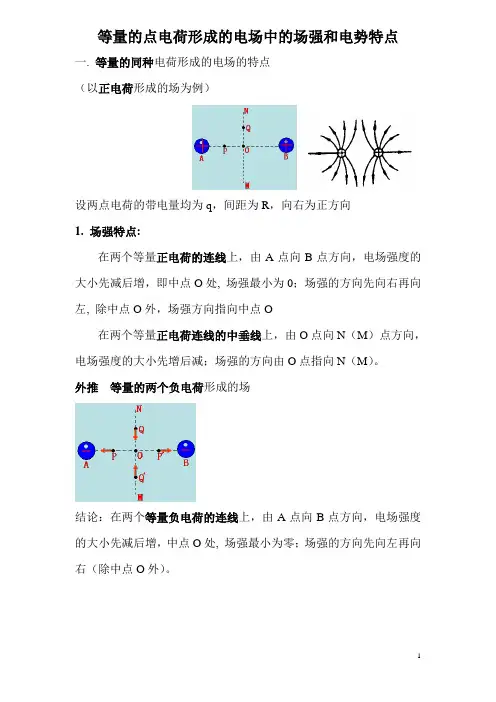
等量的点电荷形成的电场中的场强和电势特点一. 等量的同种电荷形成的电场的特点(以正电荷形成的场为例)设两点电荷的带电量均为q,间距为R,向右为正方向1.场强特点:在两个等量正电荷的连线上,由A点向B点方向,电场强度的大小先减后增,即中点O处, 场强最小为0;场强的方向先向右再向左, 除中点O外,场强方向指向中点O在两个等量正电荷连线的中垂线上,由O点向N(M)点方向,电场强度的大小先增后减;场强的方向由O点指向N(M)。
外推等量的两个负电荷形成的场结论:在两个等量负电荷的连线上,由A点向B点方向,电场强度的大小先减后增,中点O处, 场强最小为零;场强的方向先向左再向右(除中点O外)。
在等量负电荷的连线的中垂线上,由O点向N(M)点方向,电场强度的大小先增后减,场强的方向由N(M)指向O点2.电势特点:在两个等量正电荷的连线上,由A点向B点方向,电势先减后增,中点O处, 电势最小,但电势总为正。
在两个等量正电荷的连线的中垂线上,由O点向N(M)点方向,电势一直减小且大于零,即O点最大,N(M)点为零外推等量的两个负电荷形成的场在两个等量负电荷连线上,由A点向B点方向,电势先增后减,在中点O处, 电势最大但电势总为负;在两个等量负电荷连线的中垂线上,由O点向N(M)点方向,电势一直增大且小于零,即O点最小,N(M)点为零二:等量的异种电荷形成的电场的特点1.场强特点在两个等量异种电荷的连线上,由A点向B点方向,电场强度的大小先减小后增大,中点O处场强最小;场强的方向指向负电荷在两个等量异种电荷的连线的中垂线上,由O点向N(M)点方向,电场强度的大小一直在减小;场强的方向平行于AB连线指向负电荷一端2.电势特点:在两个等量异种电荷的连线上,由A点向B点方向,电势一直在减小,中点O处电势为零,正电荷一侧为正势,负电荷一侧为负势。
等量异种电荷连线的中垂线上任意一点电势均为零即等量异种电荷的连线的中垂线(面)是零势线(面)库仑定律内容表述:真空中两个静止点电荷之间的相互作用力的大小跟两个点电荷的电荷量的乘积成正比,跟它们的距离的二次方成反比.作用力的方向在两个点电荷的连线上公式: 静电力常量:k = 9.0×109 N·m2/C2库仑定律适用条件:真空中,点电荷点电荷——理想化模型,实际上是不存在的.但只要带电体本身的大小跟它们之间的距离相比可以忽略,带电体就可以看作点电荷.并非是体积小就能当点电荷(理想化研究方法)启示与小结:可以看出,万有引力公式和库仑定律公式在表面上很相似,只有质量和电荷量的区别,体现了科学的一种对称美,它们的实质区别是:首先万有引力公式计算出的力只能是相互吸引的力,绝没有相排斥的力.其次,由计算结果看出,电子和质子间的万有引力比它们之间的静电引力小的很多,因此在研究微观带电粒子间的相互作用时,主要考虑静电力,万有引力虽然存在,但相比之下非常小,所以可忽略不计电场:是力的作用媒介:电荷之间的相互作用是通过特殊形式的物质——电场发生的,电荷的周围都存在电场,电场的物质性是客观存在的,具有物质的基本属性——质量和能量。
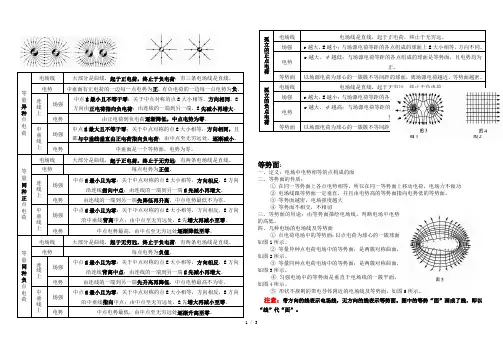
等势面:一、定义:电场中电势相等的点构成的面 二、等势面的性质:① 在同一等势面上各点电势相等,所以在同一等势面上移动电荷,电场力不做功 ② 电场线跟等势面一定垂直,并且由电势高的等势面指向电势低的等势面。
③ 等势面越密,电场强度越大 ④ 等势面不相交,不相切三、等势面的用途:由等势面描绘电场线,判断电场中电势的高低。
四、几种电场的电场线及等势面① 点电荷电场中的等势面:以点电荷为球心的一簇球面如图l 所示。
② 等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示。
③ 等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示。
④ 匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示。
⑤ 形状不规则的带电导体附近的电场线及等势面,如图5所示。
注意:带方向的线表示电场线,无方向的线表示等势面。
图中的等势“面”画成了线,即以“线”代“面”。
等 量 异 种 点 电 荷电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
电势 中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负。
连 线 上 场强 中点E 最小且不等于零;关于中点对称的点E 大小相等,方向相同,E 方向由正电荷指向负电荷;由连线的一端到另一端,E 先减小再增大。
电势 由正电荷到负电荷逐渐降低,中点电势为零。
中 垂 线 上场强 中点E 最大且不等于零;关于中点对称的点E 大小相等,方向相同,且都与中垂线垂直由正电荷指向负电荷;由中点至无穷远处,逐渐减小。
电势中垂面是一个等势面,电势为零。
等量 同 种 正 点 电 荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势 每点电势为正值。
连 线 上 场强 中点E 最小且为零;关于中点对称的点E 大小相等,方向相反,E 方向沿连线指向中点;由连线的一端到另一端E 先减小再增大。
电势 由连线的一端到另一端先降低再升高,中点电势最低不为零。
中 垂 线 上场强 中点E 最小且为零;关于中点对称的点E 大小相等,方向相反,E 方向沿中垂线背离中点;由中点至无穷远处,E 先增大再减小至零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最高,由中点至无穷远处逐渐降低至零。
等量异种点电荷电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负。
连线上场强以中点最小不等于零;关于中点对称的任意两点场强大小相等,方向相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大。
电势由正电荷到负电荷逐渐降低,中点电势为零。
中垂线上场强以中点最大;关于中点对称的任意两点场强大小相等,方向相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小。
电势中垂面是一个等势面,电势为零。
等势面(1)定义:电场中电势相等的点构成的面(2)等势面的性质:①在同一等势面上各点电势相等,所以在同一等势面上移动电荷,电场力不做功②电场线跟等势面一定垂直,并且由电势高的等势面指向电势低的等势面。
③等势面越密,电场强度越大④等势面不相交,不相切(3)等势面的用途:由等势面描绘电场线,判断电场中电势的高低。
(4)几种电场的电场线及等势面①点电荷电场中的等势面:以点电荷为球心的一簇球面如图l所示。
②等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示。
③等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示。
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示。
⑤形状不规则的带电导体附近的电场线及等势面,如图5所示。
注意:带方向的线表示电场线,无方向的线表示等势面。
图中的等势“面”画成了线,即以“线”代“面”。
常见电场电场线分布规律电场强度、电场线、电势部分基本规律总结整理:胡湛霏、几种常见电场线分布:二、 等量异种电荷电场分析1、 场强:① 在两点电荷连线上,有正电荷到负电荷,电场强度先减小后增大,中点 0的电场强度最小。
电场强度方向由正电荷指向负电荷; ② 两点电荷的连线的中垂线上,中点 0的场强最大,两侧场强依次减小。
各点电场强度方向相同。
2、 电势:① 由正电荷到负电荷电势逐渐降低;② 连线的中垂线所在的、并且与通过的所有电场线垂直的平面为一等势面; ③ 若规定无限远处电势为 0,则两点电荷连线的中垂线上各点电势即为0。
3、 电势能:(设带电粒子由正电荷一端移向负电荷一端)① 带电粒子带正电:电场力做正功,电势降低,电势能减少; ② 带电粒子带负点:电场力做负功,电势降低,电势能增加。
三、 等量同种电荷电场分析1、场强:① 两点电荷的连线上, 由点电荷起,电场强度越来越小, 到终点O 的电场强度 为0,再到另一点电荷,电场强度又越来越大;② 两点电荷连线的中垂线上, 由中点O 向两侧,电场强度越来越大,到达某一 点后电场强度又越来越小;③ 两点电荷(正)连线的中垂线上, 电场强度方向由中点 O 指向外侧,即平行 于中垂线。
2、电势:O 点电势最小,即由一个正点电荷到另一正点电荷电势先降低后升高O 点电势最大,即由一个负点电荷到另一负点电荷电势先增高后降低。
③ 其余各点电势由一般规律判断,顺着电场线方向电势逐渐降低。
连线的中垂线上, O 电电势最大,即 O 点两侧电势依次降低。
连线的中垂线上, O 点电势最小,即 O 点两侧电势依次升高①两正点电荷连线上,②两负点电荷连线上, 正点申摘奂点电%.. £3、电势能:①由电势判断:若带电粒子为正电荷,则电势越高,电势能越大;若带电粒子为负电荷,贝U 电势越高,电势能越小。
②由功能关系判断:若电场力做负功,则电势能增加;若电势能做正功,则电势能减少。
两个点电荷电场线分布示意图及场强电势特点大部分是曲线,起于无穷远,终止于负电荷;有 以中点最小为零;关于中点对称的任意两点场强 一端到另一端,先减小再增大。
最高不为零。
以中点最小为零;关于中点对称的任意两点场强 大小相等,方向相反,都沿着中垂线指向中点; 场强 由中点至无穷远处,先增大再减小至零,必有一 个位置场强最大。
中点电势最低,由中点至无穷远处逐渐升高至 电势 零。
大部分是曲线,起于正电荷,终止于无穷远;有 电场线 两条电场线是直线。
等量同种正点电场线 两条电场线是直线。
电势 每点电势为负值。
场强 大小相等,方向相反,都是背离中点;由连线的 等量同种负点电荷、、\\"山由连线的一端到另一端先升高再降低,中点电势 电势 电势 每点电势为正值。
场强 电势以中点最小为零;关于中点对称的任意两点场强 大小相等,方向相反,都是指向中点;由连线的 一端到另一端,先减小再增大。
由连线的一端到另一端先降低再升高,中点电势 电荷荷的一边每一点电势为负。
以中点最大;关于中点对称的任意两点场强大小指向负电荷:由中点至无穷远处,逐渐减小。
(以无穷远处为零电势点,场强为零)孤立点电荷电场线分布示意图及场强电势特点场强电势电场线电势最低不为零。
以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处:由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
中点电势最高,由中点至无穷远处逐渐降低至零。
大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
中垂面有正电荷的一边每一点电势为正,有负电等量异种点电以中点最小不等于零:关于中点对称的任意两点 场强 场强大小相等,方向相同,都是由正电荷指向负电势 电荷;由连线的一端到另一端,先减小再增大。
由正电荷到负电荷逐渐降低,中点电势为零。
场强 相等,方向相同,都是与中垂线垂直,由正电荷电势 中垂面是一个等势面,电势为零荷电场线直线,起于正电荷,终止于无穷远。
几种典型电场线散布表示图及场强电势特色表一、场强散布图孤立点电荷四周的电场等量异种点电荷的电场等量同种点电荷的电场+匀强电场----点电荷与带电平二、列表比较下边均以无量远处为零电势点,场强为零。
电场线直线,起于正电荷,停止于无量远。
孤立离场源电荷越远,场强越小;与场源电荷等距的各点构成的球面上场强盛小相等,方向不场强的同。
正点离场源电荷越远,电势越低;与场源电荷等距的各点构成的球面是等势面,每点的电势为电势电荷正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
电场线直线,起于无量远,停止于负电荷。
孤立离场源电荷越远,场强越小;与场源电荷等距的各点构成的球面上场强盛小相等,方向不场强的同。
负点离场源电荷越远,电势越高;与场源电荷等距的各点构成的球面是等势面,每点的电势为电势电荷负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
电场线大多数是曲线,起于无量远,停止于负电荷;有两条电场线是直线。
等量电势每点电势为负值。
同种连以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都是背叛中负点场强线点;由连线的一端到另一端,先减小再增大。
电荷上电势由连线的一端到另一端先高升再降低,中点电势最高不为零。
中以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都沿着中垂场强垂线指向中点;由中点至无量远处,先增大再减小至零,必有一个地点场强最大。
线中点电势最低,由中点至无量远处渐渐高升至零。
电势上电场线大多数是曲线,起于正电荷,停止于无量远;有两条电场线是直线。
电势每点电势为正当。
连以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都是指向中等量场强线点;由连线的一端到另一端,先减小再增大。
同种上电势由连线的一端到另一端先降低再高升,中点电势最低不为零。
正点中以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都沿着中垂电荷场强垂线指向无量远处;由中点至无量远处,先增大再减小至零,必有一个地点场强最大。
专题两个等量电荷形成电场的场强、电势的分布特点及应用1.(单选)如图1所示,在矩形ABCD的AB边和CD边中点M和N各放一个电荷,它们带等量正、负电荷.E、F是AD边和BC边中点,P、Q两点在MN连线上,MP=QN,则电场强度和电势都相同两点是().A E和FB.P和QC.A和DD.C和B2.(单选)如图2所示,一个电子沿等量异种电荷连线的中垂线由A→O→B匀速飞过,电子的重力不计,电子除了电场力以外,受到的另一个力的大小方向的变化情况为().A.先变大后变小,方向水平向左B 先变大后变小,方向水平向右C.先变小后变大,方向水平向左D.先变小后变大,方向水平向右3.(单选)两个带等量正电荷的点电荷,O为两电荷连线的中点,A点在中垂线上,若在A点由静止释放一个电子,如图3所示,关于电子的运动,正确的是().A.电子在从A向O点运动的过程中,加速度越来越大,速度越来越大B.电子在从A向O点运动的过程中,加速度越来越小,速度越来越大C 电子运动到O点时,加速度为零,速度最大D.电子通过O点后,速度越来越小,加速度越来越大,一直到速度为零4.(单选)如图4所示,有两个电量相等的正点电荷,它们连线的中点是O,C、D是中垂线上的两点,则C、D两点的场强和电势为().A.E D一定大于E C,φD一定大于φCB E D不一定大于E C,φD一定大于φCC.E D一定大于E C,φD不一定大于φCD.E D不一定大于E C,φD不一定大于φC5.(多选)如图5所示,在两等量异种点电荷的电场中,MN为两电荷连线的中垂线,a、b、c 三点所在直线平行于两电荷的连线,且a和c关于MN对称,b点位于MN上,d点位于两电荷的连线上.以下判断正确的是().A.b点场强大于d点场强B b点场强小于d点场强C a、b两点间的电势差等于b、c两点间的电势差D.试探电荷+q在a点的电势能小于在c点的电势能6.(多选)在光滑的绝缘水平面上,有一个正方形abcd,顶点a、c处分别固定一个正点电荷,电荷量相等,如图6所示.若将一个带负电的粒子置于b点,自由释放,粒子将沿着对角线bd往复运动.粒子从b点运动到d点的过程中().A 先做加速运动,后做减速运动B.先从高电势到低电势,后从低电势到高电势C.电势能与机械能之和先增大,后减小D 电势能先减小,后增大7.(2013·常州模拟试卷)(单选)如图7所示,以O为圆心的圆周上有六个等分点a、b、c、d、e、f.等量正、负点电荷分别放置在a、d两处时,在圆心O处产生的电场强度大小为E.现改变a处点电荷的位置,使O点的电场强度改变,下列叙述正确的是().A.移至c处,O处的电场强度大小不变,方向沿OeB.移至b处,O处的电场强度大小减半,方向沿OdC 移至e处,O处的电场强度大小减半,方向沿OcD.移至f处,O处的电场强度大小不变,方向沿Oe8.A、B为两个等量的正点电荷,在其连线中点放一个点电荷q(不计重力),若给该点电荷q一个初速度v方向与AB连线垂直,则该点电荷q可能的运动情况是()A.匀变速直线运动B 往复直线运动C.加速度不断减小,速度不断增大的直线运动D 加速度先增大后减小,速度不断增大的直线运动9.两个电荷量相等的正点电荷分别固定于a,b两点,将另一个正点电荷q沿着a,b连线的垂直平分线,从无限远处移到a,b连线的中点。
几种典型电场线分布示意图及场强电势特点 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】匀强电等量异种点电荷的电等量同种点电荷- - - 点电荷与带电+孤立点电荷周围的几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷 电场线直线,起于正电荷,终止于无穷远。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势 离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷 电场线直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势 离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等电场大部分是曲线,起于无穷远,终止于负电荷;有两条电场线量同种负点电荷线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
静电场中静电平衡时导体的电荷电场强度及电势分布特点下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!静电场中静电平衡时导体的电荷电场强度及电势分布特点静电场中,导体处于静电平衡时,其电荷分布和电场特性具有一些显著的特点。