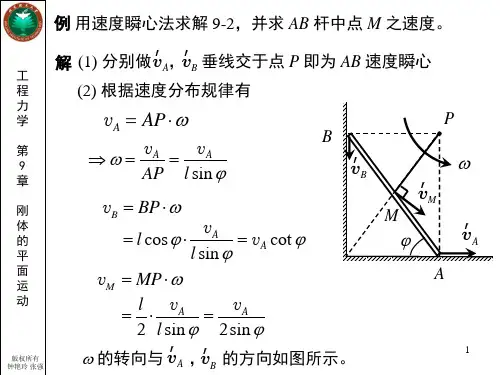
速度瞬心例题

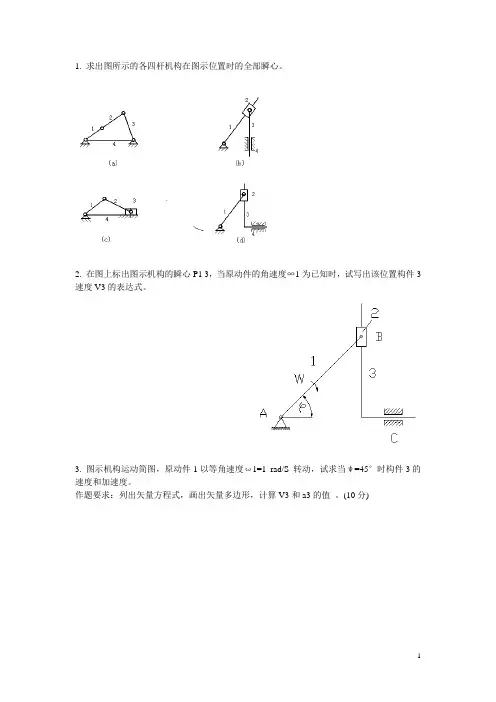
1. 求出图所示的各四杆机构在图示位置时的全部瞬心。

2. 在图上标出图示机构的瞬心P1 3，当原动件的角速度∞1为已知时，试写出该位置构件3速度V3的表达式。

3. 图示机构运动简图，原动件1以等角速度ω1=1 rad/S 转动，试求当ψ=45°时构件3的速度和加速度。

作题要求：列出矢量方程式，画出矢量多边形，计算V3和a3的值。

(10分)2题图3. 图示导杆机构的运动简图及速度多边形，已知原动件1以ω1=20rad/s逆时针等速转动，按下列要求作加速度分析：a的加速矢量方程式；1．写出求3Bp已画在图中）；2．画加速度多边形（''b3．计算构件3 的角加速度ε3的值，并将其方向标在图上。

4. 图示干草压缩机的机构运动简图（比例尺为μl）。

原动件曲柄1以等角速度ω1转动，试用矢量方程图解法求该位置活塞5的速度与加速度。

要求：1．写出C、E点速度与加速度的矢量方程式；2．画出速度与加速度矢量多边形（大小不按比例尺，但其方向与图对应）；3．据矢量多边形写出计算E点的速度V E与加速度a E的表达式。

（10分）5. 在图示机构中，原动件1以等角速度ω1转动。

试作： 1．写出B 3点的速度，加速度矢量方程式；2．在图上分别由Pb1表示（1B V ）、P ′b1′（表示2B a ）开始，画出速度，加速度多边形（法向加速度和哥氏加速度的工度任取）；3．写出构件3的角速度ω3、角加速度∝3的表达式。

6. 图示为转动导杆机构的运动简图，速度矢量图以及表示B 1点加速度的矢量1''b P 。

试作： 1．求角速度ω3的大小并指出方向；2．求相对速度V B3B2的大小并指出方向； 3．写出3B a 的矢量方向式； 4．完成加速度矢量图。

7. 图示铰链四杆机构，已知各杆尺寸及原动件角速度ω1。

试作：1b 2b 3b '1bm ms m a 2/01.0=μmmml 01.0=μm msm v /01.0=μ1ωϕ①写出点C 的速度V C 及加速度C a 的矢量方程式； ②画出速度矢量多边形（其大小随意，但方向必须正确）；8. 图示为机构运动简图及其相应的速度矢量图，用图中线段和比例尺符号写出哥氏加速度a k a4a3的表达式，并指出方向。

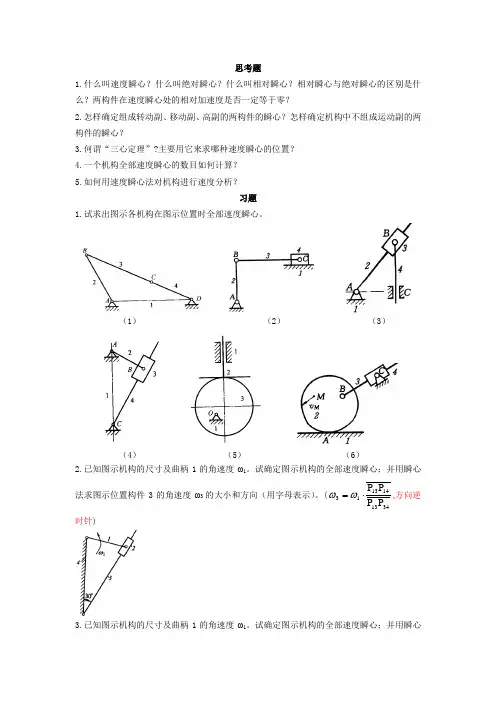
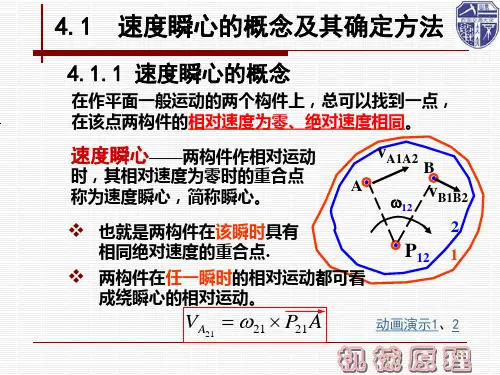
思考题1.什么叫速度瞬心？什么叫绝对瞬心？什么叫相对瞬心？相对瞬心与绝对瞬心的区别是什么？两构件在速度瞬心处的相对加速度是否一定等于零？2.怎样确定组成转动副、移动副、高副的两构件的瞬心？怎样确定机构中不组成运动副的两构件的瞬心？3.何谓“三心定理”?主要用它来求哪种速度瞬心的位置？4.一个机构全部速度瞬心的数目如何计算？5.如何用速度瞬心法对机构进行速度分析？习题1.试求出图示各机构在图示位置时全部速度瞬心。

（1） （2） （3）（4） （5） （6）2.已知图示机构的尺寸及曲柄1的角速度ω1。

试确定图示机构的全部速度瞬心；并用瞬心法求图示位置构件3的角速度ω3的大小和方向（用字母表示）。

(3413141313P P P P ⋅=ωω,方向逆时针)3.已知图示机构的尺寸及曲柄1的角速度ω1。

试确定图示机构的全部速度瞬心；并用瞬心法求图示位置滑块3的速度V 3及构件2的角速度ω2的大小和方向（用字母表示）。

(1413l 13P P ⨯⨯=μωv ,向右;2412141212P P P P ⋅=ωω,方向逆时针)4.如图凸轮机构，凸轮角速度ω1=10rad/s ，R=50mm ，L AO =20mm ，试求机构中的所有速度瞬心；并用瞬心法求当φ=0°、45°及90°时，构件2的速度v 大小及方向（需按尺寸重新画图求解）。

（φ=45°时，v 2=140mm/s ，向上）5.图示机构中，已知各构件尺寸及角速度ω2的大小和方向，试确定机构中所有速度瞬心，并用瞬心法求点D 、E 的速度V D 、V E 的大小和方向及构件4的角速度ω4的大小和方向。

(13231323122DP D l p p p p v ⋅=ω,垂直DP 13向左；24242FP AP ⋅⋅=ωEF E l v ，垂直CF 向左；ω4=ω2×AP 24/FP 24,方向逆时针)6.在图示的四杆机构中，已知AB l =65mm ，CD l =90mm ，AD BC l l ==125mm ，2ω=10/rad s ，试用瞬心法求:1)当165ϕ=︒时，点C 的速度C v ；（v C =441mm/s ）2)当165ϕ=︒时，构件3的BC 线上(或其延长线上)速度最小的一点E 的位置及其速度的大小；(v E =375mm/s )3)当C v 0=时，ϕ角之值(有两个解)。

精品文档习题>答案一.概念1.当两构件组成转动副时 ,其相对速度瞬心在转动副的圆心处; 组成移动副时 ,其瞬心在垂直于移动导路的无穷远处 ; 组成滑动兼滚动的高副时 ,其瞬心在接触点两轮廓线的公法线上 .2.相对瞬心与绝对瞬心相同点是都是两构件上相对速度为零 ,绝对速度相等的点 , 而不同点是相对瞬心的绝对速度不为零 ,而绝对瞬心的绝对速度为零 .3.速度影像的相似原理只能用于同一构件上的两点 ,而不能用于机构不同构件上的各点.4.速度瞬心可以定义为互相作平面相对运动的两构件上 ,相对速度为零 ,绝对速度相等的点 .5.3 个彼此作平面平行运动的构件共有 3 个速度瞬心 ,这几个瞬心必位于同一条直线上 . 含有 6 个构件的平面机构 ,其速度瞬心共有 15 个, 其中 5 个是绝对瞬心 ,有 9 个相对瞬心 .二.计算题1、2.关键 :找到瞬心 P36 6 Solution:The coordinates of joint B arey B =ABsinφ =0.20sin45°=0.141mx B =ABsinφ =0.20sin45°=0.141mThe vector diagram of the right Fig is drawn by representing the RTR (BBD) dyad. The vector equation, corresponding to this loop, is written asr B+r-r D=0 or r=r D-r BWhere r =BD and r=γ .When the above vectorial equation is projected on the x and y axes, two scalar equations are obtained:r*cos(3B=-0.141m φ+π )=x D-xr*sin(3B =-0.541m φ+π )=y D-yAngleφ3is obtained by solving the system of the two previous scalar equations:0.541tgφ= 0.141φ =75.36 °33The distance r isx D x Br=cos(3)=0.56mThe coordinates of joint C arex C3C=CDsin3=CDcos φ =0.17m yφ -AD=0.27mFor the next dyad RRT (CEE), the right Fig, one can write Cecos( π-φ4 )=x E - x C Cesin( -πφ4 )= y E - y C Vector diagram represent the RRT (CEE) dyad.When the system of equations is solved, the unknowns4Eφ =165.9°x=-0.114m7. Solution:The origin of the system is at A, A精品文档4and x E areφ obtained:≡0; that is,x A =y A =0.精品文档The coordinates of the R joints at B arex B =l 1 cos φ y B = l 1 sin φFor the dyad DBB (RTR), the following equations can be written with respect tothe sliding line CD:mx B - y B +n=0 y D =mx D +n1With x D =d, y D =0 from the above system, slope m of link CD and intercept n canbe calculated:l1 sin d1l1 sinm=l1cosd1n=d1l1 cosThe coordinates x C and y C of the center of the R joint C result from the system oftwo equations:l 1 sin d1l1 sinx Cy C =mx C +n=l1 cos d1d1l1 cos,222+(y C=l 3(x C - x D )- y D )Because of the quadratic equation, two solutions are abstained for x C and y C .For continuous motion of the mechanism, there are constraint relations for the Choice ofthe correct solution; that is x C < x B < x D and y C >0For the last dyad CEE (RRT), a position function can be written for joint E:222(x C -x E ) +(y C -h)=l 4The equation produces values for x E 1 and x E 2 , and the solution x E >x C is selected for continuous motion of the mechanism.。

利用瞬心法求解力学问题刘伟 （20040110911） 土木工程9班利用速度瞬心法解题，应着重注意以下几步：⑴ 分析刚体运动类型，尽是求出刚体上至少两点的速度方向。

⑵ 利用已知点的速度方向，确定速度瞬心位置。

⑶ 求出刚体绕瞬心转动的角速度，进而求出刚体上其它点的速度。

先看下面几个例题：例1，如图⑴中所示，平面四杆机构中，曲形连杆ABD 在A ，B 处，分别与曲柄OA 和杆O 1B 铰接，已知曲柄长r ，以匀角速度w 转动，两支座间的距离也是r ，BD ＝2r ，求在图示位置（OA 水平，O ，B ，D 共线且垂直），求点D 的速度。

解法⑴ 基点法：机构中的B O OA 1≠，AB OO ≠1，故杆ABD 不是作平移运动，而是做平面运动，取运动情况已知的A 点为基点，则点D 的速度为 V D ＝V A ＋V DA （a ）在上式的6个要素中，仅已知V A ＝r ω，垂直于OA 指向下，以及V DA 方向垂直连线AD ，故暂时无法求解，可设法先求得V DA 的大小，由于V DA ＝ABD AD ω，需先求得ABD ω，为此可通过研究点B 的速度V B ＝V A ＋V BA （b ）来解决，这是因为上式的6个要素中，除V A 的大小和方向及V BA 的方向已知外，还已知V B 垂直O 1B ，故可求解。

作点B 的速度四边形，如图⑴所示，由几何关系得V BA ＝V A sin45°＝ωr 22 （c ） 从而ABD ω＝2222ωω==rr AB V BA，转向为顺时针。

又由余弦定理知：sin ,10r AD =∠ADB ＝101图（1）∴V DA ＝AD ABD ω＝ωr 210 （d ） 再作点D 的速度四边形，如图㈠所示，由几何关系得V D 的大小为V D ＝ωr ADB V V V V DA A DA A 210)90cos(2022=∠--+。

对于V D 与铅直线的夹角θ，sin θ＝103)90sin(0=∠-ADB V V D DA 求得 θ＝arcsin =10371°34′。

第四章仄里机构的疏通分解之阳早格格创做基础央供相识仄里机构疏通分解的手段战要领，以及机构位子图、构件上各面的轨迹战位子的供法.掌握速度瞬心位子的决定.相识用速度瞬心供解速度的要领.掌握用相对于运动图解法做机构的速度战加速度的分解.流利掌握影像法的应用.搞浑用剖析法中的矩阵法做机构的速度战加速度的分解，末尾要达到会编步调上机做习题的程度.基础观念题与问案1.什么是速度瞬心，机构瞬心的数目怎么样估计？问：瞬心：二个构件相对于速度等于整的沉合面. K = N (N-1) / 22.速度瞬心的判决要领是什么？直瞅判决有几种？问：判决要领有二种：直瞅判决战三心定理，直瞅判决有四种：（1）二构件组成转化副的轴心.（2）二构件组成移动副，瞬心正在无贫近处.（3）杂滑动副的按触面，（4）下副接融面的公法线上.3.速度瞬心的用途是什么？问：用去供解构件的角速度战构件上面的速度，但是千万于不克不迭供加速度战角加速度，正在四杆机构中用瞬心法供连杆战从动件上任一面的速度战角速度最便当.4.仄里机构疏通分解的真质、手段战要领是什么？问：真质：构件的位子、角位移、角速度、角加速度、构件上面的轨迹、位移、速度、加速度.手段：变革现有板滞的本能，安排新板滞.要领：图解法、剖析法、真验法.5.用相对于疏通图解法供构件的速度战加速度的基根源基本理是什么？问：基根源基本理是表里力教中的刚刚体仄里疏通战面的复合疏通.6.什么是基面法？什么样的条件下用基面法？动面战基面怎么样采用？问：基面法：构件上某－面的疏通不妨认为是随其上任选某一面的移动战绕其面的转化所合成的要领.供共一构件上二面间的速度战加速度闭系时用基面法，动面战基面选正在疏通果素己知多的铰链面.7 用基面法举止疏通分解的步调是什么？问：（1）选少度比率尺绘机构疏通简图（2）选共一构件上已知疏通果素多的铰链面做动面战基面，列矢量圆程，标出已知量的大小战目标.（3）选速度战加速度比率尺及极面P、P′按已知条件绘速度战加速度多边形，供解已知量的大小战目标.（4）对于所供的量举止估计战判决目标.8 ．什么是疏通分解中的影像本理？又称什么要领？注意什么？问：影像本理：已知共－构件上二面的速度或者加速度供其余－面的速度战加速度，则那三面速度或者加速度矢端所围成的三角形与那三面正在构件上围成的三角形相似，那便称做疏通分解中的影像法，又称疏通分解中的相拟性本理.注意：三面必须正在共一构件上，对于应面排列的程序共为顺时针或者顺时针目标.9．什么是速度战加速度极面？问：正在速度战加速度多边形中千万于速度为整或者千万于加速度为整的面，而且是千万于速度或者千万于加速度的出收面.10.速度战加速度矢量式中的等号，正在速度战加速度多边形中是哪一面？问：箭头对于顶的面.11.正在机构疏通分解中应用沉合面法的基根源基本理是什么？问：面的复合疏通.12.沉合面法正在什么倩况下应用？问：二个活动构件有相对于疏通时，供沉合面的速度战加速度.13.应用沉合面举止疏通分解时，什么情况下有哥氏加速度？问：当牵连角速度战沉会面间相对于速度不等于整时，有哥氏加速度，若其中之一等于整，则哥氏加速度等于整.大小为：akB1B2 = 2ω2VB1B2目标为：VB1B2 的矢量按牵连角速度ω2目标转化900 .14.应用沉合面法举止疏通分解时的步调是什么？问：（1）采用比率尺绘机构疏通简图.（2）选疏通果素已知多的铰链面为沉合面，列速度，加速度矢量圆程.（3）选速度比率尺战速度极面绘速度多边形.（4）选加速度比率尺战加速度极面绘加速度多边形图.（5）回问所提出的问题.典型例题例3-1 图（a）战（b）分别为移动导杆机媾战正切机构的疏通简图，其少度比率尺μL＝2 mm/mm.图中的构件1均为本动件，且已知ω1＝10rad／s .试分别供出其局部瞬心面，并用瞬心法分别供出：构件3的速度V3 、构件2上速度为整的面I2 战构件2的角速度ω2.解那二个机构均为含有二个移动副的四杆机构，各有六个瞬心面.但是果导路的形状分歧，故瞬心面的位子不尽相共.（1）移动导杆机构其六个瞬心面的位子如图（a）所示.其中：P14正在A 面，P12正在B面；P23正在导路的直率核心O处（而不是正在无贫近处！那面该当注意），P∞34正在与导路笔直的无贫近处；根据三心定理，P13正在P14战P∞34连线与P12战P23连线的接面处，P24正在P14战P12连线与P23战P∞34连线的接面处.例3-1 图μL ＝2 mm / mm，μv ＝0.04 m /s / mm果为构件1的角速度ω1已知，而构件3为仄移疏通，所以可利用P13供出构件3的速度v3＝vp13＝ω1LAP13＝ω1AP13μL=10×30×2=600mm／s 目标：背左.（a）（b）构件2上速度为整的面I2 ，便是构件2 与机架4 的瞬心面P24（vP24＝0）.正在图示位子上，构件2绕P24（I2）面做瞬时定轴转化，其角速度ω2可通过瞬心面P12的速度vP12供出，即：vP12 ＝vB ＝ω1LAB ＝ω1ABμL ＝10×22×2 ＝440 mm / s∴ω2 ＝vP12 / LI2B ＝vP12 / （I2B×μL）＝440 /（20×2）= 11 rad／s目标：顺时针.（2）正切机构六个瞬心面的位子如图（b）所示.请注意利用三心定理供P13 战P24 的要领.构件3的仄移速度v3，可利用瞬心面P13 供出v3 ＝vP13 ＝ω1LAp13 ＝ω1AP13μL ＝10×38×2 ＝760 mm / s目标：背下.构件2上速度为整的面I2，即为瞬心P24 .由于构件2与构件1形成移动副，二者之间不相对于转化，果此ω2 ＝ω1 ＝10 rad / s 顺时针目标例3-2 正在图（a）所示的机构中，已知：LAB ＝38mm，LCE ＝20mm，LDE = 50mm，xD =150 mm，yD ＝60mm；构件1以顺时针等角速度ω1 ＝20 rad / s转化.试供出此机构的局部瞬心面，并用背量多边形法供出构件3 的角速度ω3 战角加速度ε3，以及面E 的速度vE 战加速度aE .解（1）供速度瞬心P14 正在A面，P12 正在B面，P34 正在D面，P∞23 正在与导路CE 相笔直的无贫近处，那四个瞬心简单供出，如图（a）所示.根据三心定理，P13 既正在P14 战P34 的连线上，又正在P12战P∞23的连线上，果此，过B（P12）面做导路CE的垂线，与AD连线的接面即为P13 面；共理，过D（P34）面做导路CE 的垂线，与AB 连线的延少线的接面即为P24 面.（2）速度分解与少度比率尺μL = 4 mm/mm，按给定条件做出机构疏通简图，如图（b）所示.正在此机构中，构件2 为做仄里疏通的构件，且疏通副B 面的疏通已知，果此，应选B2为动面，动系选正在构件3上.为供得沉合面，需将构件3 背B 面夸大，得到与B2 面沉合的、属于构件3的牵连疏通面B3 .按“沉合面法”列出的速度圆程式为：→→→vB2 = vB3 + vB2B3目标⊥AB ⊥BD ∥CE大小LABω1 ？？其中，vB2 ＝LABω1 ＝38×20 ＝760 mm / s.与速度比率尺μv ＝20 mm / s / mm.则vB2 的代表线段少度为pb2＝vB2/μv＝760/20＝38mm与速度极面P 做速度多边形pb2b3 如图（c）所示.则ω3 ＝vB3 / LBD ＝pb3μv / BDμL ＝28.5×20 / 31×4 ＝4.6 rad / s目标：顺时针.由于滑块2与导杆3之间不相对于转化，果此ω2 ＝ω3 ＝4.6 rad / s至此，正在构件3 上已经有了D 战B 二个面的速度已知（注意：D为牢固铰链，vD＝0，aD＝0，为疏通已知面，那一面易被忽略），所以，不妨用影像法去供构件3上E 面的速度.为此，正在图（c）中做△pb3e ∽△DBE ，得e 面，则vE ＝peμv ＝11.5×20 ＝230 mm / s（3）加速度分解由于动系（构件3）绕D面做定轴转化，所以存留哥氏加速度.其加速度圆程为→→→→→anB2 = anB3 + atB3 + atB2B3 + akB2B3目标B→A B→D ⊥BD ∥CE⊥CE大小LABω21 已知？？已知其中：anB2 ＝LABω21 ＝38×202 ＝15200 mm / s2 anB3 ＝LBDω23 ＝BDμLω23 ＝31×4×4.62 ＝2620 mm/s 2akB2B3 ＝2ω3vB2B3 ＝2ω3b2b3μv ＝2×4.6×13.5×20 ＝2484 mm/s2与加速度比率尺μa＝500 mm/s2/mm，选极面p′正在图（d）中依次做出上述各已知背量的代表线段.p′b2′＝anB2 / μa ＝15200 / 500 ＝30.4 mmp′n3′＝anB3 / μa ＝2620 / 500 ＝5.24 mmk′b2′＝akB2B3 3 /μa＝2484 / 500 ＝4.97 mm正在此前提上做出加速度多边形，如图（d）所示.则ε3 ＝atB3 / LBD ＝n3′b3′μa / BDμL＝39×500 / 31×4 ＝157.3 rad/s2目标：顺时针.利用影像本理，正在图（d）中，连p′b3，做△p′b3′e′∽△DBE ，得e′面，则p′e′即为aE 的代表线段，其大小为aE ＝p′e′μa ＝16×500 ＝8000 mm / s2 ＝8 m / s2例3－3 图（a）所示为一四铰链机构的机构疏通简图、速度多边形战加速度多边形，做图的比率尺分别为：μL＝2 mm/mm、μv＝20 mm/s/mm、μa＝200 mm/s2/mm.已知本动件1 以匀角速度ω1 = 10 rad / s 顺时针目标转化.央供：（1）根据二个背量多边形分别列出相映的速度战加速度背量圆程，井将各个背量标正在背量多边形中相映的代表线段中间.（2）供出构件2 战3 的角速度ω2 、ω3 战角加速度ε2 、ε3 .（3）正在构件1、2 战3 上分别供出速度为vx ＝300 mm / s（目标为p→x ）的面x1、x2 战x3 .（4）供出构件2 上速度为整的面I2 战加速度为整的面Q2 .（5）供出I2 面的加速度a I 2 战Q2 面的速度vQ2 .解（1）速度战加速度背量圆程分别为→→→vc ＝vB ＋vCB→→→→→anc 十atc ＝anB 十ancB 十atcB多边形中各线段所代表的背量如图（b）所示.（2）由图（a）中量与有闭线段，即可分别供得ω2 ＝vCB / LBC = bcμv / BCμL = 18.5×20 / 58.5×2 = 3.16 rad / s 顺时针目标ω3 ＝vC / LCD = pcμv / CDμL = 25.5×20 / 25×2 = 10.2 rad / s 顺时针目标ε2 ＝atCB / LBC = n2cμa / BCμL = 48.7×200 /58.5×2 = 83.25 rad / s2顺时针目标ε3 ＝atC / LCD = n3cμa / CDμL = 13×200 / 25×2 = 52 rad / s2顺时针目标（3）x1、x2 战x3 面的位子可用影像法本理供出：正在速度多边形中对接xb 战xc.正在机构疏通简图上分别做相似形△ ABX1∽△ pbx △ CBX2∽△ cbx △DCX3∽△ pcx即可分别供出x1、x2 战x3 三个面，如图（b）所示.（4）由于I2 面与极面p 相对于应，Q2 面与极面p 相对于应，根据影像本理，正在机构疏通简图上分别做△ BCI2∽△ bc p △ BCQ2∽△ bc p′即可供得I2 面战Q2 面的位子，如图（b）所示.（5）正在图（b）的加速度多边形中做△ bci2∽△BCI2得i2 面，对接p′i2 即为a I 2 的代表线段，则a I 2 ＝p′i2μa ＝57×200 ＝11400 mm / s2 ＝11.4 m / s2 目标：p′→ i2正在速度多边形中做△ bcq2∽△ BCQ2得q 2 面，对接pq2 即为vQ2 的代表线段，则vQ2 ＝pq2μv ＝22×20 = 440 mm / s 目标：p→ q2此例需要反过去应用背量多边形法战影像本理，解题历程虽较简朴但是央供基础观念领会，解题要领流利.其余，通过此例也不妨瞅出，正在供某一构件上速度为整的面I、加速度为整的面Q、与给定速度或者加速度相对于应的面，以及面I 的加速度aI 面Q 的速度vQ 时，应用影像法本理是－种便利的解题要领.。

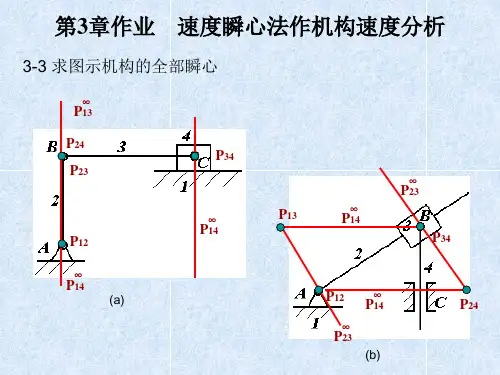
第2章习题2-1 求出图2-12所示机构中所有速度瞬心。

2-2 在图2-13所示的凸轮机构中，已知r=50mm，l OA=22mm，l AC=80mm,ψ1=90°，凸轮1的角速度ω1=10 ，逆时针转动。

试用瞬心法求从动件2的角速度ω2 。

2-3 图2-14所示四铰链运动链中，已知名构件长度l AB=55mm，l BC=40mm，l CD=50mm，l AD=25mm。

试问：（1）该运动链中是否具有双整转副构件？（2）如果具有双整转副构件，则固定哪个构件可获得曲柄摇杆机构?（3）固定哪个构件可获得双曲柄机构？（4）固定哪个构件可获得双摇杆机构？2-4 在图2-15所示的铰链四杆机构中，各杆件长度分别为l AB=28mm，l BC=52mm，l CD=50mm，l AD=72mm。

（1）若取AD为机架，求该机构的极位夹角θ，杆CD的摆角ψ和最小传动角γmin。

（2）若取AB为机架，该机构将演化为何种类型的机构？为什么？清说明这时C、D 两个转动副是整转还是摆动副？2-5 在图2-16所示机构中，已知l AB=100mm，l BC=l CD=400mm，l EF=200mm，∠BCD=90°，∠CFE=30°，ω1=100rad/s。

试求角速度ω5、速度νE4，角加速度ε5和加速度αE4。

2-6 在图2-17所示的摆动导杆机构中，∠BAC=90°，l AB60mm，l AC=120mm，曲柄AB的等角速度ω1=30rad/s。

求构件3的角速度ω3和角加速度ε3。

2-7 在图2-18所示的曲柄摇块机构中，已知l AB=30mm，l AC=100mm，l BD=50mm，ϕ=45°，等角速度ω1=10rad/s。

求点E、D的速度和加速度，构件3的角速度l DE=40mm，1ω3和角加速度ε3。

ϕ=45°，ω1=100rad/s，方向为逆时针方向，l AB=4m，2-8 在图2-19所示的机构中，已知1γ=60°。

习题 > 答案一.概念1.当两构件组成转动副时,其相对速度瞬心在转动副的圆心处;组成移动副时,其瞬心在垂直于移动导路的无穷远处;组成滑动兼滚动的高副时,其瞬心在接触点两轮廓线的公法线上.2.相对瞬心与绝对瞬心相同点是都是两构件上相对速度为零,绝对速度相等的点 ,而不同点是相对瞬心的绝对速度不为零,而绝对瞬心的绝对速度为零 .3.速度影像的相似原理只能用于同一构件上的两点,而不能用于机构不同构件上的各点.4.速度瞬心可以定义为互相作平面相对运动的两构件上,相对速度为零,绝对速度相等的点.5.3个彼此作平面平行运动的构件共有 3 个速度瞬心,这几个瞬心必位于同一条直线上 .含有6个构件的平面机构,其速度瞬心共有 15 个,其中 5 个是绝对瞬心,有 9 个相对瞬心.二.计算题1、2.关键:找到瞬心P366 Solution:The coordinates of joint B arey B=ABsinφ=0.20sin45°=0.141mx B=ABsinφ=0.20sin45°=0.141mThe vector diagram of the right Fig is drawn by representing the RTR (BBD) dyad.The vector equation, corresponding to this loop, is written asrB+r -rD =0 orr =r D-rBWherer =BD and r=γ.When the above vectorial equation is projected on the x and y axes, two scalar equations are obtained: r*cos(φ3+π)=x D -xB=-0.141mr*sin(φ3+π)=y D -y B =-0.541mAngle φ3 is obtained by solving the system of the two previous scalar equations:tgφ3=141.0541.0 ⇒φ3=75.36°The distance r isr=)cos(3πϕ+-B D x x =0.56mThe coordinates of joint C arex C =CDcosφ3=0.17m y C =CDsinφ3-AD=0.27mFor the next dyad RRT (CEE), the right Fig, one can write Cecos(π- φ4)=x E - x C Cesin(π- φ4)= y E - y CVector diagram represent the RRT (CEE) dyad.When the system of equations is solved, the unknowns φ4 and x E are obtained: φ4=165.9° x E =-0.114m7. Solution: The origin of the system is at A, A≡0; that is,x A =y A =0.The coordinates of the R joints at B are x B =l 1cosφ y B = l 1sinφFor the dyad DBB (RTR), the following equations can be written with respect to the sliding line CD:mx B - y B +n=0 y D =mx D +nWith x D =d 1, y D =0 from the above system, slope m of link CD and intercept n can be calculated:m=111cos sin d l l -ϕϕ n=ϕϕcos sin 1111l d l d -The coordinates x C and y C of the center of the R joint C result from the system of two equations:y C =mx C +n=ϕϕϕϕcos sin cos sin 1111111l d l d x d l l C -+-,(x C- xD )2+(y C- y D )2=l 23Because of the quadratic equation, two solutions are abstained for x C and y C.For continuous motion of the mechanism, there are constraint relations for the Choice of the correct solution; that is x C< x B< x D and y C>0For the last dyad CEE (RRT), a position function can be written for joint E:(x C-x E)2+(y C-h)2=l24The equation produces values for x1E and x2E, and the solution x E >x C is selected for continuous motion of the mechanism.枣元中心幼儿园教学活动评课记录。

3－１填空题：1．速度瞬心是两刚体上瞬时速度相等的重合点。

2．若瞬心的绝对速度为零，则该瞬心称为绝对瞬心；若瞬心的绝对速度不为零，则该瞬心称为相对瞬心。

3．当两个构件组成移动副时，其瞬心位于垂直于导路方向的无穷远处。

当两构件组成高副时，两个高副元素作纯滚动，则其瞬心就在接触点处；若两个高副元素间有相对滑动时，则其瞬心在过接触点两高副元素的公法线上。

4．当求机构的不互相直接联接各构件间的瞬心时，可应用三心定理来求。

5．3个彼此作平面平行运动的构件间共有 3 个速度瞬心，这几个瞬心必定位于一条直线上。

6．机构瞬心的数目K与机构的构件数N的关系是K＝N(N－1)/2 。

7．铰链四杆机构共有6个速度瞬心，其中3个是绝对瞬心。

8．速度比例尺μν表示图上每单位长度所代表的速度大小，单位为：(m/s)/mm 。

加速度比例尺μa表示图上每单位长度所代表的加速度大小，单位为(m/s2)/mm。

9．速度影像的相似原理只能应用于构件，而不能应用于整个机构。

10．在摆动导杆机构中，当导杆和滑块的相对运动为平动，牵连运动为转动时（以上两空格填转动或平动），两构件的重合点之间将有哥氏加速度。

哥氏加速度的大小为2×相对速度×牵连角速度；方向为相对速度沿牵连角速度的方向转过90°之后的方向。

P直接标注在图上)。

3－2试求出图示各机构在图示位置时全部瞬心的位置(用符号ij3－3 在图a 所示的四杆机构中，l AB =60mm,l CD =90mm ，l AD =l BC =120mm ，ω2=10rad/s ，试用瞬心法求：1）当φ＝165°时，点C 的速度v C ；2）当φ＝165°时，构件3的BC 线上速度最小的一点E 的位置及速度的大小；3）当v C ＝0时，φ角之值（有两个解）； 解：1）以选定的比例尺μl 作机构运动简图（图b ）。

2）求v C ，定出瞬心P 13的位置（图b ） v C =ω33413P P μl=34132313Bl l v P P P P μμg g g=1060583833⨯⨯⨯⨯≈2.4×174=418(mm/s) 3）定出构件3的BC 线上 速度最小的点E 的位置：E 点位置如图所示。