速度瞬心例题
- 格式:doc
- 大小:80.50 KB
- 文档页数:7

平面机构运动分析一、基本概念1、速度瞬心和机构中速度瞬心的数目1) 瞬心的定义瞬心:相对作平面运动的两构件上瞬时相对速度为零的点(即等速重合点)称为速度瞬心,简称瞬心。
瞬时等速重合点。
绝对速度瞬心:如果两构件之一是静止的,即绝对速度为零的瞬心称为绝对速度瞬心。
相对速度瞬心:如果两个构件都是运动的,即绝对速度不为零的瞬心称为相对速度瞬心。
2) 瞬心数目因为发生相对运动的任意两构件间都有一个瞬心,如果一个机构由m个构件组成,则瞬心数K为:2. 瞬心位置的确定(1)当两构件直接以运动副链接时,按定义确定:1) 当两构件组成转动副时,转动副的转动中心是它们的瞬心;2) 当两构件组成移动副时,瞬心位于导路垂线无穷远处;3) 当两构件组成纯滚动的高副时,接触点就是其速度瞬心;4) 当两构件组成滑动兼滚动的高副时,瞬心位于接触点的公法线上,具体还需据其它条件确定;(2) 对于不直接接触的构件,其瞬心可用三心定理来确定。
三心定理:作相对运动的三个构件共有三个瞬心,这三个瞬心位于一条直线上。
3、矢量图解法原理:1)用一条“有向线段”对应“一个矢量”2)作图遵循“同侧首末相连,两侧起点相同”的原则4、速度、加速度影响定理1)使用场合:统一构件,知2求3。
2)ΔBCD(机构位置图)∽Δbcd(速度多边形)∽Δb’c’d’(加速度多边形)。
3)字母排列顺序一致。
二、思考题1、机构运动分析的目的和任务是什么?图解法和解析法各有何优缺点?2、什么是速度瞬心?绝对瞬心和相对瞬心有何异同点?3.什么是“三心定理”?在确定不直接相联的两构件瞬心位置时,可能会出现什么情况(指不便于作图的情况)?三、练习题1、在图1示曲柄滑块机构中,原动件曲柄以等角速度ω1=5rad/s 逆时针转动。
已知机构尺寸:a=0.30m,b=0.6m。
1)试用瞬心法确定机构在ϕ1=60º位置时滑块3的速度2)用矢量图解法求滑块3的速度,构件2的角速度ω23)求BC上中点D的速度图1 图22、图2所示正弦机构中,已知:曲柄AB以等角速度转动,ω1=5rad/s,l AB=0.1m。



瞬 心 法一、单项选择题(每小题1分)在下列每小题的四个备选答案中选出一个正确的答案,并将其字母标号填入题干的括号内。
1、在两构件的相对速度瞬心处,瞬时重合点间的速度应为( A )。
A. 两点间相对速度为零,但两点的绝对速度不等于零B. 两点间相对速度不等于零,但其中一点的绝对速度等于零C. 两点间相对速度不等于零,且两点的绝对速度也不等于零D. 两点间的相对速度和绝对速度都等于零2、两构件作相对运动时,其瞬心是指( C )的重合点。
A. 绝对速度等于零B. 绝对速度和相对速度都等于零C. 绝对速度不一定等于零,但绝对速度相等或相对速度等于零D. 相对速度不等于零3、速度瞬心是指两构件上( B )为零的重合点。
A. 绝对速度B. 相对速度C. 绝对速度不D. 相对速度不二、填空题(每空1分)1、当两构件组成转动副时,其瞬心就是 转动中心位置 。
2、当求机构中不直接组成运动副两构件间的瞬心位置时,可应用 三心定理 来求。
三、分析题(每小题6分)1、对于下列机构的图示位置:①试确定机构的所有速度瞬心位置;②若已知原动件1的角速度ω1,试列出求从动件3运动速度ω3的表达式。
——4分113133ωωDP AP =——2分2、对于下列机构的图示位置:①试确定机构的所有速度瞬心位置;②若已知原动件1的角速度ω1,P 12P 24∞——4分0113133==ωωDP AP ——2分 3、对于下列机构的图示位置:①试确定机构的所有速度瞬心位置;②若已知原动件1的角速度ω1,试列出求从动件3运动速度v 3的表达式。
——4分1133ωAP v =——2分4、对于下列机构的图示位置:①试确定机构的所有速度瞬心位置;②若已知原动件1的角速度ω1,试列出求从动件3运动速度v 3的表达式。
——4分01133==ωAP v ——2分5、对于下列机构的图示位置:①试确定机构的所有速度瞬心位置;②若已知原动件1的角速度ω1,试列出求从动件3运动速度ω3的表达式。
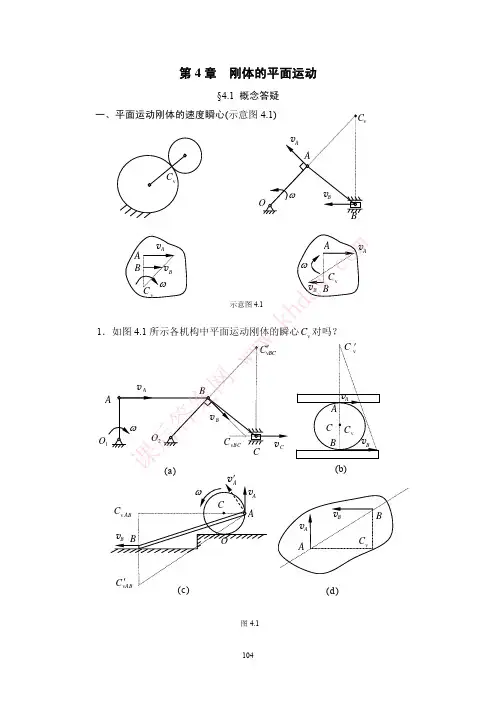
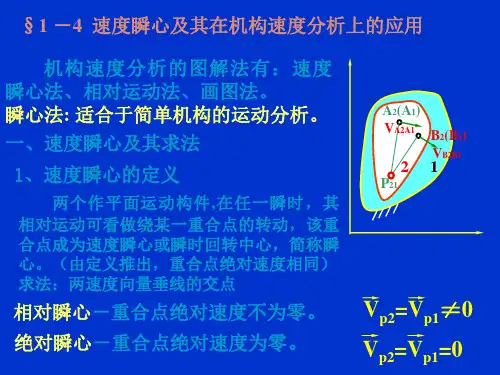


第三章典型题解析图3.1例3.1 机构尺寸如图2.2(a)所示,已知构件1的角速度为w1。
试用瞬心法求图示位置滑块的速度v5。
分析本题为多杆机构的速度分析题,可以用瞬心法和相对运动图解法求解。
但注意题目要求用瞬心法,所以应按题目要求解题。
欲求滑块5的速度,关键要找出已知速度的构件1与所求构件5的相对瞬心P15,同时确定构件1及构件5的绝对瞬心P16及P56,根据瞬心P15为构件1及构件5的瞬时等速重合点求出v p15即v5。
先把直接可确定的瞬心标出,因P15不能一下确定,所以可借助瞬心多边形依次确定。
下面介绍此方法。
解图示为六杆机构,为确定相对瞬心P15,可作出该构件的瞬心多边形如图3.2(b)所示。
在瞬心多边形中,各顶点的数字代表机构中各构件的代号,其中构件6为机架用圆圈标出,各顶点间的连线即代表相应的各瞬心(如顶点1,2的连线即代表瞬心P12)。
在瞬心多边形中,已知瞬心(如P12,P23,P16,P34,P36,P45,P56等)的相应线段用实线表示,待求的瞬心用虚线表示。
由三心定理可知,在瞬心多边形中任一个三角形三个边所代表的三个瞬心应位于一条直线上。
故可找出P13为P12,P23及P16,P36连线的交点(在图上表示即为△123与△136的公共边)。
同理,可找出下列瞬心:P26(P12-P16;P23-P36);P35(P34-P45;P36-P56);P46(P45-P56;P34-P36);P14(P13-P34;P16-P46);P15(P16-P56;P14-P45)。
(相同的脚号消去后就是所要求的脚号的瞬心。
)图3.2则v p15=v 5=w 1·1615P P (可按图上长度量取距离)[评注] 对多杆机构进行速度分析,利用速度瞬心是较方便的。
当瞬心数目较多时可借助瞬心多边形法或脚号消去法,依次找出所需瞬心的位置。
因瞬心法也属于图解法,所以应按比例准确画出所求机构位置的运动简图,所需尺寸可直接从图中量取折算。
第三章 平面机构的运动分析17 当两构件组成转动副时,其相对速度瞬心在 处;组成移动副时,其瞬心在 处;组成滑动兼滚动的高副时,其瞬心在 处.18相对瞬心与绝对瞬心相同点是 ,而不同点是 .19速度影像的相似原理只能用于 两点,而不能用于机构 的各点. 20速度瞬心可以定义为互相作平面相对运动的两构件上 的点.21 3个彼此作平面平行运动的构件共有 个速度瞬心,这几个瞬心必位于 .含有6个构件的平面机构,其速度瞬心共有 个,其中 个是绝对瞬心,有 个相对瞬心. 22 在图示机构中,已知原动件1以匀角速度ω1沿逆时针方向转动,试确定:(1)机构的全部瞬心;(2)构件3的速度v 3(需写出表达式)。
23如图所示齿轮-连杆机构中,已知齿轮2和5的齿数相等,即25z z =,齿轮2以2100ω=rad/s 顺时针方向转动,试用瞬心法求构件3的角速度ω3的大小和方向。
(取0.001l μ=m/mm 。
)第三章 平面机构的运动分析17.当两构件组成转动副时,其相对速度瞬心在 转动副的圆心 处;组成移动副时,其瞬心在 垂直于移动导路的无穷远 处;组成滑动兼滚动的高副时,其瞬心在接触点两轮廓线的公法线上.18.相对瞬心与绝对瞬心相同点是 都是两构件上相对速度为零,绝对速度相等的点 ,而不同点是 相对瞬心的绝对速度不为零,而绝对瞬心的绝对速度为零 .19.速度影像的相似原理只能用于 同一构件上的 两点,而不能用于机构 不同构件上 的各点.20.速度瞬心可以定义为互相作平面相对运动的两构件上,相对速度为零,绝对速度相等 的点.21. 3个彼此作平面平行运动的构件共有 3 个速度瞬心,这几个瞬心必位于 同一条直线上 .含有6个构件的平面机构,其速度瞬心共有 15 个,其中 5 个是绝对瞬心,有 9 个相对瞬心.22(1)求出瞬心数 (1)43622k k N -⨯>=== 瞬心如图。
(2)31314131P v v PP ω==⋅ 方向向上23(1)求出13P(2)求3ω 23P 点速度1323AB BP v l l ωω=⋅=⋅10AB l l AB μ=⋅=mm 131325BP l l BP μ=⋅=mm1332101004025AB BP l l ωω==⨯=rad/s ,逆时针方向。
第四章平面机构的运动分析基本要求了解平面机构运动分析的目的和方法,以及机构位置图、构件上各点的轨迹和位置的求法。
掌握速度瞬心位置的确定。
了解用速度瞬心求解速度的方法。
掌握用相对运动图解法作机构的速度和加速度的分析。
熟练掌握影像法的应用。
搞清用解析法中的矩阵法作机构的速度和加速度的分析,最后要达到会编程序上机作习题的程度。
基本概念题与答案1.什么是速度瞬心,机构瞬心的数目如何计算答:瞬心:两个构件相对速度等于零的重合点。
K = N (N-1) / 22.速度瞬心的判定方法是什么直观判定有几种答:判定方法有两种:直观判定和三心定理,直观判定有四种:(1)两构件组成转动副的轴心。
(2)两构件组成移动副,瞬心在无穷远处。
(3)纯滚动副的按触点,(4)高副接融点的公法线上。
3.速度瞬心的用途是什么答:用来求解构件的角速度和构件上点的速度,但绝对不能求加速度和角加速度,在四杆机构中用瞬心法求连杆和从动件上任一点的速度和角速度最方便。
4.平面机构运动分析的内容、目的和方法是什么答:内容:构件的位置、角位移、角速度、角加速度、构件上点的轨迹、位移、速度、加速度。
目的:改造现有机械的性能,设计新机械。
方法:图解法、解析法、实验法。
5.用相对运动图解法求构件的速度和加速度的基本原理是什么答:基本原理是理论力学中的刚体平面运动和点的复合运动。
6.什么是基点法什么样的条件下用基点法动点和基点如何选择答:基点法:构件上某-点的运动可以认为是随其上任选某一点的移动和绕其点的转动所合成的方法。
求同一构件上两点间的速度和加速度关系时用基点法,动点和基点选在运动要素己知多的铰链点。
7 用基点法进行运动分析的步骤是什么答:(1)选长度比例尺画机构运动简图(2)选同一构件上已知运动要素多的铰链点作动点和基点,列矢量方程,标出已知量的大小和方向。
(3)选速度和加速度比例尺及极点P、P′按已知条件画速度和加速度多边形,求解未知量的大小和方向。
(4)对所求的量进行计算和判定方向。
8 .什么是运动分析中的影像原理又称什么方法注意什么答:影像原理:已知同-构件上两点的速度或加速度求另外-点的速度和加速度,则这三点速度或加速度矢端所围成的三角形与这三点在构件上围成的三角形相似,这就称作运动分析中的影像法,又称运动分析中的相拟性原理。
注意:三点必须在同一构件上,对应点排列的顺序同为顺时针或逆时针方向。
9.什么是速度和加速度极点答:在速度和加速度多边形中绝对速度为零或绝对加速度为零的点,并且是绝对速度或绝对加速度的出发点。
10.速度和加速度矢量式中的等号,在速度和加速度多边形中是哪一点答:箭头对顶的点。
11.在机构运动分析中应用重合点法的基本原理是什么答:点的复合运动。
12.重合点法在什么倩况下应用答:两个活动构件有相对运动时,求重合点的速度和加速度。
13.应用重合点进行运动分析时,什么情况下有哥氏加速度答:当牵连角速度和重会点间相对速度不等于零时,有哥氏加速度,若其中之一等于零,则哥氏加速度等于零。
大小为: a k B1B2= 2ω2V B1B2方向为:V B1B2的矢量按牵连角速度ω2方向旋转 900。
14.应用重合点法进行运动分析时的步骤是什么答:(1)选择比例尺画机构运动简图。
(2)选运动要素已知多的铰链点为重合点,列速度,加速度矢量方程。
(3)选速度比例尺和速度极点画速度多边形。
(4)选加速度比例尺和加速度极点画加速度多边形图。
(5)回答所提出的问题。
典型例题例3-1 图(a)和(b)分别为移动导杆机构和正切机构的运动简图,其长度比例尺μL=2 mm/mm。
图中的构件1均为原动件,且已知ω1=10rad/s 。
试分别求出其全部瞬心点,并用瞬心法分别求出:构件3的速度V3、构件2上速度为零的点I2和构件2的角速度ω2。
解这两个机构均为含有两个移动副的四杆机构,各有六个瞬心点。
但因导路的形状不同,故瞬心点的位置不尽相同。
(1)移动导杆机构其六个瞬心点的位置如图(a)所示。
其中:P14在A点,P12在B点;P23在导路的曲率中心O处(而不是在无穷远处!这点应该注意),P∞34在与导路垂直的无穷远处;根据三心定理,P13在P14和P∞34连线与P12和P23连线的交点处,P24在P14和P12连线与P23和P∞34连线的交点处。
例 3-1 图μL=2 mm / mm,μv=0.04 m /s / mm因为构件1的角速度ω1已知,而构件3为平移运动,所以可利用P13求出构件3的速度 v3=v p13=ω1L AP13=ω1AP13μL=10×30×2=600mm/s 方向:向右。
(a)(b)构件2上速度为零的点I2,就是构件 2 与机架 4 的瞬心点 P24(v P24=0)。
在图示位置上,构件2绕P24(I2)点作瞬时定轴转动,其角速度ω2可通过瞬心点P12的速度v P12求出,即:v P12= v B=ω1L AB=ω1ABμL= 10×22×2 = 440 mm / s ∴ω2= v P12 / L I2B= v P12 / ( I2B×μL)= 440 /( 20×2) = 11 rad /s方向:逆时针。
(2)正切机构六个瞬心点的位置如图(b)所示。
请注意利用三心定理求P13和P24 的方法。
构件3的平移速度 v3,可利用瞬心点P13求出v3= v P13=ω1L Ap13=ω1AP13μL= 10×38×2 = 760 mm / s方向:向下。
构件 2上速度为零的点I2,即为瞬心 P24。
由于构件 2与构件 1构成移动副,二者之间没有相对转动,因此ω2=ω1= 10 rad / s 逆时针方向例3-2 在图(a)所示的机构中,已知:L AB=38mm,L CE=20mm,L DE = 50mm,x D =150 mm,y D=60mm;构件1以逆时针等角速度ω1=20 rad / s转动。
试求出此机构的全部瞬心点,并用向量多边形法求出构件 3 的角速度ω3和角加速度ε3,以及点 E 的速度v E和加速度 a E。
解(1)求速度瞬心P14在A点,P12在B点,P34在 D点,P∞23在与导路 CE 相垂直的无穷远处,这四个瞬心容易求出,如图(a)所示。
根据三心定理,P13既在P14和P34的连线上,又在P12和P ∞23的连线上,因此,过B(P12)点作导路CE的垂线,与AD连线的交点即为P13点;同理,过 D(P34)点作导路 CE 的垂线,与 AB 连线的延长线的交点即为 P24点。
(2)速度分析取长度比例尺μL = 4 mm/mm,按给定条件作出机构运动简图,如图(b)所示。
在此机构中,构件 2 为作平面运动的构件,且运动副 B 点的运动已知,因此,应选B2为动点,动系选在构件 3上。
为求得重合点,需将构件 3 向 B 点扩大,得到与 B2点重合的、属于构件3的牵连运动点B3。
按“重合点法”列出的速度方程式为:→→→v B2 = v B3 + v B2B3方向⊥AB ⊥BD ∥CE大小 L ABω1其中,v B2= L ABω1= 38×20 = 760 mm / s。
取速度比例尺μv= 20 mm / s / mm。
则 v B2的代表线段长度为pb2=v B2/μv=760/20=38mm取速度极点 P 作速度多边形 pb2b3如图(c)所示。
则ω3= v B3 / L BD= pb3μv/ BDμL=×20 / 31×4 = rad / s方向:顺时针。
由于滑块2与导杆3之间没有相对转动,因此ω2=ω3= rad / s至此,在构件 3 上已经有了 D 和 B 两个点的速度已知(注意:D为固定铰链,v D =0,a D=0,为运动已知点,这一点易被忽略),所以,可以用影像法来求构件 3上 E 点的速度。
为此,在图(c)中作△pb3e ∽△DBE ,得 e 点,则v E= pe μv=×20 = 230 mm / s(3)加速度分析由于动系(构件 3)绕 D点作定轴转动,所以存在哥氏加速度。
其加速度方程为→→→→→a n B2 = a n B3 + a t B3 + a t B2B3 + a k B2B3方向 B→A B→D ⊥BD ∥CE ⊥CE大小 L ABω21已知已知其中:a n B2= L ABω21= 38×202= 15200 mm / s2a n B3= L BDω23=BDμLω23= 31×4×= 2620 mm/s 2a k B2B3 = 2ω3v B2B3 = 2ω3b2b3μv= 2×××20 = 2484 mm/s2取加速度比例尺μa=500 mm/s2/mm,选极点p′在图(d)中依次作出上述各已知向量的代表线段。
p′b2′= a n B2/ μa= 15200 / 500 = 30.4 mmp′n3′= a n B3/ μa= 2620 / 500 = 5.24 mmk′b2′= a k B2B3 3/μa= 2484 / 500 = 4.97 mm在此基础上作出加速度多边形,如图(d)所示。
则ε3= a t B3 / L BD= n3′b3′μa/ BDμL= 39×500 / 31×4 = rad/s2 方向:顺时针。
利用影像原理,在图(d)中,连p′b3,作△p′b3′e′∽△DBE ,得 e′点,则 p′e′即为 a E的代表线段,其大小为a E= p′e′μa= 16×500 = 8000 mm / s2= 8 m / s2例 3-3 图(a)所示为一四铰链机构的机构运动简图、速度多边形和加速度多边形,作图的比例尺分别为:μL=2 mm/mm、μv=20 mm/s/mm、μa=200 mm/s2/mm。
已知原动件 1 以匀角速度ω1 = 10 rad / s 顺时针方向转动。
要求:(1)根据两个向量多边形分别列出相应的速度和加速度向量方程,井将各个向量标在向量多边形中相应的代表线段旁边。
(2)求出构件 2 和 3 的角速度ω2 、ω3和角加速度ε2、ε3。
(3)在构件 1、2 和 3 上分别求出速度为 v x= 300 mm / s(方向为 p→x )的点 x1、x2和 x3 。
(4)求出构件 2 上速度为零的点 I2和加速度为零的点 Q2 。
(5)求出 I2点的加速度 a I 2和 Q2 点的速度 v Q2 。
解( 1)速度和加速度向量方程分别为→→→v c= v B+ v CB→→→→→a n c十 a t c= a n B十 a n cB十 a t cB多边形中各线段所代表的向量如图(b)所示。