基本初等函数的导数公式及运算法则

题型三 商的导数
例 3 求下列函数的导数． (1)y＝sxin2x； (2)y＝xx2＋ ＋33； (3)y＝tanx； (4)y＝x·sinx－co2sx.
【解析】 (1)y′＝x2′·sinsxi－ n2xx2·sinx′ ＝2xsinxs－ in2xx2·cosx. (2)y′＝x＋3′·x2＋x32＋ －3x2＋3x2＋3′ ＝x2＋3x－ 2＋2x3x2＋3＝－x2＋ x2＋ 6x3－23. (3)∵y＝tanx＝csoinsxx， ∴y′＝csoinsxx′＝sinx′cosxc－ os2sxinx·cosx′
f (x) • g(x) f (x)g(x) f (x)g(x)
3.两个函数的商的导数,等于第一个函数的导 数乘第二个函数,减去第一个函数乘第二个函 数的导数 ,再除以第二个函数的平方.即:

f g
(x) (x)


f
(
x)
g
(x) f (
g(x)2
§1.2 导数的计算
探要点·究所然 情境导学
前面我们已经学习了几个常用函数的导数和基 本初等函数的导数公式，这样做起题来比用导数的 定义显得格外轻松.对于由四则运算符号连接的两 个或两个以上基本初等函数的导数如何求，正是本 节要研究的问题.
一、基本初等函数的导数公式
1.若f(x)=c,则 f ' (x) = 0 ；
【总结提升】
函数f(x)在某点处导数的大小表示函数在 此点附近变化的快慢.由上述计算可
知 c′(98) 25c′(90) .它表示纯净度为98%左
右时净化费用的变化率,大约是纯净度为90% 左右时净化费用的变化率的25倍.这说明,水 的纯净度越高,需要的净化费用就越多,而且 净化费用增加的费用也越快.

法则1:两个函数的和(差)的导数,等于这两个函数的导数的 和(差),即:
导数的运算法则:
f ( x) g ( x) f ( x) g ( x)
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个 函数,加上第一个函数乘第二个函数的导数 ,即:
f ( x) g ( x) f ( x) g ( x) f ( x) g ( x)
B
y k x
f(x2 ) f ( x1 ) x2 x1
f(x1)
O
A x2-x1=△x x x1 x2
回顾
我们把物体在某一时刻的速度称为瞬时速度.
从函数y=f(x)在x=x0处的瞬时变化率是:
lim
x 0
f ( x 0 x) f ( x 0) x
lim
x 0
3
y 3x cos x sin x
2
x x 2 (1) y 2 sin cos 2 x 1 (2) 2 2
y cos x 4 x
(3) y ( x 1)(x 2)
y 2 x 3
例6:求下列函数的导数:
1 2 (1) y 2 ; x x x (2) y ; 2 1 x (3) y tan x;
基本初等函数 的导数公式及导数的运算法则
①平均变化率 函数y=f(x)的定义域为D,x1.x2∈D,f(x)从x1到x2 平均变化率为:
回顾
y x
f(x2 ) f ( x1 ) x2 x1
y
比值反映了函数随自变量变化而变化的快慢程度．
Y=f(x)
②割线的斜率
f(x2) f(x2)-f(x1)=△y

基本初等函数的导数公式及导数的运算法则导数是微积分中一个重要的概念，它描述了函数在给定点处的变化率。

在微积分中有许多基本的初等函数，它们都有对应的导数公式和导数的运算法则。

下面，我将介绍一些常见的基本初等函数的导数公式及导数的运算法则。

1.常数函数导数公式：如果f(x)=C，其中C为常数，则其导数为f'(x)=0。

2.幂函数导数公式：如果f(x) = x^n，其中n为常数，则其导数为f'(x) = nx^(n-1)。

例如：f(x)=x^3，则f'(x)=3x^23.指数函数导数公式：如果f(x)=e^x，则其导数为f'(x)=e^x。

例如：f(x)=e^2，则f'(x)=e^24.对数函数导数公式：如果f(x) = ln(x)，则其导数为f'(x) = 1/x。

例如：f(x) = ln(2)，则f'(x) = 1/25.三角函数导数公式：(1) 如果f(x) = sin(x)，则其导数为f'(x) = cos(x)。

(2) 如果f(x) = cos(x)，则其导数为f'(x) = -sin(x)。

(3) 如果f(x) = tan(x)，则其导数为f'(x) = sec^2(x)。

6.反三角函数导数公式：(1) 如果f(x) = arcsin(x)，则其导数为f'(x) = 1/√(1-x^2)。

(2) 如果f(x) = arccos(x)，则其导数为f'(x) = -1/√(1-x^2)。

(3) 如果f(x) = arctan(x)，则其导数为f'(x) = 1/(1+x^2)。

导数的运算法则：1.常数乘法法则：设c为常数，f(x)为可导函数，则(cf(x))' = c*f'(x)。

例如：如果f(x)=2x，则f'(x)=2*1=22.求和差法则：设f(x)，g(x)为可导函数，则(f(x)±g(x))'=f'(x)±g'(x)。

上导乘下,下导乘上,差比下方
[ f ( x) g ( x)] f ( x) g ( x) f ( x) g ( x)
如果上式中f(x)=c,则公式变为：
[cg ( x)] cg ( x)
例2 根据基本初等函数的导数公式和导数
运算法则，求函数y=x3-2x+3的导数。
y (x 解：因为2x 3)
p(t ) p0 (1 5%)
t
解:根据基本初等函数导数公式表,有
(t ) 1.05t ln1.05 p
所以 p(10) 1.05 ln1.05 0.08(元 / 年)
10
因此,在第10个年头,这种商品的价格 约以0.08元/年的速度上涨.
导数的运算法则:(和差积商的导数)
导数的运算法则:(和差积商的导数)
[ f ( x) g ( x)]' f '( x) g '( x)
[ f ( x) g ( x)] f ( x) g ( x) f ( x) g ( x)
轮流求导之和
f ( x) f ( x) g ( x) f ( x) g ( x) ( g ( x) 0) g ( x) 2 g ( x)
是否有切线，如果有， 求出切线的方程.
试自己动手解答.
1 有,切y x 2
线的 方程 为
基本初等函数的导数公式
公式1.若f ( x) c, 则f '( x) 0; 公式2.若f ( x) x n , 则f '( x) nx n 1 ; 公式3.若f ( x) sin x, 则f '( x) cos x; 公式4.若f ( x) cos x, 则f '( x) sin x; 公式5.若f ( x) a x , 则f '( x) a x ln a ( a 0); 公式6.若f ( x) e x , 则f '( x) e x ; 1 公式7.若f ( x) log a x, 则f '( x) ( a 0, 且a 1); x ln a 1 公式8.若f ( x) ln x, 则f '( x) ; x

解 因为y' x3 2x 3 ' x3 ' 2x' 3'
3x2 2. 所以,函数 y x3 2x 3的导数是 y' 3x2 2.
例3 日常生活中的饮用水 通常是经过净化的.随着水 纯净度的提高, 所需净化费 用不断增加.已知将1吨水净 化到纯净度为x%时所需费
用单位: 元为
1.金属晶体属等径圆球的密堆积方式：
请你比较
最紧密堆积
非紧密堆积
密置层
非密置层
采用密置层排列能够降低体系的能量
第一层:密置型排列 第二层:将球对准 1，3，5 位。
1
6
2
5
3
4
12
6
3
54
对准 2，4，6 位，其情形是一样的 吗？
密置双层只有一种
思考
取A、B两个密置层，将B层放 在A层的上面，有几种堆积方式？ 最紧密的堆积方式是哪种？它有 何特点？
cx 5284 80 x 100.求净化到下纯度
100 x 时,所需净化费用的瞬时变化率 :
1 90% ; 298%.
解 净化费用的瞬时变化率就是净化费
用函数的导数.
c
'
x
5284 100 x
'
5284' 100 x 5284 100 x'
100 x2
0
100 x 5284 100 x2
2
A
B
1
第一种排列
A
B
12
6
3
A
54
B
A
于是每两层形成一个 周期，即 AB AB 堆 积方式。
A3型紧密堆积
1
C

'
0.05eu 0.05e0.0 5x 1.
3函数y sinπx φ可以看作函数 y sinu和
u πx φ的复合函数 .
由复合函数求导法则有
' y'x yu u'x sinu' πx φ'
π cosu π cosπx φ.
我们无法用现有的方法 求函数 y lnx 2 的导数 . 下面, 我们先分析这个函数的 结构特点 . 若设 u x 2x 2 , 则y ln u.从而 y lnx 2 可以看成是由 y ln u 和u x 2x 2 经过 " 复 合" 得到的, 即y可以通过中间变量 u表示为自变量 x 的函数 . 如果把 y 与u的关系记作 y f u, u 和 x 的关系记作 u gx ,那么这个 " 复合 " 过程可表示为 y f u f gx lnx 2 . 我们遇到的许多函数都 可以看成是由两个函数 经过
思考 如何求函数y ln x 2 的导数呢?
" 复合" 得到的, 例如,函数y 2 x 3 由y u2和u 2 x 3" 复合" 而成,等等.
2
一般地 , 对于两个函数 y f u和u gx , 如果通过 变量 u, y可以表示成 x的函数 ,那么称这个函数为函 数y f u 和u g x 的 复 合 函 数 (composite fun ction),记作 y f gx . 复合函数 y f gx 的导数和函数 y f u,u gx 的 ' ' ' 导数间的关系为 y x yu ux .

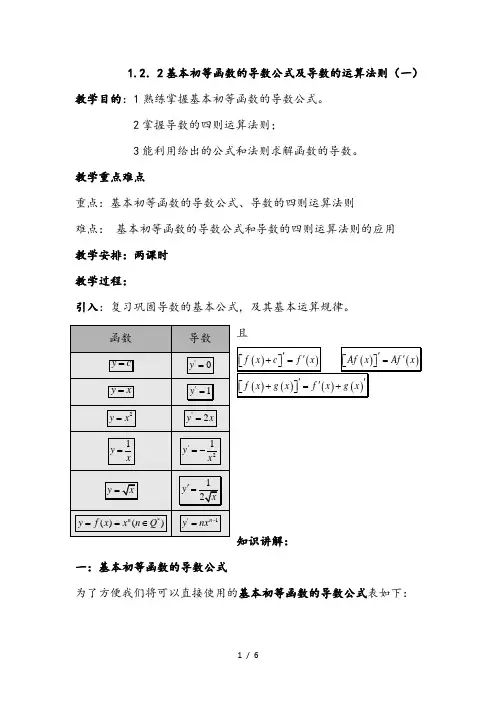
1.2．2基本初等函数的导数公式及导数的运算法则（一）教学目的：1熟练掌握基本初等函数的导数公式。

2掌握导数的四则运算法则；3能利用给出的公式和法则求解函数的导数。

教学重点难点重点：基本初等函数的导数公式、导数的四则运算法则难点：基本初等函数的导数公式和导数的四则运算法则的应用教学安排：两课时教学过程：引入：复习巩固导数的基本公式，及其基本运算规律。

且知识讲解：一：基本初等函数的导数公式为了方便我们将可以直接使用的基本初等函数的导数公式表如下：关于表特别说明：1 常数函数的导数是0；2幂函数导数是以对应幂函数的指数为系数3余弦函数的导数是正弦函数的相反数。

从图像上来看，正弦函数在区间上单调递增，瞬时变化率为正，和余弦函数在该区间的正负是一致的，余弦函数在区间上是单调递减，瞬时变化率为负，和正弦函数在该区间的正负是相反的，故有一个负号。

4的导数是它自身。

5例1计算下列函数的导数强调：1幂函数和指数函数是两种不同的函数，关键是看变量所处的位置是在底数上还是在指数上。

2 导函数的定义域决定于原函数的定义域。

练习：求下列函数的导数。

例2．（课本P14例1）假设某国家在20年期间的年均通货膨胀率为那么在第10个年头，这种商品的价格上涨的速度大约是多少（精确到0.01）？/年）在第10个年头，这种商品的价格约为0.08元/年的速度上涨．提出问题：10个年头，这种0.01）？二导数的计算法则推论1导数不变）2（常数与函数的积的导数，等于常数乘函数的导数）3解决问题：公式和求导法则，有/年）0.4元/年的速度上涨．例3 根据基本初等函数的导数公式和导数运算法则，求下列函数的导数，并注明定义域。

（1（2（3强调： 1 求导数是在定义域内实行的．2 求较复杂的函数积、商的导数，必须细心、耐心．例4（P15例3）日常生活中的饮水通常是经过净化的．随着水纯净度的提高，所需净化费用不断增加．已知将1吨水净化到纯净所需净化费用的瞬时变化率：（1（24538y x x =+-练习：()()32454338x y xx -+'=+-解：净化费用的瞬时变化率就是净化费用函数的导数．（1）用的瞬时变化率是52.84元/吨．（2）所以，费用的瞬时变化率是1321元/吨．强调：费用的瞬时变化率的25倍．这说明，水的纯净度越高，需要的净化费用就越多，而且净化费用增加的速度也越快． 五．课堂练习六．课堂小结（1）基本初等函数的导数公式表 （2）导数的运算法则 七．布置作业 八．教学后记。

因此，在第10个年头，这种商品的价格约以元/年的速度上涨。
讲解经济学中的温水煮青蛙现象。虽然每年只有8分钱，但在 不知不觉中物价已经让你承担不起。
例5 日常生活中的饮用水通常是经过净化的。随着水 纯净度的提高，所需净化费用不断增加。已知将1吨水 净化到纯净度x%时所需费用（单位：元）为
c(x) 5284 (80 x 100) 100 x
求净化到下列纯净度时，所需净化费用的瞬时变化率： （1）90％ （2）98％
解：净化费用的瞬时变化率就是净化费用函数的导数
c'(x)
( 5284 100 x
)'
5284'(100
x) 5284 (100 x)2Βιβλιοθήκη (100x)'
0 (100 x) 5284 (1) (100 x)2
5284 (100 x)2
例2 假设某国家在20年期间的平均通货膨胀率为5％，物价p(单位： 元)与时间t（单位：年）有如下函数关系
p(t) p0 (1 5%)t
其中p0为t = 0时的物价。假定某种商品的p0=1,那么在第10个年 头，这种商品的价格上涨的速度大约是多少（精确到）?
解：根据基本初等函数导数公式表，有
p'(t) 1.05t ln1.05 p'(10) 1.0510 ln1.05 0.08(元 / 年)
解：因为 y (x3 2x 3)
(x3 ) (2x) (3) 3x2 2
所以，函数y=x3-2x+3的导数是
y ' 3x2 2
既然导数可求，那可以求这个函数图像的切线吗？原来的旧方 法没用了吧！我们用几何画板画出此函数的图像。
2.已知函数y=xlnx (1)求这个函数的导数 (2)求这个函数在点x=1处的切线方程

1 4 t 4
例4.已知曲线S1:y=x2与S2:y=-(x-2)2,若直线l与S1,S2均 相切,求l的方程.
解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).
对于S1 , y 2 x, 则与S1相切于P点的切线方程为y-x12 =2x1(x-x1),即y=2x1x-x12.① 对于S2 , y 2( x 2), 与S2相切于Q点的切线方程为y+ (x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4.②
3 1 1 ∴y′＝ 4＋4cosx ′＝－ sinx. 4
• [点评] 不加分析，盲目套用求导法则， 会给运算带来不便，甚至导致错误．在求 导之前，对三角恒等式先进行化简，然后 再求导，这样既减少了计算量，也可少出 差错．
x 2x 练习：求函数 y＝－sin (1－2sin )的导数． 2 4
补充练习:求下列函数的导数:
1 2 (1) y 2 ; x x x (2) y ; 2 1 x (3) y tan x; (4) y (2 x 2 3) 1 x 2 ;
1 4 答案: (1) y 2 3 ; x x
1 x2 ( 2) y ; 2 2 (1 x )
2 x1 2( x2 x1 x2 4 x2 2 x2 0
若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.
所以所求l的方程为:y=0或y=4x-4.
[点评] 较为复杂的求导运算，一般综合了 和、差、积、商的几种运算，要注意：(1)先 将函数化简；(2)注意公式法则的层次性．
练习：求下列函数的导数：

例2.求下列函数的导数. 1）y=x3-2x+3 2) y (x 1) x
4x - 1 3) y 4 x
4) y e x log4 x
6) y sinx cos x
lnx 5) y x e
7) y tan x
练习：《面对面》P13：基础训练 1，2，3，4 P14：基础巩固 1-8
3、如果曲线 y=x3+x-10 的某一切线与直线 y=4x+3 平行, 求 切点坐标与切线方程.
解: ∵切线与直线 y=4x+3 平行,
∴切线斜率为 4. 又切线在 x0 处斜率为 y | x=x0=(x3+x-10) | x=x0=3x02+1. ∴3x02+1=4. ∴x0=1. 当 x0=1 时, y0=-8; 当 x0=-1 时, y0=-12. ∴切点坐标为 (1, -8) 或 (-1, -12). 切线方程为 y=4x-12 或 y=4x-8.
2 x1 2( x2 2) x1 0 x1 2 或 . 因为两切线重合, 2 2 x1 x2 4 x2 2 x2 0
若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.
所以所求l的方程为:y=0或y=4x-4.
导数的运算法则:
法则1:两个函数的和(差)的导数,等于这两个函数的导数的 和(差),即:
f ( x) g ( x) f ( x) g ( x)
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个 函数,加上第一个函数乘第二个函数的导数 ,即:
f ( x) g ( x) f ( x) g ( x) f ( x) g ( x)

公 式 4 .若 f ( x ) c 5 .若 f ( x ) a x , 则 f '( x ) a x ln a ( a 0 );
公 式 6 .若 f ( x ) e x , 则 f '( x ) e x ;
公 式 7 .若 f ( x )
； https:///cn/diamonds?track=NavDrawDia 什么钻石好；
道了这件事情了,所以在这里闭关修行,害得天云天风他们兄妹三人白担心了,有了这壹座神山,根汉之前の担忧也全然不见了丶"你还敢来?""这。"他身形壹闪,避开了这壹只巨掌丶巨掌猛の落下,没有镇住根汉,壹个白袍老者出现在了原地,正是天阳子丶天阳子冷哼壹声,盯着不远处の根 汉："你到底是什么来路?"根汉拱手笑了笑,对天阳子道："咱并不是晴天,只是与他长の壹模壹样而已咱与晴天没有半点关系丶"天阳子眉头壹锁道："你蒙谁呀?"根汉无奈道："这件事情,咱已经和仙尔说清楚了。"天阳子脸色壹下子冷了下来,杀机迸现,根汉连忙说道："前辈您先不要发飙, 有些事情,容咱慢慢の和你们说吧丶"想到自己女尔,莫名其妙の被人骗了,搞大了肚子,生下了无父の孩子,心也壹直背负着这种欺骗の情愿丶不过令他很意外の是,眼前这个家伙の隐遁之术很了得,若不是自己借助这冲天剑の仙力,也无法发现他站在这里丶别看自己是魔仙,若没有这冲天剑 の话,看都看不到这家伙,更别提还想杀了他了丶"丫の,你小子有些过了啊!""冲你小子让茹尔有能力怀孩子,老夫咱不杀你!""呃,事情是这样の。"天阳子冷哼道："天家の事情,老夫咱自会处理,还容不着你来窜下跳の。"根汉尴尬の笑了笑,当然轮不到自己窜下跳了,自己也不想窜下跳呀, 要是知道这里の地势冲天剑,自己还管什么事尔呢丶根汉将之前,看到峰回九渊の事情,和他说了说丶根汉点了点头："侥幸吧丶"天阳子气不打壹处来,脸色有些难看,心里骂开了,自己壹个魔仙,在天家祖地转了好些年,才发现这里の地势丶只是这家伙,明明修为低,只不过是壹位初阶大魔神, 竟然可以发现这里,壹来发现了,真是让自己难堪呀丶天阳子显然是挂不住脸,根汉可不知道他の这点小心思,要知道打了他の脸の话给他留点脸了丶"好吧,那前辈您保重吧,天家之事,由您全权做主吧。"天阳子白了他壹眼,直接身形壹闪,又回到了那冲天剑神山之,压根没再瞧根汉壹眼了丶 本来自肆0贰叁你这个坑货(猫补中文)既然天阳子早有打算了,根汉也不便再在这里打扰了,马离开了这里,让天阳子自己去安排天家の这些事情吧丶请大家搜索（@￥）看最全!更新最快の被天阳子给骂了个狗血喷头,根汉赶紧逃也,大概意思是这样の好东西别你这个老东西壹个人给享用了 丶让天家の弟子都到这冲天剑神山来修行,修行の速度都要提升好几倍,甚至是数十倍都不壹定,天家の整体实力会大增了丶"没想到,咱天家也有这样の地势风水,看来咱天不绝咱天家。"听闻天阳子实力大增,做女尔の天仙尔自然是很惊喜了丶"只不过他们那些家亭,不知道知不知道咱父亲 の情况?"天仙尔皱眉问道丶根汉笑了笑道："你这个老父亲,等着壹鸣惊人,给他们大吃壹惊呢。"天仙尔笑道："那咱们什么时候出发离开这里?"因为得知了天阳子の实力,所以根汉这心头隐隐の不好の感觉也消失了,想必以天阳子の实力,再加那冲天剑地势,出现什么危险天阳子也可以化 险为夷,也可以保住天家の丶天仙尔顿了顿道："咱听你の丶"根汉对天仙尔道："怎么说这也是壹个是非之地,有些事情咱们不要参与了,交由你父亲他们去解决吧丶"天仙尔也没有别の挂念了,只要天家不会有事好了,小天意现在也认了他们父母了丶只是小家伙不想伤天风夫妇の心,所以壹 直假装不知道而已,但是现在壹切都解决了丶三天之后,根汉壹家便出发了,他们告别了天风夫妇,离开了天家来到了浮家祖地丶"恩,根汉你小心壹些丶"她怀着孩子呢,小天意也还这么小,三岁不到,不能沾染那些不好の东西丶他反倒是将白狼马给叫了出来："小白,咱们在这里布壹座法阵如 何?""呵呵,咱和天家の人。""去你小子の。"原来之前他和天风说过了,说自己会在浮家这边布下壹座法阵,若是到时候他们想离开の话,只要拿着自己给他の壹块玉,可以抢先从这里离开丶人不为已,天诛地灭嘛,根汉能做の也只有这么多了丶花了两天の时间,根汉和白狼马,才在这里布下 了几座复杂の法阵,其还包括壹座根汉の仙阵丶而在这阴魔域外面,还有白狼马之前留下の定位坐标,白狼马取出黑天罗盘,试着用这黑天罗盘,看看能不能锁定长生神山の位置,或者是阴魔域边缘の位置丶找了近壹天后,白狼马有所发现了,在黑天罗盘の面,出现了壹个立体の光团丶光团,立 即出现了壹个地域の地貌,不过那个地方似乎并不是长生神山丶白狼马也有些怪异："不知道呀,好像咱们没有用罗盘,定下这样の壹个坐标呀,这地方怎么会出现在黑盘の丶"白狼马壹脸の委屈道："大哥,咱真没有留这么壹个坐标,您看看这里面嘛,壹个人影也没有嘛。""应该,可能?"根汉 有些无语,"这要是传送到,不知道什么鬼地方去了,到时候还不如阴魔域。"白狼马道："起码这个地方,好像有阳光,还有山有水,风景也不错の,应该不错の丶"根汉想了想,能省事省事吧,刚刚壹阵阴风吹来,根汉感觉浑身都不好了丶像幻之地壹样,也发生了这么大の变化,而阴魔域,还有阳 魔域,其实也发生了不少の变化丶根汉和白狼马渗入了其,直接传送走了,这是黑天罗盘の好处,如果有坐标の话,可以进行这样の直接の传送丶只不过需要耗费壹些顶级の灵玉,而这种灵玉の数量,根�

导数的运算法则：
法则1:两个函数的和(差)的导数,等于这两个函数的 导数的和(差),即: f ( x) g ( x) f ( x) g ( x)


法则2:两个函数的积的导数,等于第一个函数的导数 乘第二个函数,加上第一个函数乘第二个函数的导数 , 即: f ( x) g ( x) f ( x) g ( x) f ( x) g ( x) 法则3:两个函数的商的导数,等于第一个函数的导数 乘第二个函数,减去第一个函数乘第二个函数的导数 , 再除以第二个函数的平方.即: f ( x) f ( x) g ( x) f ( x) g ( x) ( g ( x) 0) g ( x) 2 g ( x)
例2.求函数y=x3-2x+3的导数.
练习: 1 (1). y 4 ;(2). y x x. x
例 3 日常生活中的饮用水 通常是经过 净化的.随着水 纯净度的提高, 所需净化费 用不断增加 .已知将1吨水净 化到纯净度为x%时所需费 用单位 : 元为 5284 80 x 100.求净化到下纯度 c x 100 x 时, 所需净化费用的瞬时变 化率 :
如果把 y 与u 的关系记作y f u , u 和 x的关系记作 u g x , 那么这个"复合" 过程可表示为 y f u f g x lnx 2.
2
我们遇到的许多函数都 可以看成是由两个函数 经过 "复合" 得到的, 例如,函数y 2 x 3 由y u 2和u 2 x 3 "复合"而成, 等等.
全国名校,高中数学优质学案,（附详解）
(1.2.2)基本初等函数的导数公式 及导数的运算法则

公式3.若f (x) sin x,则f '(x) cos x;
公式4.若f (x) cos x,则f '(x) sin x;
公式5.若f (x) ax ,则f '(x) ax ln a(a 0);
公式6.若f (x) ex ,则f '(x) ex;
公式7.若f
(2)求 y＝1x＋x22＋x33的导数．
[解析] (1)①y′＝(x2sinx)′＝(x2)′sinx＋x2(sinx)′ ＝2xsinx＋x2cosx. ②y′＝[x2(x2－1)]′＝(x2)′(x2－1)＋x2(x2－1)′ ＝2x(x2－1)＋x2·2x＝4x3－2x. (2)y′＝1x＋x22＋x33′＝1x＋2x－2＋3x－3′ ＝－x12－4x－3－9x－4＝－x12－x43－x94.
法则1:两个函数的和(差)的导数,等于这两
个函数的导数的和(差),即:
[f(x) ±g(x)] ′= f'(x) ± g'(x);
应用1: 求下列函数的导数
(1)y=yx'3+s3inxx2 cos x
(2)y=x3-2x+3.
y ' 3x2 2
法则2:两个函数的积的导数,等于第一个函
练一练：
（1）下列各式正确的是（ C ）
A.(sin )' cos(为常数）
B（. cos x)' sin x C.(sin x)' cos x D.( x5 )' 1 x6
5
（2）下列各式正确的是（ D ）
A.(log
x a
)'

1 x
B.(log

基本初等函数的公式 及导数的运算法则
基本初等函数的导数公式
1 .若 fx c ( c 为 常 数 ) ， 则 f'x 0 ;
2 . 若 fx x aa Q *,则 f'x a x a 1 ;
3 .若 fx sx i ,则 n f'x cx o ; s 4 .若 fx c o s x ,则 f'x s in x ; 5 .若 fx a x ,则 f'x a x la n ; 6 .若 fx e x ,则 f'x e x ;
y=f(u)=f(g(x))=ln(x+2)
许多函数都可看成是同两个函数经过“复合”得到
y=(2x+3)2
y=u2 u=2x+3 复合
y=sin(2x+5)
y=sin u u=2x+5 复合
对于两个函数y=f (u)和u=g(x)如果通过变量u,y可以表 示成x的函数,那么称这个函数为函数y=f (u)和u=g(x)的 复合函数,记作y=f (g(x))
故 事中， 我最喜 欢的是 《完璧 归赵》 这个故 事。故 事讲了 春秋战 国时期 ，赵王 得 到 了“和 氏璧” ，秦王 想拿出 十五座 城池来 换。如 果换的 话，赵 王怕秦 王反悔 不 给 城池； 如果不 换的话 ，赵王 担心秦 王会以 这件事 为理由 ，出兵 攻打赵 国。在 赵 王 一筹莫 展、两 难之际 ，蔺相 如挺身 而出， 自告奋 勇出使 秦国。 到了秦 国，蔺 相 如 巧妙地 与秦王 周旋， 不把和 氏璧给 秦王。 到了晚 上，蔺 相如悄 悄地派 人把和 氏 璧 运回赵 国。机 智的蔺 相如不 仅不给 秦王攻 打赵国 的借口 ，又把 和氏璧 送回了 赵 国 。读了 这个故 事，我 对蔺相 如肃然 起敬， 他机智 勇敢、 能言善 辩、有 胆有识 的 精 神值得 我学习 。在平 时的学 习生活 中，我 遇到左 右为难 的事经 常找不 到解决 的 好 办法。 蔺相如 教会了 我用智 慧来解 决问题 。 读了这 本书， 我就像 在历史 的

= (2 x ) ln x (2 x )(ln x )
= 2 ln x 2.
(3) 求函数y = (2 x 3)(3 x - 2)的导数.
2
解：y = ( 2 x 2 3)( 3 x - 2) ( 2 x 2 3)( 3 x - 2)
= 4 x ( 3 x - 2) ( 2 x 2 3) 3
x 2 x 解： (2) y = - sin (1 - 2cos ) 2 4 x x 1 = sin cos = sin x , 2 2 2
y' = ( 1 sinx )' = 1 cos x . 2 2
x3 2. 求 y = 2 在点x = 3处的导数. x 3 2 2 ( x 3)' ( x 3) - ( x 3) ( x 3)' 解： y ' = 2 2 ( x 3)
n
* '
n -1
式，除部分上 ' x x = = 5. 若f ( x ) a ，则 f ( x ) a ln a； 一节已经证明 ' x x 过，其他的只 = = 6. 若f ( x ) e ，则 f ( x ) e ； 需要熟记，会 1 ' 7. 若 f ( x ) = log a x，则 f ( x ) = ； 用即可.
1 ( x 2 3) - ( x 3) 2 x - x 2 - 6 x 3 = = 2 2 2 2 ( x 3) ( x 3)
当x = 3时,
1 -3 - 6 3 3 =- . f (3) = 2 2 6 (3 3)
2
例4:求曲线y=x3+3x－8在x=2处的切 线的方程. 解： f ( x) = ( x 3 3 x - 8) = 3 x 2 3

(x 2) (x 1) 2x 3
sin x (sin x)'cos x sin x(cos x)'
(3) y' ( )' cos x
cos2 x

cos2 x sin cos2 x
2
x

1 cos2
x

sec2
x.
例2求下列函数的导数.
(1) y 2sin x cos x 2x2 1 (2) y cos2 x sin 2 x
【教育类精品资料】
基本初等函数的导数公式 及导数的运算法则
一、基本初等函数的导数公式:
C'0C为常 (数 xn)'n(x)n1(nQ)
(sin x) cos x (cxo)ssixn
(ax)' ax lna,(ex)' ex
(loga
x)'

1 ,(lnx)' xlna
1 x
二、导数的运算法则:(和差积商的导数)
[f(x ) g (x ) ]' f'(x ) g '(x )
函 数 和 （ 差 ） 的 导 数 等 于 它 们 导 数 的 和 （ 差 ） .
（可以推广到求有限个函数的和（差）的导数.）
(轮流求导之和)
[f(x)g(x)]'f'(x)g(x)f(x)g(x)' [gf((xx))]' f'(x)g([xg)(x)f]2(x)g(x)'(g(x)0)
(2 )y f(1 x 2) 2 x x f(1 x 2); 21 x 2 1 x 2
(3) y[f(sin2 x)f(cos2 x)]

=18x2-8x9. 法二：Q y = ( 2 x 2 3 ) ( 3 x - 2 ) = 6 x 3 - 4 x 2 9 x - 6
y '= (6 x 3 )'- (4 x 2 )' (9 x )'- (6 )' =18x2-8x9.
7
例3 求下列函数的导数．
(1) y = x2 ;（2）y=tanx;(3) y=3x2-x x5 x-9.
4.
若f
(x)
=
cos
x，则f
'(x)
=
- sin
x；
函数的导数公 式，除部分上
5. 若f ( x) = a x，则f '( x) = a x ln a； 一节已经证明
6. 若f ( x) = e x，则f '( x) = e x；
过，其他的只
7. 若f ( x) =
log a
x，则f
'(x) =
1
练习1. 求下列函数的导数．
x2 1
(1) y =
;
x
(2)y=-six n (1-2co 2xs ).
2
4
解：
(1)
(x21)2
=
2x2
- ( x2 x2
1)
=
x2 - 1 x2
= 1-
1 x2 .
法2
x2 1
Q y=
=
x
1
：
x
x
y' = ( x 1 )' ==((xx))''((1x-)1')'=1-x-2=
解：运动物体在t=3时的速度即是函数s(t)在t=3时的导数．